Improvement of EMAT Butterfly Coil for Defect Detection in Aluminum Alloy Plate
Abstract
1. Introduction
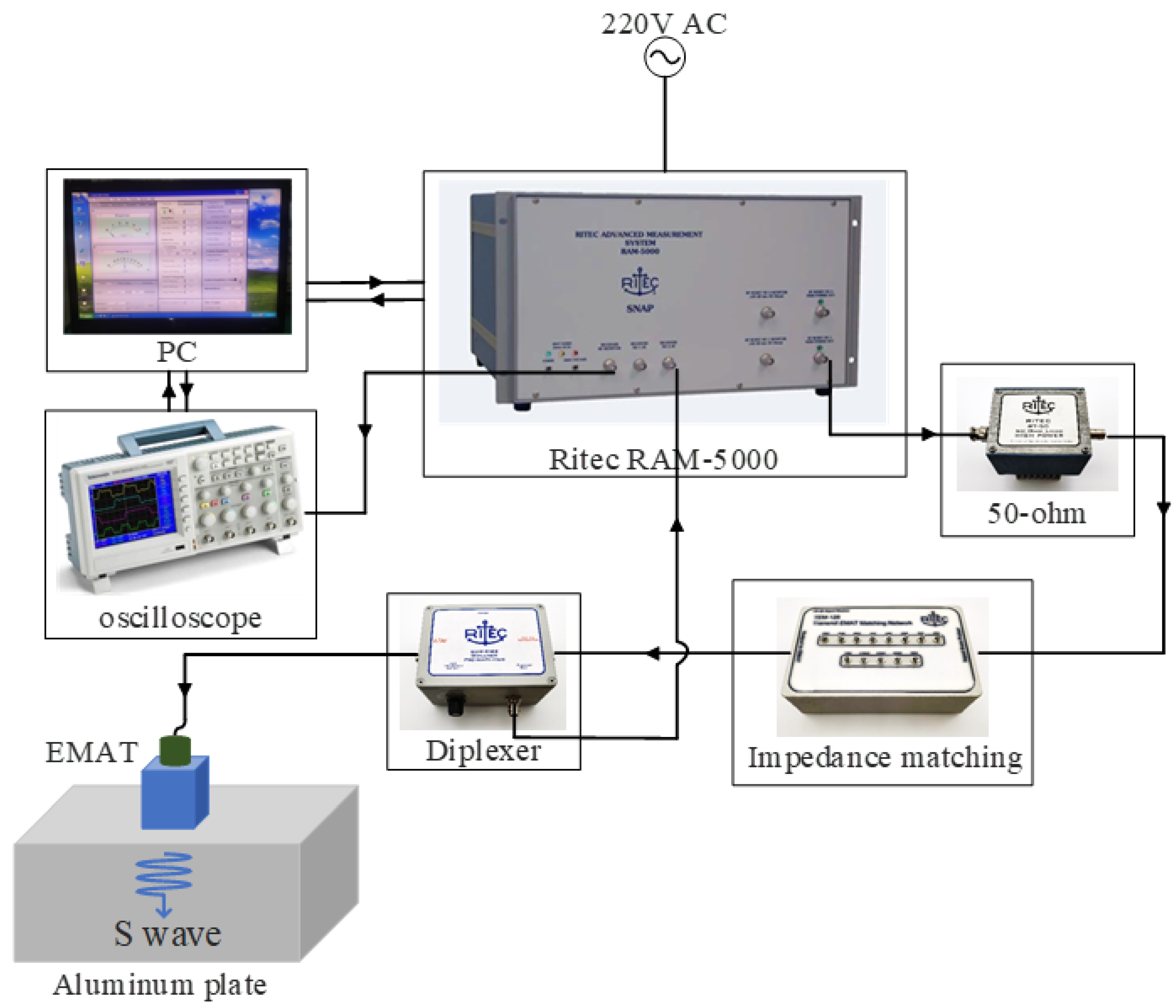
2. Equipment and Experimental Materials
2.1. Equipment
2.2. Sample with Artificial Defects
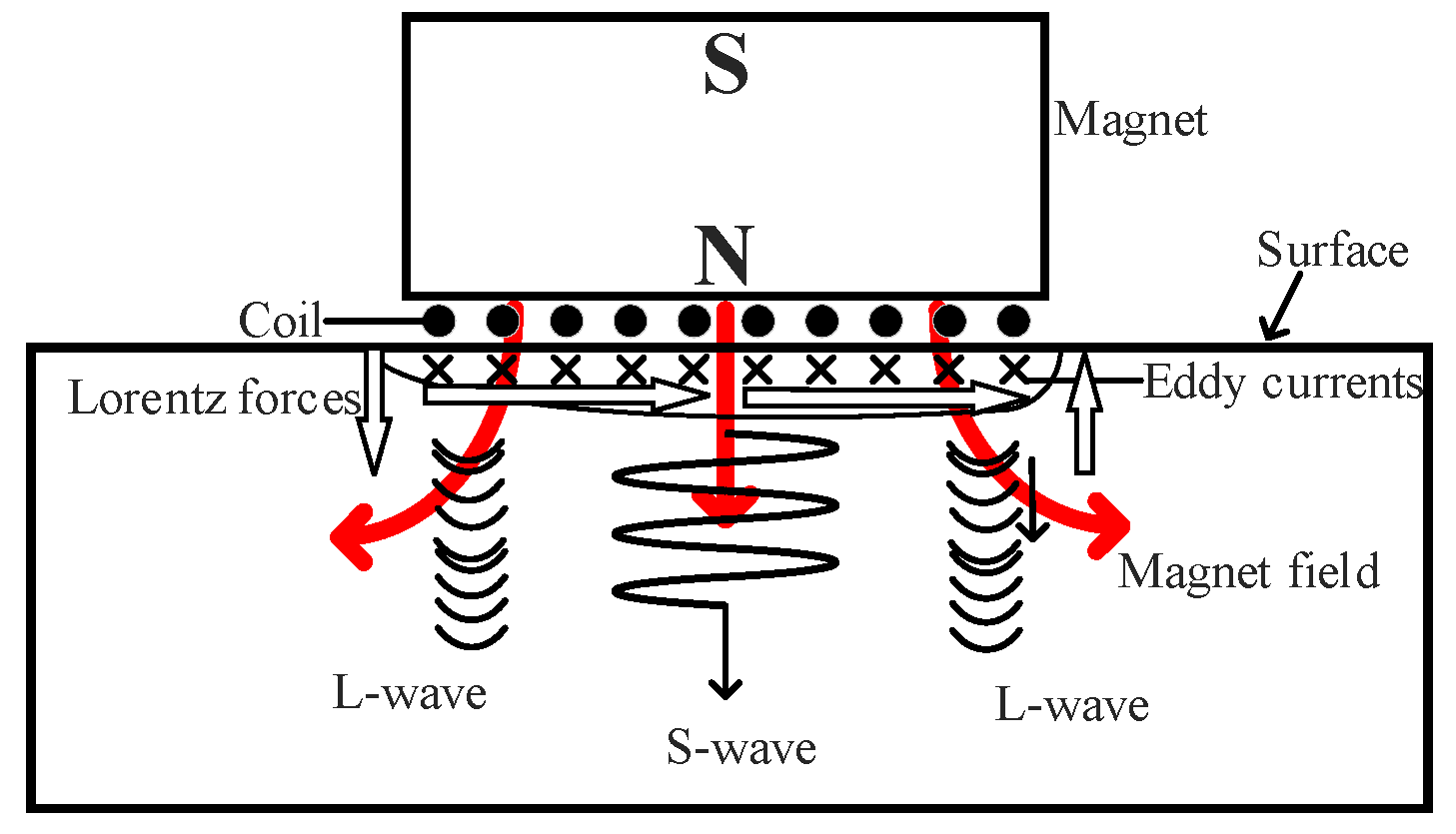
3. Principle of the Butterfly-Coil EMAT
4. FE Analysis of EMAT
4.1. FE Model
- (1)
- Establishing the geometric model: Absorbing boundary conditions were applied to the left and right interfaces of the aluminum plate to ignore the reflection of the structural boundaries. The characteristics of the aluminum plate itself were loaded through the material module. Considering the influence of mesh generation on calculation accuracy, the mesh of the air region was coarsened, and the skin-effect region of the aluminum plate was meshed with more than three layers to meet the grid requirements for analyzing high-frequency electromagnetic fields. To reduce the amount of computation, the coil region was modeled using a uniform multi-turn coil model.
- (2)
- Establishing the electromagnetic field model: The magnetic vector potential field in space was solved for the overall model through Ampere’s law, and the solution domain included the entire space. The remanence model was adopted for the B-H constitutive equation of the permanent magnet.
- (3)
- Establishing the sound-field model: In the solid mechanics module, the Lorentz force was added through the formula to achieve the transformation from the magnetic field to the force field. Appropriate step-size and relative error for transient solutions were selected to ensure the correctness and stability of the solution calculation. The working process of the transducer was the energy conversion from the electric field to the magnetic field and then to the force field realized by the EMAT.
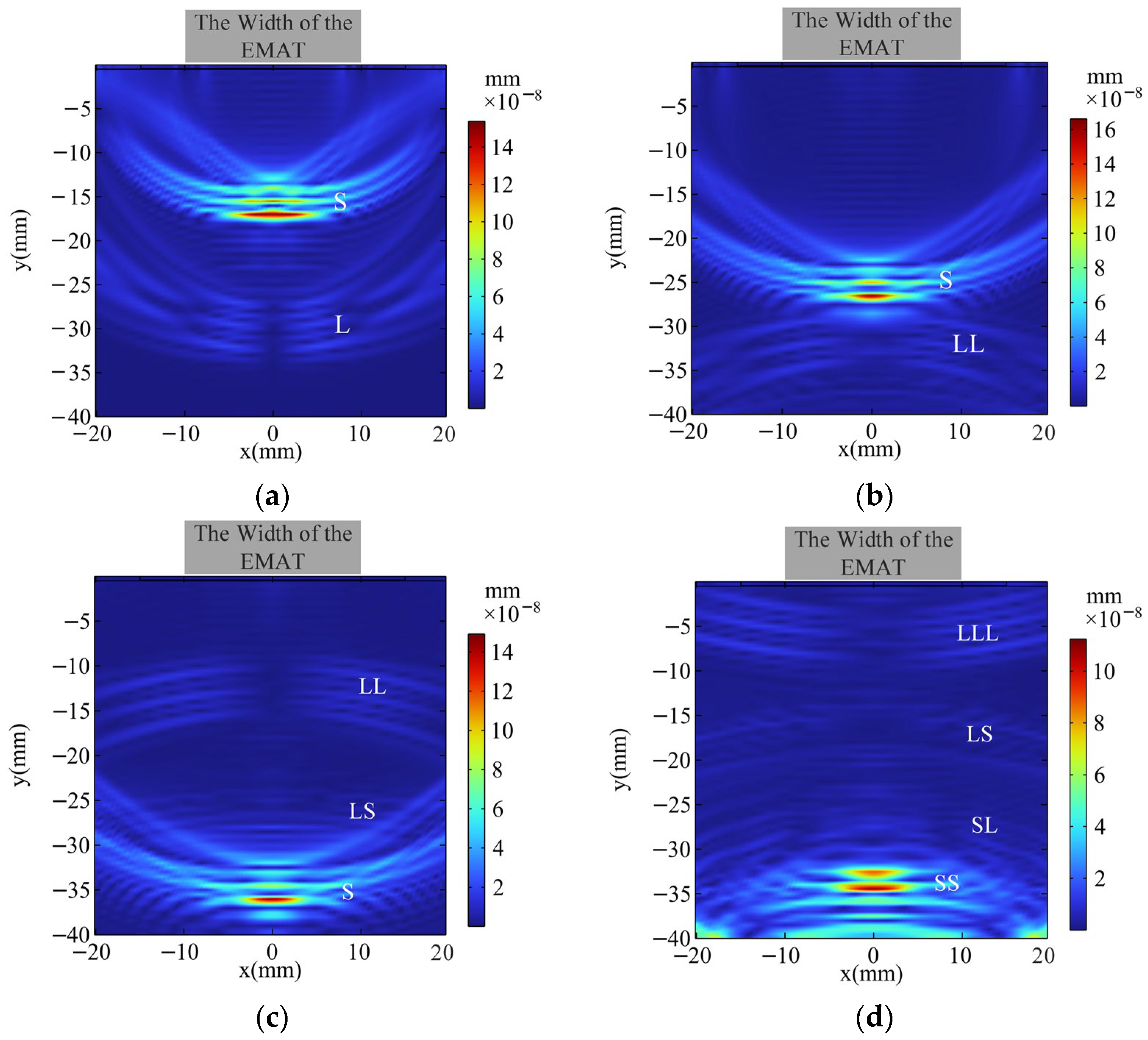
4.2. Simulation of EMAT Soundfield
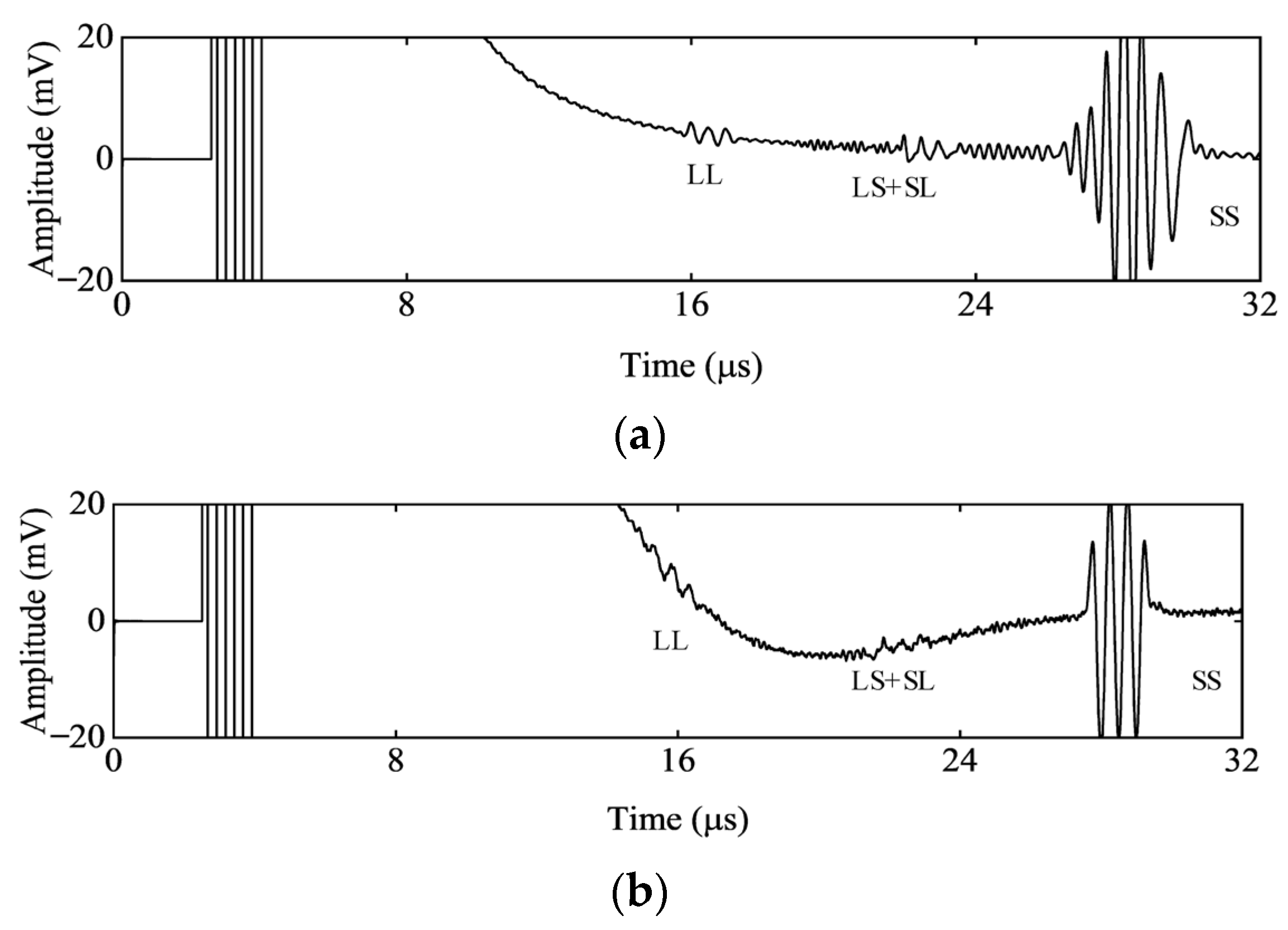
4.3. Simulation of EMAT Signals and Verification
5. Optimization of the EMAT Butterfly Coil
5.1. Design of Simulating Experiments
5.2. Results of Simulating Experiment
5.3. Analysis of Simulating Experiment Results
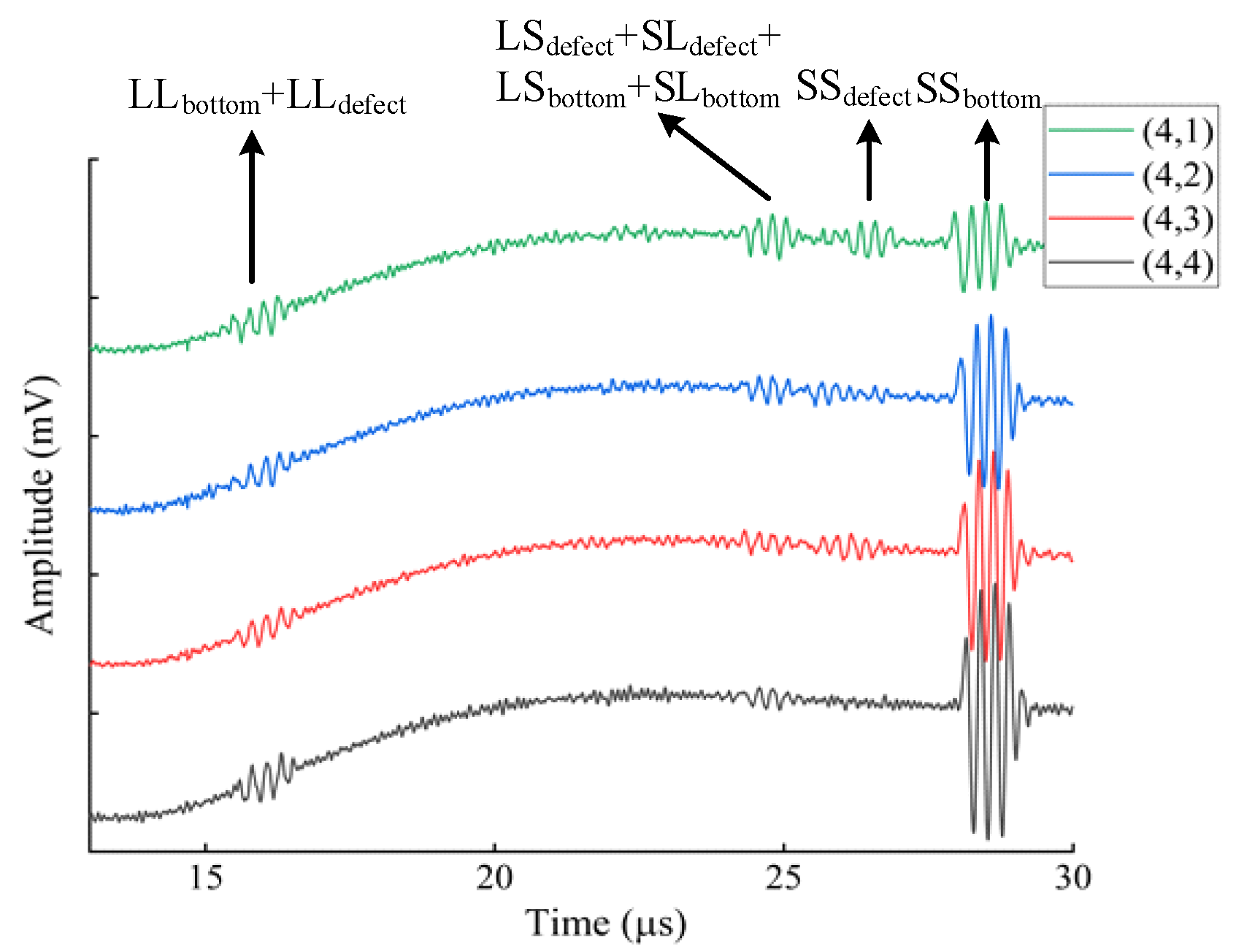
5.4. Artificial Defects Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, G.; Wang, Z.; Fan, X.; Liu, L. Research progress of aluminum alloy welding/plastic deformation composite forming technology in achieving high-strength joints. Materials 2023, 16, 7672. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M. Current trends in metallic materials for body panels and structural members used in the automotive industry. Materials 2024, 17, 590. [Google Scholar] [CrossRef]
- Zichil, V.; Grigoras, C.; Ciubotariu, V. Notches and fatigue on aircraft-grade aluminum alloys. Materials 2024, 17, 4639. [Google Scholar] [CrossRef] [PubMed]
- Bidulska, J.; Bidulsky, R.; Grande, M.A.; Kvackaj, T. Different formation routes of pore structure in aluminum powder metallurgy alloy. Materials 2019, 12, 3724. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Seleman, M.M.E.-S.; Fydrych, D.; Çam, G. Friction stir welding of aluminum in the aerospace industry: The current progress and state-of-the-art review. Materials 2023, 16, 2971. [Google Scholar] [CrossRef]
- Habibpour-Ledariali, A.; Honarvar, F. Three dimensional characterization of defects by ultrasonic time-of-flight diffraction (TOFD)technique. J. Nondestruct. Eval. 2018, 37, 14. [Google Scholar] [CrossRef]
- Chen, J.; Wu, E.; Wu, H.; Zhou, H.; Yang, K. Enhancing ultrasonic time-of-flight diffraction measurement through an adaptive deconvolution method. Ultrasonics 2019, 96, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Han, Q.; Wang, P.; Zheng, H. Modified ultrasonic time-of-flight diffraction testing with barker code excitation for sizing inclined crack. Appl. Acoust. 2018, 140, 153–159. [Google Scholar] [CrossRef]
- Zheng, G.; Zhao, Z.; Bao, Y.; Hu, F.; Zhang, H.; Zhou, Z. Three-dimensional reconstruction of transverse hole defect in plate based on TOFD inspection. Nondestruct. Test. Eval. 2024, 40, 1409–1423. [Google Scholar] [CrossRef]
- Cong, S.; Zhang, W.; Zhang, J. Analysis on ultrasonic TOFD imaging testing for ultra-thick-walled EBW joint of aluminum alloy. Procedia Eng. 2017, 207, 1910–1915. [Google Scholar] [CrossRef]
- Jin, S.; Wang, Z.; Luo, Z. TOFD detection of shallow subsurface defects in aluminum alloy thin plates by half-skip mode-converted wave. CJA 2024, 37, 454–463. [Google Scholar] [CrossRef]
- Wong, V.; Li, X.; Yousry, Y.; Philibert, M.; Jiang, C. Twice reflected ultrasonic bulk wave for surface defect monitoring. Ultrasonics 2025, 147, 107530. [Google Scholar] [CrossRef] [PubMed]
- Nanekar, P.; Kumar, A.; Jayakumar, T. SAFT-assisted sound beam focusing using phased arrays (PA-SAFT) for non-destructive evaluation. Nondestruct. Test. Eval. 2015, 30, 105–123. [Google Scholar] [CrossRef]
- Shang, F.; Chen, H.; Sun, B. Optimization analysis of acoustic field parameters in phased array ultrasonic transducers. J. Fail. Anal. Preven. 2024, 24, 1576–1587. [Google Scholar] [CrossRef]
- Lukomaki, T. Full-matrix capture with phased shift migration for flaw detection in layered objects with complex geometry. Ultrasonics 2016, 70, 201–247. [Google Scholar]
- Liu, P.; Li, X.; Li, H. Implementation of high time delay accuracy of ultrasonic phased array based on interpolation CLC filter. Sensors 2017, 17, 2322. [Google Scholar] [CrossRef]
- Petcher, P.A.; Dixon, S. Weld defect detection using PPM EMAT generated shear horizontal ultrasound. NDT E Int. 2015, 74, 58–65. [Google Scholar] [CrossRef]
- Garcia-Rodriguez, M.; Yañez, Y.; Garcia-Hernandez, M.J. Application of Golay codes to improve the dynamic range in ultrasonic Lamb waves air-coupled systems. NDT E Int. 2010, 43, 677–686. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. An SH-wave EMAT technique for gas pipeline inspection. NDT E Int. 1999, 32, 127–132. [Google Scholar] [CrossRef]
- Yusa, N.; Song, H.; Iwata, D. Probabilistic analysis of electromagnetic acoustic resonance signals for the detection of pipe wall thinning. Nondestruct. Test. Eval. 2021, 36, 1–16. [Google Scholar] [CrossRef]
- Pan, Q.; Pan, R.; Shao, C.; Chang, M.; Xu, X. Research review of principles and methods for ultrasonic measurement of axial stress in bolts. Chin. J. Mech. Eng. 2020, 33, 44–59. [Google Scholar] [CrossRef]
- Zhai, G.; Wang, K.; Wang, Y. Modeling of Lorentz forces and radiated wave fields for bulk wave electromagnetic acoustic transducers. J. Appl. Phys. 2013, 114, 55–60. [Google Scholar] [CrossRef]
- Wang, C.; Ma, J.; Wang, L.; Bai, X.; Chen, J. Research on butterfly coil EMAT sound field characteristics. J. Phys. Conf. Ser. 2024, 2815, 012006. [Google Scholar] [CrossRef]
- Sun, H.; Huang, S.; Wang, Q. Orthogonal optimal design method for point-focusing EMAT considering focal area dimensions. Sens. Actuators A Phys. 2020, 312, 112109. [Google Scholar] [CrossRef]
- Fan, Z.; Peng, S.; Wu, Y.; Yang, X. Design of S0 mode EMAT employing a dual-row linear Halbach permanent magnet array. INSIGHT 2025, 67, 13–19. [Google Scholar] [CrossRef]
- Chen, T.; Lou, T.; Lv, C.; Song, X.; Tu, J.; Wu, Q.; Zhang, X. Unidirectional focusing Rayleigh waves EMAT for plate surface defect Inspection. Nondestruct. Test. Eval. 2025, 40, 1545–1568. [Google Scholar] [CrossRef]
- Zhang, Y.; Pei, C.; Deng, J.; Liu, T.; Qu, Y.; Chen, H.; Chen, Z. A flexible EMAT enhanced with array magnetic core for inspection of curved structure. Sens. Actuators A Phys. 2024, 378, 115869. [Google Scholar] [CrossRef]
- Parra-raad, J.; Khalili, P.; Cegla, F. Shear waves with orthogonal polarizations for thickness measurement and crack detection using EMATs. NDT E Int. 2020, 111, 102212. [Google Scholar] [CrossRef]
- Martinho, L.; Kubrusly, A. A new diamond-shaped periodic permanent magnet electromagnetic acoustic transducer for side-lobe suppression of shear horizontal ultrasonic waves. Sens. Actuators A Phys. 2024, 371, 115290. [Google Scholar] [CrossRef]
- Gautam, A.; Yin, C.; Bhattacharya, B. Frequency-Division multiplexing of chevron EMAT for orthogonally polarized SH waves. IEEE Sens. J. 2024, 24, 34060–34069. [Google Scholar] [CrossRef]
- Jiang, C.; Li, Z.; Zhang, Z.; Wang, S. A new design to Rayleigh wave EMAT based on spatial pulse compression. Sensors 2023, 23, 3943. [Google Scholar] [CrossRef] [PubMed]
- Tkocz, J.; Greenshields, D.; Dixon, S. High power phased EMAT arrays for nondestructive testing of as-cast steel. NDT E Int. 2019, 102, 47–55. [Google Scholar] [CrossRef]
- Shi, W.; Tong, Y.; Lu, C.; Chen, Y.; Shen, G.; Zeng, G. Improving laser-EMAT ultrasonic energy conversion efficiency using surface constraint mechanism. Ultrasonics 2022, 124, 106729. [Google Scholar] [CrossRef] [PubMed]




| Coordinate | Diameter (mm) | Machining Depth (mm) |
|---|---|---|
| 1,1 | 5.0 | 9.0 |
| 1,2 | 4.0 | 8.9 |
| 1,3 | 3.0 | 9.1 |
| 1,4 | 2.0 | 8.8 |
| 2,1 | 5.0 | 7.1 |
| 2,2 | 4.0 | 6.8 |
| 2,3 | 3.0 | 7.0 |
| 2,4 | 2.0 | 7.0 |
| 3,1 | 5.0 | 5.1 |
| 3,2 | 4.0 | 5.1 |
| 3,3 | 3.0 | 5.0 |
| 3,4 | 2.0 | 4.9 |
| 4,1 | 5.0 | 3.0 |
| 4,2 | 4.0 | 3.1 |
| 4,3 | 3.0 | 3.2 |
| 4,4 | 2.0 | 2.9 |
| Level | (MHz) | (mm) | w (mm) |
|---|---|---|---|
| 1 | 2.5 | 0.03 | 8.0 |
| 2 | 3.0 | 0.05 | 12.0 |
| 3 | 3.5 | 0.08 | 16.0 |
| 4 | 4.0 | 0.10 | 20.0 |
| Test No. | f (MHz) | d (mm) | w (mm) |
|---|---|---|---|
| 1 | 2.5 | 0.03 | 8.0 |
| 2 | 2.5 | 0.05 | 12.0 |
| 3 | 2.5 | 0.08 | 16.0 |
| 4 | 2.5 | 0.10 | 20.0 |
| 5 | 3.0 | 0.03 | 12.0 |
| 6 | 3.0 | 0.05 | 8.0 |
| 7 | 3.0 | 0.08 | 20.0 |
| 8 | 3.0 | 0.10 | 16.0 |
| 9 | 3.5 | 0.03 | 16.0 |
| 10 | 3.5 | 0.05 | 20.0 |
| 11 | 3.5 | 0.08 | 8.0 |
| 12 | 3.5 | 0.10 | 12.0 |
| 13 | 4.0 | 0.03 | 20.0 |
| 14 | 4.0 | 0.05 | 16.0 |
| 15 | 4.0 | 0.08 | 12.0 |
| 16 | 4.0 | 0.10 | 8.0 |
| Test No. | L (mm/s) | S (mm/s) | S/L |
|---|---|---|---|
| 1 | 1.910 | 14.896 | 7.7977 |
| 2 | 2.327 | 17.192 | 7.3865 |
| 3 | 2.296 | 20.682 | 9.0067 |
| 4 | 3.628 | 15.433 | 4.2536 |
| 5 | 0.933 | 7.083 | 7.5847 |
| 6 | 2.067 | 17.115 | 8.2801 |
| 7 | 1.951 | 8.764 | 4.4912 |
| 8 | 2.468 | 21.362 | 8.6531 |
| 9 | 0.565 | 3.987 | 7.0557 |
| 10 | 0.841 | 3.683 | 4.3793 |
| 11 | 1.640 | 13.651 | 8.3233 |
| 12 | 1.120 | 10.529 | 9.3975 |
| 13 | 0.495 | 1.713 | 3.4600 |
| 14 | 0.828 | 5.065 | 6.1163 |
| 15 | 0.563 | 8.033 | 14.2480 |
| 16 | 1.057 | 16.056 | 15.1832 |
| A (f) | B (d) | C (w) | |
|---|---|---|---|
| K | 28.444 | 25.898 | 39.584 |
| 29.009 | 35.560 | 39.028 | |
| 29.156 | 36.069 | 30.832 | |
| 39.007 | 37.487 | 16.584 | |
| 7.111 | 6.475 | 9.896 | |
| 7.252 | 8.890 | 9.757 | |
| 7.289 | 9.017 | 7.708 | |
| 9.752 | 9.372 | 4.146 | |
| R | 2.641 | 2.897 | 5.750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, D.; Sun, G.; Liu, H. Improvement of EMAT Butterfly Coil for Defect Detection in Aluminum Alloy Plate. Materials 2025, 18, 3207. https://doi.org/10.3390/ma18133207
Chi D, Sun G, Liu H. Improvement of EMAT Butterfly Coil for Defect Detection in Aluminum Alloy Plate. Materials. 2025; 18(13):3207. https://doi.org/10.3390/ma18133207
Chicago/Turabian StyleChi, Dazhao, Guangyu Sun, and Haichun Liu. 2025. "Improvement of EMAT Butterfly Coil for Defect Detection in Aluminum Alloy Plate" Materials 18, no. 13: 3207. https://doi.org/10.3390/ma18133207
APA StyleChi, D., Sun, G., & Liu, H. (2025). Improvement of EMAT Butterfly Coil for Defect Detection in Aluminum Alloy Plate. Materials, 18(13), 3207. https://doi.org/10.3390/ma18133207





