Process–Structure Co-Optimization of Glass Fiber-Reinforced Polymer Automotive Front-End Module
Abstract
1. Introduction
2. Stiffness Simulation of Mounting Points and Structure Optimization
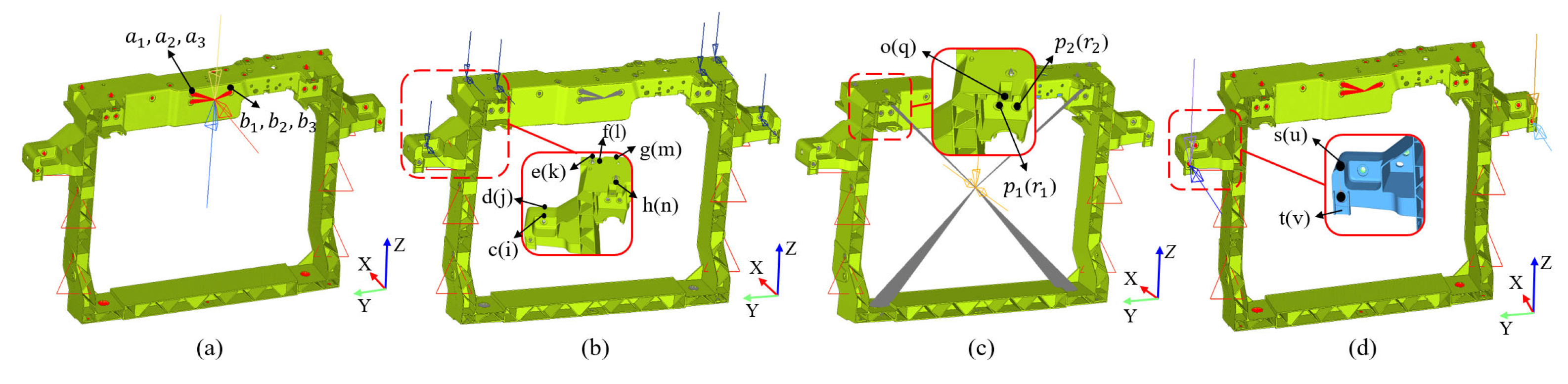
2.1. Finite Element Modeling
2.2. Analysis of Mounting Point Stiffness
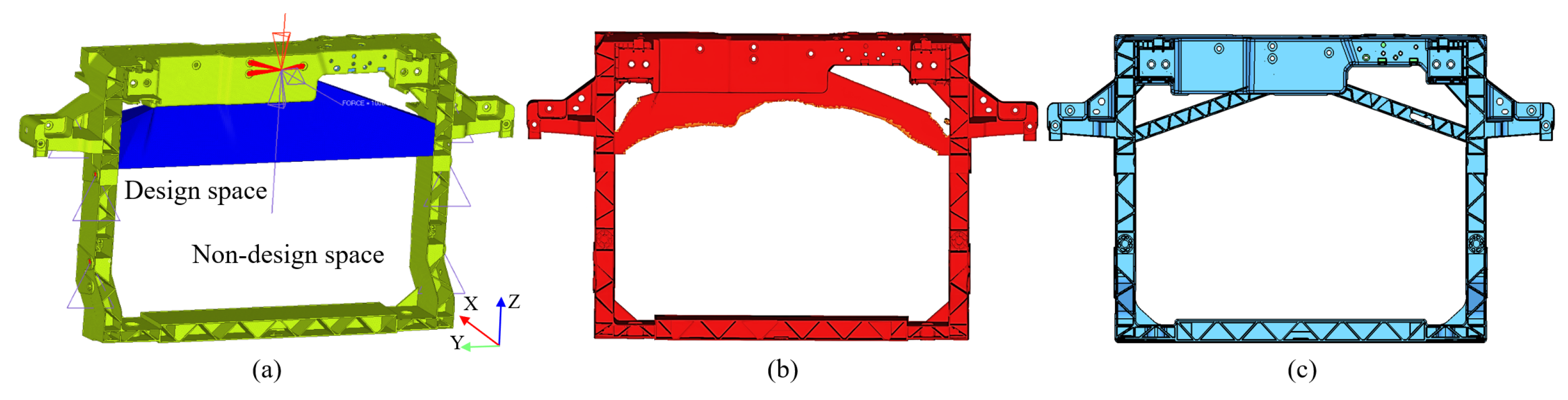
2.3. Structure Optimization
3. Design and Optimization of Injection Molding Process
3.1. Design of Injection Molding Process
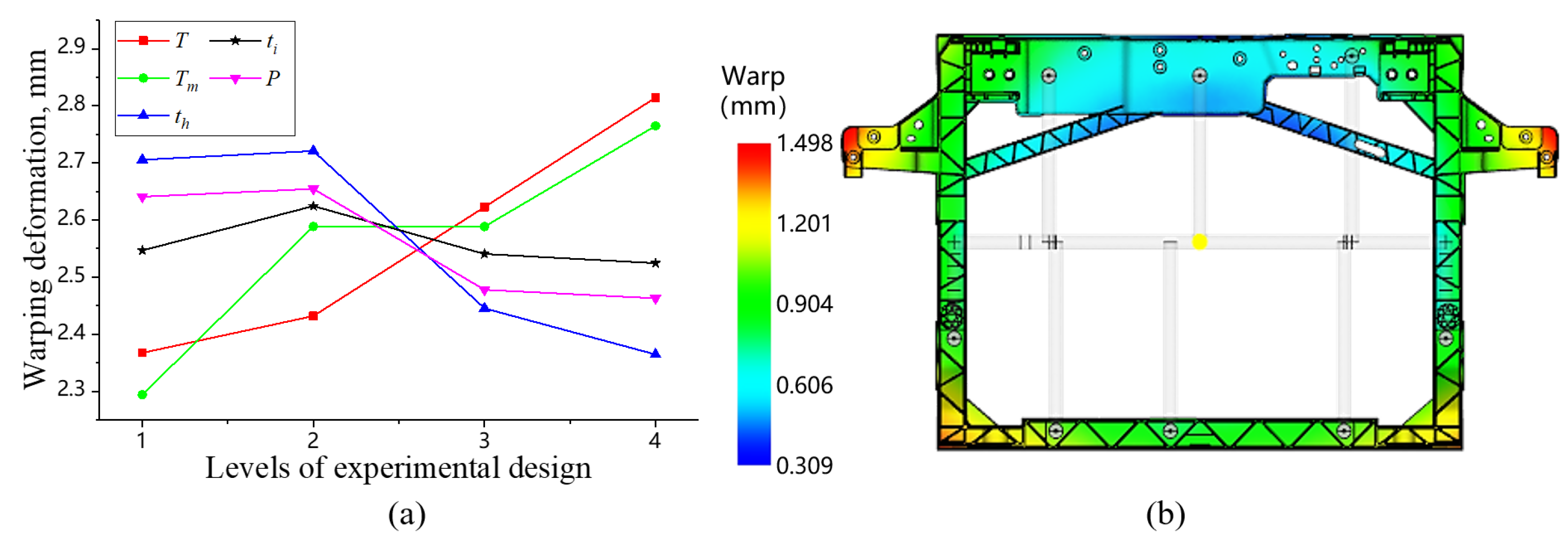
3.2. Optimization of Injection Molding Process
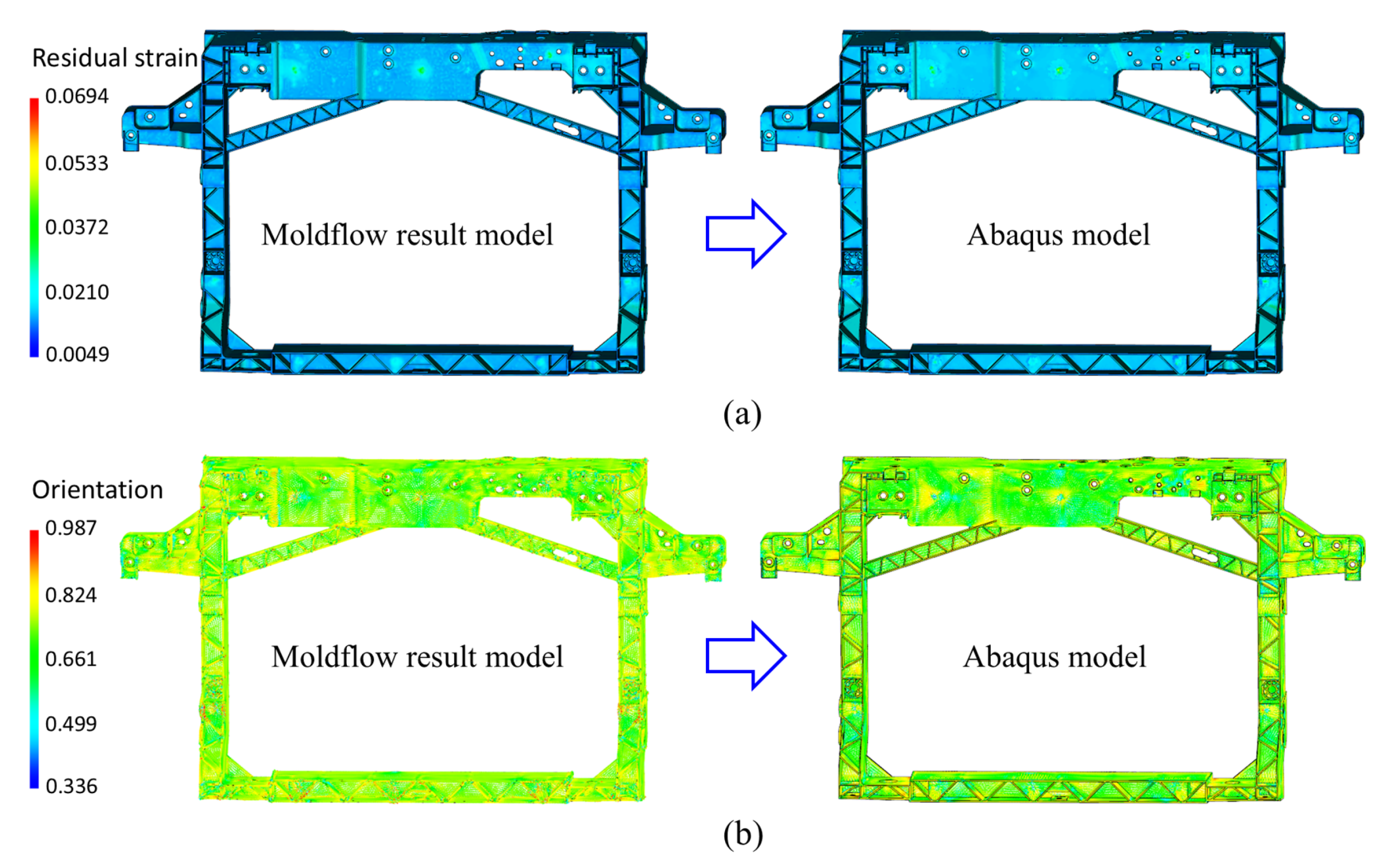
4. Performance Evaluation Mapping Injection Molding History
4.1. Mounting Point Stiffness Simulation
4.2. Test Verification and Analysis
4.3. Error Analysis of Simulation and Test
5. Conclusions
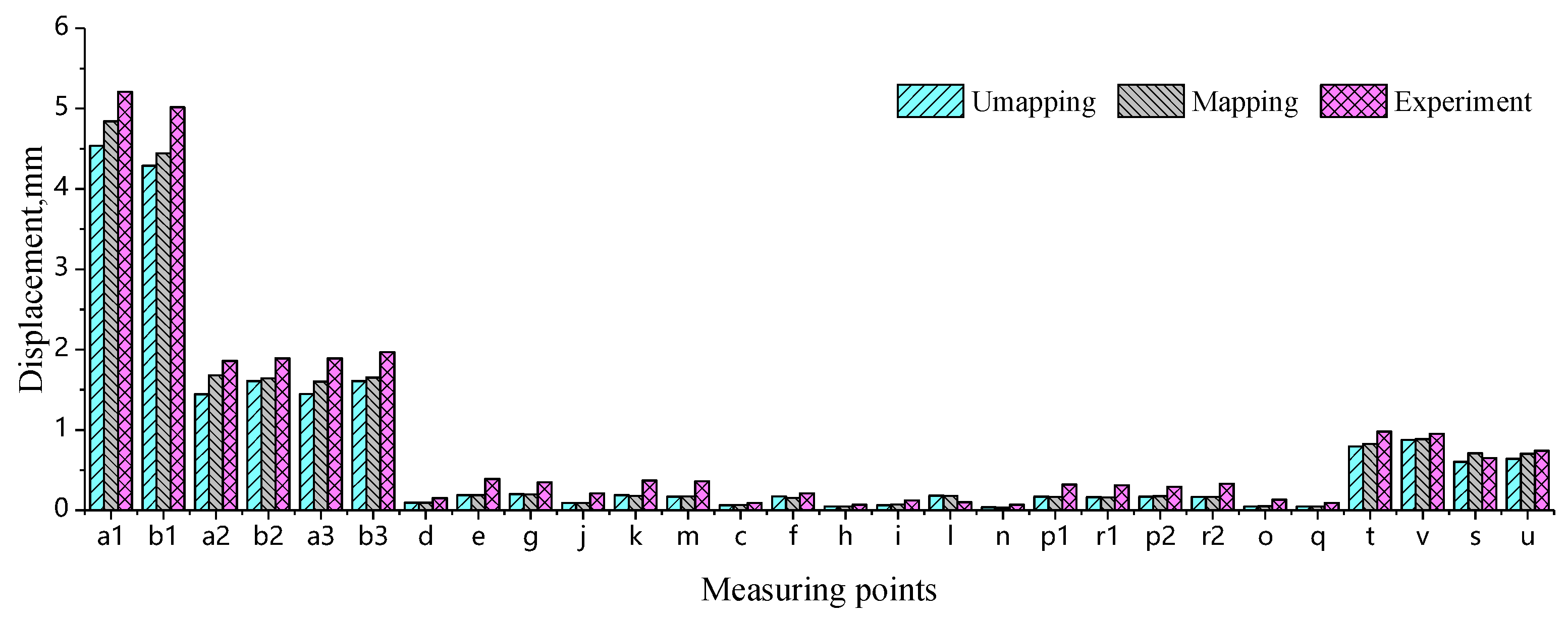
- Under ±Z-directional loading of 1000 N, the initial design of the latch mounting point exhibits a displacement of 2.254 mm, exceeding the regulatory limit (<2.0 mm). After topology optimization, the displacement is reduced to 1.609 mm. Experimental validation confirms that simulations mapping injection molding data (fiber orientation, residual stress–strain) yield results closer to the measured values, and the anisotropic model demonstrates significantly lower errors than the isotropic model.
- Case 1, which utilizes sequential valve gate control, demonstrates superior performance in both weld line quality and fiber orientation control compared to conventional gating systems. Through orthogonal experiment, the optimal process parameter combination is determined—mold temperature of 20 °C, melt temperature of 210 °C, packing pressure with 90% of injection pressure, injection time of 6 s, and packing time of 25 s—which reduces the warpage to 1.498 mm, with a 41.5% reduction compared to the average warpage obtained from the orthogonal experiment.
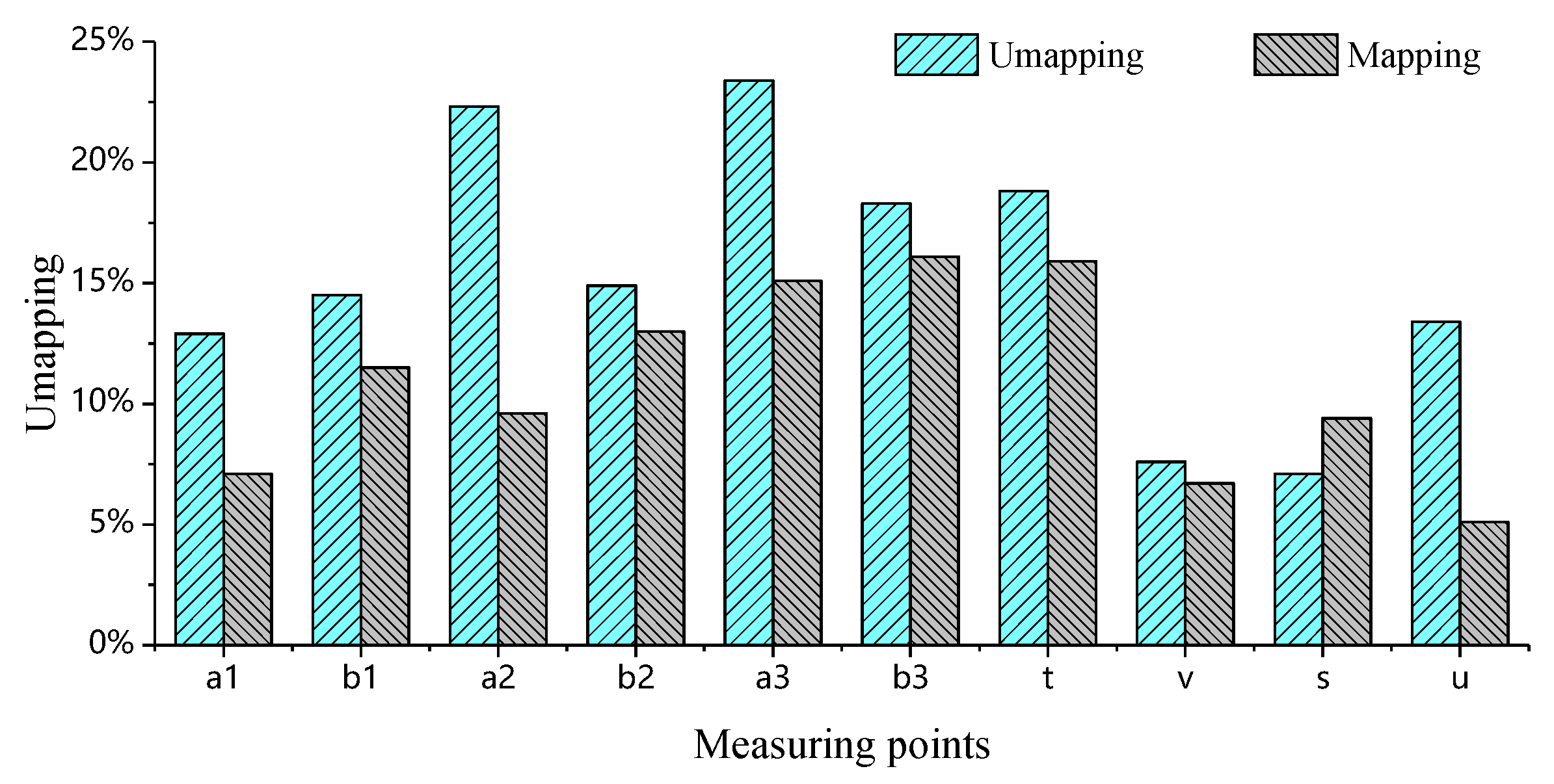
- The displacement results obtained from the simulation based on mapped injection molding historical data are closer to the experimental values, with the error decreasing as the displacement increases. When the measured displacement exceeds 0.65 mm, the simulation using mapped data demonstrates superior performance in terms of percentage error , range , and variance , validating the engineering applicability of the anisotropic simulation.
- When the tested displacement is small (<0.65 mm), significant deviations exist between simulations and measurements regardless of whether injection molding historical data is mapped, which is primarily due to systematic errors in experimental equipment and operations. Such errors are inherently unavoidable in engineering practice, necessitating reliance on large-displacement condition data as the primary basis for optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, P.; Ye, T.; Wu, Y.; Qiu, S.; Xia, E.; Liu, X.; Li, L. Unveiling the mechanical response and deformation mechanism of an extruded WE43 Magnesium alloy under high-speed impact. J. Rare Earth 2024, 42, 2303–2315. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, X.; Xiang, F.; Guo, P.; Xiang, Z.; Yang, Q. Numerical simulation of selective laser melting process of Al-Mg-Sc-Zr aluminum alloy. J. Plast. Eng. 2024, 31, 112–122. [Google Scholar] [CrossRef]
- Rajak, D.K.; Wagh, P.H.; Linul, E. Manufacturing technologies of carbon/glass fiber-reinforced polymer composites and their properties: A review. Polymers 2021, 13, 3721. [Google Scholar] [CrossRef]
- Proy, J.; Massa, F.; Notta-Cuvier, D.; Lauro, F.; Tison, T.; Spingler, G. Integrating fibers and injection molding process variability in short-natural-fiber-reinforced thermoplastics behavior: A review. Mater. Today Commun. 2021, 29, 102785. [Google Scholar] [CrossRef]
- Rabbi, M.S.; Islam, T.; Islam, G.M.S. Injection-molded natural fiber-reinforced polymer composites—A review. Int. J. Mech. Mater. Eng. 2021, 16, 15. [Google Scholar] [CrossRef]
- Mohammadi, H.; Ahmad, Z.; Mazlan, S.A.; Faizal Johari, M.A.; Siebert, G.; Petrů, M.; Rahimian Koloor, S.S. Lightweight glass fiber-reinforced polymer composite for automotive bumper applications: A review. Polymers 2022, 15, 193. [Google Scholar] [CrossRef]
- Pian, W.; Zhou, Y.; Xiao, T. A review of the feasibility of aluminum alloys, carbon fiber composites and glass fiber composites for vehicle weight reduction in the automotive industry. J. Phys. Conf. Ser. 2023, 2608, 012005. [Google Scholar] [CrossRef]
- Karataş, M.A.; Gökkaya, H. A review on machinability of carbon fiber reinforced polymer (CFRP) and glass fiber reinforced polymer (GFRP) composite materials. Def. Technol. 2018, 14, 318–326. [Google Scholar] [CrossRef]
- Alkhatib, F.; Mahdi, E.; Dean, A. Crushing response of CFRP and KFRP composite corrugated tubes to quasi-static slipping axial loading: Experimental investigation and numerical simulation. Compos. Struct. 2020, 246, 112370. [Google Scholar] [CrossRef]
- Jeong, Y.J.; Kim, H.T.; Kim, J.D.; Kim, J.H.; Kim, S.K.; Lee, J.M. Evaluation of mechanical properties of glass fiber-reinforced composites depending on length and structural anisotropy. Res. Eng. 2023, 17, 101000. [Google Scholar] [CrossRef]
- Sathishkumar, T.; Satheeshkumar, S.; Naveen, J. Glass fiber-reinforced polymer composites–A review. J. Reinf. Plast. Compos. 2014, 33, 1258–1275. [Google Scholar] [CrossRef]
- Morampudi, P.; Namala, K.K.; Gajjela, Y.K.; Barath, M.; Prudhvi, G. Review on glass fiber reinforced polymer composites. Mater. Today Proc. 2021, 43, 314–319. [Google Scholar] [CrossRef]
- Mlýnek, J.; Rahimian Koloor, S.S.; Martinec, T.; Petru, M. Fabrication of high-quality straight-line polymer composite frame with different radius parts using fiber winding process. Polymers 2021, 13, 497. [Google Scholar] [CrossRef] [PubMed]
- Fujita, Y.; Noda, S.; Takahashi, J.; Greenhalgh, E.S.; Pimenta, S. Initiation and propagation fracture toughness of injection-moulded short fibre composites under different environmental conditions. Compos. Sci. Technol. 2023, 233, 109891. [Google Scholar] [CrossRef]
- Hidayah, M.H.N.; Shayfull, Z.; Nasir, S.M.; Fathullah, M.; Hazwan, M.H.M. Warpage analysis in injection moulding process. AIP Conf. Proc. 2017, 1885, 020050. [Google Scholar] [CrossRef]
- Mao, H.; Wang, Y.; Yang, D. Study of injection molding process simulation and mold design of automotive back door panel. J Mech Sci Technol. 2022, 36, 2331–2344. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, C.; Peng, B.; Chang, C.; Cheng, H.; Lin, Y.; Shen, Y.; Wang, H. Experimental and numerical study determining the warpage phenomenon of thin-wall injection molding. Adv. Polym. Technol. 2020, 2020, 2914801. [Google Scholar] [CrossRef]
- Lee, M.; Kim, H.; Lyu, M.Y. A study on the warpage of glass fiber reinforced plastics for part design and operation condition: Part 1. Amorphous plastics. Polym.-Korea 2012, 36, 555–563. [Google Scholar] [CrossRef]
- Guo, F.L.; Hu, J.M.; Guan, T.; Fu, Y.T.; Huang, C.Y.; Li, Y.Q.; Fu, S.Y. Modeling and characterizations of mechanical behaviors of short carbon fiber and short glass fiber reinforced polyetherimide composites. Compos. Sci. Technol. 2022, 229, 109685. [Google Scholar] [CrossRef]
- Purgleitner, B.; Viljoen, D.; Kühnert, I.; Burgstaller, C. Influence of injection molding parameters, melt flow rate, and reinforcing material on the weld-line characteristics of polypropylene. Polym. Eng. Sci. 2023, 63, 1551–1566. [Google Scholar] [CrossRef]
- Lee, M.; Lee, M.; Lee, C. The effect of warpage on carbon fiber-reinforced composites (CFRP) and glass fiber-reinforced composites (GFRP) due to the operation of a rapid cooling and heating device. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 247. [Google Scholar] [CrossRef]
- Bian, Z.; Xie, P.C.; Ding, Y.M.; Yang, W.M. Effect of Processing Conditions on the Shrinkage and Warpage of Glass Fiber Reinforced PP Using Microcellular Injection Molding. Key Eng. Mater. 2012, 501, 294–299. [Google Scholar] [CrossRef]
- Kumar, B.P.; Venkataramaiah, P.; Ganesh, J.S. Optimization of process parameters in injection moulding of a polymer composite product by using gra. Mater. Today Proc. 2019, 18, 4637–4647. [Google Scholar] [CrossRef]
- Park, H.S.; Phuong, D.X.; Kumar, S. AI based injection molding process for consistent product quality. Procedia Manuf. 2019, 28, 102–106. [Google Scholar] [CrossRef]
- Kitayama, S.; Yokoyama, M.; Takano, M.; Aiba, S. Multi-objective optimization of variable packing pressure profile and process parameters in plastic injection molding for minimizing warpage and cycle time. Int. J. Adv. Manuf. Technol. 2017, 92, 3991–3999. [Google Scholar] [CrossRef]
- Kitayama, S.; Tsurita, S.; Takano, M.; Yamazaki, Y.; Kubo, Y.; Aiba, S. Multi-objective process parameters optimization in rapid heat cycle molding incorporating variable packing pressure profile for improving weldline, clam** force, and cycle time. Int. J. Adv. Manuf. Technol. 2022, 120, 3669–3681. [Google Scholar] [CrossRef]
- Tang, J.; Qiu, J.; Sakai, E.; Zhang, G.; Wu, H.; Zhang, B.; Guo, S. Effects of injection molding parameters and welding sequence on the interfacial strength of glass fiber-reinforced polypropylene. Polym. Compos. 2025. [Google Scholar] [CrossRef]
- Chauhan, V.; Kärki, T.; Varis, J. Optimization of compression molding process parameters for NFPC manufacturing using taguchi design of experiment and moldflow analysis. Processes 2021, 9, 1853. [Google Scholar] [CrossRef]
- Zhao, N.; Lian, J.; Wang, P.; Zhong, B. Recent progress in minimizing the warpage and shrinkage deformations by the optimization of process parameters in plastic injection molding: A review. Int. J. Adv. Manuf. Technol. 2022, 120, 85–101. [Google Scholar] [CrossRef]
- Öktem, H.; Shinde, D. Determination of optimal process parameters for plastic injection molding of polymer materials using multi-objective optimization. J. Mater. Eng. Perform. 2021, 30, 8616–8632. [Google Scholar] [CrossRef]
- Mukras, S.M.; Omar, H.M.; al-Mufadi, F.A. Experimental-based multi-objective optimization of injection molding process parameters. Arab. J. Sci. Eng. 2019, 44, 7653–7665. [Google Scholar] [CrossRef]
- Yang, K.; Tang, L.; Wu, P. Research on Optimization of Injection Molding Process Parameters of Automobile Plastic Front-End Frame. Adv. Mater. Sci. Eng. 2022, 2022, 5955725. [Google Scholar] [CrossRef]
- Liu, X.; Fan, X.; Guo, Y.; Man, B.; Li, L. Warpage optimization of the GFRP injection molding process parameters. Mcrosyst Technol. 2021, 27, 4337–4346. [Google Scholar] [CrossRef]
- Guo, W.; Deng, F.; Meng, Z.; Hua, L.; Mao, H.; Su, J. A hybrid back-propagation neural network and intelligent algorithm combined algorithm for optimizing microcellular foaming injection molding process parameters. J. Manuf. Process. 2020, 50, 528–538. [Google Scholar] [CrossRef]
- Dogossy, G.; Morauszki, T.; Ronkay, F. Experimental investigation and applicability of multi-stage simulations in the case of a thick-walled injection-moulded composite. Appl. Sci. 2022, 12, 8415. [Google Scholar] [CrossRef]
- Fonseca, J.H.; Quagliato, L.; Yun, S.; Han, D.; Kim, N.; Lee, H. Preliminary design of an injection-molded recycled-carbon fiber–reinforced plastic/metal hybrid automotive structure via combined optimization techniques. Struct. Multidiscip. Optim. 2021, 64, 2773–2788. [Google Scholar] [CrossRef]
- Gao, R.; Chen, H.; Hu, Z.; Cheng, X.; Gao, S.; Zhou, S.; Zhao, P. An integrated simulation method for analyzing mechanical properties of injection molded fiber-reinforced polymers. Polym. Compos. 2022, 43, 4530–4543. [Google Scholar] [CrossRef]
- Kim, D.H.; Choi, D.H.; Kim, H.S. Design optimization of a carbon fiber reinforced composite automotive lower arm. Compos. Part. B-Eng. 2014, 58, 400–407. [Google Scholar] [CrossRef]
- Park, S.W.; Choi, J.H.; Lee, B.C. Multi-objective optimization of an automotive body component with fiber-reinforced composites. Struct. Multidiscip. Optim. 2018, 58, 2203–2217. [Google Scholar] [CrossRef]
- Smith, H.; Norato, J. Topology optimization of structures made of fiber-reinforced plates. Struct. Multidiscip. Optim. 2022, 65, 58. [Google Scholar] [CrossRef]
- Blala, H.; Cheng, P.; Zhang, S.; Cheng, G.; Ruan, S.; Zhen, D.; Meng, Z. Advances and applications of metal-polymer hybrid for load-bearing body-in-white structural components: A comprehensive review. Int. J. Adv. Manuf. Technol. 2024, 133, 3023–3057. [Google Scholar] [CrossRef]
- Phiri, R.; Rangappa, S.M.; Siengchin, S.; Oladijo, O.P.; Ozbakkaloglu, T. Advances in lightweight composite structures and manufacturing technologies: A comprehensive review. Heliyon 2024, 10, e39661. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Liu, X.; Wu, Z. Mechanical properties analysis of PP-LGF40 and DC01 automotive front-end frames based on lightweight technology. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024. [Google Scholar] [CrossRef]
- Wang, L.; Tang, L.; Wu, P.; Chen, J. Research on the optimization of automobile plastic front frame structure. Adv. Mater. Sci. Eng. 2022, 2022, 2340342. [Google Scholar] [CrossRef]
- Lee, K.; Park, S.; Lee, Y.; Kim, J.; Kim, S. New concept carrier of front-end module with structural topology optimization for automotive. Adv. Mech. Eng. 2022, 14, 16878132221096201. [Google Scholar] [CrossRef]
- Li, X.J.; Zuo, Z.M.; Mi, H.Y.; Dong, B.B.; Antwi-Afari, M.F.; Liu, C.T.; Shen, C.Y. A review of research progress on the minimization of weld lines in injection molding. Int. J. Adv. Manuf. Technol. 2024, 132, 5179–5210. [Google Scholar] [CrossRef]
- Otieno, S.O.; Wambua, J.M.; Mwema, F.M.; Mharakurwa, E.T.; Jen, T.C.; Akinlabi, E.T. A predictive modelling strategy for warpage and shrinkage defects in plastic injection molding using fuzzy logic and pattern search optimization. J. Intel. Manuf. 2025, 36, 1835–1859. [Google Scholar] [CrossRef]
- Hanzlik, J.; Vanek, J.; Pata, V.; Senkerik, V.; Polaskova, M.; Kruzelak, J.; Bednarik, M. The Impact of Surface Roughness on Conformal Cooling Channels for Injection Molding. Materials 2024, 17, 2477. [Google Scholar] [CrossRef]
- Jadhav, G.; Gaval, V. Weld-line strength prediction for glass fiber reinforced polyamide-6 material through integrative simulation and its experimental validation. J. Thermoplast. Compos. Mater. 2023, 37, 2447–2463. [Google Scholar] [CrossRef]
- Isaincu, A.; Dan, M.; Ungureanu, V.; Marșavina, L. Numerical investigation on the influence of fiber orientation mapping procedure to the mechanical response of short-fiber reinforced composites using Moldflow, Digimat and Ansys software. Mater. Today: Proc. 2021, 45, 4304–4309. [Google Scholar] [CrossRef]
- Kastratović, G.; Grbović, A.; Sedmak, A.; Božić, Z.; Sedmak, S. Composite material selection for aircraft structures based on experimental and numerical evaluation of mechanical properties. Procedia Struct. Integr. 2021, 31, 127–133. [Google Scholar] [CrossRef]











| Test Item | Load | Displacement |
|---|---|---|
| Latch mounting points | +X 1000 N | ≤7 mm |
| +Z 1000 N | ≤2 mm | |
| −Z 1000 N | ≤2 mm | |
| Headlight mounting points | +X 100 N | ≤1 mm |
| −Z 100 N | ≤1 mm | |
| Radiator mounting points | +X 600 N | ≤1 mm |
| −X 600 N | ≤1 mm | |
| −Z 600 N | ≤1 mm | |
| Horn mounting points | +X 300 N | ≤2 mm |
| −Z 300 N | ≤2 mm |
| Analysis Item | Load/N | Test Point | Initial Design/mm | Optimize Case/mm | ||
|---|---|---|---|---|---|---|
| Unmapping | Mapping | Test | ||||
| Latch mounting points | +X 1000 | a1 | 5.263 | 4.536 | 4.842 | 5.21 |
| b1 | 5.030 | 4.290 | 4.443 | 5.02 | ||
| +Z 1000 | a2 | 2.008 | 1.446 | 1.682 | 1.86 | |
| b2 | 2.254 | 1.609 | 1.644 | 1.89 | ||
| −Z 1000 | a3 | 2.008 | 1.447 | 1.604 | 1.89 | |
| b3 | 2.254 | 1.609 | 1.653 | 1.97 | ||
| Headlight mounting points | +X 100 | d | 0.098 | 0.093 | 0.094 | 0.15 |
| e | 0.196 | 0.187 | 0.189 | 0.39 | ||
| g | 0.209 | 0.202 | 0.199 | 0.35 | ||
| j | 0.093 | 0.090 | 0.090 | 0.21 | ||
| k | 0.191 | 0.188 | 0.178 | 0.37 | ||
| m | 0.172 | 0.168 | 0.173 | 0.36 | ||
| −Z 100 | c | 0.074 | 0.061 | 0.067 | 0.09 | |
| f | 0.182 | 0.171 | 0.154 | 0.21 | ||
| h | 0.036 | 0.045 | 0.048 | 0.07 | ||
| i | 0.067 | 0.062 | 0.072 | 0.12 | ||
| l | 0.170 | 0.183 | 0.179 | 0.10 | ||
| n | 0.041 | 0.035 | 0.031 | 0.07 | ||
| Radiator mounting points | +X 600 | p1 | 0.167 | 0.169 | 0.166 | 0.32 |
| r1 | 0.163 | 0.163 | 0.159 | 0.31 | ||
| -X 600 | p2 | 0.167 | 0.169 | 0.175 | 0.29 | |
| r2 | 0.163 | 0.164 | 0.165 | 0.33 | ||
| −Z 600 | o | 0.046 | 0.046 | 0.051 | 0.13 | |
| q | 0.046 | 0.045 | 0.045 | 0.09 | ||
| Horn mounting points | +X 300 | t | 0.832 | 0.796 | 0.824 | 0.98 |
| v | 0.853 | 0.878 | 0.886 | 0.95 | ||
| −Z 300 | s | 0.623 | 0.604 | 0.711 | 0.65 | |
| u | 0.647 | 0.641 | 0.702 | 0.74 | ||
| Property | Value |
|---|---|
| Modulus of elasticity in the first direction E1 | 7266.9 MPa |
| Modulus of elasticity in the second direction E2 | 4488.6 MPa |
| Poisson’s ratio v12 | 0.338 |
| Poisson’s ratio v22 | 0.436 |
| Shear modulus G12 | 1621 MPa |
| Factors | (°C) | (°C) | (s) | (s) | (%) |
|---|---|---|---|---|---|
| Level 1 | 20 | 210 | 10 | 4.5 | 60 |
| Level 2 | 30 | 220 | 15 | 5.0 | 70 |
| Level 3 | 40 | 230 | 20 | 5.5 | 80 |
| Level 4 | 50 | 240 | 25 | 6.0 | 90 |
| Number | (°C) | (°C) | (s) | (s) | (%) | Warpage (mm) |
|---|---|---|---|---|---|---|
| 1 | 20 | 210 | 10 | 4.5 | 60 | 2.318 |
| 2 | 20 | 220 | 15 | 5.0 | 70 | 2.720 |
| 3 | 20 | 230 | 20 | 5.5 | 80 | 2.183 |
| 4 | 20 | 240 | 25 | 6.0 | 90 | 2.248 |
| 5 | 30 | 210 | 15 | 5.5 | 90 | 2.214 |
| 6 | 30 | 220 | 10 | 6.0 | 80 | 2.492 |
| 7 | 30 | 230 | 25 | 4.5 | 70 | 2.350 |
| 8 | 30 | 240 | 20 | 5.0 | 60 | 2.671 |
| 9 | 40 | 210 | 20 | 6.0 | 70 | 2.305 |
| 10 | 40 | 220 | 25 | 5.5 | 60 | 2.521 |
| 11 | 40 | 230 | 10 | 5.0 | 90 | 2.768 |
| 12 | 40 | 240 | 15 | 4.5 | 80 | 2.897 |
| 13 | 50 | 210 | 25 | 5.0 | 80 | 2.339 |
| 14 | 50 | 220 | 20 | 4.5 | 90 | 2.622 |
| 15 | 50 | 230 | 15 | 6.0 | 60 | 3.053 |
| 16 | 50 | 240 | 10 | 5.5 | 70 | 3.244 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Guo, P.; Tan, L.; Ye, T.; Li, L. Process–Structure Co-Optimization of Glass Fiber-Reinforced Polymer Automotive Front-End Module. Materials 2025, 18, 3121. https://doi.org/10.3390/ma18133121
Chen Z, Guo P, Tan L, Ye T, Li L. Process–Structure Co-Optimization of Glass Fiber-Reinforced Polymer Automotive Front-End Module. Materials. 2025; 18(13):3121. https://doi.org/10.3390/ma18133121
Chicago/Turabian StyleChen, Ziming, Pengcheng Guo, Longjian Tan, Tuo Ye, and Luoxing Li. 2025. "Process–Structure Co-Optimization of Glass Fiber-Reinforced Polymer Automotive Front-End Module" Materials 18, no. 13: 3121. https://doi.org/10.3390/ma18133121
APA StyleChen, Z., Guo, P., Tan, L., Ye, T., & Li, L. (2025). Process–Structure Co-Optimization of Glass Fiber-Reinforced Polymer Automotive Front-End Module. Materials, 18(13), 3121. https://doi.org/10.3390/ma18133121





