Investigation of the Impact of Clinker Grinding Conditions on Energy Consumption and Ball Fineness Parameters Using Statistical and Machine Learning Approaches in a Bond Ball Mill
Abstract
1. Introduction
2. Methods
2.1. Database Description and Preprocessing
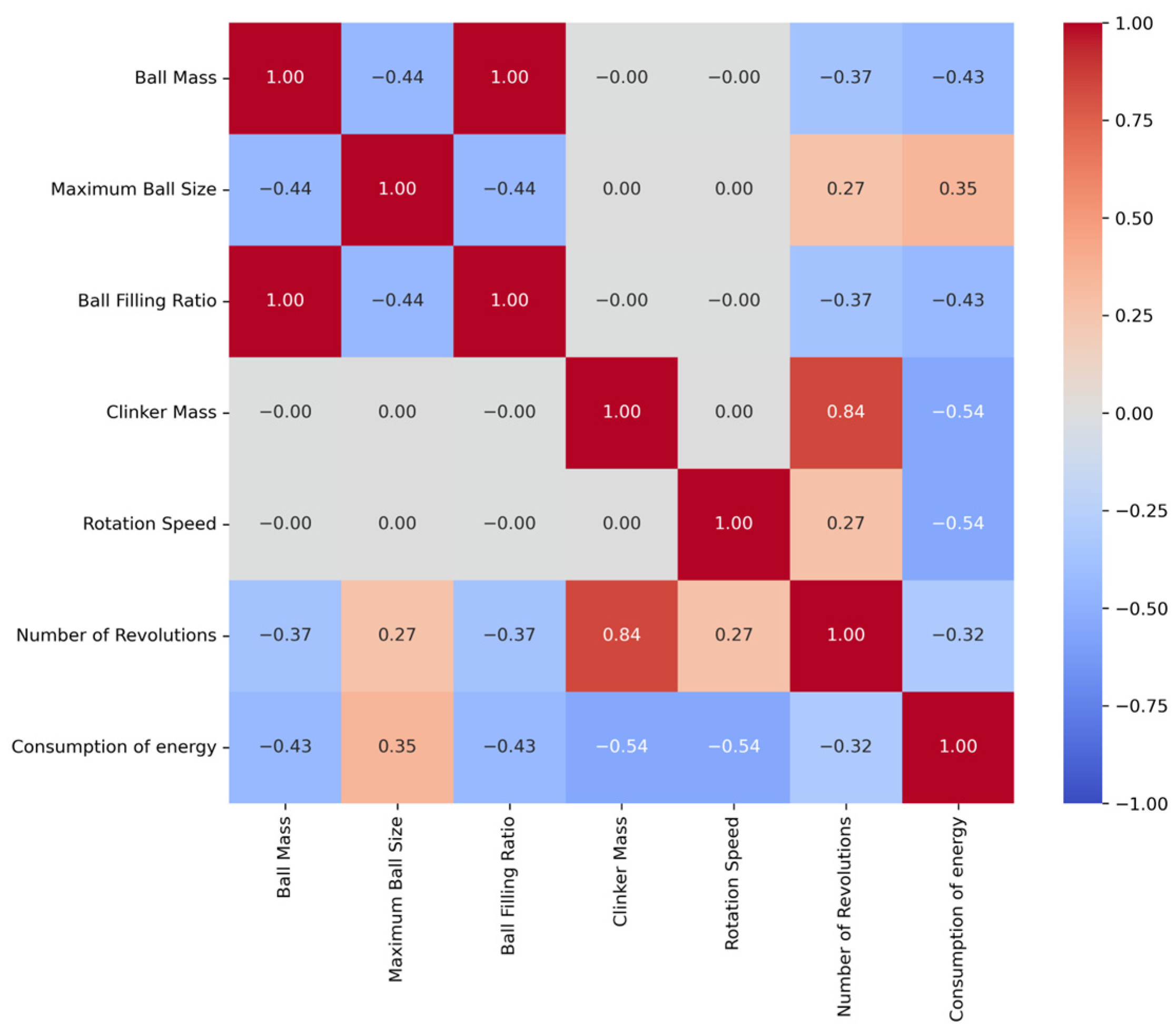
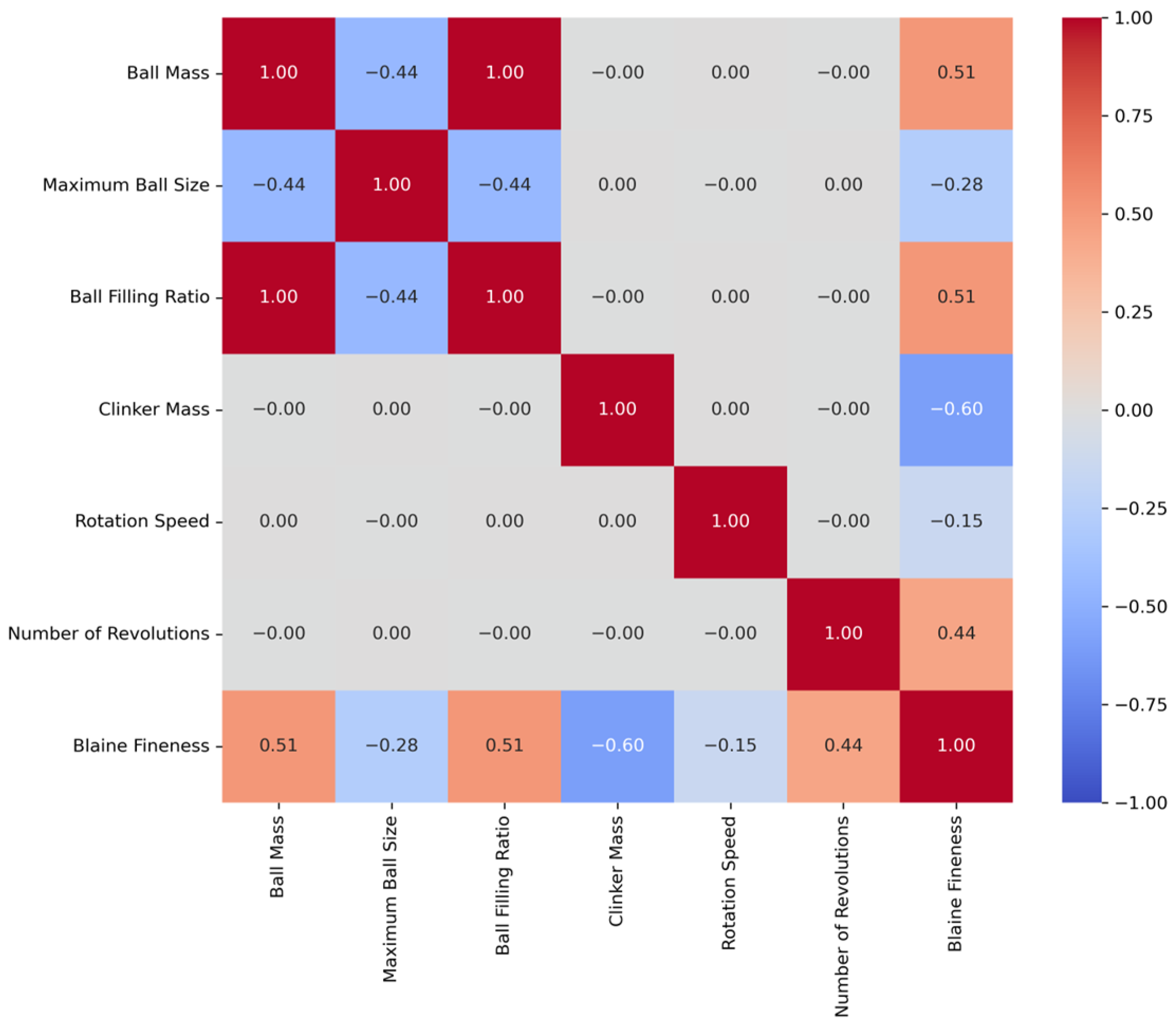
2.2. Feature Selection
2.3. Hyperparameter Tuning and Optimization
2.4. Description of Employed Techniques
2.4.1. Gradient Boosting Regressor
2.4.2. Ridge Regressor
2.4.3. Support Vector Regressor
2.4.4. Performance Evaluation of Models
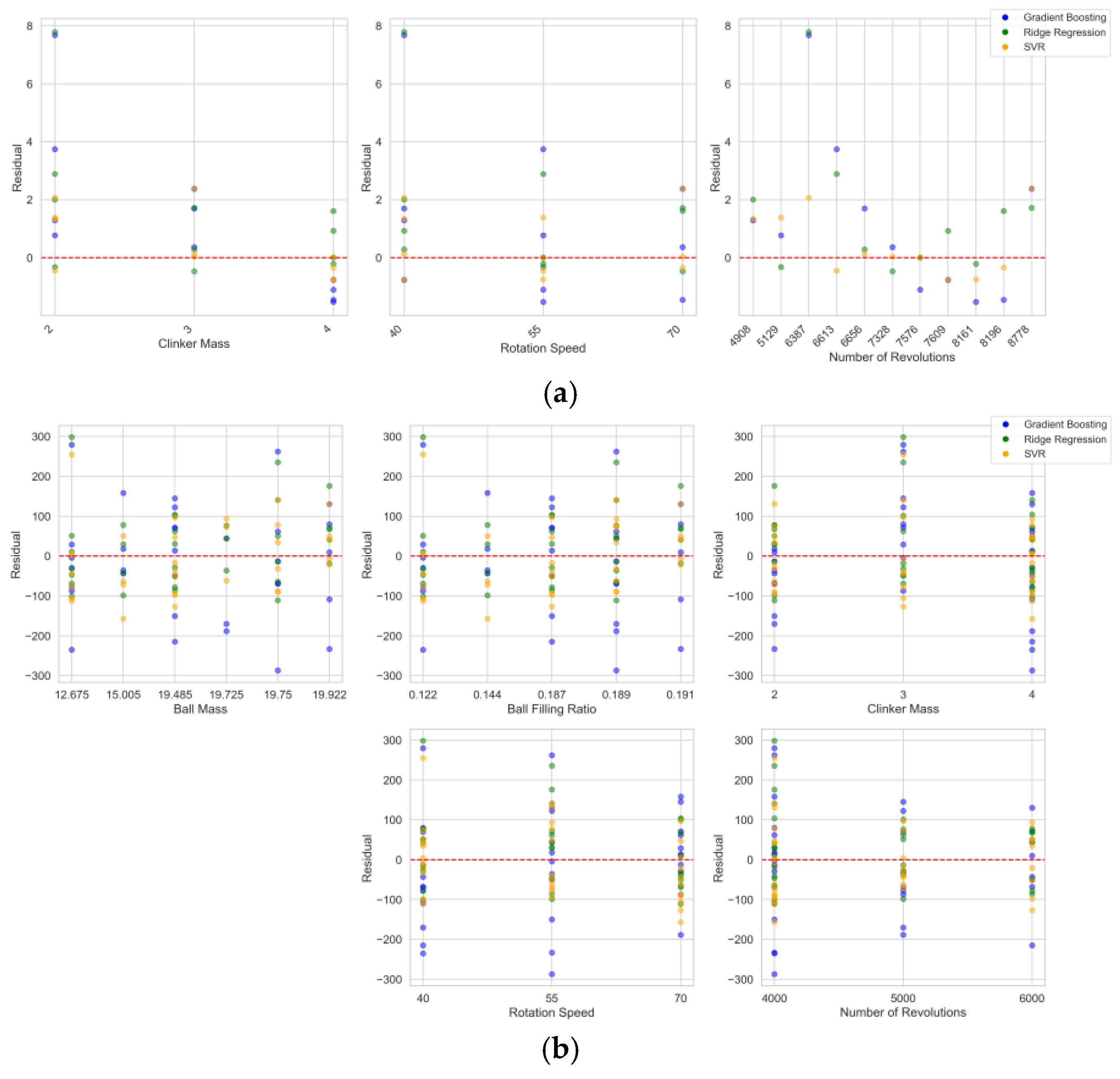
3. Results and Analysis
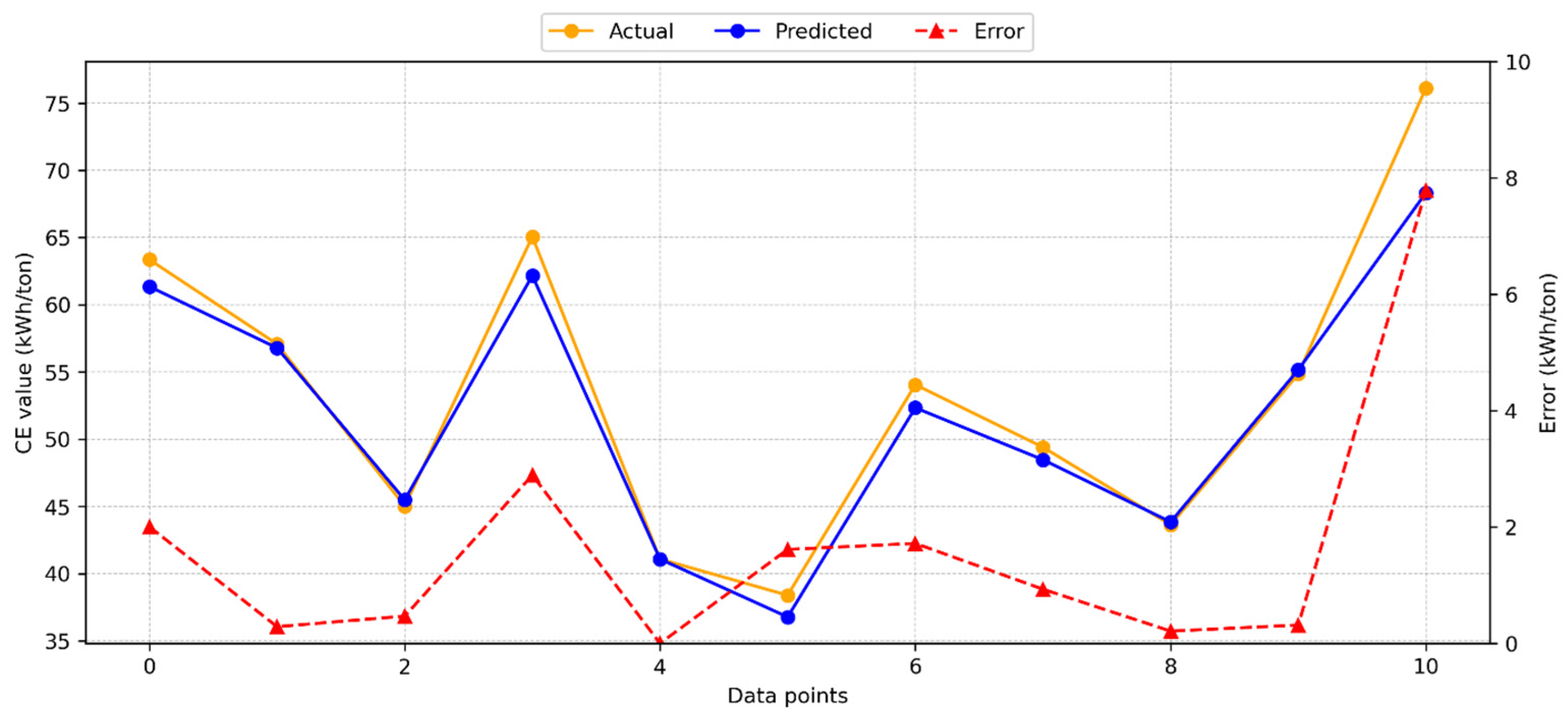
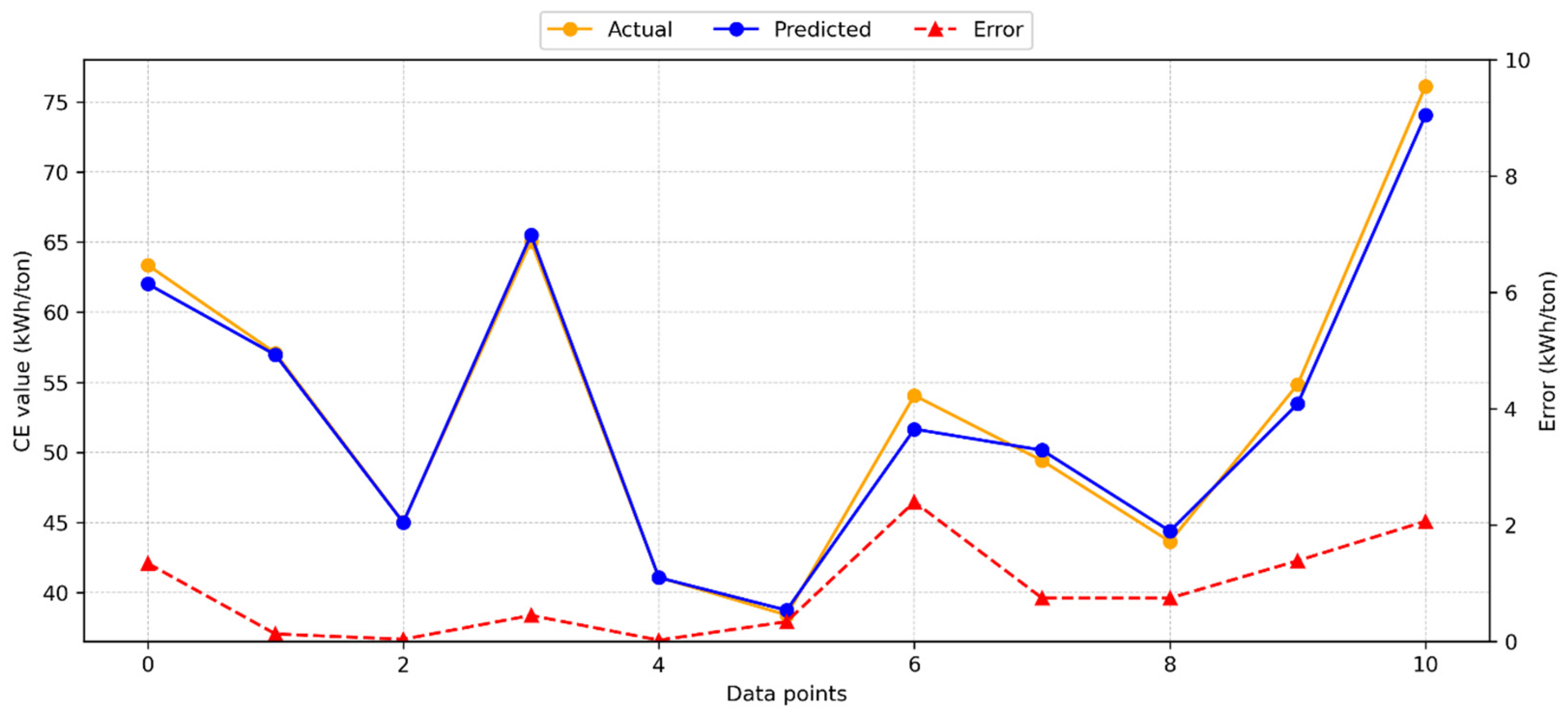
3.1. Consumption of Energy Estimation
3.1.1. Gradient Boosting Model for CE
3.1.2. Ridge Regression Model for CE
3.1.3. Support Vector Regression Model for CE
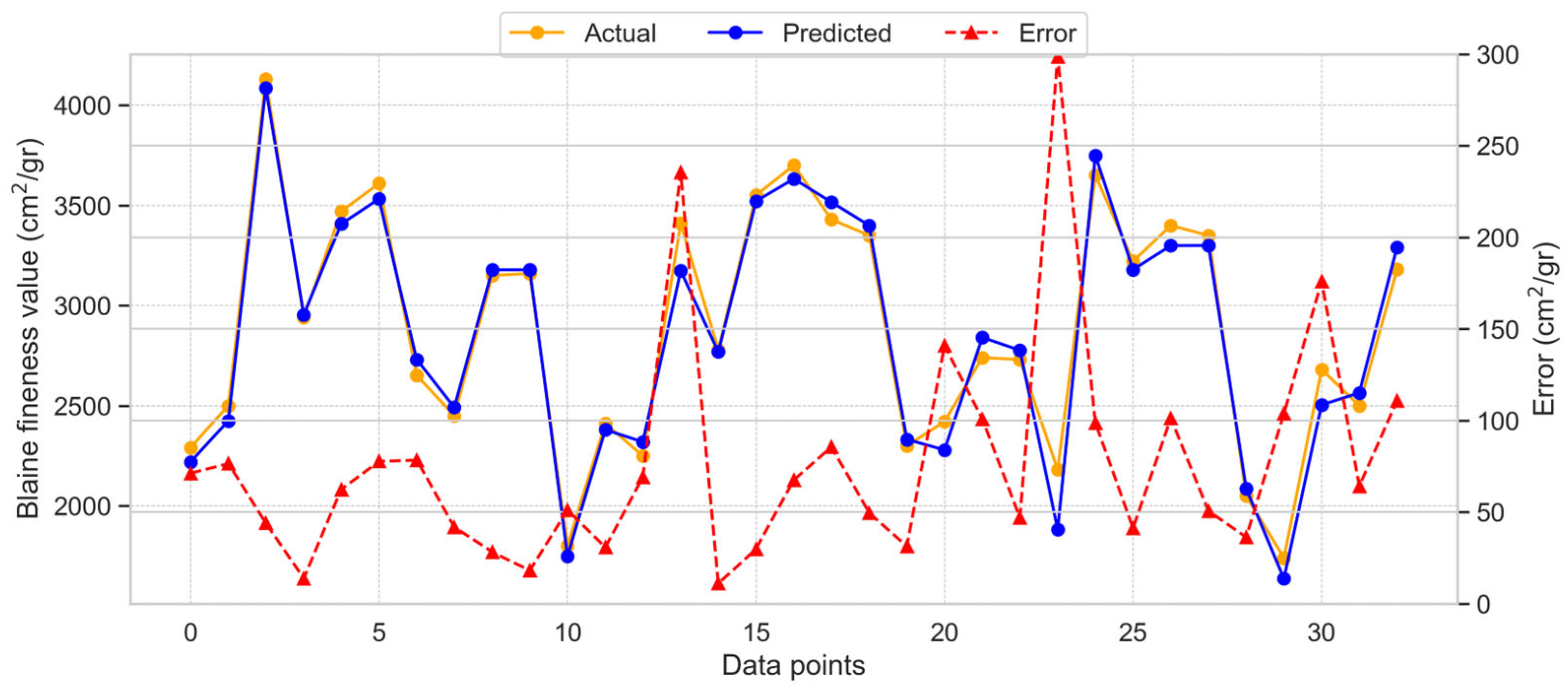
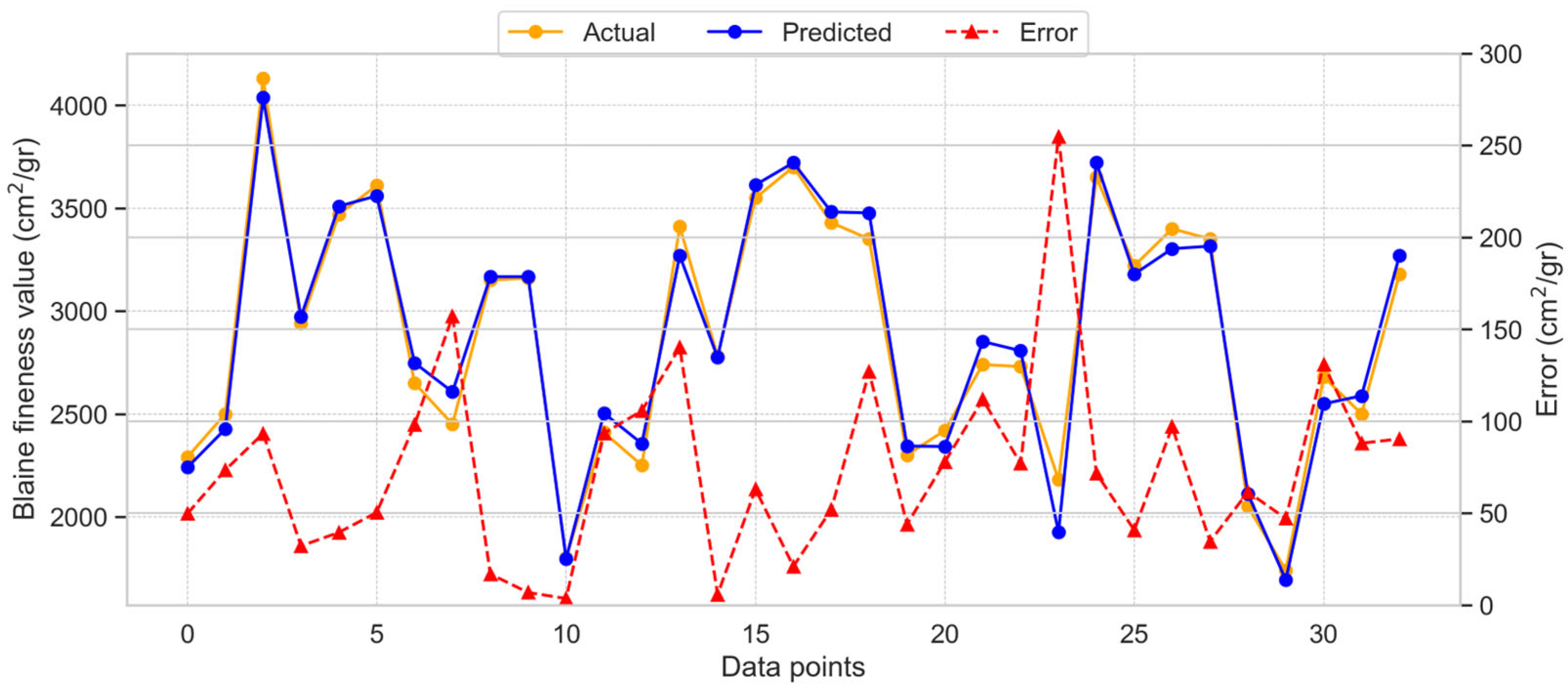
3.2. Blaine Fineness Prediction
3.2.1. Gradient Boosting Model for BF
3.2.2. Ridge Regression Model for BF
3.2.3. Support Vector Regression Model for BF
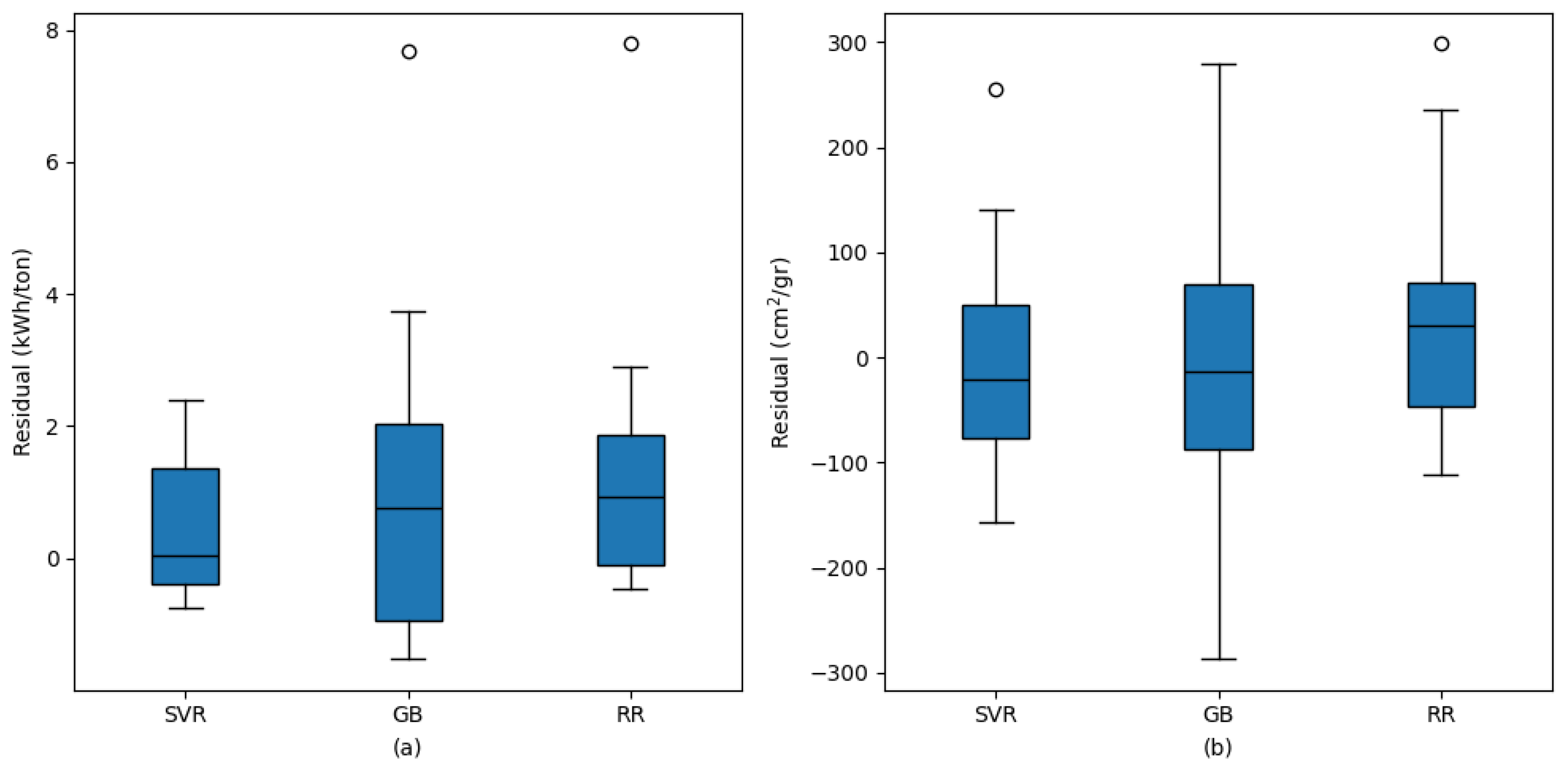
3.3. Model’s Comparison Using Statistical Performance Indicators
3.4. ML in Optimizing Cement Grinding Processes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Parameter | K-Fold Number | Avg. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Avg. | MAE | 1.14 | 1.01 | 0.86 | 0.82 | 1.00 | 0.95 | 1.10 | 1.38 | 0.83 | 2.55 | 1.16 |
| MAPE | 2.39 | 1.78 | 1.79 | 1.55 | 1.90 | 1.90 | 2.09 | 2.66 | 1.51 | 3.69 | 2.12 | |
| RMSE | 1.35 | 1.17 | 0.94 | 0.97 | 1.20 | 1.31 | 1.33 | 1.73 | 1.00 | 3.63 | 1.46 | |
| 0.96 | 0.95 | 0.97 | 0.96 | 0.87 | 0.97 | 0.90 | 0.76 | 0.97 | 0.92 | 0.92 | ||
| WAvg. | MAE | 0.77 | 0.77 | 0.64 | 0.88 | 0.98 | 0.82 | 0.99 | 1.56 | 0.83 | 2.14 | 1.04 |
| MAPE | 1.56 | 1.37 | 1.32 | 1.67 | 1.87 | 1.62 | 1.87 | 3.01 | 1.47 | 3.15 | 1.89 | |
| RMSE | 0.86 | 0.91 | 0.78 | 0.99 | 1.29 | 1.21 | 1.35 | 1.86 | 1.12 | 3.02 | 1.34 | |
| 0.98 | 0.97 | 0.98 | 0.96 | 0.85 | 0.97 | 0.90 | 0.72 | 0.97 | 0.95 | 0.92 | ||
| Model | Parameter | K-Fold Number | Avg. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Avg. | MAE | 140.35 | 118.29 | 43.12 | 92.74 | 58.74 | 77.26 | 91.42 | 136.42 | 78.09 | 249.29 | 108.57 |
| MAPE | 5.11 | 4.06 | 1.43 | 3.17 | 2.15 | 2.90 | 3.23 | 5.37 | 2.74 | 60.41 | 9.06 | |
| RMSE | 169.81 | 147.01 | 50.22 | 121.14 | 81.62 | 104.78 | 103.58 | 168.17 | 85.10 | 676.09 | 170.75 | |
| 0.95 | 0.90 | 0.99 | 0.96 | 0.98 | 0.96 | 0.96 | 0.93 | 0.97 | 0.44 | 0.90 | ||
| WAvg. | MAE | 143.78 | 119.89 | 38.07 | 88.36 | 52.19 | 66.77 | 82.77 | 129.01 | 73.23 | 245.18 | 103.93 |
| MAPE | 5.06 | 4.03 | 1.28 | 3.02 | 1.93 | 2.45 | 2.98 | 5.01 | 2.55 | 60.14 | 8.85 | |
| RMSE | 178.03 | 151.96 | 46.62 | 114.71 | 74.71 | 93.67 | 91.53 | 158.24 | 83.70 | 673.10 | 166.63 | |
| 0.94 | 0.90 | 0.99 | 0.96 | 0.98 | 0.97 | 0.97 | 0.94 | 0.97 | 0.44 | 0.91 | ||
References
- Touil, D.; Belaadi, S.; Frances, C. The specific selection function effect on clinker grinding efficiency in a dry batch ball mill. Int. J. Miner. Process. 2008, 87, 141–145. [Google Scholar] [CrossRef][Green Version]
- ICS. Cement Technology Roadmap 2009 Carbon Emission Reduction up to 2050; World Business Council for Sustainable Development: Geneva, Switzerland, 2009. [Google Scholar]
- Qian, H.Y.; Kong, Q.G.; Zhang, B.L. The effects of grinding media shapes on the grinding kinetics of cement clinker in ball mill. Powder Technol. 2013, 235, 422–425. [Google Scholar] [CrossRef]
- Mardani-Aghabaglou, A.; İlhan, M.; Özen, S. The effect of shrinkage reducing admixture and polypropylene fibers on drying shrinkage behaviour of concrete. Cem.-Wapno-Beton = Cem. Lime Concr. 2019, 24, 227–237. [Google Scholar] [CrossRef]
- Kobya, V.; Kaya, Y.; Mardani-Aghabaglou, A. Effect of amine and glycol-based grinding aids utilization rate on grinding efficiency and rheological properties of cementitious systems. J. Build. Eng. 2022, 47, 103917. [Google Scholar] [CrossRef]
- Sezer, A.; Boz, A.; Tanrinian, N. An investigation into strength and permittivity of compacted sand-clay mixtures by partial replacement of water with lignosulfonate. Acta Phys. Pol. A 2016, 130, 23–27. [Google Scholar] [CrossRef]
- Yüksel, C.; Mardani-Aghabaglou, A.; Beglarigale, A.; Yazıcı, H.; Ramyar, K.; Andiç-Çakır, Ö. Influence of water/powder ratio and powder type on alkali–silica reactivity and transport properties of self-consolidating concrete. Mater. Struct. 2016, 49, 289–299. [Google Scholar] [CrossRef]
- Coppola, L.; Bellezze, T.; Belli, A.; Bignozzi, M.C.; Bolzoni, F.; Brenna, A.; Yang, F. Binders alternative to Portland cement and waste management for sustainable construction—Part 1. J. Appl. Biomater. Funct. Mater. 2018, 16, 186–202. [Google Scholar]
- Coppola, L.; Bellezze, T.; Belli, A.; Bignozzi, M.C.; Bolzoni, F.; Brenna, A.; Yang, F. Binders alternative to Portland cement and waste management for sustainable construction–Part 2. J. Appl. Biomater. Funct. Mater. 2018, 16, 207–221. [Google Scholar]
- Ahmad, M.R.; Chen, B. Microstructural characterization of basalt fiber reinforced magnesium phosphate cement supplemented by silica fume. Constr. Build. Mater. 2020, 237, 117795. [Google Scholar] [CrossRef]
- Collivignarelli, M.C.; Abba, A.; Miino, M.C.; Cillari, G.; Ricciardi, P. A review on alternative binders, admixtures and water for the production of sustainable concrete. J. Clean. Prod. 2021, 295, 126408. [Google Scholar] [CrossRef]
- Şahin, H.G.; Biricik, Ö.; Mardani-Aghabaglou, A. Polycarboxylate-based water reducing admixture–clay compatibility; literature review. J. Polym. Res. 2022, 29, 33. [Google Scholar] [CrossRef]
- Durgun, M.Y.; Özen, S.; Karakuzu, K.; Kobya, V.; Bayqra, S.H.; Mardani-Aghabaglou, A. Effect of high temperature on polypropylene fiber-reinforced mortars containing colemanite wastes. Constr. Build. Mater. 2022, 316, 125827. [Google Scholar] [CrossRef]
- Liu, Q.; Tong, T.; Liu, S.; Yang, D.; Yu, Q. Investigation of using hybrid recycled powder from demolished concrete solids and clay bricks as a pozzolanic supplement for cement. Constr. Build. Mater. 2014, 73, 754–763. [Google Scholar] [CrossRef]
- Mardani-Aghabaglou, A.; Özen, S.; Altun, M.G. Durability performance and dimensional stability of polypropylene fiber reinforced concrete. J. Green Build. 2018, 13, 20–41. [Google Scholar] [CrossRef]
- Yiğit, B.; Salihoğlu, G.; Mardani-Aghabaglou, A.; Salihoğlu, N.K.; Özen, S. Recycling of sewage sludge incineration ashes as construction material. J. Fac. Eng. Archit. Gazi Univ. 2020, 35, 1647–1664. [Google Scholar]
- Phillip, E.; Khoo, K.S.; Yusof, M.A.W.; Rahman, R.A. Mechanistic insights into the dynamics of radionuclides retention in evolved POFA-OPC and OPC barriers in radioactive waste disposal. Chem. Eng. J. 2022, 437, 135423. [Google Scholar] [CrossRef]
- Lameck, N.S.; Kiangi, K.K.; Moys, M.H. Effects of grinding media shapes on load behaviour and mill power in a dry ball mill. Miner. Eng. 2006, 19, 1357–1361. [Google Scholar] [CrossRef]
- Erdem, A.S.; Ergün, Ş.L. The effect of ball size on breakage rate parameter in a pilot scale ball mill. Miner. Eng. 2009, 22, 660–664. [Google Scholar] [CrossRef]
- Shahbazi, B.; Jafari, M.; Parian, M.; Rosenkranz, J.; Chelgani, S.C. Study on the impacts of media shapes on the performance of tumbling mills—A review. Miner. Eng. 2020, 157, 106490. [Google Scholar] [CrossRef]
- Abdelhaffez, G.S.; Ahmed, A.A.; Ahmed, H.M. Effect of grinding media on the milling efficiency of a ball mill. Rud.-Geološko-Naft. Zb. 2022, 38, 171–177. [Google Scholar] [CrossRef]
- Kaya, Y.; Kobya, V.; Mardani, A.; Mardani, N.; Beytekin, H.E. Effect of Grinding Conditions on Clinker Grinding Efficiency: Ball Size, Mill Rotation Speed, and Feed Rate. Buildings 2024, 14, 2356. [Google Scholar] [CrossRef]
- Altun, O.; Sert, T.; Altun, D.; Toprak, A.; Kwade, A. Scale-up of Vertical Wet Stirred Media Mill (HIGmill) via Signature Plots, Stress Analyses and Energy Equations. Miner. Eng. 2024, 205, 108460. [Google Scholar] [CrossRef]
- Amiri, S.H.; Zare, S. Influence of grinding and classification circuit on the performance of iron ore beneficiation–A plant scale study. Miner. Process. Extr. Metall. Rev. 2021, 42, 143–152. [Google Scholar] [CrossRef]
- Dökme, F.; Güven, O. Bilyalı değirmenlerde hızın performansa olan etkilerinin deneysel olarak incelenmesi. Mühendis Ve Makina 2014, 38–50. [Google Scholar]
- Mukhitdinov, D.; Kadirov, Y.; Boybutayev, S.; Boeva, O.; Babakhonova, U. Simulation and control of ball mills under uncertainty conditions. J. Phys. Conf. Ser. 2024, 2697, 012041. [Google Scholar] [CrossRef]
- Mavhungu, E.; Campos, T.M.; Rocha, B.K.N.; Solomon, N.; Bergmann, C.; Tavares, L.M.; Lichter, J. Simulating large-diameter industrial ball mills from batch-grinding tests. Miner. Eng. 2024, 206, 108505. [Google Scholar] [CrossRef]
- Fortsch, D.S. Ball charge loading-impact on specific power consumption and capacity. In Proceedings of the IEEE Cement Industry Technical Conference, 2006, Conference Record, Phoenix, AZ, USA, 9–14 April 2006; pp. 1–11. [Google Scholar]
- Göktaş, İ.; Altun, O.; Toprak, N.A.; Altun, D. Element based ball mill and hydrocyclone modelling for a copper ore grinding circuit. Miner. Eng. 2023, 198, 108090. [Google Scholar] [CrossRef]
- Sridhar, C.S.; Sankar, P.S.; Prasad, R.K. Grinding kinetics, modeling, and subsieve morphology of ball mill grinding for cement industry ingredients. Part. Sci. Technol. 2016, 34, 1–8. [Google Scholar] [CrossRef]
- Altun, D.; Altun, O.; Zencirci, S. Developing a methodology to model and predict the grinding performance of the dry stirred mill. Miner. Eng. 2019, 139, 105867. [Google Scholar] [CrossRef]
- Mardani-Aghabaglou, A.; Öztürk, H.T.; Kankal, M.; Ramyar, K. Assessment and prediction of cement paste flow behavior; Marsh-funnel flow time and mini-slump values. Constr. Build. Mater. 2021, 301, 124072. [Google Scholar] [CrossRef]
- Feng, D.; Liu, Z.; Wang, X.; Chen, Y.; Chang, J.; Wei, D.; Jiang, Z. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Mustapha, I.B.; Abdulkareem, M.; Jassam, T.M.; AlAteah, A.H.; Al-Sodani, K.A.A.; Al-Tholaia, M.M.; Nabus, H.; Alih, S.C.; Abdulkareem, Z.; Ganiyu, A. Comparative Analysis of Gradient-Boosting Ensembles for Estimation of Compressive Strength of Quaternary Blend Concrete. Int. J. Concr. Struct. Mater. 2024, 18, 1–24. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Marani, A.; Nehdi, M. Machine learning prediction of compressive strength for phase change materials integrated cementitious composites. Constr. Build. Mater. 2020, 265, 120286. [Google Scholar] [CrossRef]
- Belalia Douma, O.; Boukhatem, B.; Ghrici, M.; Tagnit-Hamou, A. Prediction of properties of self-compacting concrete containing fly ash using artificial neural network. Neural Comput. Appl. 2017, 28, 707–718. [Google Scholar] [CrossRef]
- Yaman, M.A.; Abd Elaty, M.; Taman, M. Predicting the ingredients of self compacting concrete using artificial neural network. Alex. Eng. J. 2017, 56, 523–532. [Google Scholar] [CrossRef]
- Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, G.; Huang, Y.; Aslani, F.; Nener, B. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019, 210, 713–719. [Google Scholar] [CrossRef]
- Mai, H.; Nguyen, T.; Ly, H.; Tran, V. Prediction Compressive Strength of Concrete Containing GGBFS using Random Forest Model. Adv. Civ. Eng. 2021, 2021, 6671448. [Google Scholar] [CrossRef]
- Farooq, F.; Amin, M.; Khan, K.; Sadiq, M.; Javed, M.; Aslam, F.; Alyousef, R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Iftikhar, B.; Alih, S.C.; Vafaei, M.; Elkotb, M.A.; Shutaywi, M.; Javed, M.F.; Deebani, M.; Khan, I.; Aslam, F. Predictive modeling of compressive strength of sustainable rice husk ash concrete: Ensemble learner optimization and comparison. J. Clean. Prod. 2022, 348, 131285. [Google Scholar] [CrossRef]
- Sarir, P.; Chen, J.; Asteris, P.G.; Armaghani, D.J.; Tahir, M.M. Developing GEP tree-based, neuro-swarm, and whale optimization models for evaluation of bearing capacity of concrete-filled steel tube columns. Eng. Comput. 2021, 37, 1–19. [Google Scholar] [CrossRef]
- Shahmansouri, A.A.; Bengar, H.A.; Jahani, E. Predicting compressive strength and electrical resistivity of eco-friendly concrete containing natural zeolite via GEP algorithm. Constr. Build. Mater. 2019, 229, 116883. [Google Scholar] [CrossRef]
- Aslam, F.; Farooq, F.; Amin, M.N.; Khan, K.; Waheed, A.; Akbar, A.; Javed, M.F.; Alyousef, R.; Alabdulijabbar, H. Applications of gene expression programming for estimating compressive strength of high-strength concrete. Adv. Civ. Eng. 2020, 2020, 8850535. [Google Scholar] [CrossRef]
- Shah, H.A.; Rehman, S.K.U.; Javed, M.F.; Iftikhar, Y. Prediction of compressive and splitting tensile strength of concrete with fly ash by using gene expression programming. Struct. Concr. 2022, 23, 2435–2449. [Google Scholar] [CrossRef]
- Zeini, H.; Al-Jeznawi, D.; Imran, H.; Bernardo, L.; Al-Khafaji, Z.; Ostrowski, K. Random Forest Algorithm for the Strength Prediction of Geopolymer Stabilized Clayey Soil. Sustainability 2023, 15, 1408. [Google Scholar] [CrossRef]
- Zhou, J.; Su, Z.; Hosseini, S.; Tian, Q.; Lu, Y.; Luo, H.; Xu, X.; Huang, J. Decision tree models for the estimation of geo-polymer concrete compressive strength. Math. Biosci. Eng. 2024, 21, 1413–1444. [Google Scholar] [CrossRef]
- Chou, J.S.; Chiu, C.K.; Farfoura, M.; Al-Taharwa, I. Optimizing the prediction accuracy of concrete compressive strength based on a comparison of data-mining techniques. J. Comput. Civ. Eng. 2011, 25, 242–253. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Cao, M.T. Estimating strength of rubberized concrete using evolutionary multivariate adaptive regression splines. J. Civ. Eng. Manag. 2016, 22, 711–720. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T.; Hamze-Ziabari, S.M. M5′and Mars based prediction models for properties of self-compacting concrete containing fly ash. Period. Polytech. Civ. Eng. 2018, 62, 281–294. [Google Scholar] [CrossRef]
- Nasr, D.; Babagoli, R.; Rezaei, M.; Andarz, A. Evaluating the Influence of Carbon Fiber on the Mechanical Characteristics and Electrical Conductivity of Roller-Compacted Concrete Containing Waste Ceramic Aggregates Exposed to Freeze-Thaw Cycling. Adv. Mater. Sci. Eng. 2023, 2023, 1308387. [Google Scholar] [CrossRef]
- Cantu-Paz, E. Feature Subset Selection, Class Separability, and Genetic Algorithms. In Proceedings of the Genetic and evolutionary computation conference, Seattle, WA, USA, 26–30 June 2004; Springer: Berlin/Heidelberg, Germany; pp. 959–970. [Google Scholar]
- Ladha, L.; Deepa, T. Feature selection methods and algorithms. Int. J. Comput. Sci. Eng. 2011, 3, 1787–1797. [Google Scholar]
- Naqvi, G. A Hybrid Filter-Wrapper Approach for Feature Selection. Master’s Thesis, Orebro University, Örebro, Sweden, 2012. [Google Scholar]
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Bolon-Canedo, V.; Sanchez-Marono, N.; Alonso-Betanzos, A.; Benítez, J.M.; Herrera, F. A review of microarray datasets and applied feature selection methods. Inf. Sci. 2014, 282, 111–135. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Singh, S.; Patro, S.K.; Parhi, S.K. Evolutionary optimization of machine learning algorithm hyperparameters for strength prediction of high-performance concrete. Asian J. Civ. Eng. 2023, 24, 3121–3143. [Google Scholar] [CrossRef]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 847–855. [Google Scholar]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Nguyen, H.; Vu, T.; Vo, T.P.; Thai, H.T. Efficient machine learning models for prediction of concrete strengths. Constr. Build. Mater. 2021, 266, 120950. [Google Scholar] [CrossRef]
- Touzani, S.; Granderson, J.; Fernandes, S. Gradient boosting machine for modeling the energy consumption of commercial buildings. Energy Build. 2018, 158, 1533–1543. [Google Scholar] [CrossRef]
- Marquardt, D.W.; Snee, R.D. Ridge regression in practice. Am. Stat. 1975, 29, 3–20. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; 314p. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 28, 779–784. [Google Scholar]
- Durgun, H.; İnce, E.Y.; İnce, M.; Çoban, H.O.; Eker, M. Evaluation of Tree Diameter and Height Measurements in UAV Data through the Integration of Remote Sensing and Machine Learning Methods. Gazi J. Eng. Sci. (GJES)/Gazi Mühendislik Bilim. Derg. 2023, 9, 113–125. [Google Scholar]
- Ahmad, A.; Ahmad, W.; Aslam, F.; Joyklad, P. Compressive strength prediction of fly ash-based geopolymer concrete via advanced machine learning techniques. Case Stud. Constr. Mater. 2022, 16, e00840. [Google Scholar] [CrossRef]



| Parameter | Input Variables | Output | |||||
|---|---|---|---|---|---|---|---|
| Ball Mass | Maximum Ball Size | Ball Filling Ratio | Clinker Mass | Rotation Speed (rpm) | Number of Revolutions | Consumed Energy (kWh/ton) | |
| Mean | 17.76 | 58.67 | 0.17 | 3.00 | 55.00 | 7286.57 | 52.84 |
| Standard Error | 0.39 | 1.42 | 0.00 | 0.11 | 1.68 | 235.82 | 1.00 |
| Median | 19.61 | 65.00 | 0.19 | 3.00 | 55.00 | 7234.00 | 52.17 |
| Mode | 12.68 | 65.00 | 0.19 | 2.00 | 40.00 | 4510.00 | 38.40 |
| Standard Deviation | 2.88 | 10.45 | 0.03 | 0.82 | 12.36 | 1732.89 | 7.33 |
| Range | 7.25 | 28.00 | 0.07 | 2.00 | 30.00 | 7457.00 | 37.72 |
| Minimum | 12.68 | 37.00 | 0.12 | 2.00 | 40.00 | 4510.00 | 38.40 |
| Maximum | 19.92 | 65.00 | 0.19 | 4.00 | 70.00 | 11,967.00 | 76.12 |
| Parameter | Input Variables | Output | |||||
|---|---|---|---|---|---|---|---|
| Ball Mass | Maximum Ball Size | Ball Filling Ratio | Clinker Mass | Rotation Speed (rpm) | Number of Revolutions | Blaine Fineness (cm2/gr) | |
| Mean | 17.76 | 58.67 | 0.17 | 3.00 | 55.00 | 5000.00 | 2994.69 |
| Standard Error | 0.23 | 0.82 | 0.00 | 0.06 | 0.97 | 64.35 | 48.70 |
| Median | 19.61 | 65.00 | 0.19 | 3.00 | 55.00 | 5000.00 | 3050.00 |
| Mode | 12.68 | 65.00 | 0.19 | 2.00 | 40.00 | 4000.00 | 2450.00 |
| Standard Deviation | 2.86 | 10.39 | 0.03 | 0.82 | 12.29 | 819.03 | 619.87 |
| Range | 7.25 | 28.00 | 0.07 | 2.00 | 30.00 | 2000.00 | 4021.00 |
| Minimum | 12.68 | 37.00 | 0.12 | 2.00 | 40.00 | 4000.00 | 289.00 |
| Maximum | 19.92 | 65.00 | 0.19 | 4.00 | 70.00 | 6000.00 | 4310.00 |
| CE | BF | |||||
|---|---|---|---|---|---|---|
| Feature | MIR | LR | SBS | MIR | LR | SBS |
| Ball Mass | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ |
| Maximum Ball Size | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| Ball Filling Ratio | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ |
| Clinker Mass | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Rotation Speed | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Number of Revolutions | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ |
| Parameter | Gradient Boosting | Ridge Regression | Support Vector Regression | |||
|---|---|---|---|---|---|---|
| Range | Optimal Value | Range | Optimal Value | Range | Optimal Value | |
| No. of estimator | 10–300 | 200 | - | - | - | - |
| Learning rate | 0.01–1.0 | 0.5 | - | - | - | - |
| Max. depth | 1–5 | 1 | - | - | - | - |
| Max. features | 0.8–1.0 | 1.0 | - | - | - | - |
| Min. sample leaf | 1–4 | 1 | - | - | - | - |
| Min. sample split | 2–12 | 8 | - | - | - | - |
| Alpha | - | - | 0.001–100.0 | 0.1 | - | - |
| Kernel | - | - | - | - | [RBF, linear] | RBF |
| C | - | - | - | - | 0.1–100.0 | 100 |
| Epsilon | - | - | - | - | 0.01–0.5 | 0.5 |
| Parameter | Gradient Boosting | Ridge Regression | Support Vector Regression | |||
|---|---|---|---|---|---|---|
| Range | Optimal Value | Range | Optimal Value | Range | Optimal Value | |
| No. of estimator | 10–200 | 50 | - | - | - | - |
| Learning rate | 0.01–1.0 | 0.2 | - | - | - | - |
| Max. depth | 1–5 | 2 | - | - | - | - |
| Max. features | 0.8–1.0 | 0.9 | - | - | - | - |
| Min. sample leaf | 1–4 | 4 | - | - | - | - |
| Min. sample split | 2–12 | 6 | - | - | - | - |
| Alpha | - | - | 0.001–100.0 | 1 | - | - |
| Kernel | - | - | - | - | [RBF, linear] | linear |
| C | - | - | - | - | 0.1–100.0 | 100 |
| Epsilon | - | - | - | - | 0.01–0.5 | 0.01 |
| Model | Parameter | K-Fold Number | Avg. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| GB | MAE | 0.79 | 2.70 | 1.02 | 2.52 | 1.75 | 2.03 | 1.30 | 1.33 | 0.52 | 1.33 | 1.53 |
| MAPE | 1.53 | 5.23 | 2.04 | 5.08 | 2.51 | 3.82 | 2.39 | 2.45 | 1.06 | 2.76 | 2.89 | |
| RMSE | 1.02 | 3.27 | 1.23 | 3.31 | 3.07 | 2.27 | 1.55 | 1.54 | 0.60 | 1.86 | 1.97 | |
| 0.91 | 0.77 | 0.96 | 0.87 | 0.92 | 0.60 | 0.92 | 0.96 | 0.99 | 0.70 | 0.86 | ||
| RR | MAE | 1.88 | 1.98 | 1.29 | 1.88 | 2.57 | 0.86 | 2.11 | 1.03 | 1.75 | 2.28 | 1.76 |
| MAPE | 3.64 | 3.92 | 2.54 | 3.33 | 3.82 | 1.57 | 3.80 | 2.15 | 3.80 | 4.49 | 3.31 | |
| RMSE | 1.90 | 2.44 | 1.48 | 2.26 | 3.75 | 1.14 | 2.21 | 1.23 | 2.02 | 2.46 | 2.09 | |
| 0.69 | 0.87 | 0.94 | 0.94 | 0.88 | 0.90 | 0.83 | 0.97 | 0.93 | 0.47 | 0.84 | ||
| SVR | MAE | 1.05 | 1.56 | 1.18 | 1.06 | 0.97 | 1.44 | 0.72 | 1.15 | 0.15 | 1.20 | 1.05 |
| MAPE | 1.98 | 2.92 | 2.20 | 2.03 | 1.53 | 2.71 | 1.36 | 2.18 | 0.31 | 2.40 | 1.96 | |
| RMSE | 1.53 | 1.84 | 1.37 | 1.19 | 1.29 | 1.79 | 0.95 | 1.30 | 0.18 | 1.41 | 1.29 | |
| 0.80 | 0.93 | 0.95 | 0.98 | 0.99 | 0.75 | 0.97 | 0.97 | 1.00 | 0.83 | 0.92 | ||
| Model | Parameter | K-Fold Number | Avg. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| GB | MAE | 208.48 | 111.58 | 58.43 | 115.88 | 51.78 | 126.78 | 72.35 | 133.02 | 82.00 | 237.92 | 119.82 |
| MAPE | 7.33 | 3.81 | 1.97 | 3.81 | 1.77 | 4.41 | 2.61 | 4.69 | 2.85 | 59.50 | 9.27 | |
| RMSE | 304.49 | 143.42 | 71.88 | 135.00 | 70.38 | 189.62 | 86.06 | 171.58 | 96.50 | 664.70 | 193.36 | |
| 0.82 | 0.91 | 0.98 | 0.95 | 0.99 | 0.86 | 0.97 | 0.93 | 0.96 | 0.46 | 0.88 | ||
| RR | MAE | 143.75 | 157.60 | 92.75 | 102.59 | 73.00 | 75.23 | 89.02 | 126.43 | 93.27 | 244.93 | 119.86 |
| MAPE | 5.52 | 5.32 | 3.16 | 3.54 | 2.70 | 2.78 | 2.95 | 4.97 | 3.31 | 60.61 | 9.49 | |
| RMSE | 184.59 | 198.90 | 104.52 | 150.33 | 117.01 | 93.66 | 101.11 | 193.74 | 114.40 | 678.00 | 193.63 | |
| 0.94 | 0.82 | 0.96 | 0.94 | 0.96 | 0.97 | 0.96 | 0.90 | 0.94 | 0.43 | 0.88 | ||
| SVR | MAE | 127.11 | 136.37 | 86.32 | 98.74 | 77.27 | 69.78 | 80.43 | 142.63 | 86.00 | 251.11 | 115.58 |
| MAPE | 4.90 | 4.65 | 2.88 | 3.40 | 2.80 | 2.59 | 2.79 | 5.55 | 3.09 | 59.70 | 9.24 | |
| RMSE | 174.17 | 168.68 | 98.19 | 141.83 | 116.06 | 91.01 | 87.70 | 199.78 | 104.39 | 665.32 | 184.71 | |
| 0.94 | 0.87 | 0.97 | 0.95 | 0.96 | 0.97 | 0.97 | 0.90 | 0.95 | 0.45 | 0.89 | ||
| Consumption of Energy | Blaine Fineness | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | MAE (kWh/ton) | MAPE (%) | RMSE (kWh/ton) | MAE (cm2/gr) | MAPE (%) | RMSE (cm2/gr) | ||
| GB | 0.9320 | 2.070 | 3.544 | 2.863 | 0.9469 | 107.853 | 4.068 | 136.508 |
| RR | 0.9396 | 1.657 | 2.702 | 2.695 | 0.9726 | 77.068 | 2.848 | 98.028 |
| SVR | 0.9885 | 0.878 | 1.541 | 1.175 | 0.9769 | 74.420 | 2.738 | 89.929 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaya, Y.; Kobya, V.; Tabansiz-Goc, G.; Mardani, N.; Cavdur, F.; Mardani, A. Investigation of the Impact of Clinker Grinding Conditions on Energy Consumption and Ball Fineness Parameters Using Statistical and Machine Learning Approaches in a Bond Ball Mill. Materials 2025, 18, 3110. https://doi.org/10.3390/ma18133110
Kaya Y, Kobya V, Tabansiz-Goc G, Mardani N, Cavdur F, Mardani A. Investigation of the Impact of Clinker Grinding Conditions on Energy Consumption and Ball Fineness Parameters Using Statistical and Machine Learning Approaches in a Bond Ball Mill. Materials. 2025; 18(13):3110. https://doi.org/10.3390/ma18133110
Chicago/Turabian StyleKaya, Yahya, Veysel Kobya, Gulveren Tabansiz-Goc, Naz Mardani, Fatih Cavdur, and Ali Mardani. 2025. "Investigation of the Impact of Clinker Grinding Conditions on Energy Consumption and Ball Fineness Parameters Using Statistical and Machine Learning Approaches in a Bond Ball Mill" Materials 18, no. 13: 3110. https://doi.org/10.3390/ma18133110
APA StyleKaya, Y., Kobya, V., Tabansiz-Goc, G., Mardani, N., Cavdur, F., & Mardani, A. (2025). Investigation of the Impact of Clinker Grinding Conditions on Energy Consumption and Ball Fineness Parameters Using Statistical and Machine Learning Approaches in a Bond Ball Mill. Materials, 18(13), 3110. https://doi.org/10.3390/ma18133110






