Dynamic Statistical Mechanics Modeling of Percolation Networks in Conductive Polymer Composites for Smart Sensor Applications
Abstract
1. Introduction
2. Materials and Methods
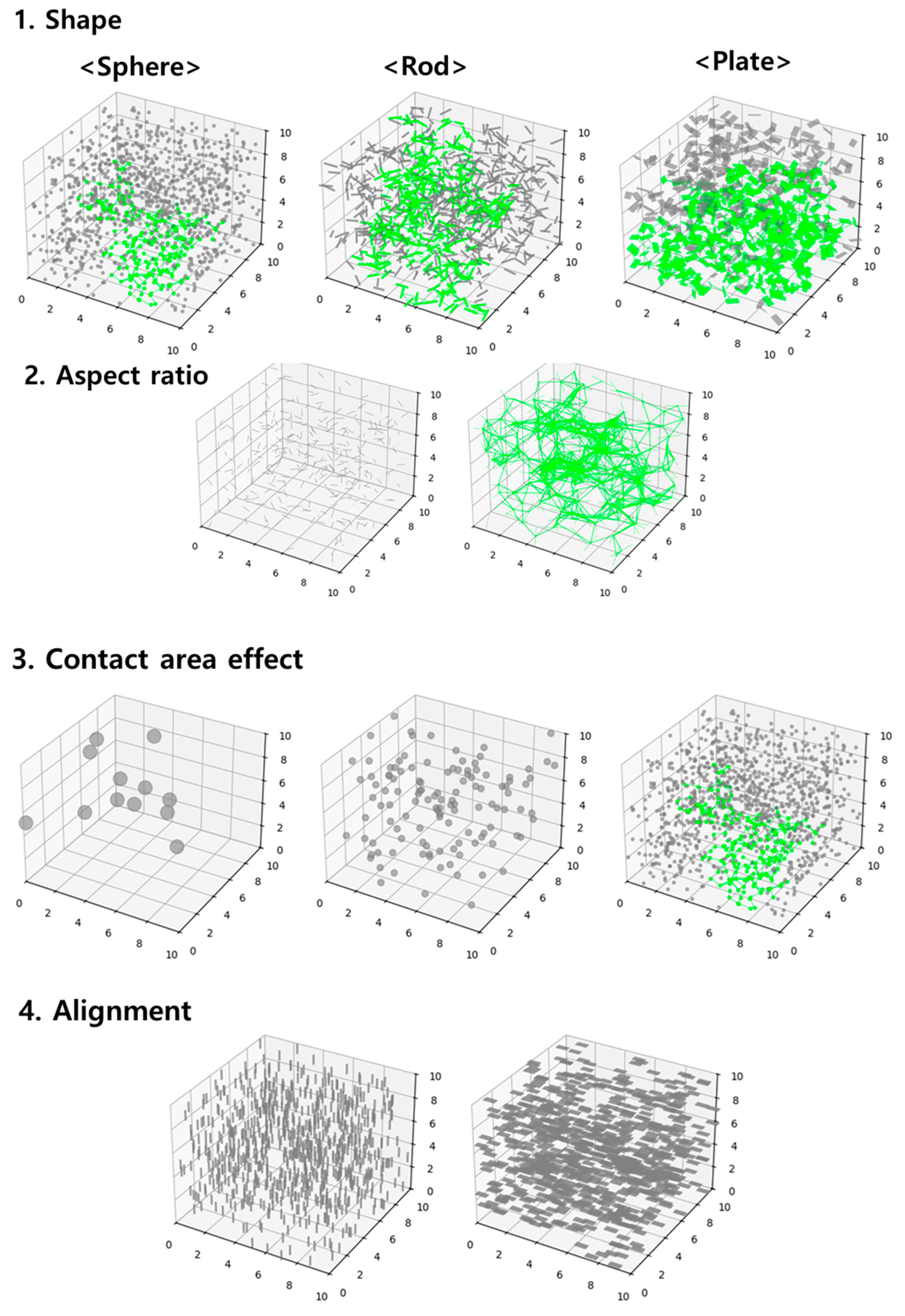
2.1. Statistical Mechanics Modeling
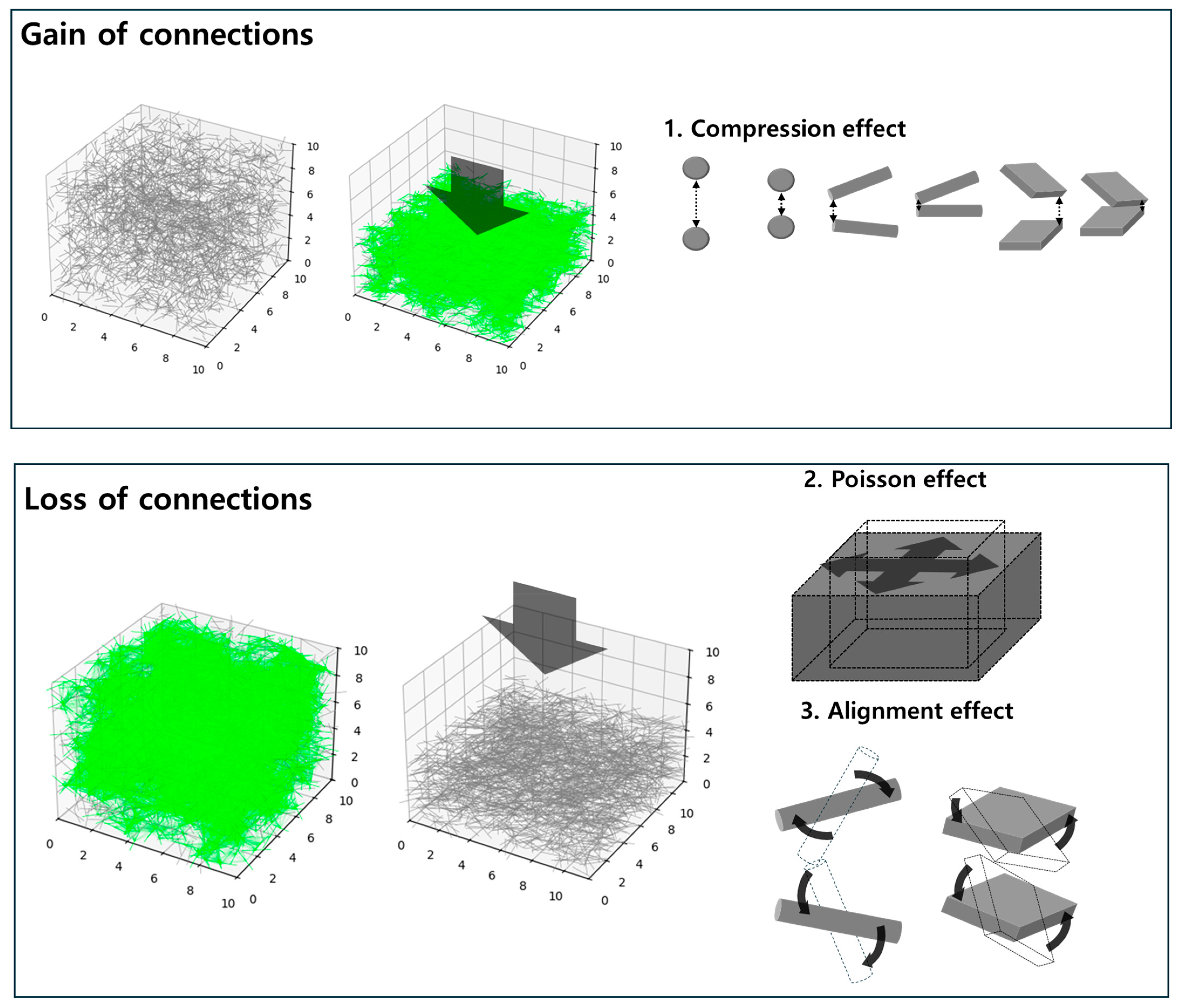
2.2. Dynamic Statistical Mechancis Modeling
2.3. Monte Carlo Computer Simulation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPC | Conductive Polymer Composite |
| AR | Aspect ratio |
References
- Chen, J.; Zhu, Y.; Huang, J.; Zhang, J.; Pan, D.; Zhou, J.; Ryu, J.E.; Umar, A.; Guo, Z. Advances in responsively conductive polymer composites and sensing applications. Polym. Rev. 2021, 61, 157–193. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, A.; Han, Y.; Li, T. Sensors based on conductive polymers and their composites: A review. Polym. Int. 2020, 69, 7–17. [Google Scholar] [CrossRef]
- Nambiar, S.; Yeow, J.T. Conductive polymer-based sensors for biomedical applications. Biosens. Bioelectron. 2011, 26, 1825–1832. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y. A review for conductive polymer piezoresistive composites and a development of a compliant pressure transducer. IEEE Trans. Instrum. Meas. 2012, 62, 495–502. [Google Scholar] [CrossRef]
- Hussain, M.; Choa, Y.; Niihara, K. Conductive rubber materials for pressure sensors. J. Mater. Sci. Lett. 2001, 20, 525–527. [Google Scholar] [CrossRef]
- Kanoun, O.; Bouhamed, A.; Ramalingame, R.; Bautista-Quijano, J.R.; Rajendran, D.; Al-Hamry, A. Review on conductive polymer/CNTs nanocomposites based flexible and stretchable strain and pressure sensors. Sensors 2021, 21, 341. [Google Scholar] [CrossRef] [PubMed]
- Ke, K.; McMaster, M.; Christopherson, W.; Singer, K.D.; Manas-Zloczower, I. Highly sensitive capacitive pressure sensors based on elastomer composites with carbon filler hybrids. Compos. Part A: Appl. Sci. Manuf. 2019, 126, 105614. [Google Scholar] [CrossRef]
- Joseph, J.; Munda, P.R.; Kumar, M.; Sidpara, A.M.; Paul, J. Sustainable conducting polymer composites: Study of mechanical and tribological properties of natural fiber reinforced PVA composites with carbon nanofillers. Polym. -Plast. Technol. Mater. 2020, 59, 1088–1099. [Google Scholar] [CrossRef]
- Lv, K.; Tian, G.; Yan, Y.; Zhou, H.; Fan, Q.; Liang, L.; Liu, N.; Wang, D.; Song, Z.; Xu, F. Stretchable carbon nanotube/Ecoflex conductive elastomer films toward multifunctional wearable electronics. Chem. Eng. J. 2024, 500, 157534. [Google Scholar] [CrossRef]
- Guler, Z.; Jackson, N. Mechanical Properties of Stretchable Multifunctional Ecoflex Composites for E-Skin Applications. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023; p. V012T013A020. [Google Scholar]
- Joshi, A.M.; Athawale, A.A. Electrically conductive silicone/organic polymer composites. Silicon 2014, 6, 199–206. [Google Scholar] [CrossRef]
- Sau, K.; Khastgir, D.; Chaki, T. Electrical conductivity of carbon black and carbon fibre filled silicone rubber composites. Die Angew. Makromol. Chem. 1998, 258, 11–17. [Google Scholar] [CrossRef]
- Lee, B.L. Electrically conductive polymer composites and blends. Polym. Eng. Sci. 1992, 32, 36–42. [Google Scholar] [CrossRef]
- Huang, J.C. Carbon black filled conducting polymers and polymer blends. Adv. Polym. Technol. J. Polym. Process. Inst. 2002, 21, 299–313. [Google Scholar] [CrossRef]
- Zhang, W.; Dehghani-Sanij, A.A.; Blackburn, R.S. Carbon based conductive polymer composites. J. Mater. Sci. 2007, 42, 3408–3418. [Google Scholar] [CrossRef]
- Halim, K.A.A.; Tee, H.W.; Badrul, F.; Salleh, M.A.A.M.; Osman, A.F.; Omar, M.F.; Zakaria, M.S. The effect of compatibiliser on the mechanical properties and electrical properties of polypropylene/carbon black (PP/CB) conductive polymer composites (CPCs). Mater. Today Proc. 2024, 109, 93–97. [Google Scholar] [CrossRef]
- Veeramuthu, L.; Venkatesan, M.; Benas, J.-S.; Cho, C.-J.; Lee, C.-C.; Lieu, F.-K.; Lin, J.-H.; Lee, R.-H.; Kuo, C.-C. Recent progress in conducting polymer composite/nanofiber-based strain and pressure sensors. Polymers 2021, 13, 4281. [Google Scholar] [CrossRef]
- Kim, S.-U.; Kim, J.-Y. Development of a Biomechanical Diagnosis and Analysis System Using a Textile Elbow Angle Sensor: Integrating Inverse Dynamics and Multi-Layer Perceptron Techniques. Processes 2025, 13, 748. [Google Scholar] [CrossRef]
- Rifa‘i, A.F.; Kaavessina, M.; Distantina, S. Mechanical, morphological, and electrical properties of polylactic acid-based conductive polymer composites through polyethylene glycol and carbon nanotubes integration. Period. Polytech. Chem. Eng. 2025, 69, 149–162. [Google Scholar] [CrossRef]
- Dubey, P.; Gupta, M.; Kundalwal, S. Conductive polymer nanocomposite incorporated with carbon nanotubes for effective electromagnetic interference shielding: A numerical study. Polym. Compos. 2024, 45, 3576–3590. [Google Scholar] [CrossRef]
- He, S.; Sun, X.; Zhang, H.; Yuan, C.; Wei, Y.; Li, J. Preparation strategies and applications of MXene-polymer composites: A review. Macromol. Rapid Commun. 2021, 42, 2100324. [Google Scholar] [CrossRef]
- Gong, K.; Zhou, K.; Qian, X.; Shi, C.; Yu, B. MXene as emerging nanofillers for high-performance polymer composites: A review. Compos. Part B Eng. 2021, 217, 108867. [Google Scholar] [CrossRef]
- Nezafat, Z.; Mirzaei, A.; Nasrollahzadeh, M.; Javanshir, S. Recent advances in MXene-based composite materials with conducting polymers for supercapacitors. J. Energy Storage 2024, 86, 111215. [Google Scholar] [CrossRef]
- Wang, M.; Gurunathan, R.; Imasato, K.; Geisendorfer, N.R.; Jakus, A.E.; Peng, J.; Shah, R.N.; Grayson, M.; Snyder, G.J. A percolation model for piezoresistivity in conductor–polymer composites. Adv. Theory Simul. 2019, 2, 1800125. [Google Scholar] [CrossRef]
- Shehzad, K.; Hussain, T.; Shah, A.T.; Mujahid, A.; Ahmad, M.N.; Sagar, R.U.R.; Anwar, T.; Nasir, S.; Ali, A. Effect of the carbon nanotube size dispersity on the electrical properties and pressure sensing of the polymer composites. J. Mater. Sci. 2016, 51, 11014–11020. [Google Scholar] [CrossRef]
- Bilotti, E.; Zhang, H.; Deng, H.; Zhang, R.; Fu, Q.; Peijs, T. Controlling the dynamic percolation of carbon nanotube based conductive polymer composites by addition of secondary nanofillers: The effect on electrical conductivity and tuneable sensing behaviour. Compos. Sci. Technol. 2013, 74, 85–90. [Google Scholar] [CrossRef]
- Huang, Y.; Xiang, B.; Ming, X.; Fu, X.; Ge, Y. Conductive mechanism research based on pressure-sensitive conductive composite material for flexible tactile sensing. In Proceedings of the 2008 International Conference on Information and Automation, Changsha, China, 20–23 June 2008; pp. 1614–1619. [Google Scholar]
- Shklovskii, B. Anisotropy of percolation conduction. Phys. Status Solidi 1978, 85, K111–K114. [Google Scholar] [CrossRef]
- Hu, Y.; Qi, H.; Yang, L.; Sheng, Y.; Xie, Y.; Ma, Q.; Shao, H.; Yu, W.; Li, D.; Dong, X. Flexible electrospun fluorescent anisotropic conductive Janus-typed nanoribbon membrane. Eur. Polym. J. 2022, 173, 111265. [Google Scholar] [CrossRef]
- Sadeghnejad, S.; Masihi, M.; King, P.; Shojaei, A.; Pishvaei, M. Effect of anisotropy on the scaling of connectivity and conductivity in continuum percolation theory. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2010, 81, 061119. [Google Scholar] [CrossRef]
- He, D.; Ekere, N. Effect of particle size ratio on the conducting percolation threshold of granular conductive–insulating composites. J. Phys. D Appl. Phys. 2004, 37, 1848. [Google Scholar] [CrossRef]
- Wu, N.; Wang, S. Conductivity percolation in carbon–carbon supercapacitor electrodes. J. Power Sources 2002, 110, 233–236. [Google Scholar] [CrossRef]
- Pan, Y.; Weng, G.; Meguid, S.; Bao, W.; Zhu, Z.-H.; Hamouda, A. Percolation threshold and electrical conductivity of a two-phase composite containing randomly oriented ellipsoidal inclusions. J. Appl. Phys. 2011, 110, 123715. [Google Scholar] [CrossRef]
- Chang, E.; Ameli, A.; Mark, L.H.; Park, C.B. Effects of uniaxial and biaxial orientation on fiber percolation in conductive polymer composites. In Proceedings of the AIP Conference Proceedings, Rodos, Greece, 23–29 September 2015. [Google Scholar]
- Lee, J.; Kwon, H.; Seo, J.; Shin, S.; Koo, J.H.; Pang, C.; Son, S.; Kim, J.H.; Jang, Y.H.; Kim, D.E. Conductive fiber-based ultrasensitive textile pressure sensor for wearable electronics. Adv. Mater. 2015, 27, 2433–2439. [Google Scholar] [CrossRef]
- Chang, E.; Ameli, A.; Alian, A.R.; Mark, L.H.; Yu, K.; Wang, S.; Park, C.B. Percolation mechanism and effective conductivity of mechanically deformed 3-dimensional composite networks: Computational modeling and experimental verification. Compos. Part B Eng. 2021, 207, 108552. [Google Scholar] [CrossRef]
- Kim, S.-U.; Kim, J.-Y. Characterizing Six Percolation Cases in Flexible Electronic Composites: A Monte Carlo-Based 3D Compressive Percolation Model for Wearable Pressure Sensors. Materials 2025, 18, 685. [Google Scholar] [CrossRef]
- Flandin, L.; Brechet, Y.; Cavaillé, J.-Y. Electrically conductive polymer nanocomposites as deformation sensors. Compos. Sci. Technol. 2001, 61, 895–901. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, L.; Wang, R.; Zhang, S.; Fu, L.; Li, M.; Xiao, Q. Advances in Monte Carlo Method for Simulating the Electrical Percolation Behavior of Conductive Polymer Composites with a Carbon-Based Filling. Polymers 2024, 16, 545. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, W.; Hu, D.; Xu, W. Percolation threshold and excluded volume of overlapping spherotetrahedral particle systems: Shape evolution from tetrahedron to sphere. Powder Technol. 2022, 408, 117713. [Google Scholar] [CrossRef]
- Smoluchowski, M. Drei vorträge über diffusion, brownsche molekularbewegung und koagulation von kolloidteilchen. Pisma Marian. Smoluchowskiego 1927, 2, 530–594. [Google Scholar]
- Bunde, A.; Dieterich, W. Percolation in composites. J. Electroceramics 2000, 5, 81–92. [Google Scholar] [CrossRef]
- Radzuan, N.A.M.; Sulong, A.B.; Sahari, J. A review of electrical conductivity models for conductive polymer composite. Int. J. Hydrog. Energy 2017, 42, 9262–9273. [Google Scholar] [CrossRef]
- Lei, C.; Xie, Z.; Wu, K.; Fu, Q. Controlled vertically aligned structures in polymer composites: Natural inspiration, structural processing, and functional application. Adv. Mater. 2021, 33, 2103495. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Wang, X.; Zhang, Y.; Zhou, M.; Hao, Y.; Jia, Z. Tuning dielectric/mechanical performance of polymeric composites for flexible electronics based on electric field-driven configurational entropy change: High throughput simulation and application. Compos. Commun. 2023, 38, 101513. [Google Scholar] [CrossRef]
- Williams, K.O. Modelling Electrical Transport in Nano-Particle Composites Using 3D Network Analysis. Master’s Thesis, University of British Columbia, Vancouver, Canada, 2014. [Google Scholar]
- Bocharov, G.S.; Eletskii, A.V. Percolation conduction of carbon nanocomposites. Int. J. Mol. Sci. 2020, 21, 7634. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Choi, S.; Oh, E.; Byun, J.; Kim, H.; Lee, B.; Lee, S.; Hong, Y. Revisit to three-dimensional percolation theory: Accurate analysis for highly stretchable conductive composite materials. Sci. Rep. 2016, 6, 34632. [Google Scholar] [CrossRef]
- Wu, H.; Ma, R.; Wang, Y.; Zhao, X.; Zhang, L.; Gao, Y. Manipulating the percolated network of nanorods in polymer matrix by adding non-conductive nanospheres: A molecular dynamics simulation. Compos. Sci. Technol. 2022, 229, 109694. [Google Scholar] [CrossRef]

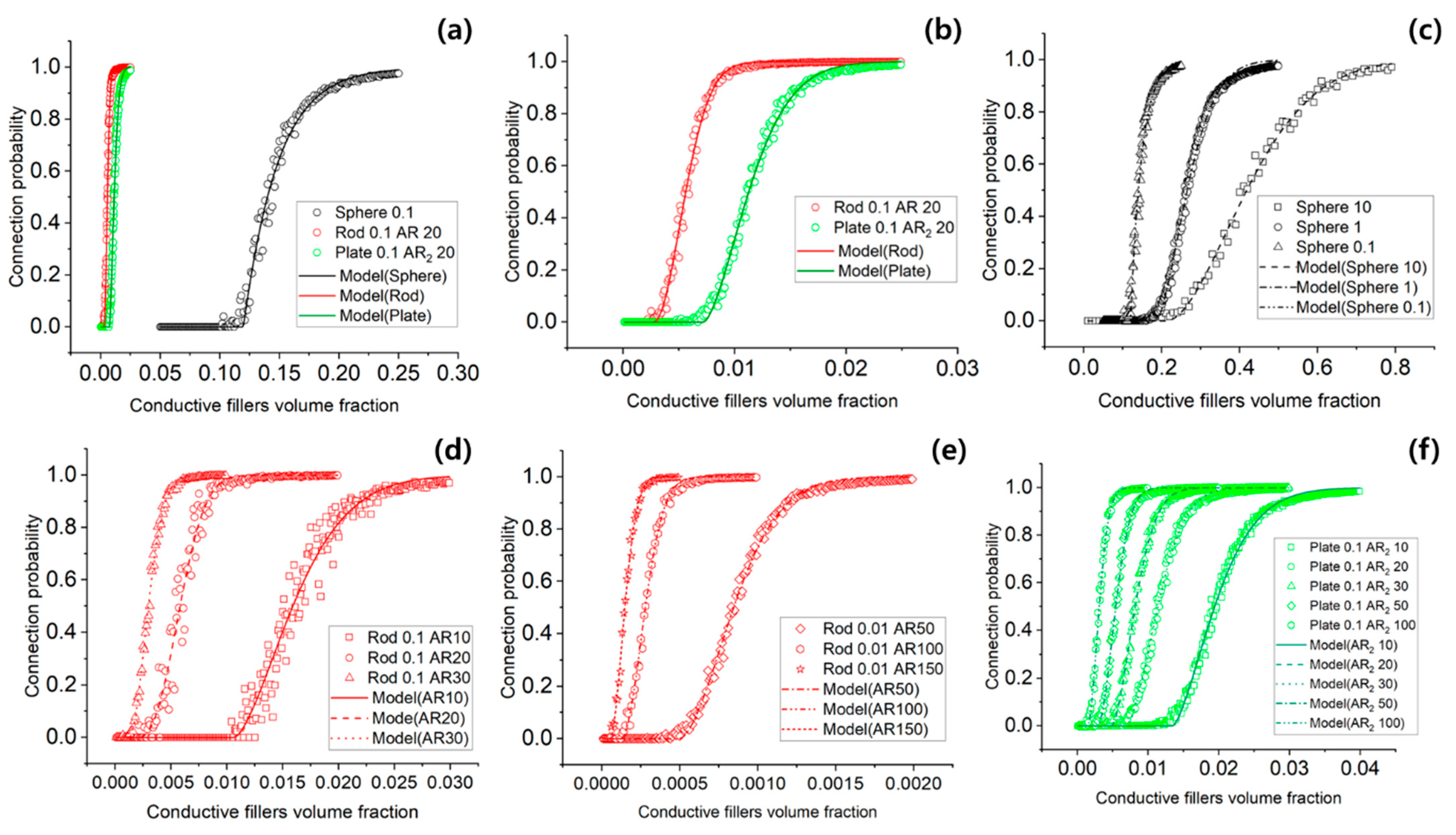
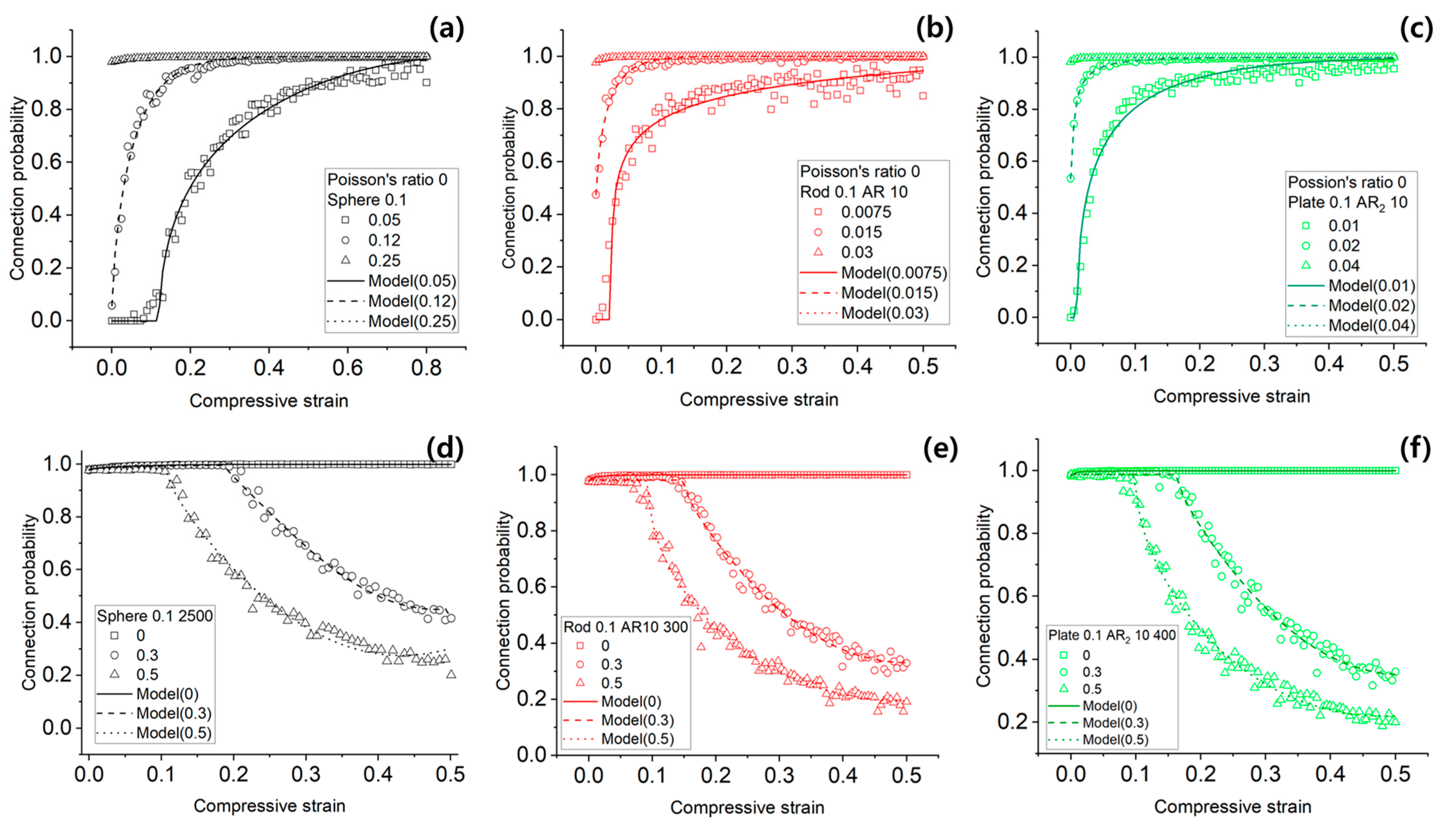
| AR (AR2) | RMSE | |||
|---|---|---|---|---|
| Sphere/0.1 | 1.02 | 1.54 | 0.11965 | 0.0308 |
| Sphere/1 | 1.6 | 2.33 | 0.18539 | 0.0394 |
| Sphere/10 | 1.73 | 2.96 | 0.2148 | 0.021 |
| Rod/0.1/10 | 1.55 | 2.78 | 0.01066 | 0.0449 |
| Rod/0.1/20 | 2.41 | 4.39 | 0.00203 | 0.0302 |
| Rod/0.1/30 | 1.86 | 3.7 | 0.00126 | 0.0163 |
| Rod/0.01/50 | 1.73 | 3.33 | 0.0005 | 0.0177 |
| Rod/0.01/100 | 1.95 | 3.93 | 0.00012 | 0.0191 |
| Rod/0.01/150 | 1.86 | 3.84 | 0.00005 | 0.0192 |
| Plate/0.1/10 | 1.5 | 1.46 | 0.01344 | 0.0194 |
| Plate/0.1/20 | 1.8 | 1.59 | 0.00669 | 0.0188 |
| Plate/0.1/30 | 1.71 | 1.48 | 0.00479 | 0.0145 |
| Plate/0.1/50 | 1.86 | 1.54 | 0.00283 | 0.0149 |
| Plate/0.1/100 | 1.85 | 1.46 | 0.00142 | 0.0179 |
| /AR(AR2) | RMSE | |||
|---|---|---|---|---|
| Sphere/0.05 | 0.51 | 0.003 | 0.00738 | 0.0346 |
| Sphere/0.12 | 0.768 | 1.566 | 0 | 0.0188 |
| Sphere/0.25 | 0.828 | 1.461 | 0 | 0.0004 |
| Rod/0.0075/10 | 0.321 | 0.712 | 0.00015 | 0.0421 |
| Rod/0.015/10 | 0.38 | 1.361 | 0.00014 | 0.0127 |
| Rod/0.03/10 | 0.494 | 1.467 | 0.00008 | 0.0004 |
| Rod/0.01/10 | 0.515 | 1.362 | 0.0001 | 0.0346 |
| Rod/0.02/10 | 0.447 | 1.356 | 0.00006 | 0.0035 |
| Rod/0.04/10 | 0.371 | 1.246 | 0.00016 | 0.0002 |
| /AR(AR2) | RMSE | ||||
|---|---|---|---|---|---|
| Sphere/0.25 | 0 | - | - | - | 0.0004 |
| 0.3 | 0.294 | - | 0.11636 | 0.0188 | |
| 0.5 | 0.248 | - | 0.10914 | 0.0253 | |
| Rod/0.03/10 | 0 | - | - | - | 0.0421 |
| 0.3 | 0.276 | 0.326 | 0.09246 | 0.0215 | |
| 0.5 | 0.161 | 0.155 | 0.09701 | 0.025 | |
| Rod/0.04/10 | 0 | - | - | - | 0.0002 |
| 0.3 | 0.251 | 0.294 | 0.10143 | 0.0238 | |
| 0.5 | 0.154 | 0.157 | 0.10285 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-U.; Kim, J.-Y. Dynamic Statistical Mechanics Modeling of Percolation Networks in Conductive Polymer Composites for Smart Sensor Applications. Materials 2025, 18, 3097. https://doi.org/10.3390/ma18133097
Kim S-U, Kim J-Y. Dynamic Statistical Mechanics Modeling of Percolation Networks in Conductive Polymer Composites for Smart Sensor Applications. Materials. 2025; 18(13):3097. https://doi.org/10.3390/ma18133097
Chicago/Turabian StyleKim, Sang-Un, and Joo-Yong Kim. 2025. "Dynamic Statistical Mechanics Modeling of Percolation Networks in Conductive Polymer Composites for Smart Sensor Applications" Materials 18, no. 13: 3097. https://doi.org/10.3390/ma18133097
APA StyleKim, S.-U., & Kim, J.-Y. (2025). Dynamic Statistical Mechanics Modeling of Percolation Networks in Conductive Polymer Composites for Smart Sensor Applications. Materials, 18(13), 3097. https://doi.org/10.3390/ma18133097







