General Prediction of Interface Chemical Bonding at Metal–Oxide Interface with the Interface Reaction Considered
Abstract
1. Introduction
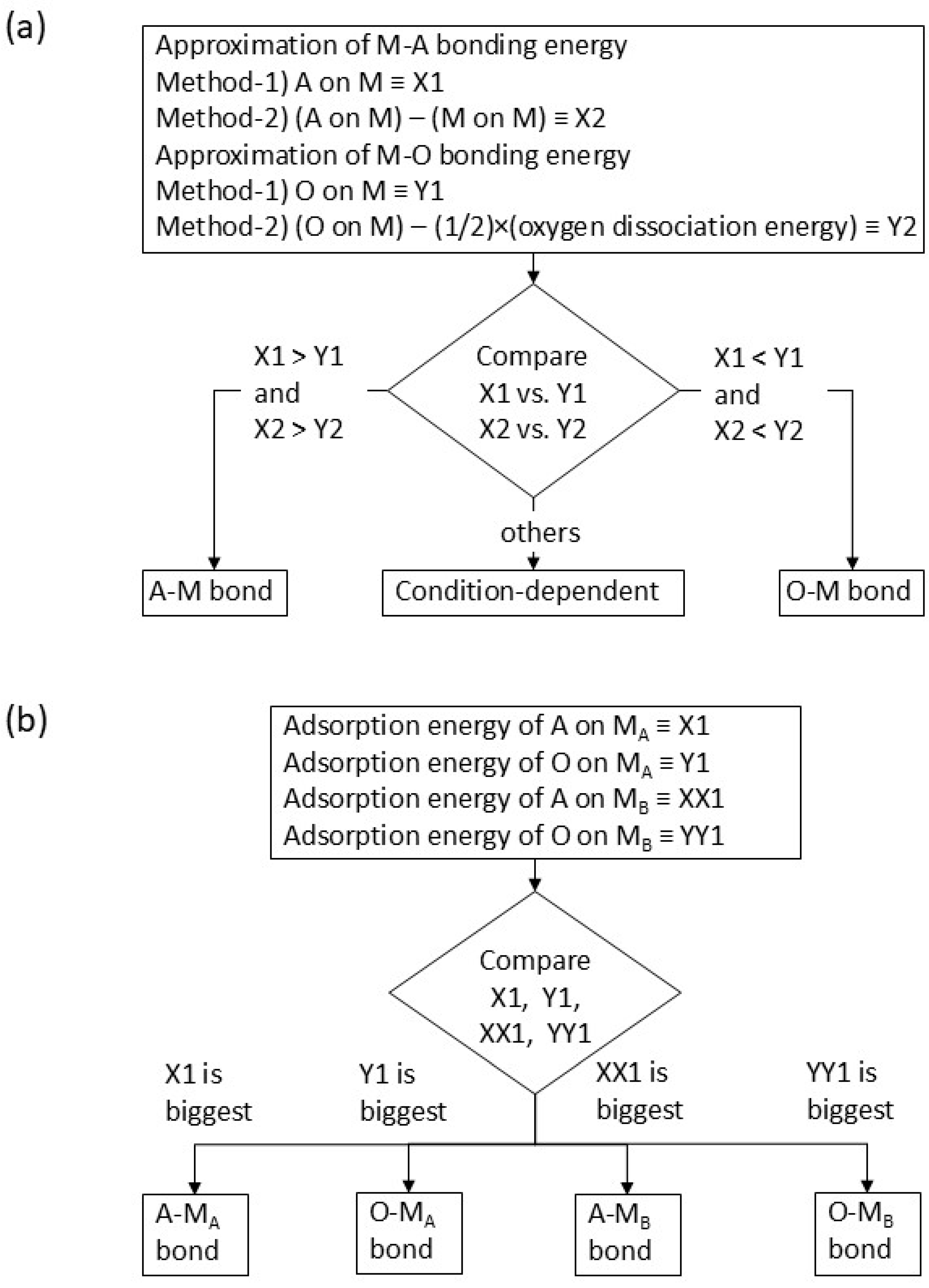
2. Overview of the Prediction Method Without an Interface Reaction
− {chemical potential of (M-A-O—) at the standard condition}
− {half of oxygen chemical potential at the standard condition}
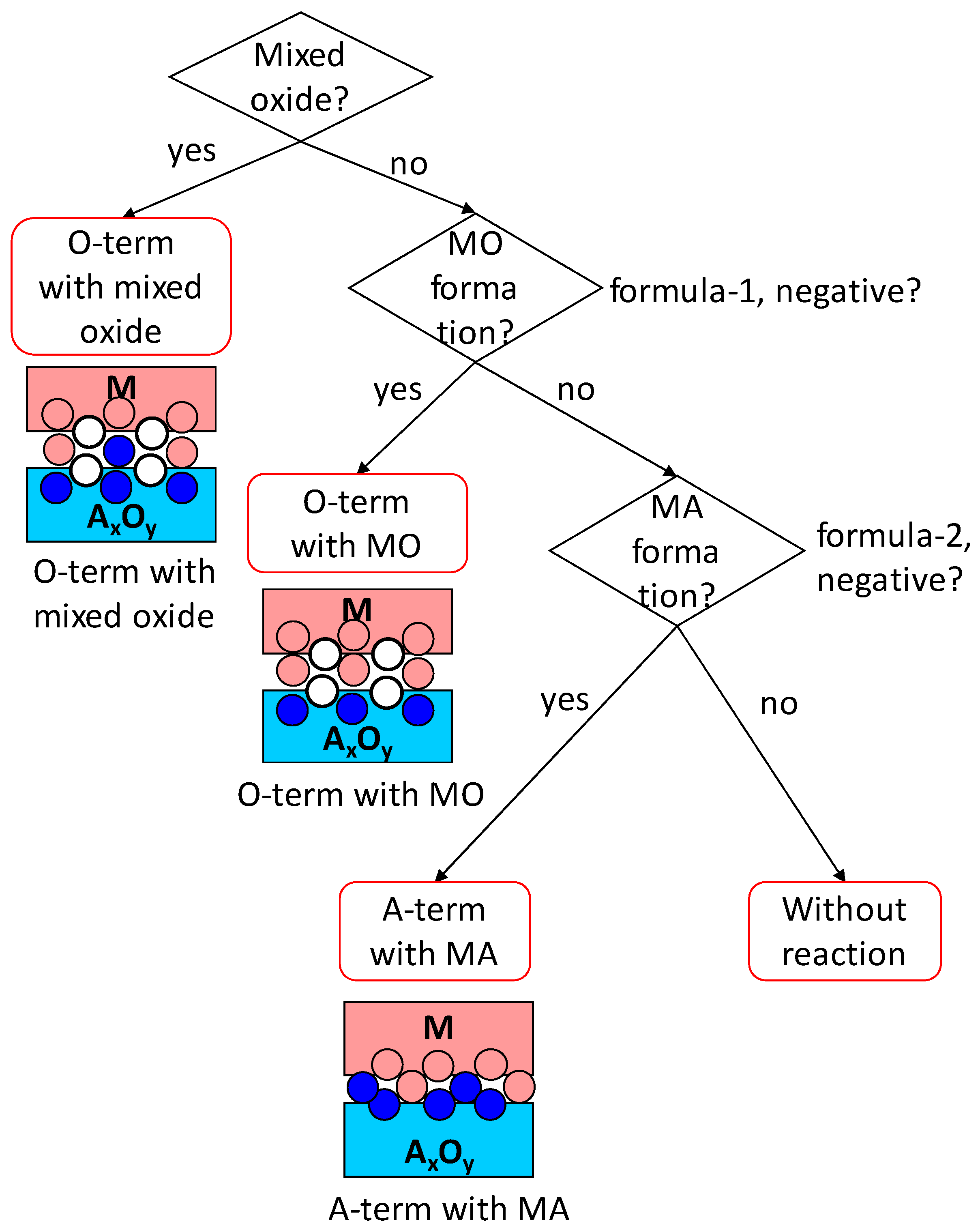
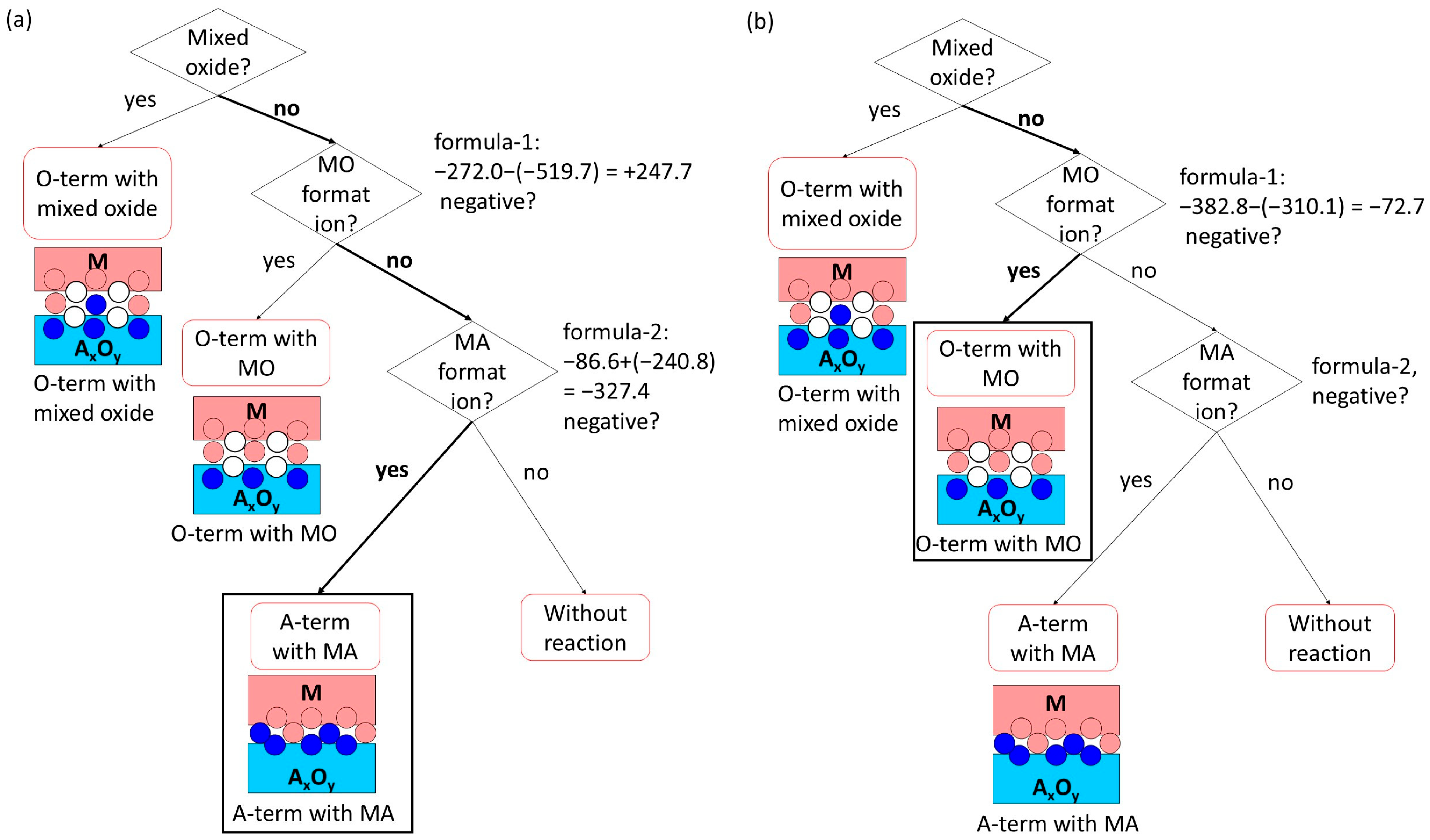
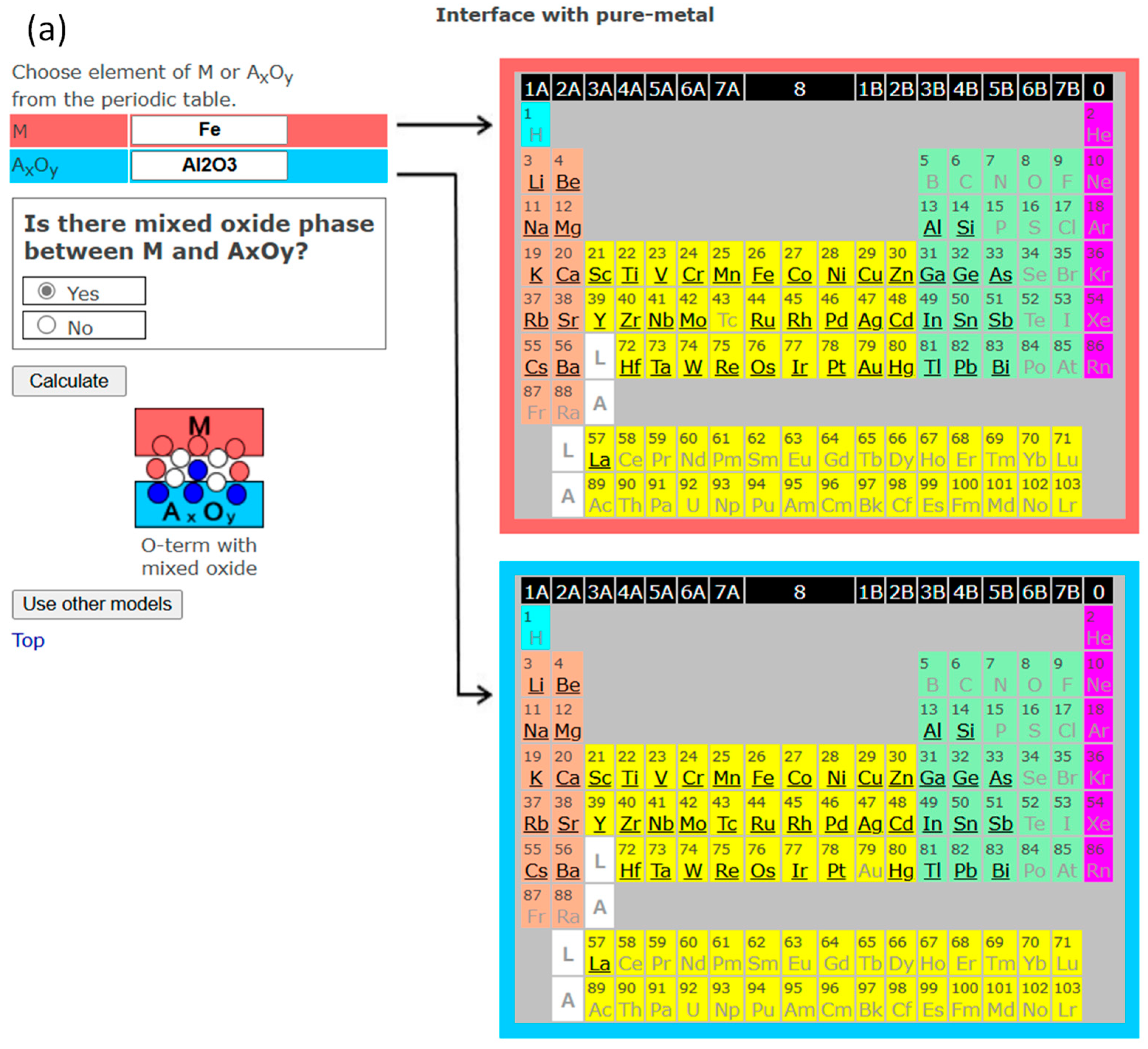
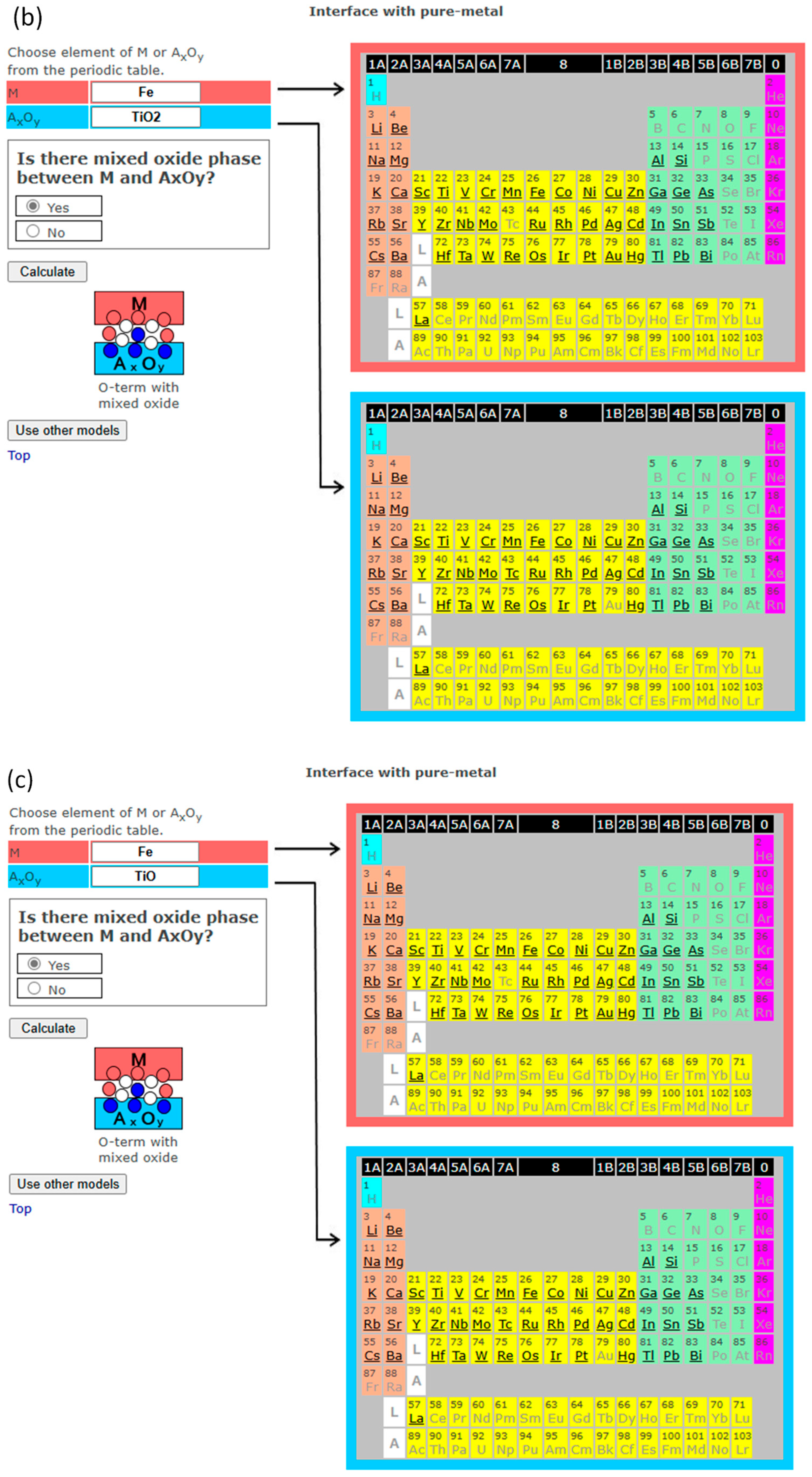
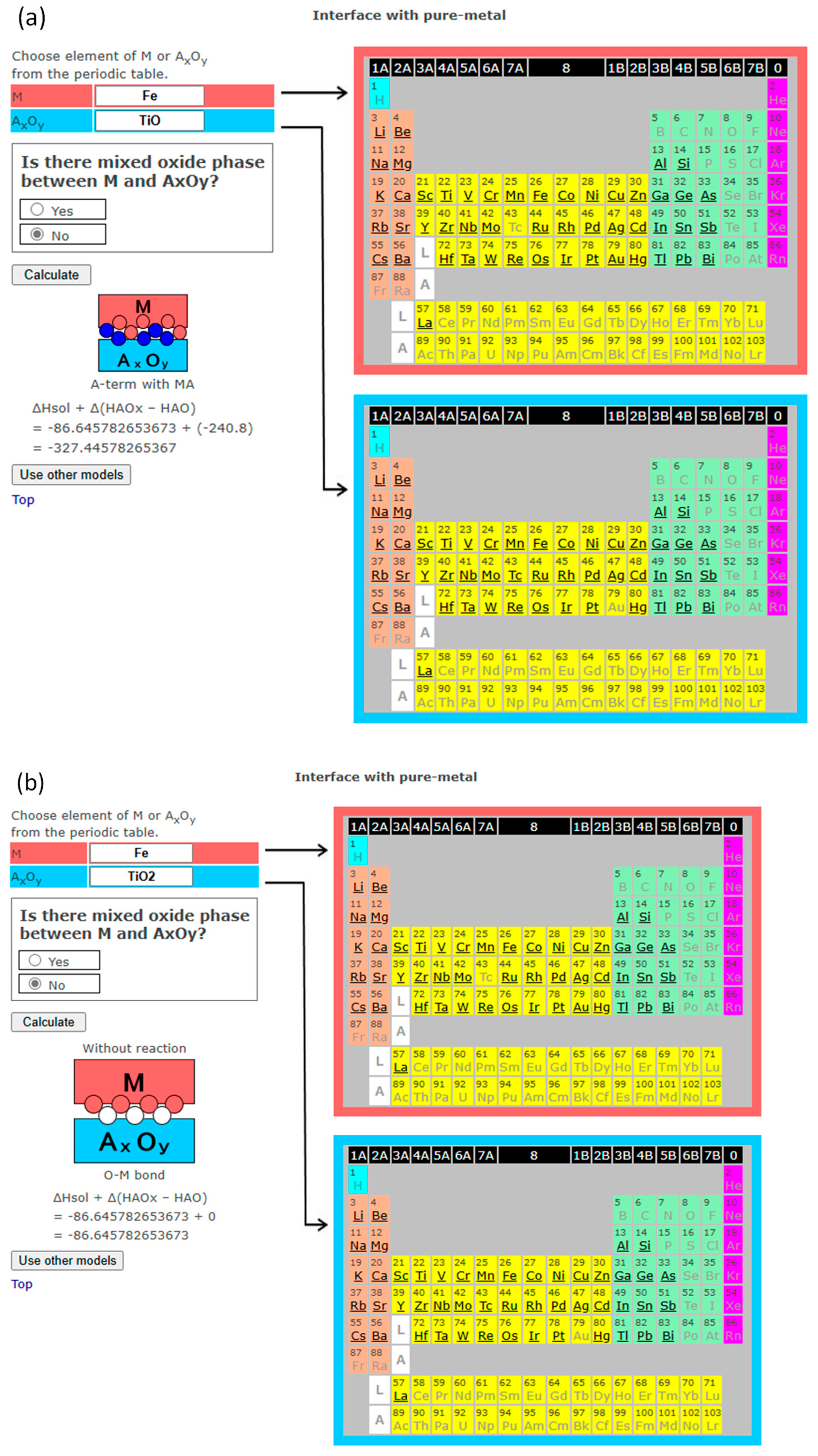
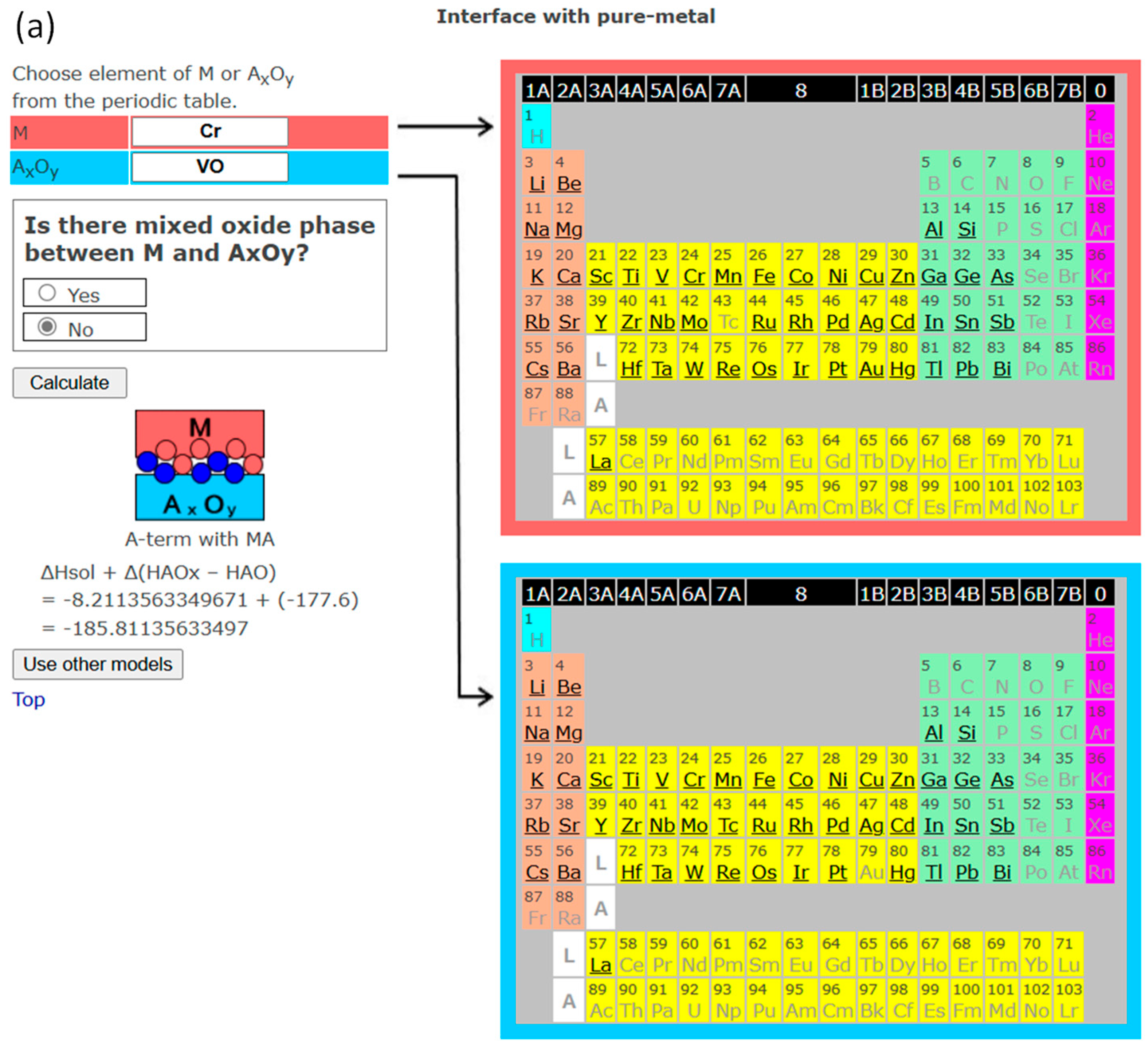
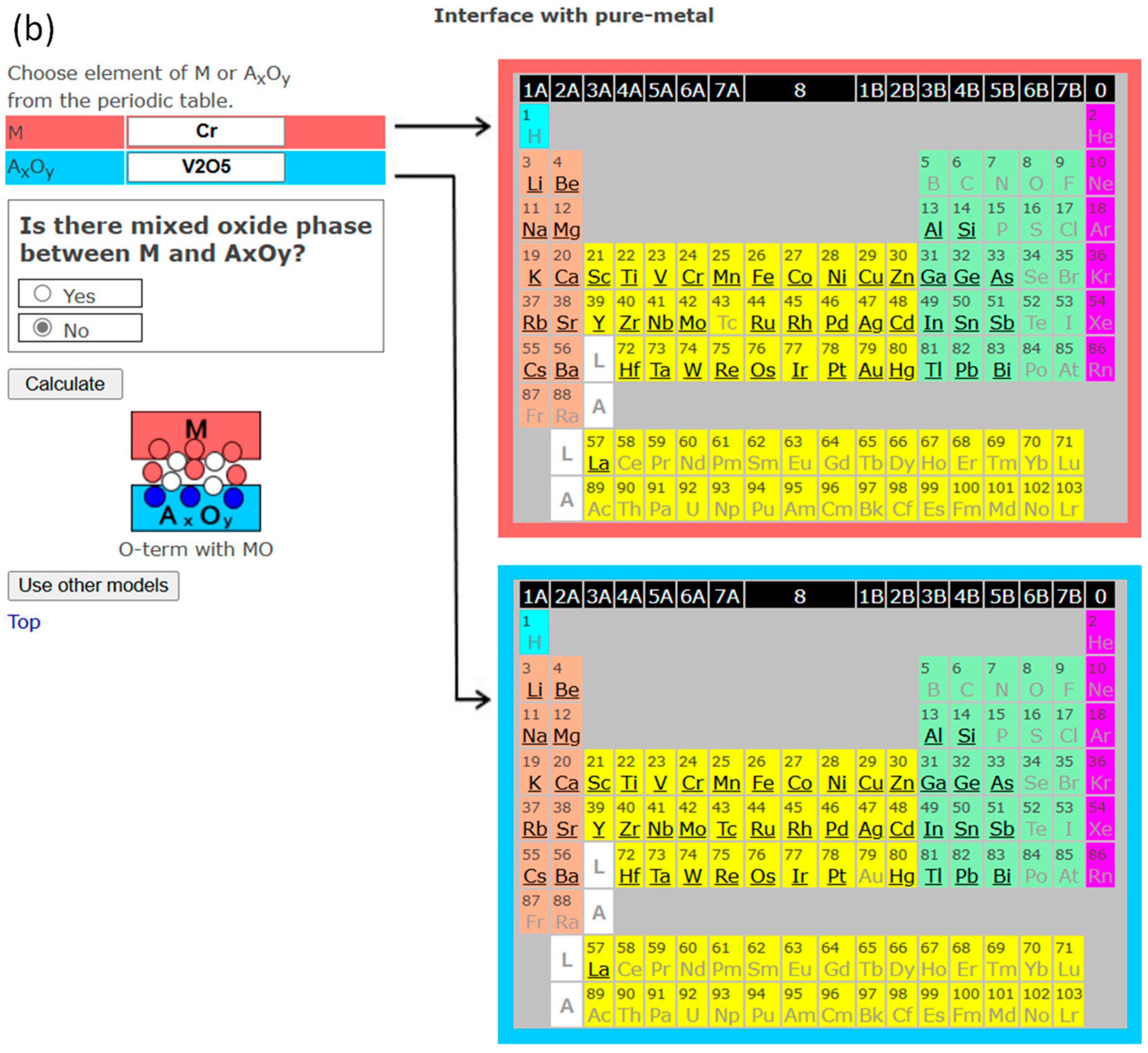
3. Interface Bonding with Interface Reaction Considered
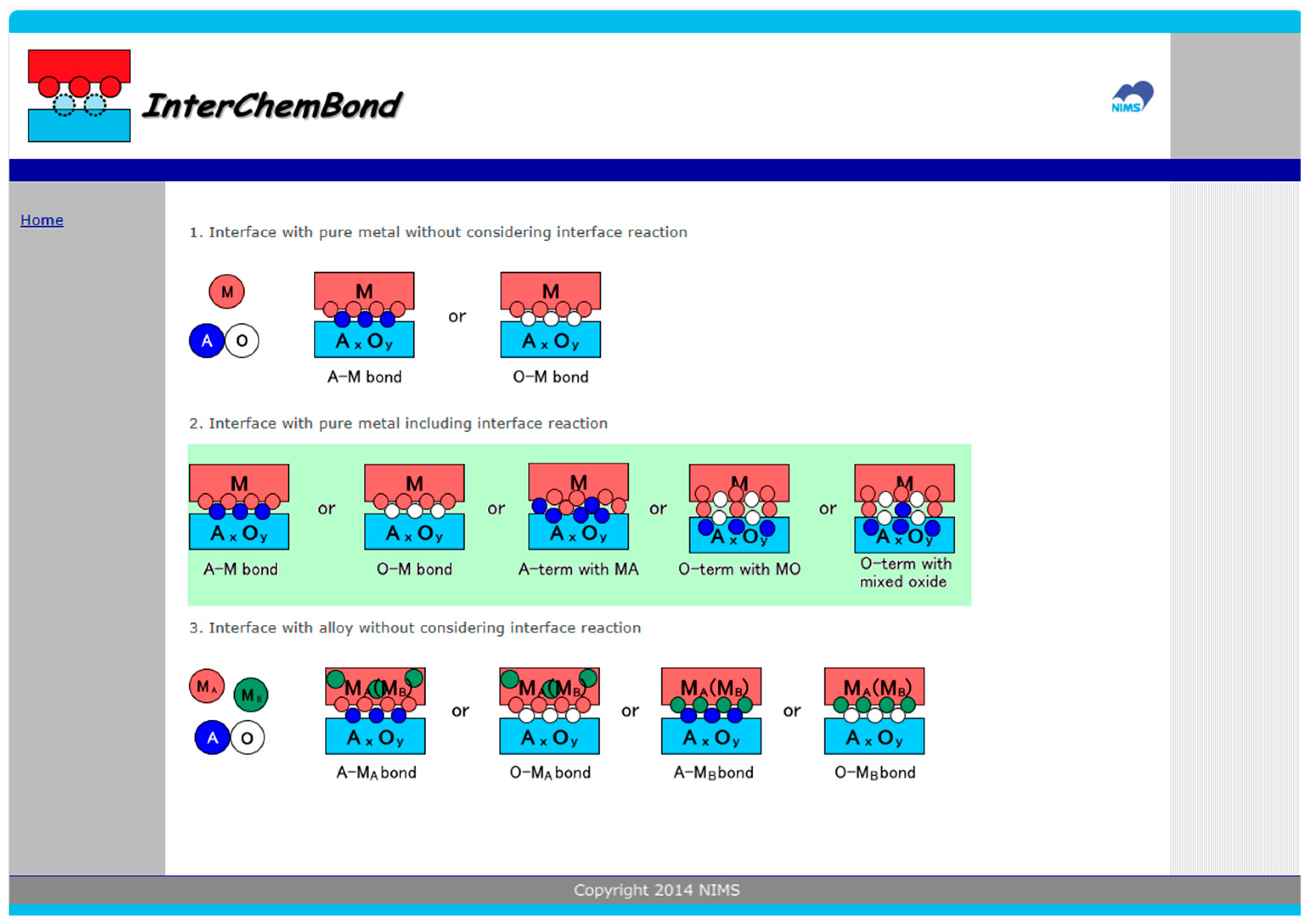
4. InterChemBond: Prediction Software
5. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alber, U.; Mullejans, H.; Ruhle, M. Wetting of copper on α-Al2O3 surfaces depending on the orientation and oxygen partial pressure. Micron 1999, 30, 101–108. [Google Scholar] [CrossRef]
- Merlin, V.; Eustathopoulos, N. Wetting and adhesion of Ni-Al alloys on α-Al2O3 single crystals. J. Mater. Sci. 1995, 30, 3619–3624. [Google Scholar] [CrossRef]
- Chatain, D.; Chabert, F.; Ghetta, V.; Fouletier, J. New experimental setup for wettability characterization under monitored oxygen activity: II, wettability of sapphire by silver-oxygen melts. J. Am. Ceram. Soc. 1994, 77, 197–201. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. First-principles study of the tensile strength and failure of α-Al2O3(0001)/Ni(111) interfaces. Phys. Rev. B 2007, 76, 075431. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. First-principles investigation of the atomic and electronic structures of α-Al2O3(0001)/Ni(111) interfaces. J. Am. Ceram. Soc. 2007, 90, 2429–2440. [Google Scholar] [CrossRef]
- Shi, S.; Tanaka, S.; Kohyama, M. Influence of interface structure on Schottky barrier heights of α-Al2O3 (0001)/Ni (111) interfaces: A first-principles study. Mater. Trans. 2006, 47, 2696–2700. [Google Scholar] [CrossRef]
- Shiraishi, K.; Nakayama, T.; Nakaoka, T.; Ohta, A.; Miyazaki, S. Theory of metal/dielectric interfaces-breakdown of Schottky barrier limits. ECS Trans. 2008, 13, 21–27. [Google Scholar] [CrossRef]
- Nagata, T.; Ahmet, P.; Yoo, Y.Z.; Yamada, K.; Tsutsui, K.; Wada, Y.; Chikyow, T. Schottky metal library for ZNO-based UV photodiode fabricated by the combinatorial ion beam-assisted deposition. Appl. Surf. Sci. 2006, 252, 2503–2506. [Google Scholar] [CrossRef]
- Asthagiri, A.; Niederberger, C.; Francis, A.J.; Porter, L.M.; Salvador, P.A.; Sholl, D.S. Thin Pt films on the polar SrTiO3 (1 1 1) surface: An experimental and theoretical study. Surf. Sci. 2003, 537, 134–152. [Google Scholar] [CrossRef]
- Yoshitake, M.; Nemsak, S.; Skala, T.; Tsud, N.; Kim, T.; Matolin, V.; Prince, K.C. Modification of terminating species and band alignment at the interface between alumina films and metal single crystals. Surf. Sci. 2010, 604, 2150–2156. [Google Scholar] [CrossRef]
- Ip, K.; Thaler, G.T.; Yang, H.; Han, S.Y.; Li, Y.; Norton, D.P.; Pearton, S.J.; Jang, S.; Ren, F. Contacts to ZnO. J. Cryst. Growth 2006, 287, 149–156. [Google Scholar] [CrossRef]
- Young, S.J.; Ji, L.W.; Chang, S.J.; Su, Y.K. ZnO metal–semiconductor–metal ultraviolet sensors with various contact electrodes. J. Cryst. Growth 2006, 293, 43–47. [Google Scholar] [CrossRef]
- Lin, T.K.; Chang, S.J.; Su, Y.K.; Huang, B.R.; Fujita, M.; Horikoshi, Y. ZnO MSM photodetectors with Ru contact electrodes. J. Cryst. Growth 2005, 281, 513–517. [Google Scholar] [CrossRef]
- Tesler, A.B.; Maoz, B.M.; Feldman, Y.; Vaskevich, A.; Rubinstein, I. Solid-state thermal dewetting of just-percolated gold films evaporated on glass: Development of the morphology and optical properties. J. Phys. Chem. C 2013, 117, 11337–11346. [Google Scholar] [CrossRef]
- Yoshitake, M.; Yagyu, S.; Chikyow, T. Novel method for the prediction of an interface bonding species at alumina/metal interfaces. J. Vac. Sci. Technol. A 2014, 32, 021102. [Google Scholar] [CrossRef]
- Yoshitake, M.; Yagyu, S.; Chikyow, T. A numerical formula for general prediction of interface bonding between alumina and aluminum-containing alloys. Int. J. Met. 2014, 2014, 120840. [Google Scholar] [CrossRef]
- Yoshitake, M. General method for predicting ZnO–metal interface termination: Extension of the method for Al2O3–metal systems. J. Vac. Sci. Technol. A 2021, 39, 063217. [Google Scholar] [CrossRef]
- Yoshitake, M. General method for predicting interface bonding at various oxide–metal interfaces. Surfaces 2024, 7, 414–427. [Google Scholar] [CrossRef]
- InterChemBond. Available online: https://interchembond.nims.go.jp (accessed on 28 April 2025).
- Miedema, A.R.; Dorleijn, J.W.F. Quantitative predictions of the heat of adsorption of metals on metallic substrates. Surf. Sci. 1980, 95, 447–464. [Google Scholar] [CrossRef]
- SurfSeg. Available online: https://surfseg.nims.go.jp (accessed on 3 April 2024).
- Yoshitake, M. Prediction of influence of oxygen in annealing atmosphere on surface segregation behavior in layered materials. Jpn. J. Appl. Phys. 2012, 51, 085601. [Google Scholar] [CrossRef]
- Brix, P.; Herzberg, G. Fine structure of the Schumann-Runge bands near the convergence limit and the dissociation energy of the oxygen molecule. Can. J. Phys. 1954, 32, 110–135. [Google Scholar] [CrossRef]
- Aller, H.T.; Yu, X.; Wise, A.; Howell, R.S.; Gellman, A.J.; McGaughey, A.J.H.; Malen, J.A. Chemical reactions impede thermal transport across metal/β-Ga2O3 interfaces. Nano Lett. 2019, 19, 8533–8538. [Google Scholar] [CrossRef] [PubMed]
- Cuculescu, E.; Evtodiev, I.; Caraman, M. Non-equilibrium charge carriers generation—Recombination mechanisms at the interface of the SnO2/GaSe heterojunction. Thin Solid Films 2009, 517, 2515–2518. [Google Scholar] [CrossRef]
- Di, L.; Li, Z.; Park, D.W.; Lee, B.; Zhang, X. Atmospheric-pressure cold plasma for synthesizing Pd/FeOx catalysts with enhanced low-temperature CO oxidation activity. Jpn. J. Appl. Phys. 2017, 56, 060301. [Google Scholar] [CrossRef]
- Ozer, O.; Missiaen, J.-M.; Laya, S.; Mitteau, R. Processing of tungsten/copper materials from W–CuO powder mixtures. Mater. Sci. Eng. A 2007, 460–461, 525–531. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Schmid Fetzer, R. Aluminium-iron-oxygen. ternary alloys. VCH 1992, 5, 325–353. [Google Scholar]
- Fujimura, T.; Tanaka, S.I. In-situ high temperature X-ray diffraction study of Fe/Al2O3 interface reactions. J. Mater. Sci. 1999, 34, 425–429. [Google Scholar] [CrossRef]
- Holdaway, M.J.; Mukhopadhyay, B. Geothermobarometry in pelitic schists: A rapidly evolving field. Am. Mineral. 1993, 78, 681–693. [Google Scholar]
- Raghavan, V. The Fe-O-Ti (iron-oxygen-titanium) system. phase diagrams ternary iron alloys. Indian Inst. Met. 1989, 5, 300–325. [Google Scholar]
- Pan, J.M.; Madey, T.E. Ultrathin Fe films on TiO2(110): Growth and reactivity. J. Vac. Sci. Technol. A 1993, 11, 1667–1674. [Google Scholar] [CrossRef]
- Cheshnitskii, S.M.; Foriev, A.A.; Sarat, L.L. Phase relationships in the V2O5-Cr2O3 system. Russ. J. Inorg. Chem. 1984, 29, 1547–1548. [Google Scholar]
| M | Al on M [kJ/mol-M] | (Al on M) − (M on M) [kJ/mol-M] | O on M [kJ/mol-O] | Al on Al | O on Al | Predicted Termination | Experimental Results from Reference | ||
|---|---|---|---|---|---|---|---|---|---|
| MB | X1 | X2 | Y1 | Y2 | XX1 | YY1 | |||
| Ti | 384 | 21 | 908.96 | 662.43 | - | - | O | O | |
| Ti | Al | 384 | 21 | 908.96 | 662.43 | 270 | 833.06 | O | Al, O |
| V | 400 | −1 | 788.34 | 541.8 | - | - | O | O | |
| Cr | 377 | 74 | 641.44 | 394.91 | - | - | O | O | |
| Fe | 392 | 76 | 528.65 | 282.12 | - | - | O | O | |
| Fe | Al | 392 | 76 | 528.65 | 282.12 | 270 | 833.06 | Al | Al |
| Co | 408 | 73 | 446.36 | 199.82 | - | - | O | O | |
| Ni | 407 | 67 | 409 | 162.46 | - | - | O | O | |
| Ni | Al | 407 | 67 | 409 | 162.46 | 270 | 833.06 | Al | Al |
| Cu | 332 | 67 | 346.47 | 99.93 | - | - | O | O | |
| Cu | Al | 332 | 67 | 346.47 | 99.93 | 270 | 833.06 | Al | Al |
| Nb | 409 | −173 | 913.07 | 666.54 | - | - | O | O | |
| Rh | 447 | 12 | 356.62 | 110.09 | - | - | Al, O | ||
| Pd | 413 | 130 | 295.06 | 48.53 | - | - | Al | ||
| Ag | 280 | 58 | 242.69 | −3.85 | - | - | Al | Al | |
| Ir | 474 | −61 | 429.98 | 183.45 | - | - | Al, O | ||
| Pt | 450 | 2 | 329.31 | 82.77 | - | - | Al, O | ||
| Au | 325 | 32 | <0 | <0 | - | - | Al |
| M | Zn on M [kJ/mol-M] | O on M [kJ/mol-O] | A on MB | O on MB | Predicted Termination | Experimental Results from References | Theory from Reference | |||
|---|---|---|---|---|---|---|---|---|---|---|
| MB | X1 | X2 | Y1 | Y2 | XX1 | YY1 | ||||
| Mg | 81 | −17 | 664.14 | 417.61 | - | - | O | O | ||
| Ti | 184 | −179 | 908.96 | 662.43 | - | - | O | O | ||
| V | 198 | −203 | 788.34 | 541.80 | - | - | O | |||
| Cr | 177 | −126 | 641.44 | 394.91 | - | - | O | O | ||
| Fe | 194 | −122 | 528.65 | 282.12 | - | - | O | O | ||
| Co | 212 | −123 | 446.36 | 199.82 | - | - | O | |||
| Ni | 211 | −129 | 409.00 | 162.46 | - | - | O | |||
| Cu | 152 | −113 | 346.47 | 99.93 | - | - | O | O | O | |
| Cu | Zn | 152 | −113 | 346.47 | 99.93 | 113 | 484.61 | Zn | Zn, O | |
| Ge | 85 | −212 | 648.70 | 402.17 | - | - | O | O | ||
| Nb | 205 | −377 | 913.07 | 666.54 | - | - | O | |||
| Pd | 221 | −62 | 295.06 | 48.53 | - | - | O | Zn | ||
| Ag | 104 | −118 | 242.69 | −3.85 | - | - | O | |||
| Ag | Zn | 104 | −118 | 242.69 | −3.85 | 113 | 484.61 | Zn | ||
| Pt | 256 | −192 | 329.31 | 82.77 | - | - | O | O | ||
| Au | 144 | −149 | <0 | <0 | - | - | Zn | Zn | Zn | |
| Oxide | Metal-A | Metal-B | Formation Enthalpy of Oxide [kJ/mol] | Formation Enthalpy of Oxide [kJ/mol-A] | Adsorption Energy [kJ/mol] | Prediction | Experiment | Theory | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AO | MA | MB | AonMA | OonMA | AonMA-MAonMA | OonMA-493.07/2 | AonMB | OonMB | |||||
| X1 | Y1 | X2 | Y2 | XX1 | YY1 | ||||||||
| MgO | Cu | 601.6 | 601.6 | 223 | 346.47 | −42 | 99.935 | - | - | O | O | O | |
| Cu | Ag | 223 | 346.47 | −42 | 99.935 | 160 | 242.69 | O-Cu | O | ||||
| Pd | 324 | 295.06 | 41 | 48.525 | - | - | Mg, O | O | O | ||||
| Ag | 160 | 242.69 | −62 | −3.845 | - | - | O | O | O | ||||
| Co | 291 | 446.36 | −44 | 199.825 | - | - | O | O | |||||
| Fe | 257 | 528.65 | −59 | 282.115 | - | - | O | O | |||||
| Ni | 295 | 409 | −45 | 162.465 | - | - | O | O | |||||
| Pt | 376 | 329.31 | −72 | 82.775 | - | - | Mg, O | O | |||||
| W | 307 | 836.67 | −388 | 590.135 | - | - | O | O | |||||
| SiO2 | Al | 910.7 | 910.7 | 359 | 833.06 | 89 | 586.525 | - | - | O | O | ||
| Au | 395 | <0 | 102 | <0 | - | - | Si | Si | |||||
| Cr2O3 | Ni | 1139.7 | 569.85 | 313 | 409 | −27 | 162.465 | - | - | O | O; O | ||
| Ga2O3 | Cr | 1089.1 | 544.55 | 363 | 641.44 | 136 | 394.905 | - | - | O | O | ||
| Y2O3 | Ge | 1905.3 | 952.65 | 389 | 648.7 | 92 | 402.165 | - | - | O | O | ||
| ZrO2 | Si | 1094.3 | 1094.32 | 476 | 885.15 | 117 | 638.615 | O | O | ||||
| Fe | 588 | 528.65 | 272 | 282.115 | - | - | Zr, O | O | |||||
| Co | 622 | 446.36 | 287 | 199.825 | - | - | Zr | O | |||||
| Ni | 629 | 409 | 289 | 162.465 | - | - | Zr | O; Zr | Zr, O; O | ||||
| Cu | 529 | 346.47 | 264 | 99.935 | - | - | Zr | O | O | ||||
| Pd | 660 | 295.06 | 377 | 48.525 | - | - | Zr | Zr | |||||
| Au | 566 | <0 | 273 | <0–493.07/2 | Zr | Zr | |||||||
| CdO | Ag | 258.4 | 258.4 | 112 | 242.69 | −110 | −3.845 | - | - | O | O | O | |
| Ag | Au | 112 | 242.69 | −110 | −3.845 | 159 | <0 | O-Ag | Au-seg | ||||
| La2O3 | Ge | 1793.7 | 896.85 | 435 | 648.7 | 138 | 402.165 | - | - | O | O | ||
| Si | 459 | 885.15 | 100 | 638.615 | - | - | O | O; O | |||||
| HfO2 | Si | 1144.7 | 1144.7 | 444 | 885.15 | 85 | 638.615 | - | - | O | O, Hf | O | |
| Si | 444 | 885.15 | 85 | 638.615 | - | - | O | Hf, O | |||||
| Pt | 671 | 329.31 | 223 | 82.775 | O | Hf, O | |||||||
| Metal Component of Oxide | Oxide | Formation Enthalpy [kJ/mol-O] | Difference of Formation Enthalpy Between AO and A1−xO [kJ/mol-A] | Metal Component of Oxide | Oxide | Formation Enthalpy [kJ/mol-O] | Difference of Formation Enthalpy Between AO and A1−xO [kJ/mol-A] |
|---|---|---|---|---|---|---|---|
| Li | Li2O | −597.9 | - | Sr | SrO | −592.0 | - |
| Be | BeO | −580.1 | - | Y | Y2O3 | −635.1 | - |
| Na | Na2O | −414.2 | - | Zr | ZrO2 | −550.3 | - |
| Mg | MgO | −601.6 | - | Nb | Nb2O5 | −379.9 | - |
| Al | Al2O3 | −558.6 | - | NbO2 | −398.1 | −153.6 | |
| Si | SiO2 | −455.4 | - | NbO | −405.8 | −390.4 | |
| K | K2O | −361.5 | - | Mo | MoO3 | −248.4 | - |
| Ca | CaO | −634.9 | - | MoO2 | −294.5 | −156.2 | |
| Sc | Sc2O3 | −636.3 | - | Tc | Tc2O7 | −159.1 | - |
| Ti | TiO2 | −472.0 | - | TcO2 | −228.9 | −99.1 | |
| Ti3O5 | −491.9 | −124.2 | Ru | RuO2 | −152.5 | - | |
| Ti2O3 | −507.0 | −59.4 | Rh | Rh2O3 | −114.3 | - | |
| TiO | −519.7 | −240.8 | Pd | PdO | −85.4 | - | |
| V | V2O5 | −310.1 | - | Ag | Ag2O2 | −12.2 | - |
| V3O5 | −386.6 | −131.0 | Ag2O | −31.1 | 3.4 | ||
| V2O3 | −406.3 | −34.9 | Cd | CdO | −258.4 | - | |
| VO | −431.8 | −177.6 | In | In2O3 | −308.6 | - | |
| Cr | CrO2 | −299.0 | - | Sn | SnO2 | −288.8 | - |
| Cr2O3 | −379.9 | −28.2 | SnO | −280.7 | −296.9 | ||
| Cr3O4 | −382.8 | −59.5 | Sb | Sb2O3 | −240.1 | - | |
| Mn | MnO2 | −260.0 | - | Cs | Cs2O | −345.8 | - |
| Mn2O3 | −319.7 | −40.5 | Ba | BaO | −548.0 | - | |
| Mn3O4 | −347.0 | −16.9 | La | La2O3 | −597.9 | - | |
| MnO | −385.2 | −77.4 | Hf | HfO2 | −572.4 | - | |
| Fe | Fe2O3 | −274.7 | - | Ta | Ta2O5 | −409.2 | - |
| Fe3O4 | −279.6 | −39.3 | W | WO3 | −281.0 | - | |
| FeO | −272.0 | −100.8 | WO2 | −294.9 | −253.2 | ||
| Co | Co2O3 | −80.8 | - | Re | Re2O7 | −177.2 | - |
| Co3O4 | −222.8 | 175.9 | ReO3 | −204.8 | −5.8 | ||
| CoO | −237.9 | −59.1 | Os | OsO4 | −98.5 | - | |
| Ni | NiO | −240.1 | - | Ir | IrO2 | −137.1 | - |
| Cu | CuO | −157.3 | - | Ir2O3 | −67.5 | −173.0 | |
| Cu2O | −168.6 | −73.0 | Pt | PtO2 | −66.7 | - | |
| Zn | ZnO | −350.5 | - | PtO | −70.0 | −63.4 | |
| Ga | Ga2O3 | −363.0 | - | Au | 0.0 | - | |
| Ge | GeO2 | −290.0 | - | Hg | HgO | −90.8 | - |
| GeO | −261.9 | −318.1 | Tl | Tl2O3 | −131.0 | - | |
| As | As2O5 | −185.0 | - | Tl2O | −178.7 | −107.2 | |
| As2O3 | −444.9 | 204.9 | Pb | PbO2 | −138.7 | - | |
| Rb | RbO2 | −139.4 | - | Pb3O4 | −179.6 | −37.9 | |
| Rb2O2 | −236.0 | −42.8 | PbO | −219.0 | −20.5 | ||
| Rb2O | −339.0 | −66.5 | Bi | Bi2O3 | −191.3 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshitake, M. General Prediction of Interface Chemical Bonding at Metal–Oxide Interface with the Interface Reaction Considered. Materials 2025, 18, 3096. https://doi.org/10.3390/ma18133096
Yoshitake M. General Prediction of Interface Chemical Bonding at Metal–Oxide Interface with the Interface Reaction Considered. Materials. 2025; 18(13):3096. https://doi.org/10.3390/ma18133096
Chicago/Turabian StyleYoshitake, Michiko. 2025. "General Prediction of Interface Chemical Bonding at Metal–Oxide Interface with the Interface Reaction Considered" Materials 18, no. 13: 3096. https://doi.org/10.3390/ma18133096
APA StyleYoshitake, M. (2025). General Prediction of Interface Chemical Bonding at Metal–Oxide Interface with the Interface Reaction Considered. Materials, 18(13), 3096. https://doi.org/10.3390/ma18133096







