Contact Resistance Modeling Under Complex Wear Conditions Based on Fractal Theory
Abstract
1. Introduction
2. Experimental Methods
2.1. Experimental Materials
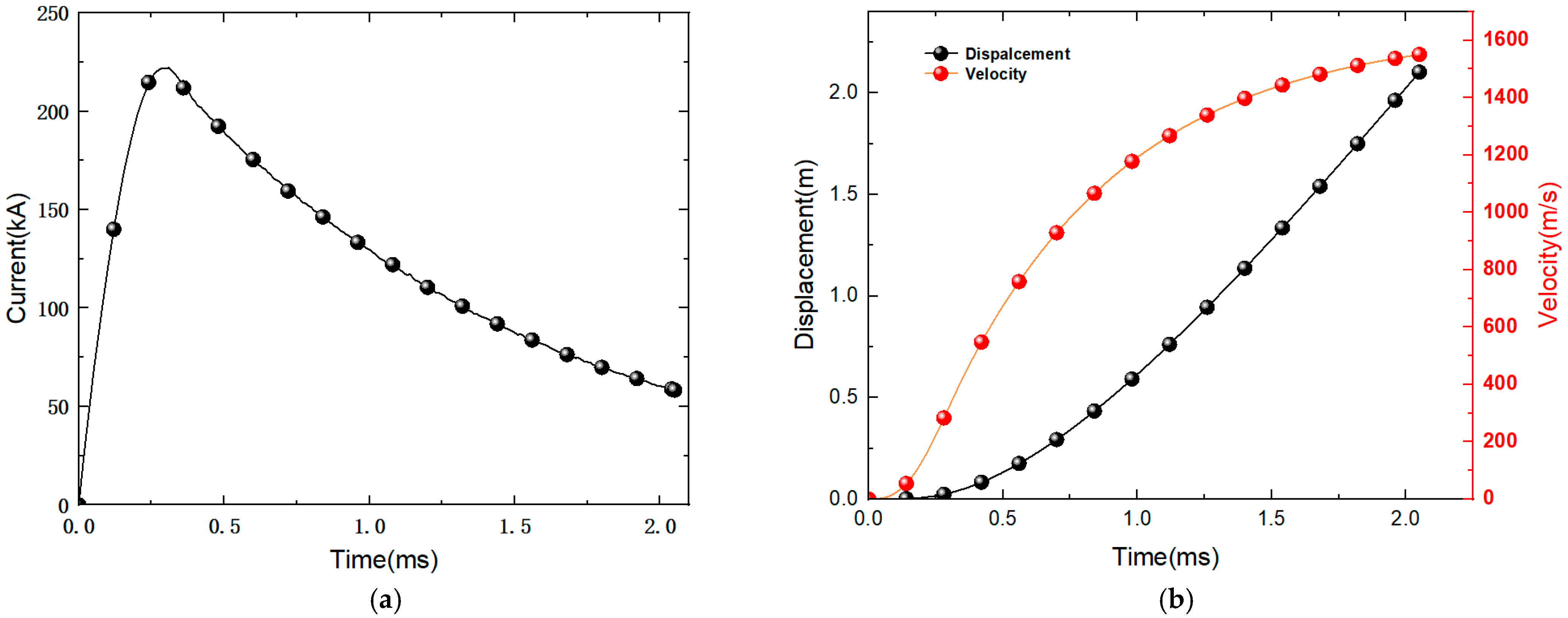
2.2. Experimental Set-Up
2.3. Surface Morphology Set-Up
2.4. Electrical Contact Resistance
3. Experimental Results
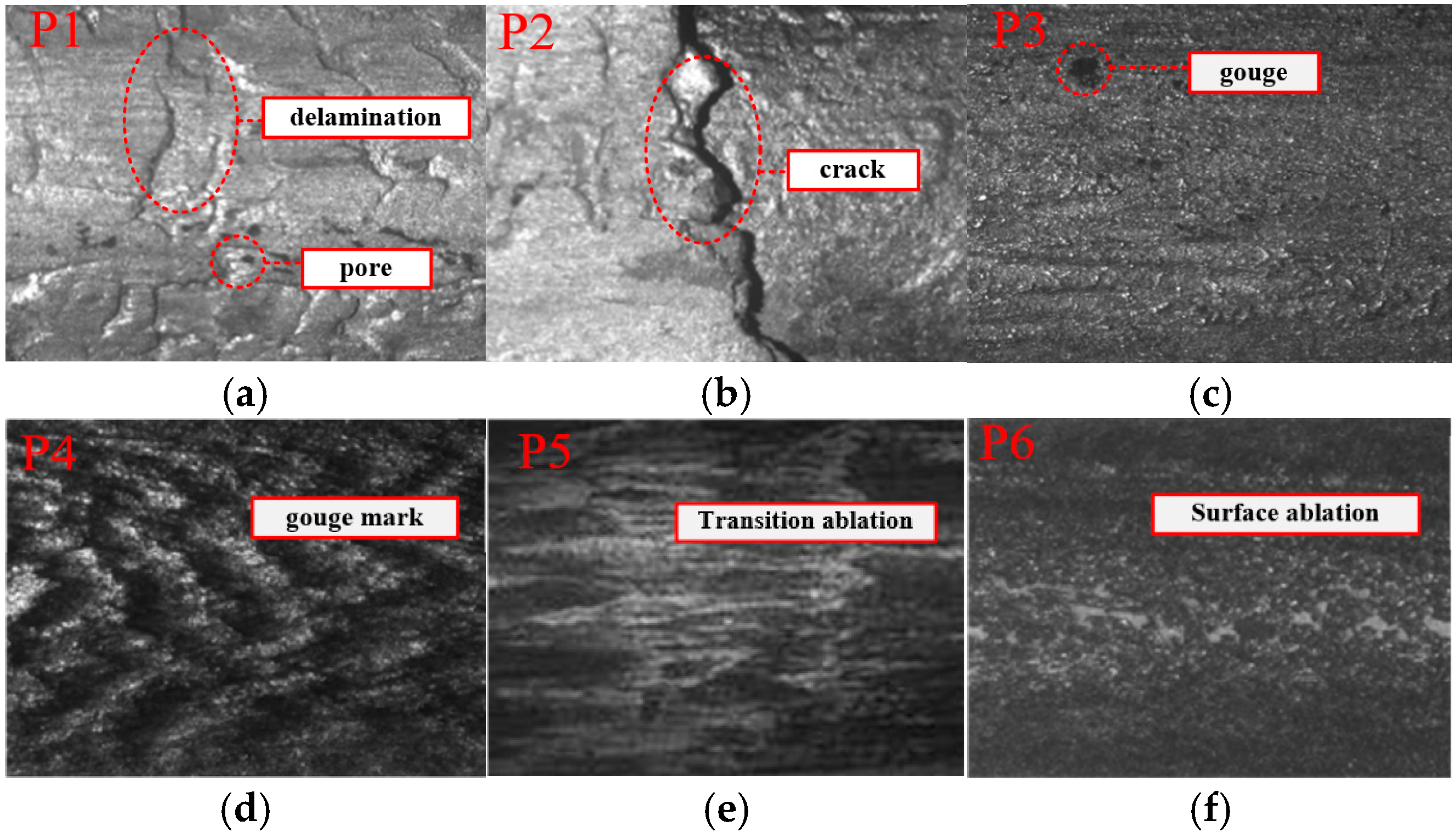
3.1. Observation of Surface Morphology
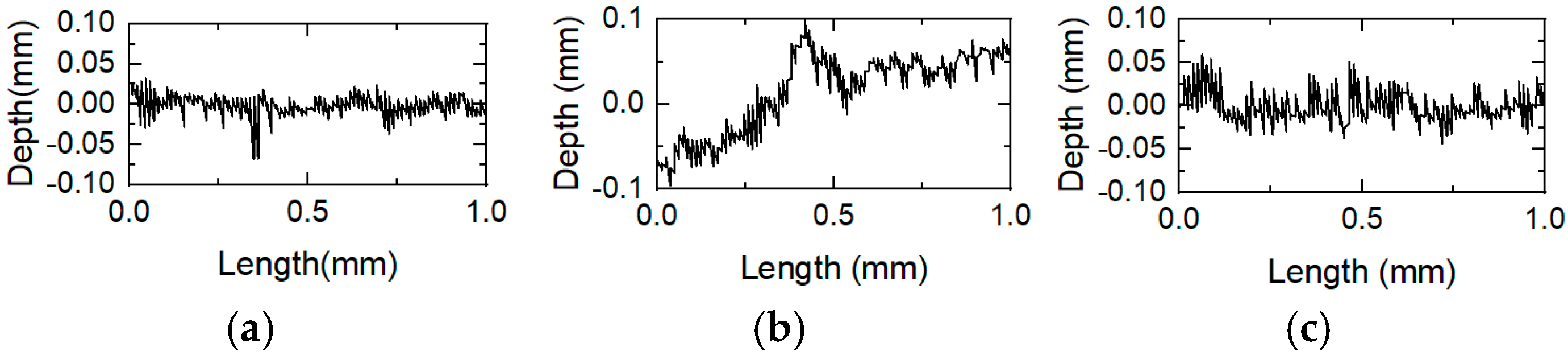
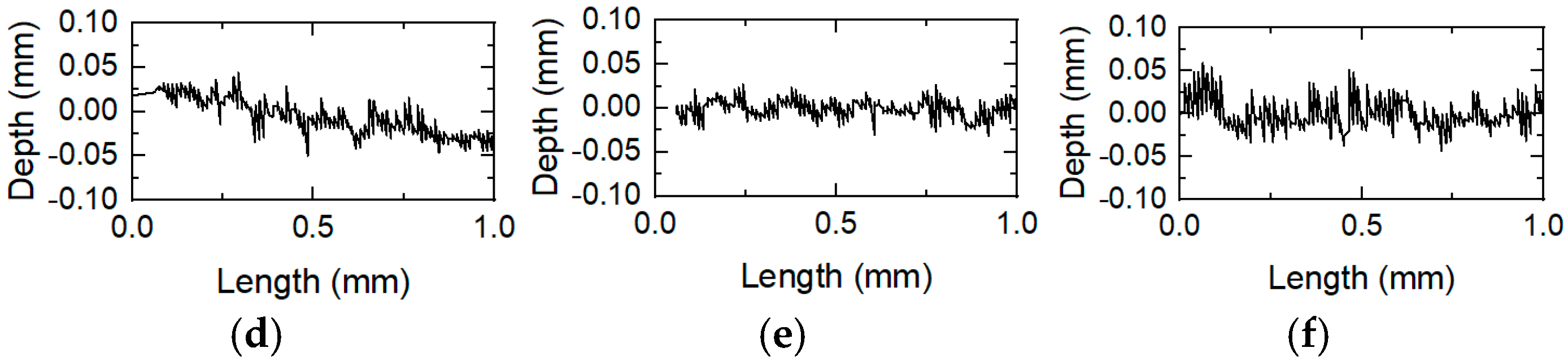
3.2. Surface Profile Micromorphology Measurement
3.3. Characteristics of Rail Surface Roughness
3.4. Research on Electrical Contact Resistance
3.4.1. Contact Resistance Equivalent Model
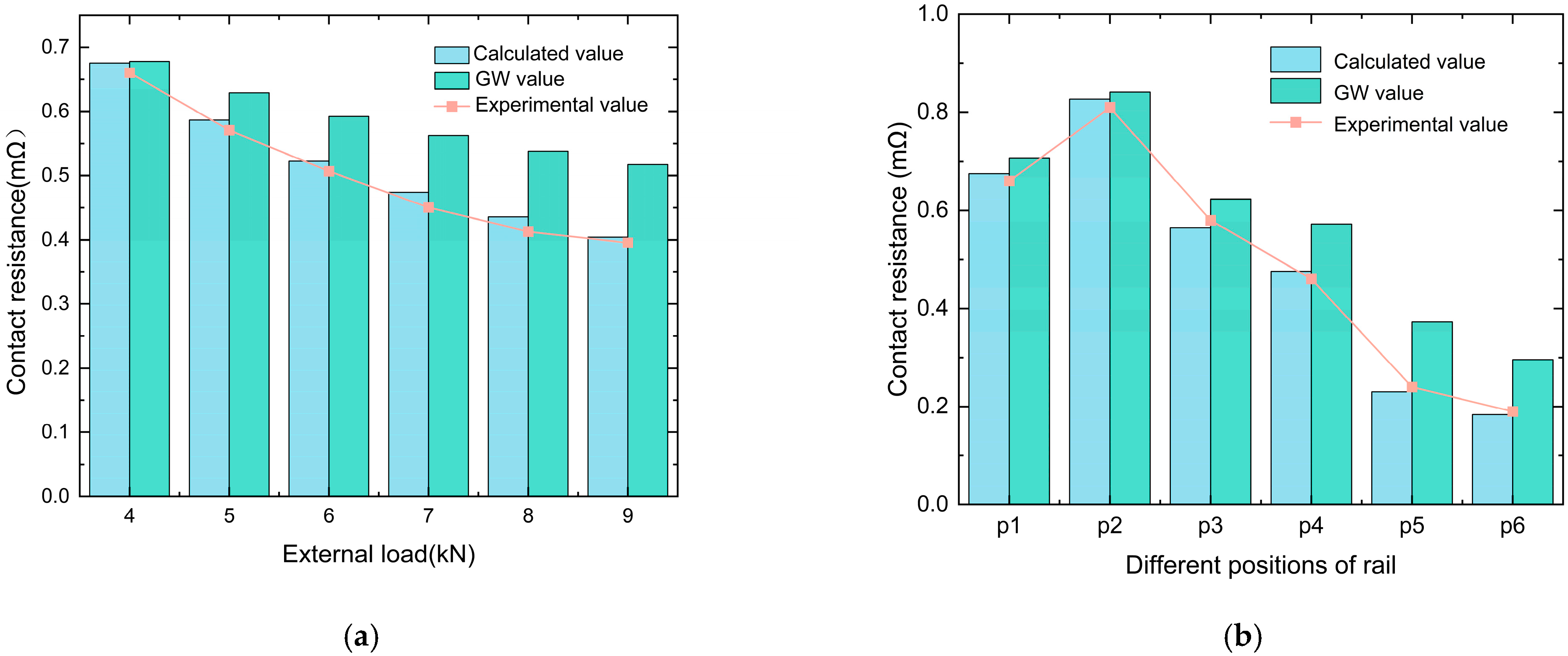
3.4.2. Contact Resistance Model Validation and Test Results
4. Conclusions
- (1)
- The front half of the rail used in the experiment is primarily affected by mechanical wear, whereas the latter half of the rail is dominated by electrical wear. Along the armature launch direction, the fluctuation range of the 2D profile of the rail surface becomes smoother and the surface roughness decreases, with the smallest fluctuation occurring at position P6.
- (2)
- Under experimental conditions, the contact resistance calculated using fractal theory shows better agreement with the experimental measurements than the GW model, demonstrating smaller errors. However, its applicability requires further verification under real engineering conditions.
- (3)
- Under experimental conditions, the greater the roughness, the more sensitive is the contact resistance to changes in external load; the smaller the roughness, the lower is the sensitivity. When the surface roughness is relatively high, the actual number of contacting asperities under the same external load is relatively low. As the external load increases, the number of contacting asperities on the rougher surface increases more significantly than that on a smoother surface. Therefore, the contact resistance of surfaces with higher roughness is more sensitive to variations in the external load.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mao, W.; Pang, T.; Guo, Z.; Bai, H.; Huang, Z.; Jin, X. Analysis of the research progress of electromagnetic railgun based on CiteSpace. IEEE Access 2024, 12, 3499–3513. [Google Scholar] [CrossRef]
- Ma, W.; Lu, J. Thinking and study of electromagnetic launch technology. IEEE Trans. Plasma Sci. 2017, 45, 1071–1077. [Google Scholar] [CrossRef]
- Mei, M.; Hou, H.; Zhang, L.; Huang, T.; Liu, S.; Zhao, Y. Numerical simulation and experimental investigation of coating influence on extrusion tap wear. Sci. Rep. 2024, 14, 18259. [Google Scholar] [CrossRef]
- Yuan, Z.; Hou, H.; Zhang, L.; Huang, T.; Liu, S.; Zhao, Y. Effect of surface roughness on friction and wear behavior of GCr15 bearing steel under different loads. Surf. Sci. Technol. 2024, 2, 28. [Google Scholar] [CrossRef]
- Yoo, S.B.; Yun, S.H.; Jo, A.J.; Cho, S.J.; Cho, H.; Lee, J.H.; Ahn, B.W. Automated measurement and analysis of sidewall roughness using three-dimensional atomic force microscopy. Appl. Microsc. 2022, 52, 1. [Google Scholar] [CrossRef]
- Lebea, L.; Ngwangwa, H.M.; Desai, D.; Nemavhola, F. Experimental investigation into the effect of surface roughness and mechanical properties of 3D-printed titanium Ti-64 ELI after heat treatment. Int. J. Mech. Mater. Eng. 2021, 16, 16. [Google Scholar] [CrossRef]
- Fujiwara, Y.; Fujii, Y.; Sawada, Y.; Okumura, S. Assessment of wood surface roughness: Comparison of tactile roughness and three-dimensional parameters derived using a robust Gaussian regression filter. J. Wood Sci. 2004, 50, 35–40. [Google Scholar] [CrossRef]
- Budhe, S.; Ghumatkar, A.; Birajdar, N.; Banea, M.D. Effect of surface roughness using different adherend materials on the adhesive bond strength. Appl. Adhes. Sci. 2015, 3, 20. [Google Scholar] [CrossRef]
- Wang, X.; Yao, P.; Zhou, H.; Fan, K.; Deng, M.; Kang, L.; Yuan, Z.; Lin, Y. Research Progress on Surface Damage and Protection Strategies of Armature–Rail Friction Pair Materials for Electromagnetic Rail Launch. Materials 2024, 17, 277. [Google Scholar] [CrossRef]
- Deucher, T.M.; Okojie, R.S. Temperature effects on electrical resistivity of selected ceramics for high-temperature packaging applications. J. Am. Ceram. Soc. 2024, 107, 2295–2303. [Google Scholar] [CrossRef]
- Gawel, K.; Taghipour Khadrbeik, M.A.; Bjørge, R.; Wenner, S.; Gawel, B.; Ghaderi, A.; Cerasi, P. Effects of water content and temperature on bulk resistivity of hybrid cement/carbon nanofiber composites. Materials 2020, 13, 2884. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Lv, J.; Liu, C. The Effect of Lubricant’s Viscosity on Reducing the Frictional-Induced Fluctuation on the Onset of Friction. Lubricants 2024, 12, 136. [Google Scholar] [CrossRef]
- Findik, F. Latest progress on tribological properties of industrial materials. Mater. Des. 2014, 57, 218–244. [Google Scholar] [CrossRef]
- Li, S.; Li, J.; Xia, S.; Zhang, Q.; Liu, P. Stage division and critical point definition of electromagnetic railgun sliding contact state. IEEE Trans. Plasma Sci. 2019, 47, 2399–2403. [Google Scholar] [CrossRef]
- Lu, T.; Hua, D.; An, B.L.; Hafeez, M.A.; Pan, J.; Chen, L.X.; Lu, J.Y.; Zhou, Q.; Zhang, C.; Liu, L. Improved anti-adhesive wear performance of rail/armature pair via interfacial energy modulation for electromagnetic launching applications. Scr. Mater. 2023, 236, 115677. [Google Scholar] [CrossRef]
- Xing, Y.; Lv, Q.; Lei, B.; Xiang, H.; Chen, J. Research on melting erosion law of a multiturn series–parallel railgun during launching period. IEEE Trans. Plasma Sci. 2018, 46, 3008–3016. [Google Scholar] [CrossRef]
- Chen, L.; He, J.; Xiao, Z.; Xia, S.; Feng, D.; Tang, L. Experimental study of armature melt wear in solid armature railgun. IEEE Trans. Plasma Sci. 2015, 43, 1142–1146. [Google Scholar] [CrossRef]
- Lu, J.; Wu, X.; Tan, S.; Zhang, Y.; Li, B. An initial survey of the life of rail for electromagnetic launch. IEEE Trans. Plasma Sci. 2018, 47, 2228–2232. [Google Scholar] [CrossRef]
- Meger, R.A.; Cairns, R.L.; Douglass, S.R.; Huhman, B.; Neri, J.M.; Carney, C.J.; Jones, H.N.; Cooper, K. EM gun bore life experiments at naval research laboratory. IEEE Trans. Plasma Sci. 2013, 41, 1533–1537. [Google Scholar] [CrossRef]
- Dong, E.; Cao, R. The inner surface profile measurement apparatus for an electromagnetic rail-gun launcher. IEEE Sens. J. 2018, 18, 4269–4274. [Google Scholar] [CrossRef]
- Gao, X.; Liu, F.; Feng, Y.; Zhang, H.; Zhan, Z. Wear characteristics of rail–armature under the action of interference fit and Lorentz force. IEEE Trans. Plasma Sci. 2020, 48, 2261–2265. [Google Scholar] [CrossRef]
- Ren, S.; Feng, G.; Liu, S. Study on wear of electromagnetic railgun. IEEE Access 2022, 10, 100955–100963. [Google Scholar] [CrossRef]
- Ceylan, D.; Güdelek, M.U.; Keysan, O. Armature shape optimization of an electromagnetic launcher including contact resistance. IEEE Trans. Plasma Sci. 2018, 46, 3619–3627. [Google Scholar] [CrossRef]
- Hartman, S.D.; Timpson, E.J.; Engel, T.G. Evaluation of electromagnetic launcher contact resistance using a design of experiments approach. IEEE Trans. Plasma Sci. 2020, 48, 571–575. [Google Scholar] [CrossRef]
- Guo, A.; Du, X.; Wang, X.; Lui, S. Calculation of Armature Melting Wear Rate Based on Contact Surface Heat Distribution. IEEE Trans. Plasma Sci. 2024, 52, 2981–2990. [Google Scholar] [CrossRef]
- Yang, F.; Zhai, X.; Zhao, Z.; Liu, H.; Peng, Z. Research on the armature–rail dynamic contact characteristics of the series enhanced electromagnetic rail launcher. IEEE Trans. Plasma Sci. 2022, 50, 1040–1047. [Google Scholar] [CrossRef]
- Yan, J.; Li, J.; Ren, R.; Chen, Y.; Wang, Y.; Chen, Y.; Huang, K. System noise suppression of muzzle voltage in augmented electromagnetic railgun based on VMD and the application in armature–rail contact characteristics. IEEE Trans. Plasma Sci. 2022, 50, 502–509. [Google Scholar] [CrossRef]
- Zhu, C.; Li, B. Analysis of sliding electric contact characteristics in augmented railgun based on the combination of contact resistance and sliding friction coefficient. Def. Technol. 2020, 16, 747–752. [Google Scholar] [CrossRef]
- Ge, X.; Cao, B.; Wang, Z.; Pei, P.; Huang, K.; Chen, Y.; Fan, W.; Zhang, T. Research on the contact characteristics between armature and rail of the enhanced electromagnetic rail gun based on the new aluminum alloy armature. IEEE Trans. Plasma Sci. 2023, 51, 3703–3708. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]



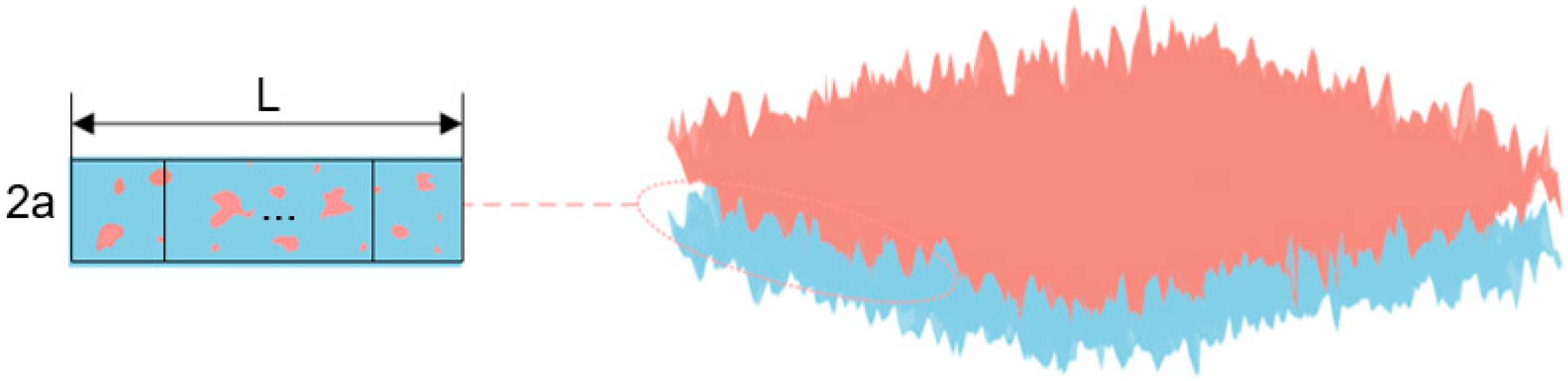

| C | Si | Mn | P | S | Cu | Ni | Cr |
|---|---|---|---|---|---|---|---|
| 0.17% | 0.23% | 1.53% | 0.013% | 0.008% | 0.008% | 0.004% | 0.22% |
| Mass Density (g/cm3) | Elastic Modulus (GPa) | Poisson’s Ratio | Conductivity (S/m) | |
|---|---|---|---|---|
| rail | 7.85 | 205 | 0.28 | 9.6 × 106 |
| armature | 2.8 | 72 | 0.30 | 3.8 × 107 |
| F (kN) | R at P1 (mΩ) | R at P2 (mΩ) | R at P3 (mΩ) | R at P4 (mΩ) | R at P5 (mΩ) | R at P6 (mΩ) |
|---|---|---|---|---|---|---|
| 4 | 0.7068 | 0.8411 | 0.6238 | 0.5724 | 0.3723 | 0.2958 |
| 5 | 0.6561 | 0.7808 | 0.5782 | 0.5313 | 0.3456 | 0.2746 |
| 6 | 0.6174 | 0.7347 | 0.5441 | 0.5004 | 0.3253 | 0.2584 |
| 7 | 0.5865 | 0.6979 | 0.5168 | 0.4750 | 0.3089 | 0.2455 |
| 8 | 0.5609 | 0.6675 | 0.4943 | 0.4543 | 0.2955 | 0.2348 |
| 9 | 0.5393 | 0.6418 | 0.4753 | 0.4368 | 0.2841 | 0.2258 |
| F (kN) | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 4 | 2.300% | 2.049% | 2.661% | 3.448% | 4.096% | 3.432% |
| 5 | 2.739% | 0.483% | 5.894% | 1.409% | 7.143% | 3.025% |
| 6 | 3.122% | 0.248% | 6.600% | 4.378% | 5.389% | 9.807% |
| 7 | 5.251% | 0.412% | 6.078% | 4.484% | 1.247% | 0.417% |
| 8 | 5.482% | 0.451% | 3.917% | 2.393% | 1.764% | 0.909% |
| 9 | 2.205% | 1.597% | 2.219% | 1.173% | 3.069% | 0.235% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Liu, X.; Jin, L.; Yan, R.; Yang, Q. Contact Resistance Modeling Under Complex Wear Conditions Based on Fractal Theory. Materials 2025, 18, 3060. https://doi.org/10.3390/ma18133060
Zhang C, Liu X, Jin L, Yan R, Yang Q. Contact Resistance Modeling Under Complex Wear Conditions Based on Fractal Theory. Materials. 2025; 18(13):3060. https://doi.org/10.3390/ma18133060
Chicago/Turabian StyleZhang, Changgeng, Xiaoxiao Liu, Liang Jin, Rongge Yan, and Qingxin Yang. 2025. "Contact Resistance Modeling Under Complex Wear Conditions Based on Fractal Theory" Materials 18, no. 13: 3060. https://doi.org/10.3390/ma18133060
APA StyleZhang, C., Liu, X., Jin, L., Yan, R., & Yang, Q. (2025). Contact Resistance Modeling Under Complex Wear Conditions Based on Fractal Theory. Materials, 18(13), 3060. https://doi.org/10.3390/ma18133060






