Possibility of Superconductivity of 6Li+ Ions in Solid Electrolytes at Room Temperature Under Coherent Acoustic Phonons
Abstract
1. Introduction
2. Model
3. Results and Discussions
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mantiram, A.; Yu, X.; Wang, S. Lithium battery chemistries enabled by solid-state electrolytes. Nat. Rev. Mater. 2017, 2, 16103. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Soft matter electrolytes: Mechanism of ionic conduction compared to liquid or solid electrolytes. Materials 2024, 17, 5134. [Google Scholar] [CrossRef]
- Kanamura, K. (Ed.) Next Generation Batteries; Springer Nature: Singapore, 2021. [Google Scholar]
- Randau, S.; Weber, D.A.; Kötz, O.; Koerver, R.; Braun, R.; Weber, A.; Ivers-Tiffée, E.; Adermann, T.; Kulisch, J.; Zeier, W.G.; et al. Benchmarking the performance of all-slid-state lithium batteries. Nat. Energy 2020, 5, 259–270. [Google Scholar] [CrossRef]
- Janek, J.; Zeier, W.G. A solid future for battery development. Nat. Energy 2016, 1, 16141. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Influence of dislocations on ionic conductivity and dendrite formation in solid electrolytes. Phys. Scr. 2023, 98, 045811. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Possibility of high ionic conductivity and high fracture toughness in all-dislocation-ceramics. Materials 2024, 17, 428. [Google Scholar] [CrossRef]
- Yasui, K. Merits and demerits of machine learning of ferroelectric, flexoelectric, and electrolytic properties of ceramic materials. Materials 2024, 17, 2512. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Toward all-dislocation-ceramics for high ionic conductivity produced by dry pressing at relatively low temperatures with and without ultrasound. J. Appl. Phys. 2024, 135, 085107. [Google Scholar] [CrossRef]
- Owens, B.B.; Argue, G.R. High-conductivity solid electrolytes: . Science 1967, 157, 308–310. [Google Scholar] [CrossRef]
- Muy, S.; Schlem, R.; Shao-Horn, Y.; Zeier, W.G. Phonon-ion interactions: Designing ion mobility based on lattice dynamics. Adv. Energy Mater. 2021, 11, 2002787. [Google Scholar] [CrossRef]
- Li, Y.; Song, S.; Kim, H.; Nomoto, K.; Kim, H.; Sun, X.; Hori, S.; Suzuki, K.; Matsui, N.; Hirayama, M.; et al. A lithium superionic conductor for millimeter-thick battery electrode. Science 2023, 381, 50–53. [Google Scholar] [CrossRef]
- Fuchs, T.; Culver, S.P.; Till, P.; Zeier, W.G. Defect-mediated conductivity enhancements in (Pn = P, Sb) using aliovalent substitutions. ACS Energy Lett. 2020, 5, 146–151. [Google Scholar] [CrossRef]
- Ling, C. Phonon-promoted superionic conduction in fluorite-structured compounds. Chem 2023, 9, 3588–3599. [Google Scholar] [CrossRef]
- He, X.; Zhu, Y.; Mo, Y. Origin of fast ion diffusion in super-ionic conductors. Nat. Commun. 2017, 8, 15893. [Google Scholar] [CrossRef] [PubMed]
- Wakamura, K. Roles of phonon amplitude and low-energy optical phonons on superionic conduction. Phys. Rev. B 1997, 56, 11593–11599. [Google Scholar] [CrossRef]
- Rice, M.J.; Roth, W.L. Ionic transport in super ionic conductors: A theoretical model. J. Solid. State Chem. 1972, 4, 294–310. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Combescot, R. Superconductivity: An Introduction; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Bednorz, J.G.; Müller, K.A. Possible high superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Schrieffer, J.R.; Brooks, J.S. (Eds.) Handbook of High-Temperature Superconductivity: Theory and Experiment; Springer: New York, NY, USA, 2007. [Google Scholar]
- Takeshita, N.; Yamamoto, A.; Iyo, A.; Eisaki, H. Zero resistivity above 150 K in at high pressure. J. Phys. Soc. Jpn. 2013, 82, 023711. [Google Scholar] [CrossRef]
- Yamamoto, A.; Takeshita, N.; Terakura, C.; Tokura, Y. High pressure effects revisited for the cuprate superconductor family with highest critical temperature. Nat. Commun. 2015, 6, 8990. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef]
- Leggett, A.J. Quantum Liquids, Bose Condensation and Cooper Pairing in Condensed-Matter Systems; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kittel, C.; Kromer, H. Thermal Physics, 2nd ed.; W.H. Freeman: New York, NY, USA, 1980. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Elsevier: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Hamao, N.; Yamaguchi, Y.; Hamamoto, K. Densification of a NASICON-type LATP electrolyte sheet by a cold-sintering process. Materials 2021, 14, 4737. [Google Scholar] [CrossRef]
- Dai, P.; Liu, Y.; Yi, S.; Zhou, S.; Liu, Y.; Gao, T.; Cao, G.; Zhao, S. Cold-sintering assisted process enables densified and robust fine-grained electrolytes for solid-state batteries. J. Power Sources 2024, 618, 235169. [Google Scholar] [CrossRef]
- Monchak, M.; Hupfer, T.; Senyshyn, A.; Boysen, H.; Chernyshov, D.; Hansen, T.; Schell, K.G.; Bucharsky, E.C.; Hoffmann, M.J.; Ehrenberg, H. Lithium diffusion pathway in (LATP) superionic conductor. Inorg. Chem. 2016, 55, 2941–2945. [Google Scholar] [CrossRef]
- Zhang, Z.-W.; Pethick, C.J. Proton superconductivity in pasta phases in neutron star crusts. Phys. Rev. C 2021, 103, 055807. [Google Scholar] [CrossRef]
- Sedrakian, D.M.; Sedrakian, A.D.; Zharkov, G.F. Type I superconductivity of protons in neutron stars. Mon. Not. R. Astron. Soc. 1997, 290, 203–207. [Google Scholar] [CrossRef]
- Tuoriniemi, J.; Juntunen-Nurmilaukas, K.; Uusvuori, J.; Pentti, E.; Salmela, A.; Sebedash, A. Superconductivity in lithium below 0.4 millikelvin at ambient pressure. Nature 2007, 447, 187–189. [Google Scholar] [CrossRef]
- Atkins, P.W. Physical Chemistry, 2nd ed.; Oxford University Press: Oxford, UK, 1982. [Google Scholar]
- Misochko, O.V. Coherent phonons and their properties. J. Exp. Theor. Phys. 2001, 92, 246–259. [Google Scholar] [CrossRef]
- Ventura-Velázquez, C.; Ávila, B.J.; Kyoseva, E.; Rodríguez-Lara, B.M. Robust optomechanical state transfer under composite phase driving. Sci. Rep. 2019, 9, 4382. [Google Scholar] [CrossRef]
- Misochko, O.V.; Hase, M.; Ishioka, K.; Kitajima, M. Transient Bose-Einstein condensation of phonons. Phys. Lett. A 2004, 321, 381–387. [Google Scholar] [CrossRef]
- Garrett, G.A.; Rojo, G.; Sood, A.K.; Whitaker, J.F.; Merlin, R. Vacuum squeezing of solids: Macroscopic quantum states driven by light pulses. Science 1997, 275, 1638–1640. [Google Scholar] [CrossRef]
- Ruello, P.; Gusev, V.E. Physical mechanisms of coherent acoustic phonons generation by ultrafast laser action. Ultrasonics 2015, 56, 21–35. [Google Scholar] [CrossRef] [PubMed]
- Thomsen, C.; Grahn, H.T.; Maris, H.J.; Tauc, J. Surface generation and detection of phonons by picosecond light pulses. Phys. Rev. B 1986, 34, 4129–4138. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- McQuarrie, D.A.; Simon, J.D. Physical Chemistry: A Molecular Approach; University Science Books: Melville, NY, USA, 1997. [Google Scholar]
- Murray, É.D.; Fritz, D.M.; Wahlstrand, J.K.; Fahy, S.; Reis, D.A. Effect of lattice anharmonicity on high-amplitude phonon dynamics in photoexcited bismuth. Phys. Rev. B 2005, 72, 060301(R). [Google Scholar] [CrossRef]
- Andreev, A.F.; Lifshitz, I.M. Quantum theory of defects in crystals. Sov. Phys. JETP 1969, 29, 1107–1113. [Google Scholar]
- Galli, D.E.; Reatto, L. Vacancies in solid 4He and Bose Einstein condensation. J. Low Temp. Phys. 2001, 124, 197–207. [Google Scholar] [CrossRef]
- Burns, C.A.; Goodkind, J.M. The role of vacancies in solid 4He. Phys. B 1994, 194–196, 949–950. [Google Scholar] [CrossRef]
- Leggett, A.J. Can a solid be “superfluid”? Phys. Rev. Lett. 1970, 25, 1543–1546. [Google Scholar] [CrossRef]
- Gautam, S.K.; Singh, F.; Sulania, I.; Singh, R.G.; Kulriya, P.K.; Pippel, E. Micro-Raman study on the softening and stiffening of phonons in rutile titanium dioxide film: Competing effects of structural defects, crystallite size, and lattice strain. J. Appl. Phys. 2014, 115, 143504. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Delehaye, M.; Laurent, S.; Grier, A.T.; Pierce, M.; Rem, B.S.; Chevy, F.; Salomon, C. A mixture of Bose and Fermi superfluids. Science 2014, 345, 1035–1038. [Google Scholar] [CrossRef]
- Wright, O.B.; Kawashima, K. Coherent phonon detection from ultrafast surface vibrations. Phys. Rev. Lett. 1992, 69, 1668–1671. [Google Scholar] [CrossRef] [PubMed]
- Makhrinov, V.; Maksut, Z.; Yazici, A.; Almagambetov, A.; Grossan, B.; Shafiee, M. Superconducting microresonator signal denoising using machine learning. IEEE Trans. Appl. Supercond. 2025, 35, 2400411. [Google Scholar] [CrossRef]
- Pratticò, D.; Laganà, F.; Oliva, G.; Fiorillo, A.S.; Pullano, S.A.; Calcagno, S.; De Carlo, D.; Foresta, F.L. Integration of LSTM and U-net models for monitoring electrical absorption with a system of sensors and electronic circuits. IEEE Trans. Instrum. Meas. 2025, 74, 2533311. [Google Scholar] [CrossRef]
- Cheng, T.K.; Vidal, J.; Zeiger, H.J.; Dresselhaus, G.; Ippen, E.P. Mechanism for displacive excitation of coherent phonons in Sb, Bi, Te, and . Appl. Phys. Lett. 1991, 59, 1923–1925. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Stanton, C.J. Theory of coherent phonon oscillations in semiconductors. Phys. Rev. Lett. 1994, 73, 3243–3246. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Kuttruff, H. Acoustics, an Introduction; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Yasui, K. Acoustic Cavitation and Bubble Dynamics; Springer: Cham, Switzerland, 2018. [Google Scholar]
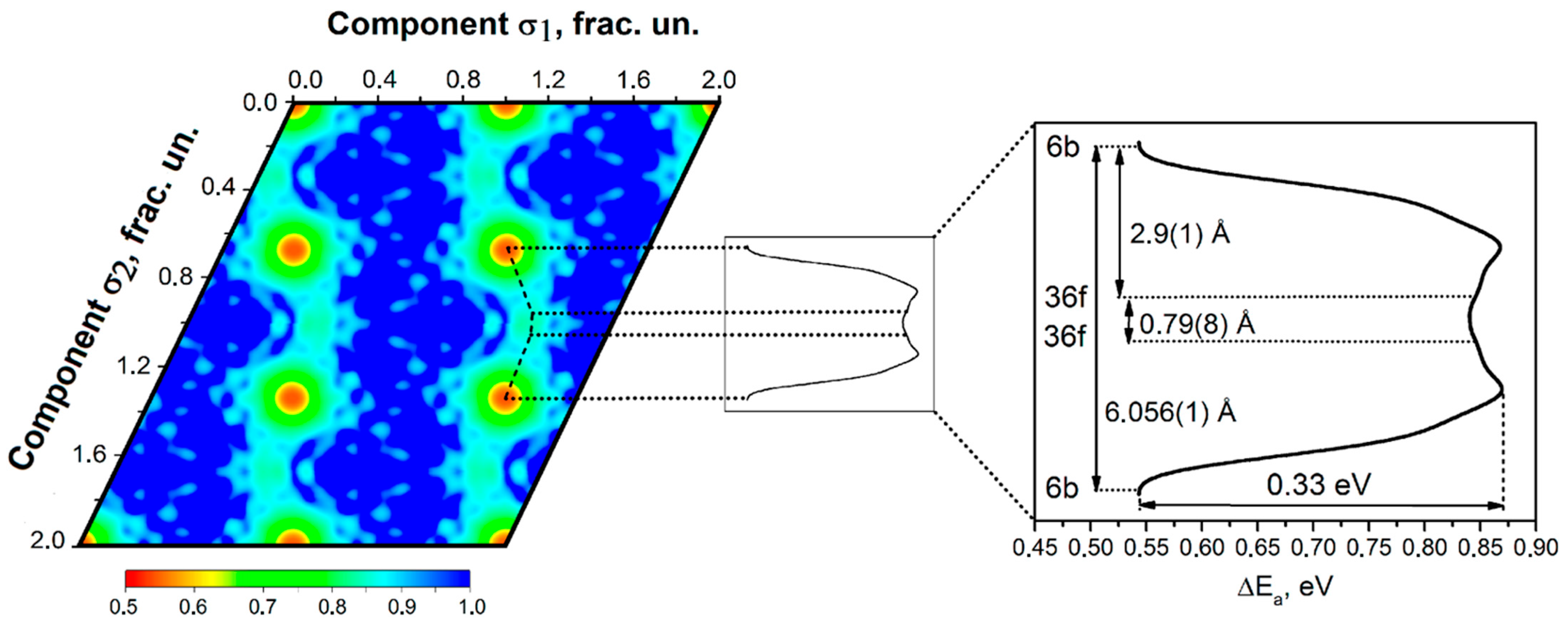
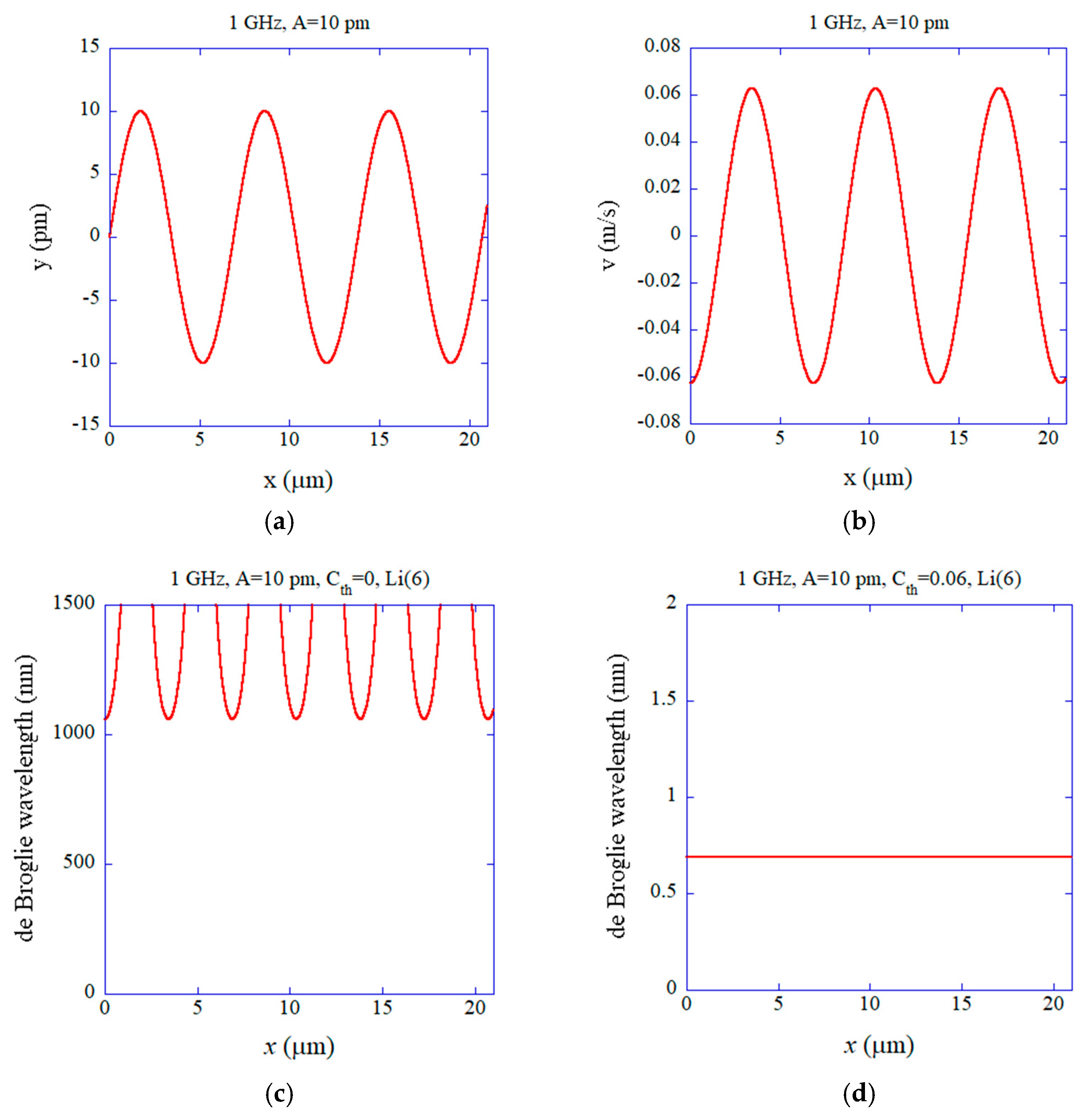
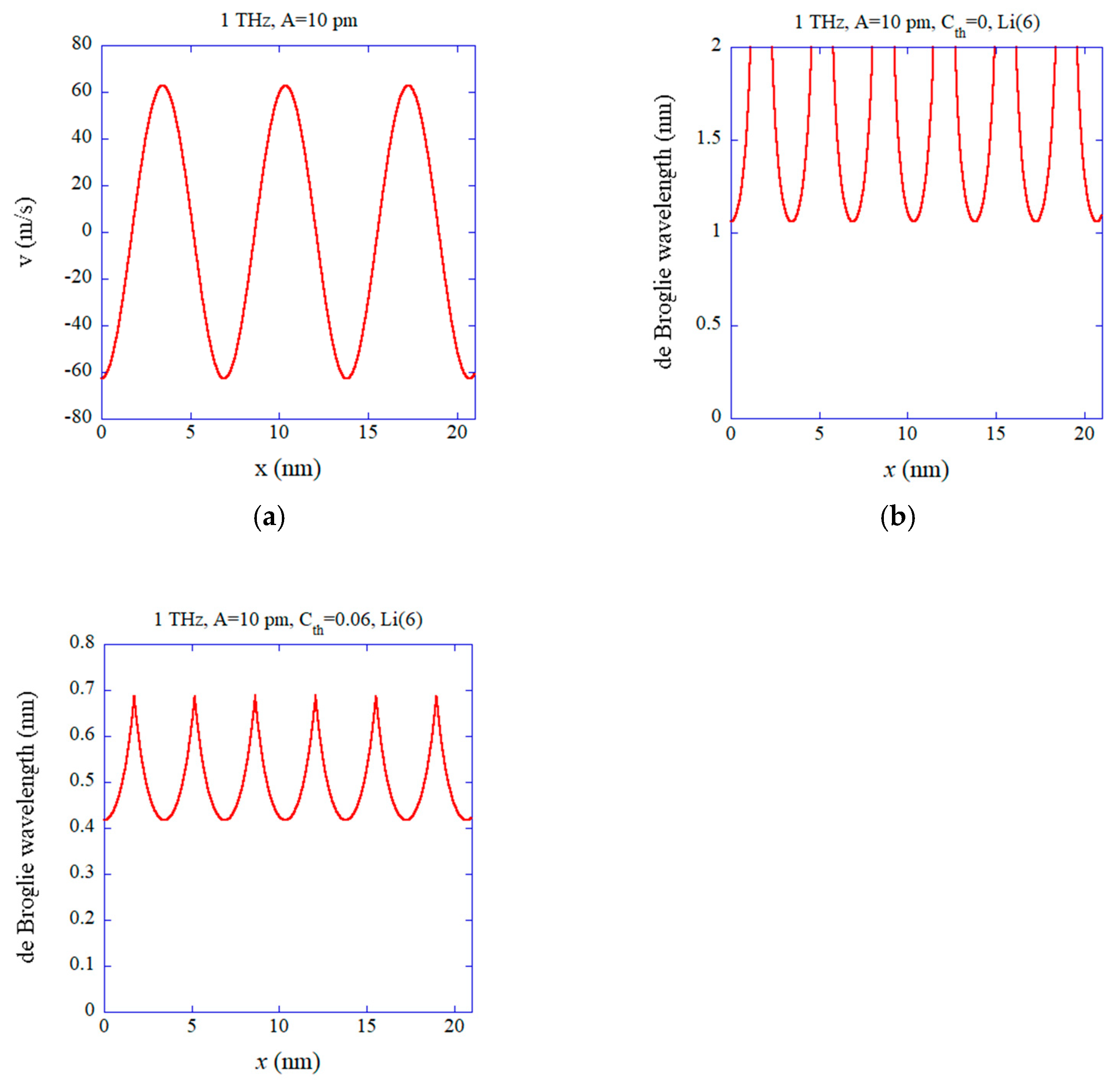
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasui, K. Possibility of Superconductivity of 6Li+ Ions in Solid Electrolytes at Room Temperature Under Coherent Acoustic Phonons. Materials 2025, 18, 3058. https://doi.org/10.3390/ma18133058
Yasui K. Possibility of Superconductivity of 6Li+ Ions in Solid Electrolytes at Room Temperature Under Coherent Acoustic Phonons. Materials. 2025; 18(13):3058. https://doi.org/10.3390/ma18133058
Chicago/Turabian StyleYasui, Kyuichi. 2025. "Possibility of Superconductivity of 6Li+ Ions in Solid Electrolytes at Room Temperature Under Coherent Acoustic Phonons" Materials 18, no. 13: 3058. https://doi.org/10.3390/ma18133058
APA StyleYasui, K. (2025). Possibility of Superconductivity of 6Li+ Ions in Solid Electrolytes at Room Temperature Under Coherent Acoustic Phonons. Materials, 18(13), 3058. https://doi.org/10.3390/ma18133058





