Review of Molecular Dynamics Simulation of Bimetallic Interfacial Behavior
Abstract
1. Introduction
2. Molecular Dynamics Simulation of Al/Cu Bimetallic Interfacial Behavior
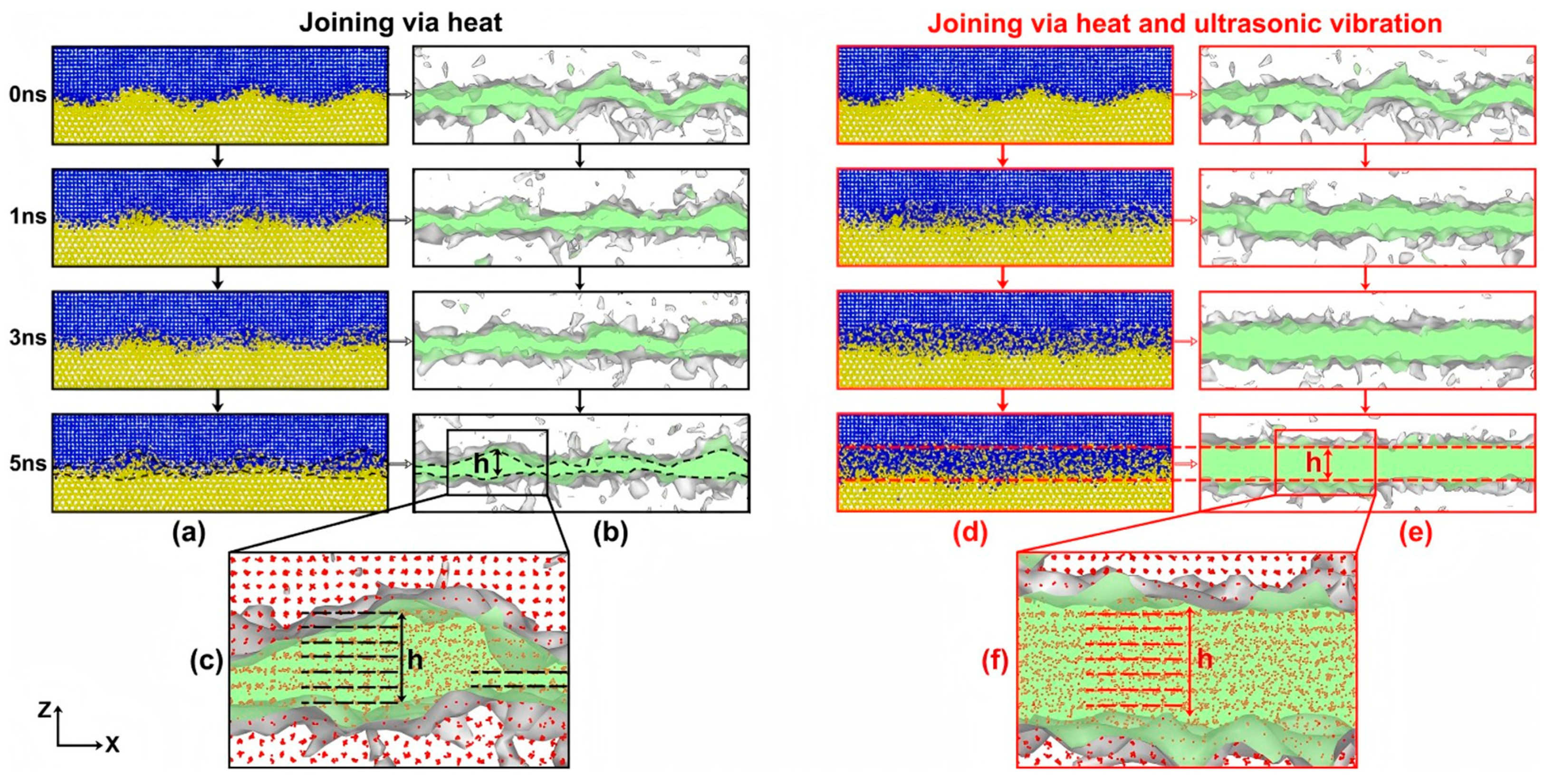
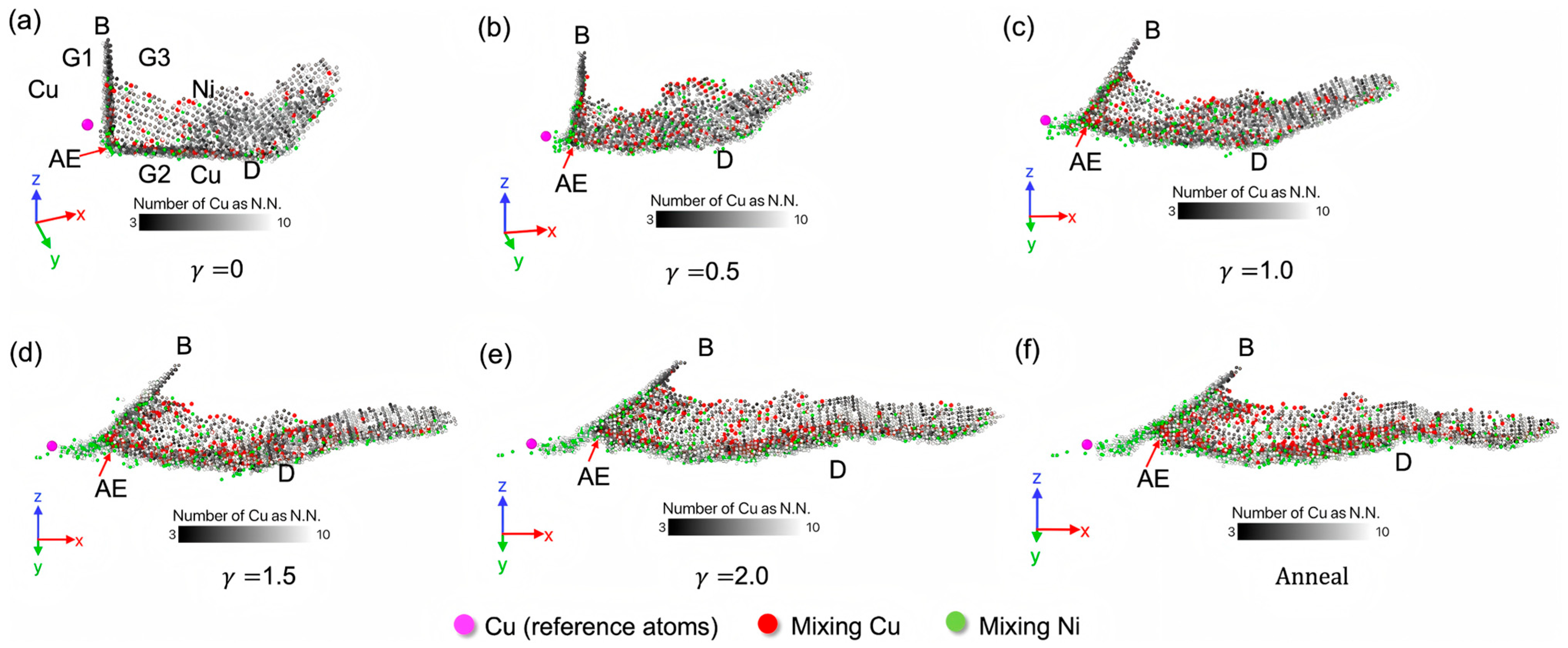
2.1. Interface Formation Process of Al/Cu Bimetallic Systems
- Internal Influencing Factors
- External Influencing Factors
2.2. Mechanical Behavior of Al/Cu Bimetallic Interfaces
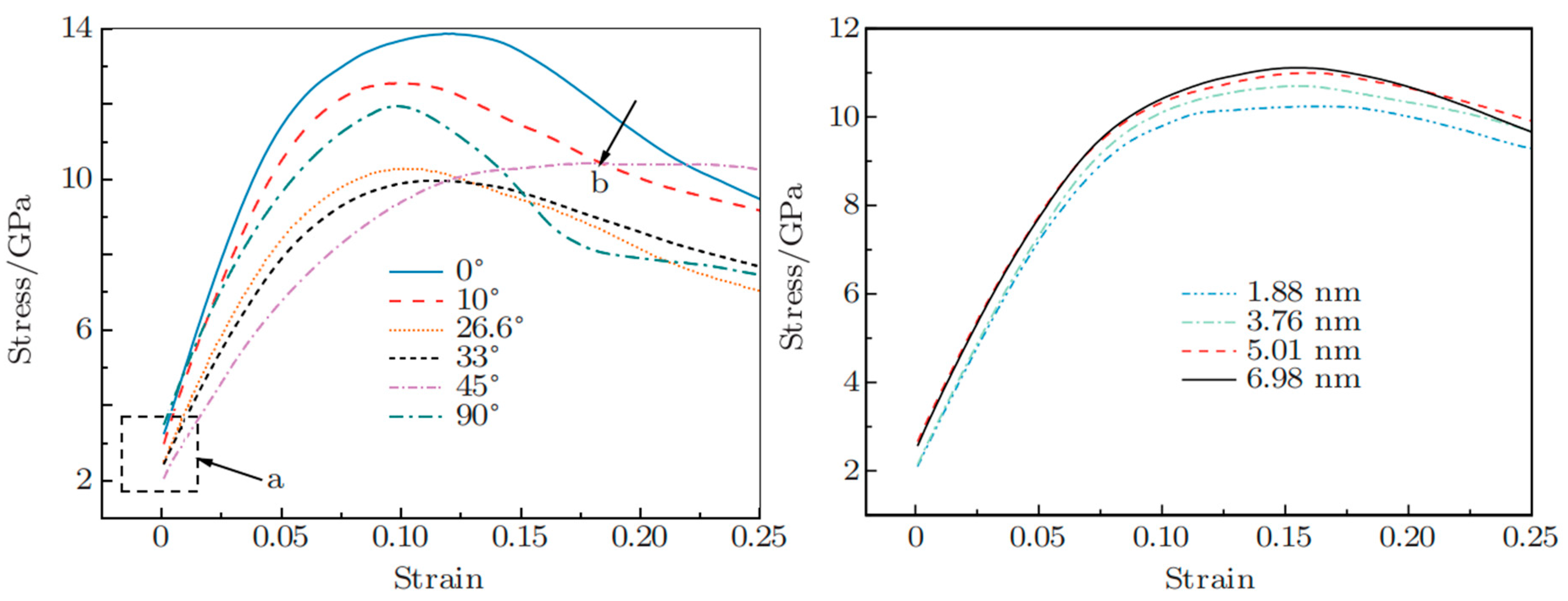
2.2.1. Tensile Behavior
- Internal Influencing Factors
- External Influencing Factors
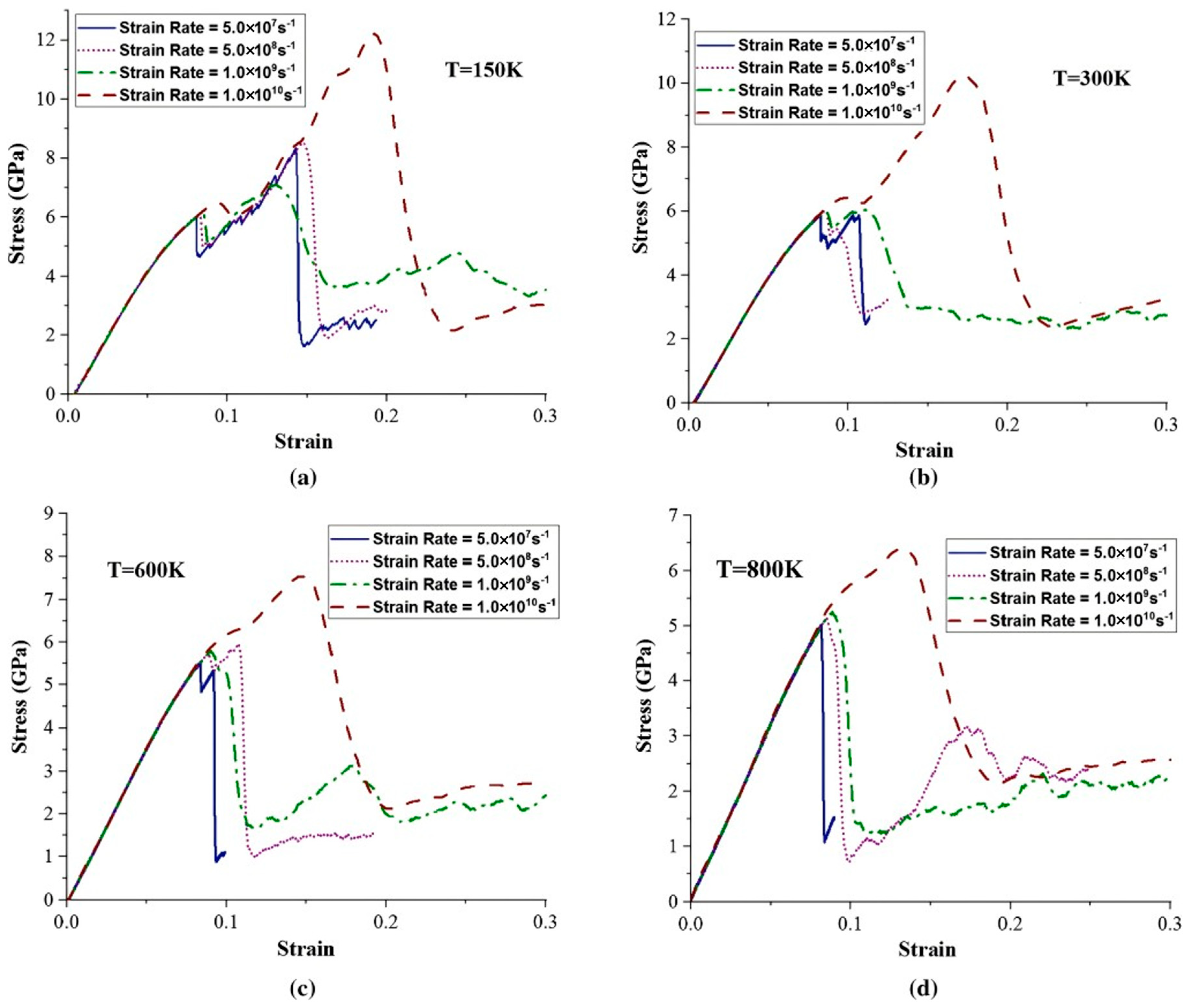
2.2.2. Compression Behavior
- Internal Influencing Factors
- External Influencing Factors
3. Molecular Dynamics Simulation of Al/Mg Bimetallic Interfacial Behavior
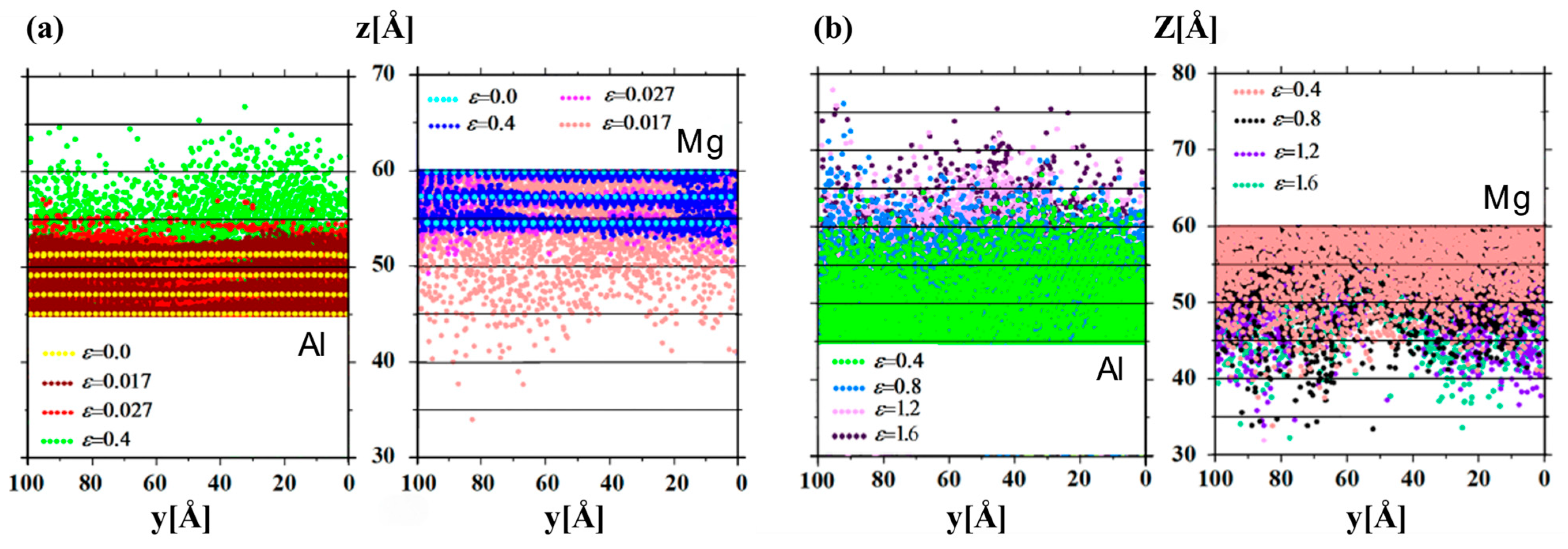
3.1. Interface Formation Process of Al/Mg Bimetallic Systems
- External Influencing Factors
3.2. Mechanical Behavior of Al/Mg Bimetallic Interfaces
3.2.1. Tensile Behavior
- Internal Influencing Factors
- External Influencing Factors
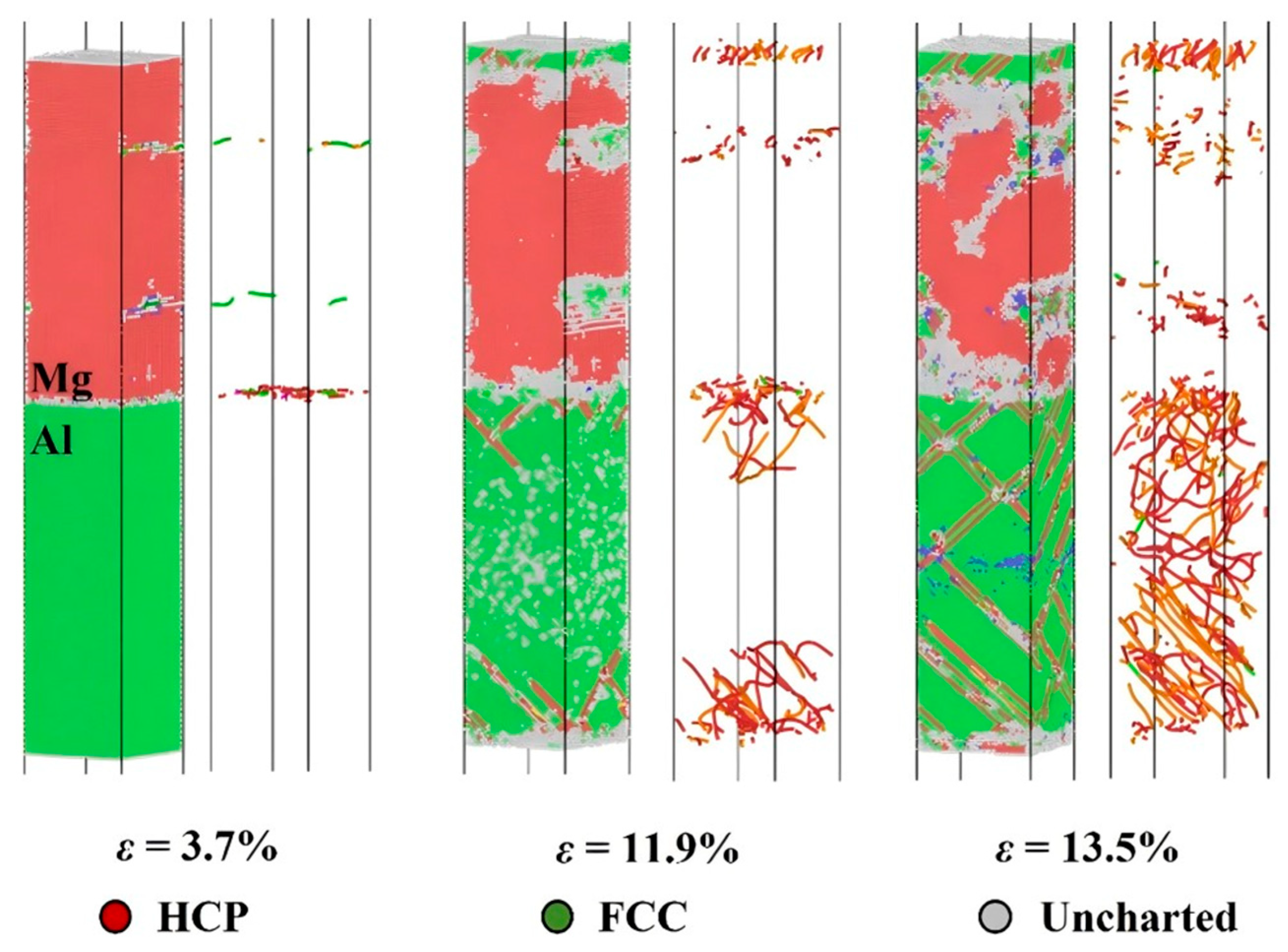
3.2.2. Compression Behavior
- Internal Influencing Factors
- External Influencing Factors
4. Molecular Dynamics Simulation of Al/Ni Bimetallic Interfacial Behavior
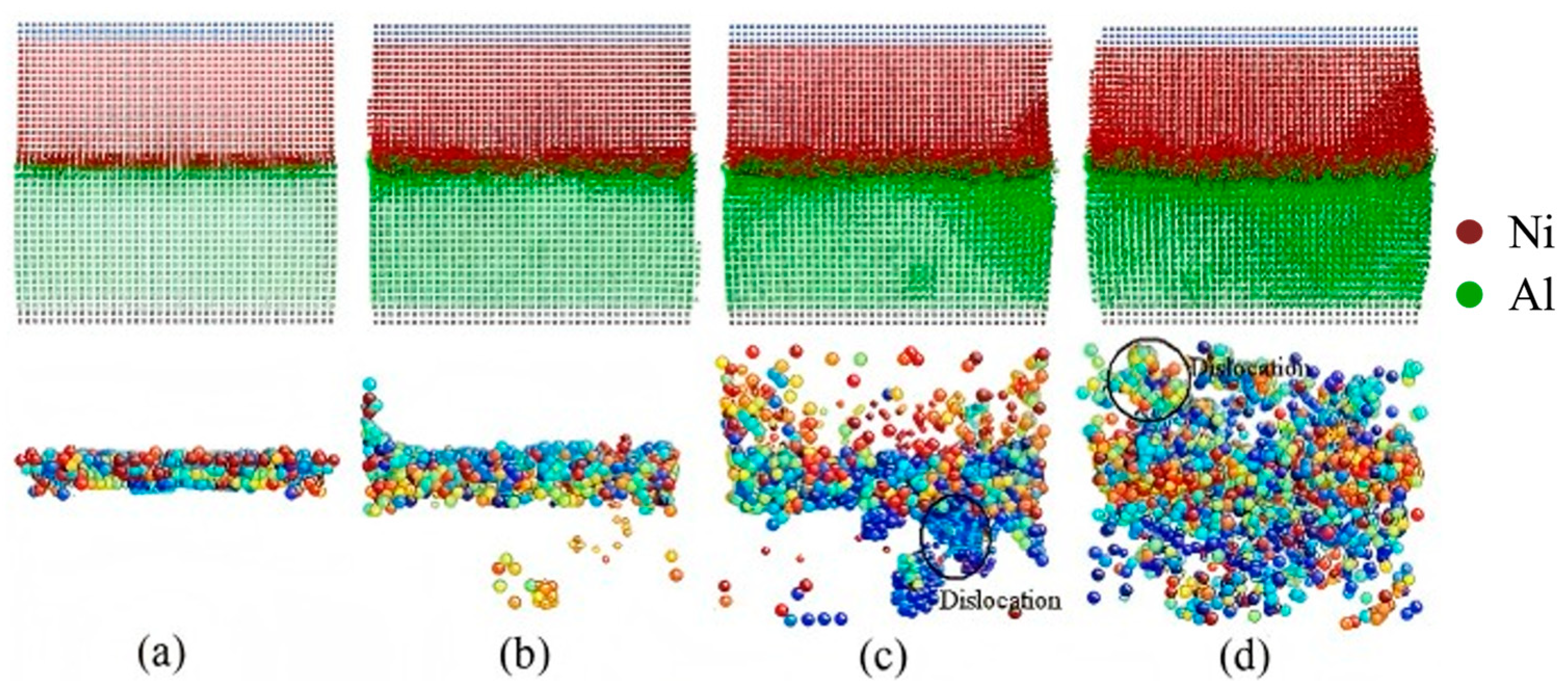
4.1. Interface Formation Process of Al/Ni Bimetallic Systems
- External Influencing Factors
4.2. Mechanical Behavior of Al/Ni Bimetallic Interfaces
Tensile Behavior
- Internal Influencing Factors
- External Influencing Factors
5. Molecular Dynamics Simulation of Al/Ti Bimetallic Interfacial Behavior
5.1. Interface Formation Process of Al/Ti Bimetallic Systems
- Internal Influencing Factors
- External Influencing Factors
5.2. Mechanical Behavior of Al/Ti Bimetallic Interfaces
5.2.1. Tensile Behavior
- Internal Influencing Factors
- External Influencing Factors
5.2.2. Compression Behavior
- Internal Influencing Factors
6. Molecular Dynamics Simulation of Al/Fe Bimetallic Interfacial Behavior
6.1. Interface Formation Process of Al/Fe Bimetallic Systems
- External Influencing Factors
6.2. Mechanical Behavior of Al/Fe Bimetallic Interfaces
Compression Behavior
- External Influencing Factors
7. Molecular Dynamics Simulation of Cu/Ni Bimetallic Interfacial Behavior
7.1. Interface Formation Process of Cu/Ni Bimetallic Systems
- External Influencing Factors
7.2. Mechanical Behavior of Cu/Ni Bimetallic Interfaces
Tensile Behavior
- Internal Influencing Factors
- External Influencing Factors
8. Molecular Dynamics Simulation of Fe/Cu Bimetallic Interfacial Behavior
8.1. Interface Formation Process of Fe/Cu Bimetallic Systems
- External Influencing Factors
8.2. Mechanical Behavior of Fe/Cu Bimetallic Interfaces
Tensile Behavior
- Internal Influencing Factors
- External Influencing Factors
9. Conclusions and Perspectives
9.1. Conclusions
9.2. Perspectives
- (1)
- Machine learning interatomic potentials to optimize potential functions: The key to materials simulation lies in the interatomic potentials, which are crucial for accurately predicting and understanding the physicochemical properties of materials. Classical MD simulations usually rely on experimental data or potential energy surfaces fitted by approximate methods to describe the atomic forces, and although they can match experimental results in many cases, their applicability and accuracy are still limited, especially in complex solid-liquid systems where it is difficult to describe the bonding and breaking of chemical reactions. Therefore, the construction and optimization of interatomic potentials using machine learning methods has become an effective means to describe the atomic-scale behavior of materials more accurately.
- (2)
- Applied energy field-assisted interfacial bonding: It mainly includes explosion bonding and electromagnetic pulse bonding. Explosions or electromagnetic pulses produce transient tilted collisions and plastic deformations at the composite interface, thus enhancing the interfacial bonding. MD simulations can provide an in-depth analysis of the effects of these applied energy fields on the interfacial atomic diffusion, interfacial structure evolution, and bond strength, thus providing new ideas and methods for optimizing the properties of bimetallic materials.
- (3)
- Improvement of stress–strain curves: When using LAMMPS version 29 August 2024 Stable Release to carry out simulation studies, it was found that there was a certain degree of difference between the obtained stress–strain curves and the corresponding curves obtained through actual experiments, which was manifested in the fact that the curves obtained from the simulation showed a wavy pattern at the final stage. In view of this situation, suitable fitting algorithms can be used to re-fit the stress–strain curve based on machine learning and other means, so that it can better reproduce the mechanical behavior of the experiment, thus improving the reliability and scientific validity of the simulation.
- (4)
- Multi-scale simulation methods: The interfacial behavior of bimetallic systems represents a complex multiscale and multiphysics process, necessitating cross-scale simulation analysis. To overcome inherent scale limitations in simulations, an integrated computational framework combining DFT calculations, MD simulations, phase-field methods, and finite element modeling has been established. This approach enables the following: a DFT calculation of Al/Mg interfacial binding energy; MD simulations of dynamic interface evolution to provide diffusion barriers and interfacial energy parameters for mesoscale models; phase-field simulations of matrix/interface microstructural evolution yielding equivalent mechanical properties for finite element inputs; and ultimately, finite element modeling based on mesoscale features to predict mechanical responses of Al/Mg bimetal—thereby achieving coordinated cross-scale design of interfacial performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basem, A.; Jasim, D.J.; Bansal, P.; Qasim, M.; Brisset, B. Creep properties of bimetal Al/SiC/Cu composites fabricated via accumulative roll bonding process. J. Cent. South Univ. 2024, 31, 3807–3818. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, J.; Jiang, W.M.; Xu, Y.C.; Li, Q.Q.; Liu, W.W.; Yao, S.; Yao, P.K.; Fan, Z.T. Microstructure characteristic, formation mechanism and mechanical properties of AZ91D/A356 bimetallic interface with a novel Ni-Cr composite coating. J. Alloys Compd. 2024, 1005, 176121. [Google Scholar] [CrossRef]
- Yang, P.A.; Cai, R.; Ruan, H.B.; Zhang, N.Q.; Huang, X.; Li, R.; Zhang, Y.X.; Lu, Y.; Zhou, Z.H. Bimagnetic metal constructed core-shell structure of Fe@Co nanowires for multi-band microwave absorption. Prog. Nat. Sci. Mater. Int. 2024, 34, 354–361. [Google Scholar] [CrossRef]
- Wang, M.F.; Peng, B.; Sun, J.; Wang, X.W.; Li, G.L.; Wang, X.L.; Jie, J.C.; Li, T.J. Simultaneously enhancing mechanical and bonding property of Cu-Ni-Si/1010 steel bimetal laminated composites via annealing. Mater. Charact. 2025, 223, 114908. [Google Scholar] [CrossRef]
- Guan, F.; Jiang, W.M.; Li, G.Y.; Zhu, J.W.; Wang, G.L.; Jie, G.L.; Fan, Z.T. Effect of vibration on interfacial microstructure and mechanical properties of Mg/Al bimetal prepared by a novel compound casting. J. Magnes. Alloys 2022, 10, 2296–2309. [Google Scholar] [CrossRef]
- Prasad, S.V.S.; Prasad, B.S.; Verma, K.; Mishra, R.K.; Kumar, V.; Singh, S. The role and significance of Magnesium in modern day research-A review. J. Magnes. Alloy. 2022, 10, 1–61. [Google Scholar] [CrossRef]
- Zhao, S.J.; Chen, C.T.; Liang, H.; Wang, S.H.; Kimura, F.; Kajihara, Y. Investigation of the influence of aluminum surficial water on aluminum-plastic hybrids through a combined experimental and simulation approach. Appl. Surf. Sci. 2024, 656, 159694. [Google Scholar] [CrossRef]
- Li, G.Y.; Guan, F.; Jiang, W.M.; Xu, Y.C.; Zhang, Z.; Fan, Z.T. Effects of mechanical vibration on filling and solidification behavior, microstructure and performance of Al/Mg bimetal by lost foam compound casting. China Foundry 2023, 20, 469–479. [Google Scholar] [CrossRef]
- Hoseini-Athar, M.M.; Tolaminejad, B. Interface morphology and mechanical properties of Al-Cu-Al laminated composites fabricated by explosive welding and subsequent rolling process. Met. Mater. Int. 2016, 22, 670–680. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Chen, L.J.; Ren, Q.L.; Du, H.Q.; Wei, Y.S.; Shi, Y.N.; Hou, X.M.; Wang, J.H.; Jin, P.P. Deformation behavior and strengthening mechanisms of a novel powder metallurgy Ni-based superalloy during in-situ tensile testing. Mater. Sci. Eng. A 2025, 926, 147942. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, S.; Hu, Y.; Meng, Q.H.; Fu, B.; Zhao, Y.W.; Wu, C.L.; Li, G.M.; Qin, J.; Wang, J.P. Effects of welding current on microstructure evolution and mechanical behavior of WC-Co/X32 steel joints by resistance spot welding. Int. J. Refract. Met. Hard Mater. 2025, 128, 107048. [Google Scholar] [CrossRef]
- Bu, W.G.; He, P.F.; Hao, J.M.; Wang, R.; Hu, Z.F.; Mo, J.Y.; Liang, X. Achieving superior mechanical properties by regulating nano-phases in cast Al-Li alloys: Experimental and simulation. Mater. Des. 2025, 252, 113782. [Google Scholar] [CrossRef]
- Li, G.Y.; Jiang, W.M.; Guan, F.; Zhu, J.W.; Yu, Y.; Fan, Z.T. Improving mechanical properties of AZ91D magnesium/A356 aluminum bimetal prepared by compound casting via a high velocity oxygen fuel sprayed Ni coating. J. Magnes. Alloys 2022, 10, 1075–1085. [Google Scholar] [CrossRef]
- Pu, Z.; Liu, D.R.; Chen, T.; Guan, J.; Guo, Z. Multiscale simulation and experimental investigation of nanoparticles dispersion during laser surface remelting of SiC/Mg-9Al composites. Surf. Coat. Technol. 2025, 502, 131988. [Google Scholar] [CrossRef]
- Ajithkumar, S.; Arulmurugan, B.; Meiyazhagan, R. Welding of nickel alloys interface by finite element modeling and artificial intelligence and envisage by patent landscape. Int. J. Interact. Des. Manuf. (IJIDeM) 2025, in press. [Google Scholar] [CrossRef]
- Krylova, K.A.; Safina, L.R.; Rusalev, Y.V.; Baimova, J.A. The impact of composite graphene/Ni coating on nanoindentation of Ni: Deformation mechanism. Surf. Interfaces 2025, 61, 106093. [Google Scholar] [CrossRef]
- Feng, L.; Liu, R.L.; Ma, K.; Zhao, Y.C.; Fu, X.; Zhang, X.; Ling, Y.; Li, J. Tensile properties and molecular dynamics simulation of FeCrMnAlxCu high-entropy alloys. Vacuum 2025, 238, 114219. [Google Scholar] [CrossRef]
- Kang, Y.Y.; Liu, W.W.; Wang, X.Y.; Cai, Z.Y.; Li, J.; Leng, X.S.; Chen, H. Effect of Fe content on corrosion behavior of heat-resistance alloys in high-temperature supercritical carbon dioxide. Appl. Surf. Sci. 2025, 693, 162821. [Google Scholar] [CrossRef]
- Lehtinen, A.; Granberg, F.; Laurson, L.; Nordlund, K.; Alava, M.J. Multiscale modeling of dislocation-precipitate interactions in Fe: From molecular dynamics to discrete dislocations. Phys. Rev. E 2016, 93, 013309. [Google Scholar] [CrossRef]
- Lee, S.-M.; Baek, J.-H.; Yu, M.-H.; Jeon, S.-W.; Choi, W.-S.; Heo, S.-P.; Yang, M.-H.; Park, J.-H. Multi-scale (macro-meso-micro) progressive failure simulation of the carbon fiber braided structure under quasi-static mechanical loading. Int. J. Precis. Eng. Manuf. Green Technol. 2024, in press. [Google Scholar] [CrossRef]
- Ma, T.; Gong, G.; Cao, H.; Shi, J.; Wei, X.; Zhang, L. Exploring multi-scale damage mechanisms in 8Cr4Mo4V alloy by molecular dynamics simulations and experiments. Mater. Today Commun. 2024, 41, 110862. [Google Scholar] [CrossRef]
- Ding, J.Q.; Du, N.Z.; Wei, X.B.; Li, X.Q.; Chen, Z.; Lu, S.Q.; Zhang, H.; Feng, C.; Chen, K.; Qiao, J.; et al. Insights into friction behavior of textured amorphous carbon and lubricant composite system: Dependence on the lubricant viscosity and textured shape. Prog. Nat. Sci. Mater. Int. 2023, 33, 616–624. [Google Scholar] [CrossRef]
- Xie, C.; Bai, S.J.; Liu, X.; Zhang, M.H.; Du, J.K. Stress-corrosion coupled damage localization induced by secondary phases in bio-degradable Mg alloys: Phase-field modeling. J. Magnes. Alloys 2024, 12, 361–383. [Google Scholar] [CrossRef]
- Staublin, P.; Mukherjee, A.; Warren, J.A.; Voorhees, P.W. Phase-field model for anisotropic grain growth. Acta Mater. 2022, 237, 118169. [Google Scholar] [CrossRef]
- Evers, L.P.; Brekelmans, W.A.M.; Geers, M.G.D. Non-local crystal plasticity model with intrinsic SSD and GND effects. J. Mech. Phys. Solids 2004, 52, 2379–2401. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, W.; Li, B.; Liu, M.B. Investigation on behavior of crack penetration/deflection at interfaces in intelligent coating system. Appl. Math. Mech. 2015, 36, 465–474. [Google Scholar] [CrossRef]
- Djurabekova, F.; Domingos, R.; Cerchiara, G.; Castin, N.; Vincent, E.; Malerba, L. Artificial intelligence applied to atomistic kinetic Monte Carlo simulations in Fe–Cu alloys. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2006, 255, 8–12. [Google Scholar] [CrossRef]
- Ji, Y.C.; Fu, X.Q.; Ding, F.; Xu, Y.T.; He, Y.; Ao, M.; Xiao, F.L.; Chen, D.H.; Dey, P.; Qin, W.T.; et al. Artificial intelligence combined with high-throughput calculations to improve the corrosion resistance of AlMgZn alloy. Corros. Sci. 2024, 233, 112062. [Google Scholar] [CrossRef]
- Zhang, G.W.; Zhang, Y.G.; Xu, H.; Yu, H. Strong bonding effect and Zn segregation at Al/Fe bimetallic composite interface: A first-principles study. J. Mater. Res. 2023, 38, 3078–3088. [Google Scholar] [CrossRef]
- Obot, I.B.; Haruna, K.; Saleh, T.A. Atomistic simulation: A unique and powerful computational tool for corrosion inhibition research. Arab. J. Sci. Eng. 2019, 44, 1–32. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, L.; Wang, X.P.; Liu, B.; Zhang, Y.Y.; Lv, X.S.; Du, T. Interfacial regulation to improve interface heat transfer of Al/diamond composites based on molecular dynamics simulations. Diam. Relat. Mater. 2025, 153, 112029. [Google Scholar] [CrossRef]
- Ma, Y.; Xue, Q.; Kong, M.W.; Wang, T.; Fang, X.G.; Chen, Z.J. Study of atomic diffusion behavior in diffusion welding of NiTi alloy-based on molecular dynamics. Mater. Today Commun. 2024, 41, 110965. [Google Scholar] [CrossRef]
- Yuan, H.; Bao, H.W.; Zhao, Q.H.; Guo, Z.; Li, Y.; Ma, F. Oxygen modification enhanced bonding behaviors in Cu/graphene interface: First principles calculations. Surf. Interfaces 2025, 58, 105866. [Google Scholar] [CrossRef]
- Ding, Z.Y.; Jiu, Y.T.; Long, W.M.; Zhong, S.J.; Hou, J.T.; Ren, X.F.; Zhao, J.C.; Zhang, G.X.; Wei, S.Z. Microstructural evolution and bonding characteristics of Ag/Cu interface in Ag/Cu bimetallic strips fabricated via diffusion welding. J. Iron Steel Res. Int. 2025, 32, 1468–1476. [Google Scholar] [CrossRef]
- Li, H.; Huang, Z.; Xu, D.; Shen, Q.; Chen, F. Atomic-scale interfacial strengthening mechanism of nano intermetallic compounds in Ti-Ni bimetallic alloys. Mech. Mater. 2025, 205, 105329. [Google Scholar] [CrossRef]
- Huang, Y.X.; Huang, H.; Xu, X.P.; Wu, M.; Yu, Y.Q.; Duan, N. Analysis of diffusion in Fe/4H-SiC by molecular dynamics method. Precis. Eng. 2025, 95, 286–297. [Google Scholar] [CrossRef]
- Liu, G.J.; Li, J.L.; Yang, L.; Zhang, Y.S. Reactive molecular dynamics study on interfacial reaction behavior of Fe-Cr-Ni alloy. Electrochim. Acta 2025, 530, 146380. [Google Scholar] [CrossRef]
- Ren, J.Q.; Zhang, X.Y.; Gui, Y.C.; Wang, Q.; Zhang, X.D.; Lu, X.F. Mechanical response and plastic deformation in the B2-NiAl/Fe interface: Molecular dynamics analysis. J. Mater. Eng. Perform. 2024, 34, 4925–4933. [Google Scholar] [CrossRef]
- Yang, J.W.; Xie, C.H.; Zhang, J.; Ding, Z.Y.; Qiao, J. An atomic insight into effect of grain boundary on diffusion behavior of Cu/Al dissimilar materials undergoing ultrasonic welding. J. Iron Steel Res. Int. 2024, 31, 2555–2567. [Google Scholar] [CrossRef]
- Zhang, J.P.; Mao, A.X.; Wang, J.F.; Liu, C.Y.; Xie, J.P.; Jia, Y. Grain boundary heredity from Cu/Al solid–liquid interface via diffusion during the solidification processes. Chem. Phys. 2022, 552, 111369. [Google Scholar] [CrossRef]
- Chen, S.D.; Ke, F.J.; Zhou, M.; Bai, Y.L. Atomistic investigation of the effects of temperature and surface roughness on diffusion bonding between Cu and Al. Acta Mater. 2007, 55, 3169–3175. [Google Scholar] [CrossRef]
- Han, X.J.; Guo, Q.N.; Yang, S.E.; Wang, M.X.; Wang, J.F.; Liu, Q.; Wang, L.; Gu, G.; Qian, X. Molecular dynamics simulation of the effects of temperature and holding time on interfacial diffusion and mechanical properties of Cu/Al thin films. Hot Work. Process 2019, 48, 102–107. [Google Scholar] [CrossRef]
- Cui, Y.F.; Wang, W.Y.; Xie, J.P.; Wang, A.Q.; Mao, Z.P.; Gao, M. Molecular dynamics analysis of the diffusion process of the Cu/Al2Cu/Al system. J. Heat Treat. Mater. 2023, 44, 167–175. [Google Scholar] [CrossRef]
- Mao, A.X.; Zhang, J.P.; Yao, S.C.; Wang, A.Q.; Wang, W.Y.; Li, Y.; Qiao, C.; Xie, J.; Jia, Y. The diffusion behaviors at the Cu-Al solid-liquid interface: A molecular dynamics study. Results Phys. 2020, 16, 102998. [Google Scholar] [CrossRef]
- Qian, X.F.; Guo, Q.N.; Yang, S.E.; Wang, M.X.; Liu, Q.; Wang, J.F. Molecular dynamics simulation of connection and tensile properties of Cu/Al casting interface. Trans. Nonferrous Met. Soc. China 2020, 30, 2886–2900. [Google Scholar] [CrossRef]
- Li, J.R.; Chu, F.Q.; Feng, Y.H. Effect of atomic diffusion on interfacial heat transfer and tensile property of copper/aluminum composites. Mater. Today Commun. 2023, 36, 106757. [Google Scholar] [CrossRef]
- Li, Q.H.; Dong, Z.B.; Ji, S.D.; Yang, L.S.; Tao, C.C.; Zhou, S.Z.; Hu, G. Effects of welding parameter on atom-scale interfacial diffusion behavior of Al/Cu dissimilar friction stir welding. Physica Status solidi (b) 2021, 258, 2100123. [Google Scholar] [CrossRef]
- Chen, S.Y.; Wu, Z.W.; Liu, K.X.; Li, X.J.; Luo, N.; Lu, G.X. Atomic diffusion behavior in Cu-Al explosive welding process. J. Appl. Phys. 2013, 113, 044901. [Google Scholar] [CrossRef]
- Li, J.R.; Feng, Y.H.; Zhang, M.Y.; Sun, F.Y.; Chu, F.Q. Formation and effect of intermetallic compounds in the interface of copper/aluminum composites under rolling conditions. J. Mater. Res. Technol. 2024, 28, 1734–1742. [Google Scholar] [CrossRef]
- Bian, X.Q.; Wang, A.Q.; Xie, J.P.; Liu, P.; Mao, Z.P.; Chen, Y.; Liu, Z.; Gao, Y. Atomic-scale deformation mechanisms of nano-polycrystalline Cu/Al layered composites: A molecular dynamics simulation. J. Mater. Res. Technol. 2023, 24, 1177–1189. [Google Scholar] [CrossRef]
- Bian, X.Q.; Wang, A.Q.; Xie, J.P.; Liu, P.; Mao, Z.P.; Liu, Z.W. Effect of Al2Cu constituent layer thickness discrepancy on the tensile mechanical behavior of Cu/Al2Cu/Al layered composites: A molecular dynamics simulation. Nanotechnology 2023, 34, 445702. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, A.Q.; Guo, Z.S.; Xie, J.P. Molecular dynamics study of deformation mechanism of interfacial microzone of Cu/Al2Cu/Al composites under tension. Nanotechnol. Rev. 2022, 11, 1158–1166. [Google Scholar] [CrossRef]
- Wang, A.Q.; Bian, X.Q.; Mao, Z.P.; Hou, Y.X.; Xie, J.P.; Liu, P.; Liu, Z. Effect of solid solution and vacancies on the mechanical properties of Cu(Al)/Al2Cu/(Cu)Al layered gradient heterostructures. Phys. B: Condens. Matter 2024, 680, 415845. [Google Scholar] [CrossRef]
- Pang, W.W.; Xin, K.; Liu, A.S.; Chen, R.B.; Yu, S.Y. The effect of interface orientation on deformation behavior of Cu/Al multilayer during tensile process. Mater. Today Commun. 2023, 34, 105133. [Google Scholar] [CrossRef]
- Wang, X.L.; Cheng, G.; Zhang, Y.; Wang, Y.X.; Liao, W.J.; Venkatesh, T.A. On the evolution of nano-structures at the Al–Cu interface and the influence of annealing temperature on the interfacial strength. Nanomaterials 2022, 12, 3658. [Google Scholar] [CrossRef]
- Wang, M.D.; Zhang, J.P.; Wang, A.Q.; Liang, T.T.; Xie, J.P. Molecular dynamics study on the deformation mechanism of Cu–Zr/Al laminated composites. J. Mater. Res. Technol. 2024, 33, 3894–3900. [Google Scholar] [CrossRef]
- Jin, Y.H.; Hu, B.R.; Luo, P.; Wang, H.L.; Luo, X.F. Simulation of atomic diffusion and mechanical properties at the interface of copper/aluminum friction stir welded joints. J. Lanzhou Univ. Technol. 2024, 50, 7–16. [Google Scholar] [CrossRef]
- Pang, W.W.; Xin, K.; Liu, A.S.; Yu, S.Y.; Feng, X.T. The effect of loading axes on deformation behavior of Cu/Al multilayer. Phys. Lett. A 2023, 458, 128587. [Google Scholar] [CrossRef]
- Gao, X.B.; Abbas, W.N.; Al-zahy, Y.M.A.; Al-Bahrani, M.; Kumar, N.; Hanoon, Z.A.; Salahshour, S.; Pirmoradian, M. Application of electric field to aluminum/copper/aluminum trilayer nanocomposites and determination of mechanical properties: A molecular dynamics approach. Phys. A: Stat. Mech. Its Appl. 2024, 653, 130104. [Google Scholar] [CrossRef]
- Liu, X.P.; Yan, J.H. Influence of interface on deformation compatibility of a heterogeneous Cu/Al nanoscale multilayer. Mater. Today Commun. 2024, 40, 109510. [Google Scholar] [CrossRef]
- Yin, F.X.; Zhao, Y.Z.; Yu, S.Y.; Pang, W.W. Molecular dynamics studies on the interface evolution characteristics and deformation mechanisms of Cu/Al multilayers during compression process. J. Appl. Phys. 2019, 125, 025112. [Google Scholar] [CrossRef]
- Zhang, T.T.; Wang, W.X.; Zhou, J.; Cao, X.Q.; Xie, R.S.; Wei, Y. Molecular dynamics simulations and experimental investigations of atomic diffusion behavior at bonding interface in an explosively welded Al/Mg alloy composite plate. Acta Metall. Sin. (Engl. Lett.) 2017, 30, 983–991. [Google Scholar] [CrossRef]
- Li, Y.; Lv, X.Q.; Li, X.Y. Diverse yielding regimes of two Mg-Al composite structures predicted by molecular dynamics simulations. Mater. Today Commun. 2024, 39, 109298. [Google Scholar] [CrossRef]
- Li, Z.; Shen, T.; Hu, X.; Zhang, L.; Jia, X.; Li, J.; Zhang, C. The plastic deformation mechanism in nano-polycrystalline Al/Mg layered composites: A molecular dynamics study. Nanomaterials 2024, 14, 114. [Google Scholar] [CrossRef] [PubMed]
- Lv, X.Q.; Li, X.Y.; Liu, H.B. Coherent-interface-induced second hardening deformation of Al–Mg–Al nanolayers by molecular dynamics simulations. Phys. Chem. Chem. Phys. 2022, 24, 10373–10377. [Google Scholar] [CrossRef]
- Pogorelko, V.V.; Mayer, A.E. Tensile strength of Fe–Ni and Mg–Al nanocomposites: Molecular dynamic simulations. J. Phys. Conf. Ser. 2018, 946, 012043. [Google Scholar] [CrossRef]
- Xu, Y.C.; Jiang, W.M.; Li, Q.Q.; Niu, Y.Q.; Yu, L.H.; Li, G.Y.; Fan, Z. Significantly improved bonding strength of Al/Mg bimetallic interface by compound casting via FeCoNiCrCu high entropy alloy coating. J. Mater. Res. Technol. 2024, 30, 6870–6876. [Google Scholar] [CrossRef]
- Li, X.Y.; Lv, X.Q.; Wang, Y.S.; Yang, J.; Liu, H.B. Nonuniform-to-uniform structural transitions induced by ultrasonic vibrations. Nanoscale 2023, 15, 4899–4909. [Google Scholar] [CrossRef]
- Li, Z.; Shen, T.; Li, J.H.; Xia, S.Q.; Yu, L.; Zhang, C. Developing a dual-mode confined layer slip model for Al/Mg composites with incoherent FCC/HCP interfaces: Insights from molecular dynamics studies. Next Mater. 2025, 6, 100433. [Google Scholar] [CrossRef]
- Polyakova, P.V.; Pukhacheva, J.A.; Shcherbinin, S.A.; Baimova, J.A.; Mulyukov, R.R. Fabrication of Magnesium-Aluminum Composites under High-Pressure Torsion: Atomistic Simulation. Appl. Sci. 2021, 11, 6801. [Google Scholar] [CrossRef]
- Zhang, C.G.; Wang, H.; Qiu, Y.S. Study of Ni/Al interface diffusion by molecular dynamics simulation. Engineering 2011, 3, 227–232. [Google Scholar] [CrossRef]
- Hu, Z.J.; Zhang, J.J.; Yan, Y.D.; Yan, J.H.; Sun, T. Molecular dynamics simulation of tensile behavior of diffusion bonded Ni/Al nanowires. J. Mech. Sci. Technol. 2013, 27, 43–46. [Google Scholar] [CrossRef]
- Dai, Y.M.; Dai, Y.J. A MD study on the temperature influence on Ni/Al interface at initial diffusion time. Appl. Mech. Mater. 2014, 496–500, 21–25. [Google Scholar] [CrossRef]
- Dai, Y.M.; Zhu, S.L.; Wang, F.H. Study on Ni/Al interface diffusion at initial time by using molecular dynamics method. Adv. Mater. Res. 2012, 391–392, 42–45. [Google Scholar] [CrossRef]
- Smith, G.D.; Bedrov, D.; Hooper, J. Molecular dynamics simulations of isothermal reactions in Al/Ni nanolaminates. J. Chem. Phys. 2019, 150, 214702. [Google Scholar] [CrossRef] [PubMed]
- Linde, A.; Politano, O.; Baras, F. Study of the reactive dynamics of nanometric metallic multilayers using molecular dynamics: The Al-Ni system. Defect Diffus. Forum 2012, 323–325, 89–94. [Google Scholar] [CrossRef]
- Politano, O.; Baras, F.; Mukasyan, A.S.; Vadchenko, S.G.; Rogachev, A.S. Microstructure development during NiAl intermetallic synthesis in reactive Ni–Al nanolayers: Numerical investigations vs. TEM observations. Surf. Coat. Technol. 2013, 215, 485–492. [Google Scholar] [CrossRef]
- Kunwar, A.; Yousefi, E.; Zuo, X.J.; Sun, Y.Q.; Seveno, D.; Guo, M.X.; Moelans, N. Multi-phase field simulation of Al3Ni2 intermetallic growth at liquid Al/solid Ni interface using MD computed interfacial energies. Int. J. Mech. Sci. 2022, 215, 106930. [Google Scholar] [CrossRef]
- Kolli, S.; Yousefi, E.; Sun, Y.Q.; Kunwar, A.; Guo, M.X.; Moelans, N.; Seefeldt, M.; Seveno, D. Fracture mechanisms of Ni-Al interfaces–A nanoscale view. Mater. Today Commun. 2022, 32, 103967. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, Y.S. Atomic diffusion behavior within and between layers in Al/Ni nanolaminates under electro-thermo-mechanical multifield coupling. Sci. China: Technol. Sci. 2024, 54, 315–332. [Google Scholar] [CrossRef]
- Qiao, C.; Fu, X.N.; Chi, R.Z.; Guo, Y.Y.; Wang, Q.X.; Liu, C.Y.; Wang, F.; Jia, Y. Inhibition effect on the evolution of a twist grain boundary for an Al/Ni bimetal interface under torsion. RSC Adv. 2015, 5, 102400–102408. [Google Scholar] [CrossRef]
- Zheng, D.L.; Chen, S.D.; Soh, A.K.; Ma, Y. Molecular dynamics simulations of glide dislocations induced by misfit dislocations at the Ni/Al interface. Comput. Mater. Sci. 2010, 48, 551–555. [Google Scholar] [CrossRef]
- Moon, S.; Paek, J.H.; Jang, Y.H.; Kang, K. Mixing behavior of Ti–Al interface during the ultrasonic welding process and its welding strength: Molecular dynamics study. Heliyon 2024, 10, e25116. [Google Scholar] [CrossRef]
- Liu, J.Y.; Zhang, L.Q. Investigation on the diffusion behaviors and mechanical properties of the Ti/Al interface using molecular dynamics simulation. J. Mater. Eng. Perform. 2023, 33, 2920–2939. [Google Scholar] [CrossRef]
- Tang, F.L.; Zhou, J.; Bao, H.W.; Lu, W.J.; Rui, Z.Y. Molecular dynamics simulation of interfacial behavior in Ti-Al diffusion-bonded joints under tensile loading. J. Lanzhou Univ. Technol. 2015, 41, 1–6. [Google Scholar] [CrossRef]
- Wang, H.N.; Zhang, H.; Liu, R.; Li, Y.M.; Zhan, H.F. Molecular dynamic simulation of characteristics and mechanical properties of hot-pressed Ti/Al interfaces. J. Plast. Eng. 2024, 31, 131–139. [Google Scholar] [CrossRef]
- Malekpour, F.; Aghili, S.; Panjepour, M.; Meratian, M.; Alizadeh, J. Theoretical and experimental study on the formation mechanisms of TiAl: Using the method of molecular dynamics simulation and SPS method. JOM 2023, 75, 4894–4909. [Google Scholar] [CrossRef]
- Kiselev, S.; Ryashin, N. Ti-Al intermetallic compounds synthesis in coatings deposited by cold spraying. AIP Conf. Proc. 2016, 1770, 030093. [Google Scholar] [CrossRef]
- Kiselev, S.P.; Ryashin, N.S.; Maximovsky, E.A.; Kiselev, V.P.; Filippov, A.A.; Polukhin, A.A. Simulation of Ti-Al intermetallic compound synthesis using cold spraying. AIP Conf. Proc. 2017, 1893, 030036. [Google Scholar] [CrossRef]
- An, M.R.; Song, H.Y.; Deng, Q.; Su, M.J.; Liu, Y.M. Influence of interface with mismatch dislocations on mechanical properties of Ti/Al nanolaminate. J. Appl. Phys. 2019, 125, 165307. [Google Scholar] [CrossRef]
- Lu, X.C.; Ran, H.; Cheng, Q.; Guo, F.J.; Huang, C.X. Underlying mechanisms of enhanced plasticity in Ti/Al laminates at elevated temperatures: A molecular dynamics study. J. Mater. Res. Technol. 2024, 28, 31–42. [Google Scholar] [CrossRef]
- An, M.R.; Deng, Q.; Su, M.J.; Song, H.Y.; Li, Y.L. Dependence of deformation mechanisms on layer spacing in multilayered Ti/Al composite. Mater. Sci. Eng. A 2017, 684, 491–499. [Google Scholar] [CrossRef]
- Chen, S.Q.; Wang, H.N.; Yan, P.X.; Li, S.F.; Zhang, H.; Zhan, H.F. Molecular dynamics simulation of temperature and Ti volume fraction on compressive properties of Ti/Al layered composites. Metals 2024, 14, 1182. [Google Scholar] [CrossRef]
- El Chlouk, Z.; Kassem, W.; Shehadeh, M.; Hamade, R.F. On the mechanical response and intermetallic compound formation in Al/Fe interface: Molecular dynamics analyses. Philos. Mag. 2020, 100, 3041–3060. [Google Scholar] [CrossRef]
- Luo, Q.; Liu, W.; Li, W.H.; Gu, Q.F.; Wang, B.J.; Li, Q. Revisiting selective nucleation at heterophase interfaces in Fe–Al solid-liquid reaction. J. Mater. Res. Technol. 2022, 17, 452–458. [Google Scholar] [CrossRef]
- Liu, S.Y.; Xu, H.; Zhang, B.H.; Zhang, G.W.; Bai, L.; Song, H.Q.; Zhang, D.; Chang, C.; Yu, H.; Yang, C.L. The Effect of the Cu Interlayer on the Interfacial Microstructure and Mechanical Properties of Al/Fe Bimetal by Compound Casting. Materials 2023, 16, 5469. [Google Scholar] [CrossRef]
- El Chlouk, Z.G.; Shehadeh, M.A.; Hamade, R.F. The effect of strain rate and temperature on the mechanical behavior of Al/Fe interface under compressive loading. Metall. Mater. Trans. A 2020, 51, 2573–2589. [Google Scholar] [CrossRef]
- Chen, N.J.; Devaraj, A.; Mathaudhu, S.N.; Hu, S.Y. Atomic mixing mechanisms in nanocrystalline Cu/Ni composites under continuous shear deformation and thermal annealing. J. Mater. Res. Technol. 2023, 27, 6792–6798. [Google Scholar] [CrossRef]
- Sun, J.X.; Xu, J.G.; Wang, Y.P. Atomic-scale interfacial dynamics in Cu-Ni diffusion bonding: A molecular dynamics study. Ordnance Mater. Sci. Eng. 2013, 36, 68–71. [Google Scholar] [CrossRef]
- Pang, W.W.; Yang, K.; Liu, A.S.; Han, F.Y. The effect of Fe solute atom on interface structure and deformation behavior of Cu/FexNi1-x layered composites by molecular dynamics. Mater. Today Commun. 2024, 40, 110161. [Google Scholar] [CrossRef]
- Chen, G.; Wang, C.J.; Zhang, P. The role of interface in uniaxial tensile process of nano-scale bilayer Cu/Ni. Comput. Mater. Sci. 2017, 131, 21–27. [Google Scholar] [CrossRef]
- Weng, S.Y.; Ning, H.M.; Hu, N.; Yan, C.; Fu, T.; Peng, X.H. Strengthening effects of twin interface in Cu/Ni multilayer thin films–A molecular dynamics study. Mater. Des. 2016, 111, 1–8. [Google Scholar] [CrossRef]
- Fu, T.; Peng, X.H.; Weng, S.Y.; Zhao, Y.B.; Gao, F.S.; Deng, L.J.; Wang, Z. Molecular dynamics simulation of effects of twin interfaces on Cu/Ni multilayers. Mater. Sci. Eng. A 2016, 658, 1–7. [Google Scholar] [CrossRef]
- Yang, M.; Xu, J.G.; Song, H.Y.; Zhang, Y.G. Effects of tilt interface boundary on mechanical properties of Cu/Ni nanoscale metallic multilayer composites. Chin. Phys. B 2015, 24, 096202. [Google Scholar] [CrossRef]
- Chen, S.D.; Zhou, Y.K.; Soh, A.K. Molecular dynamics simulations of mechanical properties for Cu(001)/Ni(001) twist boundaries. Comput. Mater. Sci. 2012, 61, 239–242. [Google Scholar] [CrossRef]
- Wu, C.D.; Huang, B.X.; Li, H.X. Effects of interfacial defect on deformation and mechanical properties of Cu/Ni bilayer—A molecular dynamics study. Thin Solid Film. 2020, 707, 138050. [Google Scholar] [CrossRef]
- Chong, C.; Chen, S.D.; Wu, Y.Z.; Huang, H.X. Strain-rate-dependent deformation mechanisms in nanocrystalline Cu/Ni bilayer thin films: A molecular dynamics study. Mater. Eng. 2015, 43, 60–66. [Google Scholar] [CrossRef]
- Zhang, G.W.; Kang, Y.Y.; Wang, M.J.; Xu, H.; Jia, H.M. Atomic diffusion behavior and diffusion mechanism in Fe–Cu bimetal casting process studied by molecular dynamics simulation and experiment. Mater. Res. Express 2020, 7, 096519. [Google Scholar] [CrossRef]
- Zhang, G.W.; Wang, M.J.; Yu, H.; Xu, H.; Wan, A. Molecular dynamics and experimental investigation on the interfacial binding mechanism in the Fe/Cu1-x-Nix bimetallic interface. Nanomaterials 2022, 12, 3245. [Google Scholar] [CrossRef]
- Zheng, H.Y.; Sun, J.W.; Guo, N.; Wang, M.J. Atomic research on the diffusion behavior, mechanical properties and fracture mechanism of Fe/Cu solid–liquid interface. Coatings 2022, 12, 1299. [Google Scholar] [CrossRef]
- Hammood, H.S.; Irhayyim, S.S.; Awad, A.Y.; Abdulhadi, H.A. Influence of multiwall carbon nanotube on mechanical and wear properties of Copper–Iron composite. Int. J. Automot. Mech. Eng. 2020, 17, 7570–7576. [Google Scholar] [CrossRef]
- Chen, W.; Hu, X.H.; Hu, Q.; Zou, J.; Guo, W.; Lu, D.P. A novel liquid-liquid method for preparing bimetallic composites using liquid phase separation phenomenon. Vacuum 2024, 219, 112765. [Google Scholar] [CrossRef]
- Feng, J.R.; Dai, K.D.; Zhou, Q.; Xie, J.; Yang, R.J.; Bataev, I.A.; Chen, P. Formation of bonding interface in explosive welding-a molecular dynamics approach. J. Phys. Condens. Matter 2019, 31, 415403. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.J.; Mi, S.T.; Sun, L.; Yang, L.Y.; Gong, H.R. Mechanical properties and dislocation evolution of Cu–Fe interfaces from molecular dynamics simulation. Mater. Chem. Phys. 2021, 262, 124270. [Google Scholar] [CrossRef]
- Lin, Z.J.; Pang, W.W.; Xin, K.; Feng, X.T.; Yin, F.X. The effect of loading strain rates on deformation behavior of Cu/Fe composite. Phys. Lett. A 2021, 388, 127070. [Google Scholar] [CrossRef]
- Wang, S.; Cai, X.; Wang, Z.; Ju, J.; Zhou, J.; Xue, F. The inhibition mechanism of liquid metal embrittlement cracks in the Fe-Cu system by Al: Atomistic simulations and calculations. J. Mater. Sci. 2023, 58, 12673–12684. [Google Scholar] [CrossRef]
- Yang, H.K.; Qiu, J.; Cao, C.; Li, Y.D.; Song, Z.X.; Liu, W.J. Theoretical design and experimental study of the interlayer of Al/Mg bimetallic composite plate by solid-liquid cast rolling. Mater. Sci. Eng. A 2022, 835, 142677. [Google Scholar] [CrossRef]
- Xie, J.S.; Zhang, J.H.; You, Z.H.; Liu, S.J.; Guan, K.; Wu, R.Z.; Wang, J.; Feng, J. Towards developing Mg alloys with simultaneously improved strength and corrosion resistance via RE alloying. J. Magnes. Alloys 2021, 9, 41–56. [Google Scholar] [CrossRef]
- Li, G.Q.; Li, D.Y.; Zhang, N.Y.; Fan, X.N.; Zhang, H.M. Study on in situ formation of intermetallic compounds and oxygen adsorption of Ni/Al coating. J. Therm. Spray Technol. 2023, 32, 1828–1839. [Google Scholar] [CrossRef]
- Kuryntsev, S. A review: Laser welding of dissimilar materials (Al/Fe, Al/Ti, Al/Cu)—Methods and techniques, microstructure and properties. Materials 2022, 15, 122. [Google Scholar] [CrossRef]
- Hao, Z.L.; Li, X.; Liu, J.L.; Xie, Y.M.; Wen, Q.; Meng, X.C.; Huang, Y.; Wan, L. Expanding-welding: A hybrid deformation and welding process for joining dissimilar metals. J. Mater. Process. Technol. 2022, 303, 117535. [Google Scholar] [CrossRef]
- Wu, P.F.; Liu, R.X.; Li, W.B.; Zhang, W.; Wei, J.R.; Zhou, Q.H.; Wei, T.; Kardani, A.; Lin, Z.D.; Xiao, Y.; et al. Interface optimization by introducing Ti for strengthening graphene network/copper composites: New insight from MD simulations. Carbon 2025, 236, 120109. [Google Scholar] [CrossRef]
- Wu, P.F.; Kardani, A.; Liu, M.B.; Lin, Z.D.; Bagherifard, S. Exploring the bonding mechanism in cold spray deposition of engineered graphene nanoplates-Ni nanocomposite powder. Compos. Part A 2025, 191, 108741. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.J.; Zhao, J.; Qin, S.H.; Wei, W.Q.; Zhai, B.; Wang, Z.N.; Liu, G. Effect of Electric Field on the Microstructure and Properties of NiAl Alloy Sheet Prepared by Foil Reaction Synthesis. J. Mater. Eng. Perform. 2023, 33, 4570–4578. [Google Scholar] [CrossRef]

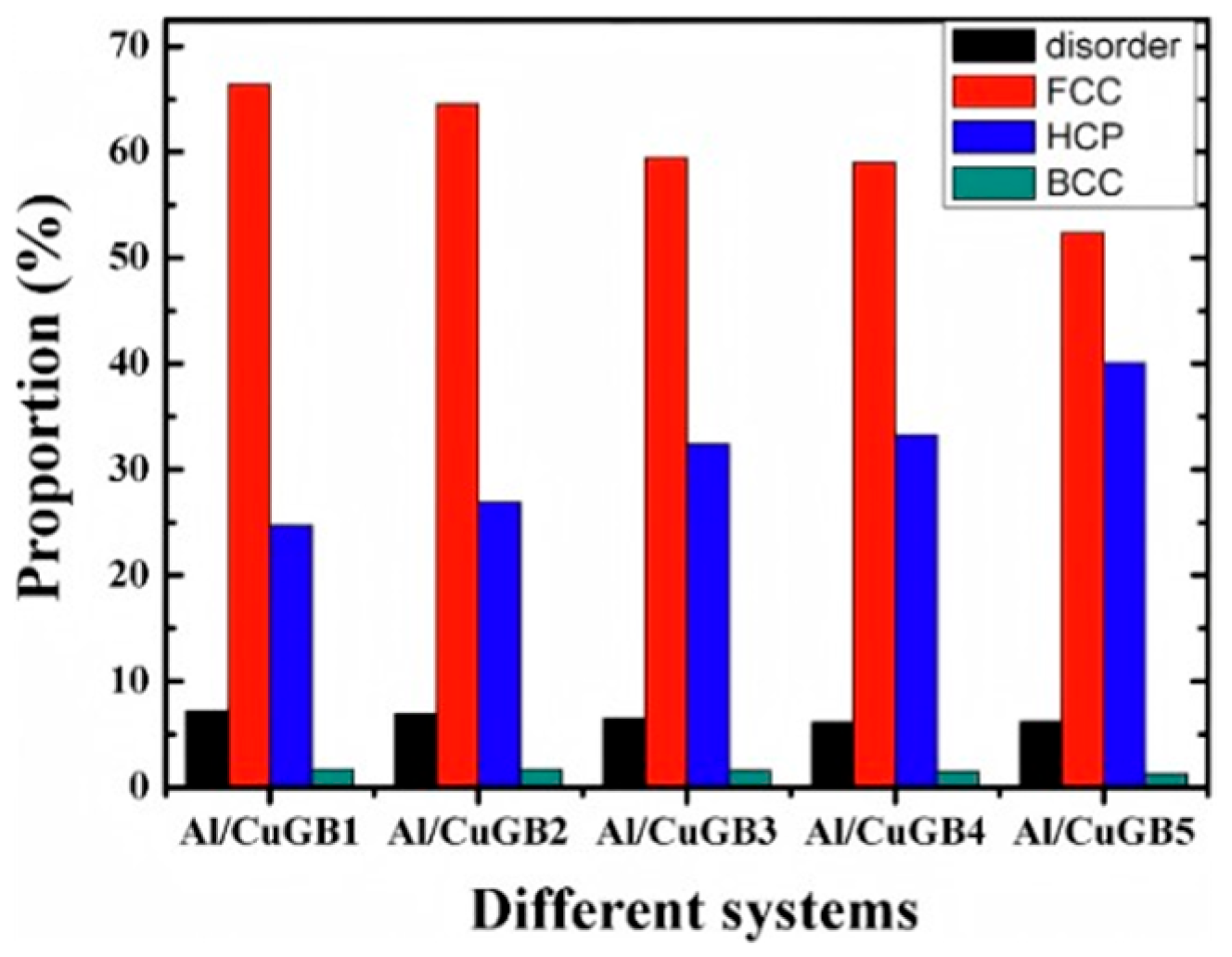


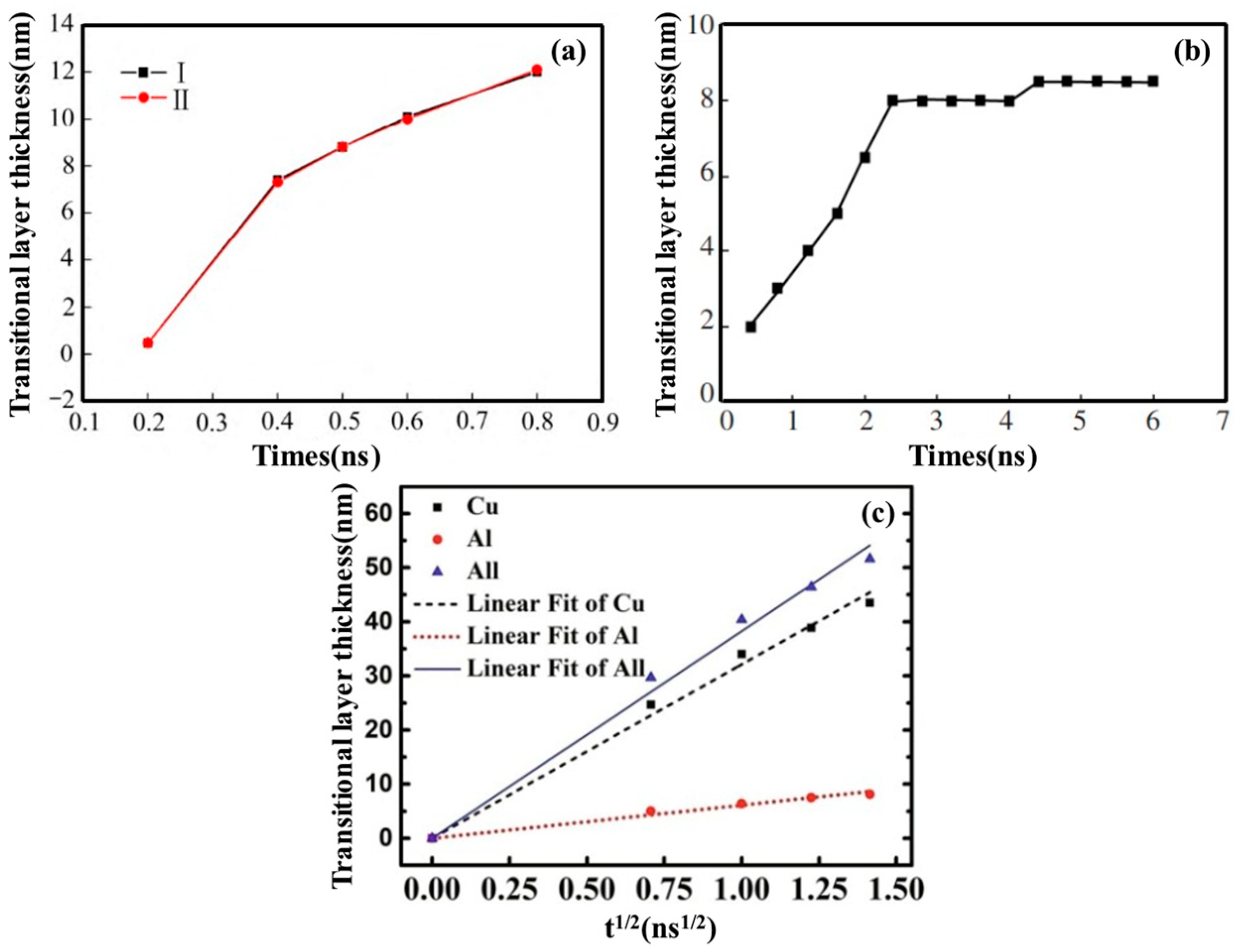
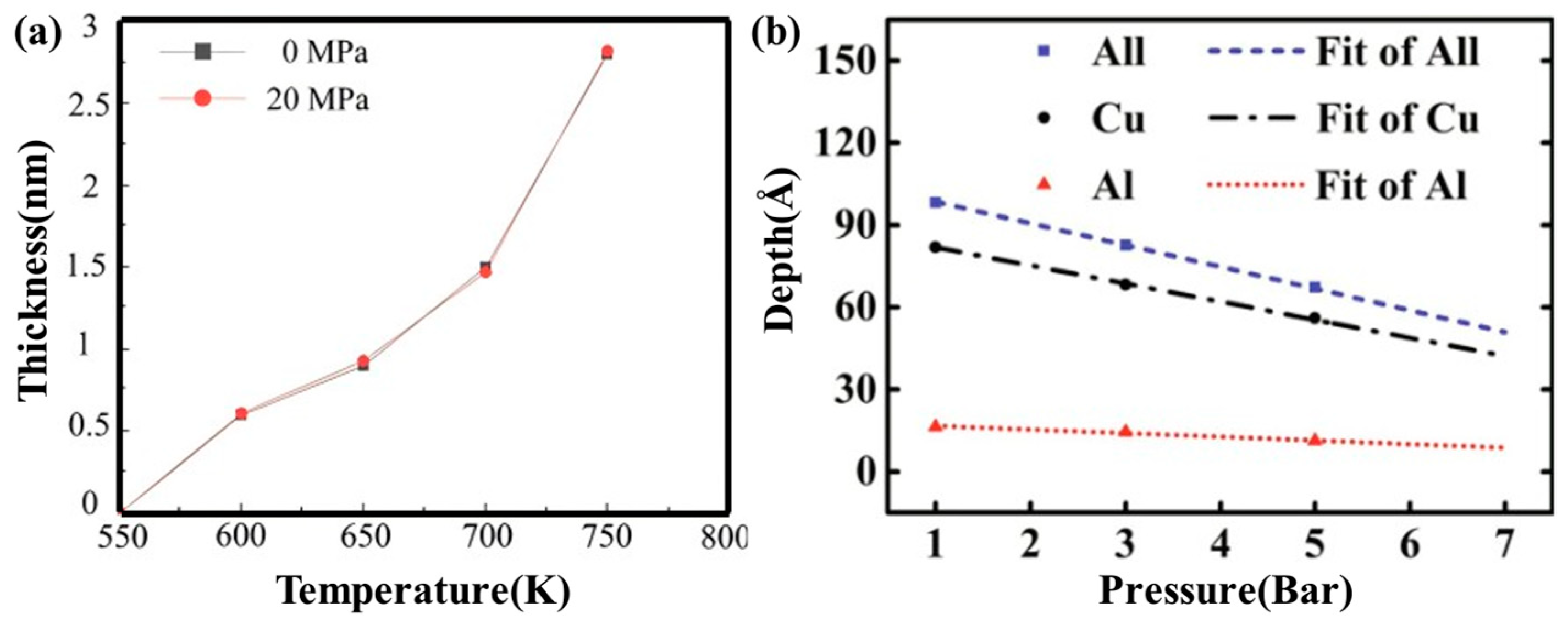
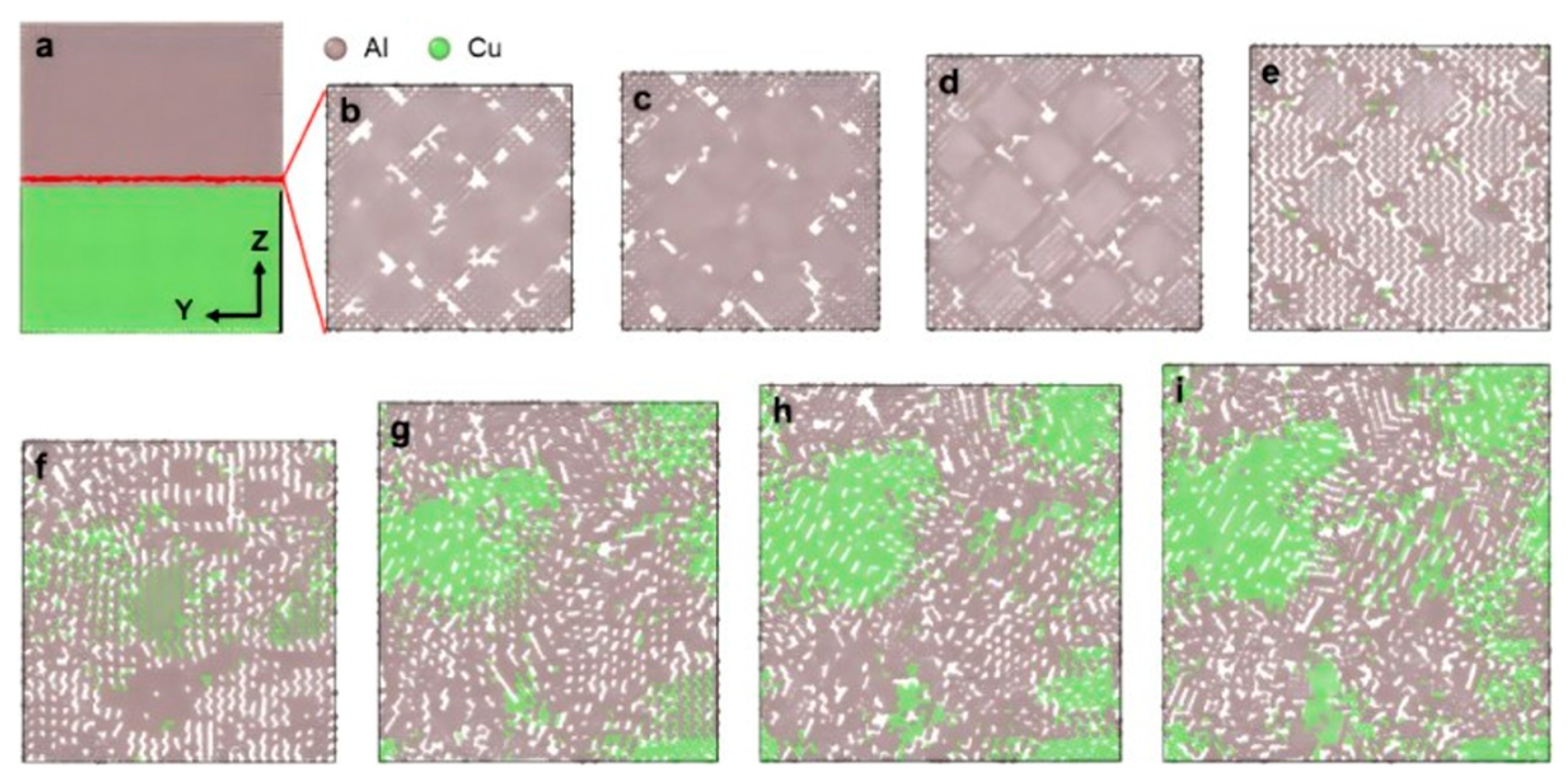
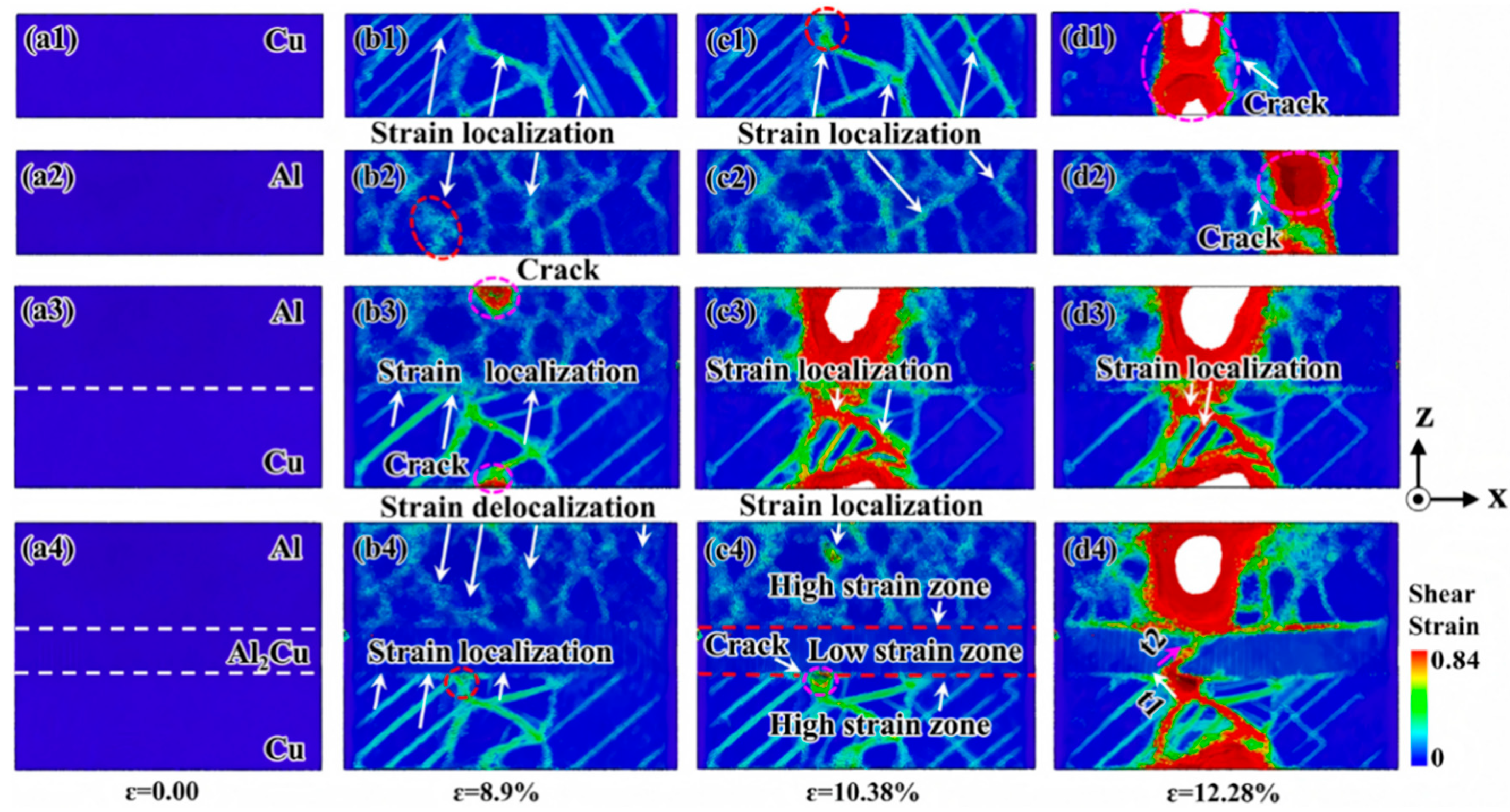
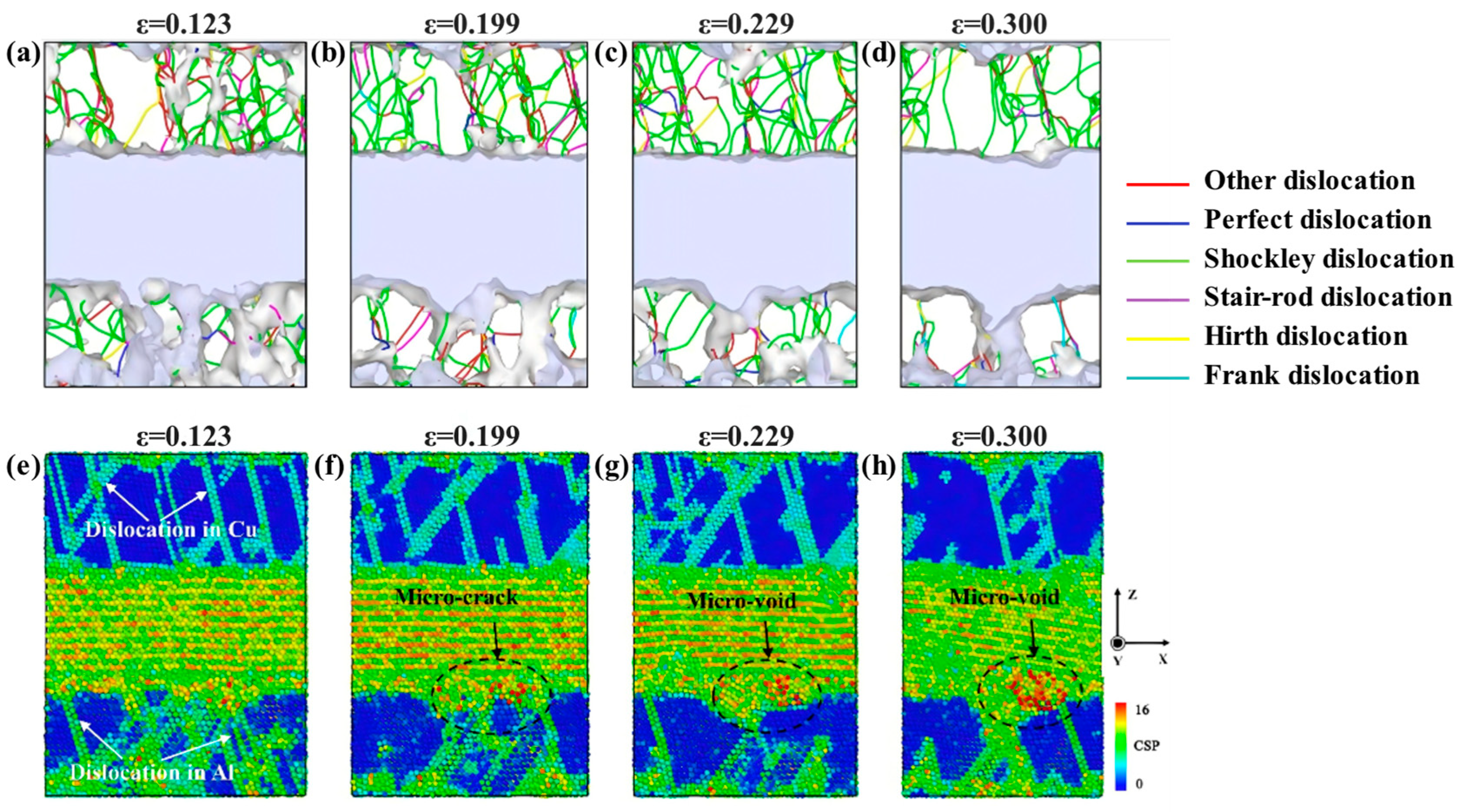
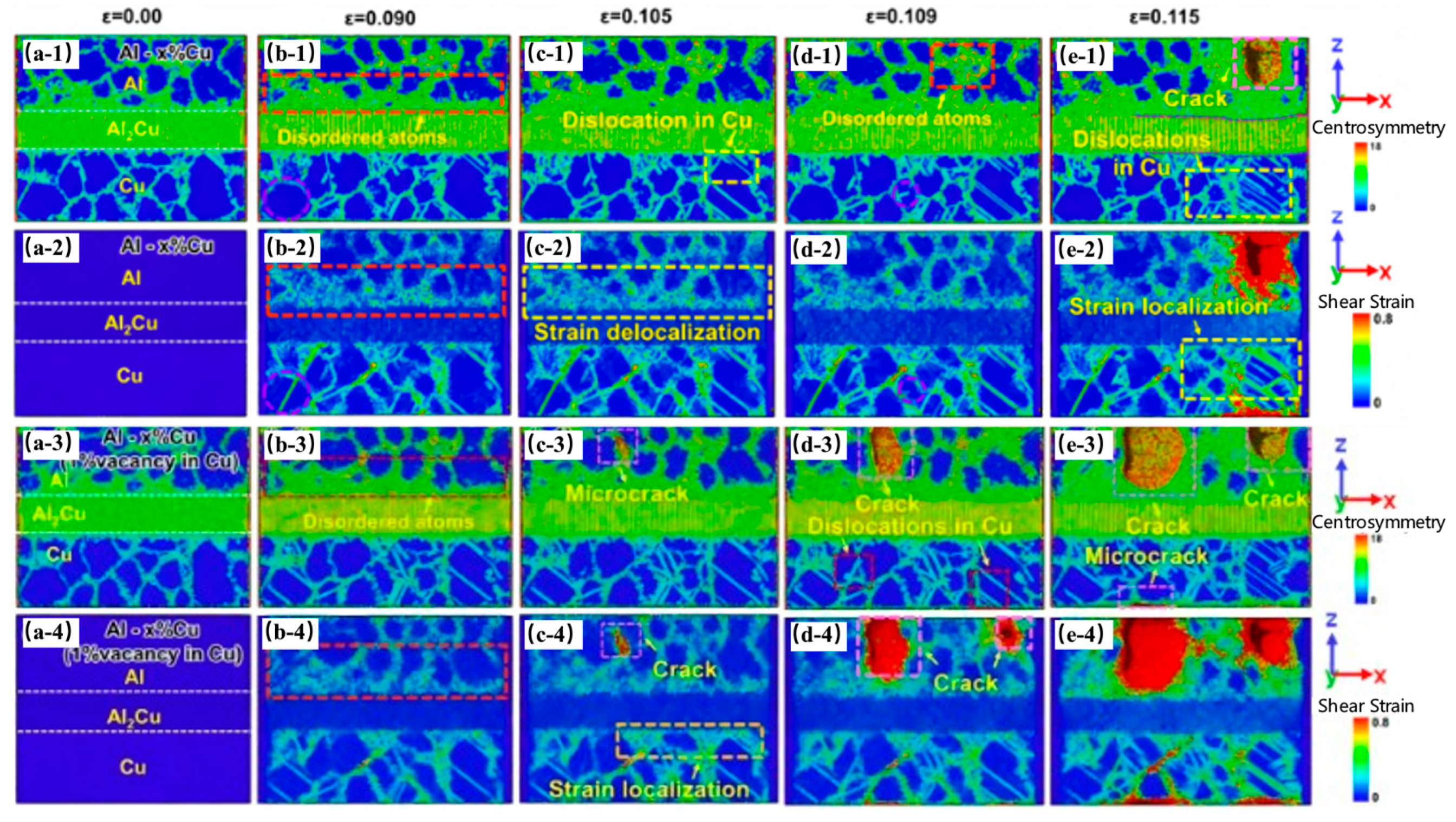
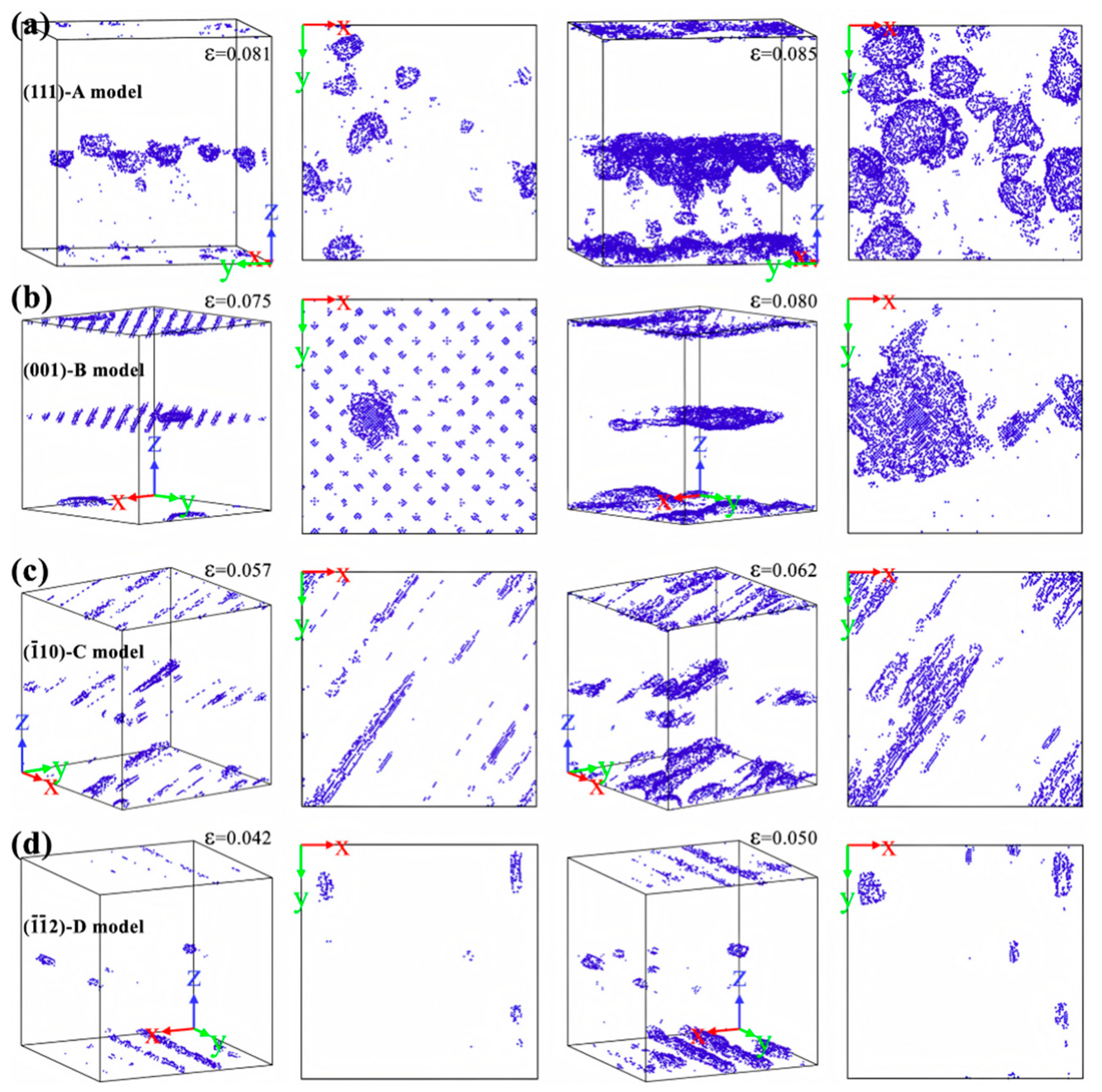
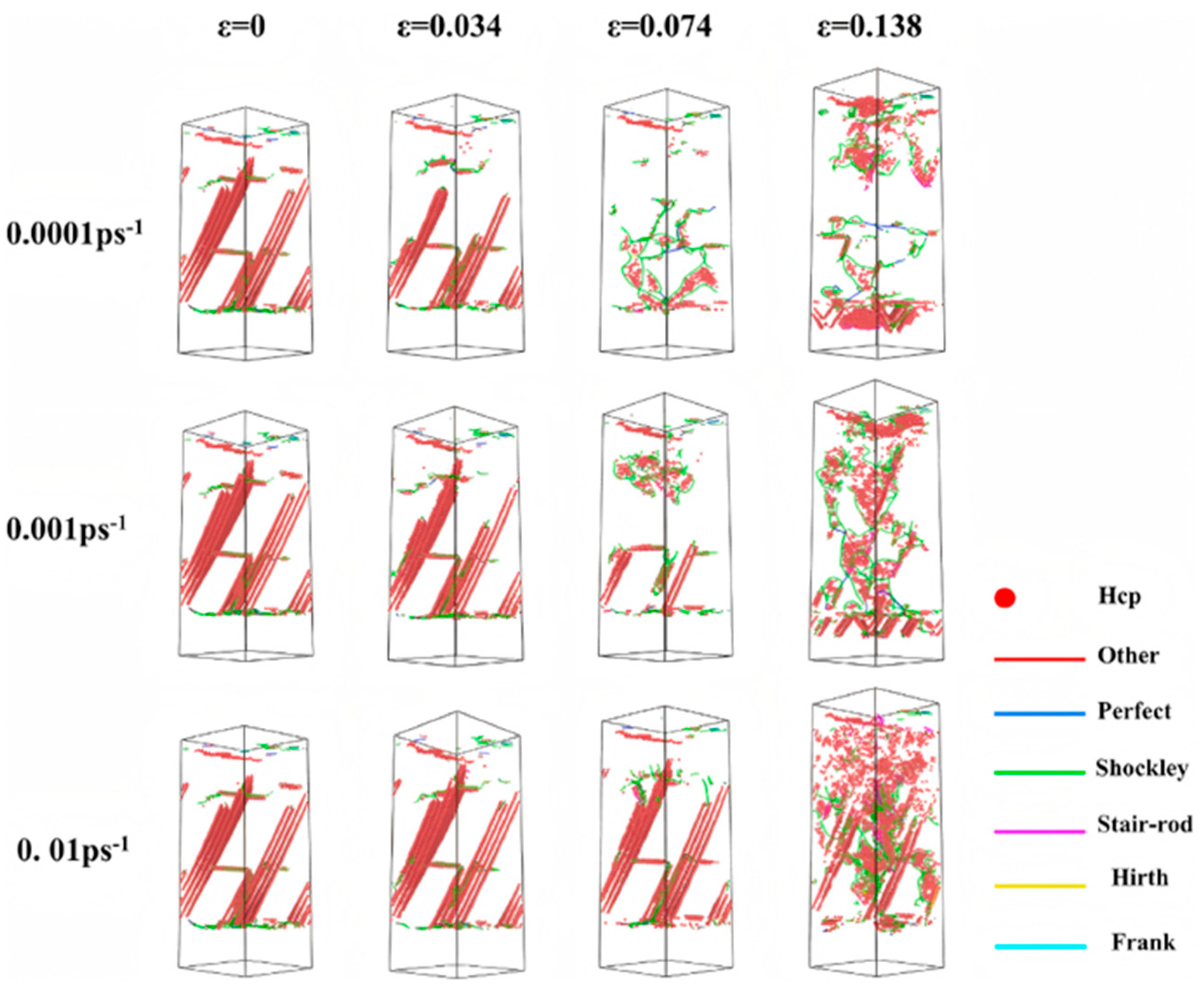
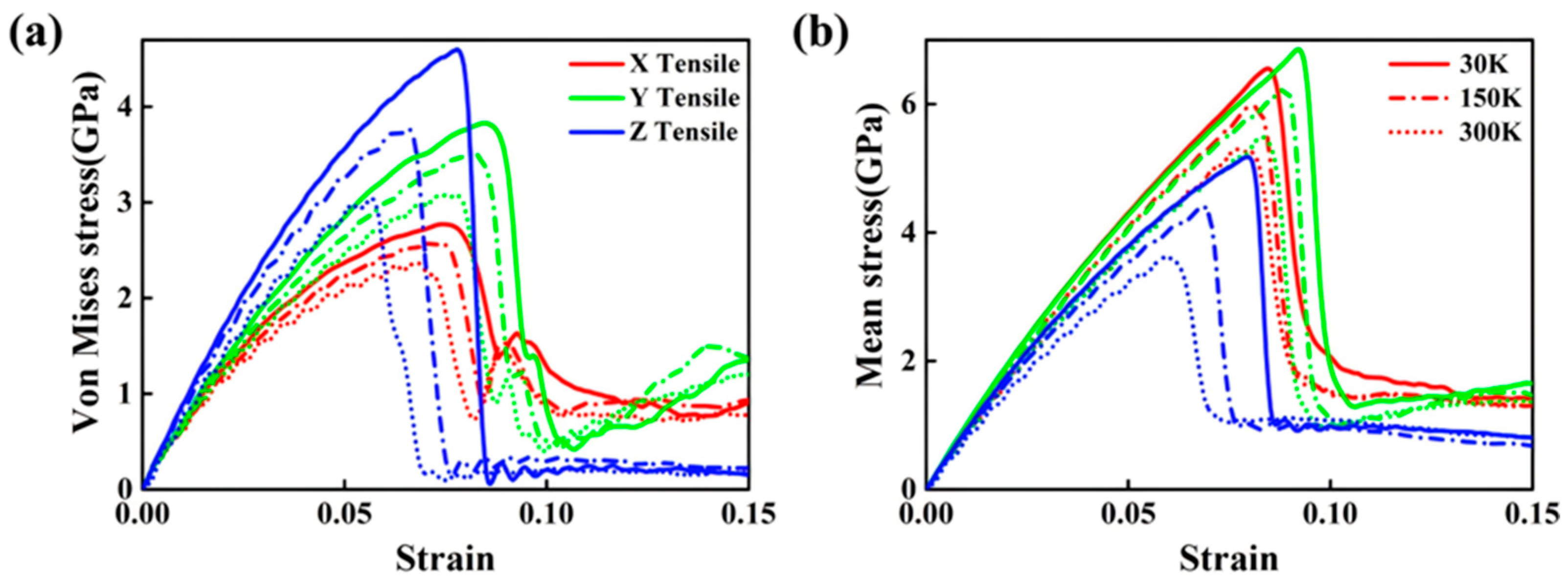
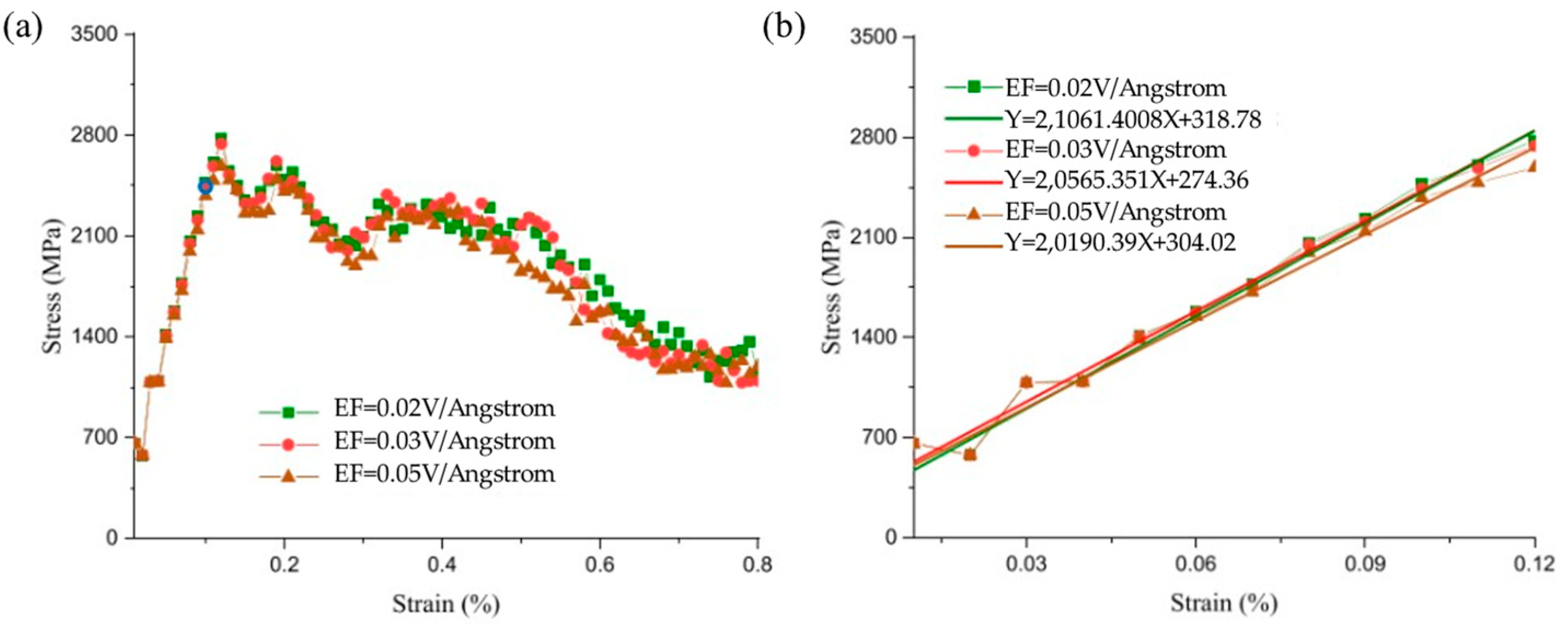
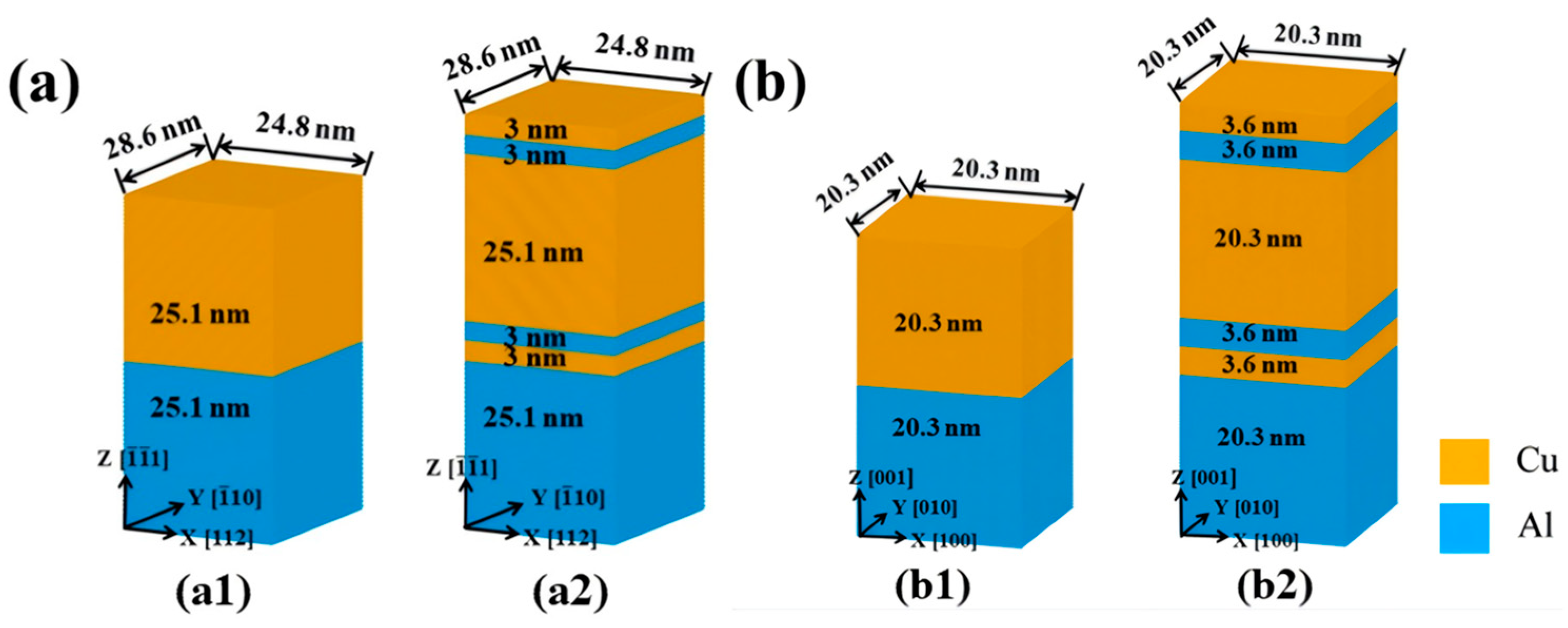
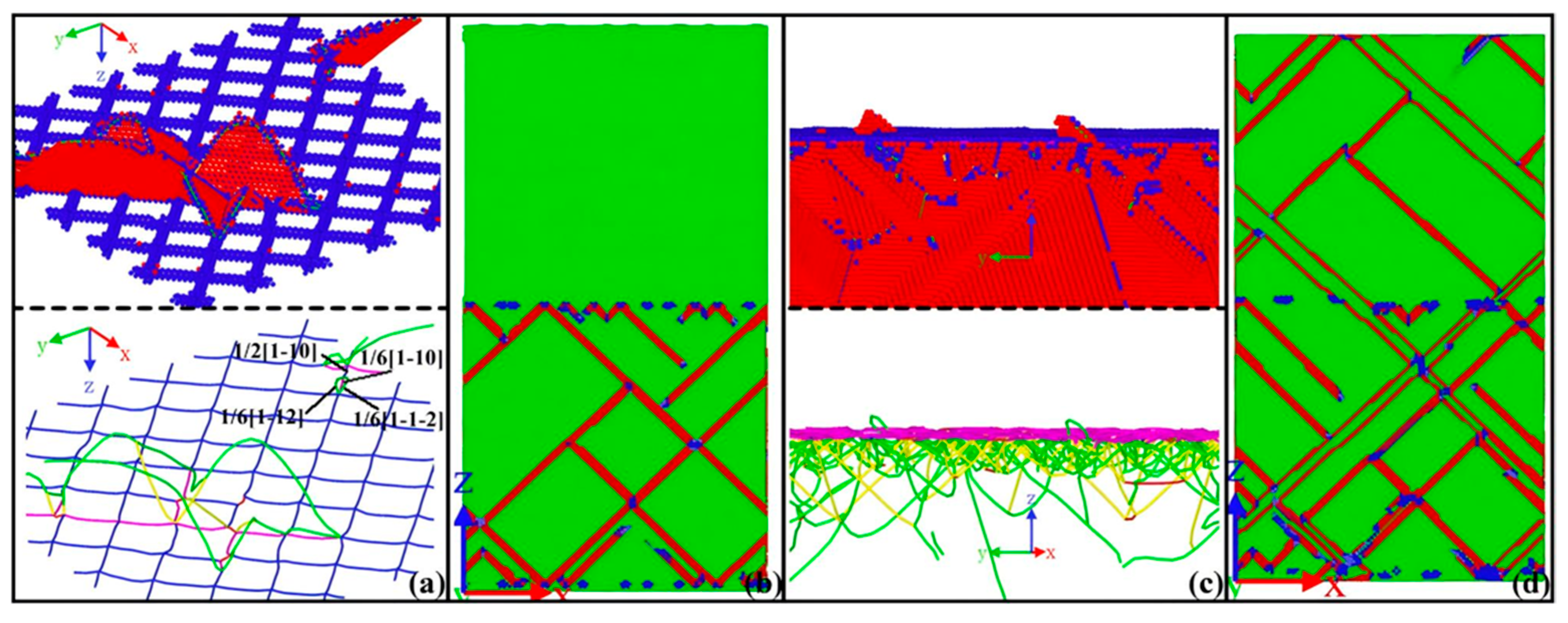
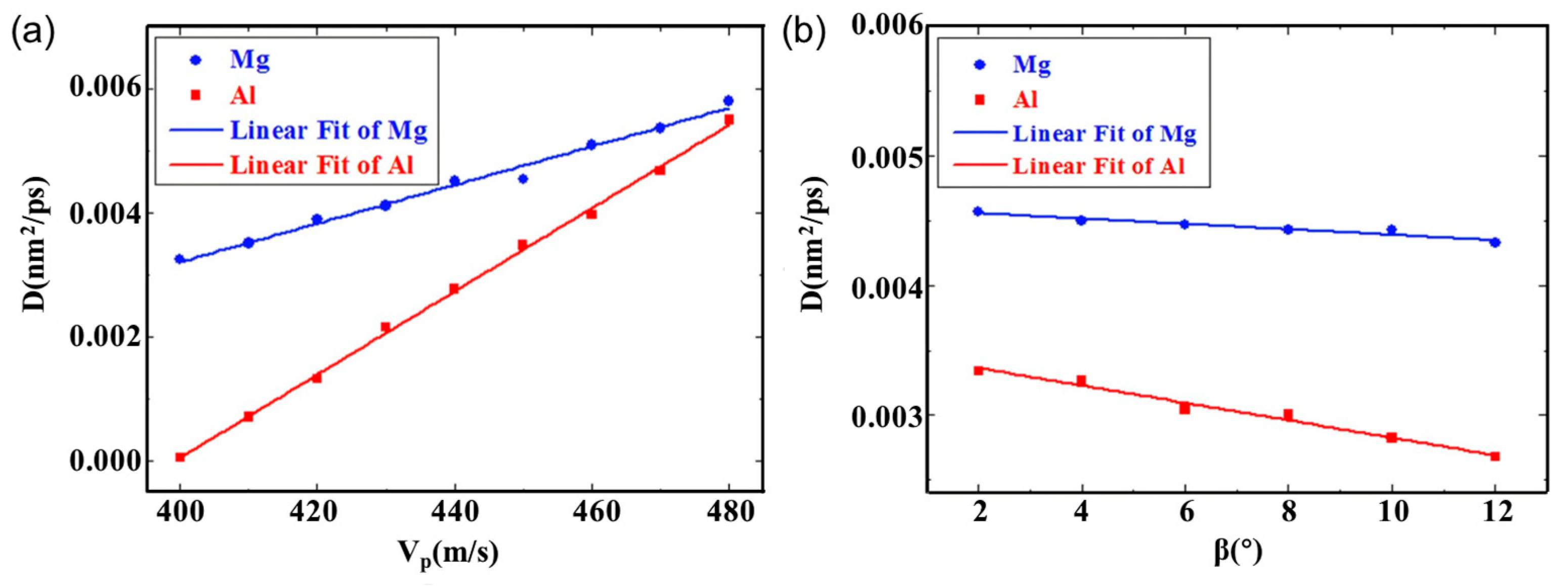
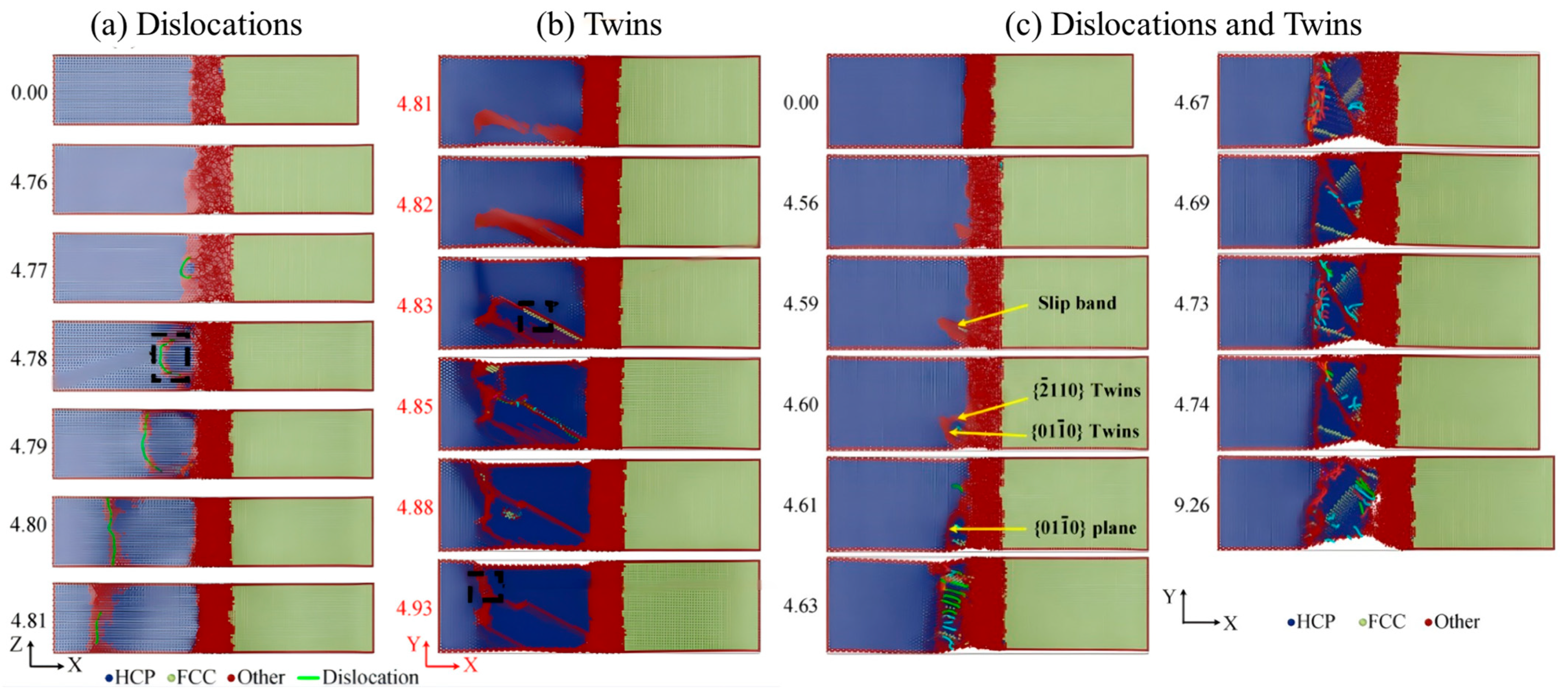

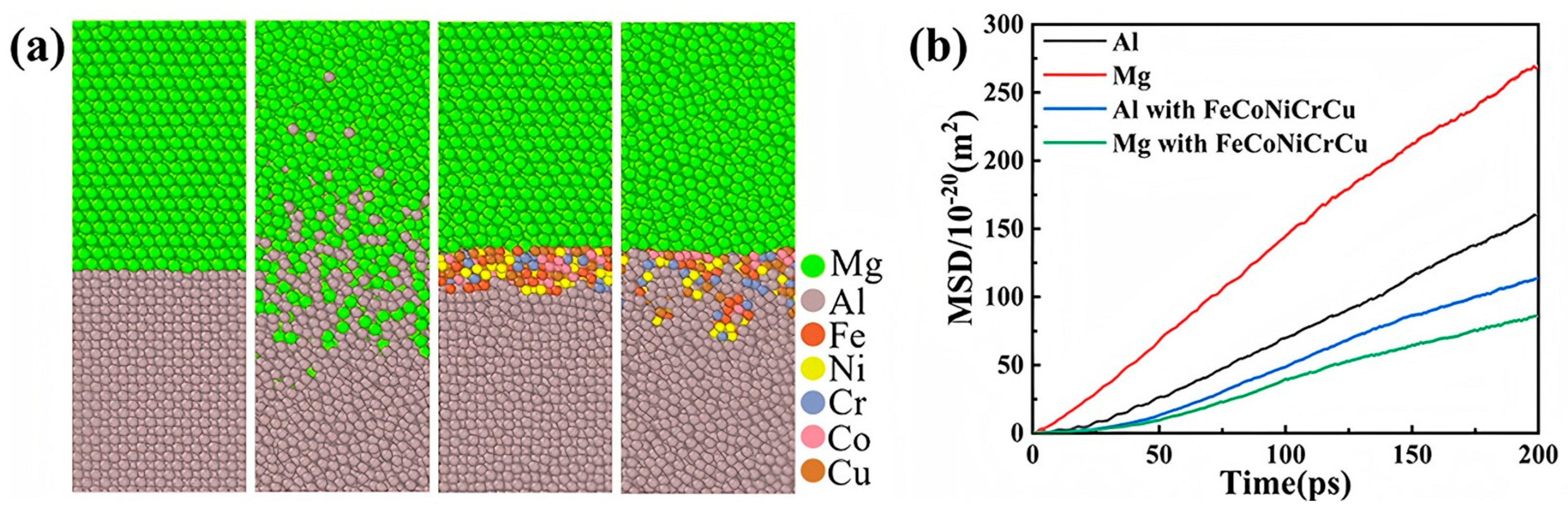
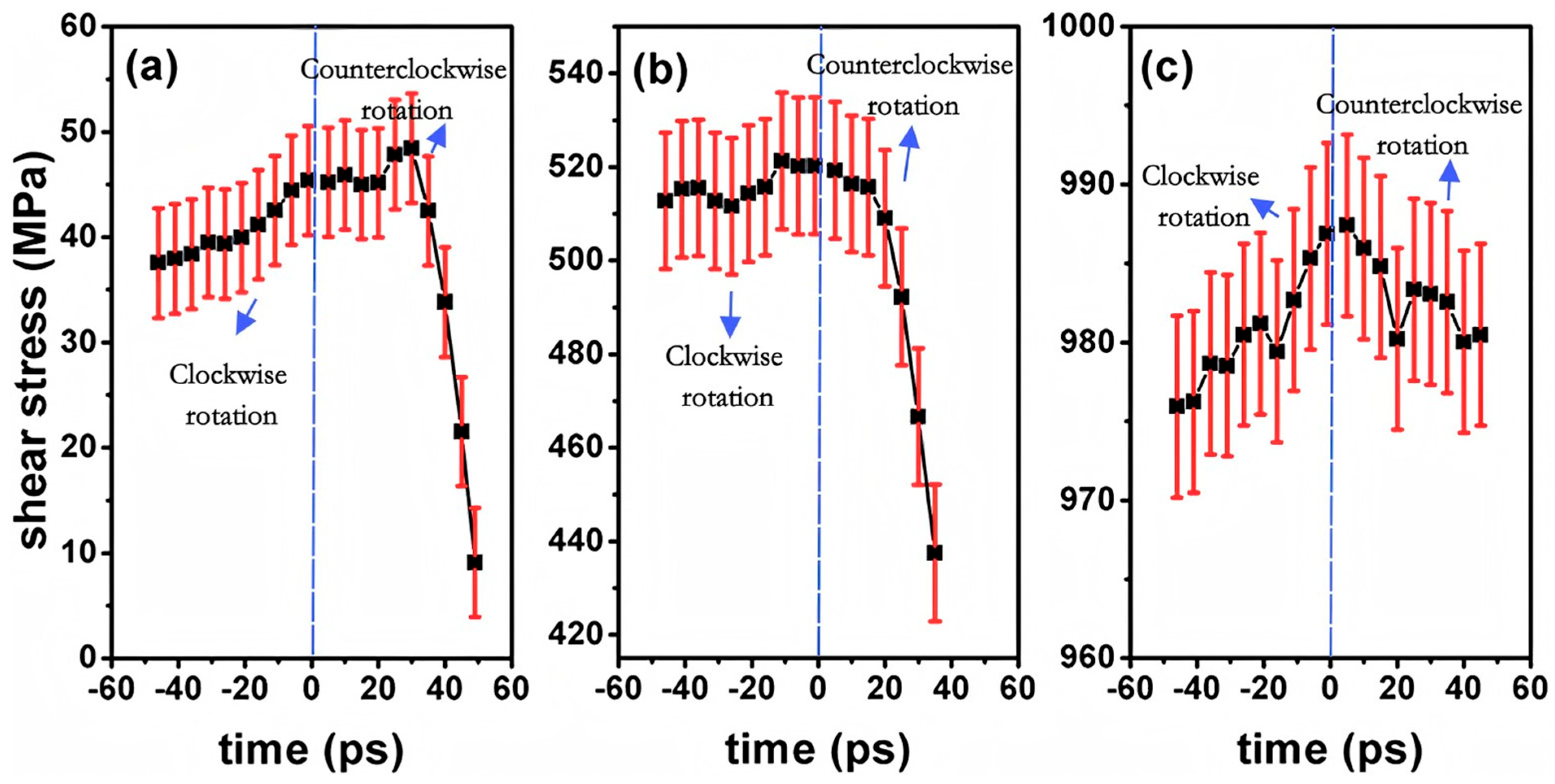

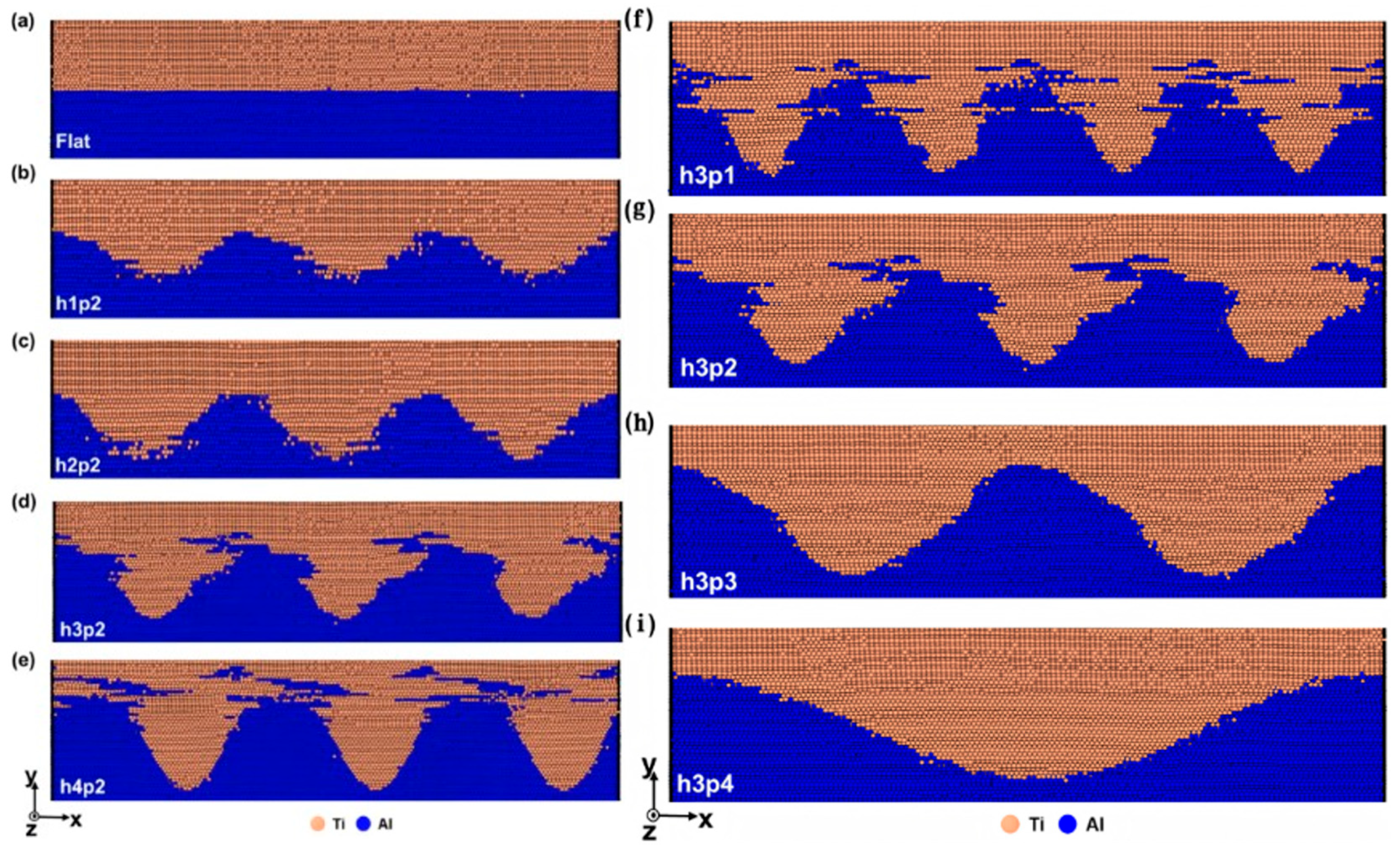


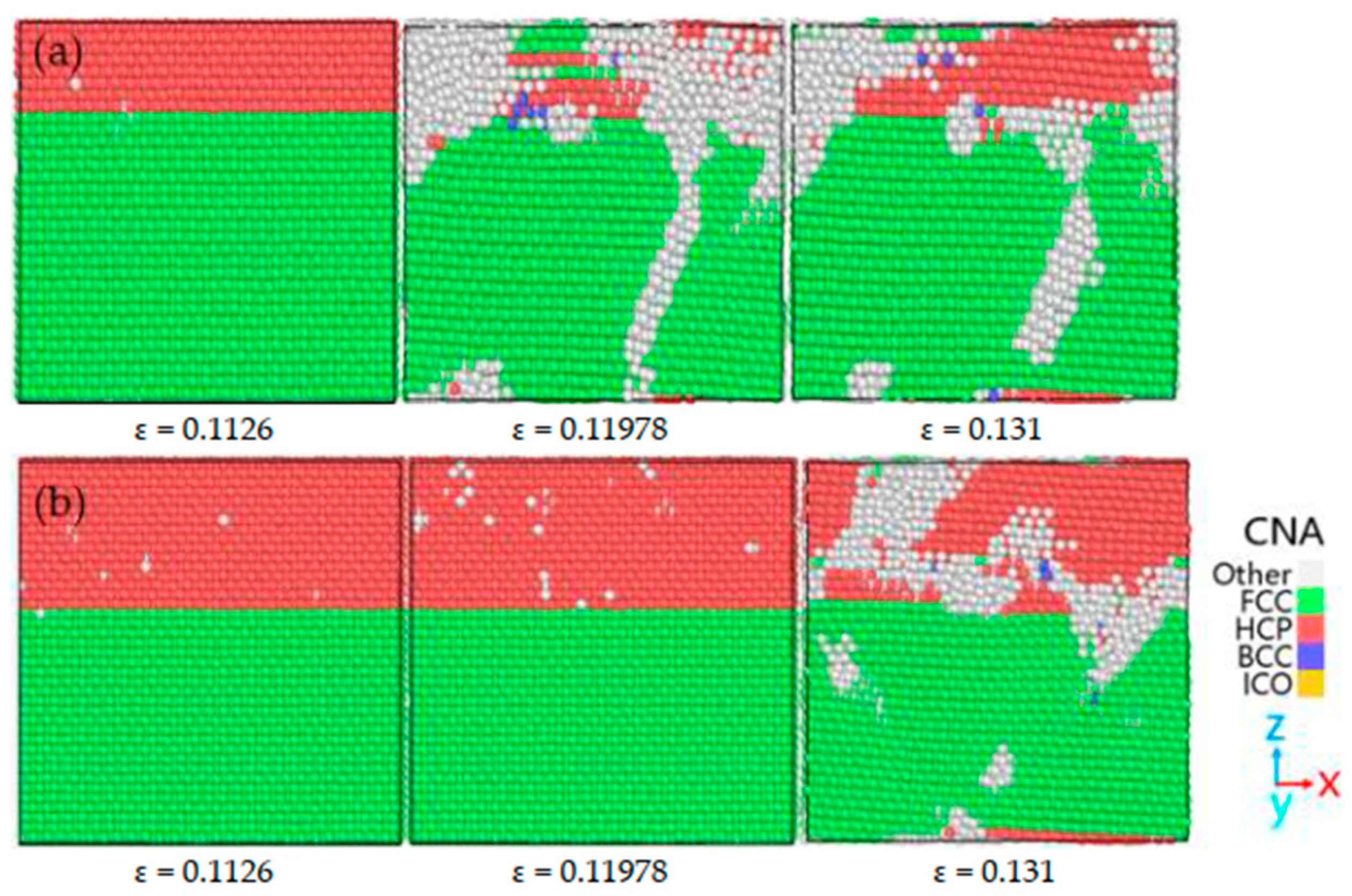
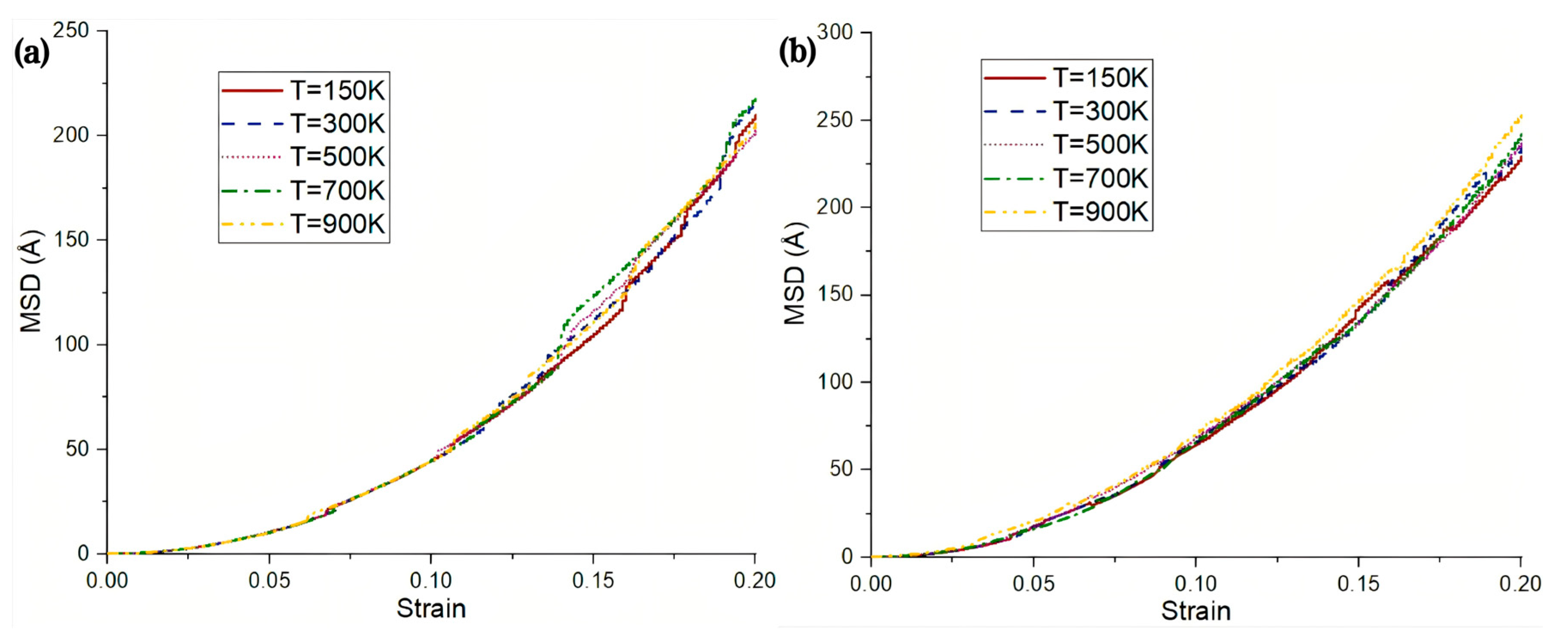


| Researcher | Temperature/K | Diffusion Coefficient of Al/(m2·s−1) | Diffusion Coefficient of Cu/(m2·s−1) | Atoms Conditions |
|---|---|---|---|---|
| Han XJ et al. [42] | 650 | 9.64471 × 10−12 | 2.19764 × 10−12 | Al (solid) Cu (solid) diffusion bonding |
| 700 | 2.78636 × 10−11 | 5.00352 × 10−12 | ||
| 750 | 6.24829 × 10−9 | 5.05976 × 10−10 | ||
| 800 | 6.85999 × 10−9 | 1.04891 × 10−9 | ||
| Cui YF et al. [43] | 873 | 3.08 × 10−12 | 1.73 × 10−9 | Al (solid → liquid) Cu (solid) Existence of IMCs |
| 893 | 8.05 × 10−12 | 1.86 × 10−9 | ||
| 913 | 4.49 × 10−11 | 1.94 × 10−9 | ||
| 933 | 2.68 × 10−10 | 2.05 × 10−9 | ||
| 953 | 5.15 × 10−10 | 2.17 × 10−9 | ||
| Mao AX et al. [44] | 800 | 1.3140 × 10−9 | 2.12 × 10−11 | Al (liquid) Cu (solid) |
| 850 | 1.5785 × 10−9 | 1.004 × 10−10 | ||
| 900 | 1.7770 × 10−9 | 2.434 × 10−10 | ||
| 950 | 2.0755 × 10−9 | 4.833 × 10−10 | ||
| Qian XF et al. [45] | 953 | 6.3017 × 10−9 | 9.475465 × 10−9 | Al (liquid) Cu (solid) |
| 973 | 7.28007 × 10−9 | 1.0293025 × 10−8 | ||
| 993 | 8.36446 × 10−9 | 1.0813525 × 10−8 | ||
| 1013 | 9.388485 × 10−9 | 1.1257745 × 10−8 | ||
| 1033 | 1.0975015 × 10−8 | 1.1947165 × 10−8 |
| Models | Crystal Orientation Along x-Axis | Crystal orientation Along the y-Axis | Crystal orientation Along the z-Axis | Lattice Mismatch | In-Plane Mismatch Along x-Axis | In-Plane Mismatch Along y-Axis |
|---|---|---|---|---|---|---|
| (111)-A | [] | [] | [111] | 11.35% | 15.38 | 8.879 |
| (001)-B | [100] | [010] | [001] | 11.35% | 21.75 | 21.75 |
| ()-C | [] | [111] | [] | 11.35% | 8.879 | 25.11 |
| ()-D | [111] | [] | [] | 11.35% | 25.11 | 15.38 |
| Mechanical Properties | Homogenous Sample with () Interface | Heterogenous Sample with () Interface | Homogenous Sample with (001) Interface | Heterogenous Sample with (001) Interface |
|---|---|---|---|---|
| Young’s moduli | 127.6 GPa | 129.3 GPa | 33.8 GPa | 31.9 GPa |
| Yielding strengths | 9.5 GPa | 8.4 GPa | 1.5 GPa | 1.3 GPa |
| Diffusion Coefficients | Ideal Interface | Rough Interface |
|---|---|---|
| DAl (m2/s) | 2.6667 × 10−9 | 2.4333 × 10−9 |
| DTi (m2/s) | 1.65 × 10−11 | 1.47 × 10−11 |
| Tensile Direction | Interface or Pure Metal | Tensile Strength (GPa) |
|---|---|---|
| X (Parallel to the interface) | Cu()/Fe(110)-KS | 9.68 |
| Cu()/Fe(110)-NW | 6.64 | |
| pure Cu along [011] | 6.28 | |
| pure Fe along [] | 35.64 | |
| pure Fe along [001] | 9.90 | |
| Y (Parallel to the interface) | Cu()/Fe(110)-KS | 11.08 |
| Cu()/Fe(110)-NW | 11.25 | |
| pure Cu along [] | 10.74 | |
| pure Fe along [] | 22.30 | |
| pure Fe along [] | 26.82 | |
| Z (Vertical to the interface) | Cu()/Fe(110)-KS | 10.25 |
| Cu()/Fe(110)-NW | 11.99 | |
| pure Cu along [] | 13.08 | |
| pure Fe along [110] | 26.82 |
| Different Systems | Diffusion Coefficient (m2·s−1) | Simulated Condition | |
|---|---|---|---|
| Al or Fe | Cu or Mg or Ti | ||
| Al/Mg [62] | 278 × 10−11 | 451 × 10−11 | β = 10° |
| 334 × 10−11 | 456 × 10−11 | Vp = 440 m/s | |
| Al/Ni [124] | 0.43 | 0.27 | 0 V/Å |
| 0.46 | 0.31 | 5 × 10−11 V/Å | |
| 0.56 | 0.36 | 1 × 10−10 V/Å | |
| 0.92 | 0.58 | 2 × 10−10 V/Å | |
| Al/Ti [84,86,87] | 266.67 × 10−11 | 1.65 × 10−11 | ideal interface |
| 243.33 × 10−11 | 1.47 × 10−11 | rough interface | |
| 35.5 × 10−11 | 27.3 × 10−11 | 600 K and 50 MPa | |
| 19.2 × 10−11 | 329.0 × 10−11 | 1340 K | |
| Fe/Cu [108,110] | 0.644 × 10−11 | 303.1 × 10−11 | 1373 K |
| 1.227 × 10−11 | 336.4 × 10−11 | 1423 K | |
| 2.711 × 10−11 | 368.2 × 10−11 | 1473 K | |
| 4.806 × 10−11 | 394.8 × 10−11 | 1523 K | |
| 10.084 × 10−11 | 446.4 × 10−11 | 1573 K | |
| 0.353 × 10−11 | 491.7 × 10−11 | (100) | |
| 0.464 × 10−11 | 549.6 × 10−11 | (110) | |
| 0.554 × 10−11 | 512.6 × 10−11 | (111) | |
| Types | Research Contents |
|---|---|
| Al/Cu | Atomic diffusion behavior [39,40,42,45,46,57] |
| Coefficient of diffusion [42,44,45] | |
| Diffusion depth [44] | |
| Rate of diffusion [44] | |
| Activation energy of diffusion [57] | |
| Diffusion mechanism [57] | |
| Transitional layer thickness [41,42,44,45,47,57] | |
| Plastic deformation mechanism [39,50,52,54,56,57,58] | |
| Tensile strength [41,42,45,51,52,55,56,57,58,59] | |
| Yield strength [42,45,46,58] | |
| Young’s modulus [59] | |
| Broken mode [51,52,55,56] | |
| Shear strength [55] | |
| Interface reinforcement mechanism [53] | |
| The solidification process [40] | |
| Al/Mg | Atomic diffusion behavior [62,67] |
| Coefficient of diffusion [62] | |
| Diffusion rate [62] | |
| Diffusion layer thickness [67] | |
| Modulus of elasticity [64] | |
| Plastic deformation mechanism [64] | |
| Tensile property [63] | |
| Shear strength [67] | |
| Breaking mechanism or mode [63,66,67] | |
| Interface reinforcement mechanism [64] | |
| Al/Ni | Atomic diffusion behavior [71,73,74,75] |
| Coefficient of diffusion [75] | |
| Diffusion rate [73,74] | |
| Diffusion mechanism [75,80] | |
| Diffusion layer thickness [72,73,74] | |
| Intermetallic compound formation species [76,78] | |
| Formation mechanism of intermetallic compounds [77] | |
| Tensile property [72] | |
| Plastic deformation mechanism [72] | |
| Interface dislocation behavior [81] | |
| Evolution behavior of crystal boundary [81] | |
| Al/Ti | Dispersal behavior [85] |
| Diffusion constant [84,86] | |
| Formation mechanism of intermetallic compounds [87,88,89] | |
| Tensile property [85,86] | |
| Broken mode [84,86] | |
| Plastic deformation mechanism [86,90,92] | |
| Structural evolution [90,92] | |
| Compression performance [93] | |
| Al/Fe | Atomic diffusion behavior [94,96] |
| Studies on intermetallic compound generation [94] | |
| Formation mechanism of intermetallic compounds [95] | |
| Anti-shear performance [96] | |
| Cu/Ni | Diffusion mechanism [98] |
| Transitional layer thickness [99] | |
| Tensile property [99,104,106,107] | |
| Anti-shear performance [106] | |
| Plastic deformation mechanism [98,100,101,106] | |
| Interface reinforcement mechanism [101,102] | |
| Structural evolution [98,105] | |
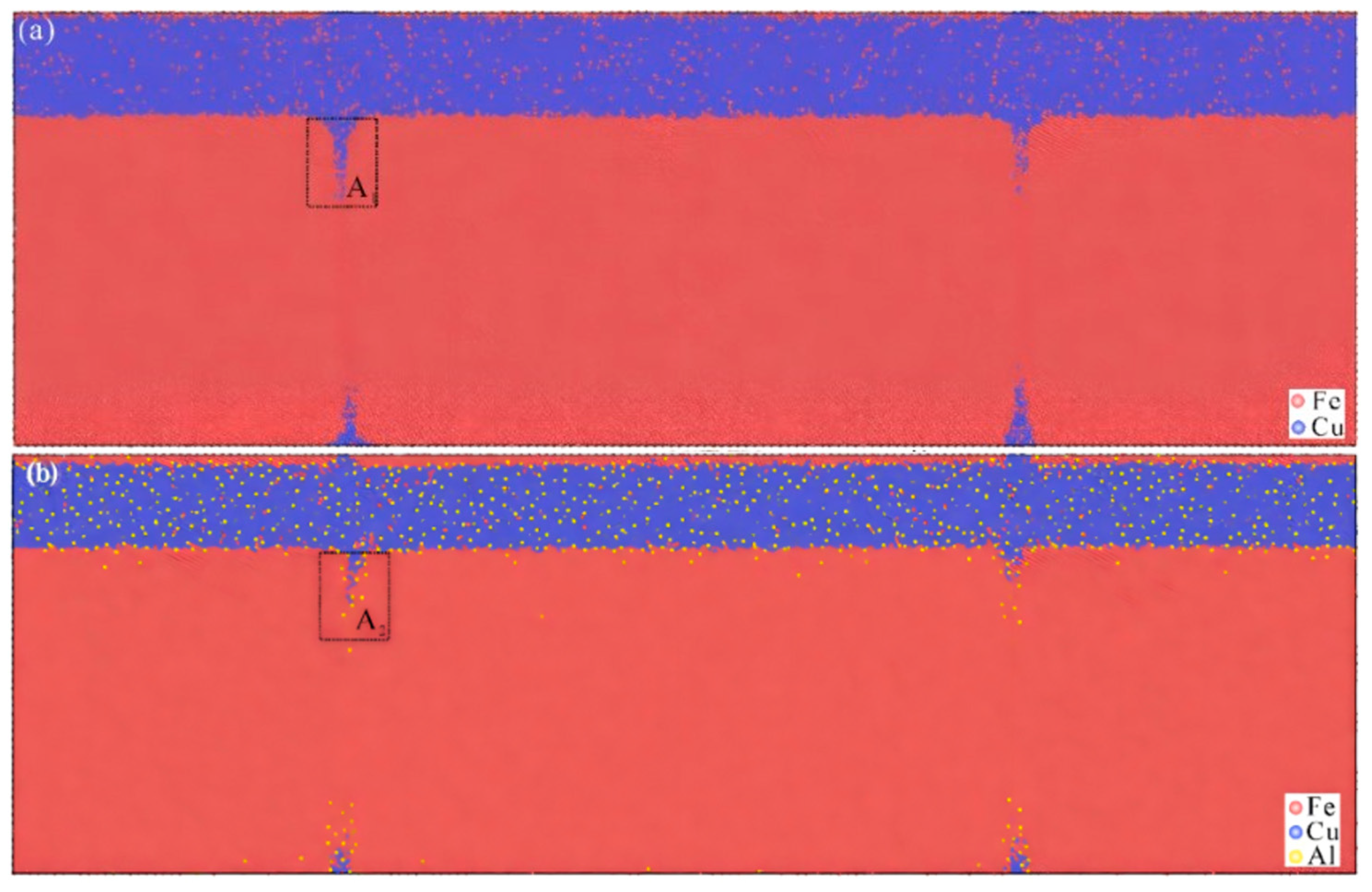
| Fe/Cu | Coefficient of diffusion [108,109,110] |
| Diffusion depth [108] | |
| Diffusion rate [116] | |
| Diffusion mechanism [108] | |
| Diffusion length [108,109,110] | |
| Tensile property [110] | |
| Plastic deformation mechanism [115] | |
| Connectionism [113] | |
| Interface reinforcement mechanism [109] | |
| Combined interface type [113] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, Y.; Li, G.; Jiang, W.; Wang, J.; Kang, X.; Zeng, Q.; Yao, S.; Yao, P. Review of Molecular Dynamics Simulation of Bimetallic Interfacial Behavior. Materials 2025, 18, 3048. https://doi.org/10.3390/ma18133048
Wang X, Wang Y, Li G, Jiang W, Wang J, Kang X, Zeng Q, Yao S, Yao P. Review of Molecular Dynamics Simulation of Bimetallic Interfacial Behavior. Materials. 2025; 18(13):3048. https://doi.org/10.3390/ma18133048
Chicago/Turabian StyleWang, Xiaoqiong, Yuejia Wang, Guangyu Li, Wenming Jiang, Jun Wang, Xing Kang, Qiantong Zeng, Shan Yao, and Pingkun Yao. 2025. "Review of Molecular Dynamics Simulation of Bimetallic Interfacial Behavior" Materials 18, no. 13: 3048. https://doi.org/10.3390/ma18133048
APA StyleWang, X., Wang, Y., Li, G., Jiang, W., Wang, J., Kang, X., Zeng, Q., Yao, S., & Yao, P. (2025). Review of Molecular Dynamics Simulation of Bimetallic Interfacial Behavior. Materials, 18(13), 3048. https://doi.org/10.3390/ma18133048









