Development of Constitutive Relationship for Thermomechanical Processing of FeCrAl Alloy to Predict Hot Deformation Behavior
Abstract
1. Introduction
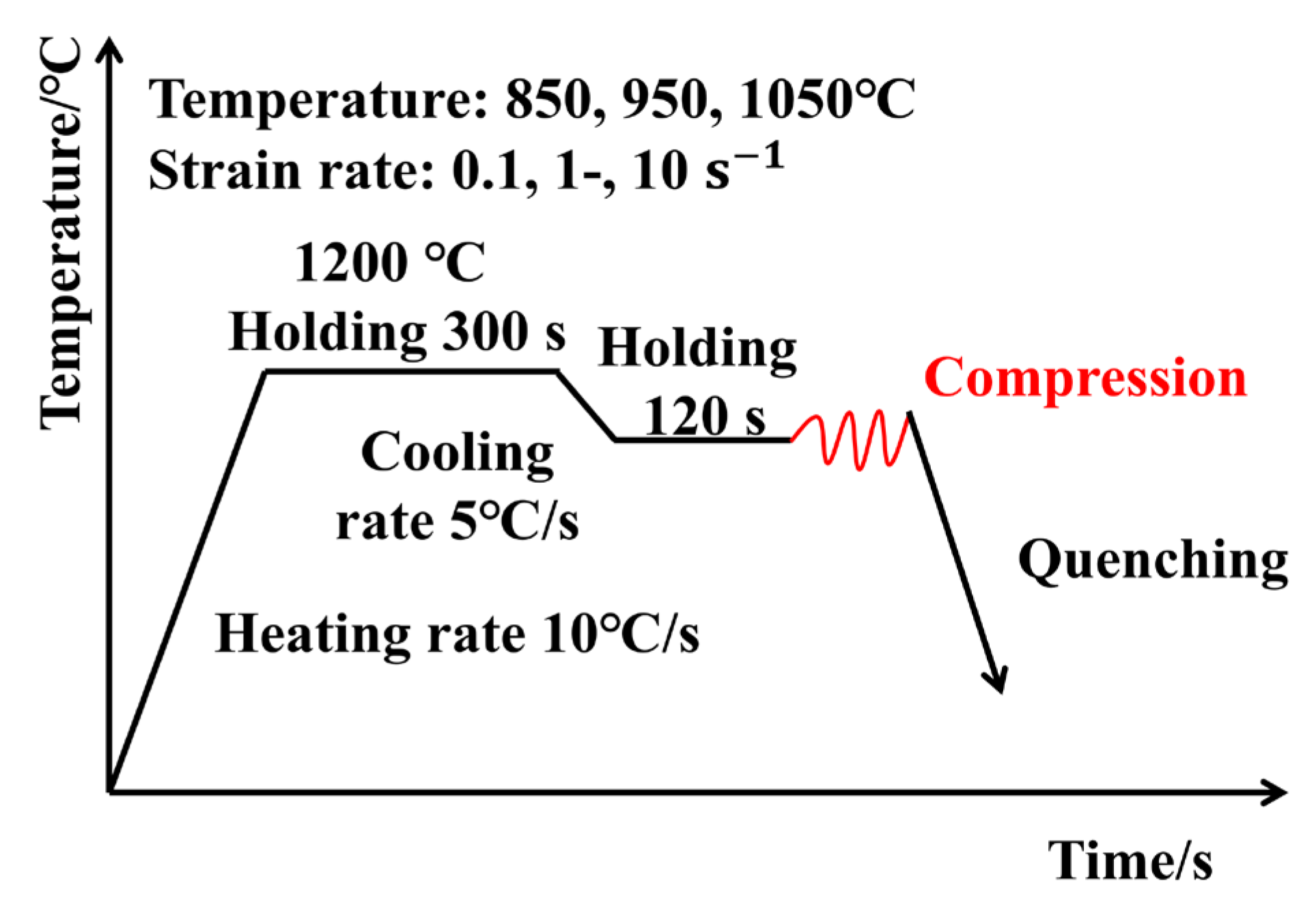
2. Materials and Methods
3. Results and Discussion
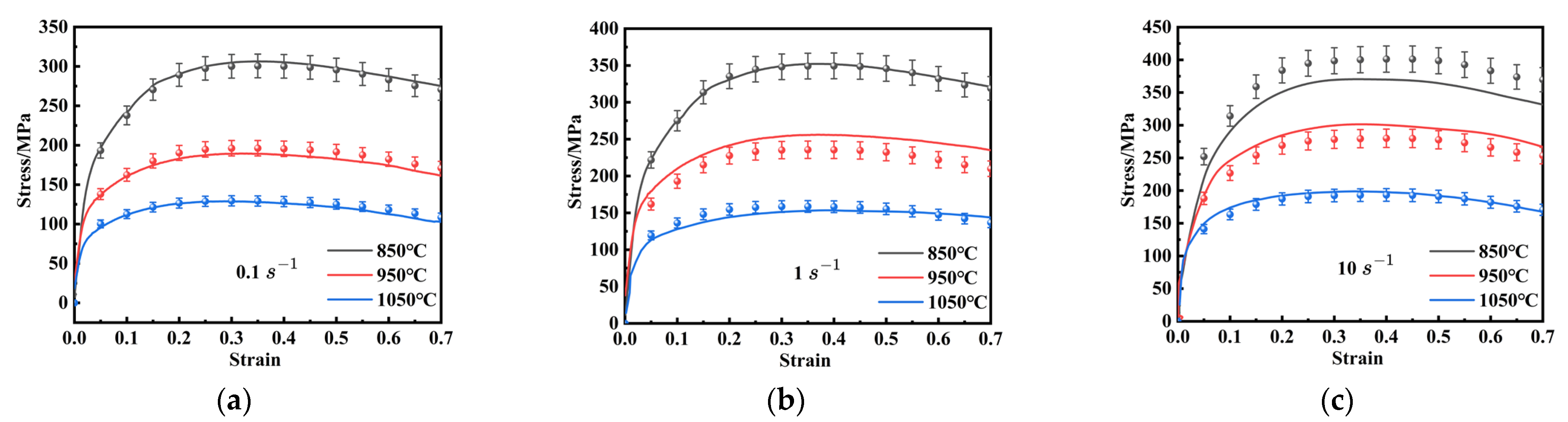
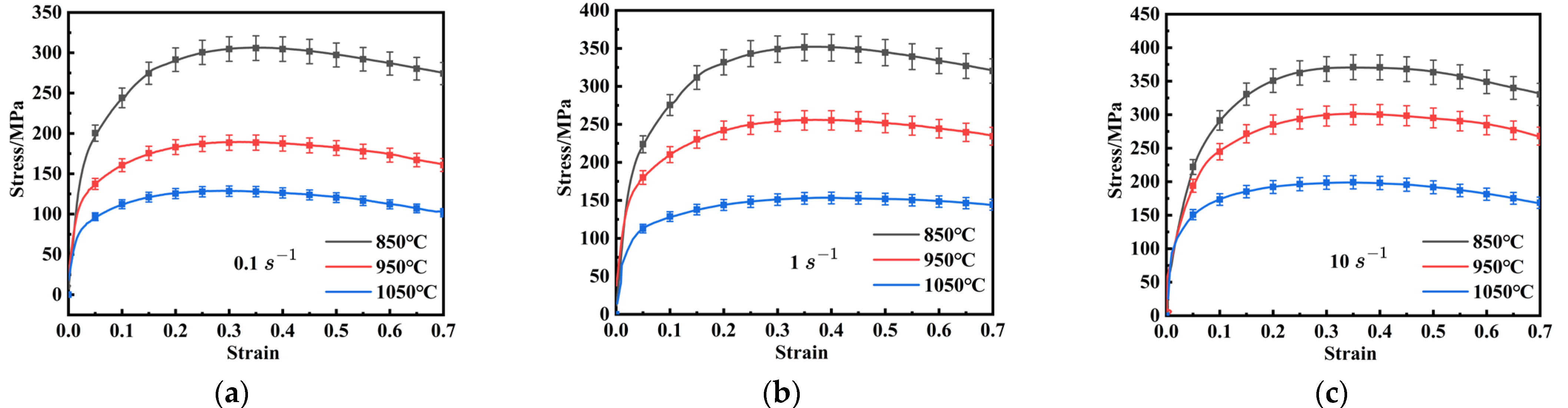
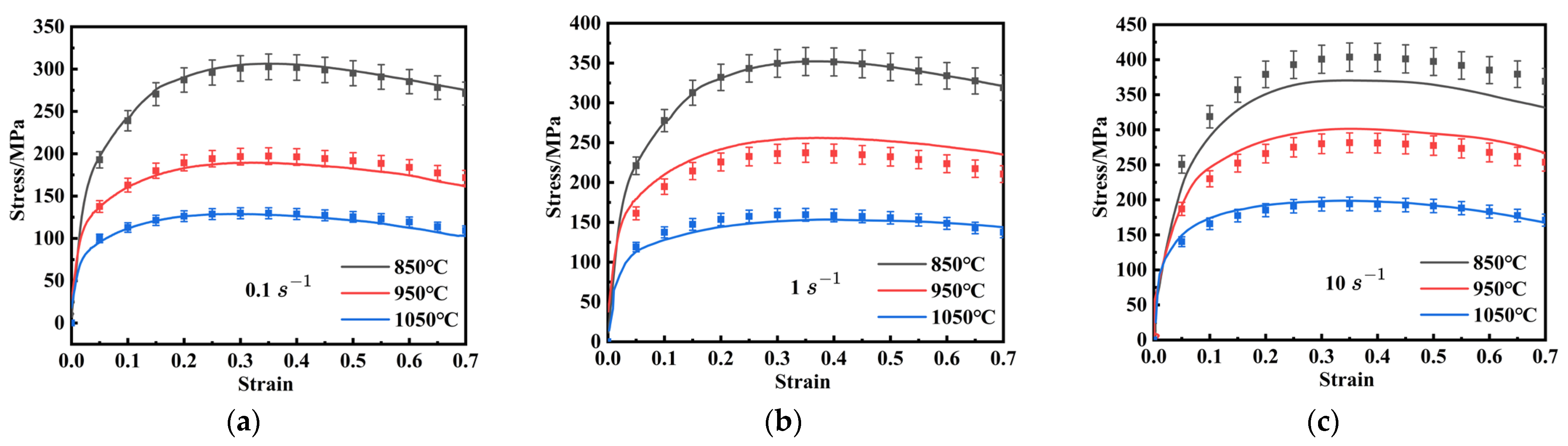
3.1. Flow Stress Curves
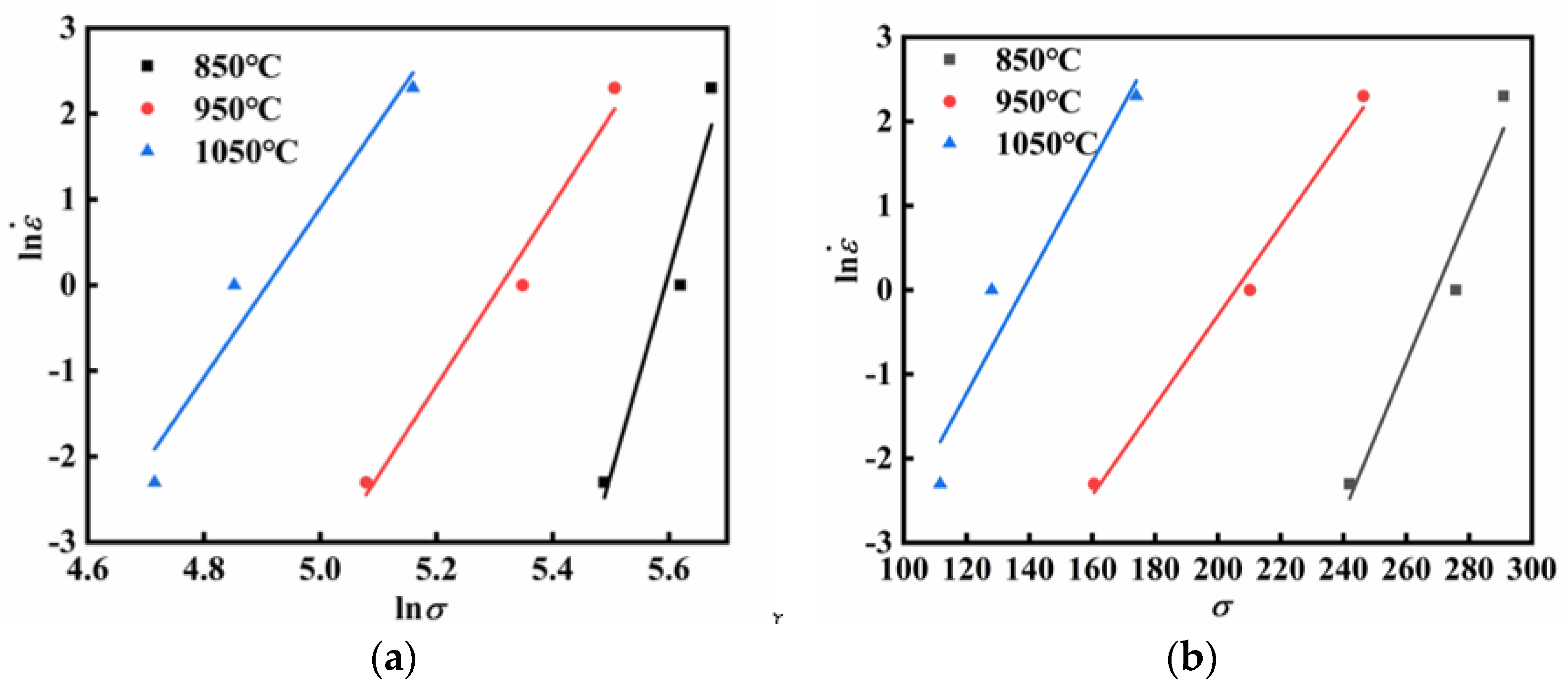
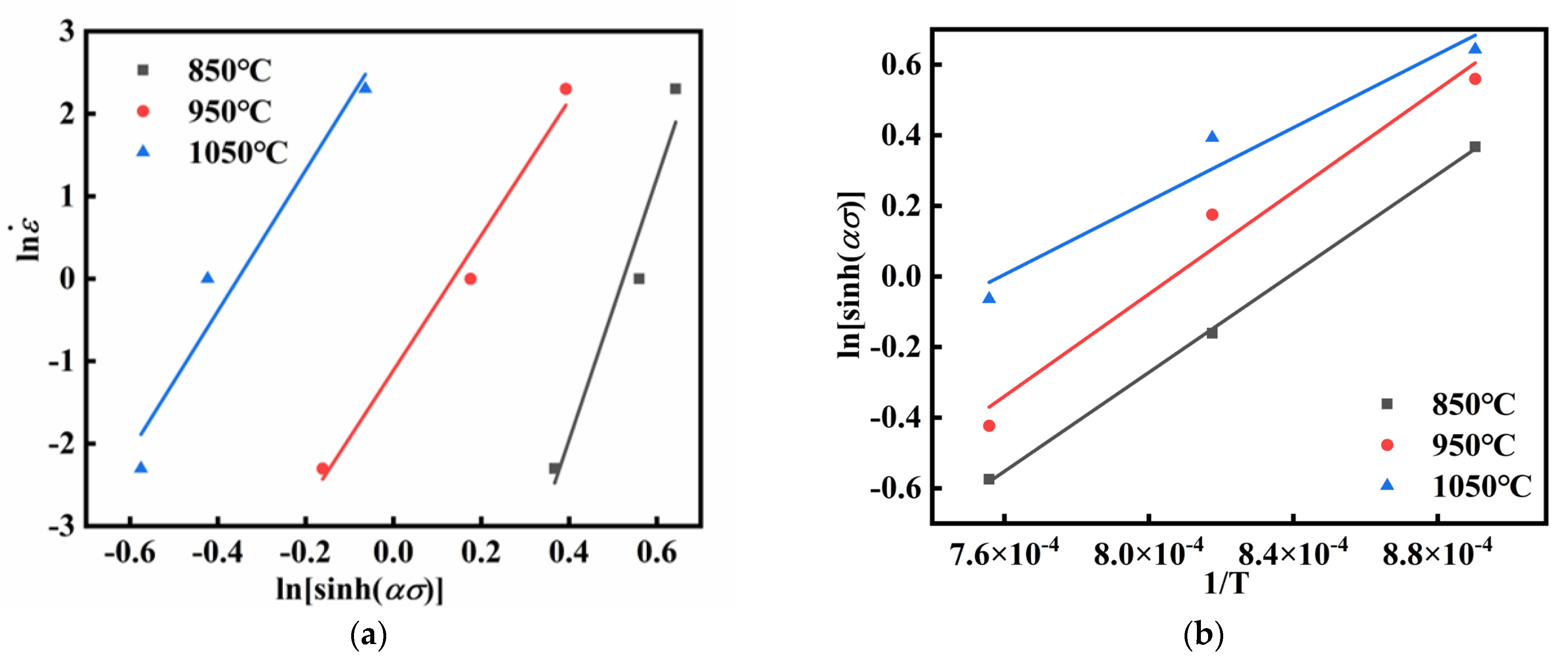
3.2. Improved Arrhenius-Type Constitutive Model
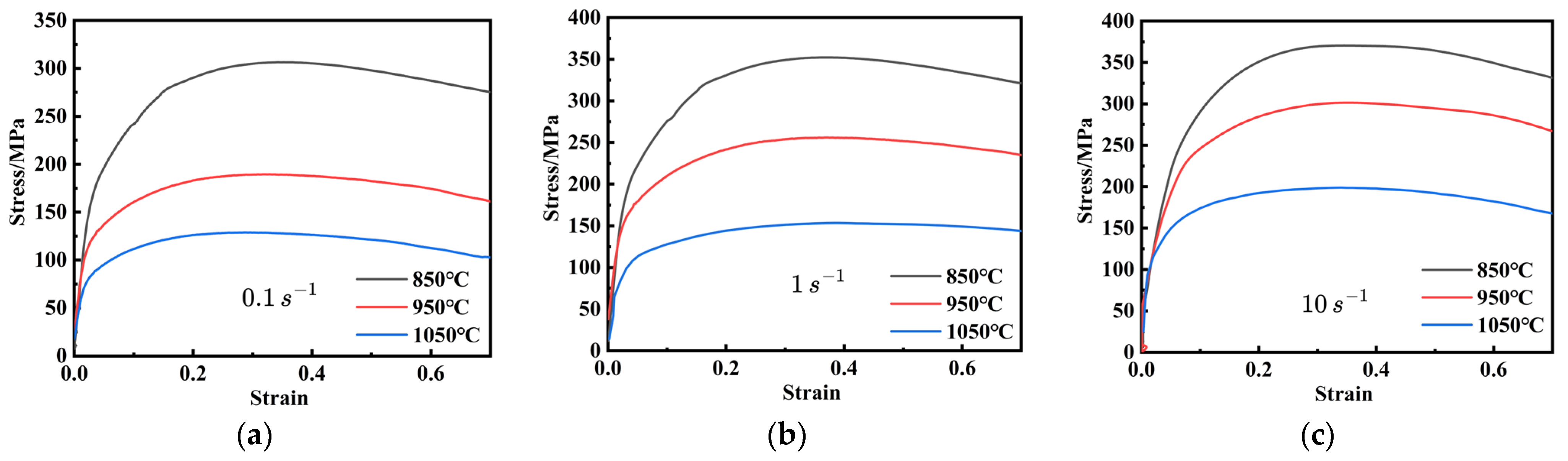
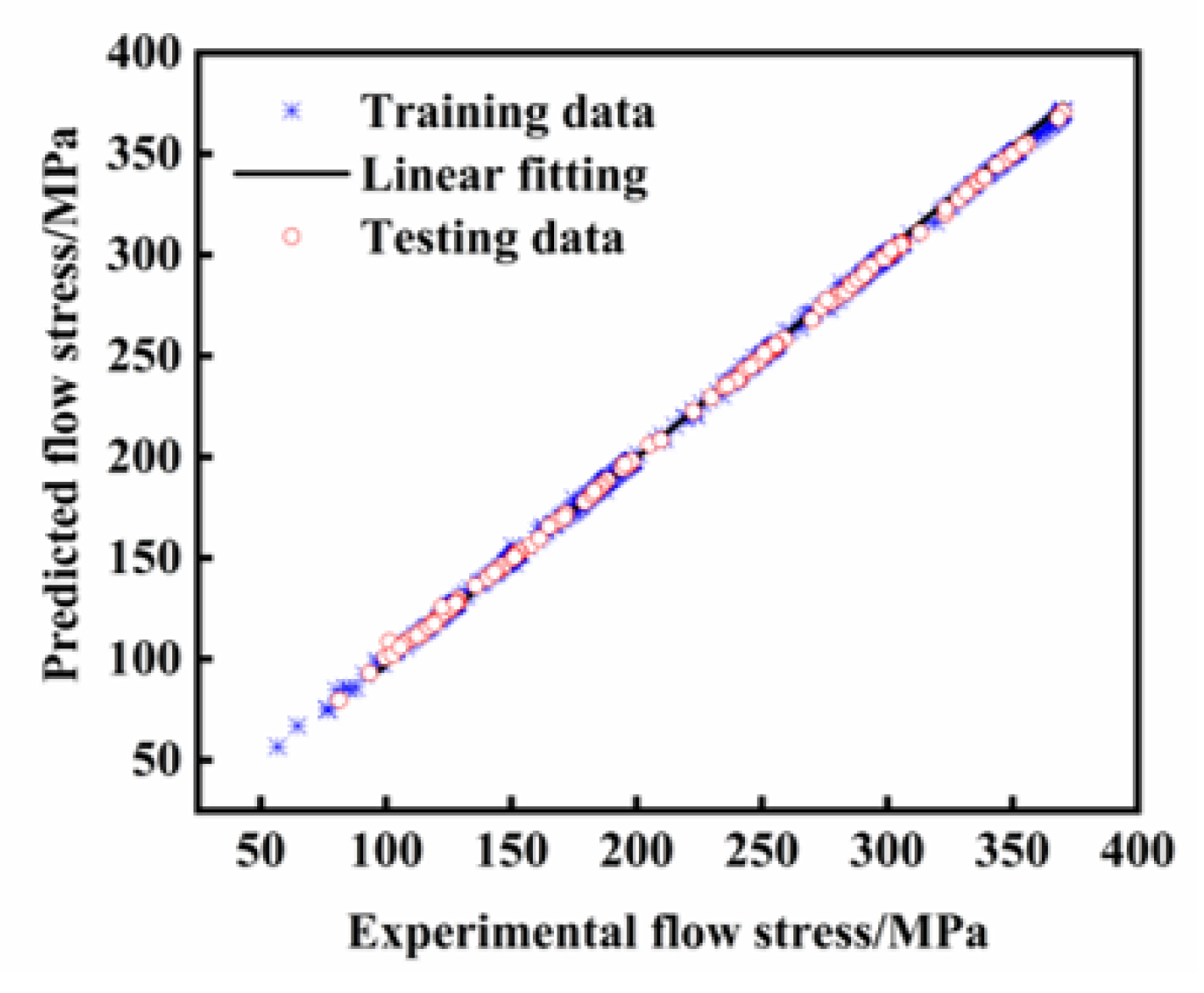
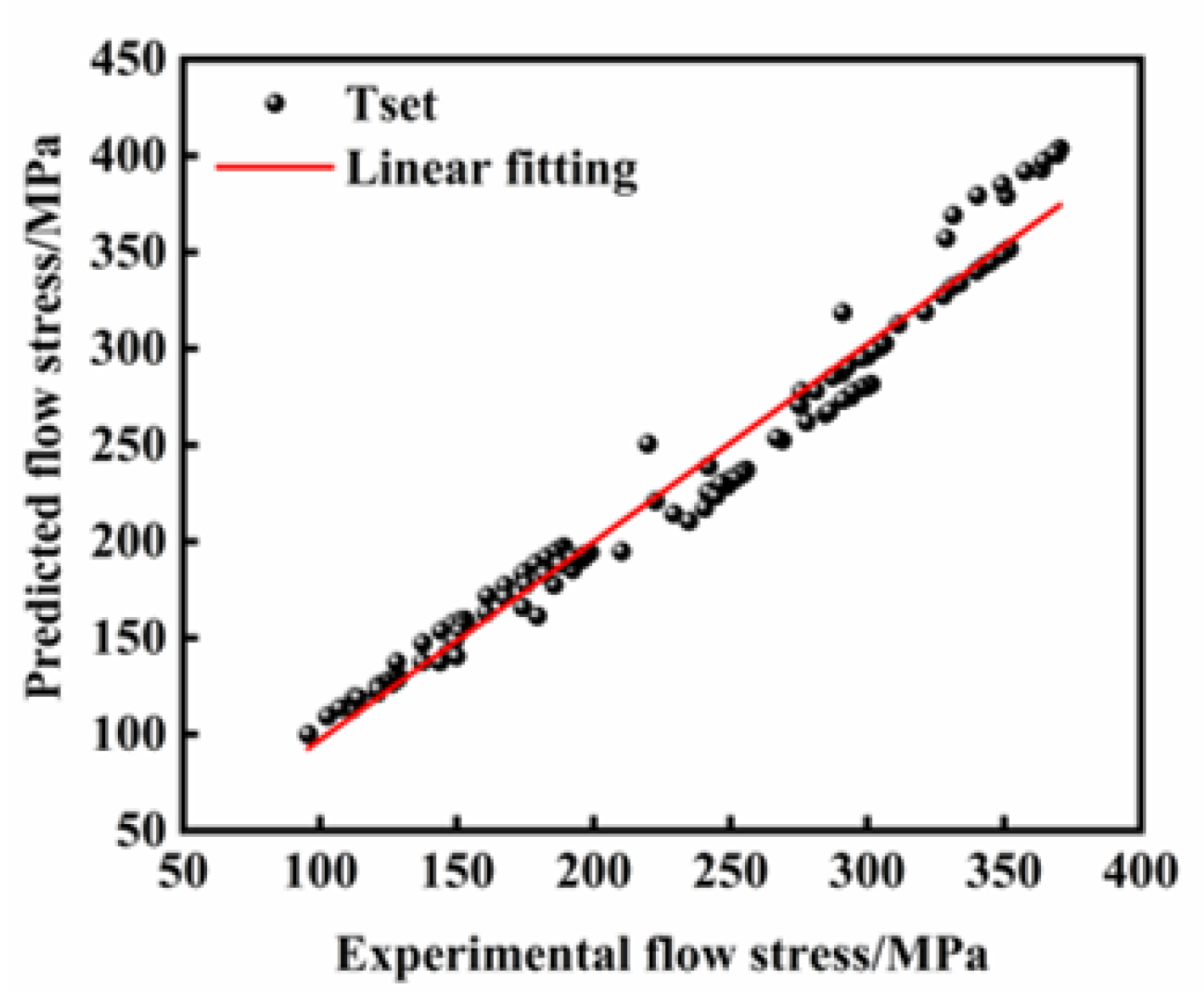
3.3. Development of ANN Model
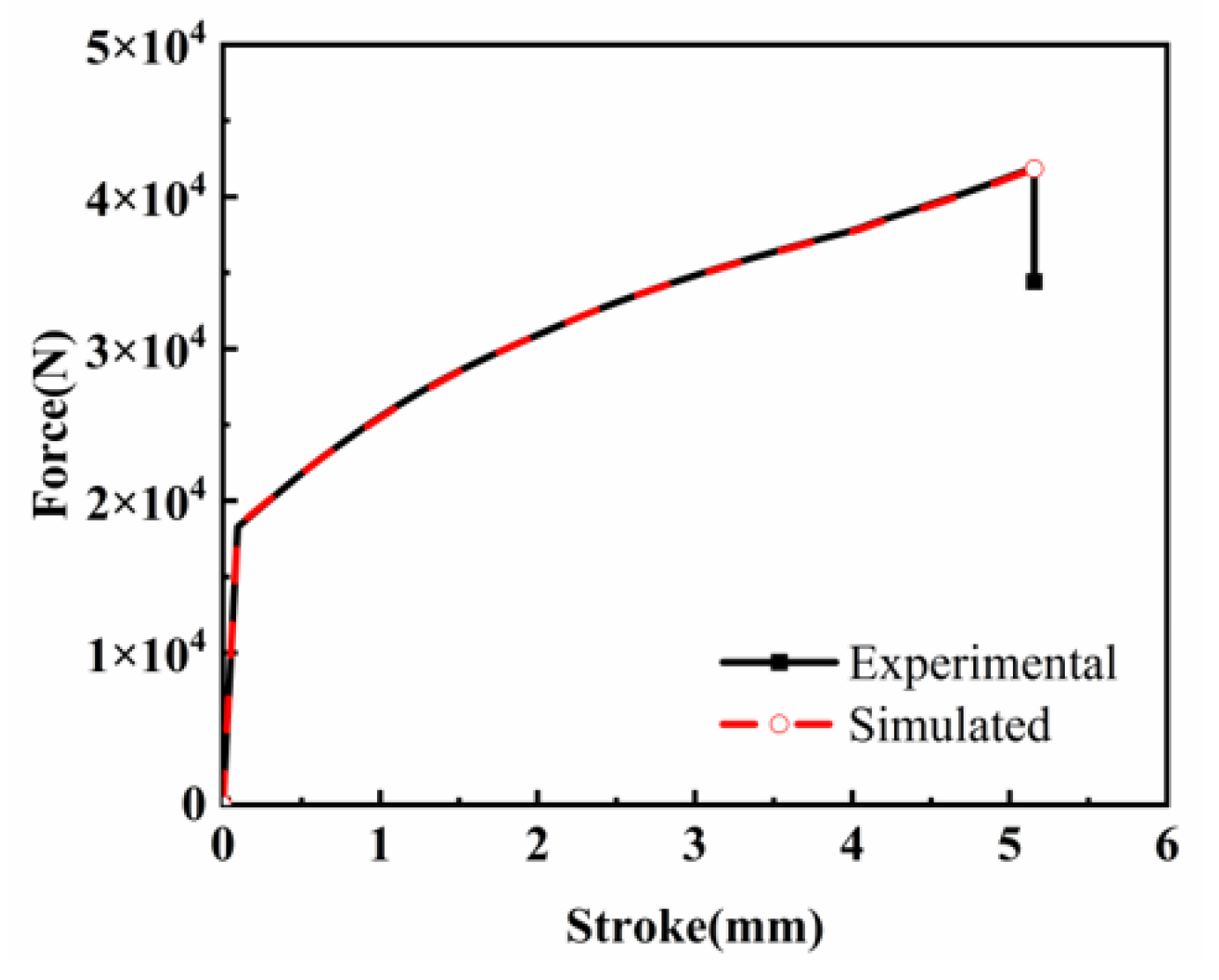
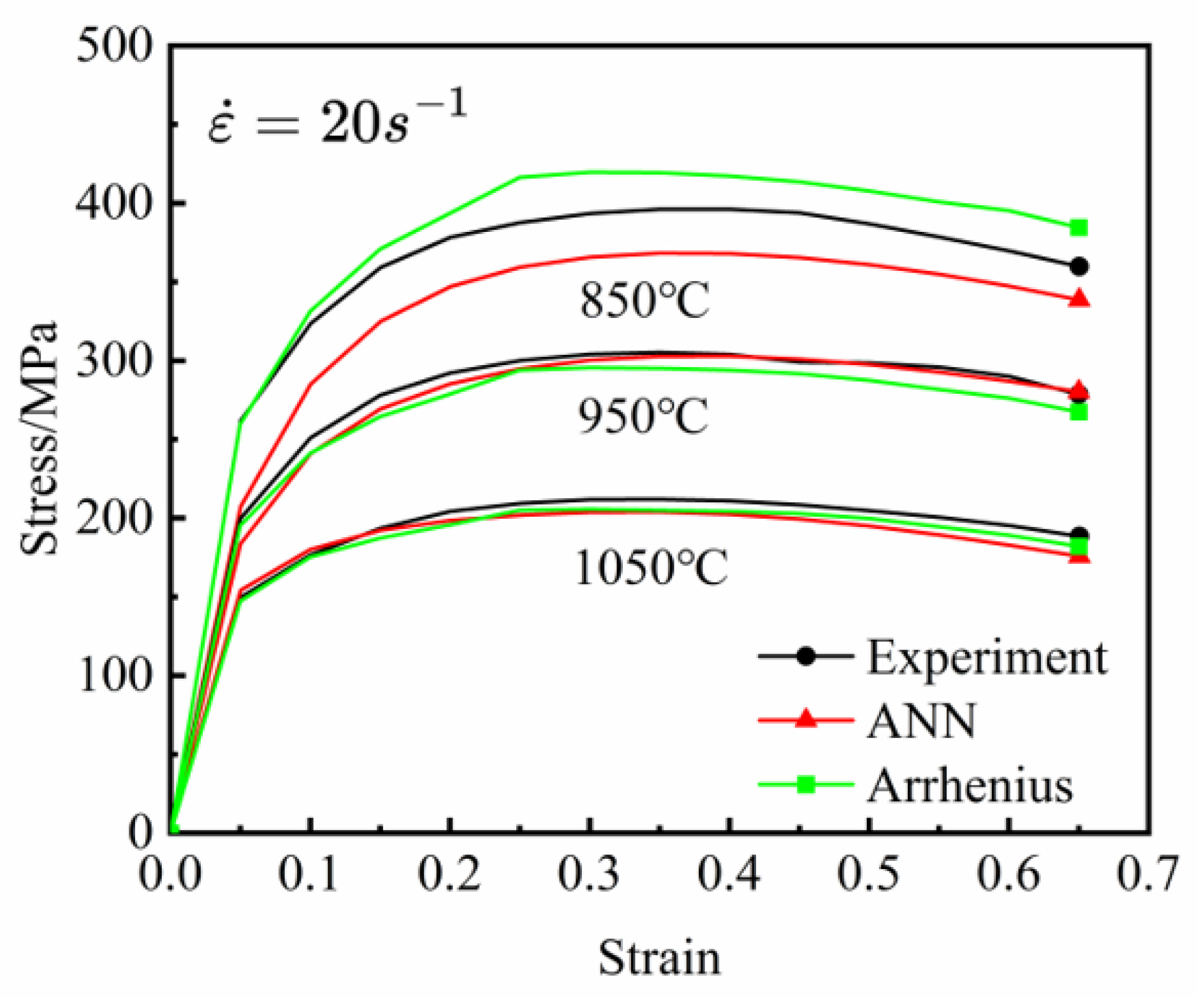
3.4. Compression Test Simulation and Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| Polynomial | R (%) | AARE (%) | RMSE (MPa−1) |
|---|---|---|---|
| 5-order | 98.47 | 4.30 | 14.52 |
| 8-order | 98.49 | 4.30 | 14.47 |
Appendix B
References
- Dryepondt, S.; Unocic, K.A.; Hoelzer, D.T.; Massey, C.P.; Pint, B.A. Development of low-Cr ODS FeCrAl alloys for accident-tolerant fuel cladding. J. Nucl. Mater. 2018, 501, 59–71. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Liu, H.; Du, P.; Zhang, R.; Wang, Q. Dynamic precipitation of laves phase and grain boundary features in warm deformed FeCrAl alloy: Effect of Zr. Acta Metall. Sin. (Engl. Lett.) 2021, 34, 1734–1746. [Google Scholar] [CrossRef]
- Raj, B.; Vijayalakshmi, M. Ferritic steels and advanced ferritic–martensitic steels. Compr. Nucl. Mater. 2012, 4, 97–121. [Google Scholar]
- Terrani, K.A.; Zinkle, S.J.; Snead, L.L. Advanced oxidation-resistant iron-based alloys for LWR fuel cladding. J. Nucl. Mater. 2014, 448, 420–435. [Google Scholar] [CrossRef]
- Gamble, K.A.; Barani, T.; Pizzocri, D.; Hales, J.D.; Terrani, K.A.; Pastore, G. An investigation of FeCrAl cladding behavior under normal operating and loss of coolant conditions. J. Nucl. Mater. 2017, 491, 55–66. [Google Scholar] [CrossRef]
- Sun, Z.; Yamamoto, Y. Processability evaluation of a Mo-containing FeCrAl alloy for seamless thin-wall tube fabrication. Mater. Sci. Eng. A 2017, 700, 554–561. [Google Scholar] [CrossRef]
- Stott, F.H.; Wood, G.C.; Stringer, J. The influence of alloying elements on the development and maintenance of protective scales. Oxid. Met. 1995, 44, 113–145. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Gussev, M.N.; Kim, B.; Byun, T.S. Optimized Properties on Base Metal and Thin-Walled Tube of Generation II ATF FeCrAl (No. ORNL/TM-2015/414); Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2015. [Google Scholar]
- Yamamoto, Y.; Pint, B.A.; Terrani, K.A.; Field, K.G.; Yang, Y.; Snead, L.L. Development and property evaluation of nuclear grade wrought FeCrAl fuel cladding for light water reactors. J. Nucl. Mater. 2015, 467, 703–716. [Google Scholar] [CrossRef]
- Haghdadi, N.; Cizek, P.; Beladi, H.; Hodgson, P.D. A novel high-strain-rate ferrite dynamic softening mechanism facilitated by the interphase in the austenite/ferrite microstructure. Acta Mater. 2017, 126, 44–57. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Constitutive relationships for hot deformation of austenite. Acta Mater. 2011, 59, 6441–6448. [Google Scholar] [CrossRef]
- He, Y.; Deng, Z.; Liu, J.; Yan, B.; Chen, C. Hot-deformation characteristics and dynamic softening of as-cast FeCrAl alloy. J. Mater. Res. Technol. 2020, 9, 6632–6641. [Google Scholar] [CrossRef]
- Liu, D.; Lu, Z.; Yu, J.; Shi, C.; Xiao, H.; Liu, W.; Jiang, S. Hot deformation behavior and microstructure evolution of NiAl-9HfO2 composite. Intermetallics 2021, 139, 107344. [Google Scholar] [CrossRef]
- Hu, M.; Sun, Y.; He, J.; Li, C.; Li, H.; Yu, L.; Liu, Y. Hot deformation behaviour and microstructure evolution of Al-3% Mg2Si alloy. Mater. Charact. 2022, 183, 111623. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Shi, Z.; Yan, X.; Duan, C. Characterization of hot deformation behavior of GH925 superalloy using constitutive equation, processing map and microstructure observation. J. Alloys Compd. 2015, 652, 30–38. [Google Scholar] [CrossRef]
- Mandal, S.; Rakesh, V.; Sivaprasad, P.V.; Venugopal, S.; Kasiviswanathan, K.V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 500, 114–121. [Google Scholar] [CrossRef]
- Cao, Y.; Di, H.S.; Misra, R.D.K.; Zhang, J. Hot deformation behavior of alloy 800H at intermediate temperatures: Constitutive models and microstructure analysis. J. Mater. Eng. Perform. 2014, 23, 4298–4308. [Google Scholar] [CrossRef]
- Wu, H.; Wen, S.P.; Huang, H.; Wu, X.L.; Gao, K.Y.; Wang, W.; Nie, Z.R. Hot deformation behavior and constitutive equation of a new type Al–Zn–Mg–Er–Zr alloy during isothermal compression. Mater. Sci. Eng. A 2016, 651, 415–424. [Google Scholar] [CrossRef]
- Sun, T.; Sun, L.; Teng, H.; Liu, W.; Wang, R.; Zhao, X.; Zhou, J. Constitutive model and microstructure evolution of Ti65 titanium alloy. Materials 2024, 17, 2409. [Google Scholar] [CrossRef]
- Fang, X.Q.; Wang, J.B.; Liu, S.Y.; Wen, J.Z.; Song, H.Y.; Liu, H.T. Microstructure Evolution, Hot Deformation Behavior and Processing Maps of an FeCrAl Alloy. Materials 2024, 17, 1847. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Luo, W.; Du, P.; Wang, X.; Pei, J.; Zhang, R.; Liu, H. Discontinous and continuous dynamic recrystallization of Fe-12.5 Cr–4Al–2Mo-0.03 Nb-0.08 Y alloy during hot deformation. J. Mater. Res. Technol. 2024, 28, 831–843. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, Z.; Zu, G.; Du, W.; Zhang, X.; Jiang, L. Flow behaviour and constitutive modelling of a ferritic stainless steel at elevated temperatures. Met. Mater. Int. 2016, 22, 474–487. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, Z.; Sun, H.; Zou, L.; Wang, M.; Li, S. Hot deformation behavior and processing map of a 9Cr ferritic/martensitic ODS steel. J. Nucl. Mater. 2014, 455, 139–144. [Google Scholar] [CrossRef]
- Mandal, S.; Sivaprasad, P.V.; Murthy, K.P.N.; Raj, B. Modeling constitutive behavior of a 15Cr-15Ni-2.2 Mo-Ti modified austenitic stainless steel under hot compression using artificial neural network. In Proceedings of the International Conference on Statistical Mechanics of Plasticity and Related Instabilities POS (SMPRI 2005), Bangalore, India, 31 August–2 September 2005; Volume 59. [Google Scholar]
- Kumar, Y.; Kaur, K.; Singh, G. Machine learning aspects and its applications towards different research areas. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 9–10 January 2020; pp. 150–156. [Google Scholar]
- Karimzadeh, M.; Malekan, M.; Mirzadeh, H.; Saini, N.; Li, L. Hot deformation behavior analysis of as-cast CoCrFeNi high entropy alloy using Arrhenius-type and artificial neural network models. Intermetallics 2024, 168, 108240. [Google Scholar] [CrossRef]
- Churyumov, A.Y.; Kazakova, A.A. Prediction of true stress at hot deformation of high manganese steel by artificial neural network Modeling. Materials 2023, 16, 1083. [Google Scholar] [CrossRef]
- Liang, F.R.; Gao, Z.Y.; Chai, F.; Su, H.; Luo, X.B. Investigation on predicting flow stress of a Cu-containing steel based on machine learning algorithms. Mater. Today Commun. 2025, 46, 112728. [Google Scholar] [CrossRef]
- Xu, J.; Sun, C.; Liang, H.; Qian, L.; Wang, C. Constitutive Model for Hot Deformation Behavior of Fe-Mn-Cr-Based Alloys: Physical Model, ANN Model, Model Optimization, Parameter Evaluation and Calibration. Metals 2025, 15, 512. [Google Scholar] [CrossRef]
- Liu, H.L.; Ma, M.Y.; Liu, L.L.; Wei, L.L.; Chen, L.Q. Effect of W addition on hot deformation and precipitation behaviors of 19Cr2Mo ferritic stainless steel. J. Iron Steel Res. Int. 2019, 26, 425–434. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Liu, H.; Wang, Q.; Zhang, R. Effects of Zr on high temperature deformation and dynamic precipitation of laves phase in Fe–13Cr–5Al–2Mo–0.5Nb–0.4Ta alloy. Results Phys. 2021, 22, 103945. [Google Scholar] [CrossRef]
- Zhao, H.; Qi, J.; Su, R.; Zhang, H.; Chen, H.; Bai, L.; Wang, C. Hot deformation behaviour of 40CrNi steel and evaluation of different processing map construction methods. J. Mater. Res. Technol. 2020, 9, 2856–2869. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, X.; Zhao, T.; Zhou, Z.; Qiu, Y.; Wang, F.; Luo, R. Application of Four Different Models for Predicting the High-Temperature Flow Behavior of 1420 Al–Li Alloy. Metals 2022, 12, 2029. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Su, Z.; Wan, L.; Sun, C.; Cai, Y.; Yang, D. Hot deformation behavior of AZ80 magnesium alloy towards optimization of its hot workability. Mater. Charact. 2016, 122, 90–97. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Ashtiani, H.R.; Shahsavari, P. A comparative study on the phenomenological and artificial neural network models to predict hot deformation behavior of AlCuMgPb alloy. J. Alloys Compd. 2016, 687, 263–273. [Google Scholar] [CrossRef]
- Huang, W.; Lei, L.; Fang, G. Comparison between four flow stress models characterizing the constitutive behavior of hot deformation of 40 Mn steel. J. Mater. Eng. Perform. 2021, 30, 9149–9164. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Quan, G.Z.; Lv, W.Q.; Mao, Y.P.; Zhang, Y.W.; Zhou, J. Prediction of flow stress in a wide temperature range involving phase transformation for as-cast Ti–6Al–2Zr–1Mo–1V alloy by artificial neural network. Mater. Des. 2013, 50, 51–61. [Google Scholar] [CrossRef]
- Fangpo, L.; Ning, L.; Xiaojian, R.; Song, Q.; Caihong, L.; Jianjun, W.; Yang, X.; Bin, W. Arrhenius constitutive equation and artificial neural network model of flow stress in hot deformation of offshore steel with high strength and toughness. Mater. Technol. 2023, 38, 2264670. [Google Scholar] [CrossRef]
- Haihao, T.; Yufeng, X.; Tao, S.; Deyu, Z.; Lei, C. Flow Stress Prediction of Near-beta Ti-55511 Alloy During Isothermal Compression Based on Corrected Arrhenius Model with Material Parameter Evolution and BP-ANN Model. RARE Met. Mater. Eng. 2023, 52, 823–833. [Google Scholar]
- Pantalé, O. Development and implementation of an ANN based flow law for numerical simulations of thermo-mechanical processes at high temperatures in FEM software. Algorithms 2023, 16, 56. [Google Scholar] [CrossRef]






| C | Si | Mn | P | S | Cr | Nb | Al | Fe |
|---|---|---|---|---|---|---|---|---|
| 0.020 | 0.058 | 0.066 | 0.200 | 0.015 | 23.01 | 0.045 | 5.000 | Balance |
| True Strain | n | Q (J/mol) | |||
|---|---|---|---|---|---|
| 0.05 | 0.00578817 | 0.0978 | 11.78032 | 583,094.175 | 56.48958 |
| 0.10 | 0.00480784 | 0.0705 | 10.39722 | 585,825.067 | 56.80832 |
| 0.15 | 0.00434381 | 0.0659 | 10.77661 | 650,994.569 | 63.27652 |
| 0.20 | 0.00417564 | 0.0614 | 10.47091 | 648,180.364 | 62.84802 |
| 0.25 | 0.00408467 | 0.0590 | 10.27589 | 648,081.784 | 62.76339 |
| 0.30 | 0.00403675 | 0.0577 | 10.15583 | 647,236.520 | 62.65377 |
| 0.35 | 0.00403047 | 0.0572 | 10.05910 | 644,882.840 | 62.39976 |
| 0.40 | 0.00405917 | 0.0568 | 9.906700 | 638,400.738 | 61.72825 |
| 0.45 | 0.00411368 | 0.0565 | 9.73116 | 631,297.919 | 60.99076 |
| 0.50 | 0.00419438 | 0.0568 | 9.56919 | 624,389.253 | 60.24838 |
| 0.55 | 0.00429911 | 0.0585 | 9.60889 | 6,251,977.097 | 60.18814 |
| 0.60 | 0.00439022 | 0.0583 | 9.29741 | 6,198,135.363 | 59.75589 |
| 0.65 | 0.004532131 | 0.0591 | 9.08570 | 6,179,084.598 | 59.54815 |
| 0.70 | 0.004686720 | 0.0609 | 9.03063 | 6,250,485.214 | 60.22132 |
| 3-m-n-1 | nv | T (min) | R | AARE (%) | RMSE (MPa) | Prod |
|---|---|---|---|---|---|---|
| 3-9-4-1 | 81 | 78 | 0.9996 | 1.22 | 2.51 | 2.791 |
| 3-10-5-1 | 101 | 80 | 0.9998 | 0.90 | 1.93 | 2.125 |
| 3-11-6-1 | 123 | 81 | 0.9998 | 0.83 | 1.72 | 1.905 |
| 3-12-8-1 | 161 | 82 | 0.9997 | 0.70 | 1.99 | 2.110 |
| Model | R | AARE (%) | RMSE (MPa) |
|---|---|---|---|
| ANN | 0.9995 | 0.70 | 1.99 |
| Arrhenius | 0.9846 | 4.30 | 14.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Chen, S.; Du, S.; Yu, J.; Zhang, Y. Development of Constitutive Relationship for Thermomechanical Processing of FeCrAl Alloy to Predict Hot Deformation Behavior. Materials 2025, 18, 3007. https://doi.org/10.3390/ma18133007
Li C, Chen S, Du S, Yu J, Zhang Y. Development of Constitutive Relationship for Thermomechanical Processing of FeCrAl Alloy to Predict Hot Deformation Behavior. Materials. 2025; 18(13):3007. https://doi.org/10.3390/ma18133007
Chicago/Turabian StyleLi, Chuan, Shuang Chen, Shiyu Du, Juhong Yu, and Yiming Zhang. 2025. "Development of Constitutive Relationship for Thermomechanical Processing of FeCrAl Alloy to Predict Hot Deformation Behavior" Materials 18, no. 13: 3007. https://doi.org/10.3390/ma18133007
APA StyleLi, C., Chen, S., Du, S., Yu, J., & Zhang, Y. (2025). Development of Constitutive Relationship for Thermomechanical Processing of FeCrAl Alloy to Predict Hot Deformation Behavior. Materials, 18(13), 3007. https://doi.org/10.3390/ma18133007




