Method for Determining Contact Temperature of Tool Rake Face During Orthogonal Turning of Ti-6Al-4V Alloy
Abstract
1. Introduction
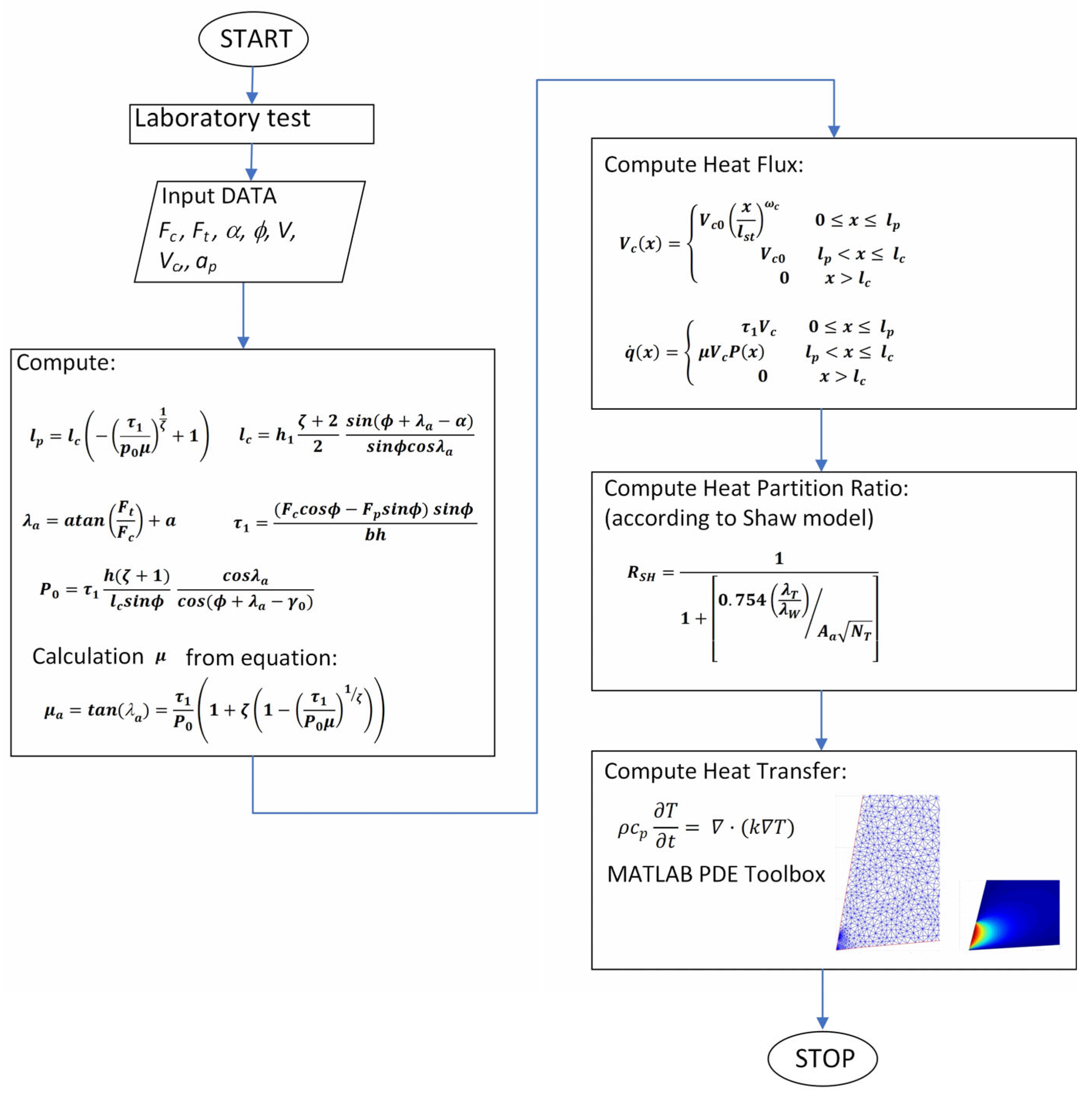
2. Methodology
3. Materials and Methods
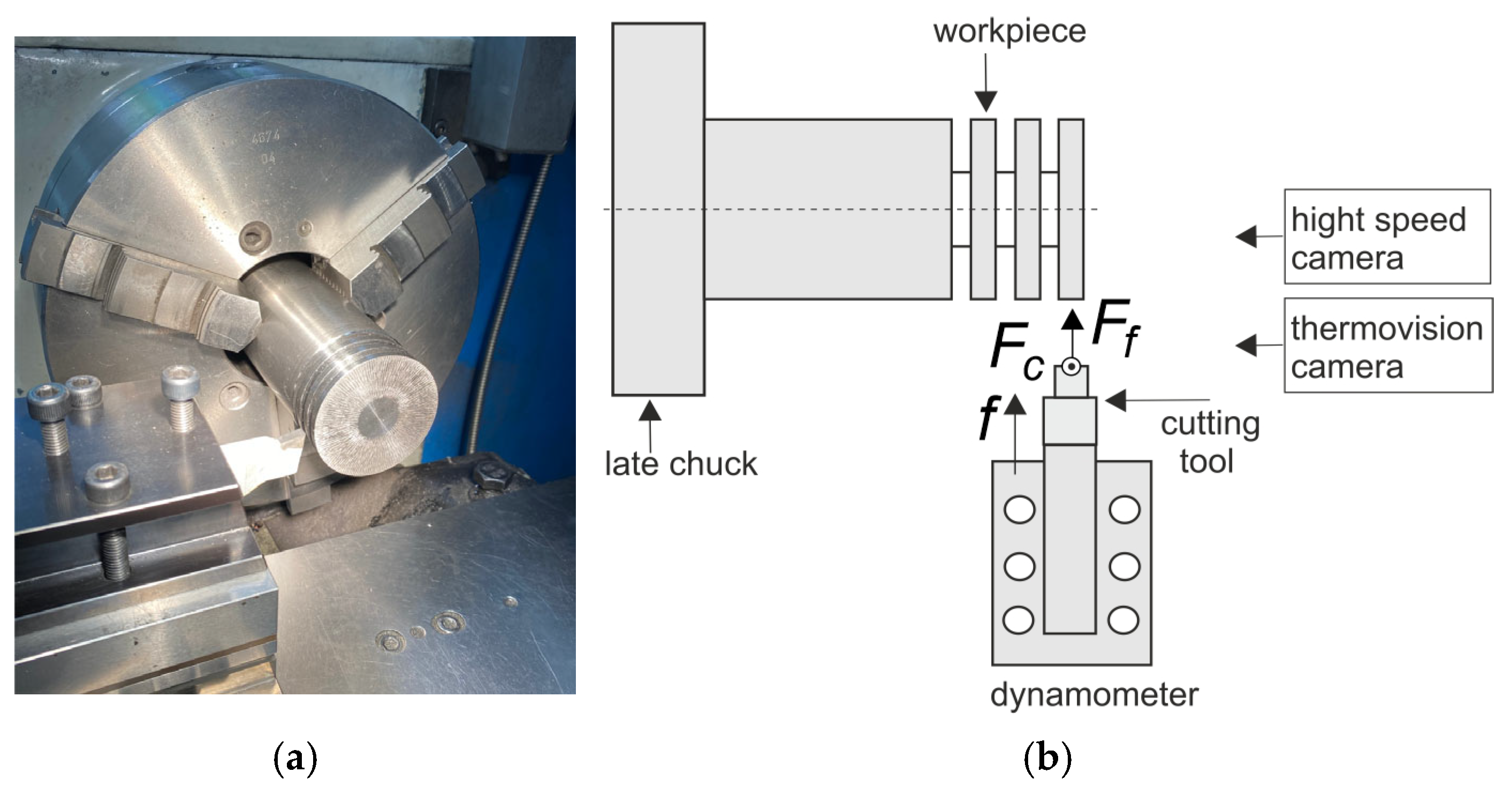
3.1. Materials
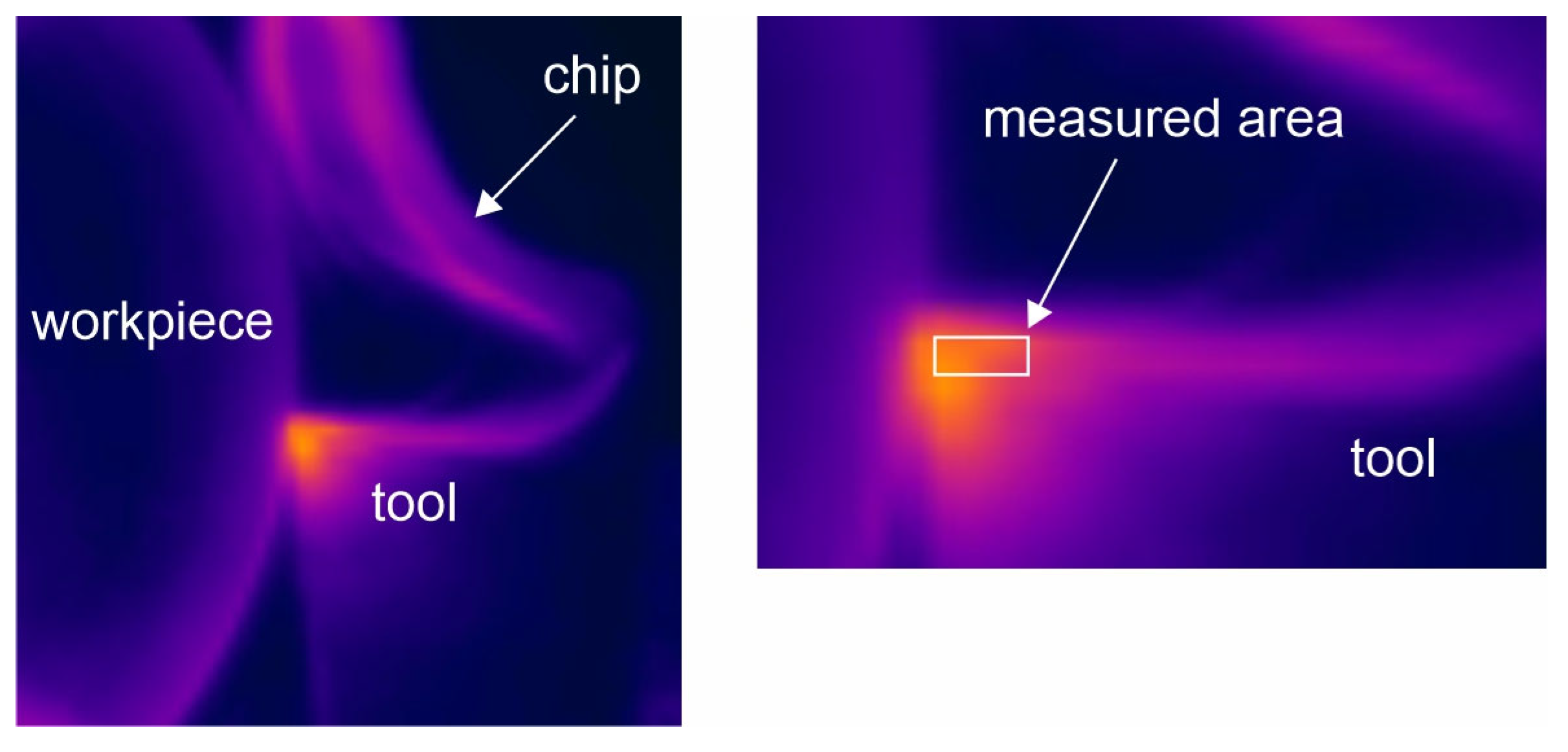
3.2. Methods
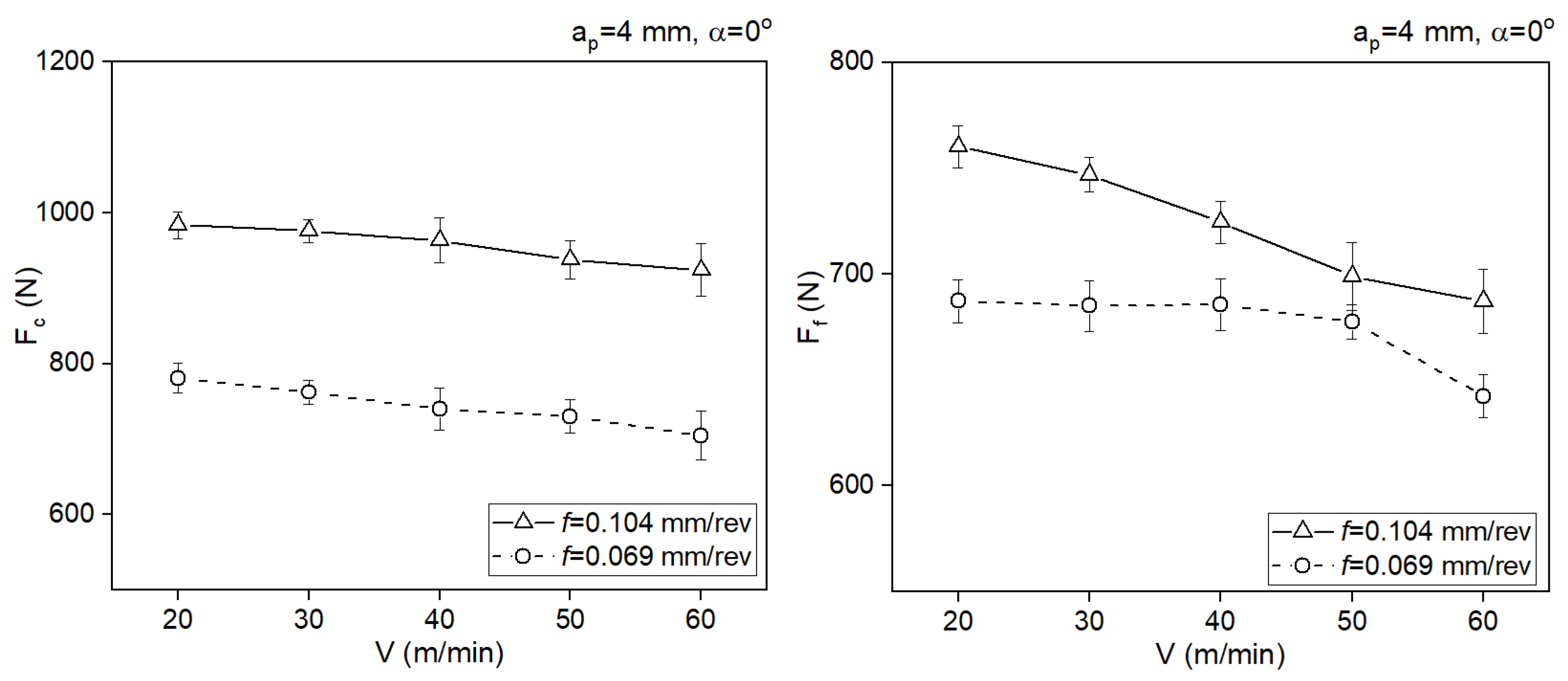
4. Results
- ○
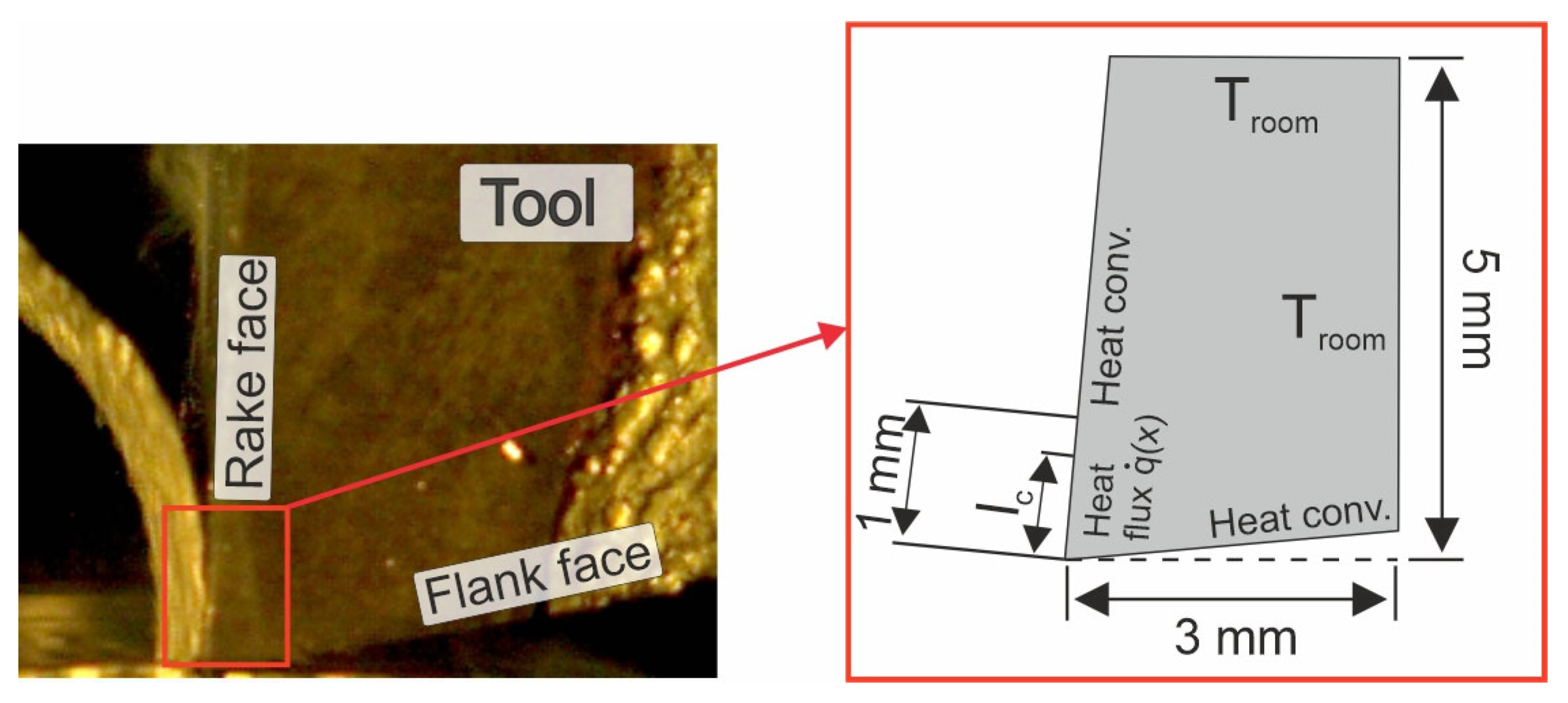
- Tool geometrical dimensions were according to Figure 17;
- ○
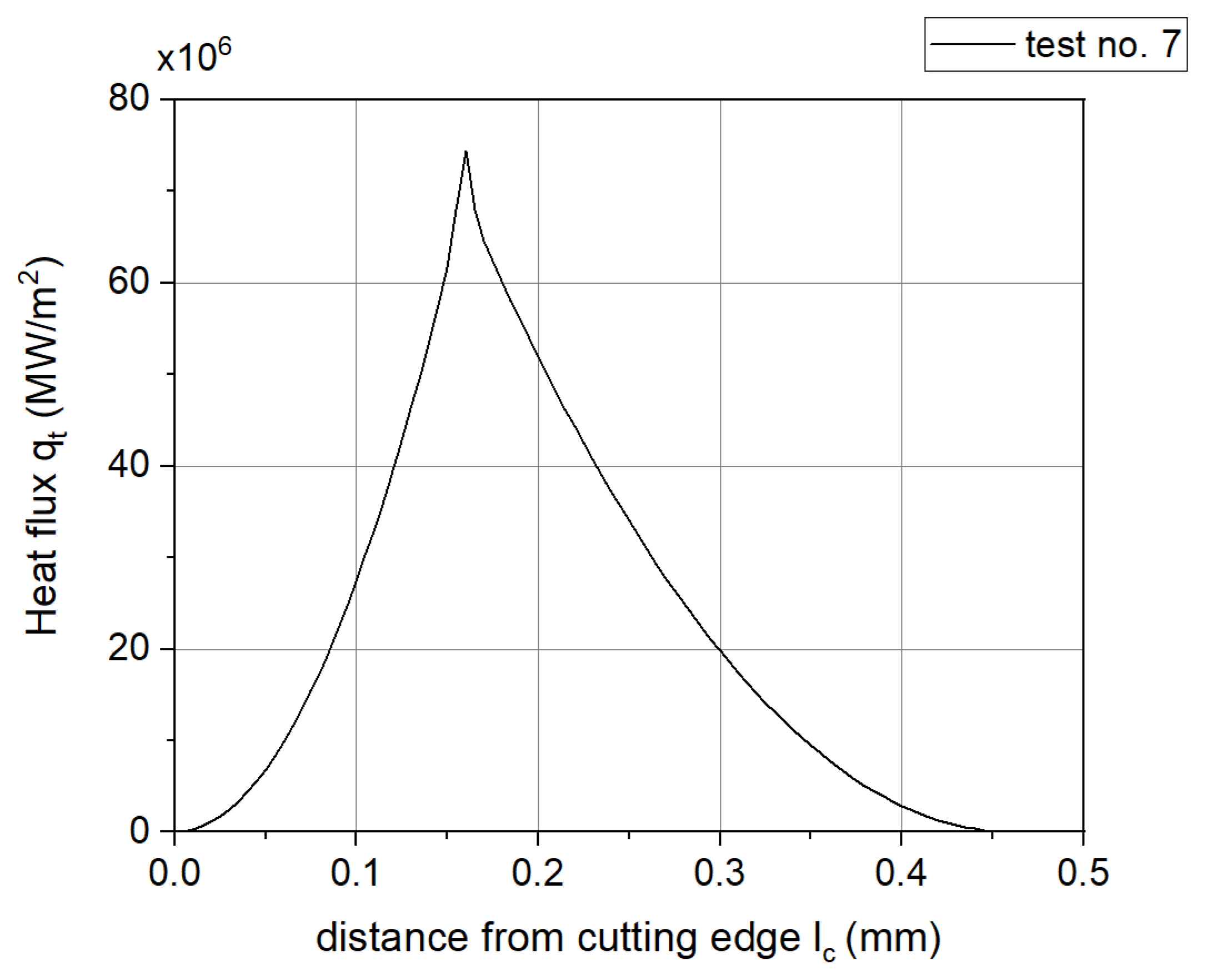
- Heat flux propagation was considered only on the rake face, within the chip–tool contact area, according to Figure 17;
- ○
- Dor the remaining part of the rake face and for the flank face, the convection coefficient used was hconv = 10 W/m2;
- ○
- The temperature set for the outer tool edges was Troom = 20 °C.
- -
- The boundary conditions were constant, according to Figure 17;
- -
- The superimposition and densification methods of the FEM mesh on the tool significantly affected the calculation time.
5. Conclusions
- ○
- The presented method is an original approach for the quick determination of the temperature on the tool rake face. The input data used in the method are the experimentally measured values of the cutting forces, the rake angle, and the cutting parameters.
- ○
- The model has some limitations. It is an orthogonal model of a 2D cutting process. In addition, it is based on the average heat partition ratio according to Shaw’s method and does not account for the tool’s core temperature.
- ○
- With a correctly calibrated model, differences may result from the fact that the thermovision camera measures the flank of the tool where the temperature is lower than in the central part of the rake face.
- ○
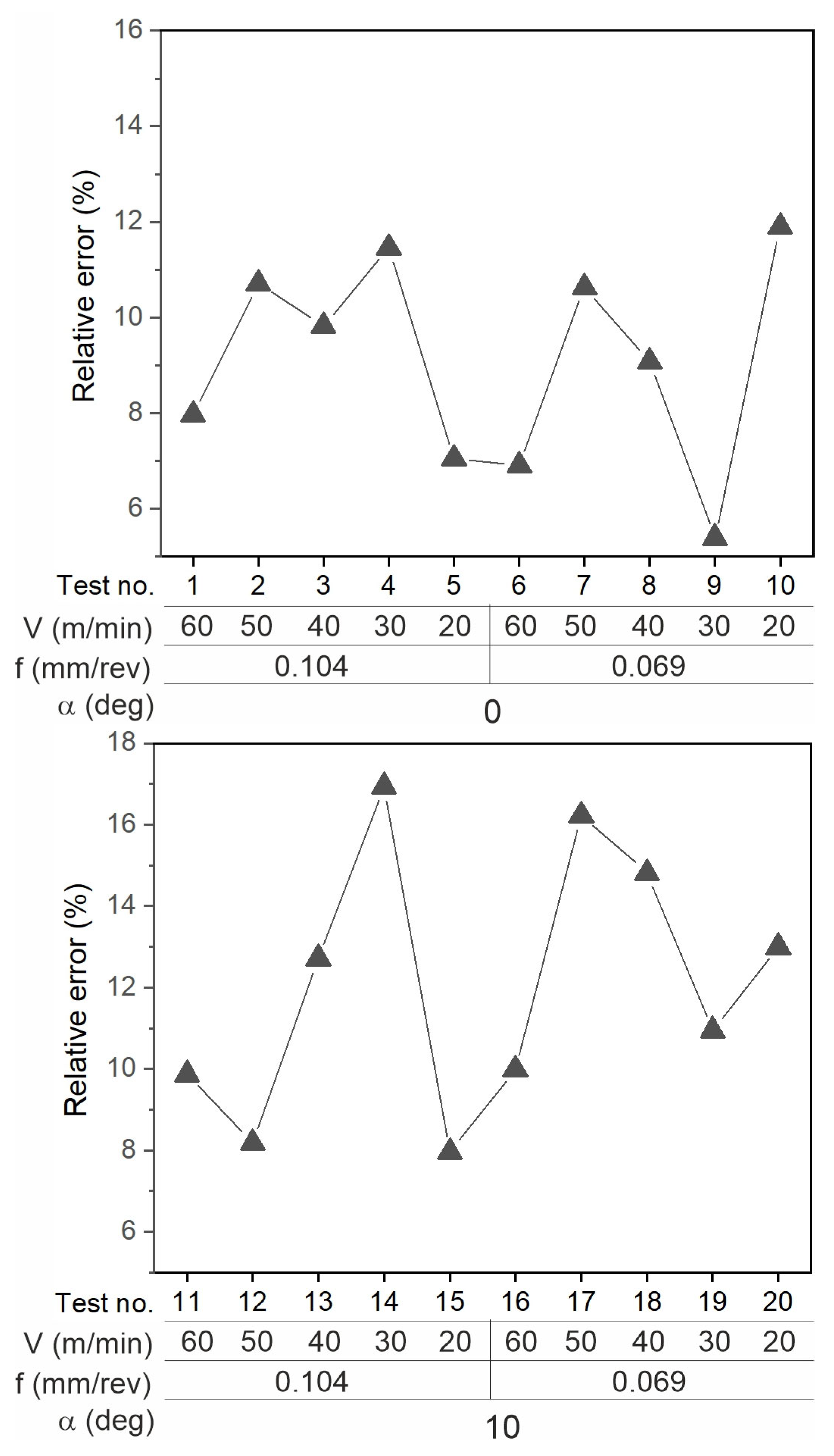
- The experimental values of the contact temperature are lower than those calculated, but the difference is small, ranging from 24 °C to 53 °C for α = 0°, and from 33 °C to 73° for α = 10°, which is a 17% difference, indicating a good fit of the results and confirming the correctness of the adopted model.
- ○
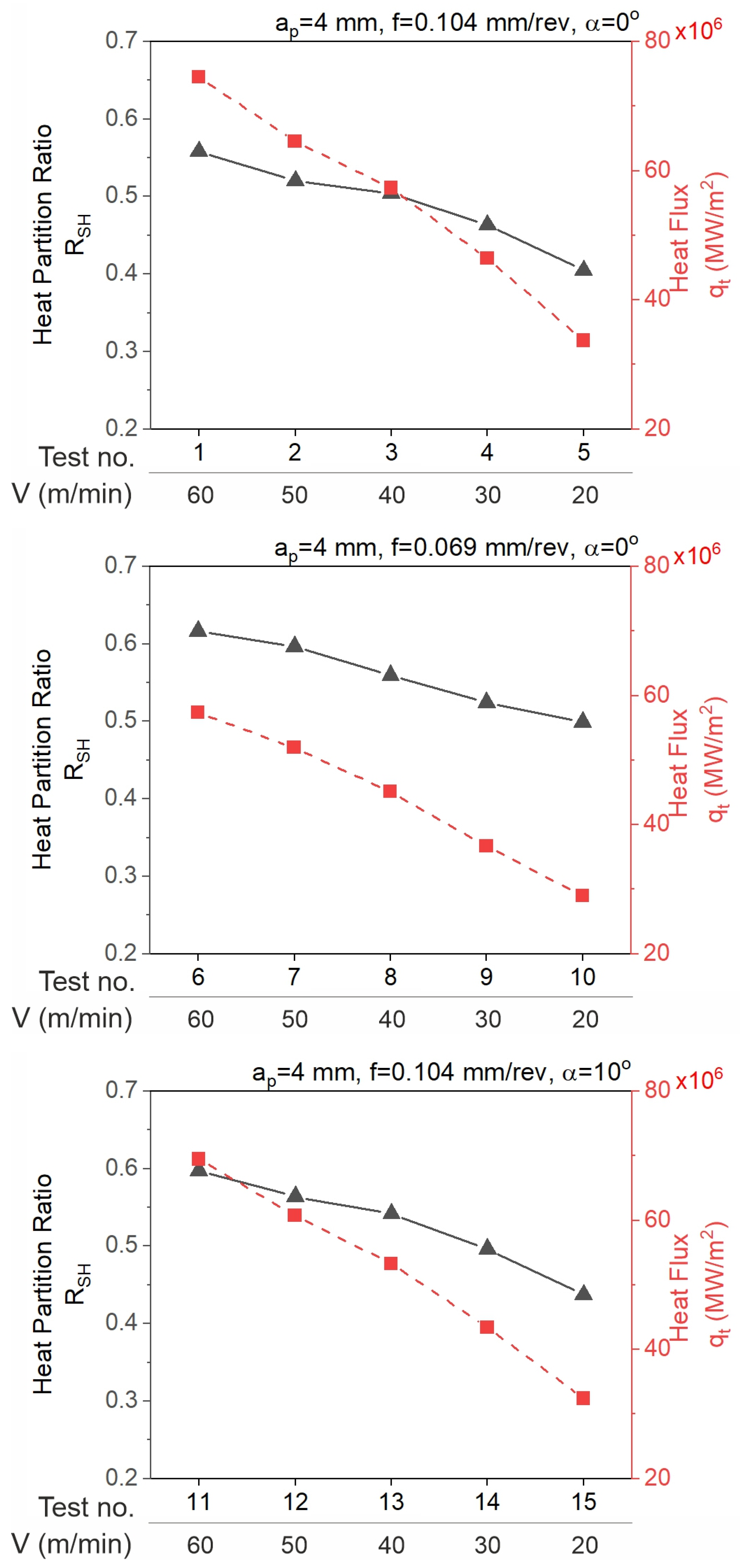
- The heat partition ratio for the tool (1-RSH) decreases as the cutting speed increases. The greatest value of the ratio was determined in test 5 (0.596) and the smallest value in test 6 (0.383).
- ○
- The minimum heat flux value propagating to the tool was determined in test 20 and was equal to 28.680 MW/m2, which was 38.5% of the maximum value (in test 1, 74.452 MW/m2).
- ○
- In addition, the model can be further improved by including reliable models of heat division and the tool core temperature in the algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process: Part I—Temperature rise distribution due to shear 456 plane heat source. Int. J. Mech. Sci. 2000, 42, 1715–1752. [Google Scholar] [CrossRef]
- Karpat, Y.; Özel, T. Predictive analytical and thermal modeling of orthogonal cutting process—Part I: Predictions of tool forces, stresses, and temperature distributions. J. Manuf. Sci. Eng. 2006, 128, 435–444. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, J.; Cao, S.; Song, X.; Yan, X.; Nie, F.; Peng, Z. Wear behavior of coated cermet/carbide tools during high-speed turning of 18CrNiMo7-6 steel and its associated surface integrity evaluations. Wear 2025, 576–577, 206121. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part II: Temperature rise distribution due to frictional 458 heat source at the tool–chip interface. Int. J. Mech. Sci. 2001, 43, 57–88. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part III: Temperature rise distribution due to the 460 combined effects of shear plane heat source and the tool–chip interface frictional heat source. Int. J. Mech. Sci. 2001, 43, 89–107. [Google Scholar] [CrossRef]
- Karpat, Y.; Özel, T. Predictive analytical and thermal modeling of orthogonal cutting process—Part II: Effect of tool flank wear on tool forces, stresses, and temperature distributions. J. Manuf. Sci. Eng. 2006, 128, 445–453. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, L.; Ye, Y.; Chi, Y.; Gao, L.; Zha, X.; Huang, T.; Zhang, Y.; Ding, H.; Ye, C. Exploring the strengthening mechanisms of additive manufactured metals treated by ultrasonic nanocrystal surface modification. Int. J. Fatigue 2025, 190, 108609. [Google Scholar] [CrossRef]
- Davies, M.A.; Ueda, T.; M’Saoubi, R.; Mullany, B.; Cooke, A.L. On The Measurement of Temperature in Material Removal Processes. CIRP Ann. 2007, 5, 581–604. [Google Scholar] [CrossRef]
- Barlier, C.; Lescalier, C.; Mosian, A. Continuous Flank Wear Measurement of Turning Tools by Integrated Microthermocouple. CIRP Ann. 1997, 46, 35–38. [Google Scholar] [CrossRef]
- Basti, A.; Obikawa, T.; Shinozuka, J. Tools with built-in thin film thermocouple sensors for monitoring cutting temperature. Int. J. Mach. Tools Manuf. 2007, 47, 793–798. [Google Scholar] [CrossRef]
- Hoyne, A.C.; Nath, C.; Kapoor, S.G. On cutting temperature measurement during titanium machining with an atomization-based cutting fluid spray system. J. Manuf. Sci. Eng. 2015, 137, 024502. [Google Scholar] [CrossRef]
- Davies, M.; Cao, Q.; Cooke, A.; Ivester, R. On the Measurement and Prediction of Temperature Fields in Machining AISI 1045 Steel. CIRP Ann. 2003, 52, 77–80. [Google Scholar] [CrossRef]
- Li, T.; Long, H.; Shi, T.; Yang, J.; Duan, J. Cutting temperature measurement using a novel near-infrared two-color pyrometer under dry and wet cutting of Ti-6Al-4V alloy. J. Mater. Process. Technol. 2022, 309, 117751. [Google Scholar] [CrossRef]
- Abouridouane, M.; Klocke, F.; Döbbeler, B. Analytical temperature prediction for cutting steel. CIRP Ann. 2016, 65, 77–80. [Google Scholar] [CrossRef]
- Arrazola, P.J.; Aristimuno, P.; Soler, D.; Childs, T. Metal cutting experiments and modelling for improved determination of chip/tool contact temperature by infrared thermography. CIRP Ann. 2015, 64, 57–60. [Google Scholar] [CrossRef]
- Soler, D.; Childs, T.H.C.; Arrazola, P.J. A Note on Interpreting Tool Temperature Measurements from Thermography. Mach. Sci. Technol. 2015, 19, 174–181. [Google Scholar] [CrossRef]
- Chen, W.C.; Tsao, C.C.; Liang, P.W. Determination of temperature distributions on the rake face of cutting tools using a remote method. Int. Commun. Heat Mass Transf. 1997, 24, 161–170. [Google Scholar] [CrossRef]
- Kumar, B.V.R.M.; Reddy, K.; Kumar, C.R. Finite element model based on abaqus/explicit to analyze the temperature effects of turning. Int. J. Appl. Eng. Res. 2016, 11, 5728–5734. [Google Scholar]
- Ding, H.; Shin, Y. Multi-physics modeling and simulations of surface microstructure alteration in hard turning. J. Mater. Process. Technol. 2013, 213, 877–886. [Google Scholar] [CrossRef]
- Liu, G.; Huang, C.; Su, R.; Özel, T.; Liu, Y.; Xu, L. 3D FEM simulation of the turning process of stainless steel 17-4PH with differently texturized cutting tools. Int. J. Mech. Sci. 2019, 155, 417–429. [Google Scholar] [CrossRef]
- Ojal, N.; Copenhaver, R.; Cherukuri, H.P.; Schmitz, T.L.; Devlugt, K.T.; Jaycox, A.W. A Realistic Full-Scale 3D Modeling of Turning Using Coupled Smoothed Particle Hydrodynamics and Finite Element Method for Predicting Cutting Forces. J. Manuf. Mater. Process. 2022, 6, 33. [Google Scholar] [CrossRef]
- Qiu, X.; Cheng, X.; Dong, P.; Peng, H.; Xing, Y.; Zhou, X. Sensitivity Analysis of Johnson-Cook Material Constants and Friction Coefficient Influence on Finite Element Simulation of Turning Inconel 718. Materials 2019, 12, 3121. [Google Scholar] [CrossRef] [PubMed]
- Komvopoulos, K.; Erpenbeck, S.A. Finite Element Modeling of Orthogonal Metal Cutting. J. Manuf. Sci. Eng. 1991, 113, 253–267. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B. The effects of coolant on the cutting temperature, surface roughness and tool wear in turning operations of Ti6Al4V alloy. Mech. Based Des. Struct. Mach. 2023, 52, 3277–3299. [Google Scholar] [CrossRef]
- Özel, T.; Ulutan, D. Prediction of Machining Induced Residual Stresses in Turning of Titanium and Nickel Based Alloys with Experiments and Finite Element Simulations. CIRP Ann. 2012, 61, 547–550. [Google Scholar] [CrossRef]
- Alammari, Y.; Weng, J.; Saelzer, J.; Biermann, D. Transient Temperature at Tool–Chip Interface during Initial Period of Chip Formation in Orthogonal Cutting of Inconel 718. Materials 2024, 17, 2232. [Google Scholar] [CrossRef]
- Karaguzel, U. Transient multi-domain thermal modeling of interrupted cutting with coated tools. Int. J. Adv. Manuf. Technol. 2021, 116, 345–361. [Google Scholar] [CrossRef]
- Ślusarczyk, Ł. Experimental-Analytical Method for Temperature Determination in the Cutting Zone during Orthogonal Turning of GRADE 2 Titanium Alloy. Materials 2021, 14, 4328. [Google Scholar] [CrossRef]
- Ozlu, E.; Molinari, A.; Budak, E. Two-zone analytical contact model applied to orthogonal cutting. Mach. Sci. Technol. 2010, 14, 323–343. [Google Scholar] [CrossRef]
- Bahi, S.; Nouari, M.; Moufki, A.; El Mansori, M.; Molinari, A. A new friction law for sticking and sliding contacts in machining. Tribol. Int. 2011, 44, 764–771. [Google Scholar] [CrossRef]
- Grzesik, W. Modelling of Heat Generation and Transfer in Metal Cutting: A Short Review. J. Mach. Eng. 2020, 20, 24–33. [Google Scholar] [CrossRef]
- Grzesik, W.; Nieslony, P. Physics based modelling of interface temperatures in machining with multilayer coated tools at moderate cutting speeds. Int. J. Mach. Tools Manuf. 2004, 9, 889–901. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, H.P.; Chang, J.; Wei, B. Experimental study of surface tension, specific heat and thermal diffusivity of liquid and solid titanium. Chem. Phys. Lett. 2015, 639, 105–108. [Google Scholar] [CrossRef]
- Twardowska, A.; Ślusarczyk, Ł.; Kowalski, M. Impact of Deposition of the (TiBx/TiSiyCz)x3 Multilayer on M2 HSS on the Cutting Force Components and Temperature Generated in the Machined Area during the Milling of 316L Steel. Materials 2022, 15, 746. [Google Scholar] [CrossRef] [PubMed]











| Symbol | Ti | C | Fe | N | Al | O | V | H | Other |
|---|---|---|---|---|---|---|---|---|---|
| %wt. | bal | 0.08 | 0.03 | 0.05 | 5.5–6.75 | 0.20 | 3.5–4.5 | 0.015 | 0.40 |
| Symbol | Cutting Parameters | Parameter Values | |||||
|---|---|---|---|---|---|---|---|
| A | f (mm/rev) | 0.069 | 0.104 | ||||
| B | V (m/min) | 20 | 30 | 40 | 50 | 60 | |
| Test No. | F (mm/rev) | V (m/min) | ap (mm) | α (degs) |
|---|---|---|---|---|
| 1 | 0.104 | 60 | 4 | 0 |
| 2 | 0.104 | 50 | 4 | 0 |
| 3 | 0.104 | 40 | 4 | 0 |
| 4 | 0.104 | 30 | 4 | 0 |
| 5 | 0.104 | 20 | 4 | 0 |
| 6 | 0.069 | 60 | 4 | 0 |
| 7 | 0.069 | 50 | 4 | 0 |
| 8 | 0.069 | 40 | 4 | 0 |
| 9 | 0.069 | 30 | 4 | 0 |
| 10 | 0.069 | 20 | 4 | 0 |
| 11 | 0.104 | 60 | 4 | 10 |
| 12 | 0.104 | 50 | 4 | 10 |
| 13 | 0.104 | 40 | 4 | 10 |
| 14 | 0.104 | 30 | 4 | 10 |
| 15 | 0.104 | 20 | 4 | 10 |
| 16 | 0.069 | 60 | 4 | 10 |
| 17 | 0.069 | 50 | 4 | 10 |
| 18 | 0.069 | 40 | 4 | 10 |
| 19 | 0.069 | 30 | 4 | 10 |
| 20 | 0.069 | 20 | 4 | 10 |
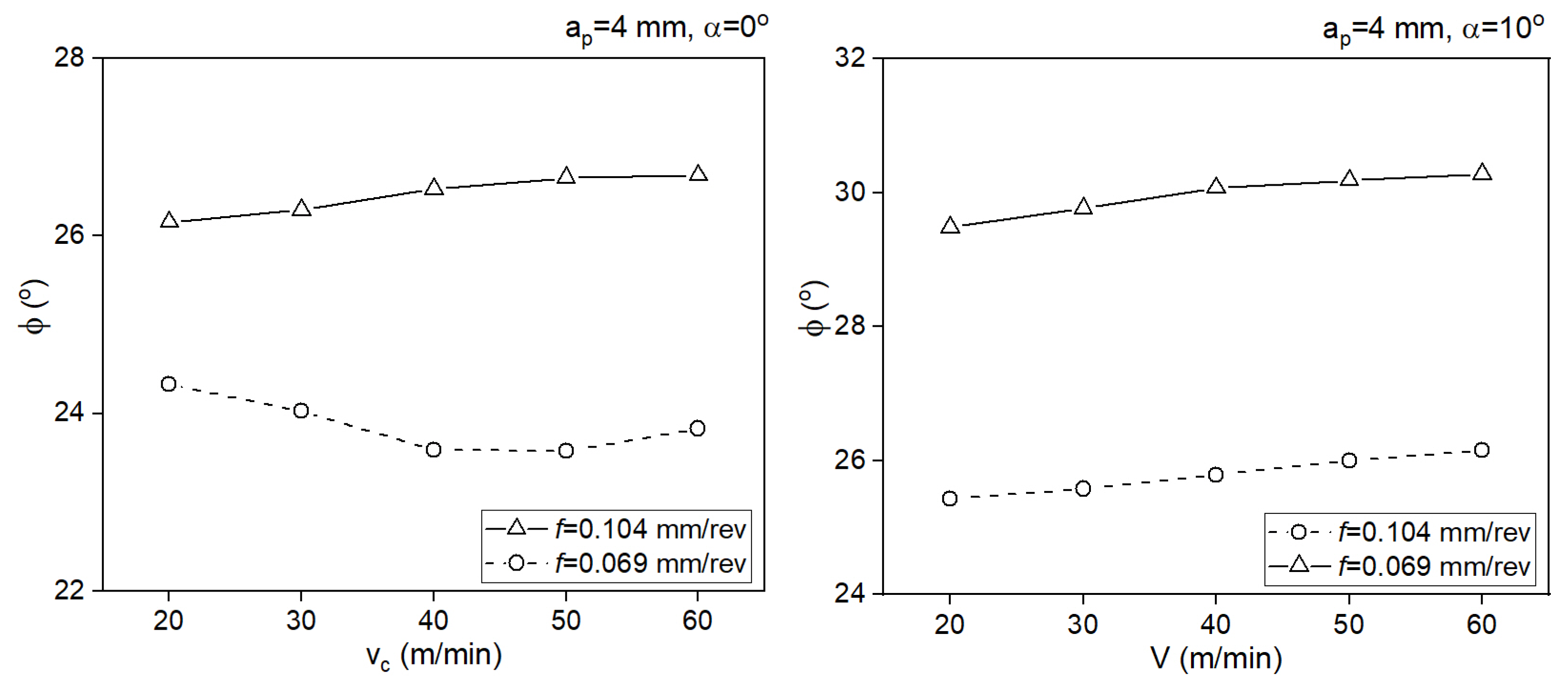
| Test No. | Fc (N) | Ft (N) | ϕ (degs) | τ1 (MPa) |
|---|---|---|---|---|
| 1 | 924.3 | 687.2 | 26.68 | 558.4 |
| 2 | 938.0 | 699.0 | 26.65 | 565.9 |
| 3 | 963.5 | 724.5 | 26.53 | 578.1 |
| 4 | 976.3 | 746.9 | 26.29 | 579.7 |
| 5 | 984.0 | 760.2 | 26.16 | 580.8 |
| 6 | 705.0 | 642.3 | 23.83 | 564.2 |
| 7 | 730.2 | 677.3 | 23.58 | 577.3 |
| 8 | 740.0 | 685.5 | 23.59 | 585.5 |
| 9 | 762.2 | 685.0 | 24.03 | 615.5 |
| 10 | 781.0 | 687.1 | 24.33 | 639.7 |
| 11 | 762.1 | 430.2 | 30.28 | 534.8 |
| 12 | 774.3 | 440.3 | 30.19 | 541.4 |
| 13 | 782.5 | 449.1 | 30.07 | 544.6 |
| 14 | 796.3 | 468.2 | 29.77 | 547.5 |
| 15 | 810.0 | 487.2 | 29.49 | 550.5 |
| 16 | 584.8 | 451.8 | 26.16 | 520.3 |
| 17 | 589.3 | 460.4 | 26.00 | 520.7 |
| 18 | 598.8 | 475.0 | 25.79 | 524.1 |
| 19 | 596.3 | 480.2 | 25.58 | 517.1 |
| 20 | 601.3 | 489.3 | 25.43 | 518.0 |
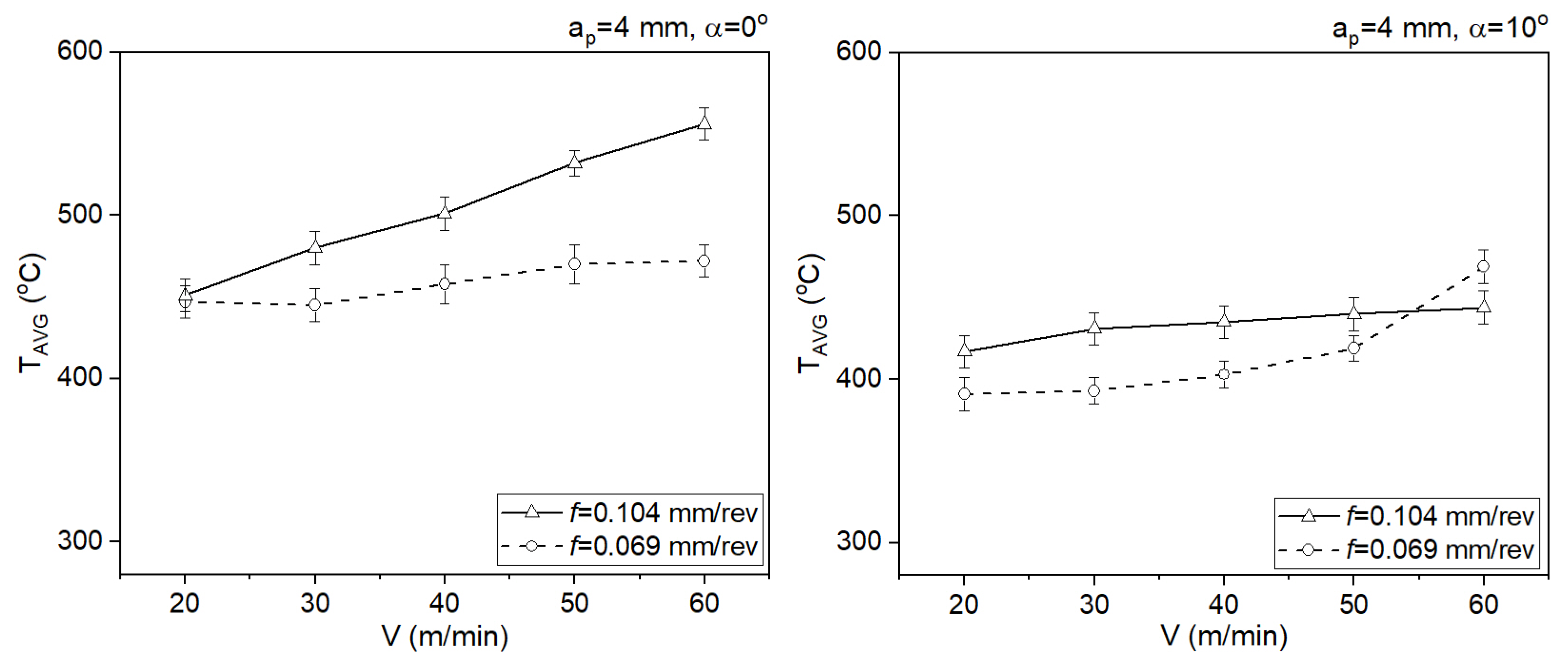
| Test No. | (m/min) | (°C) |
|---|---|---|
| 1 | 30.2 | 556 |
| 2 | 25.1 | 532 |
| 3 | 20.0 | 501 |
| 4 | 14.8 | 480 |
| 5 | 9.8 | 451 |
| 6 | 26.5 | 472 |
| 7 | 21.8 | 470 |
| 8 | 17.5 | 458 |
| 9 | 13.4 | 445 |
| 10 | 9.0 | 447 |
| 11 | 32.3 | 444 |
| 12 | 26.8 | 440 |
| 13 | 21.3 | 435 |
| 14 | 15.8 | 431 |
| 15 | 10.4 | 417 |
| 16 | 27.5 | 469 |
| 17 | 22.8 | 419 |
| 18 | 18.1 | 403 |
| 19 | 13.4 | 393 |
| 20 | 8.9 | 391 |
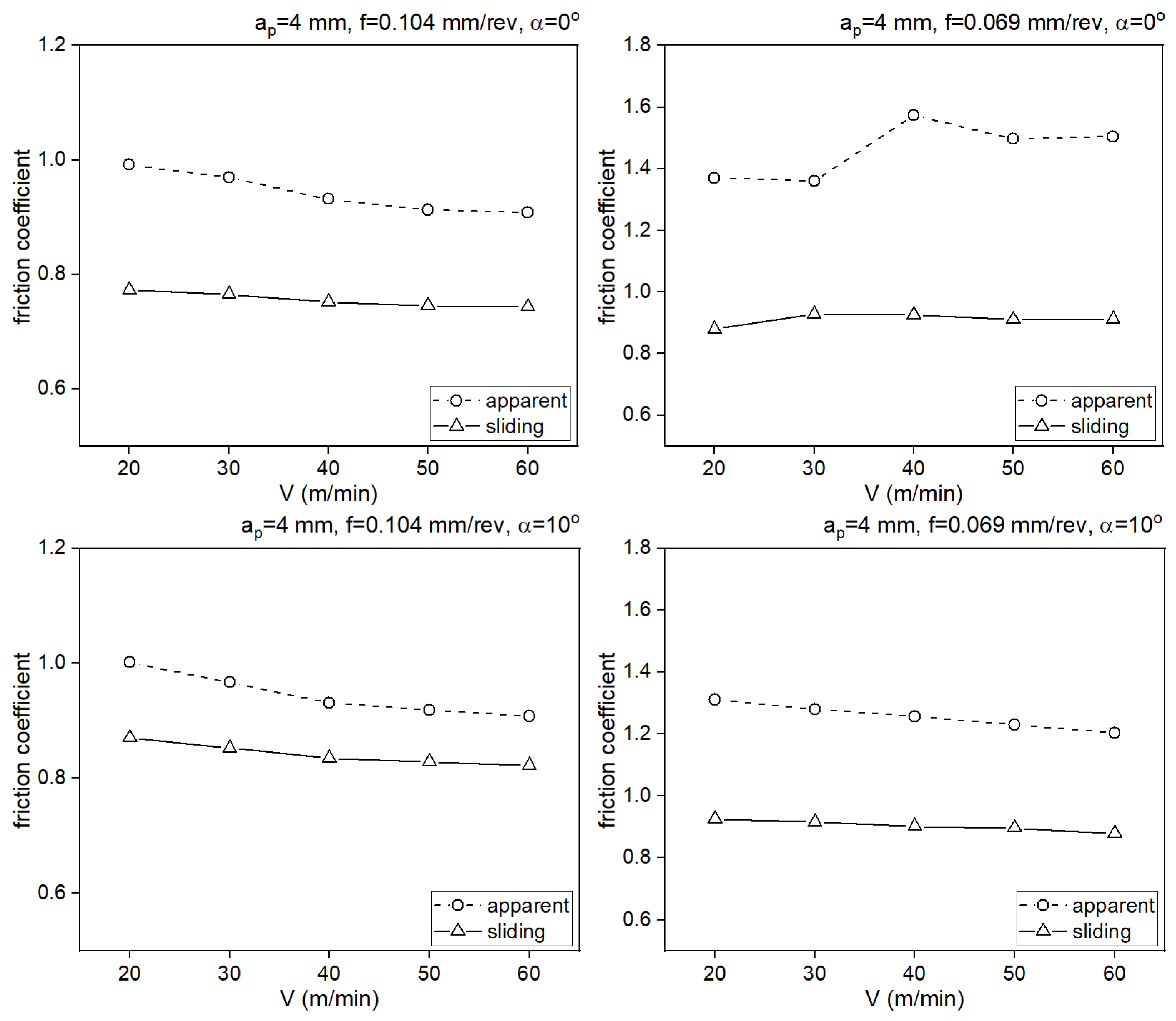
| Test No. | (MPa) | ||
|---|---|---|---|
| 1 | 1344.3 | 0.743 | 0.908 |
| 2 | 1361.2 | 0.745 | 0.913 |
| 3 | 1386.2 | 0.752 | 0.931 |
| 4 | 1381.3 | 0.765 | 0.969 |
| 5 | 1378.9 | 0.773 | 0.992 |
| 6 | 1251.1 | 0.912 | 1.504 |
| 7 | 1269.7 | 0.910 | 1.496 |
| 8 | 1288.7 | 0.926 | 1.574 |
| 9 | 1373.5 | 0.928 | 1.360 |
| 10 | 1440.9 | 0.880 | 1.370 |
| 11 | 1098.7 | 0.823 | 0.908 |
| 12 | 1108.5 | 0.828 | 0.918 |
| 13 | 1110.2 | 0.835 | 0.931 |
| 14 | 1103.3 | 0.853 | 0.967 |
| 15 | 1096.9 | 0.870 | 1.001 |
| 16 | 893.8 | 0.879 | 1.203 |
| 17 | 887.6 | 0.896 | 1.230 |
| 18 | 883.9 | 0.902 | 1.257 |
| 19 | 862.7 | 0.916 | 1.280 |
| 20 | 857.6 | 0.925 | 1.310 |
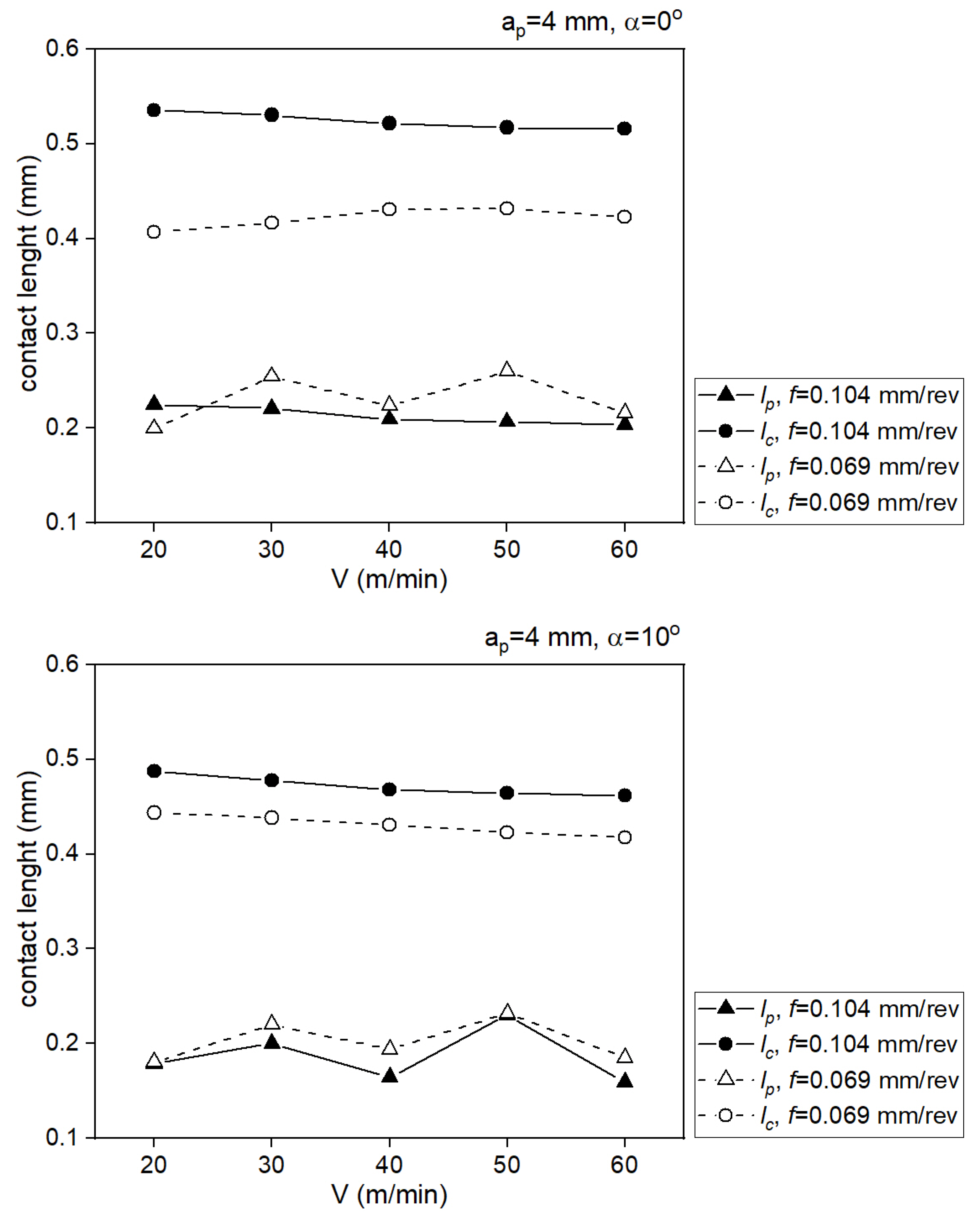
| Test No. | (mm) | (mm) |
|---|---|---|
| 1 | 0.516 | 0.204 |
| 2 | 0.517 | 0.206 |
| 3 | 0.521 | 0.209 |
| 4 | 0.530 | 0.221 |
| 5 | 0.535 | 0.225 |
| 6 | 0.423 | 0.216 |
| 7 | 0.431 | 0.260 |
| 8 | 0.431 | 0.224 |
| 9 | 0.416 | 0.254 |
| 10 | 0.407 | 0.200 |
| 11 | 0.461 | 0.159 |
| 12 | 0.464 | 0.242 |
| 13 | 0.468 | 0.164 |
| 14 | 0.478 | 0.249 |
| 15 | 0.488 | 0.179 |
| 16 | 0.417 | 0.185 |
| 17 | 0.423 | 0.232 |
| 18 | 0.430 | 0.194 |
| 19 | 0.438 | 0.241 |
| 20 | 0.444 | 0.180 |
| Material | Property | Equation or Value |
|---|---|---|
| WC-Co | Thermal conductivity | |
| Specific heat (Jkg−1K−1) | ||
| Density (kgm−3) | ρ = | |
| Ti-6Al-4V | Thermal conductivity | |
| Thermal diffusivity |
| Test No. | RSH | Heat Flux (MW/m2) | Heat Flux qc (MW/m2) | Heat Flux qt (MW/m2) |
|---|---|---|---|---|
| 1 | 0.558 | 168.390 | 93.938 | 74.452 |
| 2 | 0.520 | 139.080 | 74.529 | 64.551 |
| 3 | 0.504 | 115.445 | 58.161 | 57.284 |
| 4 | 0.463 | 87.710 | 41.323 | 46.386 |
| 5 | 0.404 | 56.535 | 22.865 | 33.670 |
| 6 | 0.617 | 149.522 | 92.193 | 57.329 |
| 7 | 0.596 | 127.725 | 75.796 | 51.929 |
| 8 | 0.560 | 102.402 | 57.307 | 45.095 |
| 9 | 0.524 | 79.330 | 42.662 | 36.668 |
| 10 | 0.499 | 57.860 | 28.880 | 28.980 |
| 11 | 0.597 | 172.469 | 103.039 | 69.430 |
| 12 | 0.564 | 142.904 | 82.166 | 60.738 |
| 13 | 0.542 | 116.225 | 62.952 | 53.273 |
| 14 | 0.496 | 88.073 | 44.657 | 43.416 |
| 15 | 0.437 | 57.489 | 25.128 | 32.361 |
| 16 | 0.615 | 143.265 | 88.071 | 55.195 |
| 17 | 0.525 | 117.835 | 63.198 | 43.925 |
| 18 | 0.553 | 94.785 | 52.369 | 42.416 |
| 19 | 0.510 | 74.635 | 38.589 | 36.045 |
| 20 | 0.453 | 52.423 | 23.744 | 28.680 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ślusarczyk, Ł.; Twardowska, A. Method for Determining Contact Temperature of Tool Rake Face During Orthogonal Turning of Ti-6Al-4V Alloy. Materials 2025, 18, 2980. https://doi.org/10.3390/ma18132980
Ślusarczyk Ł, Twardowska A. Method for Determining Contact Temperature of Tool Rake Face During Orthogonal Turning of Ti-6Al-4V Alloy. Materials. 2025; 18(13):2980. https://doi.org/10.3390/ma18132980
Chicago/Turabian StyleŚlusarczyk, Łukasz, and Agnieszka Twardowska. 2025. "Method for Determining Contact Temperature of Tool Rake Face During Orthogonal Turning of Ti-6Al-4V Alloy" Materials 18, no. 13: 2980. https://doi.org/10.3390/ma18132980
APA StyleŚlusarczyk, Ł., & Twardowska, A. (2025). Method for Determining Contact Temperature of Tool Rake Face During Orthogonal Turning of Ti-6Al-4V Alloy. Materials, 18(13), 2980. https://doi.org/10.3390/ma18132980







