Experimental Verification of the Model for Estimating the Corrosion Current of Reinforcement in an RC Element
Abstract
1. Introduction
2. Theoretical Model
3. Calculation Approach
4. Laboratory Tests
| Assay | Maximum Content of Elements, % | % | ||||||
|---|---|---|---|---|---|---|---|---|
| C | Mn | Si | P | S | Cu | N | ||
| steel smelting | 0.220 | 1.600 | 0.550 | 0.050 | 0.050 | 0.800 | 0.012 | 0.500 |
| finished product | 0.240 | 1.650 | 0.600 | 0.055 | 0.055 | 0.850 | 0.013 | 0.520 |
5. Analysis of the Obtained Results
6. Discussion
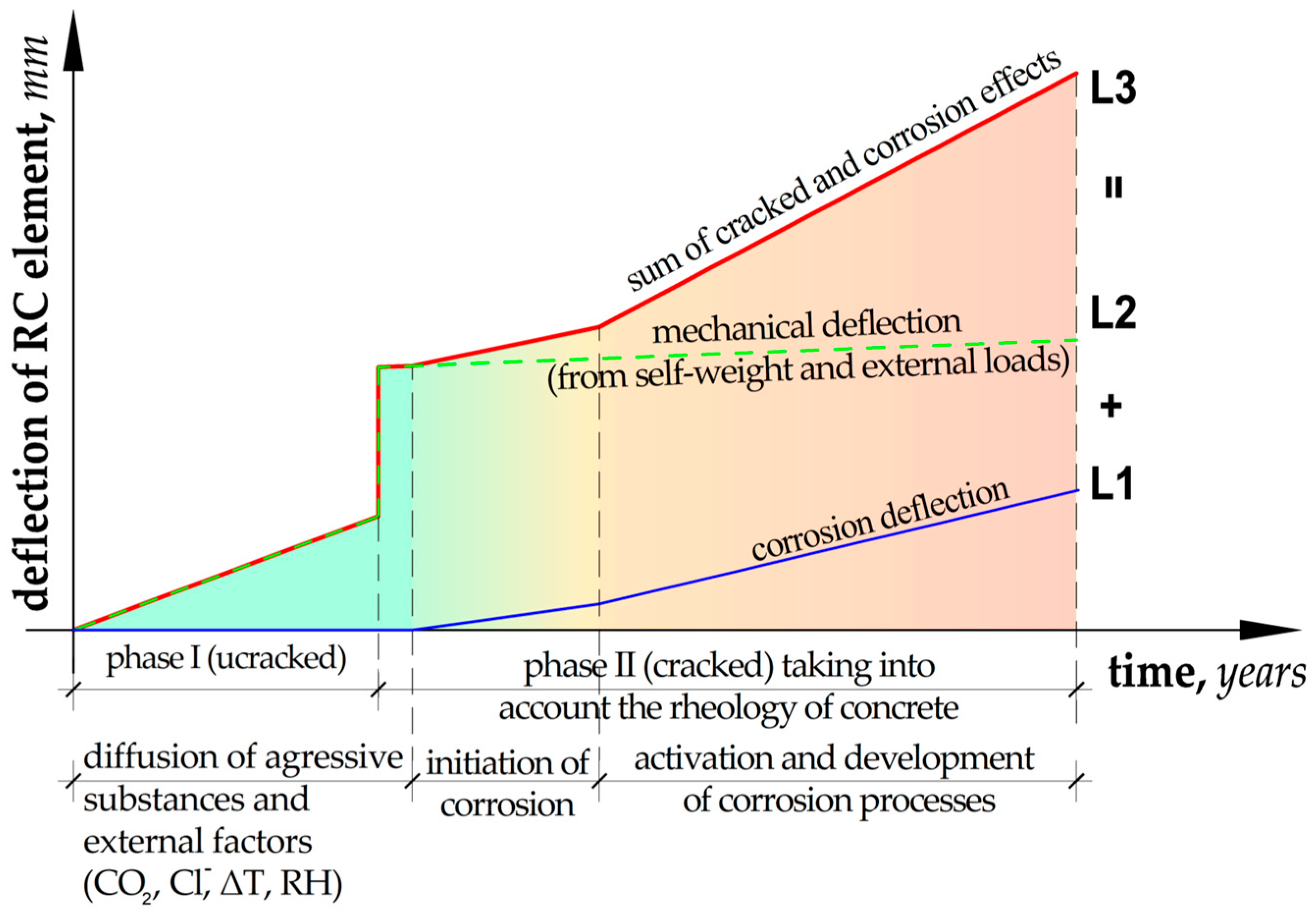
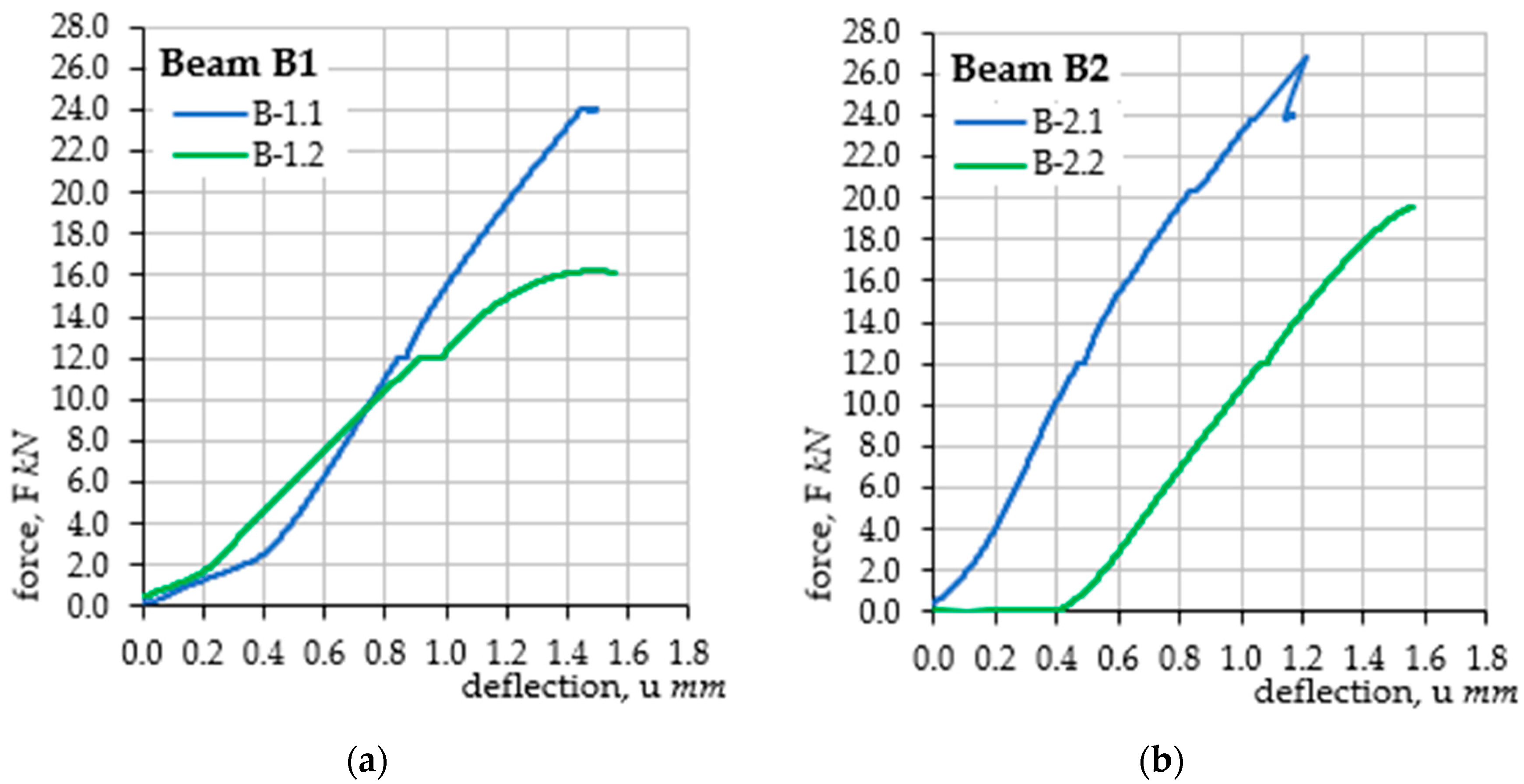
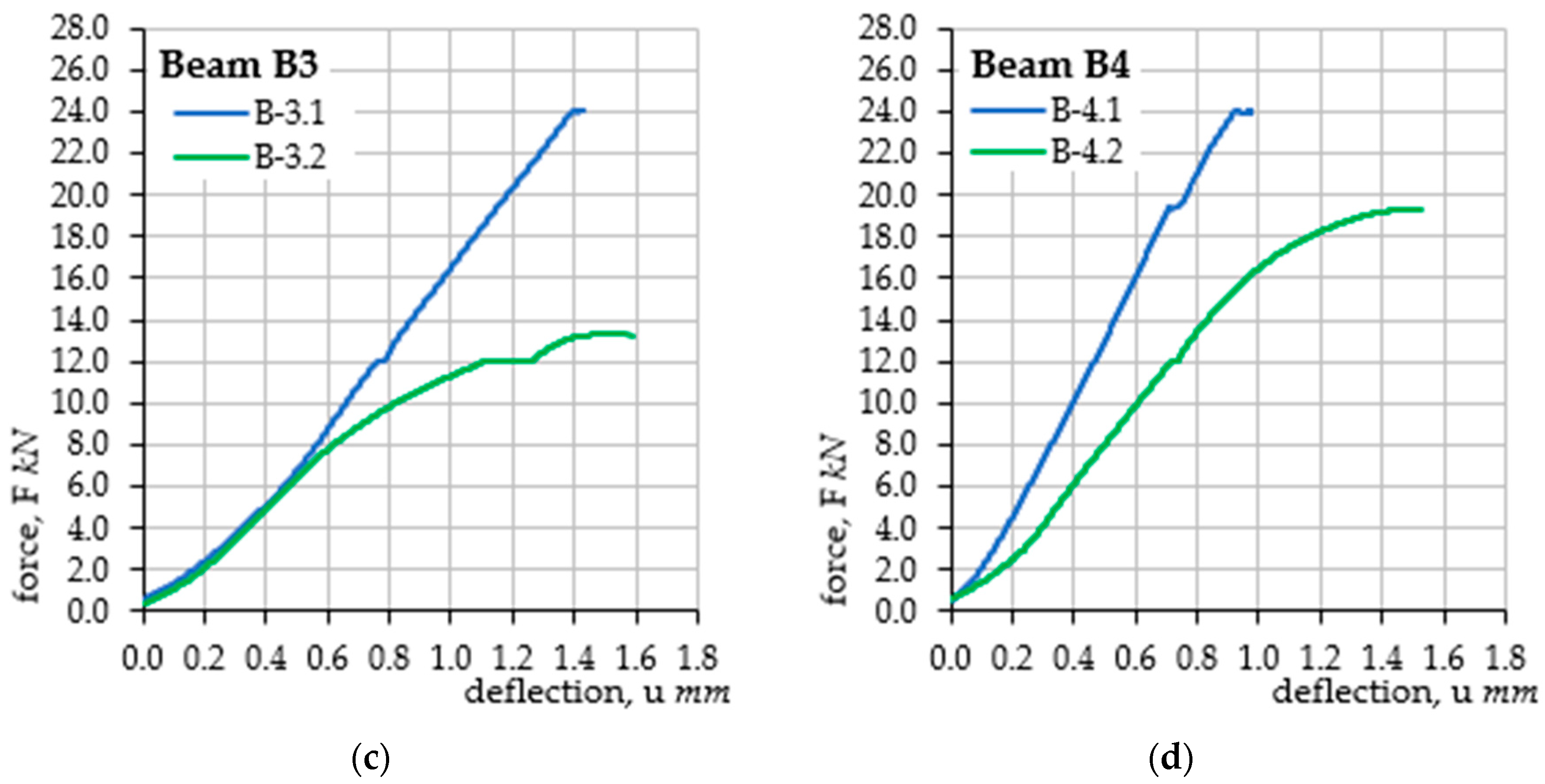
- The progressing corrosion process causes an increase in the deflections of the elements loaded in the same way, which is consistent with the results of the tests [23,27,29,30,31]. This is confirmed by the graphs of the evolution of changes in the displacement of the point in the middle of the span of the analyzed beams as a function of the concentrated force. The obtained deflection in the second loading cycle (after the accelerated corrosion test) is greater than the deflection in the first cycle (before the accelerated corrosion test) with the same external force (see Figure 6).
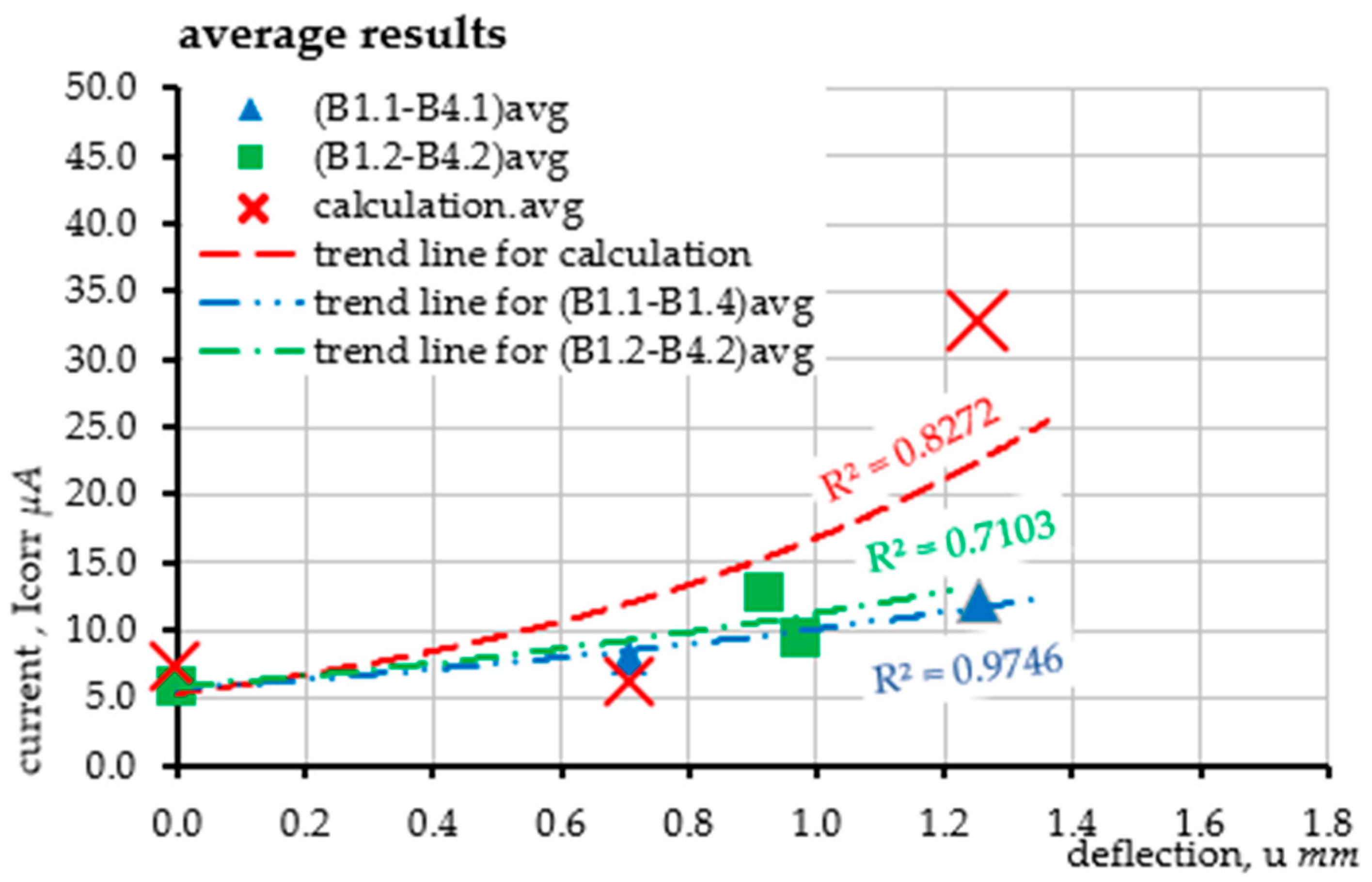
- The proposed method for estimating the level of the corrosion current intensity of the reinforcement was verified based on the analysis of beam deflections and simultaneous measurement of the actual value of the corrosion current intensity. The deflection, which was the basis for determining the curvature of the element, and then the changes in stiffness in the corroded element, provided the basis for estimating the corrosion current intensity using Faraday’s law. The obtained results were comparably similar to the results of laboratory measurements. A more accurate illustration of the obtained results was obtained based on generating exponential functions of the trend line for each series of tests. Thanks to this, the course of the evolution of changes in the corrosion current intensity as a function of the element deflection was generated using the proposed method. The graphs of the obtained functions mostly reflect the actual state of changes in the corrosion current intensity. The result that deserves special attention are the graphs obtained for beam B1 in the second load cycle, where the course of changes in the current intensity obtained in the tests has a very high compliance with the graph obtained for the proposed calculation method. In the remaining cases, the graphs are also similar but have slightly larger scatters.
- In each analyzed case, in the first range, the level of corrosion current intensity is lower than the actual values; then, it increases, finally reaching values higher than the actual state. These differences are small and result from simplifications of the theoretical model, which in the case of the estimation method is considered a fully satisfactory result. Differences in the individual stages of the impact result directly from the simplification used at the stage of performing analytical calculations, consisting of omitting the range of the first phase of the work of the bent element (until the beam cracks) due to cyclic loads of the same elements, which, after the first cycle, were plastically deformed-cracked.
- Finally, it was considered that the estimation results performed within the proposed new research method reflect the actual state of the corrosion current intensity level in the element well. The proposed method is an element supporting existing, advanced diagnostic methods, while its advantage over other methods is the absolute non-invasiveness in the structure. This method is fully based on external measurements of deflections or deformations of the structure, which must be performed with very high accuracy (including optical image analysis methods). The coefficient of determination obtained for the calculated values of the corrosion current intensity for most cases at the level of about 0.9 is considered a satisfactory result. Fitting the function with an error oscillating around 10% can be considered acceptable for the method representing the estimation approach. Only the trend line fitting in the case of beam B4 is burdened with larger errors due to the uncertainties of the model parameters that are burdened with corrosion processes. Progressive deflection is the sum of mechanical deflections (from external loads and self-weight) and rheological and corrosive phenomena. In addition, the effects of concrete cover cracking due to corrosion and changes in adhesion at the steel–concrete interface are an additional element of the model, which requires in-depth verification at later stages of its development. Therefore, an additional issue is the application of probabilistic issues, including the Monte Carlo method or interval numbers, to the assessment of phenomena burdened with large uncertainties, such as the corrosion process. Due to the complexity of corrosion issues and the mechanics of cracking the structure, which reduce the stiffness of the element, the method can only be used on the basis of precise deflection measurements. Optical measurement and image analysis methods may prove helpful in this situation (e.g., including optical methods, self-learning technology or AI). In addition, this method can be expanded to include analysis of the obtained images and the automatic determination of the corrosion rate of the reinforcement using mobile applications. This is a topic that is planned to be developed in further research.
7. Conclusions
- The corrosion process that occurs causes an increase in the deflection of the element, which is caused by the change in the stiffness of the reinforced concrete element due to the coupled phenomenon of the loss of reinforcement mass and changes in Young’s modulus. This phenomenon confirms the correctness of the assumptions made in the theoretical model, and the obtained results are consistent with similar studies in this area [29,30,31].
- The proposed theoretical method confirms the possibility of estimating the level of reinforcement corrosion current intensity based on the deflection of reinforced concrete elements in a completely non-invasive way, solely on the basis of the analysis of the deformation of the structure, which is the original element of this method.
- The presented method, together with the function describing the evolution of changes in the corrosion current in relation to the measured deflection, can be used in the diagnostics of structures for the purposes of the preliminary estimation of the corrosion level. As part of the development of the theoretical model of this method, we plan to apply solutions that take into account the uncertainty of the model parameters (e.g., the Monte Carlo method) and the influence of concrete cover cracking on deflection phenomena (including changes in adhesion forces between steel and concrete). The last element planned in the course of this research is the verification and application of this method for reinforced concrete elements operating in real-world conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| initial mass of rebar, g | |
| final mass of rebar, g | |
| mass loss, g | |
| average mass loss, g | |
| percentage mass loss, % | |
| corrosion degree, % | |
| ultimate force, kN | |
| stress in reinforcing steel, MPa | |
| stress in reinforcing steel causing first crack, MPa | |
| α | deformation parameter, - |
| factor taking into account time and nature of external impact, - | |
| flexural stiffness of corroded reinforced concrete cross-section, kN | |
| modulus of inertia of corroded reinforced concrete cross-section, | |
| Young’s modulus of corroded reinforced concrete cross-section, GPa | |
| bending moment, characteristic value, kNm | |
| curvature of deflection, 1/m | |
| critical bending moment, kNm | |
| radius of deflection curvature, m | |
| time, time increase, year | |
| density of reinforcing steel, g/ | |
| effective length of element, m | |
| area of side surface of bar identical to the area of electrochemically active areas, | |
| effective electrochemical equivalent of reinforcing steel, determined experimentally, g/(μAyear) | |
| Young’s modulus taking into account concrete rheology, GPa | |
| mean secant Young’s modulus of concrete, GPa | |
| concrete creep coefficient, - | |
| density of corrosion current intensity, μA/ | |
| change in cross-sectional area of reinforcement, | |
| change in volume of reinforcement, | |
| cross-sectional area concrete, | |
| Young’s modulus of reinforcing steel, GPa | |
| coefficient taking into account the ratio of Young’s moduli of reinforcing steel and concrete, - | |
| distance from the center of gravity to the extreme tensile fibers of a reinforced concrete cross-section, cm |
References
- Arredondo-Rea, S.P.; Corral-Higuera, R.; Gómez-Soberón, J.M.; Gámez-García, D.C.; Bernal-Camacho, J.M.; Rosas-Casarez, C.A.; Ungsson-Nieblas, M.J. Durability parameters of reinforced recycled aggregate concrete: Case study. Appl. Sci. 2019, 9, 617. [Google Scholar] [CrossRef]
- Bazant, Z.P. Physical model for steel corrosion in concrete sea structures—Theory. J. Struct. Div. ASCE 1979, 105, 1137–1153. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P. Modeling Chloride Penetration in Saturated Concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Bui, H.T.; Maekawa, K.; Tan, K.H. Analytical model of corrosion-induced cracks in concrete considering time-varying deformations of layers, mechanical properties of rust. Constr. Build. Mater. 2022, 316, 125883. [Google Scholar] [CrossRef]
- Maekawa, K.; Ishida, T.; Kishi, T. Multi-scale Modeling of Concrete Performance. J. Adv. Concr. Technol. 2003, 1, 91–126. [Google Scholar] [CrossRef]
- Raczkiewicz, W.; Bacharz, M.; Bacharz, K.; Teodorczyk, M. Reinforcement Corrosion Testing in Concrete and Fiber Reinforced Concrete Specimens Exposed to Aggressive External Factors. Materials 2023, 16, 1174. [Google Scholar] [CrossRef]
- Cerný, R.; Rovnaníková, P. Transport Processes in Concrete; CRC Press: London, UK; New York, NY, USA, 2002. [Google Scholar]
- Caijun, S.; Qiang, Y.; Fuqiang, H.; Xiang, H. Transport and Interactions of Chlorides in Cement-Based Materials; CRC Press: Boca Raton, FL, USA, 2019; ISBN 9780429466557. [Google Scholar]
- Raczkiewicz, W. The Galvanostatic Pulse Method in Laboratory Tests and Diagnostics of the Durability of Reinforced Concrete Structures; Kielce University of Technology: Kielce, Poland, 2022; ISBN 978-83-66678-34-7. [Google Scholar]
- Michel, A.; Pease, B.J.; Peterová, A.; Geiker, M.R.; Stang, H.; Thybo, A.E.A. Penetration of corrosion products and corrosion-induced cracking in reinforced cementitious materials: Experimental investigations and numerical simulations. Cem. Concr. Compos. 2014, 47, 75–86. [Google Scholar] [CrossRef]
- Krykowski, T.; Jaśniok, T.; Recha, F.; Karolak, M. A Cracking Model for Reinforced Concrete Cover, Taking Account of the Accumulation of Corrosion Products in the ITZ Layer, and Including Computational and Experimental Verification. Materials 2020, 13, 5375. [Google Scholar] [CrossRef] [PubMed]
- Šavija, B.; Luković, M.; Pacheco, J.; Schlangen, E. Cracking of the concrete cover due to reinforcement corrosion: A two-dimensional lattice model study. Constr. Build. Mater. 2013, 44, 626–638. [Google Scholar] [CrossRef]
- Jamshidi, F.; Dehestani, M. Time to cracking in concrete cover length due to reinforcement corrosion via a simplified fracture mechanics approach. Constr. Build. Mater. 2020, 258, 119588. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, W.; Tang, Z.; Huang, Q. Experimental and numerical investigation of chloride-induced reinforcement corrosion and mortar cover cracking. Cem. Concr. Compos. 2020, 111, 103620. [Google Scholar] [CrossRef]
- Capozucca, R. Damage to reinforced concrete due to reinforcement corrosion. Constr. Build. Mater. 1995, 9, 295–303. [Google Scholar] [CrossRef]
- Fischer, C. Auswirkungen der Bewehrungskorrosion auf den Verbund Zwischen Stahl und Beton; Institut für Werkstoffe im Bauwesen der Universität Stuttgart: Stuttgart, Germany, 2012. [Google Scholar]
- El Alami, E.; Fekak, F.E.; Garibaldi, L.; Moustabchir, H.; Elkhalfi, A.; Scutaru, M.L.; Vlase, S. Numerical Study of the Bond Strength Evolution of Corroded Reinforcement in Concrete in Pull-Out Tests. Appl. Sci. 2022, 12, 654. [Google Scholar] [CrossRef]
- Lee, H.S.; Noguchi, T.; Tomosawa, F. Evaluation of the bond properties between concrete and reinforcement as a function of the degree of reinforcement corrosion. Cem. Concr. Res. 2002, 32, 1313–1318. [Google Scholar] [CrossRef]
- Almusallam, A.A. Effect of degree of corrosion on the properties of reinforcing steel bars. Constr. Build. Mater. 2001, 15, 361–368. [Google Scholar] [CrossRef]
- Zhou, B.; Sun, X.; Zou, D.; Wang, H. Evaluation of corrosion morphology on mechanical properties of reinforcing steel bars using numerical simulation and simplified analytical model. J. Build. Eng. 2022, 52, 104380. [Google Scholar] [CrossRef]
- Moreno, E.; Cobo, A.; Palomo, G.; González, M.N. Mathematical models to predict the mechanical behavior of reinforcements depending on their degree of corrosion and the diameter of the rebars. Constr. Build. Mater. 2014, 61, 156–163. [Google Scholar] [CrossRef]
- Andrade, C. Some historical notes on the research in corrosion of reinforcement. Hormigón Y Acero 2018, 69, 21–28. [Google Scholar] [CrossRef]
- Benjamin, I.; Kennedy, C.; Wurah, I.F. Effects of Corrosion on Mechanical Properties of Reinforcing Steel Residual Flexural Strength. Sch. Int. J. Chem. Mater. Sci. 2021, 4, 158–173. [Google Scholar] [CrossRef]
- Zhu, W.; François, R.; Poon, C.S.; Dai, J.G. Influences of corrosion degree and corrosion morphology on the ductility of steel reinforcement. Constr. Build. Mater. 2017, 148, 297–306. [Google Scholar] [CrossRef]
- Lee, H.S.; Cho, Y.S. Evaluation of the mechanical properties of steel reinforcement embedded in concrete specimen as a function of the degree of reinforcement corrosion. Int. J. Fract. 2009, 157, 81–88. [Google Scholar] [CrossRef]
- Bahleda, F.; Prokop, J.; Koteš, P.; Wdowiak-Postulak, A. Mechanical Properties of Corroded Reinforcement. Buildings 2023, 13, 855. [Google Scholar] [CrossRef]
- Negrutiu, C.; Sosa, I.P.; Constantinescu, H.; Heghes, B. Crack Analysis of Reinforced High Strength Concrete Elements in Simulated Aggressive Environments. Procedia Technol. 2016, 22, 4–12. [Google Scholar] [CrossRef][Green Version]
- Shen, J.; Gao, X.; Li, B.; Du, K.; Jin, R.; Chen, W.; Xu, Y. Damage evolution of RC beams under simultaneous reinforcement corrosion and sustained load. Materials 2019, 12, 627. [Google Scholar] [CrossRef] [PubMed]
- Recha, F. Estimation method of corrosion current density of RC elements. Open Eng. 2023, 13, 20220430. [Google Scholar] [CrossRef]
- Grandić, D.; Bjegović, D.; Grandić, I.Š. Deflection of reinforced concrete beams simultaneously subjected to sustained load and reinforcement corrosion. In Proceedings of the Structural Engineers World Congress 2011, Las Vegas, NV, USA, 14–16 April 2011. [Google Scholar]
- Jin, X.; Tong, J.; Tian, Y.; Jin, N. Time-varying relative displacement field on the surface of concrete cover caused by reinforcement corrosion based on DIC measurement. Constr. Build. Mater. 2018, 159, 695–703. [Google Scholar] [CrossRef]
- Ye, H.; Fu, C.; Jin, N.; Jin, X. Performance of reinforced concrete beams corroded under sustained service loads: A comparative study of two accelerated corrosion techniques. Constr. Build. Mater. 2018, 162, 286–297. [Google Scholar] [CrossRef]
- De Sitter, W.R. CEB-RILEM Workshop Report. In Durability of Concrete Structures; CEB-Bulletin: Kopenhaga, Denmark, 1983. [Google Scholar]
- Li, L.; Mahmoodian, M.; Khaloo, A.; Sun, Z. Risk-Cost Optimized Maintenance Strategy for Steel Bridge Subjected to Deterioration. Sustainability 2022, 14, 436. [Google Scholar] [CrossRef]
- PN-EN 1992-1-1; Design of Concrete Structures. Part 1-1: General Rules and Rules for Buildings. Polish Committee for Standardization Standard: Warsaw, Poland, 2008.
- FIB. FIB Model Code for Concrete Structures 2010; Walraven, J., Ed.; International Federation for Structural Concrete (FIB): Lausanne, Switzerland, 2013; ISBN 9783433604090. [Google Scholar]
- PN-EN 206+A1: 2016-12; Concrete: Requirements, Properties, Production and Conformity. Polish Committee for Standardization Standard: Warsaw, Poland, 2016.
- Kubik, J. Thermodiffusion Flows in a Solid with a Dominant Constituent; Ruhr-Universität Bochum: Bochum, Germany, 1985; Volume 44. [Google Scholar]
- Ring, G. GalvaPulse. User Manual. Available online: https://www.germanninstruments.com/wp-content/uploads/2022/02/GalvaPulse-GP-TDS-01.pdf (accessed on 20 May 2025).
- Chen, E.; Berrocal, C.G.; Fernandez, I.; Löfgren, I.; Lundgren, K. Assessment of the mechanical behaviour of reinforcement bars with localised pitting corrosion by Digital Image Correlation. Eng. Struct. 2020, 219, 110936. [Google Scholar] [CrossRef]
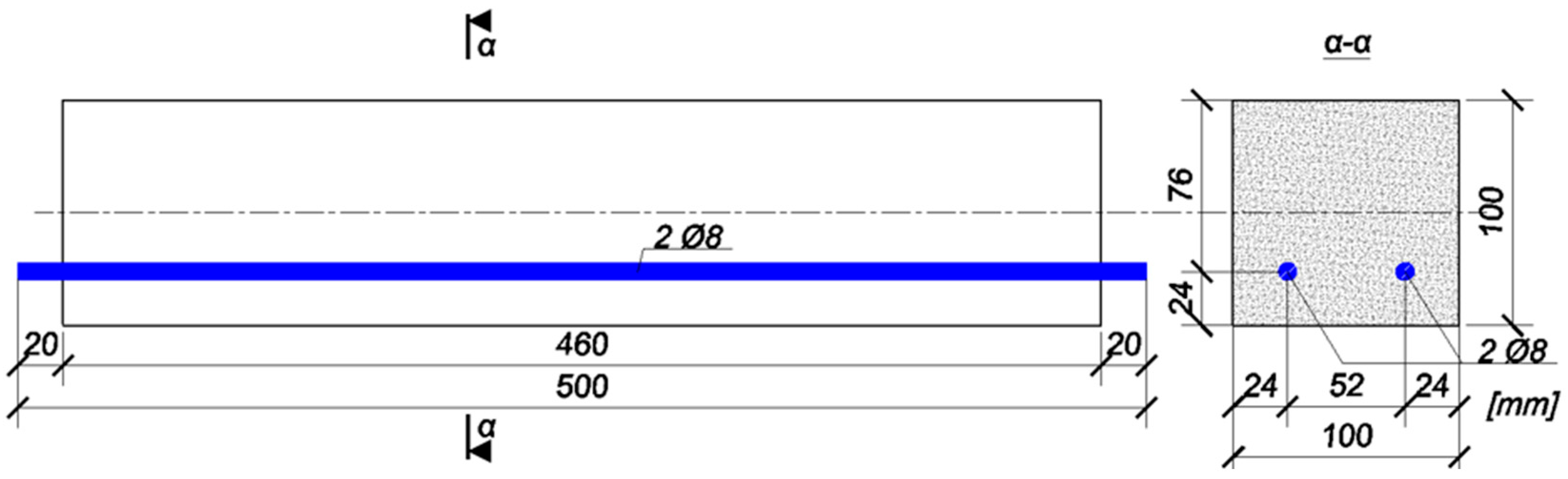
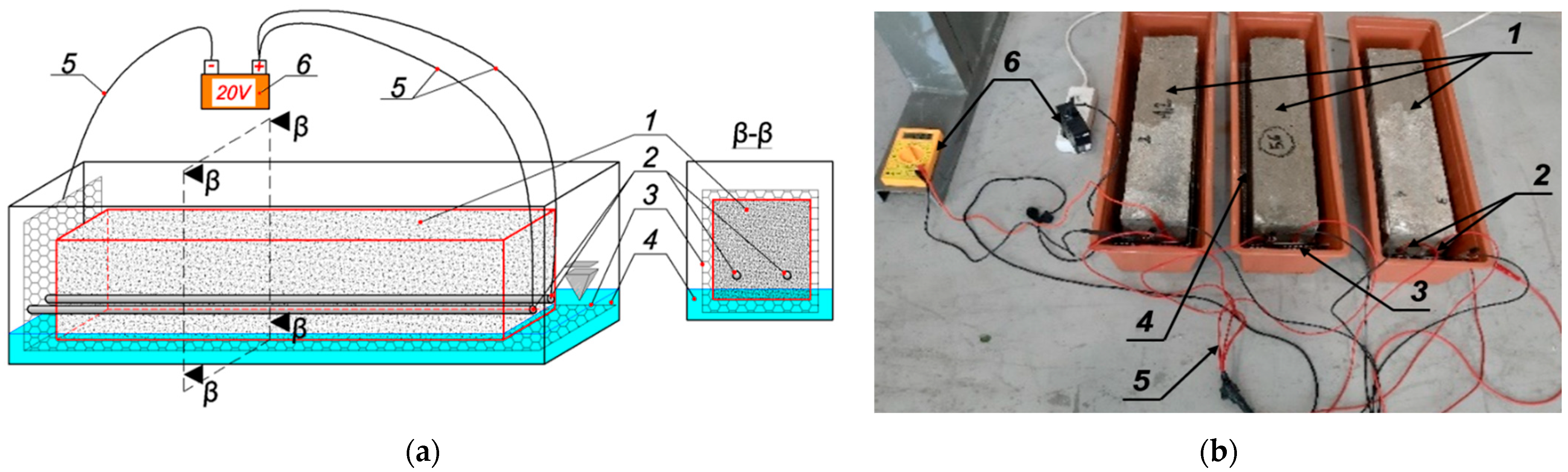
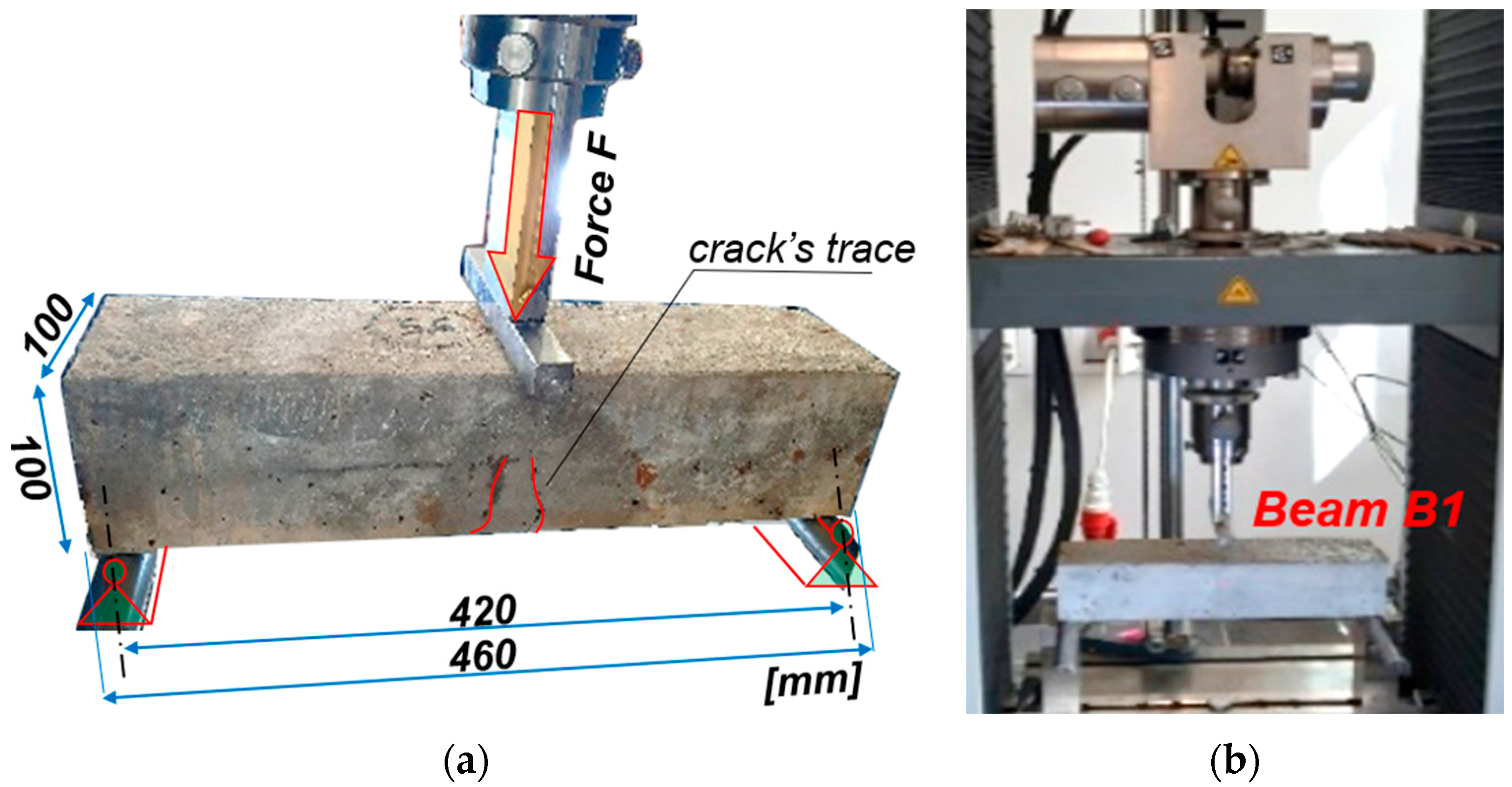


| Scenario | Sample | Dimension mm | kN | MPa | MPa |
|---|---|---|---|---|---|
| Beam’s concrete | 150 × 150 | 1141.328 | 50.726 | 48.788 | |
| 1122.253 | 49.878 | ||||
| 1089.341 | 48.415 | ||||
| 1038.008 | 46.134 |
| Scenario—Beam’s Number | Rebar’s Number | g | g | g | g | % | % | year | μA | year) | rok) | year) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beam B1 | 194.91 | 186.75 | 8.16 | 8.490 | 4.19 | 4.33 | 0.0082192 | 18.75 | 0.005294933 | 0.00641009 | 0.0065178 | |
| 196.88 | 188.06 | 8.82 | 4.48 | 14.26 | 0.007525245 | |||||||
| Beam B2 | 194.85 | 188.36 | 6.49 | 5.980 | 3.33 | 3.08 | 13.12 | 0.00601842 | 0.00582204 | |||
| 193.66 | 188.19 | 5.47 | 2.82 | 11.83 | 0.005625669 | |||||||
| Beam B3 | 196.26 | 190.49 | 5.77 | 5265 | 2.94 | 2.70 | 16.36 | 0.004291055 | 0.00419338 | |||
| 193.73 | 188.97 | 4,76 | 2.46 | 14.14 | 0.00409571 | |||||||
| Beam B4 | 194.00 | 187.70 | 6.30 | 5.305 | 3.25 | 2.73 | 6.77 | 0.011322009 | 0.00964568 | |||
| 195.16 | 190.85 | 4.31 | 2.21 | 6.58 | 0.007969352 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Recha, F.; Raczkiewicz, W.; Bacharz, K.; Wójcicki, A.; Bujňáková, P.; Koteš, P. Experimental Verification of the Model for Estimating the Corrosion Current of Reinforcement in an RC Element. Materials 2025, 18, 2945. https://doi.org/10.3390/ma18132945
Recha F, Raczkiewicz W, Bacharz K, Wójcicki A, Bujňáková P, Koteš P. Experimental Verification of the Model for Estimating the Corrosion Current of Reinforcement in an RC Element. Materials. 2025; 18(13):2945. https://doi.org/10.3390/ma18132945
Chicago/Turabian StyleRecha, Faustyn, Wioletta Raczkiewicz, Kamil Bacharz, Artur Wójcicki, Petra Bujňáková, and Peter Koteš. 2025. "Experimental Verification of the Model for Estimating the Corrosion Current of Reinforcement in an RC Element" Materials 18, no. 13: 2945. https://doi.org/10.3390/ma18132945
APA StyleRecha, F., Raczkiewicz, W., Bacharz, K., Wójcicki, A., Bujňáková, P., & Koteš, P. (2025). Experimental Verification of the Model for Estimating the Corrosion Current of Reinforcement in an RC Element. Materials, 18(13), 2945. https://doi.org/10.3390/ma18132945









