Bearing Capacity and Reinforced Measures of Bolted Joints for Pultruded Composite Square Tubes
Abstract
1. Introduction
1.1. Test Specimen and Preparation
1.2. Manufacturing Procedures
1.3. Material Properties
1.4. Experimental Set-Up and Loading Procedure
2. Experimental Results and Discussion
2.1. Failure Modes
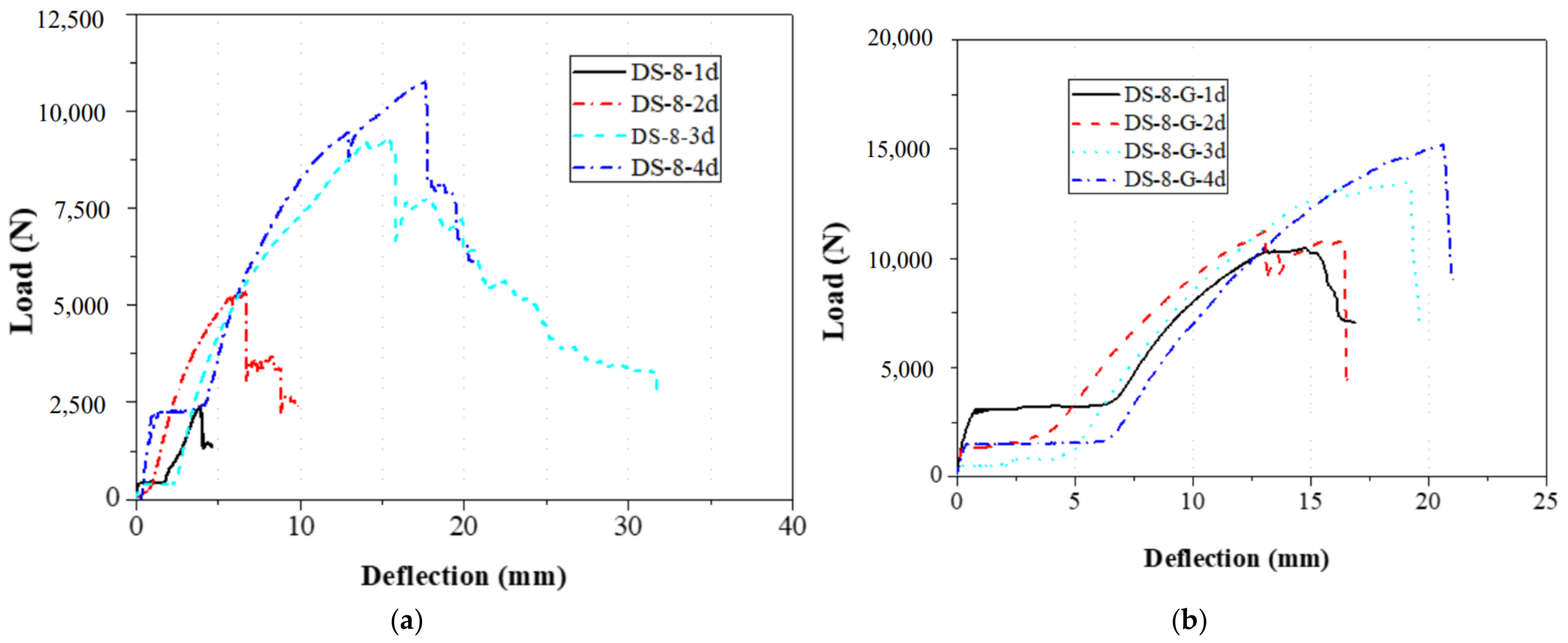
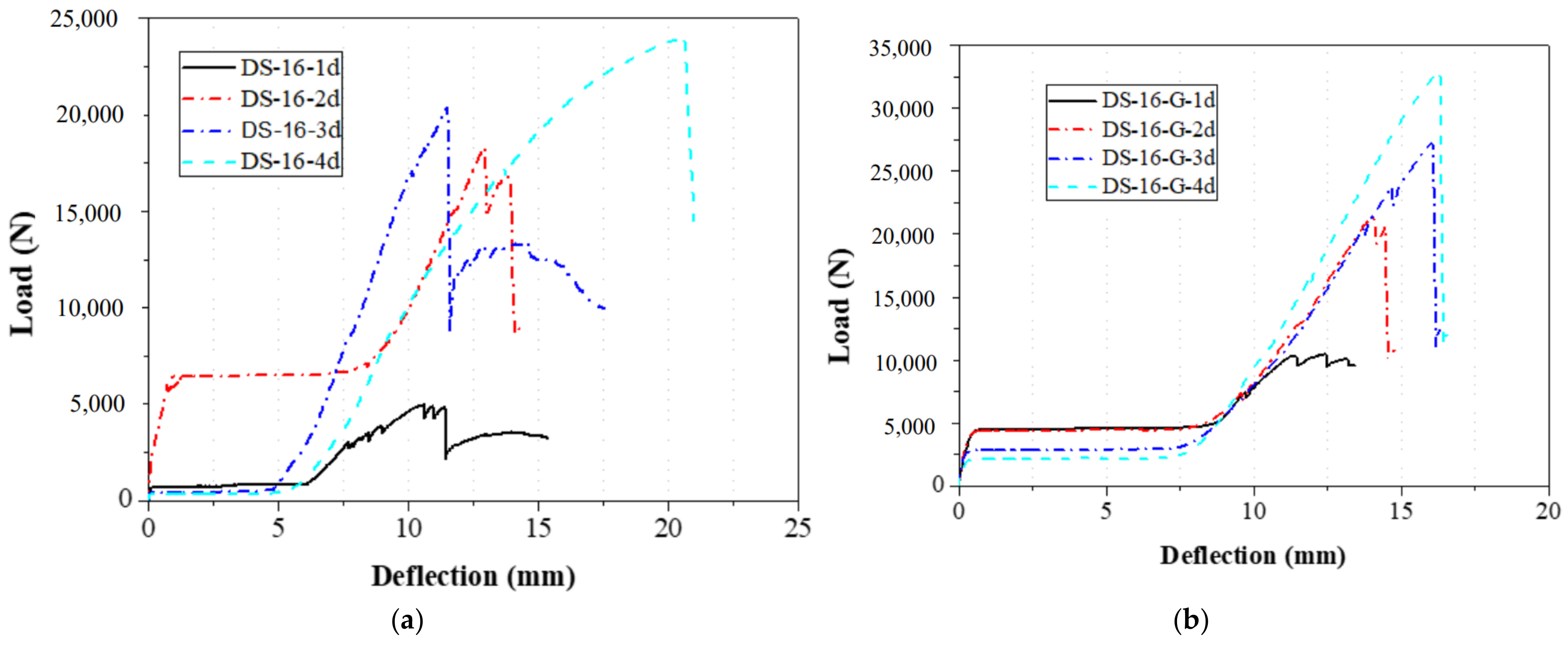
2.2. Load and Displacement Relationship
2.2.1. Effect of the Gasket
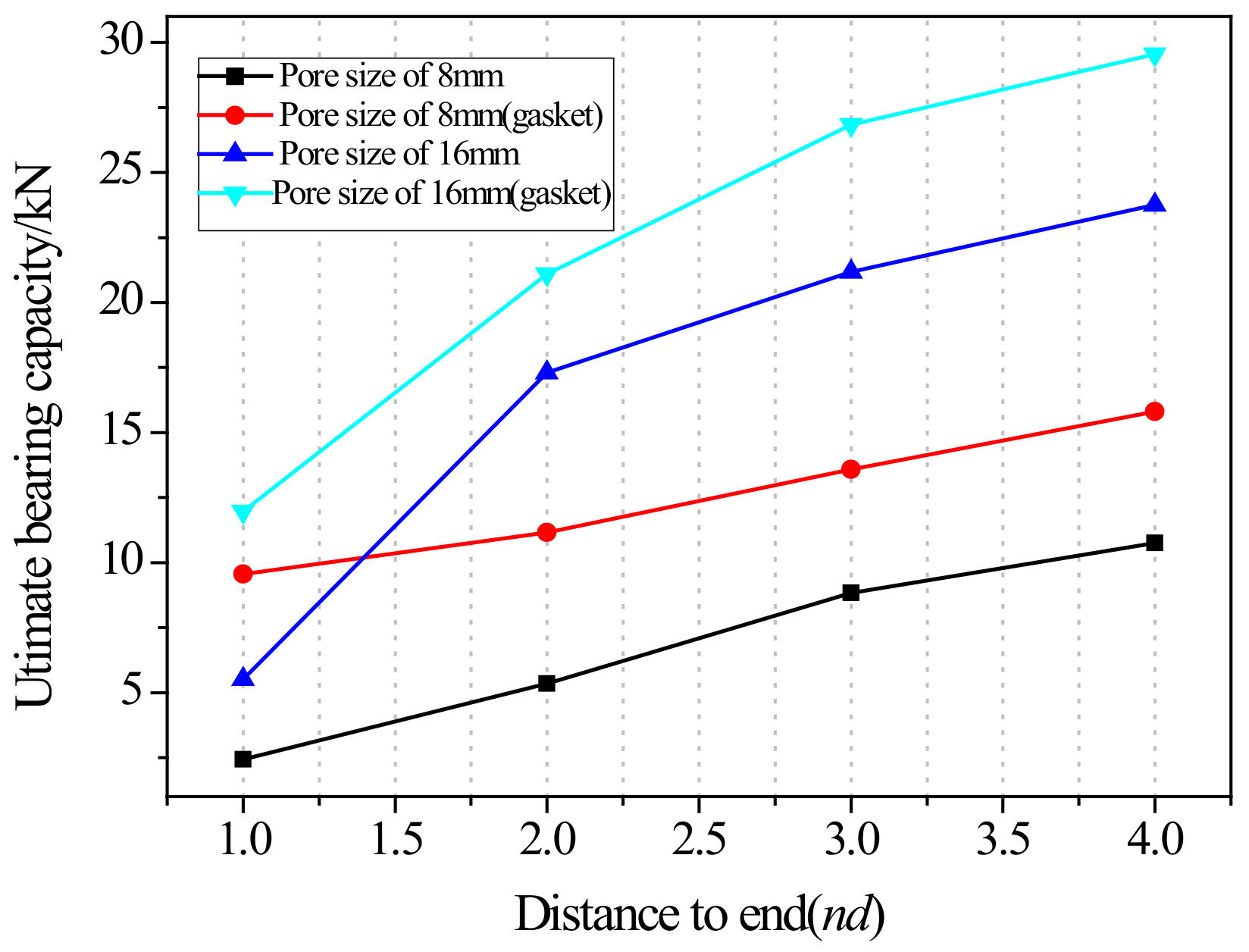
2.2.2. Effect of the Distance from Bolt Hole to the End
2.2.3. Effect of the Bolt Diameter
3. Theoretical Analysis
3.1. Capacity of Single Bolt Joints
3.2. Capacity of Double Bolts Joints
3.3. Capacity of Joint with Gasket
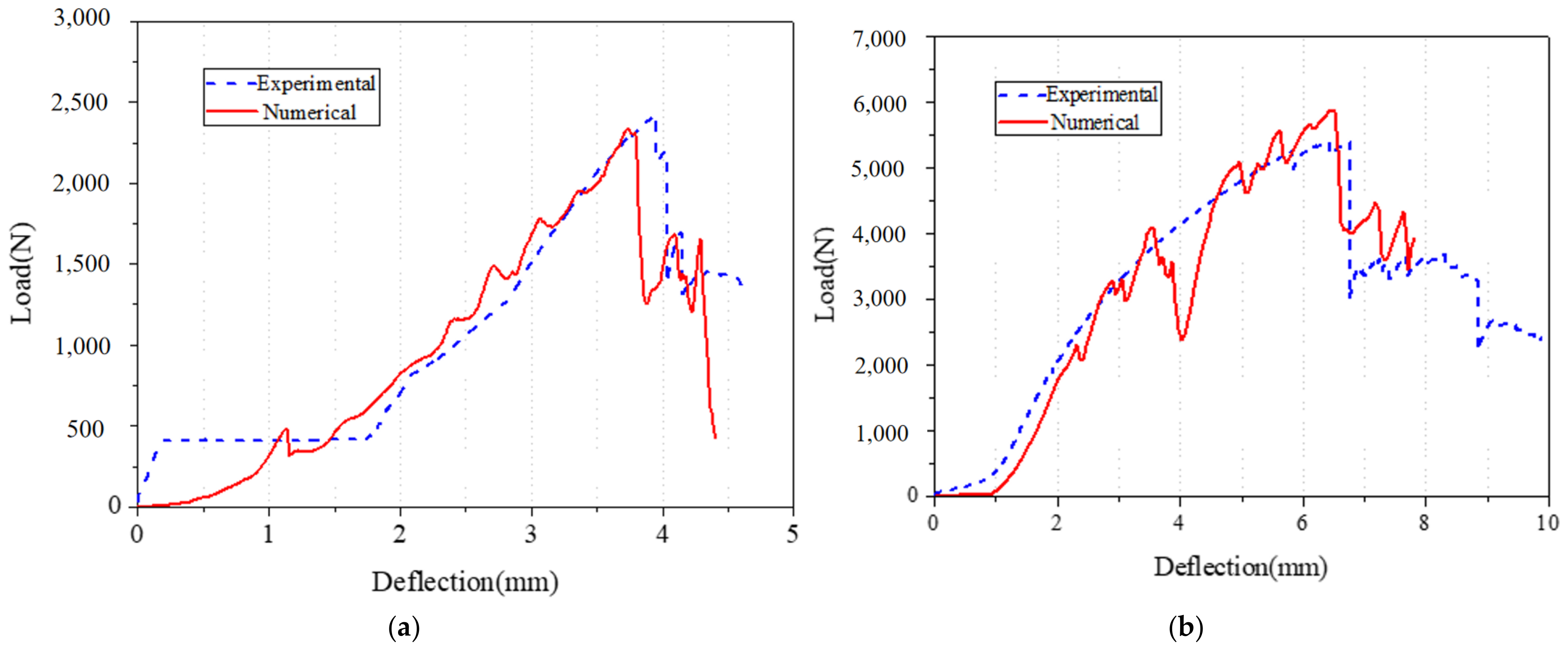
3.4. Validation of Theoretical Prediction
4. Numerical Simulation and Discussion
4.1. Modeling Details
4.2. Loading and Boundary Conditions
4.3. Contact Definition
4.4. Validation and Discussion
5. Conclusions
- Geometric effects (normalized): Geometric parameters had a significant impact on joint capacity. For single-bolt specimens without gaskets, increasing the normalized edge distance (e.g., from 1 d to 4 d) led to an increase in bearing capacity by a factor of 4.4 for 8 mm bolts and 4.3 for 16 mm bolts. For double-bolt specimens, increasing bolt spacing from 2 d to 3 d resulted in a capacity increase of over 100%, indicating strong sensitivity to spatial configuration;
- The introduction of multiaxial fiber-reinforced gaskets yielded up to a 295% improvement in load-bearing capacity in short edge distance scenarios. However, the effectiveness diminished as edge distance or bolt spacing increased. For instance, with 8 mm bolts, the enhancement dropped from 295% at 1 d to 47% at 4 d, revealing a clear trend of reduced marginal benefit with increasing clearance;
- As the edge distance increased, the dominant failure mode gradually shifted from shear failure to local extrusion failure. This transition highlights a nonlinear relationship between geometry and structural failure mechanisms;
- Theoretical predictions showed strong consistency with experimental results, with most peak load errors under 10%. Finite element simulations also demonstrated excellent agreement with test data, confirming the robustness of the numerical model;
- The use of multiaxial gaskets provides a practical and effective strengthening strategy for composite joints. Its advantages in stress redistribution and damage suppression make it well-suited for high-demand applications such as bridge nodes, aerospace fastener zones, and structural truss systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, A.N.; Xu, G.W.; Liu, X.G. Effect of polyurea coating on low-velocity impact properties of unidirectional carbon fiber-reinforced polymer composite plates. Structures 2024, 61, 106090. [Google Scholar] [CrossRef]
- Qi, S.; Alajarmeh, O.; Alhawamdeh, M.; Shelley, T.; Schubel, P.; Rendle-Short, K.; Zeng, X. Formation of non-uniform fibre distribution and its effect on the flexural performance of pultruded GFRP box beams. Compos. Struct. 2024, 327, 117695. [Google Scholar] [CrossRef]
- Shrikant, M.H. Durability and long-term performance of fiber reinforced polymer (FRP) composites: A review. Structures 2024, 60, 105881. [Google Scholar]
- Chen, J.Y.; Fang, H.; Gao, F.; Liu, W. Flexural performance of composite grid panels with deep ribs. J. Reinf. Plast. Compos. 2020, 39, 443–458. [Google Scholar] [CrossRef]
- Stazi, F.; Giampaoli, M.; Nisi, L.; Rossi, M.; Munafò, P. Mechanical performance reduction of GFRP specimens with polyester matrix exposed to continuous condensation. Compos. Part B Eng. 2016, 99, 330–339. [Google Scholar] [CrossRef]
- Turvey, G.J.; Zhang, Y. Mechanical properties of pultruded GFRP WF, channel and angle profiles for limit state/permissible stress design. Compos. Part B Eng. 2018, 148, 260–271. [Google Scholar] [CrossRef]
- Konstantinos, K.; Soňa, R.; Krejčí, O.; Kalendová, A. Thermal analysis of postcured aramid fiber/epoxy composites. Rev. Adv. Mater. Sci. 2021, 60, 479–489. [Google Scholar]
- Ungureanu, D.; Țăranu, N.; Lupășteanu, V.; Isopescu, D.N.; Oprișan, G.; Mihai, P. Experimental and numerical investigation of adhesively bonded single lap and thick adherents joints between pultruded GFRP composite profiles. Compos. Part B Eng. 2018, 146, 49–59. [Google Scholar] [CrossRef]
- Abdelkerim, D.S.E.; Wang, X.; Ibrahim, H.A.; Wu, Z. Static and fatigue behavior of pultruded FRP multi-bolted joints with basalt FRP and hybrid steel-FRP bolts. Compos. Struct. 2019, 220, 324–337. [Google Scholar] [CrossRef]
- Dicuonzo, A.; Laudiero, F.; Minghini, F. Design and construction of a temporary structure composed by FRP pultruded profiles. In Proceedings of the Fourth International Conference on FRP Composites in Civil Engineering, Zurich, Switzerland, 21 July 2008. [Google Scholar]
- Godat, A.; Légeron, F.; Gagné, V.; Marmion, B. Use of FRP pultruded members for electricity transmission towers. Compos. Struct. 2013, 105, 408–421. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Markopoulos, Y.P.; Vlachos, D.E.; Katerelos, D.; Galiotis, C.; Tsiknias, T.; Zacharopoulos, D.; Karalekas, D.; Chronis, P.; Kalomallos, D. Design and construction of a vehicular bridge made of glass/polyester pultruded box beams. Plast. Rubber Compos. 2005, 34, 201–207. [Google Scholar] [CrossRef]
- Keller, T.; Bai, Y.; Vallée, T. Long-term performance of a glass fiber-reinforced polymer truss bridge. J. Compos. Constr. 2007, 11, 99–108. [Google Scholar] [CrossRef]
- Fang, H.; Bai, Y.; Liu, W.; Qi, Y.; Wang, J. Connections and structural applications of fibre reinforced polymer composites for civil infrastructure in aggressive environments. Compos. Part B Eng. 2019, 164, 129–143. [Google Scholar] [CrossRef]
- Mosallam, A. Design Guide for FRP Composite Connections; American Society of Civil Engineers: Reston, VA, USA, 2011. [Google Scholar]
- Girão Coelho, A.M.; Mottram, J.T. A review of the behaviour and analysis of bolted connections and joints in pultruded fibre reinforced polymers. Mater. Des. 2015, 74, 86–107. [Google Scholar] [CrossRef]
- Whitney, J.M.; Nuismer, R.J. Stress fracture criteria for laminated composites containing stress concentrations. J. Compos. Mater. 1974, 8, 253–265. [Google Scholar] [CrossRef]
- Collings, T.A. The strength of bolted joints in multi-directional CFRP laminates. Composites 1977, 8, 43–55. [Google Scholar] [CrossRef]
- Chang, F.K.; Scott, R.A.; Springer, G.S. Failure of composite laminates containing pin loaded holes—Method of solution. J. Compos. Mater. 1984, 18, 255–278. [Google Scholar] [CrossRef]
- Chang, F.K.; Scott, R.A.; Springer, G.S. The effect of laminate configuration on characteristic lengths and rail shear strength. J. Compos. Mater. 1984, 18, 290–296. [Google Scholar] [CrossRef]
- Starikov, R.; Schön, J. Quasi-static behaviour of composite joints with protruding-head bolts. Compos. Struct. 2001, 51, 411–425. [Google Scholar] [CrossRef]
- Ireman, T.; Ranvik, T.; Eriksson, I. On damage development in mechanically fastened composite laminates. Compos. Struct. 2000, 49, 151–171. [Google Scholar] [CrossRef]
- McCarthy, C.T.; McCarthy, M.A. Three-dimensional finite element analysis of single-bolt, single-lap composite bolted joints: Part II—Effects of bolt-hole clearance. Compos. Struct. 2005, 71, 159–175. [Google Scholar] [CrossRef]
- Sun, H.T.; Chang, F.K.; Qing, X. The response of composite joints with bolt-clamping loads, Part I: Model development. J. Compos. Mater. 2002, 36, 47–67. [Google Scholar] [CrossRef]
- Aktaş, A. Bearing strength of carbon epoxy laminates under static and dynamic loading. Compos. Struct. 2005, 67, 485–489. [Google Scholar] [CrossRef]
- Turvey, G.J.; Wang, P. Failure of pultruded GRP single-bolt tension joints under hot–wet conditions. Compos. Struct. 2007, 77, 514–520. [Google Scholar] [CrossRef]
- Bai, Y. Novel joint for assembly of all-composite space truss structures: Conceptual design and preliminary study. J. Compos. Constr. 2013, 17, 130–138. [Google Scholar] [CrossRef]
- Luo, F.J.; Bai, Y.; Yang, X.; Lu, Y. Bolted sleeve joints for connecting pultruded FRP tubular components. J. Compos. Constr. 2016, 20, 04015024. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Q.; Chen, H.; Xu, L. Experimental investigation of novel pre-tightened teeth connection technique for composite tube. Steel Compos. Struct. 2017, 23, 161–172. [Google Scholar] [CrossRef]
- ASTM D3039:2014; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D695:2015; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- Clarke, J.L. Structural Design of Polymer Composites: Eurocomp Design Code and Background Document; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Consiglio Nazionale Delle Ricerche. Guide for the Design and Construction of Structures Made of FRP Pultruded Elements; CNR-DT 205, Advisory Committee on Technical Recommendations for Constructions; Italian National Research Council: Rome, Italy, 2007. [Google Scholar]
- Hart-Smith, L.J. Mechanically-fastened joints for advanced composites—Phenomenological considerations and simple analyses. In Fibrous Composite Materials; Springer: Boston, MA, USA, 1980; pp. 543–574. [Google Scholar]
- McCarthy, M.A.; McCarthy, C.T.; Padhi, G.S. A simple method for determining the effects of bolt–hole clearance on load distribution in single-column multi-bolt composite joints. Compos. Struct. 2006, 73, 78–87. [Google Scholar] [CrossRef]
- Feo, L.; Marra, G.; Mosallam, A.S. Stress analysis of multi-bolted joints for FRP pultruded composite structures. Compos. Struct. 2012, 94, 3769–3780. [Google Scholar] [CrossRef]
- Cowper, G.R.; Symonds, P.S. Strain hardening and strain rate effect in the impact loading of cantilever beams. Small Bus. Econ. 1957, 31, 235–263. [Google Scholar]
- Jones, N. Structural Impact; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Chang, F.K.; Chang, K.Y. Post-failure analysis of bolted composite joints in tension or shear-out mode failure. J. Compos. Mater. 1987, 21, 809–833. [Google Scholar] [CrossRef]
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress concentrations. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]

















| Specimen | L (mm) | t0 (mm) | t (mm) | d (mm) | e (mm) |
|---|---|---|---|---|---|
| DS-8 | 300 | 5 | 0 | 8 | 8 (1 d); 16 (2 d); 24 (3 d); 32 (4 d) |
| DS-8-G | 300 | 5 | 3 | 8 | 8 (1 d); 16 (2 d); 24 (3 d); 32 (4 d) |
| DS-16 | 300 | 5 | 0 | 16 | 16 (1 d); 32 (2 d); 48 (3 d); 64 (4 d) |
| DS-16-G | 300 | 5 | 3 | 16 | 16 (1 d); 32 (2 d); 48 (3 d); 64 (4 d) |
| Specimen | L (mm) | t0 (mm) | t (mm) | d (mm) | e (mm) | I (mm) |
|---|---|---|---|---|---|---|
| SS-8 | 300 | 5 | 0 | 8 | 16 | 16 (2 d); 24 (3 d); 32 (4 d) |
| SS-8-G | 300 | 5 | 3 | 8 | 16 | 16 (2 d); 24 (3 d); 32 (4 d) |
| SS-16 | 300 | 5 | 0 | 16 | 16 | 32 (2 d); 48 (3 d); 64 (4 d) |
| SS-16-G | 300 | 5 | 3 | 16 | 16 | 32 (2 d); 48 (3 d); 64 (4 d) |
| Components | Properties | Sheets | Gaskets |
|---|---|---|---|
| Tension | Yield strength (MPa) | 416.2 | 315.70 |
| Young’s modulus (GPa) | 38.8 | 30.15 | |
| Compression | Yield strength (MPa) | 337.27 | 223.74 |
| Young’s modulus (GPa) | 20.92 | 16.01 |
| Specimen | t (mm) | d (mm) | e (mm) | Ultimate Load | Failure Mode |
|---|---|---|---|---|---|
| DS-8-1d | 0 | 8 | 8 (1 d) | 2.4 | Shear failure |
| DS-8-2d | 0 | 8 | 16 (2 d) | 5.4 | Shear failure |
| DS-8-3d | 0 | 8 | 24 (3 d) | 8.8 | Shear failure |
| DS-8-4d | 0 | 8 | 32 (4 d) | 10.8 | Shear and extrusion failure |
| DS-8-G-1d | 3 | 8 | 8 (1 d) | 9.6 | Shear failure |
| DS-8-G-2d | 3 | 8 | 16 (2 d) | 11.2 | Shear failure |
| DS-8-G-3d | 3 | 8 | 24 (3 d) | 13.6 | Shear failure |
| DS-8-G-4d | 3 | 8 | 32 (4 d) | 15.8 | Extrusion damage |
| DS-16-1d | 0 | 16 | 16 (1 d) | 5.5 | Shear failure |
| DS-16-2d | 0 | 16 | 32 (2 d) | 17.3 | Shear failure |
| DS-16-3d | 0 | 16 | 48 (3 d) | 21.2 | Shear and extrusion failure |
| DS-16-4d | 0 | 16 | 64 (4 d) | 23.8 | Extrusion damage |
| DS-16-G-1d | 3 | 16 | 16 (1 d) | 12.0 | Shear failure |
| DS-16-G-2d | 3 | 16 | 32 (2 d) | 21.1 | Shear failure |
| DS-16-G-3d | 3 | 16 | 48 (3 d) | 26.8 | Extrusion damage |
| DS-16-G-4d | 3 | 16 | 64 (4 d) | 29.6 | Splitter and extrusion damage |
| Specimen | t (mm) | d (mm) | e (mm) | I (mm) | Ultimate Load | Failure Mode |
|---|---|---|---|---|---|---|
| SS-8-2d | 0 | 8 | 16 | 16 (2 d) | 7.5 | Shear failure |
| SS-8-3d | 0 | 8 | 16 | 24 (3 d) | 8.2 | Shear failure |
| SS-8-4d | 0 | 8 | 16 | 32 (4 d) | 16.3 | Shear failure |
| SS-8-G-2d | 3 | 8 | 16 | 16 (2 d) | 17.3 | Shear failure |
| SS-8-G-3d | 3 | 8 | 16 | 24 (3 d) | 17.5 | Extrusion damage |
| SS-8-G-4d | 3 | 8 | 16 | 32 (4 d) | 22.3 | Extrusion damage |
| SS-16-2d | 0 | 16 | 16 | 32 (2 d) | 10.9 | Shear failure |
| SS-16-3d | 0 | 16 | 16 | 48 (3 d) | 22.6 | Splitter failure |
| SS-16-4d | 0 | 16 | 16 | 64 (4 d) | 25.6 | Shear failure |
| SS-16-G-2d | 3 | 16 | 16 | 32 (2 d) | 19.7 | Shear failure |
| SS-16-G-3d | 3 | 16 | 16 | 48 (3 d) | 29.2 | Extrusion damage |
| SS-16-G-4d | 3 | 16 | 16 | 64 (4 d) | 28.2 | Extrusion damage |
| Specimen | Ultimate Load (kN) | Deviation % | Specimen | Ultimate Load (kN) | Deviation % | ||
|---|---|---|---|---|---|---|---|
| Experimental | Theoretical | Experimental | Theoretical | ||||
| DS-8-1d | 2.42 | 2.48 | 2.5 | DS-8-G-1d | 9.56 | 7.32 | −23.2 |
| DS-8-2d | 5.35 | 4.96 | −7.3 | DS-8-G-2d | 11.16 | 13.37 | 20.4 |
| DS-8-3d | 8.83 | 7.44 | −15.7 | DS-8-G-3d | 13.59 | 16.29 | 20.1 |
| DS-8-4d | 10.76 | 10.56 | −11.1 | DS-8-G-4d | 15.81 | 19.32 | 22.6 |
| DS-16-1d | 5.51 | 4.96 | −9.8 | DS-16-G-1d | 11.97 | 13.37 | 17.2 |
| DS-16-2d | 17.31 | 10.56 | −38.9 | DS-16-G-2d | 21.10 | 19.32 | −9.8 |
| DS-16-3d | 21.18 | 14.90 | −29.3 | DS-16-G-3d | 26.84 | 32.65 | 22.6 |
| DS-16-4d | 23.76 | 19.90 | −16.2 | DS-16-G-4d | 29.56 | 40.24 | 36.1 |
| SS-8-2d | 7.54 | 6.78 | −10.3 | SS-8-G-2d | 17.27 | 15.23 | −12.9 |
| SS-8-3d | 8.18 | 8.39 | 2.6 | SS-8-G-3d | 17.53 | 18.01 | 2.7 |
| SS-8-4d | 16.28 | 18.11 | 18.9 | SS-8-G-4d | 22.27 | 26.97 | 21.2 |
| SS-16-2d | 10.86 | 8.54 | −21.6 | SS-16-G-2d | 19.73 | 20.12 | 2.0 |
| SS-16-3d | 22.56 | 22.89 | 1.5 | SS-16-G-3d | 29.19 | 28.47 | −2.5 |
| SS-16-4d | 25.64 | 30.56 | 19.2 | SS-16-G-4d | 28.15 | 35.34 | 26.5 |
| Property | LS-DYNA Parameter | Experimental Value | |
|---|---|---|---|
| Square Tube | Reinforcing Gasket | ||
| Density | RO | 1.8 g/cm3 | 1.8 g/cm3 |
| Modulus in the longitudinal direction | EA | 38.8 GPa | 30.15 GPa |
| Modulus in the transverse direction | EB | 38.8 GPa | 30.15 GPa |
| Modulus in the C direction | EC | 8.12 GPa | 7.68 GPa |
| Shear modulus | GAB | 2.5 GPa | 2.5 GPa |
| Shear modulus | GAC | 1.5 GPa | 1.5 GPa |
| Shear modulus | GBC | 1.5 GPa | 1.5 GPa |
| Poisson’s ratio | PRBA | 0.15 | 0.15 |
| Longitudinal tensile strength | XT | 416.2 MPa | 315.7 MPa |
| Transverse tensile strength | YT | 416.2 MPa | 315.7 MPa |
| Compressive strength in the longitudinal direction | XC | 337.3 MPa | 223.7 MPa |
| Compressive strength in the transverse direction | YC | 337.3 MPa | 223.7 MPa |
| Shear strength | SC | 55 MPa | 55 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Zhang, X.; Xie, Z.; Fang, H.; Qi, Y.; Song, W. Bearing Capacity and Reinforced Measures of Bolted Joints for Pultruded Composite Square Tubes. Materials 2025, 18, 2936. https://doi.org/10.3390/ma18132936
Han J, Zhang X, Xie Z, Fang H, Qi Y, Song W. Bearing Capacity and Reinforced Measures of Bolted Joints for Pultruded Composite Square Tubes. Materials. 2025; 18(13):2936. https://doi.org/10.3390/ma18132936
Chicago/Turabian StyleHan, Juan, Xinchen Zhang, Zhitian Xie, Hai Fang, Youjun Qi, and Wei Song. 2025. "Bearing Capacity and Reinforced Measures of Bolted Joints for Pultruded Composite Square Tubes" Materials 18, no. 13: 2936. https://doi.org/10.3390/ma18132936
APA StyleHan, J., Zhang, X., Xie, Z., Fang, H., Qi, Y., & Song, W. (2025). Bearing Capacity and Reinforced Measures of Bolted Joints for Pultruded Composite Square Tubes. Materials, 18(13), 2936. https://doi.org/10.3390/ma18132936






