Predicting Rheological Properties of Asphalt Modified with Mineral Powder: Bagging, Boosting, and Stacking vs. Single Machine Learning Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials and Sample-Making
2.1.1. Preparation of Emulsified Asphalt
2.1.2. Preparation of Emulsified Asphalt Residue
2.1.3. Mineral Powders
2.2. Test Methods
3. Methods
3.1. Data Preprocessing
3.2. ML Models
3.2.1. K-Nearest Neighbors Regression (KNN)
3.2.2. Bayesian Ridge (BR)
3.2.3. Decision Tree (DT)
- Select an initial dataset as the root node.
- Evaluate each feature’s splitting effect and choose the optimal one.
- Split the dataset into subsets based on the splitting feature’s values, creating child nodes.
- Repeat steps (ii) and (iii) for each child node until the stopping criteria are met.
- Prune the DT by removing unnecessary nodes or branches to enhance generalization.
3.2.4. Random Forest (RF)
3.2.5. Extreme Gradient Boosting (XGB)
3.3. Stacking
3.4. Evaluation Indicators
3.5. K-Fold Cross-Validation and Bayesian Optimization
3.6. Shapley Additive Explanations (SHAP) Analysis
4. Results and Analysis
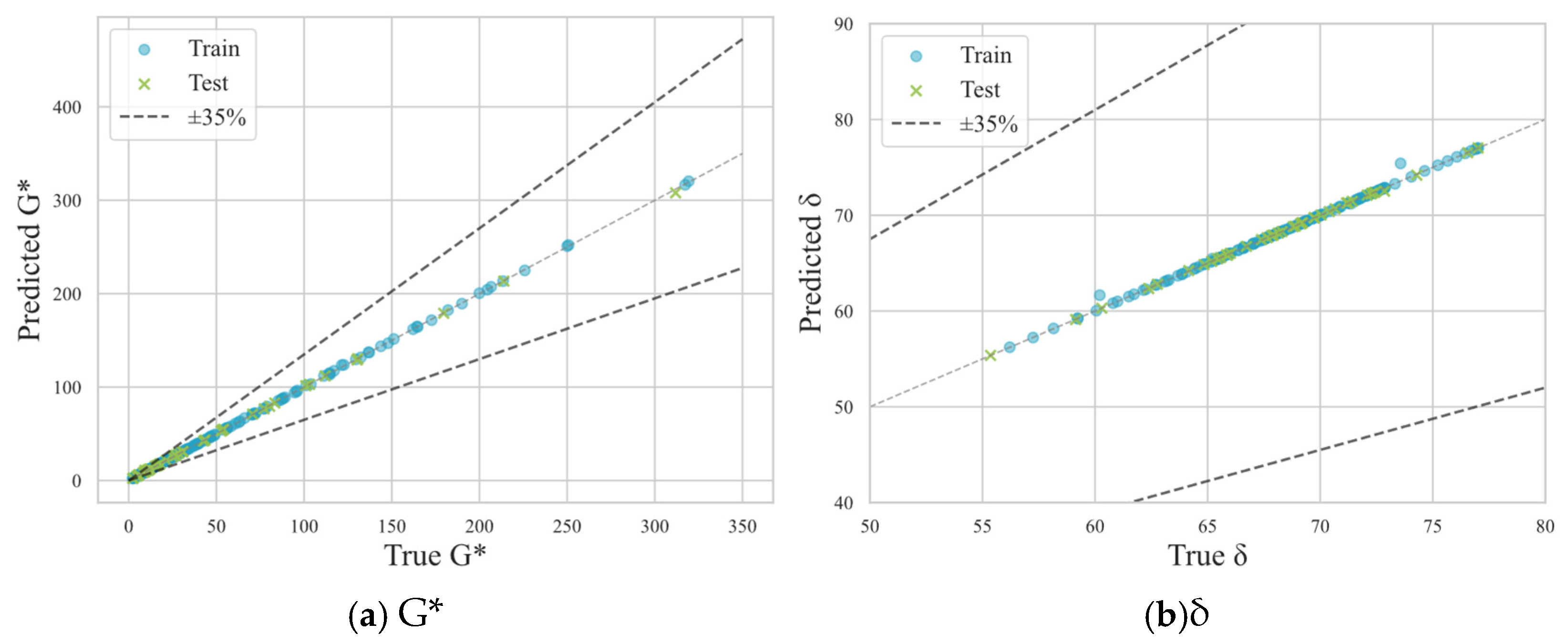
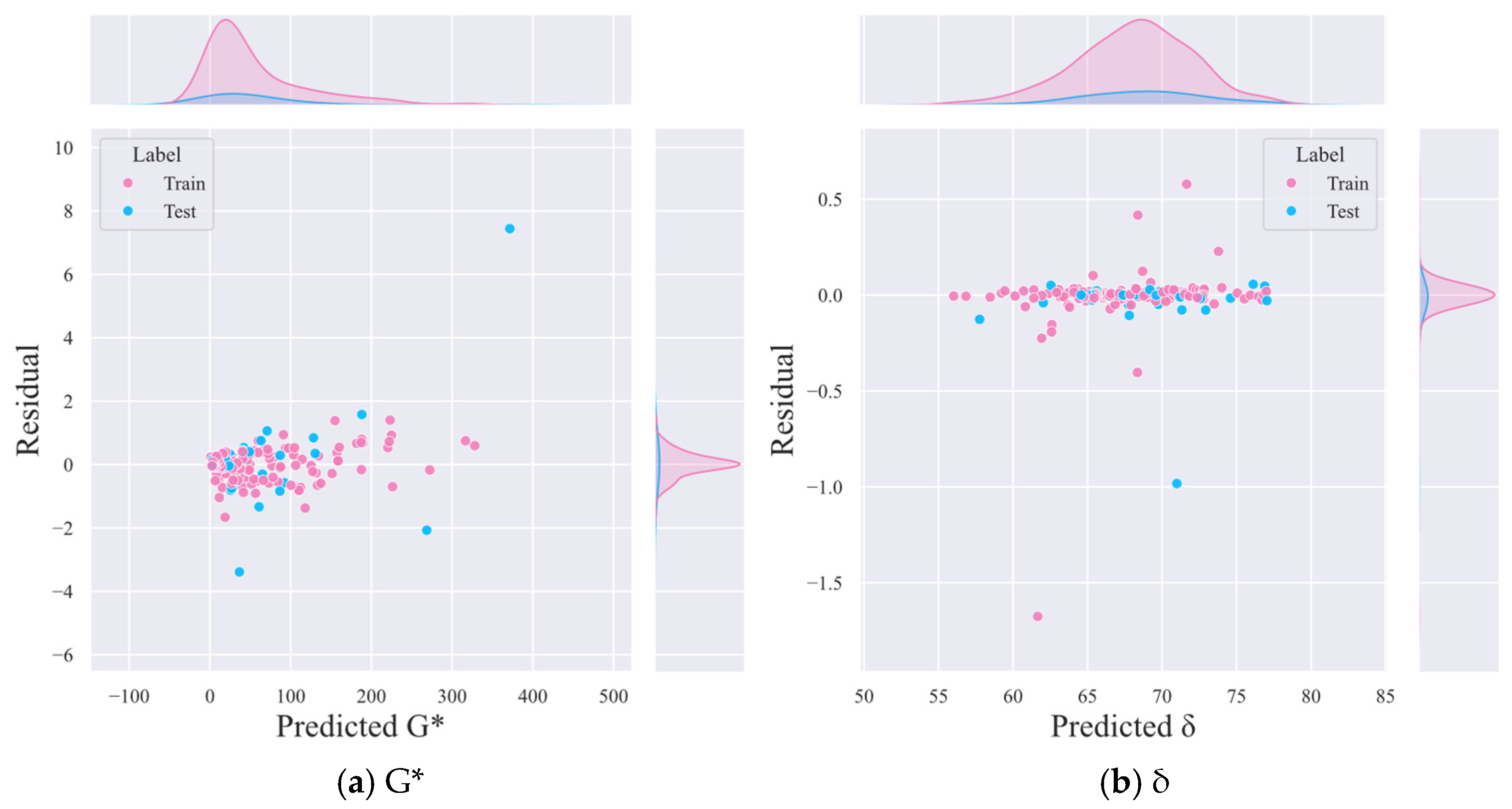
4.1. Comparison of Model Prediction Performance
4.2. Prediction
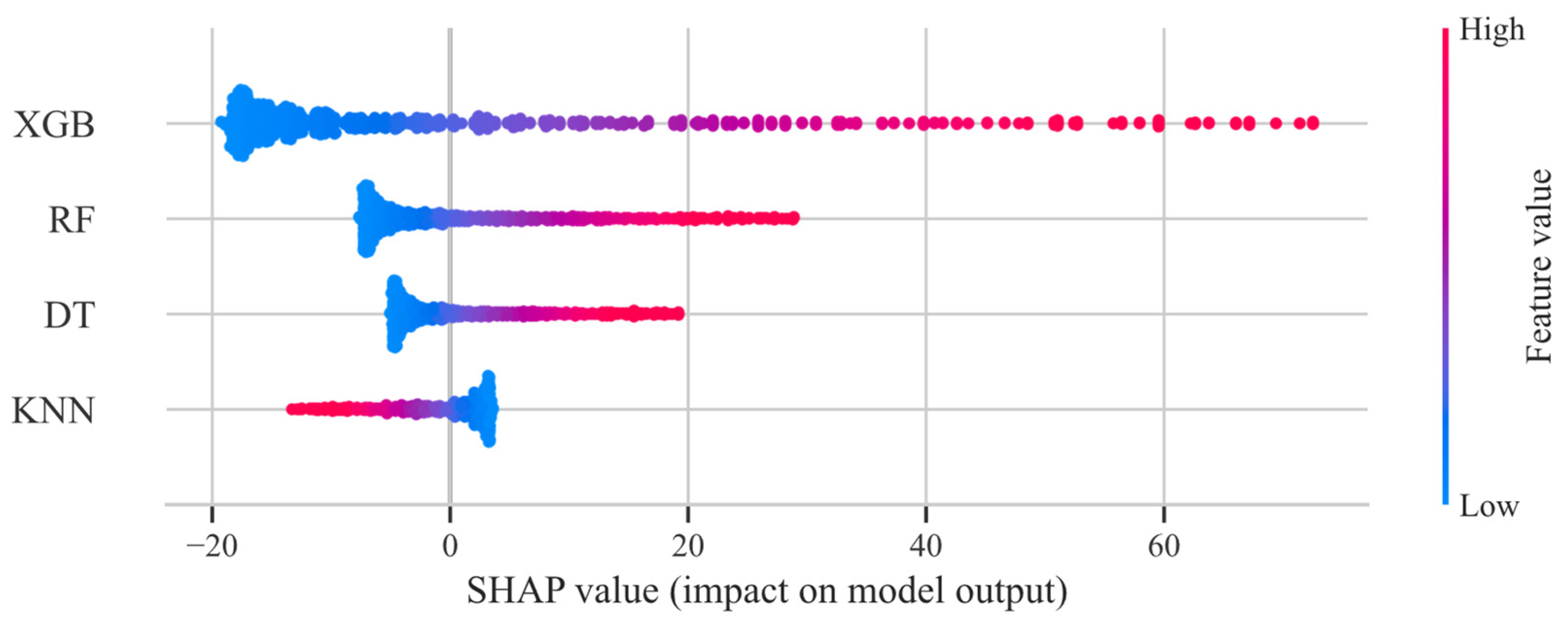
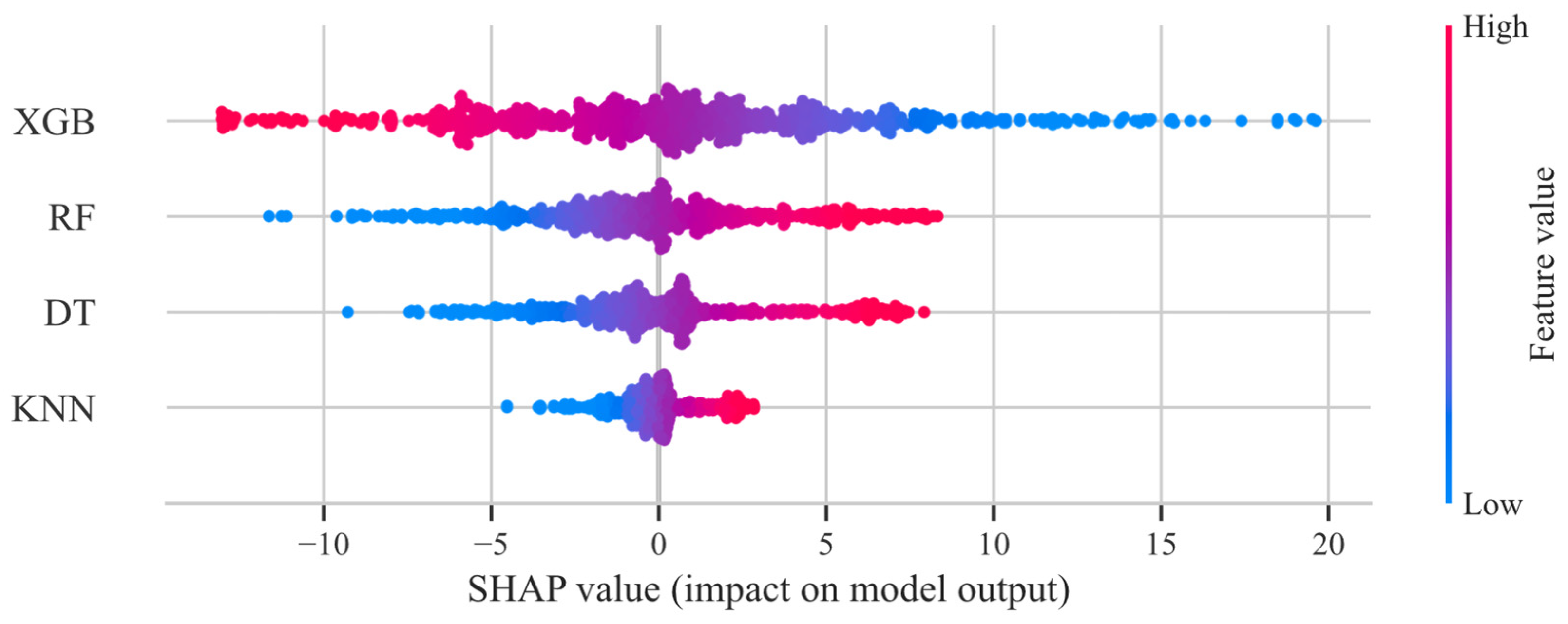
4.3. SHAP Analysis
4.3.1. Base Learners
4.3.2. Meta-Learner
5. Conclusions and Prospects
- Ensemble learning models, particularly the stacking model, outperformed single ML models in terms of prediction accuracy and generalization ability. The stacking model shows its superiority in R2 (0.9727 for G* and 0.9990 for δ) MAE, MAPE, and RMSE, demonstrating its robustness and reliability. This finding corroborates prior research [16,17,18,19,20], emphasizing the effectiveness of ensemble methods in modeling complex non-linear relationships within material-science datasets.
- SHAP analysis revealed that temperature and mineral powder type are the most significant factors affecting the rheological properties of modified asphalt. Among the mineral powders tested, the ranking of G* and δ enhancement is as follows: granite (GN) > diabase (DB) > limestone (LS). This indicates GN’s potential for improving the high-temperature stability of asphalt mixtures. This finding is consistent with the results of Xu et al. [27], who reported that mineral powder can significantly enhance the high-temperature performance of emulsified asphalt. Their study also revealed that the order of effectiveness for this improvement is as follows: GN > DB > LS.
- The SHAP analysis also provided valuable insights into the contributions of different base learners in the stacking model. XGBoost was identified as the most influential base learner, while KNN exhibited limitations in certain scenarios, highlighting the importance of model selection and integration in ensemble learning.
- The findings of this study have significant implications for the design and optimization of asphalt mixtures. The stacking model offers a data-driven approach to predict the rheological behavior of mineral powder-modified asphalt, which can aid in selecting optimal materials and improving pavement performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, P.; Huang, S.; Zhou, C.; Xu, Z.; Wu, Y. Preparation process and performance of polyurethane modified bitumen investigated using machine learning algorithm. Artif. Intell. Rev. 2023, 56, 6775–6800. [Google Scholar] [CrossRef]
- Kong, W.; Huang, W.; Guo, W.; Wei, Y. Modification of MEPDG rutting model based on RIOHTrack data. Int. J. Pavement Eng. 2023, 24, 2201500. [Google Scholar] [CrossRef]
- Wu, X.; Ji, Z.; Milani, G.; Kang, A.; Liu, M.; Zhang, Y.; Kou, C. Numerical and experimental study on the low temperature rheological performance of basalt fiber reinforced asphalts. Constr. Build. Mater. 2024, 412, 134869. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Sakanlou, F.; Sohrabi, M. Laboratory investigation of using liquid anti-stripping additives on the performance characteristics of asphalt mixtures. Int. J. Pavement Res. Technol. 2019, 12, 269–276. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L.; Dong, S.; You, Z.; Zhang, Q.; Hu, S.; Bi, J. Assessment of testing methods for higher temperature performance of emulsified asphalt. J. Clean. Prod. 2022, 375, 134101. [Google Scholar] [CrossRef]
- Zhao, P.; Liang, H.; Wu, W.; Yang, Y.; Liu, Y.; Li, C.; Meng, W.; Zhang, R.; Song, X.; Wang, C.; et al. Rheological properties of high-asphalt-content emulsified asphalt. Constr. Build. Mater. 2024, 419, 135511. [Google Scholar] [CrossRef]
- Liu, B.; Shi, J.; He, Y.; Yang, Y.; Jiang, J.; He, Z. Factors influencing the demulsification time of asphalt emulsion in fresh cement emulsified asphalt composite binder. Road Mater. Pavement Des. 2022, 23, 477–490. [Google Scholar] [CrossRef]
- Tang, F.; Xu, G.; Ma, T.; Kong, L. Study on the Effect of Demulsification Speed of Emulsified Asphalt based on Surface Characteristics of Aggregates. Materials 2018, 11, 1488. [Google Scholar] [CrossRef]
- Xing, B.; Fan, W.; Zhuang, C.; Qian, C.; Lv, X. Effects of the morphological characteristics of mineral powder fillers on the rheological properties of asphalt mastics at high and medium temperatures. Powder Technol. 2019, 348, 33–42. [Google Scholar] [CrossRef]
- Kopylov, V.E.; Burenina, O.N. Physical and Mechanical Properties of Asphalt Concrete Modified with Activated Mineral Powders. IOP Conf. Ser. Mater. Sci. Eng. 2020, 753, 022037. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Y.; Sun, W.; Nair, H.; Lane, D.S.; Wang, L. Effect of coarse aggregate morphology on the mechanical properties of stone matrix asphalt. Constr. Build. Mater. 2017, 152, 48–56. [Google Scholar] [CrossRef]
- Cosme, R.L.; Teixeira, J.E.S.L.; Calmon, J.L. Use of frequency sweep and MSCR tests to characterize asphalt mastics containing ornamental stone residues and LD steel slag. Constr. Build. Mater. 2016, 122, 556–566. [Google Scholar] [CrossRef]
- Guo, T.; Chen, H.; Tang, D.; Ding, S.; Wang, C.; Wang, D.; Chen, Y.; Li, Z. Rheological Properties of Composite Inorganic Micropowder Asphalt Mastic. Coatings 2023, 13, 1068. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Atakan, M.; Valentin, J.; Yıldız, K. Effect of number and surface area of the aggregates on machine learning prediction performance of recycled hot-mix asphalt. Constr. Build. Mater. 2024, 445, 137788. [Google Scholar] [CrossRef]
- Hosseini, A.S.; Hajikarimi, P.; Gandomi, M.; Nejad, F.M.; Gandomi, A.H. Optimized machine learning approaches for the prediction of viscoelastic behavior of modified asphalt binders. Constr. Build. Mater. 2021, 299, 124264. [Google Scholar] [CrossRef]
- Majidifard, H.; Jahangiri, B.; Buttlar, W.G.; Alavi, A.H. New machine learning-based prediction models for fracture energy of asphalt mixtures. Measurement 2019, 135, 438–451. [Google Scholar] [CrossRef]
- AL-Jarazi, R.; Rahman, A.; Ai, C.; Al-Huda, Z.; Ariouat, H. Development of prediction models for interlayer shear strength in asphalt pavement using machine learning and SHAP techniques. Road Mater. Pavement Des. 2024, 25, 1720–1738. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Zheng, C.; Zhou, D.; Wang, L. Optimizing asphalt mix design through predicting effective asphalt content and absorbed asphalt content using machine learning. Constr. Build. Mater. 2022, 325, 126607. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Wang, Z.; Fanijo, E.O.; Wang, L. Involving prediction of dynamic modulus in asphalt mix design with machine learning and mechanical-empirical analysis. Constr. Build. Mater. 2023, 407, 133610. [Google Scholar] [CrossRef]
- Veiga, R.K.; Veloso, A.C.; Melo, A.P.; Lamberts, R. Application of machine learning to estimate building energy use intensities. Energy Build. 2021, 249, 111219. [Google Scholar] [CrossRef]
- Aldrees, A.; Awan, H.H.; Javed, M.F.; Mohamed, A.M. Prediction of water quality indexes with ensemble learners: Bagging and boosting. Process Saf. Environ. Prot. 2022, 168, 344–361. [Google Scholar] [CrossRef]
- Satoła, A.; Satoła, K. Performance comparison of machine learning models used for predicting subclinical mastitis in dairy cows: Bagging, boosting, stacking, and super-learner ensembles versus single machine learning models. J. Dairy Sci. 2024, 107, 3959–3972. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Liu, G.; Sun, J.; Bavirisetti, D.P.; Xiao, G. PSO-Stacking improved ensemble model for campus building energy consumption forecasting based on priority feature selection. J. Build. Eng. 2023, 72, 106589. [Google Scholar] [CrossRef]
- Talebi, H.; Bahrami, B.; Ahmadian, H.; Nejati, M.; Ayatollahi, M.R. An investigation of machine learning algorithms for estimating fracture toughness of asphalt mixtures. Constr. Build. Mater. 2024, 435, 136783. [Google Scholar] [CrossRef]
- Hajihosseinlou, M.; Maghsoudi, A.; Ghezelbash, R. Stacking: A novel data-driven ensemble machine learning strategy for prediction and mapping of Pb-Zn prospectivity in Varcheh district, west Iran. Expert Syst. Appl. 2024, 237, 121668. [Google Scholar] [CrossRef]
- Xu, W.; Luo, R. Evaluation of interaction between emulsified asphalt and mineral powder using rheology. Constr. Build. Mater. 2022, 318, 125990. [Google Scholar] [CrossRef]
- Olasehinde, O.O.; Johnson, O.V.; Olayemi, O.C. Evaluation of Selected Meta Learning Algorithms for the Prediction Improvement of Network Intrusion Detection System. In Proceedings of the 2020 International Conference in Mathematics, Computer Engineering and Computer Science (ICMCECS), Lagos, Nigeria, 18–21 March 2020; pp. 1–7. [Google Scholar]
- Huang, S.; Lin, Y.; Chinde, V.; Ma, X.; Lian, J. Simulation-based performance evaluation of model predictive control for building energy systems. Appl. Energy 2021, 281, 116027. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Data-driven estimation of building energy consumption with multi-source heterogeneous data. Appl. Energy 2020, 268, 114965. [Google Scholar] [CrossRef]
- Gong, M.; Wang, J.; Bai, Y.; Li, B.; Zhang, L. Heat load prediction of residential buildings based on discrete wavelet transform and tree-based ensemble learning. J. Build. Eng. 2020, 32, 101455. [Google Scholar] [CrossRef]
- Zeng, Z.; Underwood, B.S.; Kim, Y.R. A state-of-the-art review of asphalt mixture fracture models to address pavement reflective cracking. Constr. Build. Mater. 2024, 443, 137674. [Google Scholar] [CrossRef]
- Zeng, Z.; Kim, Y.R.; Underwood, B.S.; Guddati, M. Asphalt mixture fatigue damage and failure predictions using the simplified viscoelastic continuum damage (S-VECD) model. Int. J. Fatigue 2023, 174, 107736. [Google Scholar] [CrossRef]



| Property | MQ65 | EM520 |
|---|---|---|
| Physical form, 25 °C | Brown liquid | |
| Emulsifier type | Cation, slow-breaking, and quick-curing | |
| Solid content (%) | 100 | |
| Density (g/cm3) | 1.026 | 1.050 |
| Viscosity (mPa·s), 25 °C | 7400 | ≤90,000 |
| Property Indices | Specific Surface Area (SSA) | D10 (μm) | D25 (μm) | D50 (μm) | D75 (μm) |
|---|---|---|---|---|---|
| LS | 2.108 | 1.249 | 2.282 | 4.557 | 8.423 |
| DB | 2.419 | 1.106 | 1.867 | 3.514 | 5.965 |
| GN | 1.791 | 1.396 | 2.475 | 5.178 | 8.781 |
| Evaluation Indicators | BR | KNN | DT | RF | XGB | Stacking | |
|---|---|---|---|---|---|---|---|
| G* | R2 | 0.7315 | 0.9973 | 0.9990 | 0.9995 | 0.9996 | 0.9727 |
| MAE | 24.133 | 0.6751 | 0.6738 | 0.4551 | 0.6493 | 8.5964 | |
| MAPE | 1.5368 | 0.0248 | 0.0159 | 0.0113 | 0.0154 | 0.3719 | |
| RMSE | 32.351 | 3.1549 | 1.8610 | 1.3694 | 1.1635 | 10.146 | |
| δ | R2 | 0.6043 | 0.9864 | 0.9982 | 0.9984 | 0.9988 | 0.9990 |
| MAE | 1.9182 | 0.0885 | 0.0443 | 0.0374 | 0.0649 | 0.0409 | |
| MAPE | 0.0286 | 0.0013 | 0.0007 | 0.0006 | 0.0010 | 0.0006 | |
| RMSE | 2.5391 | 0.4712 | 0.1721 | 0.1612 | 0.1368 | 0.1276 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Xu, Z.; Li, X.; Liu, B.; Fan, X.; Ding, H.; Xu, W. Predicting Rheological Properties of Asphalt Modified with Mineral Powder: Bagging, Boosting, and Stacking vs. Single Machine Learning Models. Materials 2025, 18, 2913. https://doi.org/10.3390/ma18122913
Huang H, Xu Z, Li X, Liu B, Fan X, Ding H, Xu W. Predicting Rheological Properties of Asphalt Modified with Mineral Powder: Bagging, Boosting, and Stacking vs. Single Machine Learning Models. Materials. 2025; 18(12):2913. https://doi.org/10.3390/ma18122913
Chicago/Turabian StyleHuang, Haibing, Zujie Xu, Xiaoliang Li, Bin Liu, Xiangyang Fan, Haonan Ding, and Wen Xu. 2025. "Predicting Rheological Properties of Asphalt Modified with Mineral Powder: Bagging, Boosting, and Stacking vs. Single Machine Learning Models" Materials 18, no. 12: 2913. https://doi.org/10.3390/ma18122913
APA StyleHuang, H., Xu, Z., Li, X., Liu, B., Fan, X., Ding, H., & Xu, W. (2025). Predicting Rheological Properties of Asphalt Modified with Mineral Powder: Bagging, Boosting, and Stacking vs. Single Machine Learning Models. Materials, 18(12), 2913. https://doi.org/10.3390/ma18122913







