Advances in Solidification Processing in Steady Magnetic Field
Highlights
- The SMF affects alloy solidification via various magnetic effects;
- Recent progress in alloy solidification in the SMF is reviewed;
- The SMF will be one of the most advanced techniques for tailoring solidification.
Abstract
1. Introduction
2. Main Magnetic Effects During Solidification
2.1. Magnetic Damping
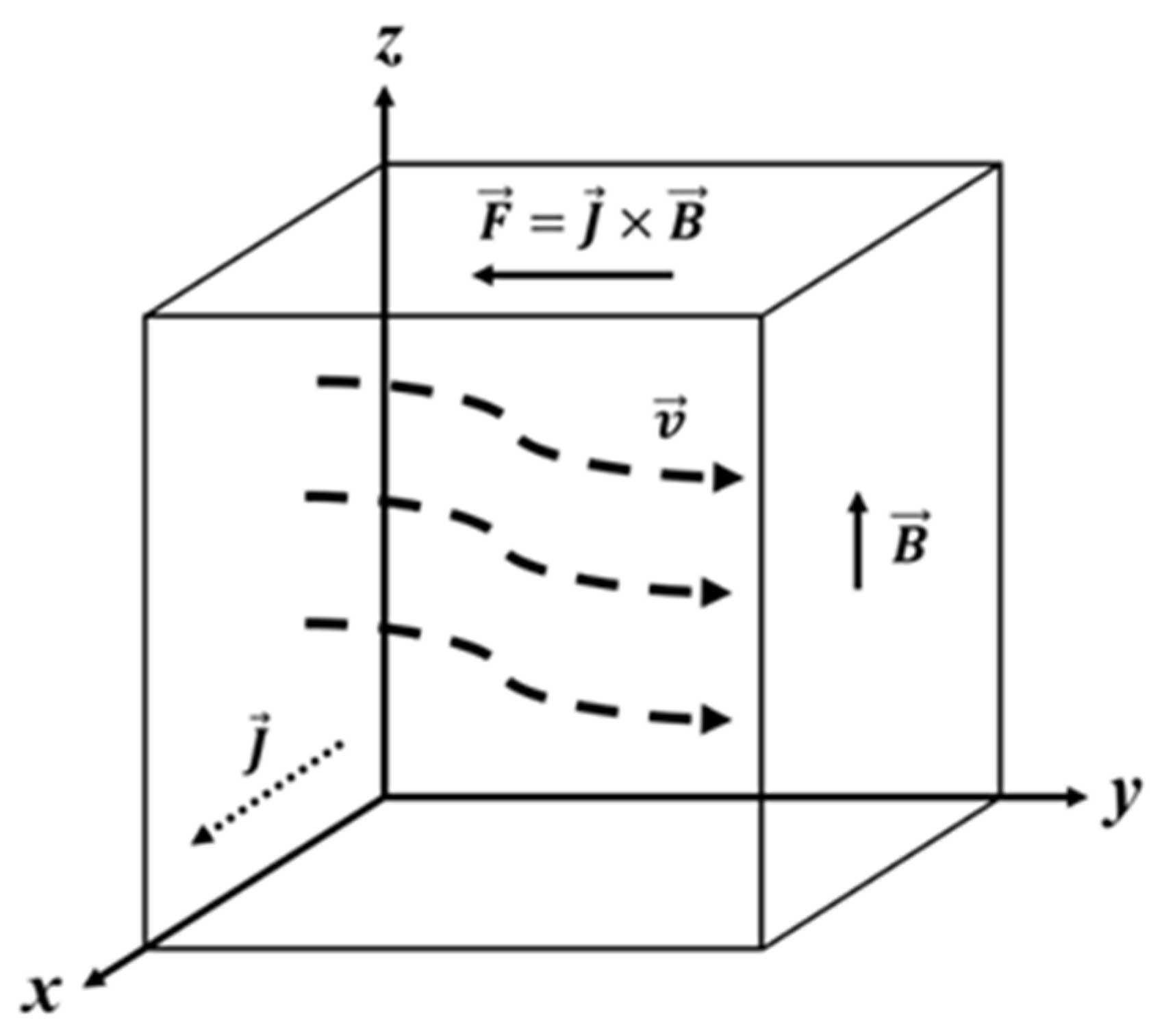
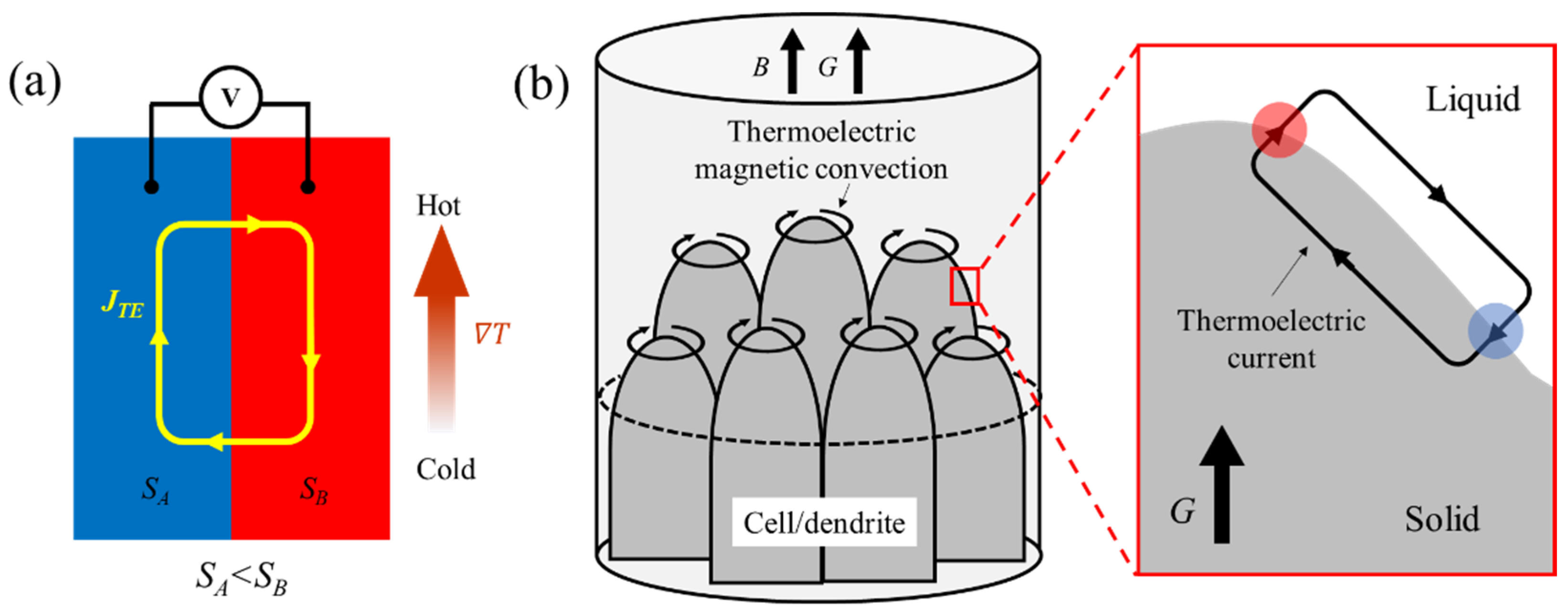
2.2. Thermoelectric Magnetic Convection
2.3. Magnetic Orientation
2.4. Magnetic Field-Controlled Diffusion
3. Undercooling in SMF
| Materials | Magnetic Field Intensity | Degree of Undercooling | Ref. |
|---|---|---|---|
| Pure Aluminum | 12 T | 21.6 °C | [70] |
| 6 T | 10 °C | [3] | |
| Pure Antimony | 6 T | 9.6 °C | [4] |
| 11.5 T | 5 °C | [69] | |
| Pure Tin | 6 T | 7.6 °C | [4] |
| Pure Zinc | 6 T | 5.9 °C | [4] |
| Ni-90wt.%Cu | 11.5 T | 8 °C | [69] |
| Al-25at.%Cu | 12 T | 2.7 °C | [71] |
| Al-38wt.%Cu | 12 T | 10 °C | [72] |
| Al-4.5wt.%Cu | 2 T | 2 °C | [73] |
| 4 T | 3 °C | [73] | |
| 6 T | 3.9 °C | [74] | |
| 8 T | 5 °C | [73] | |
| Al-26wt.%Cu | 6 T | 7.3 °C | [74] |
| Al-45wt.%Cu | 6 T | 6.7 °C | [74] |
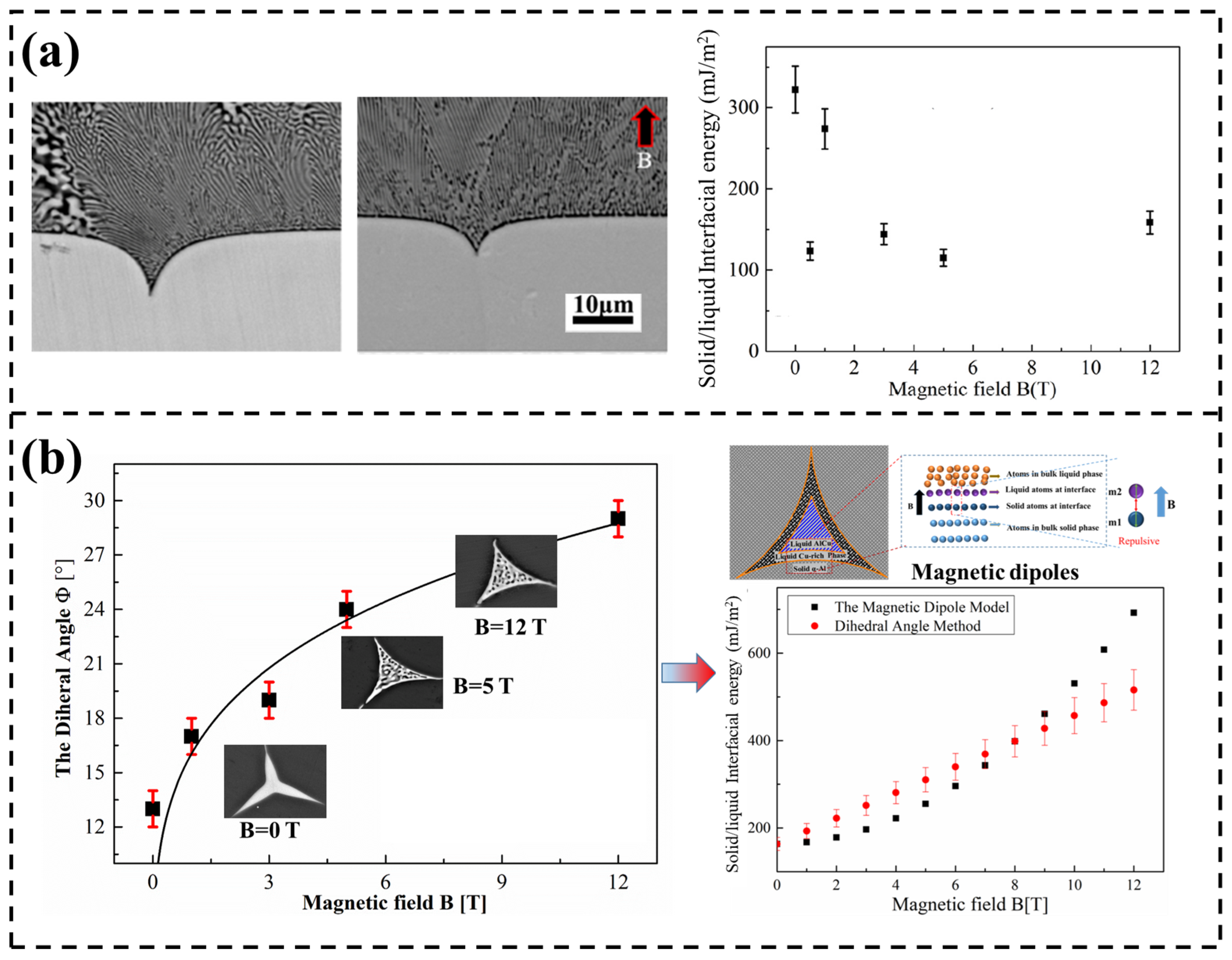
4. Interfacial Free Energy in SMFs
5. Microsegregation in SMF
6. Microstructure Evolution in SMF
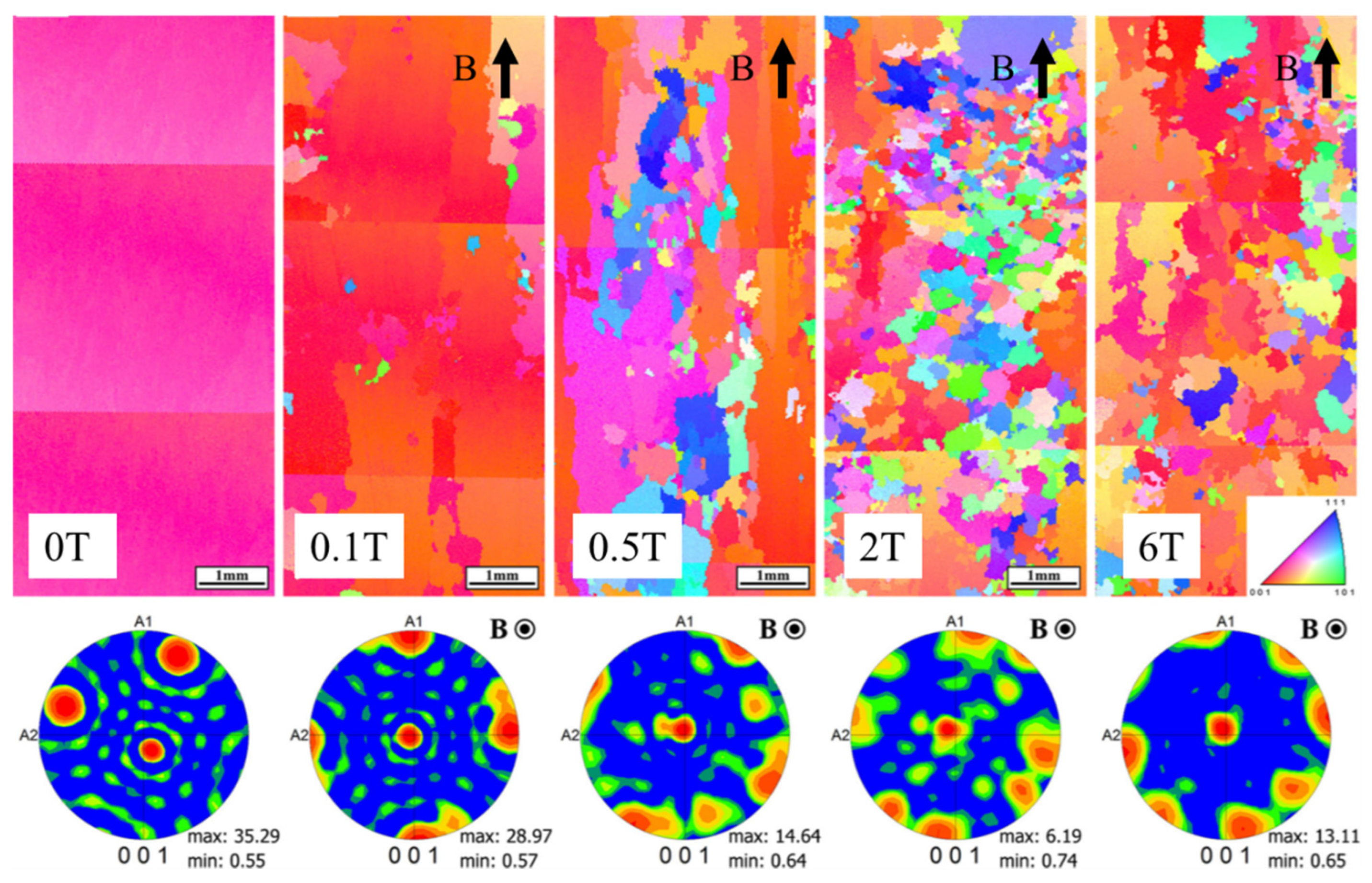
7. Summary and Prospective
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SMF | Steady magnetic field |
| EPM | Electromagnetic Processing of Materials |
| MD | Magnetic damping |
| TEMC | Thermoelectric magnetic convection |
| MHD | Magnetohydrodynamics |
| TEC | Thermoelectric current |
| TEMF | Thermoelectric magnetic force |
| SLIFE | Solid–liquid interfacial free energy |
| IGBG | Improved grain boundary groove |
| DAM | Dihedral angle method |
| CET | Columnar-to-equiaxed transition |
References
- Asai, S. Recent development and prospect of electromagnetic processing of materials. Sci. Technol. Adv. Mater. 2000, 1, 191–200. [Google Scholar] [CrossRef]
- Joo, H.D.; Kim, S.U.; Shin, N.S.; Koo, Y.M. An effect of high magnetic field on phase transformation in Fe–C system. Mater. Lett. 2000, 43, 225–229. [Google Scholar] [CrossRef]
- Li, C.J.; Guo, R.; Yuan, Z.J.; Xuan, W.D.; Ren, Z.M.; Zhong, Y.B.; Li, X.; Wang, H.; Wang, Q.L. Magnetic-field dependence of nucleation undercoolings in non-magnetic metallic melts. Philos. Mag. Lett. 2015, 95, 37–43. [Google Scholar] [CrossRef]
- Guo, R.; Li, C.J.; He, S.Y.; Wang, J.; Xuan, W.D.; Li, X.; Zhong, Y.B.; Ren, Z.M. Enhanced undercooling of para-and diamagnetic metal melts in steady magnetic field. Jpn. J. Appl. Phys. 2018, 57, 080301. [Google Scholar] [CrossRef]
- Morikawa, H.; Sassa, K.; Asai, S. Control of precipitating phase alignment and crystal orientation by imposition of a high magnetic field. Mater. Trans. JIM 1998, 39, 814–818. [Google Scholar] [CrossRef]
- Asai, S.; Sassa, K.; Tahashi, M. Crystal orientation of non-magnetic materials by imposition of a high magnetic field. Sci. Technol. Adv. Mater. 2003, 4, 455–460. [Google Scholar] [CrossRef]
- Lu, Z.; Fautrelle, Y.; Ren, Z.; Li, X. Influence of a transverse static magnetic field on the orientation and peritectic reaction of Cu-10.5 at.% Sn peritectic alloy. Sci. Rep. 2018, 8, 10641. [Google Scholar] [CrossRef]
- Youdelis, W.V.; Colton, D.R.; Cahoon, J. On the theory of diffusion in a magnetic field. Can. J. Phys. 1964, 42, 2217–2237. [Google Scholar] [CrossRef]
- Yuan, Z.J.; Ren, Z.M.; Li, C.J.; Xiao, Q.; Wang, Q.L.; Dai, Y.M.; Wang, H. Effect of high magnetic field on diffusion behavior of aluminum in Ni–Al alloy. Mater. Lett. 2013, 108, 340–342. [Google Scholar] [CrossRef]
- Shercliff, J.A. Thermoelectric magnetohydrodynamics. J. Fluid Mech. 1979, 91, 231–251. [Google Scholar] [CrossRef]
- Davidson, P.A. An Introduction to Magnetohydrodynamics; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Moreau, R.; Laskar, O.; Tanaka, M.; Camel, D. Thermoelectric magnetohydrodynamic effects on solidification of metallic alloys in the dendritic regime. Mater. Sci. Eng. A 1993, 173, 93–100. [Google Scholar] [CrossRef]
- Tewari, S.N.; Shah, R. Macrosegregation during dendritic arrayed growth of hypoeutectic pb-sn alloys: Influence of primary arm spacing and mushy zone length. Metall. Mater. Trans. A 1996, 27, 1353–1362. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Tanimoto, Y. Magneto-Science: Magnetic Field Effects on Materials: Fundamentals and Applications; Kodansha: Tokyo, Japan, 2006. [Google Scholar]
- Cowling, T.G. Magnetohydrodynamics. Rep. Prog. Phys. 1962, 25, 244. [Google Scholar] [CrossRef]
- Oreper, G.M.; Szekely, J. The effect of an externally imposed magnetic field on buoyancy driven flow in a rectangular cavity. J. Cryst. Growth 1983, 64, 505–515. [Google Scholar] [CrossRef]
- Ha, M.Y.; Lee, H.G.; Seong, S.H. Numerical simulation of three-dimensional flow, heat transfer, and solidification of steel in continuous casting mold with electromagnetic brake. J. Mater. Process. Technol. 2003, 133, 322–339. [Google Scholar] [CrossRef]
- Li, B.; Tsukihashi, F. Numerical Estimation of the Effect of the Magnetic Field Application on the Motion of Inclusion in Continuous Casting of Steel. ISIJ Int. 2003, 43, 923–931. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, M. Numerical Simulation of the Effects of Electromagnetic Brake and Argon Gas Injection on the Three-dimensional Multiphase Flow and Heat Transfer in Slab Continuous Casting Mold. ISIJ Int. 2008, 48, 584–591. [Google Scholar] [CrossRef]
- Chedzey, H.A.; Hurle, D.T.J. Avoidance of growth-striae in semiconductor and metal crystals grown by zone-melting techniques. Nature 1966, 210, 933. [Google Scholar] [CrossRef]
- Utech, H.P.; Flemings, M.C. Elimination of solute banding in indium antimonide crystals by growth in a magnetic field. J. Appl. Phys. 1966, 37, 2021–2024. [Google Scholar] [CrossRef]
- Frohberg, G.; Kraatz, K.H.; Weber, H. Proc. Vacancies & Interstitials in Metals; Trans Tech Publlcations Ltd.: Bäch, Switzerland, 1984. [Google Scholar]
- Cahoon, J.R.; Youdelis, W.V. Application of a magnetic field to suppress convective velocities during liquid diffusion. Can. Metall. Q. 1969, 8, 39–40. [Google Scholar] [CrossRef]
- Khine, Y.Y.; Banish, R.M.; Alexander, J.I.D. Convective effects during diffusivity measurements in liquids with an applied magnetic field. Int. J. Thermophys. 2002, 23, 649–666. [Google Scholar] [CrossRef]
- Miyake, T.; Inatomi, Y.; Kuribayashi, K. Measurement of diffusion coefficient in liquid metal under static magnetic field. Jpn. J. Appl. Phys. 2002, 41, L811. [Google Scholar] [CrossRef]
- Botton, V.; Lehmann, P.; Bolcato, R.; Moreau, R. Measurement of solute diffusivities. Part III. From solutal convection dominated transport to quasi-diffusive transport. Int. J. Heat Mass Transf. 2004, 47, 2457–2467. [Google Scholar] [CrossRef]
- Tewari, S.N.; Shah, R.; Song, H. Effect of magnetic field on the microstructure and macrosegregation in directionally solidified Pb-Sn alloys. Metall. Mater. Trans. A 1994, 25, 1535–1544. [Google Scholar] [CrossRef]
- Lehmann, P.; Moreau, R.; Camel, D.; Bolcato, R. Modification of interdendritic convection in directional solidification by a uniform magnetic field. Acta Mater. 1998, 46, 4067–4079. [Google Scholar] [CrossRef]
- Fautrelle, Y.; Wang, J.; Salloum-Abou-Jaoude, G.; Abou-Khalil, L.; Reinhart, G.; Li, X.; Ren, Z.M.; Nguyen-Thi, H. Thermo-Electric-Magnetic Hydrodynamics in Solidification: In Situ Observations and Theory. JOM 2018, 70, 764–771. [Google Scholar] [CrossRef]
- Gel’fgat, Y.M.; Gorbunov, L.A. An additional source of forced convection in semiconductor melts during single-crystal growth in magnetic fields. Sov. Phys. Dokl. 1989, 34, 470–473. [Google Scholar]
- Khine, Y.Y.; Walker, J.S. Thermoelectric magnetohydrodynamic effects during Bridgman semiconductor crystal growth with a uniform axial magnetic field. J. Cryst. Growth 1998, 183, 150–158. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Ren, Z.M. Influence of thermoelectric effects on the solid-liquid interface shape and cellular morphology in the mushy zone during the directional solidification of Al-Cu alloys under a magnetic field. Acta Mater. 2007, 55, 3803–3813. [Google Scholar] [CrossRef]
- Savitsky, E.M.; Torchinova, R.S.; Turanov, S.A. Effect of crystallization in magnetic field on the structure and magnetic properties of Bi-Mn alloys. J. Cryst. Growth 1981, 52, 519–523. [Google Scholar] [CrossRef]
- Mikelson, A.E.; Karklin, Y.K. Control of crystallization processes by means of magnetic fields. J. Cryst. Growth 1981, 52, 524–529. [Google Scholar] [CrossRef]
- Wang, J.; Long, Z.; Jiang, P.; Fautrelle, Y.; Li, X. Microstructure, Crystallographic Orientation and Mechanical Property in AlCoCrFeNi2.1 Eutectic High-Entropy Alloy Under Magnetic Field-Assisted Directional Solidification. Metall. Mater. Trans. A 2020, 51, 3504–3517. [Google Scholar] [CrossRef]
- Zhao, R.; Chen, C.; Shuai, S.; Hu, T.; Fautrelle, Y.; Liao, H.; Lu, J.; Wang, J.; Ren, Z. Enhanced mechanical properties of Ti6Al4V alloy fabricated by laser additive manufacturing under static magnetic field. Mater. Res. Lett. 2022, 10, 530–538. [Google Scholar] [CrossRef]
- Luo, Y.; Shan, Y.; Xiong, S.; Wang, Y.; Xiao, X.; He, X.; Zhou, H. Preparation and construction mechanism of thermal conductive epoxy-based composite via magnetic field induced orientation. J. Appl. Polym. Sci. 2024, 141, e54783. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Wei, L.; Xia, F. The Influence of Magnetic Field Orientation on the Efficacy and Structure of Ni-W-SiC Coatings Produced by Magnetic Field-Assisted Electrodeposition. Coatings 2024, 14, 1272. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, T.; Zhang, B.; Dahlström, A.; Li, S.; Wang, K.; Mu, W.; Wang, Q. Crystal orientation-induced Al grain coalescence coarsening during isothermal semisolid annealing of Al-15 wt% Cu alloys under high magnetic fields. J. Mater. Res. Technol. 2025, 35, 6825–6835. [Google Scholar] [CrossRef]
- Li, X.; Ren, Z.; Wang, H.; Deng, K.; Xu, K. Effects of high magnetic field on solidification structure of Al~ 3Ni phase in Al-Ni alloy. Chin. J. Nonferrous Met. 2006, 16, 476. [Google Scholar]
- Li, X.; Ren, Z.; Fautrelle, Y.; Zhang, Y.; Esling, C. Morphological instabilities and alignment of lamellar eutectics during directional solidification under a strong magnetic field. Acta Mater. 2010, 58, 1403–1417. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Q.; Gao, A.; Zhang, C.; Li, D.; He, J. Crystal orientation and grain alignment in a hypoeutectic Mn–Sb alloy under high magnetic field conditions. J. Alloys Compd. 2009, 481, 755–760. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, T.; Zhang, C.; Gao, A.; Li, D.; He, J. Effects of high magnetic fields on solidified structures of Mn-90.4 wt% Sb hypoeutectic alloy. Sci. Technol. Adv. Mater. 2009, 10, 014606. [Google Scholar] [CrossRef]
- Legrand, B.A.; Chateigner, D.; Bathie, R.P.; Tournier, R. Orientation of samarium–cobalt compounds by solidification in a magnetic field. J. Alloys Compd. 1998, 275–277, 660–664. [Google Scholar] [CrossRef]
- Han, Y.; Ban, C.; Guo, S.; Liu, X.; Ba, Q.; Cui, J. Alignment behavior of primary Al3Fe phase in Al–Fe alloy under a high magnetic field. Mater. Lett. 2007, 61, 983–986. [Google Scholar] [CrossRef]
- Rivoirard, S.; Barthem, V.M.T.S.; Garcin, T.; Beaugnon, E.; Miranda, P.E.V.; Givord, D. Texturing hard Nd-Fe-B powdered ribbons in high magnetic field. J. Phys. Conf. Ser. 2009, 156, 012009. [Google Scholar] [CrossRef]
- Rivoirard, S. High Steady Magnetic Field Processing of Functional Magnetic Materials. JOM 2013, 65, 901–909. [Google Scholar] [CrossRef]
- Mayaguchi, M.; Tanimoto, Y. Magnetoscience; Kodansha: Tokyo, Japan, 2006. [Google Scholar]
- Li, L.; Zhang, Y.; Esling, C.; Jiang, H.; Zhao, Z.; Zuo, Y.; Cui, J. Influence of a high magnetic field on the precipitation behavior of the primary Al3Fe phase during the solidification of a hypereutectic Al-3.31 wt% Fe alloy. J. Cryst. Growth 2012, 339, 61–69. [Google Scholar] [CrossRef]
- Li, L.; Suo, Y.; Zhang, R.; Ban, C.; Zhang, H.; Liu, T.; Esling, C.; Cui, J. A crystallographic investigation on the growth of Al4Sr crystals under a high magnetic field. J. Appl. Phys. 2019, 125, 245108. [Google Scholar] [CrossRef]
- Li, L.; Ban, C.; Shi, X.; Zhang, H.; Zuo, Y.; Zhu, Q.; Wang, X.; Zhang, H.; Cui, J.; Nagaumi, H. Effects of a high magnetic field on the primary zinc-rich crystals in hypoeutectic Zn-Sn alloy. J. Cryst. Growth 2017, 463, 59–66. [Google Scholar] [CrossRef]
- Li, L.; Zhang, R.; Ban, C.; Zhang, H.; Liu, T.; Zhang, H.; Wang, X.; Esling, C.; Cui, J. Growth behavior of Zn-rich phase in Zn-Mg alloy under a high magnetic field. Mater. Charact. 2019, 151, 191–202. [Google Scholar] [CrossRef]
- Li, L.; Lv, G.; Suo, Y.; Liang, W.; Liu, T.; Wang, X.; Cui, J. Effect of a high magnetic field on the macro- and microstructures of Zn-Mg alloy during semi-solid isothermal annealing process. J. Cryst. Growth 2021, 554, 125947. [Google Scholar] [CrossRef]
- Youdelis, W.V.; Cahoon, J.R. Diffusion in a magnetic field. Can. J. Phys. 1970, 48, 805–808. [Google Scholar] [CrossRef]
- Nakamichi, S.; Tsurekawa, S.; Morizono, Y.; Watanabe, T.; Nishida, M.; Chiba, A. Diffusion of carbon and titanium in γ-iron in a magnetic field and a magnetic field gradient. J. Mater. Sci. 2005, 40, 3191–3198. [Google Scholar] [CrossRef]
- Wang, S.J.; Wu, Y.; Zhao, X.; Zuo, L. Effect of a high magnetic field on carbon diffusion in γ-iron. Mater. Trans. 2011, 52, 139–141. [Google Scholar] [CrossRef]
- He, S.; Li, C.; Yuan, Z.; Xuan, W.; Wang, J.; Ren, Z. Magnetic-Field-Induced Liquid–Solid Interface Transformation and Its Effect on Microsegregation in Directionally Solidified Ni-Cr Alloy. Metall. Mater. Trans. A 2020, 51, 4592–4601. [Google Scholar] [CrossRef]
- Wang, Q.; Li, D.G.; Wang, K.; Wang, Z.Y.; He, J.C. Effects of high uniform magnetic fields on diffusion behavior at the Cu/Al solid/liquid interface. Scr. Mater. 2007, 56, 485–488. [Google Scholar] [CrossRef]
- Li, D.G.; Wang, Q.; Liu, T.; Li, G.J.; He, J.C. Growth of diffusion layers at liquid Al–solid Cu interface under uniform and gradient high magnetic field conditions. Mater. Chem. Phys. 2009, 117, 504–510. [Google Scholar] [CrossRef]
- Li, C.J.; Yuan, Z.J.; Guo, R.; Xuan, W.D.; Ren, Z.M.; Zhong, Y.B.; Li, X.; Wang, H.; Wang, Q.L. Reaction diffusion in Ni–Al diffusion couples in steady magnetic fields. J. Alloys Compd. 2015, 641, 7–13. [Google Scholar] [CrossRef]
- Philibert, J.M. Atom Movements-Diffusion and Mass Transport in Solids; EDP Sciences: Les Ulis, France, 2012. [Google Scholar]
- Long, Z.; Wang, J.; Fautrelle, Y.; Li, X. Repeated nucleation behaviors of pure bismuth under a high magnetic field. J. Alloys Compd. 2020, 831, 154746. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, X.; Xu, X.; Lin, X.; Liu, L. A review on the effect of external fields on solidification, melting and heat transfer enhancement of phase change materials. J. Energy Storage 2020, 31, 101567. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Xu, X.; Zhang, S. Research progress in nucleation and supercooling induced by phase change materials. J. Energy Storage 2020, 27, 101156. [Google Scholar] [CrossRef]
- Luo, J.; Luo, H.; Zhao, T.; Wang, R. Effect of magnetic field on dislocation morphology and precipitation behaviour in ultrafine-grained 7075 aluminium alloy. J. Mater. Sci. Technol. 2021, 93, 128–146. [Google Scholar] [CrossRef]
- Wang, L.; Long, Z.; Hou, L.; Yan, S.; Sun, B.; Li, X. Effects of a high magnetic field on single-phase interface evolution, additional interfacial energy and nucleation undercooling in Al-based alloy. J. Mater. Sci. Technol. 2023, 154, 43–53. [Google Scholar] [CrossRef]
- Hasegawa, M.; Asai, S. Effects of static magnetic field on undercooling of a copper melt. J. Mater. Sci. 1992, 27, 6123–6126. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Zhou, Y.L.; Gao, J.R.; He, J.C. Undercooling of Pure Cu and Ge Melts in a Static Magnetic Field. Mater. Sci. Forum 2010, 649, 281–286. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Q.; Liu, F.; Li, G.; He, J. Nucleation behavior of bulk Ni–Cu alloy and pure Sb in High magnetic fields. J. Cryst. Growth 2011, 321, 167–170. [Google Scholar] [CrossRef]
- Li, C.J.; Yang, H.; Ren, Z.M.; Ren, W.L.; Wu, Y.Q. On nucleation temperature of pure aluminum in magnetic fields. Prog. Electromagn. Res. 2010, 15, 45–52. [Google Scholar] [CrossRef]
- Li, C.J.; Yang, H.; Ren, Z.M.; Ren, W.L.; Wu, Y.Q. Application of differential thermal analysis to investigation of magnetic field effect on solidification of Al–Cu hypereutectic alloy. J. Alloys Compd. 2010, 505, 108–112. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, X.; Guo, M.; Li, C.; Vleugels, J.; Ren, Z.; Van der Biest, O.; Blanpain, B. Strong magnetic field effect on surface tension associated with an interfacial magnetic pressure. J. Phys. Chem. C 2012, 116, 17676–17681. [Google Scholar] [CrossRef]
- He, S.; Li, C.; Guo, R.; Xuan, W.; Ren, Z.; Li, X.; Zhong, Y. Microsegregation Formation in Al–Cu Alloy under Action of Steady Magnetic Field. ISIJ Int. 2018, 58, 899–904. [Google Scholar] [CrossRef]
- Guo, R.; Li, C.; He, S.; Wang, J.; Xuan, W.; Li, X.; Zhong, Y.; Ren, Z. Effect of steady magnetic field on undercooling of Al-Cu alloy melts. EPL (Europhys. Lett.) 2019, 126, 46001. [Google Scholar] [CrossRef]
- Li, C.J.; Ren, Z.M.; Ren, W.L.; Deng, K.; Cao, G.H.; Zhong, Y.B.; Wu, Y.Q. Design and application of differential thermal analysis apparatus in high magnetic fields. Rev. Sci. Instrum. 2009, 80, 073907. [Google Scholar] [CrossRef]
- Li, C.J.; Ren, Z.M.; Ren, W.L.; Wu, Y.Q. Effect of High Magnetic Field on Nucleation and Growth of Primary Phase in Hypoeutectic Binary Alloys. J. Iron Steel Res. Int. 2012, 19, 297–300. [Google Scholar]
- Wang, J.; He, Y.; Li, J.; Kou, H.; Beaugnon, E. Strong magnetic field effect on the nucleation of a highly undercooled Co-Sn melt. Sci. Rep. 2017, 7, 4958. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.; Guo, R.; Shuai, S.; Wang, J.; Xia, M.; Li, J.; Ren, Z.; Li, J.; Wang, Q. Influence of static magnetic field on the heterogeneous nucleation behavior of Al on single crystal Al2O3 substrate. Materialia 2020, 13, 100847. [Google Scholar] [CrossRef]
- Turnbull, D. Correlation of Liquid-Solid Interfacial Energies Calculated from Supercooling of Small Droplets. J. Chem. Phys. 1950, 18, 769. [Google Scholar] [CrossRef]
- Jones, D.R.H. The free energies of solid-liquid interfaces. J. Mater. Sci. 1974, 9, 1–17. [Google Scholar] [CrossRef]
- Jones, H. An Evaluation of Measurements of Solid/Liquid Interfacial Energies in Metallic Alloy Systems by the Groove Profile Method. Metall. Mater. Trans. A 2007, 38, 1563–1569. [Google Scholar] [CrossRef]
- Glicksman, M.E.; Vold, C.L. Determination of absolute solid-liquid interfacial free energies in metals. Acta Metall. 1969, 17, 1–11. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Karma, A.; Asta, M.A.; Sun, D.Y. From atoms to dendrites. JOM 2004, 56, 49–54. [Google Scholar] [CrossRef]
- Liu, J.; Davidchack, R.L.; Dong, H.B. Molecular dynamics calculation of solid–liquid interfacial free energy and its anisotropy during iron solidification. Comput. Mater. Sci. 2013, 74, 92–100. [Google Scholar] [CrossRef]
- Nourian-Avval, A.; Asadi, E. On the quantification of phase-field crystals model for computational simulations of solidification in metals. Comput. Mater. Sci. 2017, 128, 294–301. [Google Scholar] [CrossRef]
- Kaptay, G. On the solid/liquid interfacial energies of metals and alloys. J. Mater. Sci. 2018, 53, 3767–3784. [Google Scholar] [CrossRef]
- Kaptay, G. A coherent set of model equations for various surface and interface energies in systems with liquid and solid metals and alloys. Adv. Colloid Interface Sci. 2020, 283, 102212. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Cao, Y.; Lippmann, S.; Ren, Z.; Rettenmayr, M. Reduced Wettability of Solids by a Liquid Ga–In–Sn Alloy in a Steady Magnetic Field. J. Phys. Chem. C 2018, 122, 27451–27455. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, T.; Lu, Z.; Li, G.; Yuan, S.; Hirota, N.; Ren, Z.; Wang, Q. Wetting Transition in a Molten Metal and Solid Substrate System in High Magnetic Fields. Metall. Mater. Trans. A 2020, 51, 2333–2343. [Google Scholar] [CrossRef]
- Miao, P.; Liu, T.; Lu, Z.; Sun, H.; Wang, J.; Yuan, S.; Wang, Q. Wetting of α-Al2O3 by molten Al-2wt.%Cu under high magnetic fields. Surf. Interfaces 2024, 48, 104325. [Google Scholar] [CrossRef]
- Miao, P.; Liu, T.; Tang, P.; Wang, J.; Yuan, S.; Mu, W.; Wang, Q. Dynamic wetting behavior of molten Al on α-Al2O3 substrate during heating in high magnetic field. Colloids Surf. A: Physicochem. Eng. Asp. 2024, 682, 132938. [Google Scholar] [CrossRef]
- Huang, C.; Shuai, S.; Wang, P.; Liu, X.; Wang, J.; Ren, Z. The effect of static magnetic field on solid–liquid interfacial free energy of Al–Cu alloy system. Scr. Mater. 2020, 187, 232–236. [Google Scholar] [CrossRef]
- Huang, C.; Shuai, S.; Wang, J.; Shi, L.; Li, S.; Nan, R.; Li, C.; Wang, J.; Ren, Z. Magnetic field-induced variation of solid/liquid interfacial energy of solid Al2Cu and Al-Cu eutectic melt. J. Alloys Compd. 2023, 941, 168977. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.; Shuai, S.; Wang, J.; Nan, R.; Guo, R.; Li, S.; Li, C.; Chen, C.; Ren, Z. The effect of static magnetic field on solid/liquid interfacial energies of Al-Cu studied by dihedral angle method. Metall. Mater. Trans. A 2023, 54A, 3401. [Google Scholar] [CrossRef]
- Witt, A.F.; Herman, C.J.; Gatos, H.C. Czochralski-type crystal growth in transverse magnetic fields. J. Mater. Sci. 1970, 5, 822–824. [Google Scholar] [CrossRef]
- Youdelis, W.V.; Dorward, R.C. Directional solidification of aluminium–copper alloys in a magnetic field. Can. J. Phys. 1966, 44, 139–150. [Google Scholar] [CrossRef]
- Li, X.; Gagnoud, A.; Ren, Z.M.; Fautrelle, Y.; Debray, F. Effect of strong magnetic field on solid solubility and microsegregation during directional solidification of Al–Cu alloy. J. Mater. Res. 2013, 28, 2810–2818. [Google Scholar] [CrossRef]
- Shen, Z.; Zhou, B.; Zhong, Y.; Zheng, T.; Ren, W.; Lei, Z.; Ren, Z. Revealing influence mechanism of a transverse static magnetic field on the refinement of primary dendrite spacing during directional solidification. J. Cryst. Growth 2019, 517, 54–58. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Q.; Liu, T.; He, J.C. Effects of High Magnetic Fields on Solidified Microstructure and Solute Element Distribution in Al-Cu Alloy. J. Northeast. Univ. Nat. Sci. 2013, 34, 57–61. [Google Scholar]
- Song, J.Y.; Zhao, X.; Zhang, Y.D.; Esling, C.; Zuo, L. Influence of a High Magnetic Field on the Solubility of Ferrite and the Amount of Pearlite. Steel Res. Int. 2011, 82, 836–838. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, H.; Fan, G.; Liu, C.; Huang, T.; Yang, W.; Zhang, J.; Liu, L.; Fu, H. Tailoring Microstructure and Microsegregation in a Directionally Solidified Ni-Based SX Superalloy by a Weak Transverse Static Magnetic Field. Acta Metall. Sin. (Engl. Lett.) 2022, 35, 1164–1174. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, L.; Li, X.; Su, H.; Zhang, J. Solute segregation behavior of nickel-based single crystal superalloys directionally solidified under transverse static magnetic field. Mater. Charact. 2023, 200, 112914. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Zhang, X.; Chen, C.; Meng, J.; Yu, J.; Wang, J.; Ren, Z. Influence of Longitudinal Static Magnetic Field on Microstructure and Microsegregation During Directional Solidification of DD98M Alloy. Acta Metall. Sin. 2024, 60, 1595–1606. [Google Scholar]
- Zhang, C.; Zhou, Y.; Shen, C.; Ren, W.; Yuan, X.; Ding, B.; Lu, H.; Lei, Z.; Zhong, Y.; Zhang, A. Effects of longitudinal magnetic field on primary dendrite spacing and segregation of directionally solidified single crystal superalloy. Prog. Nat. Sci. Mater. Int. 2024, 34, 26–36. [Google Scholar] [CrossRef]
- Hou, L.; Dai, Y.C.; Fautrelle, Y.; Li, Z.B.; Ren, Z.M.; Esling, C.; Li, X. Evolution of microstructure and microsegregation in Ni-Mn-Ga alloys directionally solidified under axial magnetic field. J. Alloys Compd. 2018, 758, 54–61. [Google Scholar] [CrossRef]
- Ren, W.L.; Lu, L.; Yuan, G.Z.; Xuan, W.D.; Zhong, Y.B.; Yu, J.B.; Ren, Z.M. The effect of magnetic field on precipitation phases of single-crystal nickel-base superalloy during directional solidification. Mater. Lett. 2013, 100, 223–226. [Google Scholar] [CrossRef]
- Ren, W.; Niu, C.; Ding, B.; Zhong, Y.; Yu, J.; Ren, Z.; Liu, W.; Ren, L.; Liaw, P.K. Improvement in creep life of a nickel-based single-crystal superalloy via composition homogeneity on the multiscales by magnetic-field-assisted directional solidification. Sci. Rep. 2018, 8, 1452. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Ren, W.L.; Dong, J.W.; Li, X.; Ren, Z.M.; Cao, G.H.; Zhong, Y.B.; Deng, K.; Lei, Z.S.; Guo, J.T. Effect of high magnetic field on the primary dendrite arm spacing and segregation of directionally solidified superalloy DZ417G. J. Alloys Compd. 2009, 487, 612–617. [Google Scholar] [CrossRef]
- Chen, R. Effect of external magnetic field on the microstructure and strength of laser-welded aluminum to titanium. J. Mater. Sci. 2020, 55, 4054–4064. [Google Scholar] [CrossRef]
- He, S.; Li, C.; Guo, R.; Xuan, W.; Wang, J.; Ren, Z. Evolution of microsegregation in directionally solidified Al–Cu alloys under steady magnetic field. J. Alloys Compd. 2019, 800, 41–49. [Google Scholar] [CrossRef]
- He, S.; Zhan, T.; Li, C.; Xuan, W.; Wang, J.; Ren, Z. Enhanced Dendrite Coarsening and Microsegregation in AlCu Alloy under a Steady Magnetic Field. Mater. Trans. 2019, 60, 1921–1927. [Google Scholar] [CrossRef]
- Wang, P.; Shuai, S.; Huang, C.; Liu, X.; Fu, Y.; Wang, J.; Ren, Z. Revealing the influence of high magnetic field on the solute distribution during directional solidification of Al-Cu alloy. J. Mater. Sci. Technol. 2021, 88, 226–232. [Google Scholar] [CrossRef]
- He, S.; Shevchenko, N.; Eckert, S. In situ observation of directional solidification in Ga-In alloy under a transverse DC magnetic field. In Proceedings of the MCWASP XV 2020, Jönköping, Sweden, 22–23 June 2020; p. 012025. [Google Scholar]
- Brody, H.D. Solute Redistribution in Dendritic Solidification. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1965. [Google Scholar]
- Voller, V.R.; Beckermann, C. Approximate models of microsegregation with coarsening. Metall. Mater. Trans. A 1999, 30, 3016–3019. [Google Scholar] [CrossRef]
- He, S. Effect of Steady Magnetic Field on Microsegregation Formation During Solidification of Binary Hypoeutectic Alloy. Ph.D. Thesis, Shanghai University, Shanghai, China, 2021. [Google Scholar]
- Zhao, Y.; Su, H.; Zhang, J.; Liu, L.; Fu, H. Recent Progress on Directional Solidification of Nickel-BasedSuperalloys with Magnetic Field. Mater. Mech. Eng. 2021, 45, 1–7. [Google Scholar]
- Hu, Y.; Zhao, H.; Yu, X.; Li, J.; Zhang, B.; Li, T. Research Progress of Magnetic Field Regulated Mechanical Property of Solid Metal Materials. Metals 2022, 12, 1988. [Google Scholar] [CrossRef]
- Wang, Q.; Zhai, L.L.; Zhang, L.; Zhang, J.W.; Ban, C.Y. Effect of steady magnetic field on microstructure and properties of laser cladding Ni-based alloy coating. J. Mater. Res. Technol. 2022, 17, 2145–2157. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, H.; Zhang, Z.; Wang, Y.; Zhu, B.; Zhao, H. A review of the microstructure and properties of superalloys regulated by magnetic field. J. Mater. Res. Technol. 2024, 30, 9285–9317. [Google Scholar] [CrossRef]
- Zhou, H.; Song, C.; Yang, Y.; Han, C.; Wang, M.; Xiao, Y.; Liu, Z. The microstructure and properties evolution of SS316L fabricated by magnetic field-assisted laser powder bed fusion. Mater. Sci. Eng. A 2022, 845, 143216. [Google Scholar] [CrossRef]
- Lehmann, P.; Moreau, R.; Camel, D.; Bolcato, R. A simple analysis of the effect of convection on the structure of the mushy zone in the case of horizontal Bridgman solidification. Comparison with experimental results. J. Cryst. Growth 1998, 183, 690–704. [Google Scholar] [CrossRef]
- Li, X.; Gagnoud, A.; Ren, Z.; Fautrelle, Y.; Moreau, R. Investigation of thermoelectric magnetic convection and its effect on solidification structure during directional solidification under a low axial magnetic field. Acta Mater. 2009, 57, 2180–2197. [Google Scholar] [CrossRef]
- Li, X.; Du, D.; Gagnoud, A.; Ren, Z.; Fautrelle, Y.; Moreau, R. Effect of multi-scale thermoelectric magnetic convection on solidification microstructure in directionally solidified Al-Si alloys under a transverse magnetic field. Metall. Mater. Trans. A 2014, 45, 5584–5600. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Ren, Z.M. Influence of an axial high magnetic field on the liquid-solid transformation in Al-Cu hypoeutectic alloys and on the microstructure of the solid. Acta Mater. 2007, 55, 1377–1386. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Ren, Z.M.; Gagnoud, A.; Moreau, R.; Zhang, Y.D.; Esling, C. Effect of a high magnetic field on the morphological instability and irregularity of the interface of a binary alloy during directional solidification. Acta Mater. 2009, 57, 1689–1701. [Google Scholar] [CrossRef]
- Liu, H.; Xuan, W.; Xie, X.; Yu, J.; Wang, J.; Ren, Z. Effect of a high magnetic field on the microstructure in directionally solidified two-phase Ni3Al alloys. Mater. Lett. 2017, 189, 131–135. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Zaidat, K.; Gagnoud, A.; Ren, Z.M.; Moreau, R.; Zhang, Y.D.; Esling, C. Columnar-to-equiaxed transitions in Al-based alloys during directional solidification under a high magnetic field. J. Cryst. Growth 2010, 312, 267–272. [Google Scholar] [CrossRef]
- Li, X.; Gagnoud, A.; Fautrelle, Y.; Ren, Z.M.; Moreau, R.; Zhang, Y.D.; Esling, C. Dendrite fragmentation and columnar-to-equiaxed transition during directional solidification at lower growth speed under a strong magnetic field. Acta Mater. 2012, 60, 3321–3332. [Google Scholar] [CrossRef]
- Xuan, W.D.; Ren, Z.M.; Li, C.J. Effect of a high magnetic field on microstructures of Ni-based superalloy during directional solidification. J. Alloys Compd. 2015, 620, 10–17. [Google Scholar] [CrossRef]
- Hou, Y.; Ren, Z.M.; Zhang, Z.Q.; Ren, X.F. Columnar to Equiaxed Transition during Directionally Solidifying GCr18Mo Steel Affected by Thermoelectric Magnetic Force under an Axial Static Magnetic Field. ISIJ Int. 2019, 59, 60–68. [Google Scholar] [CrossRef]
- Mangelinck-Noël, N.; Nguyen-Thi, H.; Reinhart, G.; Schenk, T.; Cristiglio, V.; Dupouy, M.D.; Gastaldi, J.; Billia, B.; Härtwig, J.; Baruchel, J. In situ analysis of equiaxed growth of aluminium–nickel alloys by x-ray radiography at ESRF. J. Phys. D: Appl. Phys. 2005, 38, A28. [Google Scholar] [CrossRef]
- Liu, D.R.; Mangelinck-Noël, N.; Gandin, C.A.; Zimmermann, G.; Sturz, L.; Thi, H.N.; Billia, B. Structures in directionally solidified Al–7 wt.% Si alloys: Benchmark experiments under microgravity. Acta Mater. 2014, 64, 253–265. [Google Scholar] [CrossRef]
- Spittle, J.A. Columnar to equiaxed grain transition in as solidified alloys. Int. Mater. Rev. 2006, 51, 247–269. [Google Scholar] [CrossRef]
- Li, X.; Gagnoud, A.; Fautrelle, Y.; Moreau, R.; Du, D.; Ren, Z.; Lu, X. Effect of a transverse magnetic field on solidification structures in unmodified and Sr-modified Al-7wtpctSi alloys during directional solidification. Metall. Mater. Trans. A 2016, 47, 1198–1214. [Google Scholar] [CrossRef]
- Wang, J.; Fautrelle, Y.; Ren, Z.M.; Li, X.; Nguyen-Thi, H.; Mangelinck-Noel, N.; Salloum Abou Jaoude, G.; Zhong, Y.B.; Kaldre, I.; Bojarevics, A.; et al. Thermoelectric magnetic force acting on the solid during directional solidification under a static magnetic field. Appl. Phys. Lett. 2012, 101, 251904. [Google Scholar] [CrossRef]
- Wang, J. Study on Influence of Interaction Between Thermoelectric Currens and Magnetic Field During Directional Solidification of Binary Alloy. Ph.D. Thesis, Shanghai University, Shanghai, China, 2014. [Google Scholar]
- Liu, H.; Xuan, W.; Xie, X.; Li, C.; Wang, J.; Yu, J.; Li, X.; Zhong, Y.; Ren, Z. Columnar-to-Equiaxed Transition and Equiaxed Grain Alignment in Directionally Solidified Ni3Al Alloy Under an Axial Magnetic Field. Metall. Mater. Trans. A 2017, 48, 4193–4203. [Google Scholar] [CrossRef]
- Hou, Y.; Ren, Z.; Zhang, Z.; Xuan, W.; Wang, J.; Yu, J.; Ren, X. Effects of axial static magnetic field on columnar to equiaxed transition in directionally solidified low carbon steel. Ironmak. Steelmak. 2020, 47, 398–404. [Google Scholar] [CrossRef]
- Nishinga, T. Handbook of Crystal Growth; Elsevier: Amsterdam, The Netherlands, 2015; Volume II. [Google Scholar]
- Hoshi, K.; Isawa, N.; Suzuki, T.; Ohkubo, Y. Czochralski Silicon Crystals Grown in a Transverse Magnetic Field. J. Electrochem. Soc. 1985, 132, 693. [Google Scholar] [CrossRef]
- Shimura, F. Semiconductor Silicon Crystal Technology; Academic Press: San Diego, CA, USA, 2012. [Google Scholar]
- Terashima, K.; Fukuda, T. A new magnetic-field applied pulling apparatus for LEC GaAs single crystal growth. J. Cryst. Growth 1983, 63, 423–425. [Google Scholar] [CrossRef]
- Park, Y.J.; Min, S.K.; Hahn, S.H.; Yoon, J.K. Application of an axial magnetic field to vertical gradient freeze GaAs single crystal growth. J. Cryst. Growth 1995, 154, 10–18. [Google Scholar] [CrossRef]
- Lyubimova, T.P.; Croell, A.; Dold, P.; Khlybov, O.A.; Fayzrakhmanova, I.S. Time-dependent magnetic field influence on GaAs crystal growth by vertical Bridgman method. J. Cryst. Growth 2004, 266, 404–410. [Google Scholar] [CrossRef]
- Gorbunov, L.; Klyukin, A.; Pedchenko, A.; Feodorov, A. Melt flow instability and vortex structures in Czochralski growth under steady magnetic fields. Energy Convers. Manag. 2002, 43, 317–326. [Google Scholar] [CrossRef]
- Bliss, D.F. Indium Phosphide: Crystal Growth and Defect Control by Applying Steady Magnetic Fields in Springer Handbook of Crystal Growth; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Miyazawa, Y. Effect of magnetic field on melt flow and crystal growth of oxide crystals. Prog. Cryst. Growth Charact. Mater. 1999, 38, 261–272. [Google Scholar] [CrossRef]
- Frank-Rotsch, C.; Dropka, N.; Kießling, F.M.; Rudolph, P. Semiconductor Crystal Growth under the Influence of Magnetic Fields. Cryst. Res. Technol. 2020, 55, 1900115. [Google Scholar] [CrossRef]
- Liu, L.; Kakimoto, K. Partly three-dimensional global modeling of a silicon Czochralski furnace. I. Principles, formulation and implementation of the model. Int. J. Heat Mass Transf. 2005, 48, 4481–4491. [Google Scholar] [CrossRef]
- Kalaev, V.V. Combined effect of DC magnetic fields and free surface stresses on the melt flow and crystallization front formation during 400 mm diameter Si Cz crystal growth. J. Cryst. Growth 2007, 303, 203–210. [Google Scholar] [CrossRef]
- Vizman, D.; Watanabe, M.; Friedrich, J.; Müller, G. Influence of different types of magnetic fields on the interface shape in a 200 mm Si-EMCZ configuration. J. Cryst. Growth 2007, 303, 221–225. [Google Scholar] [CrossRef]
- Qi, C.; Wang, J.; Li, D.; Li, Z.; Li, J.; Wang, J.; Wen, Y.; Wang, L.; Jiang, Z.; Liu, L. Study on power consumption and heat transfer paths in Czochralski silicon crystal growth based on global 3D numerical simulation. CrystEngComm 2024, 26, 5531–5540. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, Y.; Yan, J.; Qin, M. Progress in modeling of fluid flows in crystal growth processes. Prog. Nat. Sci. 2008, 18, 1465–1473. [Google Scholar] [CrossRef]
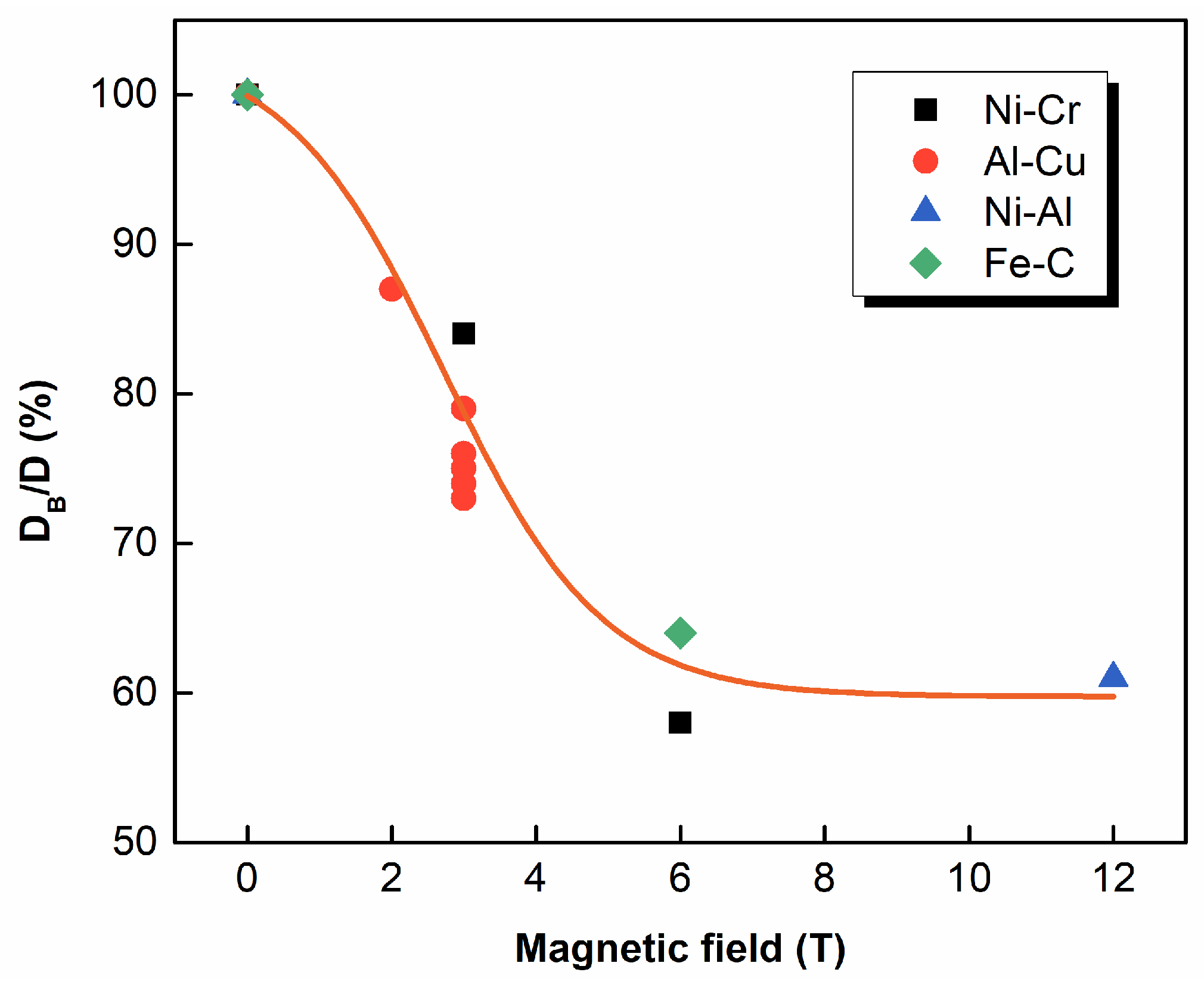
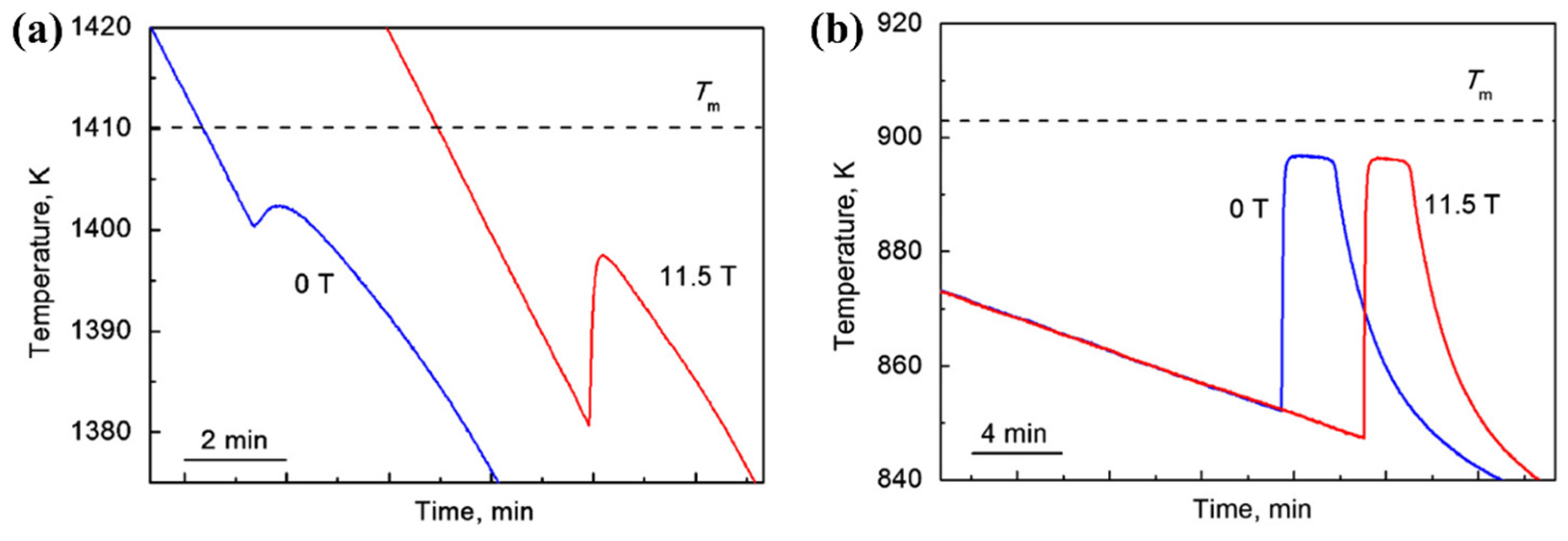
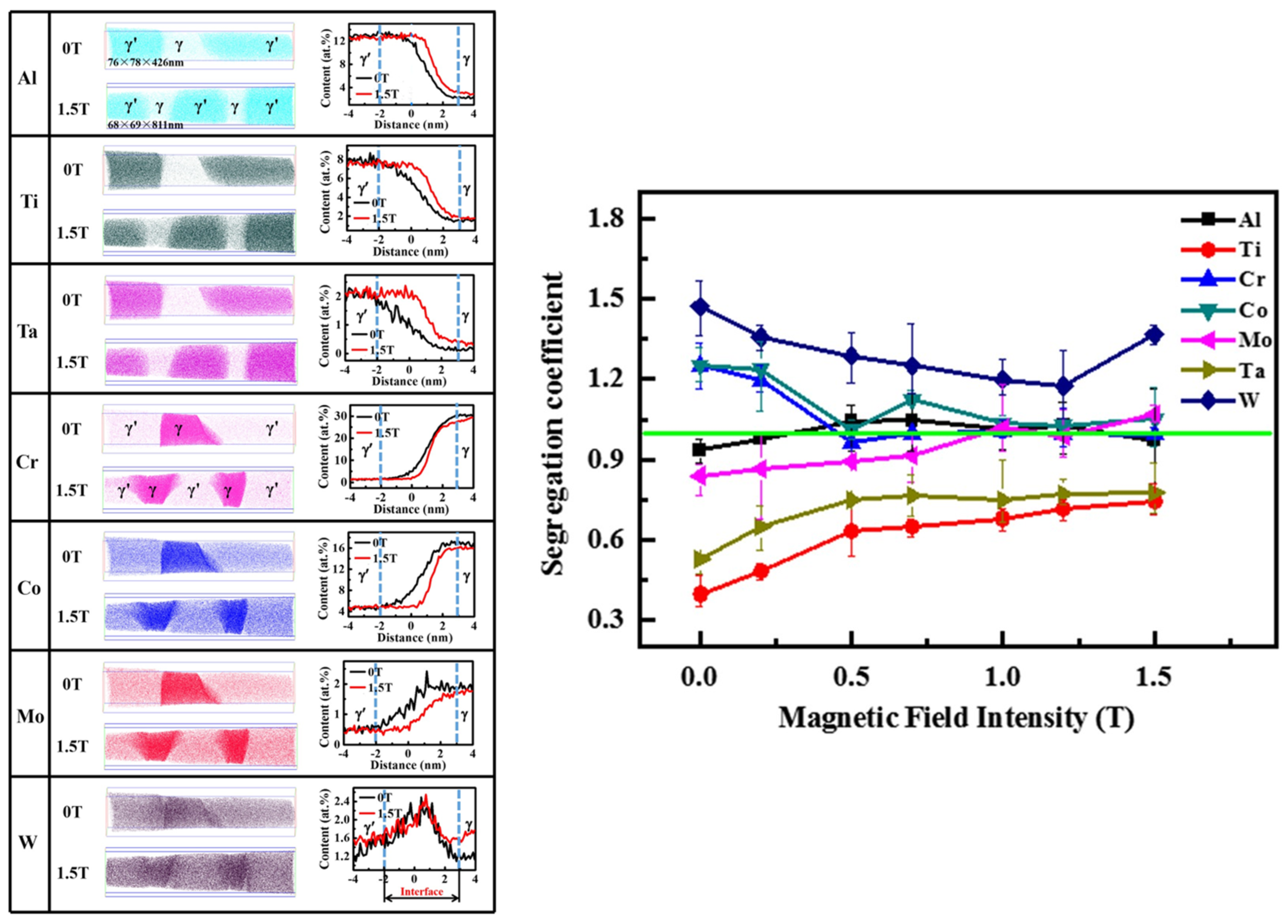
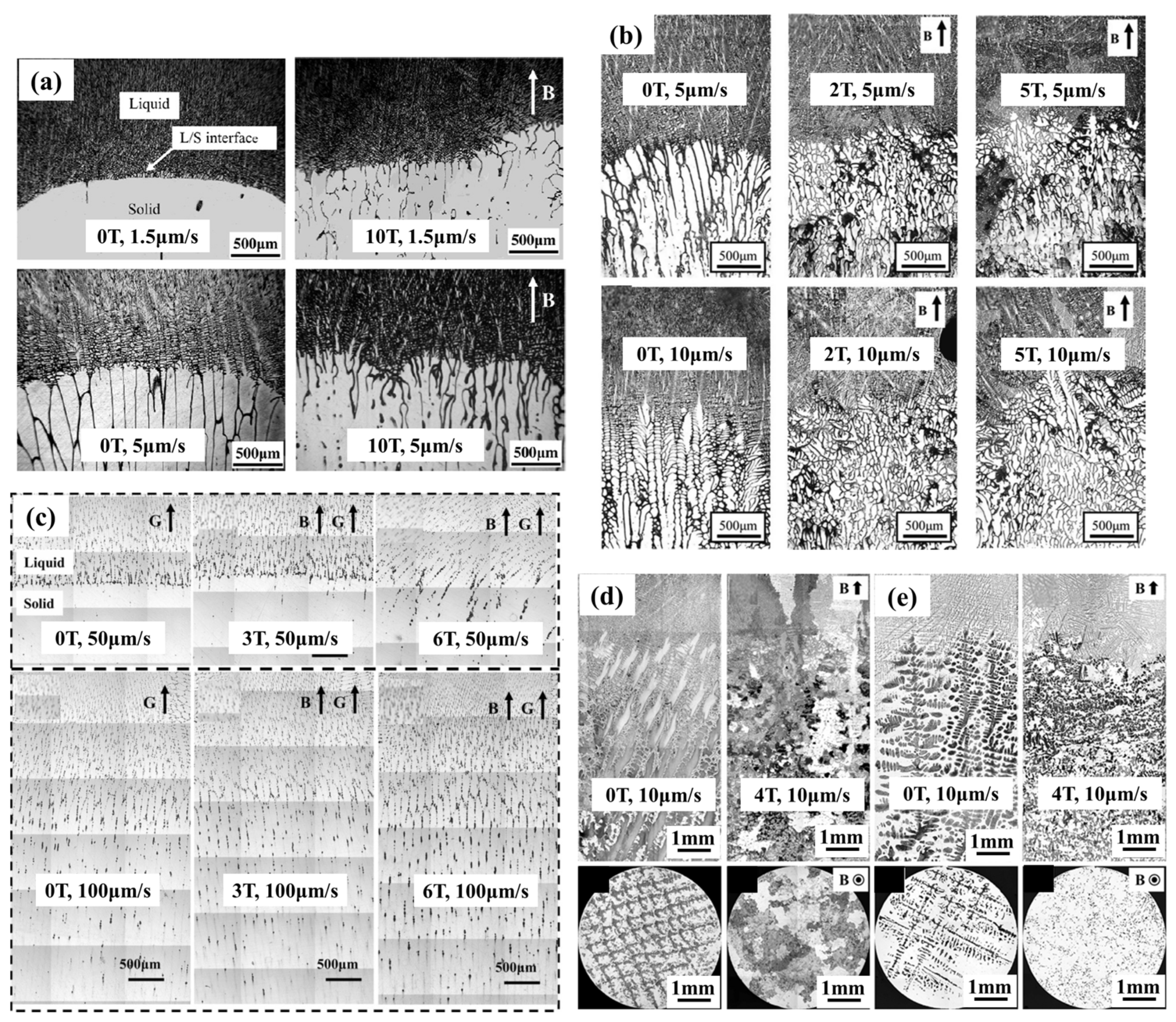
| Substance | SMF Intensity | Orientation Relationship (z-Axis and B) | Ref. |
|---|---|---|---|
| NiAl3 (orthorhombic) | 10 T | Parallel | [34,40] |
| BiMnx (hexagonal) | 10 T | Parallel | [33] |
| CuAl2 (tetragonal) | 10 T | Parallel | [41] |
| Zinc (hexagonal) | 1 T | Parallel | [34] |
| Bismuth (hexagonal) | 5~12 T | Perpendicular | [14] |
| SbMn (hexagonal) | 12 T | Parallel | [42,43] |
| Co17Sm2 (hexagonal) | 2.5 T | Parallel | [44] |
| FeAl3 (monoclinic) | 12 T | <543> parallel to B | [45] |
| Nd2BFe14 (tetragonal) | 5 T | Parallel | [46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Huang, C.; Li, C. Advances in Solidification Processing in Steady Magnetic Field. Materials 2025, 18, 2886. https://doi.org/10.3390/ma18122886
He S, Huang C, Li C. Advances in Solidification Processing in Steady Magnetic Field. Materials. 2025; 18(12):2886. https://doi.org/10.3390/ma18122886
Chicago/Turabian StyleHe, Shengya, Chenglin Huang, and Chuanjun Li. 2025. "Advances in Solidification Processing in Steady Magnetic Field" Materials 18, no. 12: 2886. https://doi.org/10.3390/ma18122886
APA StyleHe, S., Huang, C., & Li, C. (2025). Advances in Solidification Processing in Steady Magnetic Field. Materials, 18(12), 2886. https://doi.org/10.3390/ma18122886