Prediction of Compressive Strength of Concrete Considering Pore Relative Humidity
Abstract
1. Introduction
2. Prediction of Pore Humidity
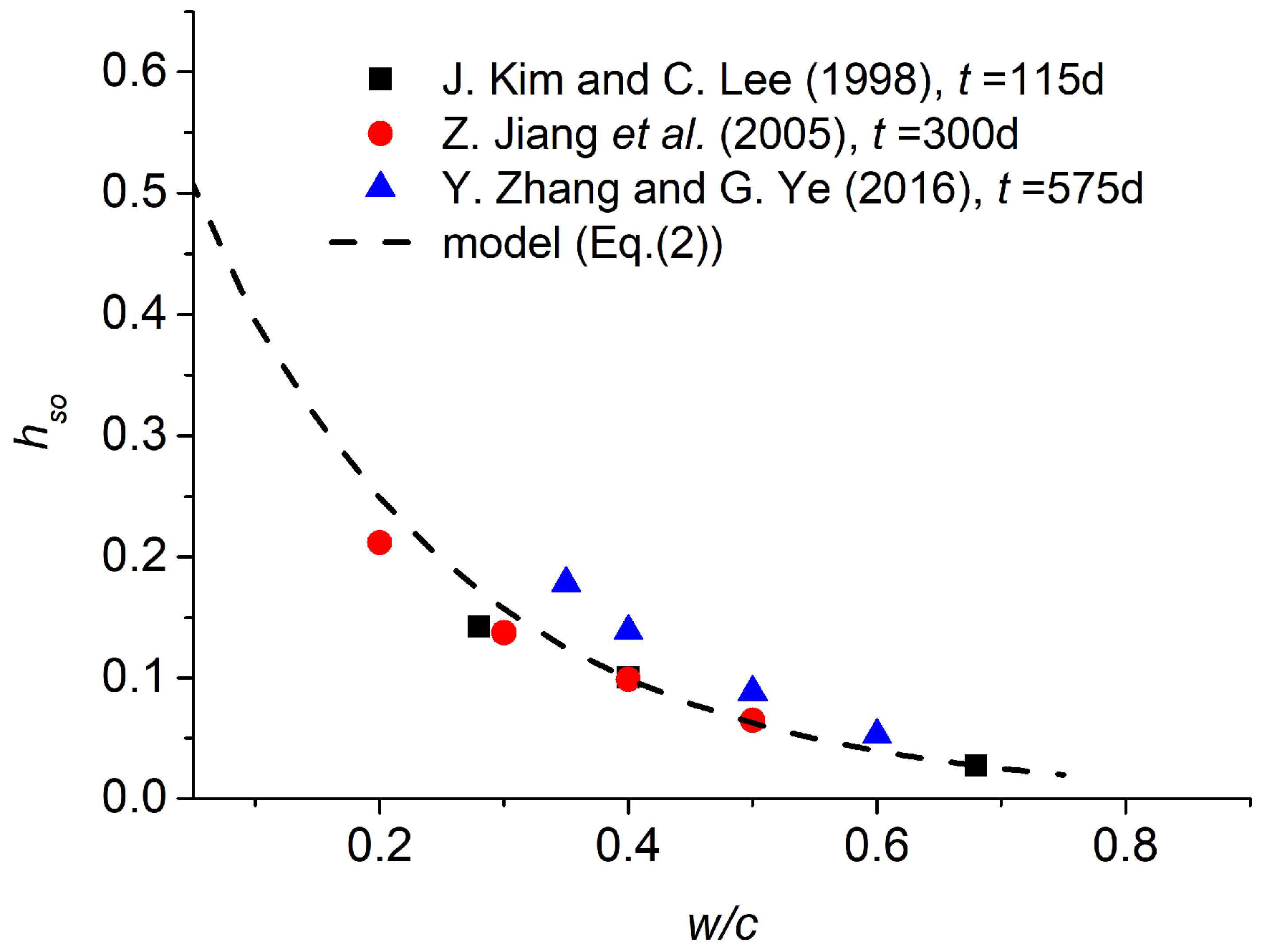
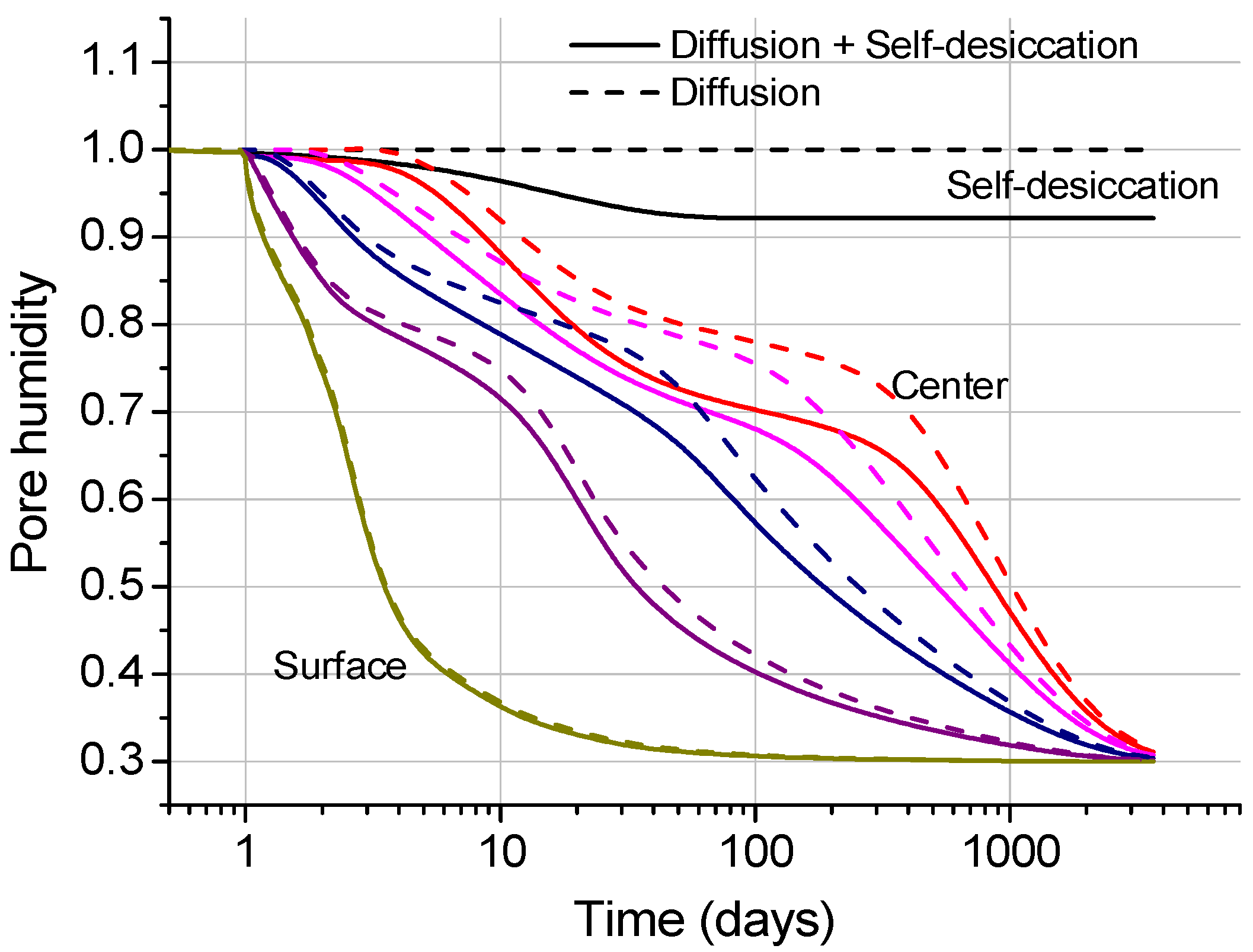
2.1. Self-Desiccation
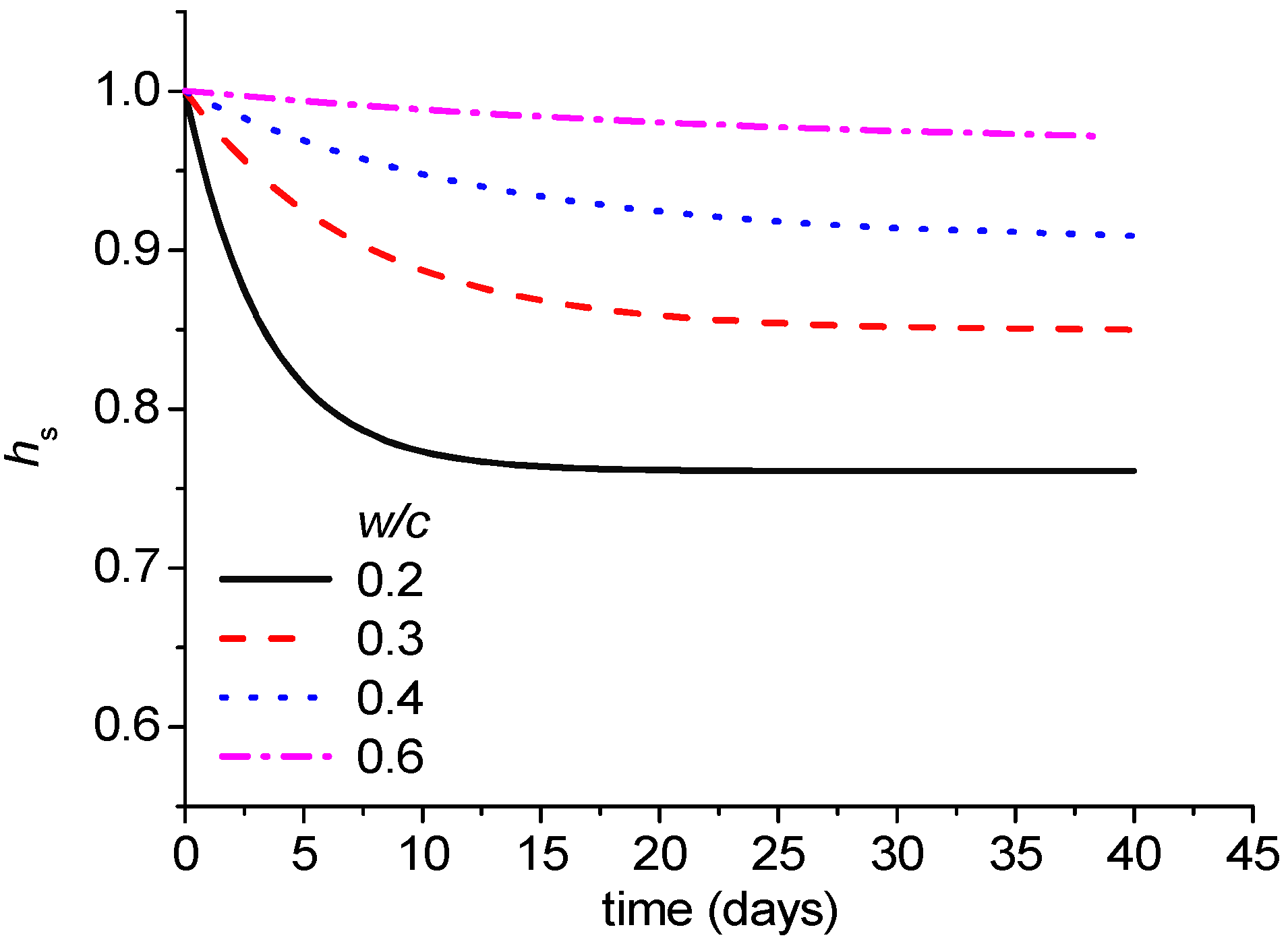
2.2. Diffusion
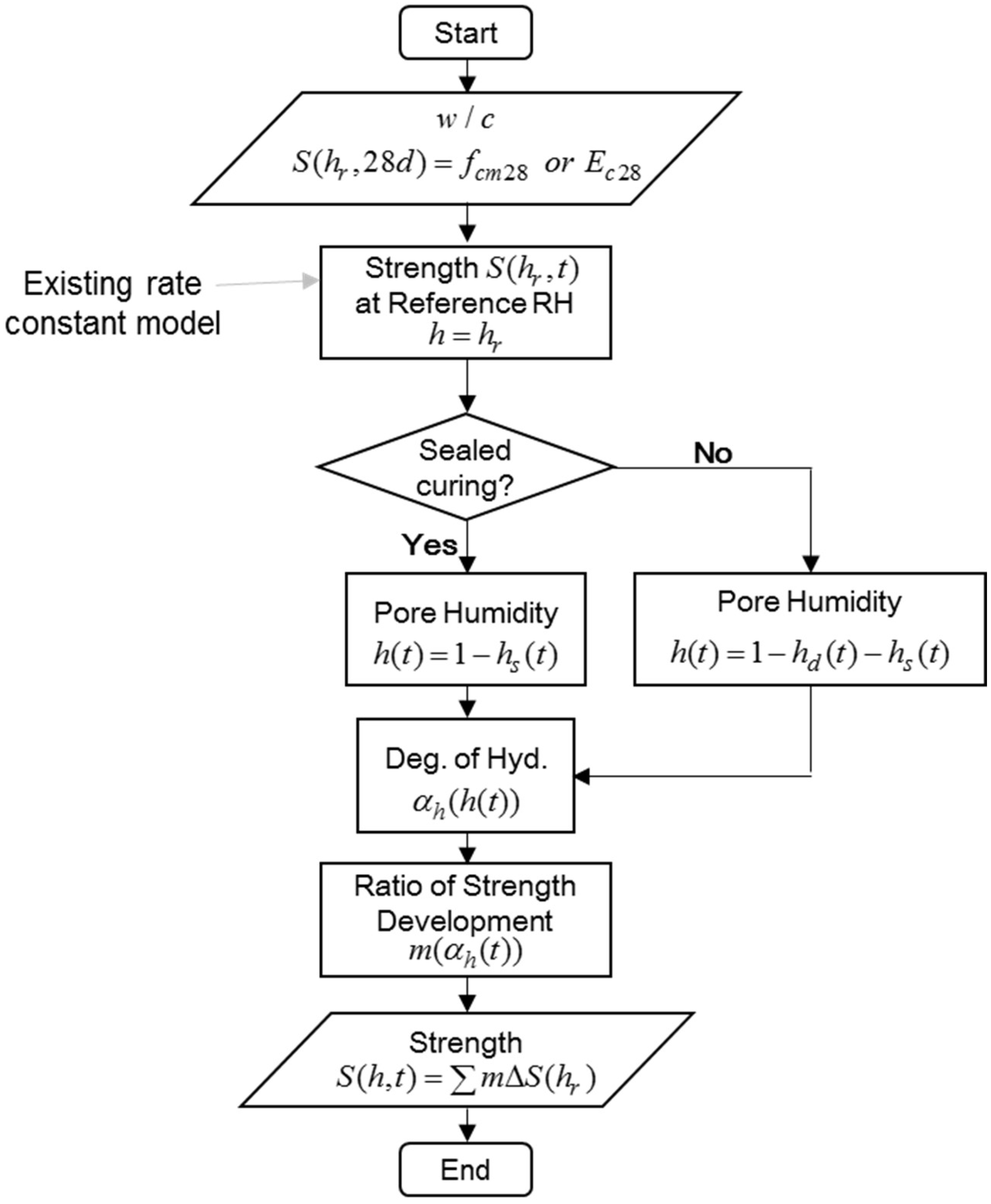
3. Prediction of Compressive Strength Considering Pore Humidity
3.1. Rate Constant Model with Apparent Activation Energy
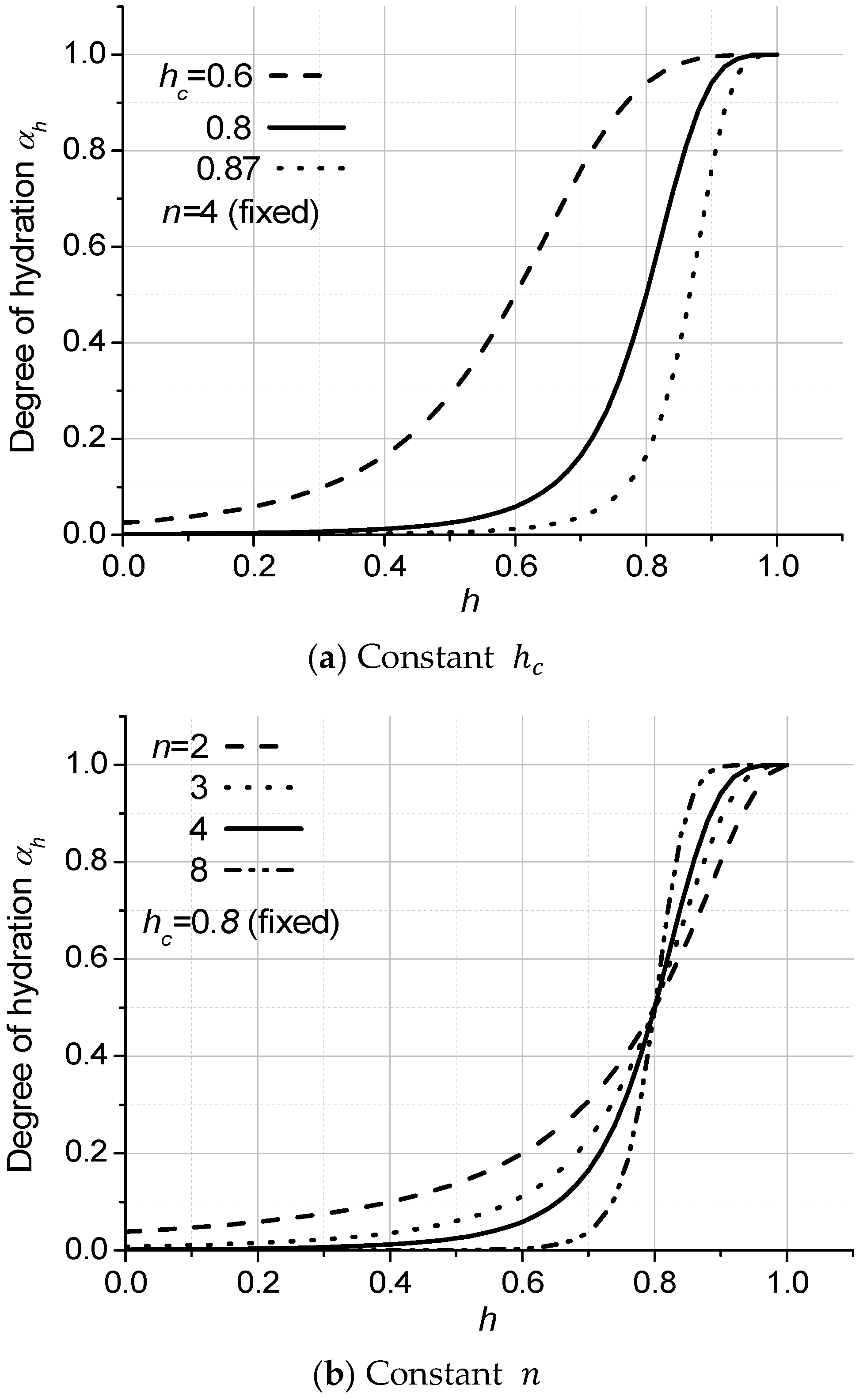
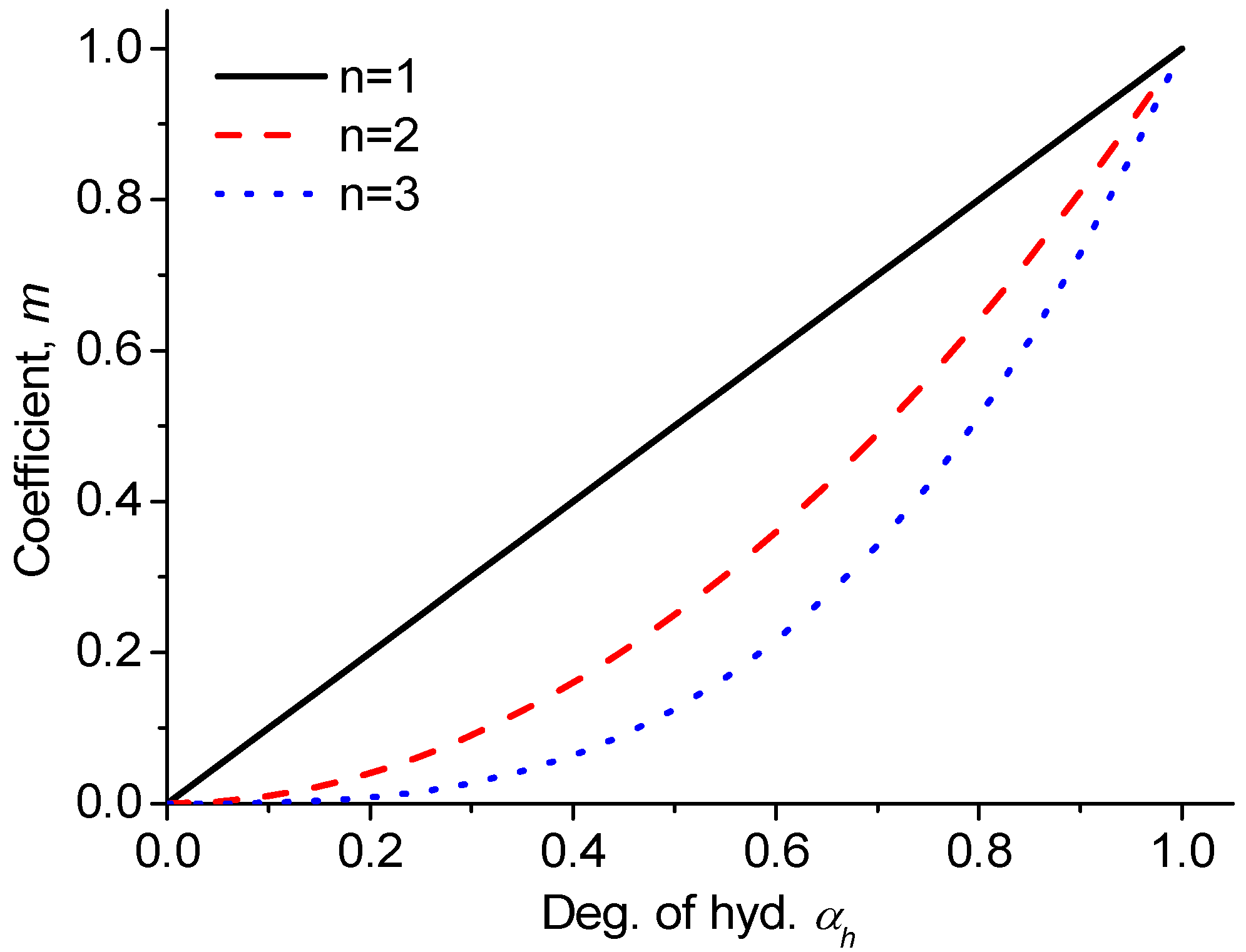
3.2. Degree of Hydration Depending on Pore Humidity
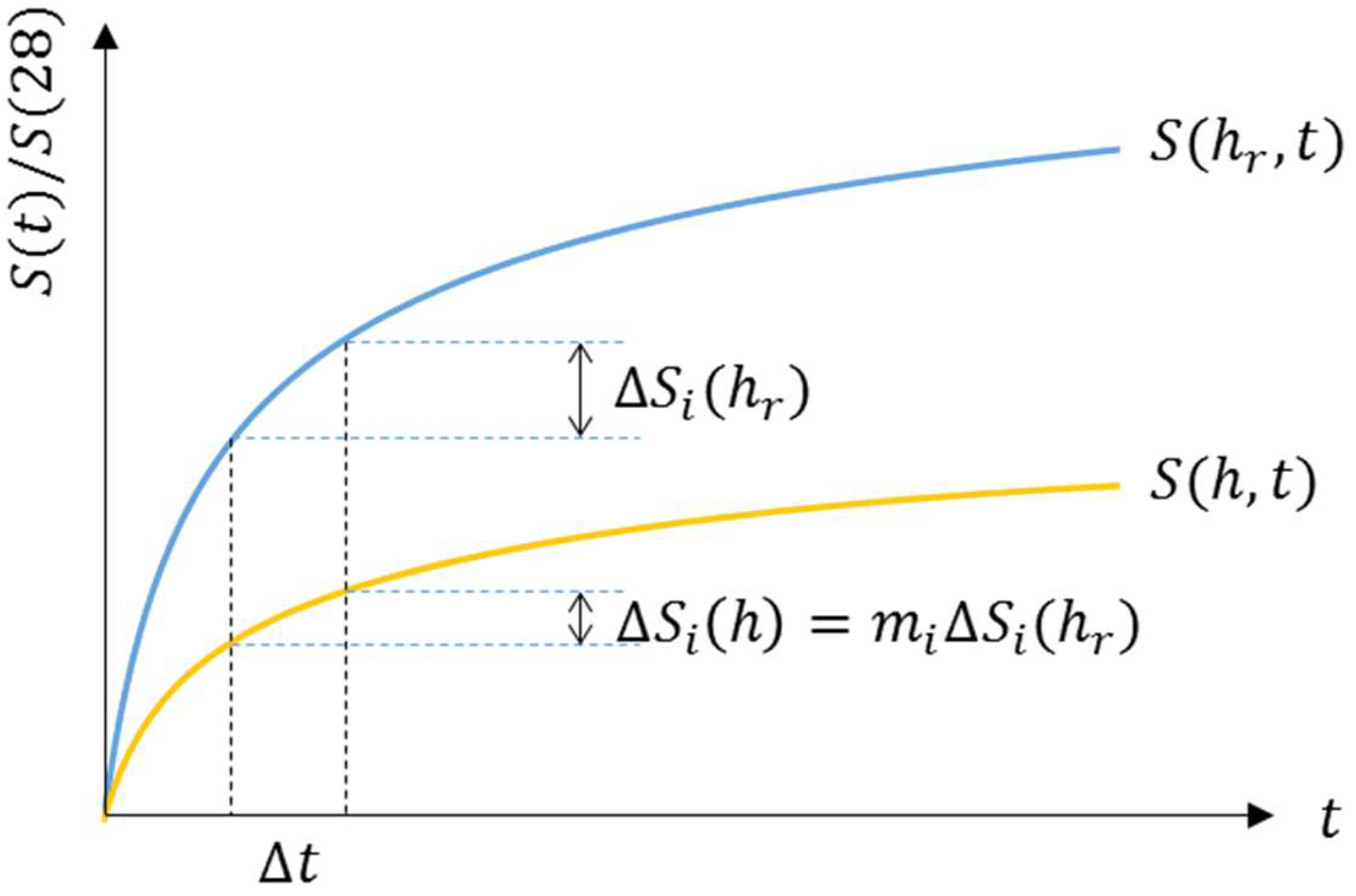
3.3. Relationship Between Compressive Strength and Degree of Hydration
3.4. Development of Prediction Method
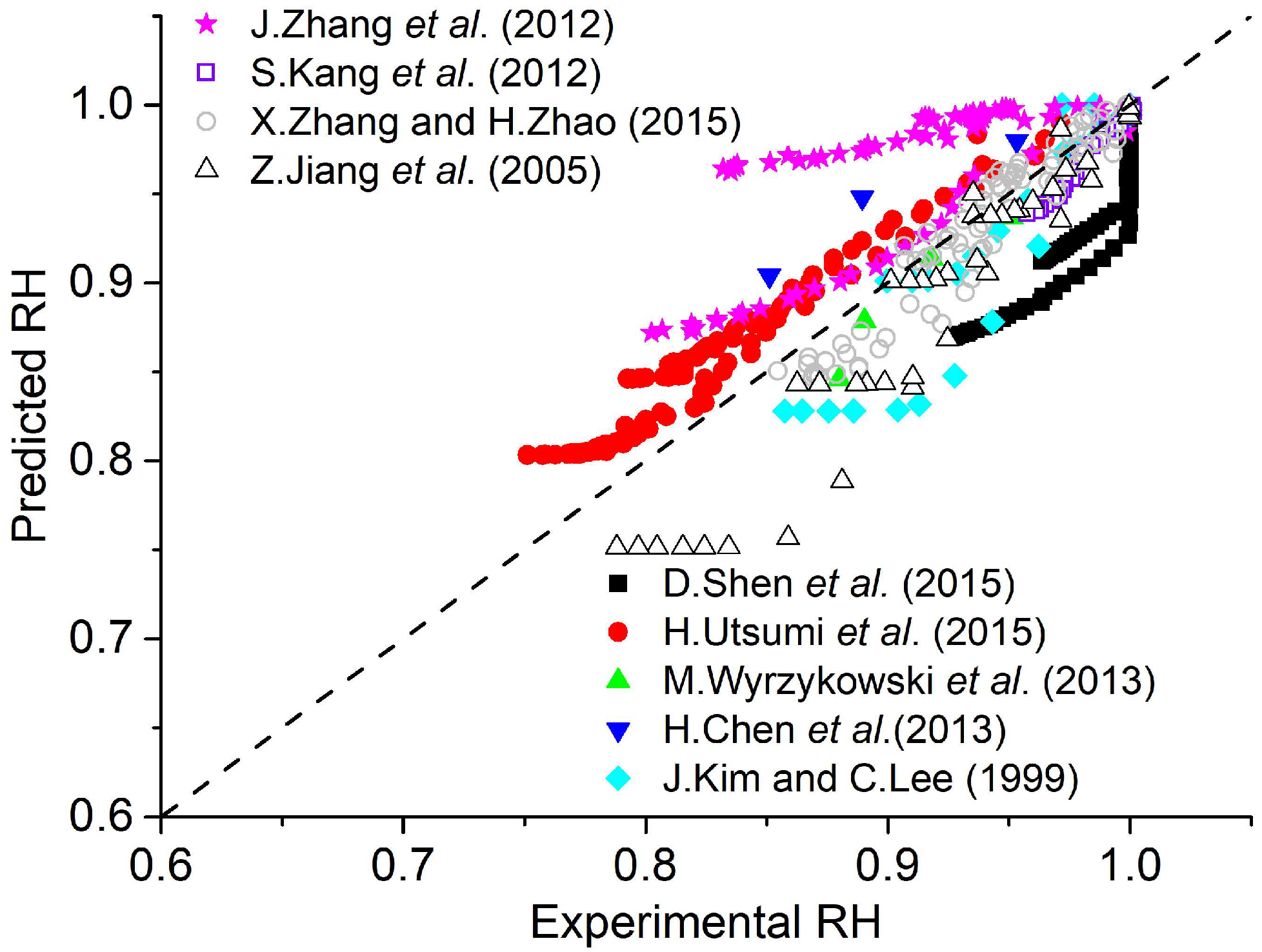
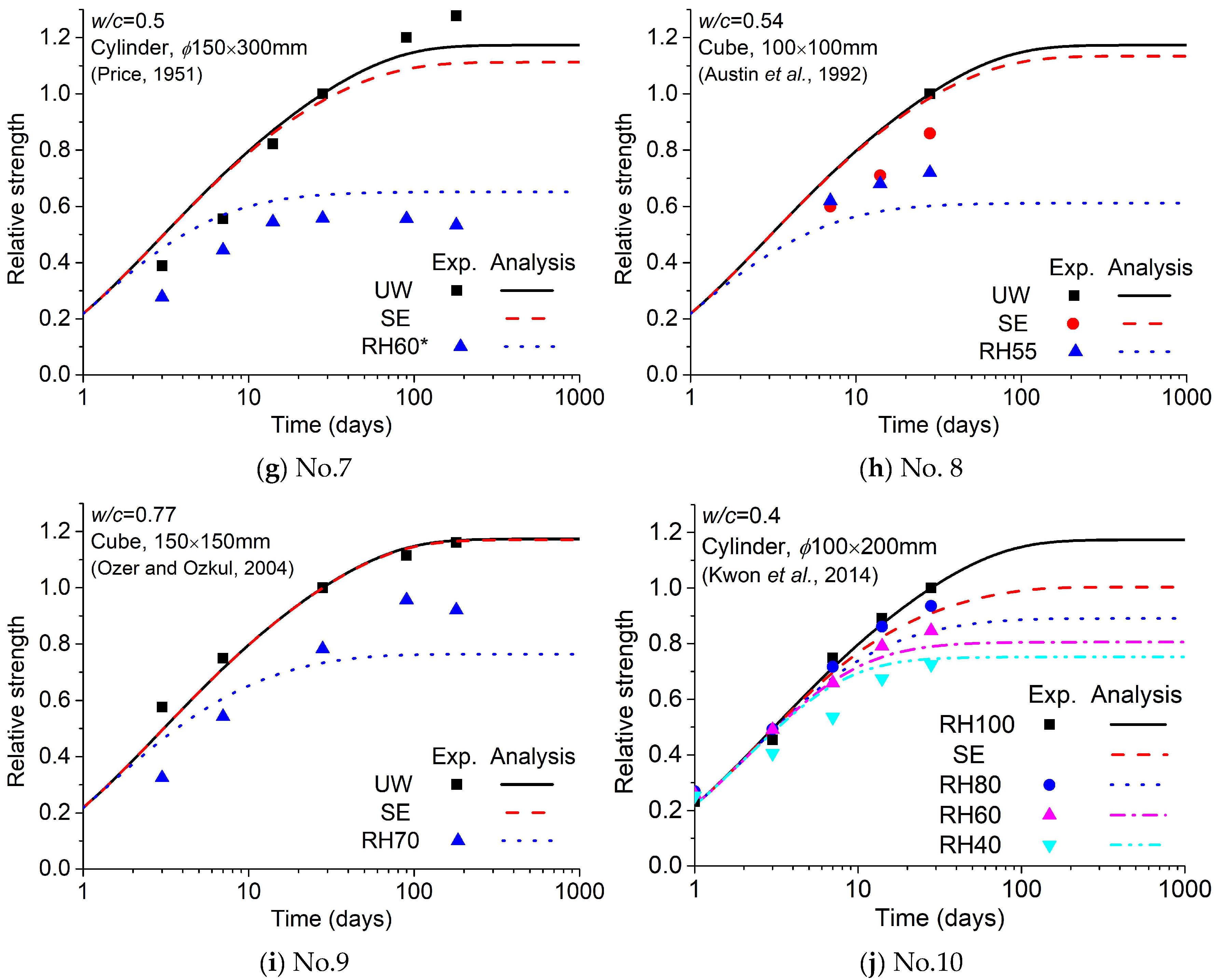
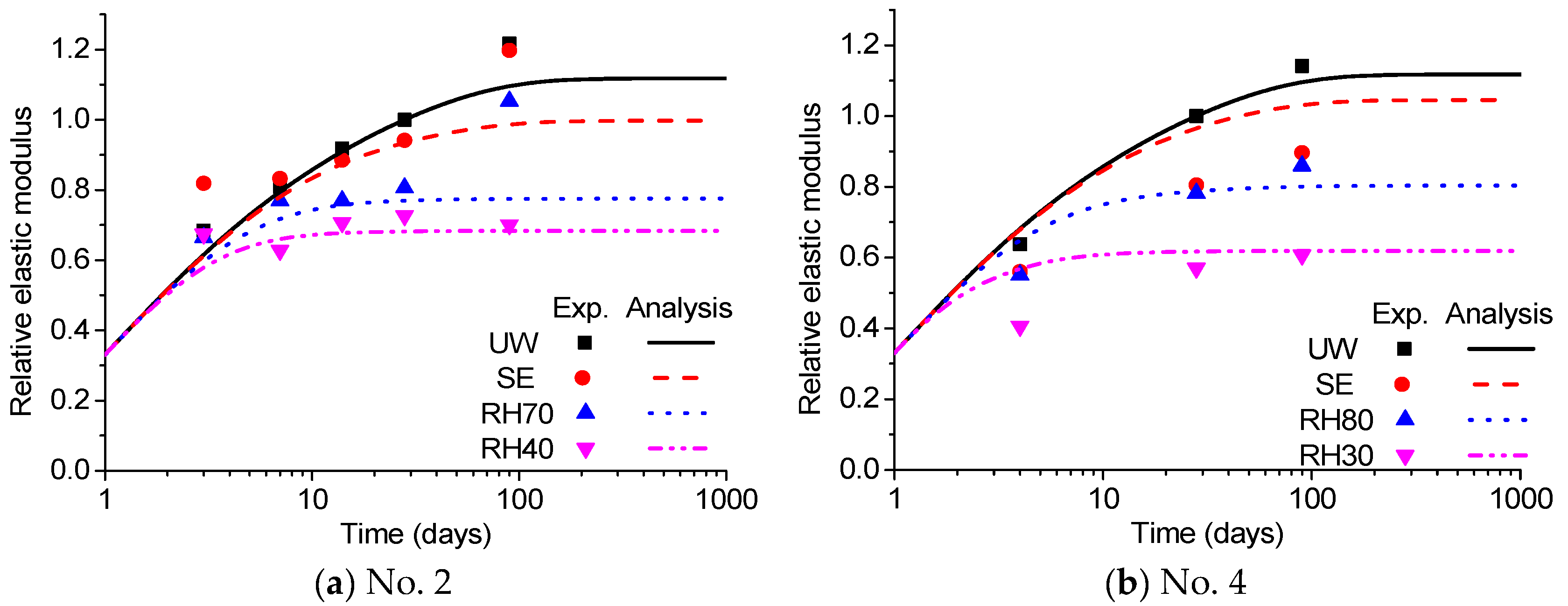
3.5. Verification of Prediction Method
4. Conclusions
- The degree of hydration and the development of mechanical properties change with pore relative humidity. The relationships of pore humidity with the degree of hydration and the development of mechanical properties are suggested and verified by the experimental results. The relationships show that the degree of hydration changes rapidly around 80% pore humidity, and the increase in mechanical properties at a given pore relative humidity is proportional to the cube of the degree of hydration compared to the increase under 100%% pore humidity.
- The proposed step-by-step analysis incorporates both the concrete properties and the corresponding humidity distribution at each stage. Since the prediction model for concrete properties is based on internal humidity distribution, it can be applied to assess concrete’s properties regardless of its shape or exposure conditions, as long as the humidity distribution is available through diffusion analysis. Therefore, the proposed model is applicable to various structural sections and geometries, even those with complex or nonstandard configurations.
- There are some assumptions for analyzing the humidity and properties of concrete in this study. In addition to comments about assumptions, some suggestions for further study are given below:
- The self-desiccation model is an important factor that affects the strength development of sealed concrete, but it currently has some uncertainties.
- The diffusion coefficient of concrete at an early age is one of the important factors that affect moisture diffusion and should be observed more thoroughly for various cases.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Persson, B. Moisture in concrete subjected to different kinds of curing. Mater. Struct. 1997, 30, 533–544. [Google Scholar] [CrossRef]
- Powers, T.C. A discussion of cement hydration in relation to the curing of concrete. Proc. Highw. Res. Board 1947, 27, 178. [Google Scholar]
- Paillere, A.M.; Buil, M.; Serrano, J.J. Effect of fiber addition on the autogenous shrinkage of silica fume concrete. ACI Mater. J. 1989, 86, 139–144. [Google Scholar]
- Xi, Y.; Bažant, Z.P.; Jennings, H. Moisture diffusion in cementitious materials: Adsorption isotherms. Adv. Cem. Based Mater. 1994, 1, 248–257. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Najjar, L.J. Nonlinear water diffusion in nonsaturated concrete. Mater. Struct. 1972, 5, 3–20. [Google Scholar] [CrossRef]
- Sakata, K. A study on moisture diffusion in drying and drying shrinkage of concrete. Cem. Concr. Res. 1983, 13, 216–224. [Google Scholar] [CrossRef]
- Akita, H.; Fujiwara, T.; Ozaka, Y. A practical procedure for the analysis of moisture transfer within concrete due to drying. Mag. Concr. Res. 1997, 49, 129–137. [Google Scholar] [CrossRef]
- Persson, B. Hydration and strength of high performance concrete. Adv. Cem. Based Mater. 1996, 3, 107–123. [Google Scholar] [CrossRef]
- Persson, B. Self-desiccation and chloride migration. In Proceedings of the Third International Research Seminar, Lund, Sweden, 14–15 June 2002. [Google Scholar]
- Persson, B. Self-desiccation and its importance in concrete technology. Mater. Struct. 1997, 30, 293–305. [Google Scholar] [CrossRef]
- Persson, B.; Fagerlund, G. Self-desiccation and its importance in concrete technology. In Proceedings of the Third International Research Seminar, Lund, Sweden, 14–15 June 2002. [Google Scholar]
- Persson, B. Consequence of cement constituents, mix composition and curing conditions for self-desiccation in concrete. Mater. Struct. 2000, 33, 352–362. [Google Scholar] [CrossRef]
- Kim, J.K.; Lee, C.S. Moisture diffusion of concrete considering self-desiccation at early ages. Cem. Concr. Res. 1999, 29, 1921–1927. [Google Scholar] [CrossRef]
- Kim, J.K.; Lee, C.S. Moisture diffusion and self-desiccation of concrete at early ages. In Proceedings of the Korea Concrete Institute Spring Conference, Cheongju, Republic of Korea, 2 May 1998. [Google Scholar]
- Jiang, Z.; Sun, Z.; Wang, P. Autogenous relative humidity change and autogenous shrinkage of high-performance cement pastes. Cem. Concr. Res. 2005, 35, 1539–1545. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, G. Development of interior relative humidity due to self-desiccation in blended cementitious system. In Proceedings of the International RILEM Conference on Materials, Systems and Structures in Civil Engineering, Lyngby, Denmark, 15–29 August 2016. [Google Scholar]
- Zhang, X.; Zhao, H. Characterization of Moisture Diffusion in Cured Concrete Slabs at Early Ages. Adv. Mater. Sci. Eng. 2015, 2015, 154394. [Google Scholar] [CrossRef]
- Shen, D.; Wang, T.; Chen, Y.; Wang, M.; Jiang, G. Effect of internal curing with super absorbent polymers on the relative humidity of early-age concrete. Constr. Build. Mater. 2015, 99, 246–253. [Google Scholar] [CrossRef]
- Wyrzykowski, M.; Lura, P. Moisture dependence of thermal expansion in cement-based materials at early ages. Cem. Concr. Res. 2013, 53, 25–35. [Google Scholar] [CrossRef]
- Chen, H.; Wyrzykowski, M.; Scrivener, K.; Lura, P. Prediction of self-desiccation in low water-to-cement ratio pastes based on pore structure evolution. Cem. Concr. Res. 2013, 49, 38–47. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, D.; Han, Y. Micromechanical modeling on autogenous and drying shrinkages of concrete. Constr. Build. Mater. 2012, 29, 230–240. [Google Scholar] [CrossRef]
- Kang, S.-T.; Kim, J.-S.; Lee, Y.; Park, Y.-D.; Kim, J.-K. Moisture diffusivity of early age concrete considering temperature and porosity. KSCE J. Civ. Eng. 2012, 16, 179–188. [Google Scholar] [CrossRef]
- Utsumi, H.; Misaka, T.; Moteki, W. Prediction Model of Internal Relative Humidity During Self-desiccation in Hardened Cement Pastes. Concr. Res. Technol. 2015, 26, 11–19. [Google Scholar] [CrossRef][Green Version]
- Pihlajavaara, S.E.; Vaisanen, M. Numerical Solution of Diffusion Equation with Diffusivitg Concentration Dependent; State Institute for Technical Research: Helsinki, Finland, 1965. [Google Scholar]
- Federation Internationale du Beton (FIB). FIB Model Code for Concrete Structures 2010; Ernst&Sohn: Berlin, Germany, 2013. [Google Scholar]
- Bažant, Z.P. Mathematical models for creep and shrinkage of concrete. In Creep and Shrinkage in Concrete Structures; John Wiley&Sons: Hoboken, NJ, USA, 1982; pp. 163–256. [Google Scholar]
- Bažant, Z.P.; Chern, J.C. Concrete creep at variable humidity: Constitutive law and mechanism. Mater. Struct. 1985, 18, 1–20. [Google Scholar] [CrossRef]
- Zhang, J.; Hou, D.; Gao, Y.; Wei, S. Determination of Moisture Diffusion Coefficient of Concrete at Early Age from Interior Humidity Measurements. Dry. Technol. Int. J. 2011, 29, 689–696. [Google Scholar] [CrossRef]
- Sun, B.; Noguchi, T.; Cai, G.; Chen, Q. Prediction of early compressive strength of mortars at different curing temperature and relative humidity by a modified maturity method. Struct. Concr. 2021, 22, E732–E744. [Google Scholar] [CrossRef]
- Sun, B.; Noguchi, T.; Cai, G.; Zhao, W. Effect of temperature and relative humidity on the development of the compressive strength of surface-layer cement mortar. Constr. Build. Mater. 2021, 281, 122626. [Google Scholar] [CrossRef]
- Samouh, H.; Roziere, E.; Loukili, A. Experimental and numerical study of the relative humidity effect on drying shrinkage and cracking of self-consolidating concrete. Cem. Concr. Res. 2019, 115, 519–529. [Google Scholar] [CrossRef]
- Shafaie, V.; Ghodousian, O.; Ghodousian, A.; Homayounfar, M.; Rad, M.M. Slant shear tests and fuzzy logic integration for evaluating shear bond strength in SCC and FRSCC repair applications. Case Stud. Constr. Mater. 2025, 22, e04176. [Google Scholar] [CrossRef]
- Kwon, S.H.; Jang, K.P.; Bang, J.-W.; Kim, Y.Y. Prediction of concrete compressive strength considering humidityand temperature in the construction of nuclear power plants. Nucl. Eng. Des. 2014, 27, 23–29. [Google Scholar] [CrossRef]
- Tank, R.C.; Carino, N.J. Rate Constant Functions for Strength Development of Concrete. ACI Mater. J. 1991, 88, 74–83. [Google Scholar]
- Bernhardt, J. Hardening of Concrete at Different Temperatures. In Proceedings of the RILEM Symposium on Winter Concreting, Copenhagen, Danish, 1 February 1956. [Google Scholar]
- Han, S.H. Effect of Temperature and Aging on the Mechanical Properties of Concrete; Korea Advanced Institute of Science and Technology: Daejeon, Republic of Korea, 2001. [Google Scholar]
- Kjellsen, K.O.; Detwiler, R.J. Later Age Strength Prediction by a Modified Maturity Method. ACI Mater. J. 1993, 90, 220–227. [Google Scholar]
- Chanvillard, G.; D’Aloia, L. Concrete Strength Estimation at Early Ages: Modification of the Method of Equivalent Age. ACI Mater. J. 1996, 94, 520–530. [Google Scholar]
- Jonasson, J. Early Strength Growth in Concrete-Preliminary Test Results Concerning Hardening at Elevated Temperature. In Proceedings of the RILEM Symposium on Winter Concreting, Espoo, Finland, 25–27 November 1985. [Google Scholar]
- Moon, Y.H. Prediction of Concrete Strength with Different Curing Temperature and Time; Korea Advanced Institute of Science and Technology: Daejeon, Republic of Korea, 1998. [Google Scholar]
- Kim, J.K.; Moon, Y.H.; Eo, S.H. Compressive Strength Development of Concrete with Different Curing Time and Temperature. Cem. Concr. Res. 1998, 28, 1761–1773. [Google Scholar] [CrossRef]
- Klieger, P. Effect of Mixing and Curing Temperature on Concrete Strength. ACI J. Proc. 1958, 54, 1063–1081. [Google Scholar]
- Brooks, J.J.; Al-Kaisi, A.F. Early Strength Development of Portland and Slag Cement Concretes Cured at Elevated Temperatures. ACI Mater. J. 1990, 87, 503–506. [Google Scholar]
- Park, J.M. Prediction of Adiabatic Temperature Rise and Compressive Strength of Concrete; Korea Advanced Institute of Science and Technology: Daejeon, Republic of Korea, 2014. [Google Scholar]
- Kim, Y.H. Material Properties of Concrete Cured Under Different Relative Humidities; Korea Advanced Institute of Science and Technology: Daejeon, Republic of Korea, 2013. [Google Scholar]
- Kwon, K. The Effect of the Humidity on Axial Compressive Strength of Concrete Column Section with Different Sizes; Korea Advanced Institute of Science and Technology: Daejeon, Republic of Korea, 2015. [Google Scholar]
- Kim, J.Y. Long-Term Behavior of Concrete Cured in Various Conditions; Korea Advanced Institute of Science and Technology: Daejeon, Republic of Korea, 2015. [Google Scholar]
- Bonavetti, V.; Donza, H.; Rahhal, V.; Irassar, E. Influence of initial curing on the properties of concrete containing limestone blended cement. Cem. Concr. Res. 2000, 30, 703–708. [Google Scholar] [CrossRef]
- Price, W.H. Factors influencing concrete strength. ACI J. 1951, 47, 417–432. [Google Scholar] [CrossRef]
- Austin, S.A.; Robins, P.J.; Issaad, A. Influence of curing methods on the strength and permeability of GGBFS concrete in a simulated arid climate. Cem. Concr. Compos. 1992, 14, 157–167. [Google Scholar] [CrossRef]
- Ozer, B.; Ozkul, M.H. The influence of initial water curing on the strength development of ordinary portland and pozzolanic cement concretes. Cem. Concr. Res. 2004, 34, 13–18. [Google Scholar] [CrossRef]
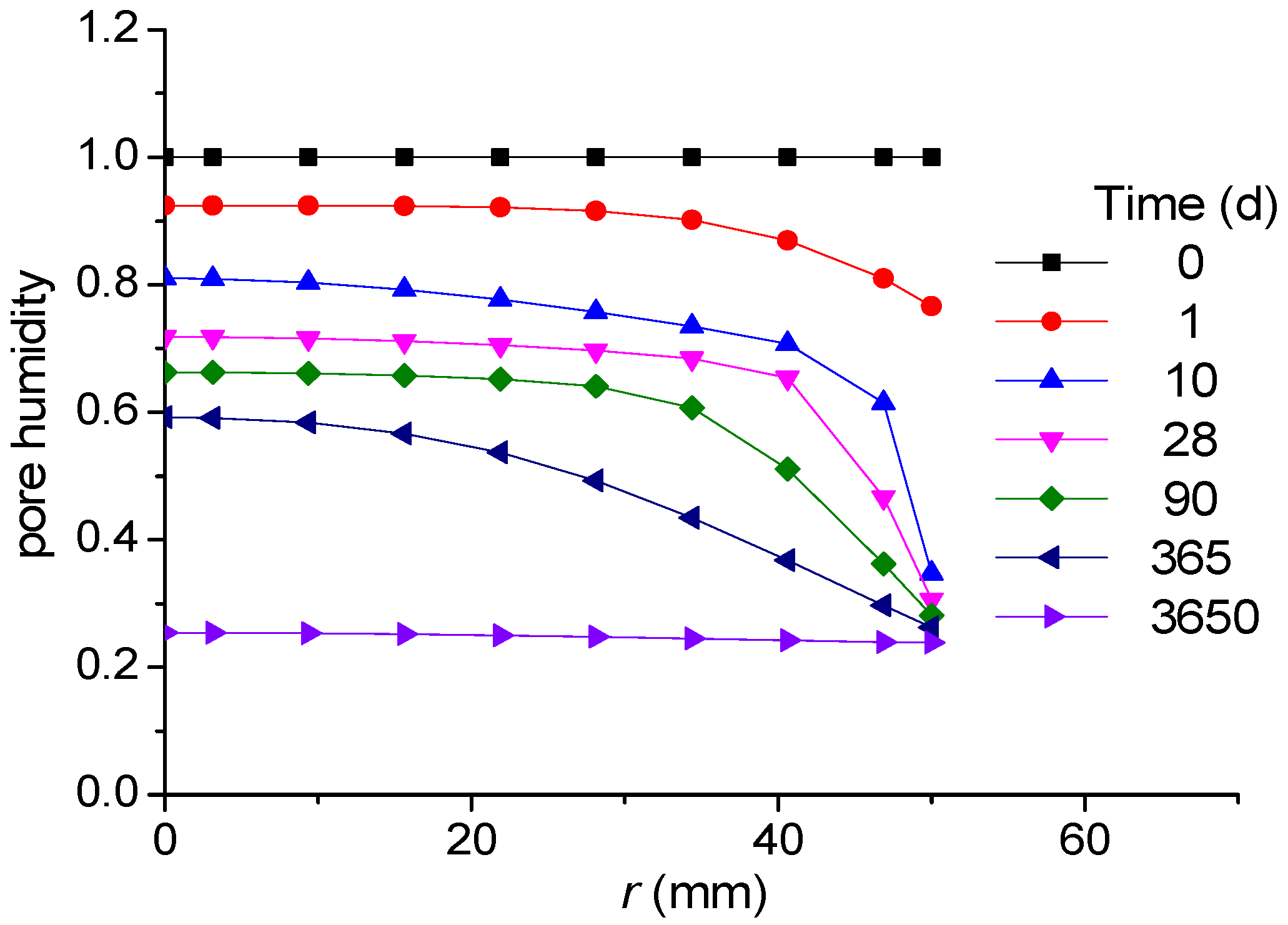
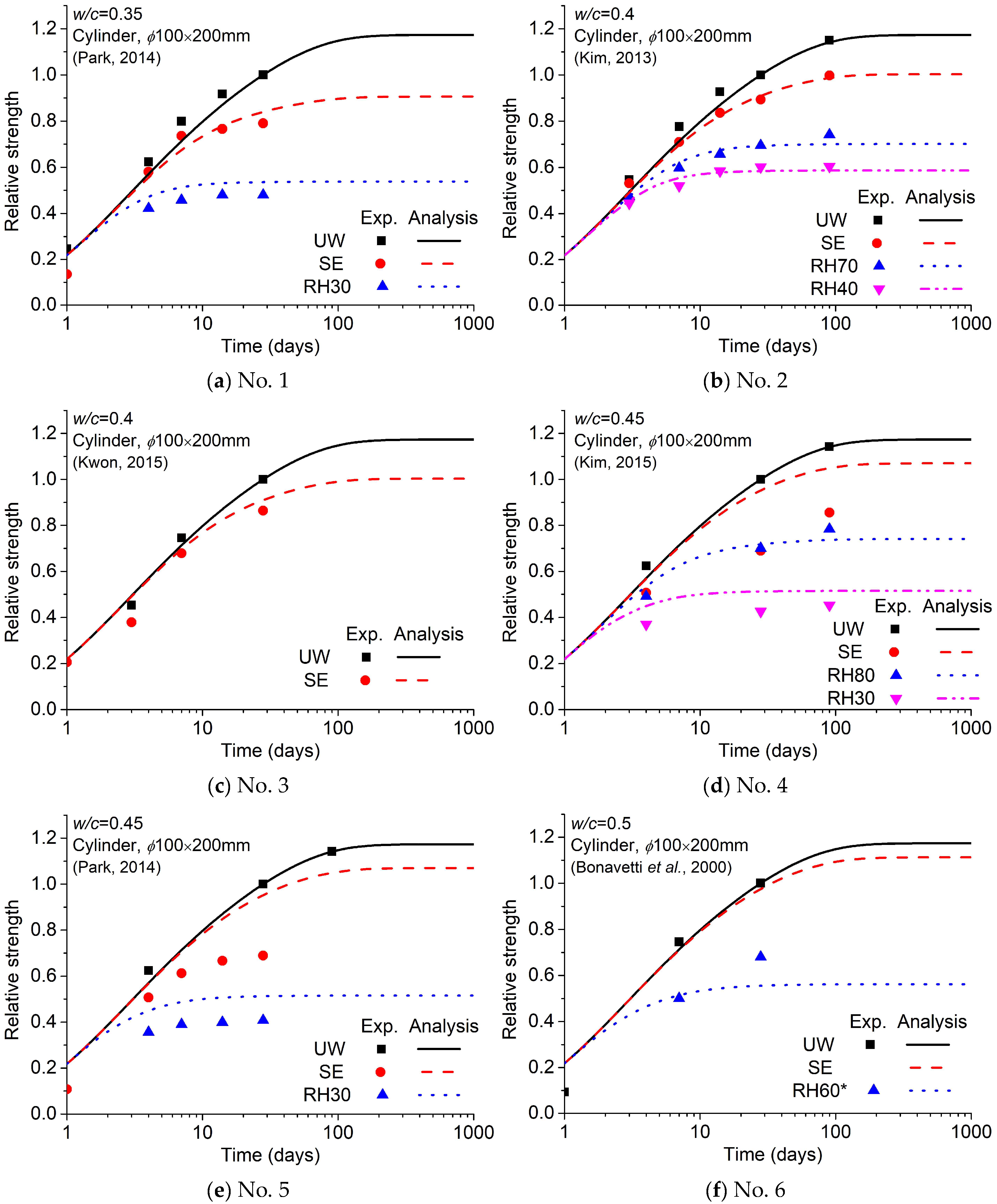

| Variable | Value | |
|---|---|---|
| Diffusion coefficient | 15 | |
| 0.05 | ||
| 0.8 | ||
| Degree of hydration | 2 | |
| 0.8 | ||
| Coefficient, | 3 | |
| No. | Type/Size of Specimen | Ambient Humidity | Ref. | |||
|---|---|---|---|---|---|---|
| 1 | 0.35 | 7.3 | 0.5 | Cylinder/100 | 30% | Park (2014) [44] |
| 2 | 0.4 | 9.7 | 0.5 | Cylinder/100 | 40%, 70% | Kim (2013) [45] |
| 3 | 0.4 | 9.7 | 1.0 | Cylinder/100 | Kwon (2015) [46] | |
| 4 | 0.45 | 9.9 | 1.2 | Cylinder/100 | 30%, 80% | Kim (2015) [47] |
| 5 | 0.45 | 9.9 | 1.2 | Cylinder/100 | 30% | Park (2014) [44] |
| 6 | 0.5 | 9.0 | 2.3 | Cylinder/100 | Air condition * | Bonavetti et al. (2000) [48] |
| 7 | 0.5 | 8.4 | 2.3 | Cylinder/150 | Air condition * | Price (1951) [49] |
| 8 | 0.54 | 7.1 | 3.2 | Cube/100 | 55% | Austin et al. (1992) [50] |
| 9 | 0.77 | 10 | 3.2 | Cube/150 | 70% | Ozer and Ozkul (2004) [51] |
| 10 | 0.4 | 7.7 | 0.1 | Cylinder/100 | 40%, 60%, 80% | Kwon et al. (2014) [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, G. Prediction of Compressive Strength of Concrete Considering Pore Relative Humidity. Materials 2025, 18, 2859. https://doi.org/10.3390/ma18122859
An G. Prediction of Compressive Strength of Concrete Considering Pore Relative Humidity. Materials. 2025; 18(12):2859. https://doi.org/10.3390/ma18122859
Chicago/Turabian StyleAn, Gyeonghee. 2025. "Prediction of Compressive Strength of Concrete Considering Pore Relative Humidity" Materials 18, no. 12: 2859. https://doi.org/10.3390/ma18122859
APA StyleAn, G. (2025). Prediction of Compressive Strength of Concrete Considering Pore Relative Humidity. Materials, 18(12), 2859. https://doi.org/10.3390/ma18122859