Selecting the Optimal Calculation Method and Chemical Reagents in Surface Energy Tests of Asphalt Materials
Abstract
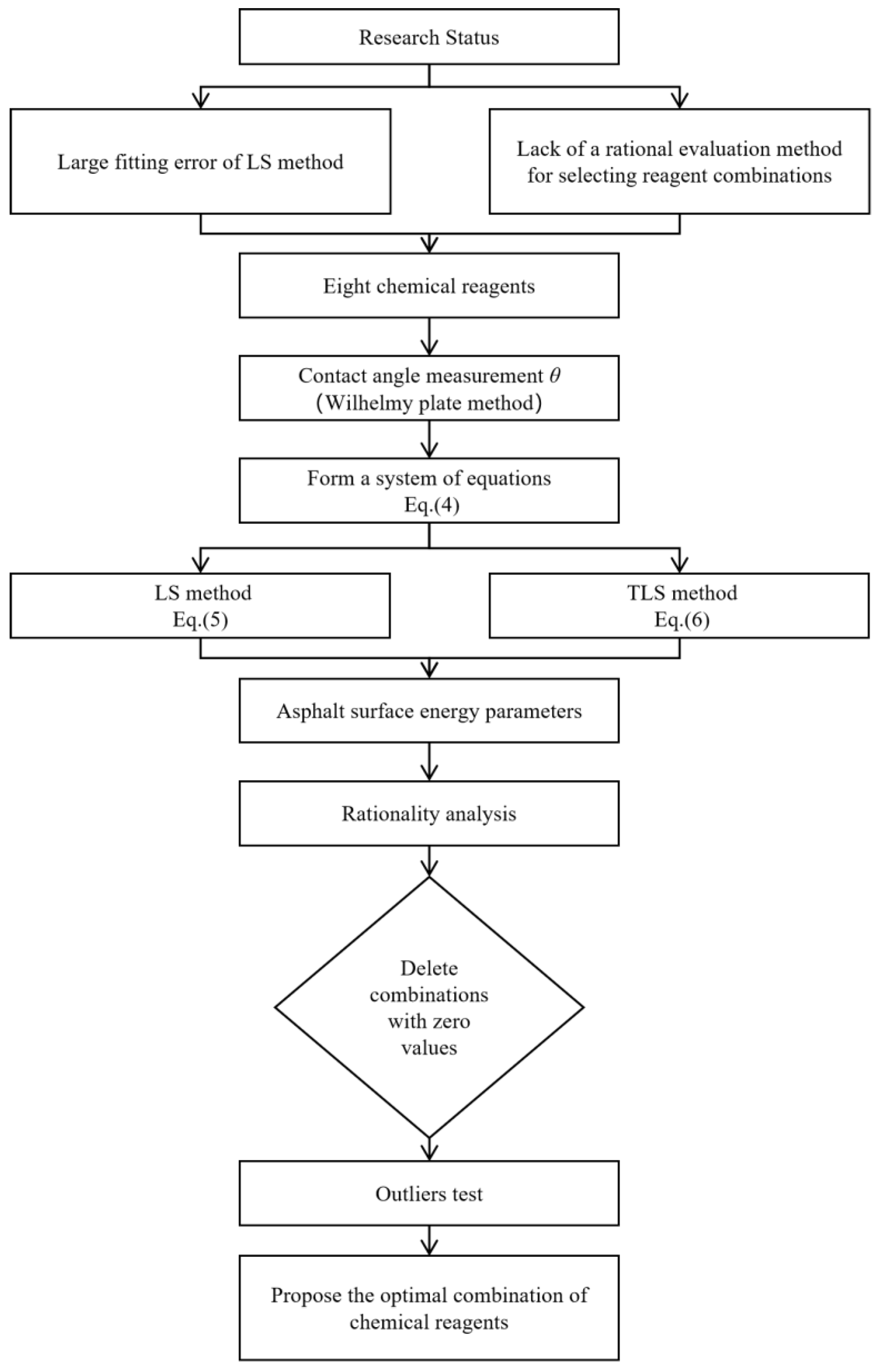
1. Introduction
- (1)
- When the LS method is used to solve asphalt surface energy parameters, the optimal fitting method is not used, which causes a large fitting error between the calculated and real values of asphalt surface energy parameters;
- (2)
- There is a lack of a reasonable and effective evaluation method for selecting different reagent combinations.
2. Contact Angle Test
2.1. Reagent Selection
- The chemical reagent is a single, homogeneous, and pure liquid reagent and does not dissolve or react with asphalt material.
- In order to solve asphalt surface energy parameters using simultaneous equations, the surface energy parameters of chemical reagents must be known;
- Chemical reagent droplets can form a stable contact angle on the surface of asphalt film slides; that is, the total surface energy of the chemical reagent is greater than that of asphalt material.
- Highly polar reagents (such as water and formamide): They dominate the polar interactions and sensitively reflect the polar components ( and ) of asphalt.
- Moderately polar reagents (such as ethylene glycol and glycerol): They balance the polar and nonpolar interactions and are used to adjust the condition number of the equation set.
- Weakly polar/nonpolar reagents (such as diiodomethane and n-octanol): They mainly contribute nonpolar dispersion forces and constrain the component of asphalt.
2.2. Asphalt Preparation
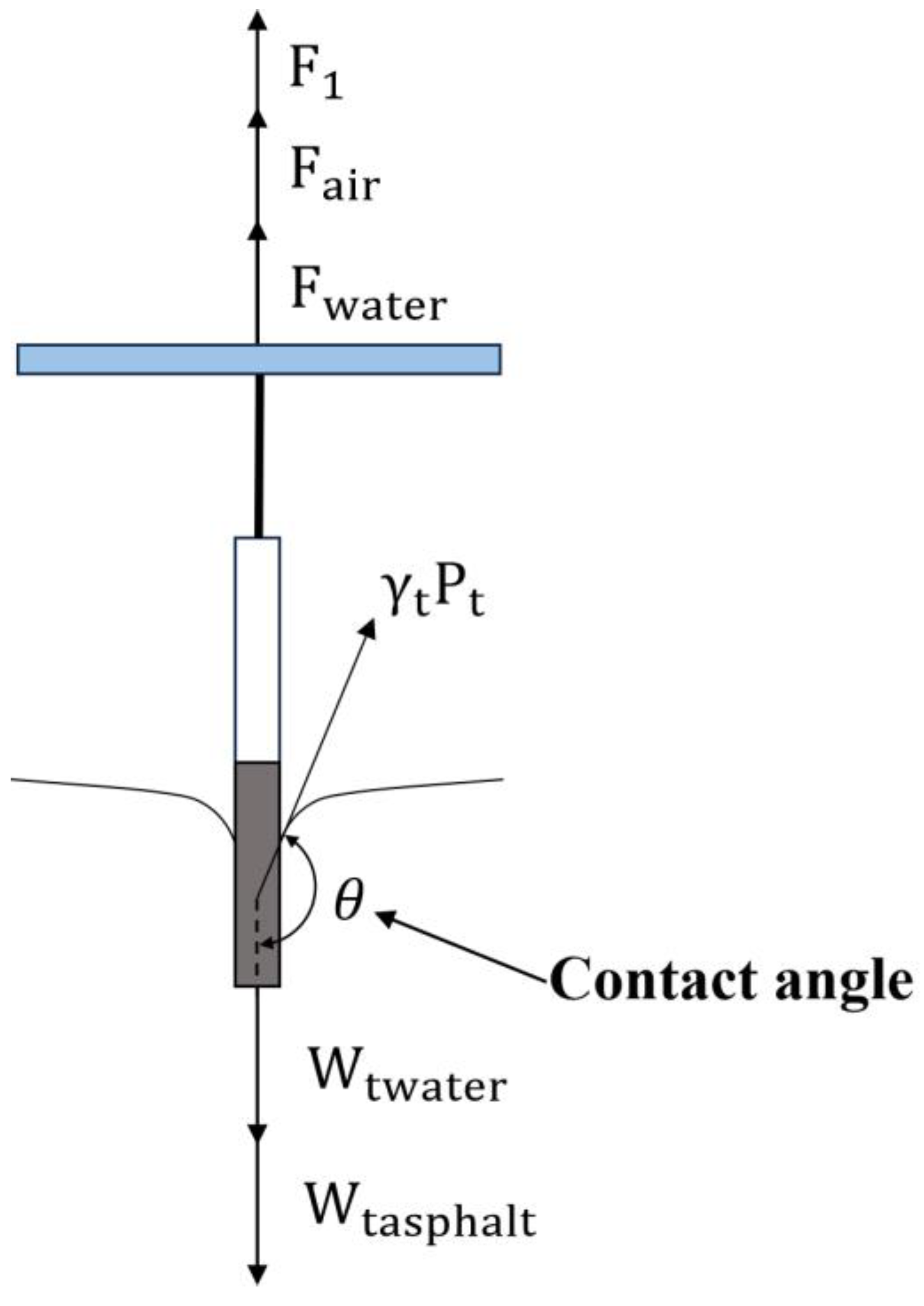
2.3. Measurement Method
3. Calculation of Asphalt Surface Energy Parameters
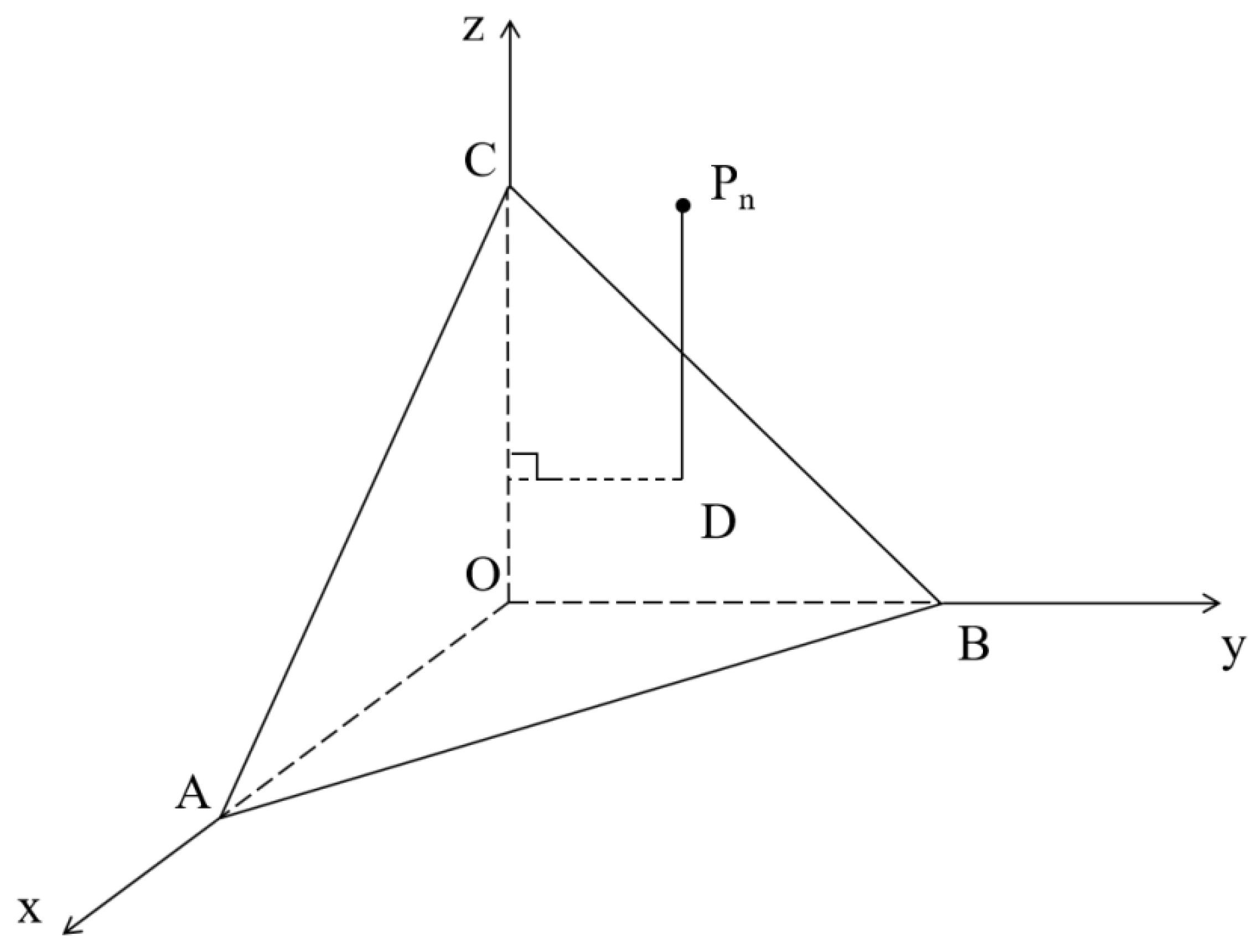
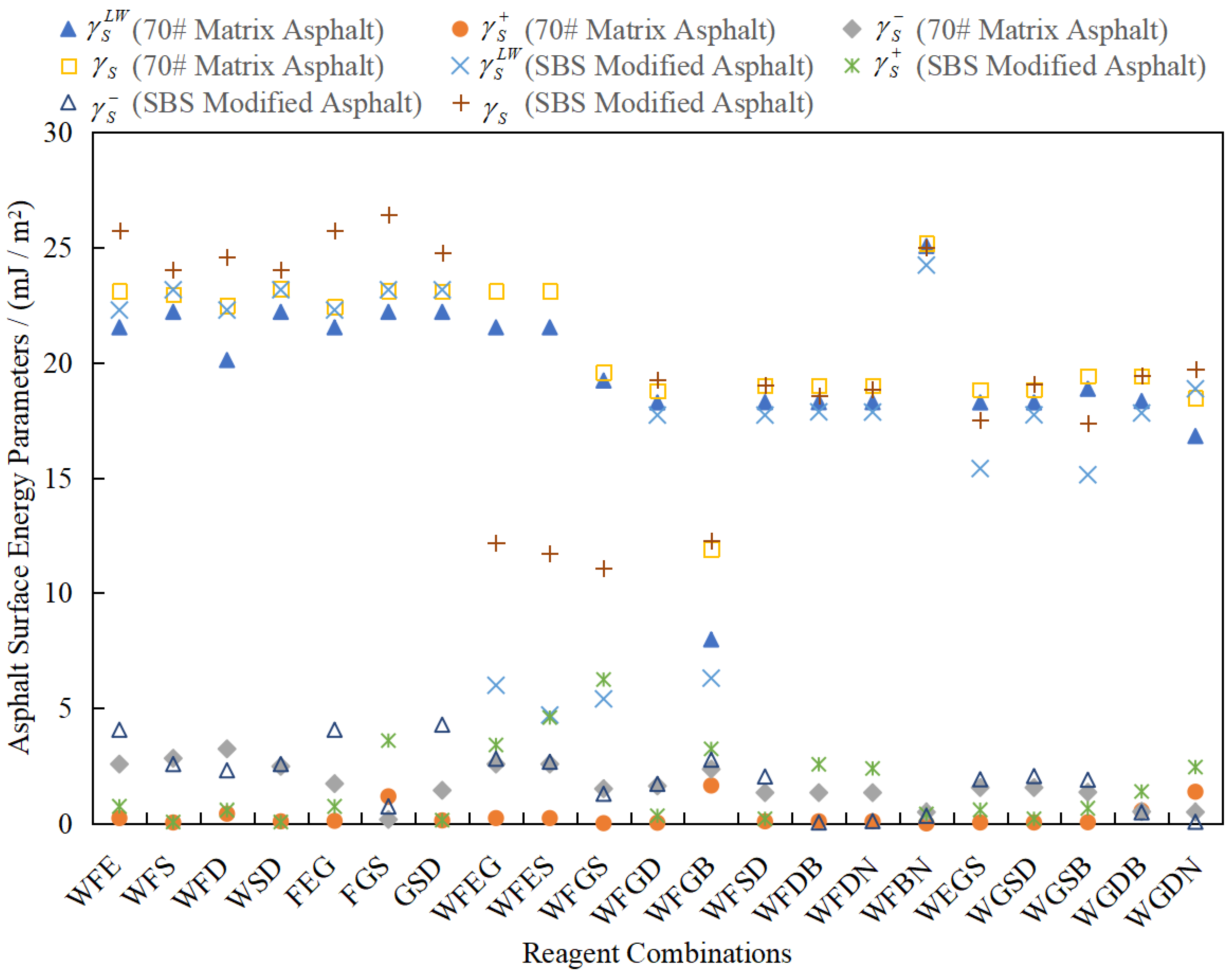
3.1. Calculation Principle of Asphalt Surface Energy Parameters
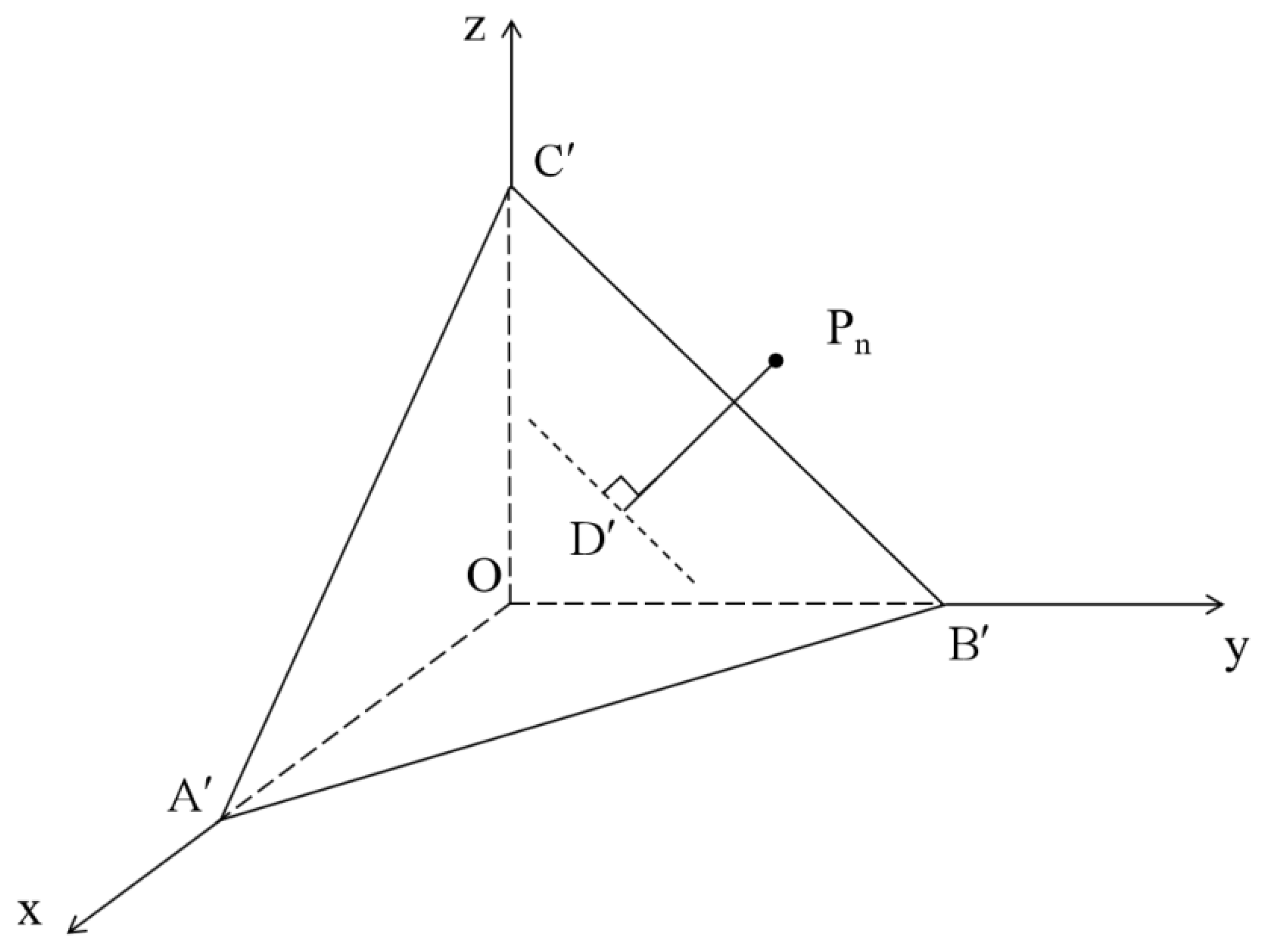
3.2. Calculation of Asphalt Surface Energy Parameters Using TLS
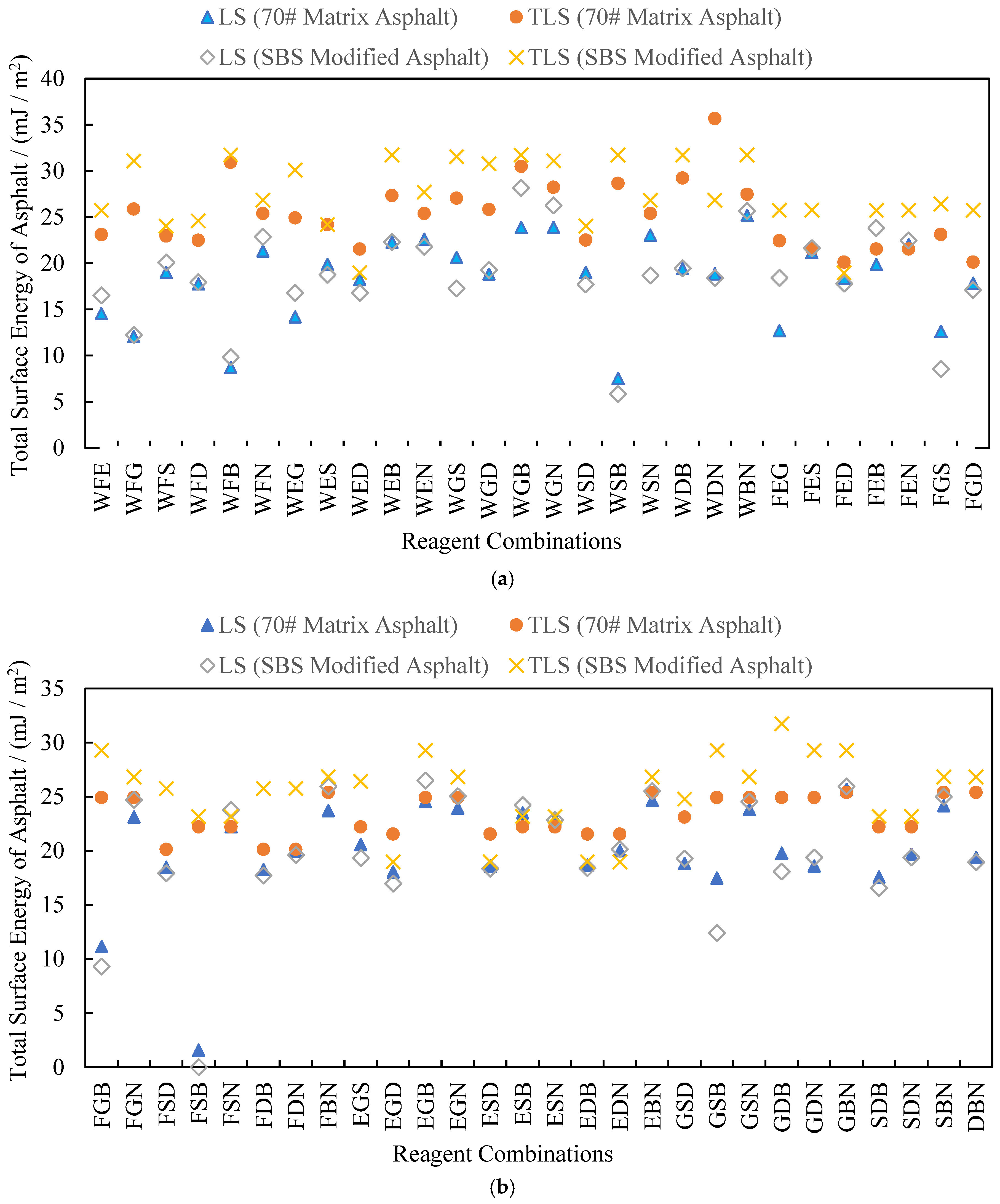
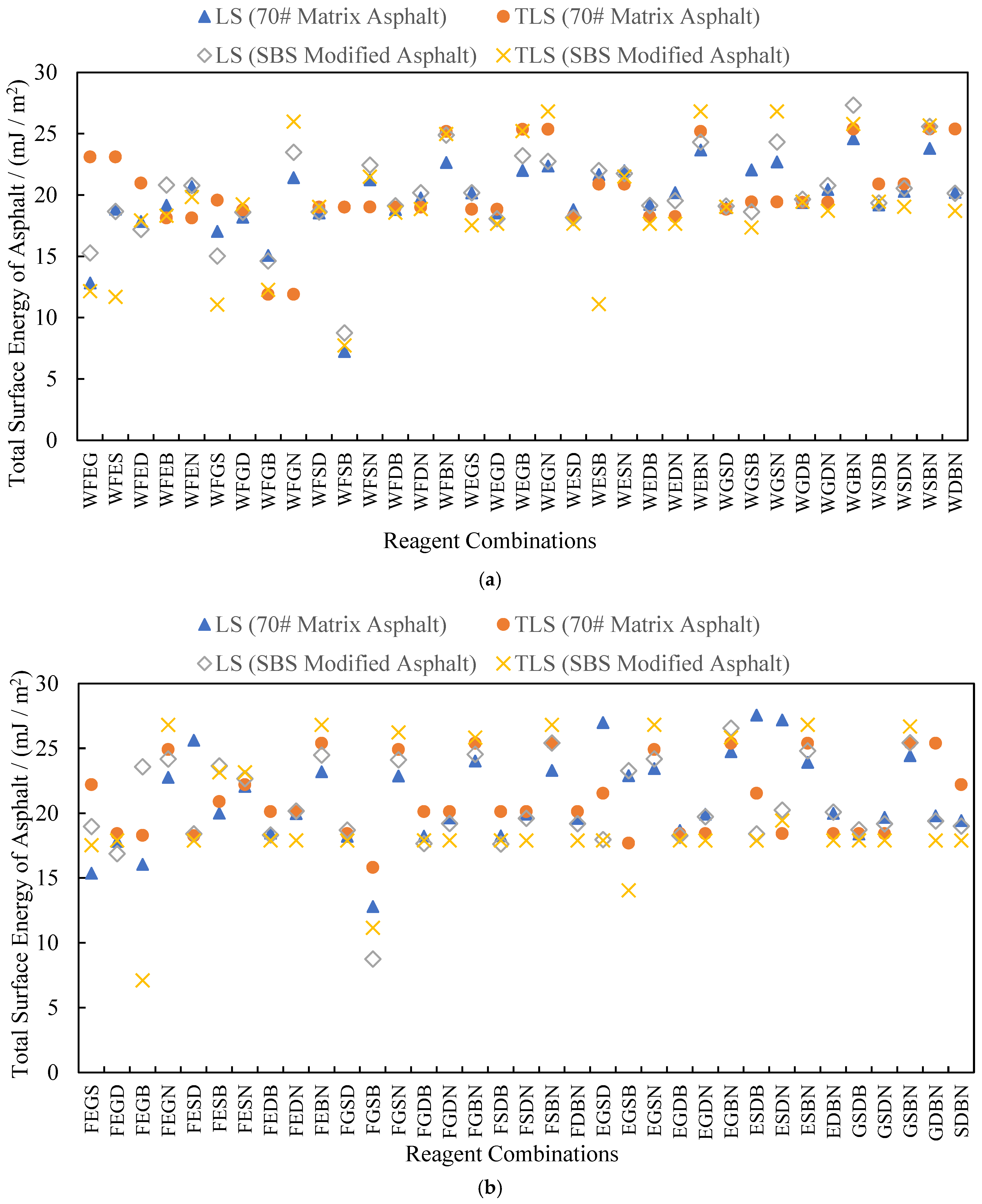
3.3. Analysis of Test Results
4. Optimization of Reagent Combinations
4.1. Rationality Analysis of Calculated Results
4.2. Testing for Outliers in the Calculated Results
4.3. Analysis of Results
- (1)
- Based on three basic principles, eight chemical reagents with known surface energy parameters were preliminarily selected: W, F, E, G, S, D, B, and N. Then, 126 reagent combinations were formed randomly.
- (2)
- After the contact angles were measured using the Wilhelmy plate method and the asphalt surface energy parameters were determined using TLS, the rationality of the calculated results for all reagent combinations was analyzed, and those that were obviously unreasonable were eliminated. Finally, 21 reagent combinations that met the requirements were identified.
- (3)
- Through the leap degree test, the reagent combination scheme with the fewest outliers was selected from the 21 reagent combinations so as to achieve the research purpose of this study.
5. Conclusions
- (1)
- Compared to the LS method, the TLS method is more suitable for solving the linear equations established using the Young–Dupre equation. The TLS approach reduces the fitting error between the calculated and real values of asphalt surface energy parameters and improves the accuracy and stability of the calculated results. The coefficients of variation of the total surface energy of the 70# matrix asphalt and SBS-modified asphalt calculated using TLS are 15.92% and 24.65%, respectively, which are 21.65% and 6.45% reductions compared to those obtained with the LS method. The LS method only minimizes the single-axis (Z-axis) error, while the TLS method minimizes the full-dimensional vertical error, especially in ill-conditioned equations (for example, the change rate of the calculated values for the FSB combination is reduced from 23,060% to an acceptable range).
- (2)
- In this study, the number of outliers in the calculated results was determined by analyzing the rationality of the calculated results and using the leap degree test method. Finally, among 126 reagent combinations, the optimal reagent combination scheme was determined to be WFSD; there were no outliers in the calculated results of asphalt surface energy parameters, which were closer to the real values. For the 70# matrix asphalt and SBS-modified asphalt, compared to the most commonly used reagent combination, WFEG, the error rate of the reagent combination WFSD in calculating the total surface energy of asphalt was reduced by 17.71% and 64.80%, respectively.
- (3)
- The leap degree test method can quickly and accurately determine the reagent combination with the fewest outliers, and the selected resolution is more reasonable and reliable. Therefore, it can be used to select the optimal reagent combination. These research results can provide an experimental basis for the accurate calculation of asphalt surface energy parameters and assist in accurately analyzing the performance of adhesion between asphalt and aggregate. Thus, surface energy tests for more kinds of asphalt, asphalt binders, and aggregates will be conducted in the future, and the optimal reagent combination scheme suitable for surface energy tests of different road materials will be explored based on classification.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Asphalt Type | Surface Energy Parameter | Leap Degree | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 70# Matrix Asphalt | WF GB | WF GD | WE GS | WG SD | WF SD | WF DB | WF DN | WG DB | WG DN | WG SB | WF GS | WFD | WSD | FEG | WFE | WF EG | WF ES | FGS | GSD | WFS | WF BN | |
| 1.12 | 0.67 | 0.75 | 0.80 | 0.83 | 0.86 | 0.88 | 0.89 | 0.9 | 0.92 | 0.94 | 0.95 | 0.94 | 0.93 | 0.94 | 0.94 | 0.95 | 0.95 | 0.95 | 0.98 | \ | ||
| WF BN | WE GS | WF GD | WF GS | WG SD | WFS | WG SB | WF DB | WF DN | WF SD | FEG | GSD | WSD | WFE | WF EG | WF ES | WFD | WG DB | WG DN | FGS | WF GB | ||
| 1.22 | 1.44 | 0.93 | 0.80 | 0.83 | 0.99 | 1.34 | 0.89 | 0.90 | 1.01 | 1.03 | 1.07 | 1.18 | 0.93 | 0.94 | 1.33 | 1.09 | 0.95 | 1.44 | 1.15 | \ | ||
| FGS | WF BN | WG DB | WG DN | WF SD | WF DB | WF DN | WG SB | GSD | WF GS | WE GS | WSD | WF GB | FEG | WF GD | WG SD | WFE | WF EG | WF ES | WFS | WFD | ||
| 0.93 | 0.69 | 0.75 | 1.85 | 0.83 | 0.86 | 0.89 | 0.93 | 0.93 | 0.93 | 0.92 | 0.94 | 0.96 | 1.11 | 0.96 | 0.96 | 0.94 | 0.95 | 0.98 | 0.99 | \ | ||
| WF GB | WF GD | WE GS | WG SD | WF SD | WF DB | WF DN | WG DB | WG DN | WG SB | WF GS | FEG | WFD | WSD | WFS | GSD | WFE | WF EG | WF ES | FGS | WF BN | ||
| 1.18 | 0.67 | 0.75 | 0.81 | 0.83 | 0.86 | 0.89 | 0.89 | 0.90 | 0.91 | 0.99 | 0.92 | 0.93 | 0.94 | 0.94 | 0.94 | 0.94 | 0.95 | 0.95 | 0.97 | \ | ||
| SBS-Modified Asphalt | WF ES | WF GS | WF EG | WG SB | WF GB | WE GS | WF GD | WF SD | WG SD | WG DB | WF DN | WG DN | WF DB | WFD | FEG | WFE | WSD | GSD | WFS | FGS | WF BN | |
| 0.57 | 0.73 | 0.78 | 1.75 | 0.85 | 0.97 | 0.88 | 0.89 | 0.90 | 0.91 | 0.92 | 0.92 | 1.05 | 0.93 | 0.94 | 0.96 | 0.94 | 0.95 | 0.95 | 0.96 | \ | ||
| WFS | WSD | GSD | WG SD | WF SD | WF GD | WF BN | WFD | WE GS | WG SB | WFE | FEG | WG DB | WF DN | WG DN | WF DB | WF GB | WF EG | FGS | WF ES | WF GS | ||
| 0.50 | 1.34 | 1.01 | 0.81 | 1.25 | 1.03 | 1.15 | 0.91 | 0.97 | 0.99 | 0.92 | 1.45 | 1.41 | 0.95 | 0.97 | 1.09 | 0.97 | 0.97 | 1.06 | 0.95 | \ | ||
| WF DB | WG DN | WF DN | WF BN | WG DB | FGS | WF GS | WF GD | WG SB | WE GS | WF SD | WG SD | WFD | WFS | WSD | WF ES | WF GB | WF EG | FEG | WFE | GSD | ||
| 0.76 | 0.93 | 2.22 | 1.13 | 1.21 | 1.41 | 1.13 | 0.97 | 0.91 | 0.95 | 0.92 | 1.00 | 1.00 | 0.93 | 0.96 | 0.96 | 0.95 | 1.11 | 0.95 | 0.97 | \ | ||
| WF GS | WF ES | WF EG | WF GB | WG SB | WE GS | WF DB | WG DN | WF DN | WF SD | WG SD | WF GD | WG DB | WSD | WFS | WFD | GSD | WF BN | FEG | WFE | FGS | ||
| 0.53 | 0.69 | 0.76 | 1.08 | 0.84 | 0.90 | 0.88 | 0.89 | 0.91 | 0.91 | 0.92 | 0.93 | 1.04 | 0.93 | 0.95 | 0.94 | 0.95 | 0.96 | 0.95 | 0.96 | \ | ||
| Reagent Combination | WFE | WFS | WFD | WSD | FEG | FGS | GSD | WF EG | WF ES | WF GS | WF GD | WF GB | WF SD | WF DB | WF DN | WF BN | WE GS | WG SD | WG SB | WG DB | WG DN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Outliers | 4 | 4 | 3 | 3 | 3 | 4 | 3 | 3 | 4 | 3 | 1 | 4 | 0 | 1 | 1 | 4 | 1 | 1 | 1 | 1 | 2 |
References
- D3625/D3625M–12; Standard Practice for Effect of Water on Bituminous-Coated Aggregate Using Boiling Water. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2020.
- Zhang, Y.; Luo, X.; Luo, R.; Lytton, R.L. Crack initiation in asphalt mixtures under external compressive loads. Constr. Build. Mater. 2014, 72, 94–103. [Google Scholar] [CrossRef]
- Alfalah, A.; Ali, A.; Mehta, Y. Estimating tensile strength ratio of asphalt mixtures using surface free energy (sfe) and fourier transform infrared attenuated total reflectance (ftir-atr). Constr. Build. Mater. 2023, 409, 133900. [Google Scholar] [CrossRef]
- Liu, L.; Liu, L.; Yu, Y. Study of factors influencing moisture susceptibility of warm-mix asphalt using the surface free energy approach. Polymers 2023, 15, 2798. [Google Scholar] [CrossRef]
- Tu, C.; Xi, L.; Luo, R.; Huang, T.; Luo, J. Effect of water vapor concentration on adhesion between asphalt and aggregate. Mater. Struct. 2022, 55, 237. [Google Scholar] [CrossRef]
- Little, D.N.; Bhasin, A. Using Surface Energy Measurements to Select Materials for Asphalt Pavements; Texas A & M University: Austin, TX, USA, 2006. [Google Scholar]
- Dong, J.; Zhang, K.; Liang, S.; Ma, H.; Huang, T.; Luo, R. Evaluation of moisture sensitivity of asphalt mixtures based on surface energy of asphalt mastic. J. Mater. Civ. Eng. 2024, 36, 04024191. [Google Scholar] [CrossRef]
- Mitchell, B.S. An introduction to materials engineering and science: For chemical and materials engineers. Chem. Eng. 2003, 2003, 976. [Google Scholar]
- Elphingstone, G.M., Jr. Adhesion and Cohesion in Asphalt-Aggregate Systems. Ph.D. Thesis, Texas A & M University, Austin, TX, USA, 1997. [Google Scholar]
- Cheng, D.X. Surface Free Energy of Asphalt-Aggregate System and Performance Analysis of Asphalt Concrete Based on Surface Free Energy. Ph.D. Thesis, Texas A & M University, Austin, TX, USA, 2002. [Google Scholar]
- Bhasin, A. Development of Methods to Quantify Bitumen-Aggregate Adhesion and Loss of Adhesion Due to Water. Ph.D. Thesis, Texas A & M University, Austin, TX, USA, 2006. [Google Scholar]
- Tu, C.; Luo, R.; Huang, T. Influence of infiltration velocity on the measurement of the surface energy components of asphalt binders using the Wilhelmy plate method. J. Mater. Civ. Eng. 2021, 33, 04021243. [Google Scholar] [CrossRef]
- Chibowski, E. Perea-Carpio R. Problems of contact angle and solid surface free energy determination. Adv. Colloid Interface Sci. 2002, 98, 245–264. [Google Scholar] [CrossRef] [PubMed]
- Luo, R.; Zhang, D.; Zeng, Z.; Lytton, R.L. Effect of surface tension on the measurement of surface energy components of asphalt binders using the Wilhelmy plate method. Constr. Build. Mater. 2015, 98, 900–909. [Google Scholar] [CrossRef]
- Li, Q.; Xu, L.; Chen, X.; Li, W.; Li, Y.; Wang, H.; Liu, K. Study on the adhesion performance of biochar-modified asphalt based on surface free energy and atomic force microscopy. Coatings 2024, 14, 1390. [Google Scholar] [CrossRef]
- Schuster, J.M.; Schvezov, C.E.; Rosenberger, M.R. Analysis of the results of surface free energy measurement of Ti6Al4V by different methods. Procedia Mater. Sci. 2015, 8, 732–741. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, R. Using the surface free energy (sfe) method to investigate the effects of additives on moisture susceptibility of asphalt mixtures. Int. J. Adhes. Adhes. 2019, 95, 102437. [Google Scholar] [CrossRef]
- Little, D.N. Asphalt Research Consortium Quarterly Technical Progress Report from July to September. Research report; Texas A & M University: Texas, TX, USA, 2011. [Google Scholar]
- Al-Rawashdeh, A.S.; Sargand, S. Performance assessment of a warm asphalt binder in the presence of water by using surface free energy concepts and nanoscale techniques. J. Mater. Civ. Eng. 2014, 26, 803–811. [Google Scholar] [CrossRef]
- Singh, D.; Mishra, V. Different methods of selecting probe liquids to measure the surface free energy of asphalt binders. Constr. Build. Mater. 2018, 175, 448–457. [Google Scholar] [CrossRef]
- Hefer, A.W.; Bhasin, A.; Little, D.N. Bitumen surface energy characterization using a contact angle approach. J. Mater. Civ. Eng. 2006, 18, 759–767. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Lin, R.; Mui, M.; Neumann, A.W. Low-rate dynamic and static contact angles and the determination of solid surface tensions. Colloids Surf. A: Physicochem. Eng. Asp. 1996, 116, 63–77. [Google Scholar] [CrossRef]
- Ma, F.; Fu, Z.; Wang, L.L. Asphalt-aggregate adhesion work of natural asphalt modified asphalt. Int. J. Pavement Res. Technol. 2014, 7, 456–460. [Google Scholar]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing. China, 2011.
- ASTM D1331-14; Standard Test Methods for Surface and Interfacial Tension of Solutions of Paints, Solvents, Solutions of Surface-active Agents, and Related Materials. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2017.
- Kurt, O.; Arslan, O. Geometric interpretation and precision analysis of algebraic ellipse fitting using least squares method. Acta Geod. Et Geophys. Hung. 2012, 47, 430–440. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of total least-squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Gu, T.; Lin, S.; Fang, B.; Luo, T. An improved total least square calibration method for straightness error of coordinate measuring machine. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 1665–1672. [Google Scholar] [CrossRef]
- Ord, K. Outliers in statistical data. Int. J. Forecast. 1996, 12, 175–176. [Google Scholar] [CrossRef]
- Arthur, Z.; Peter, F. There and back again: Outlier detection between statistical reasoning and data mining algorithms. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1280. [Google Scholar]
- Onoz, B.; Oguz, B. Assessment of Outliers in Statistical Data Analysi; Springer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Wang, X.; Zeng, R.; Zou, F.; Huang, F.; Jin, B. A highly efficient framework for outlier detection in urban traffic flow. IET Intell. Transp. Syst. 2021, 12, 1494–1507. [Google Scholar] [CrossRef]
| Chemical Reagent (Abbreviation) | Surface Energy Parameter/(mJ/m2) | ||||
|---|---|---|---|---|---|
| Distilled Water (W) | 21.80 | 51.00 | 25.50 | 25.50 | 72.80 |
| Formamide (F) | 39.00 | 19.00 | 2.28 | 39.60 | 58.00 |
| Ethylene Glycol (E) | 29.00 | 19.00 | 3.00 | 30.10 | 48.00 |
| Glycerol (G) | 34.00 | 30.00 | 3.92 | 57.40 | 64.00 |
| Dimethyl Sulfoxide (S) | 36.00 | 8.00 | 0.50 | 32.00 | 44.00 |
| Diiodomethane (D) | 50.80 | 0 | 0.01 | 0 | 50.80 |
| Benzyl Alcohol (B) | 28.60 | 11.40 | 0.95 | 34.20 | 40.00 |
| N-Octanol (N) | 27.50 | 0 | 0 | 3.97 | 27.50 |
| Property | Asphalt Material | Technical Requirement | |||||
|---|---|---|---|---|---|---|---|
| 70# Matrix Asphalt | SBS (I-D Type)-Modified Asphalt | 70# Matrix Asphalt | SBS (I-D Type)-Modified Asphalt | ||||
| Penetration at 25 °C, 0.1 mm | 64.0 | 53.0 | 60.0–70.0 | 40.0–60.0 | |||
| Softening Point (TR&B), °C | 47.0 | 66.0 | ≥46.0 | ≥60.0 | |||
| Ductility, cm | 10 °C | 35.0 | / | ≥20.0 | / | ||
| 5 °C | / | 41.0 | / | ≥20.0 | |||
| Dynamic Viscosity at 60 °C, (Pa·s) | 208.4 | / | ≥180.0 | / | |||
| Kinematic Viscosity at 135 °C, (Pa·s) | / | 2.8 | / | ≤3.0 | |||
| Wax Content (Distillation Method),% | 1.6 | / | ≤2.2 | / | |||
| Flash Point, °C | 295.0 | 255.0 | ≥260.0 | ≥230.0 | |||
| Solubility,% | 99.8 | 99.4 | ≥99.5 | ≥99.0 | |||
| Density, (g/cm3) | 1.04 | 1.07 | / | / | |||
| Residue after RTFOT | Quality Loss | −0.07 | −0.12 | ≤±0.80 | ≤±1.00 | ||
| Penetration Ratio at 25 °C,% | 67.0 | 75.0 | ≥61.0 | ≥65.0 | |||
| Ductility, cm | 10 °C | 11.0 | / | ≥6.0 | / | ||
| 5 °C | / | 22.0 | / | ≥15.0 | |||
| Test Method | Asphalt Material | Chemical Reagent | |||||||
|---|---|---|---|---|---|---|---|---|---|
| W | F | E | G | S | D | B | N | ||
| Wilhelmy Plate Method | 70# Matrix Asphalt | 104.33 | 91.96 | 87.64 | 95.20 | 73.44 | 78.21 | 66.54 | 22.84 |
| SBS-Modified Asphalt | 101.43 | 89.06 | 91.30 | 90.81 | 71.79 | 79.23 | 59.59 | 12.82 | |
| Asphalt Types | Asphalt Surface Energy Component with a Calculated Value of 0 | Examples of Reagent Combinations |
|---|---|---|
| 70# Matrix Asphalt | WFN, WEG, FES, FGN, EGSD, ESBN, SDBN, etc. | |
| FED, FGB, EBN, GDB, SDN, FEGS, SDBN, etc. | ||
| SBS-Modified Asphalt | WFSB | |
| WFB, WEB, FED, EGN, WESN, FESB, ESBN, etc. | ||
| FSN, GSB, SDN, FGSD, EGSN, GSBN, SDBN, etc. |
| Asphalt Type | Calculation Method of Equation | Reagent Combination | Asphalt Surface Energy Parameter/(mJ/m2) | |||||
|---|---|---|---|---|---|---|---|---|
| 70# Matrix Asphalt | TLS | WFSD | 18.28 | 0.10 | 1.33 | 0.73 | 19.01 | 17.71% |
| WFEG | 21.53 | 0.24 | 2.57 | 1.57 | 23.10 | |||
| SBS-Modified Asphalt | TLS | WFSD | 18.72 | 0.21 | 2.03 | 1.32 | 20.04 | 64.80% |
| WFEG | 5.99 | 3.40 | 2.80 | 6.17 | 12.16 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, L.; Tu, C.; Ding, G. Selecting the Optimal Calculation Method and Chemical Reagents in Surface Energy Tests of Asphalt Materials. Materials 2025, 18, 2833. https://doi.org/10.3390/ma18122833
Niu L, Tu C, Ding G. Selecting the Optimal Calculation Method and Chemical Reagents in Surface Energy Tests of Asphalt Materials. Materials. 2025; 18(12):2833. https://doi.org/10.3390/ma18122833
Chicago/Turabian StyleNiu, Longchang, Chongzhi Tu, and Gongying Ding. 2025. "Selecting the Optimal Calculation Method and Chemical Reagents in Surface Energy Tests of Asphalt Materials" Materials 18, no. 12: 2833. https://doi.org/10.3390/ma18122833
APA StyleNiu, L., Tu, C., & Ding, G. (2025). Selecting the Optimal Calculation Method and Chemical Reagents in Surface Energy Tests of Asphalt Materials. Materials, 18(12), 2833. https://doi.org/10.3390/ma18122833





