Calculating Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate by Finite Element Method Based on Energy Methods
Abstract
1. Introduction
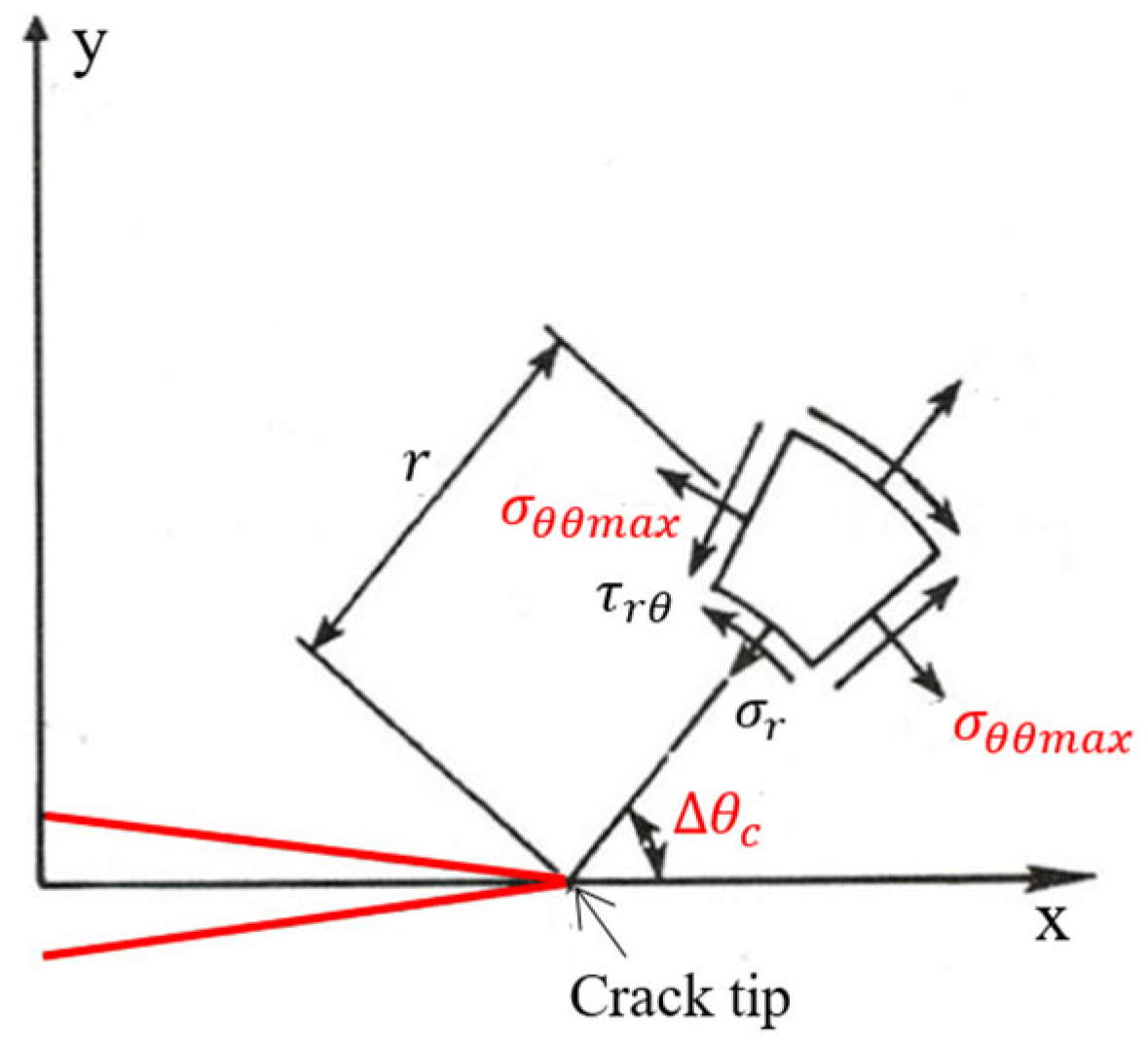
2. Method to Calculate the Propagation Direction of the Crack
2.1. The Theory of Maximum Tangential Normal Stress
2.2. The Theory of Minimum Strain Energy Density
2.3. Theory of Maximum Energy Release
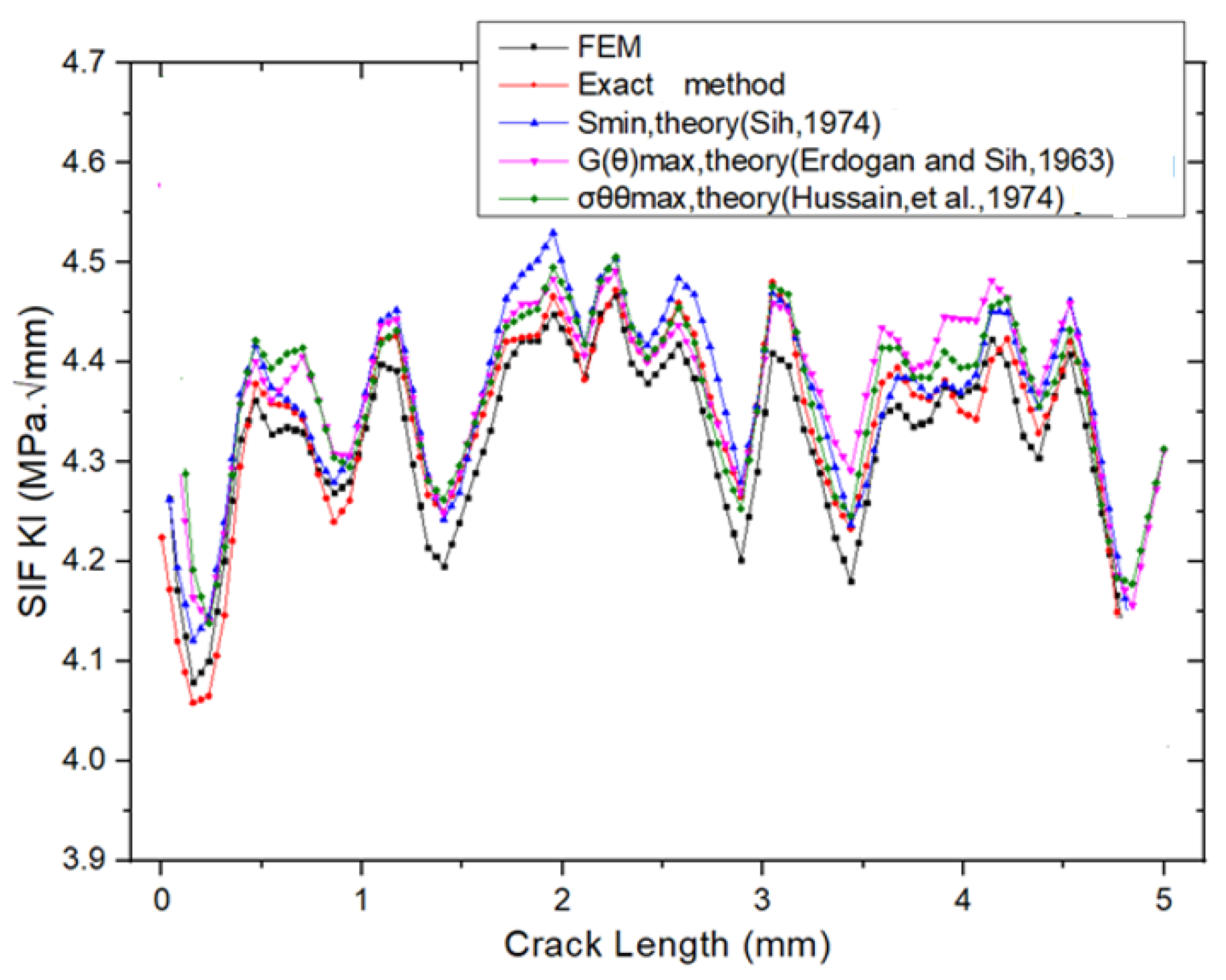
2.4. Comparison Between Three Methods of Calculating Crack Propagation Direction
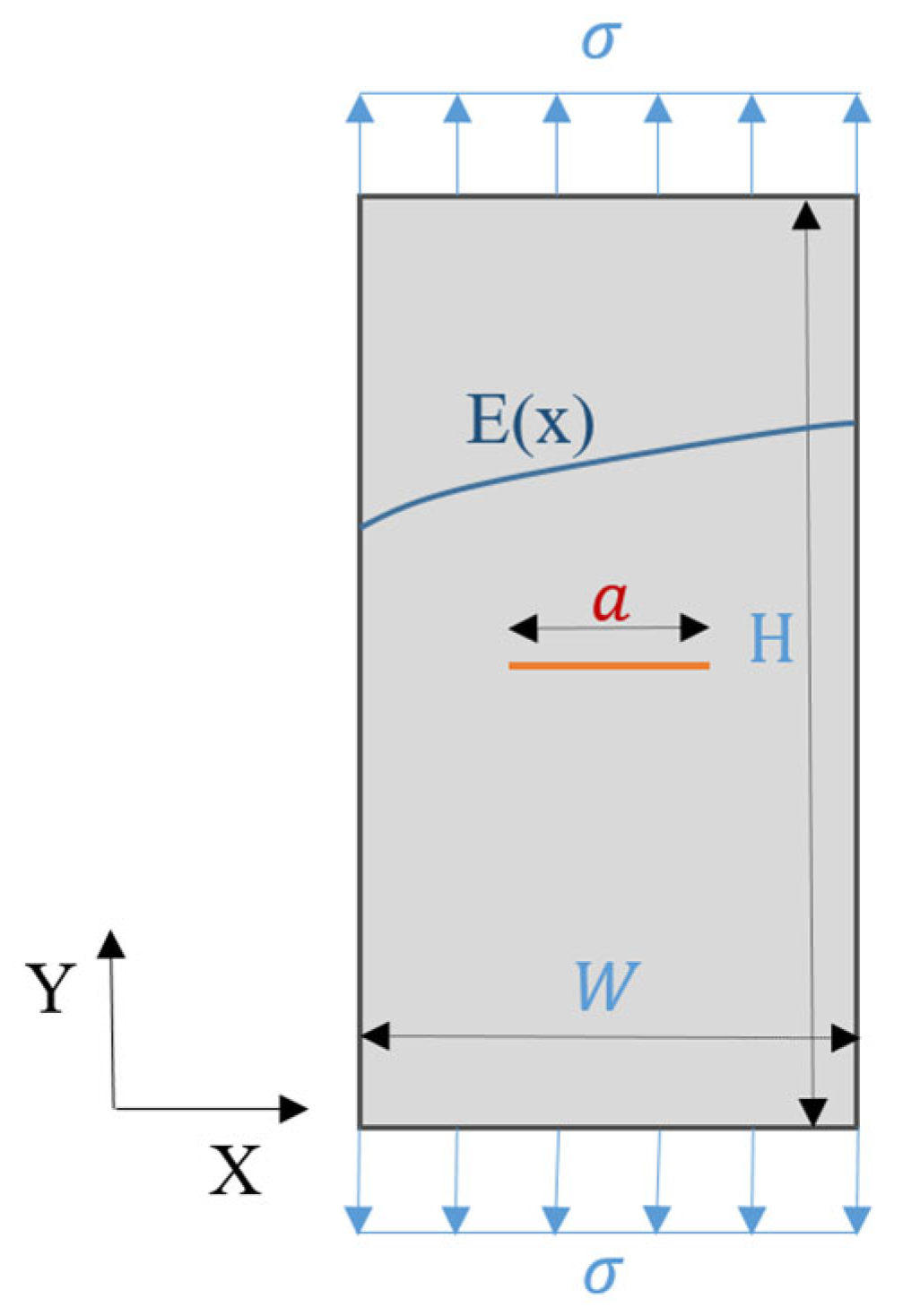
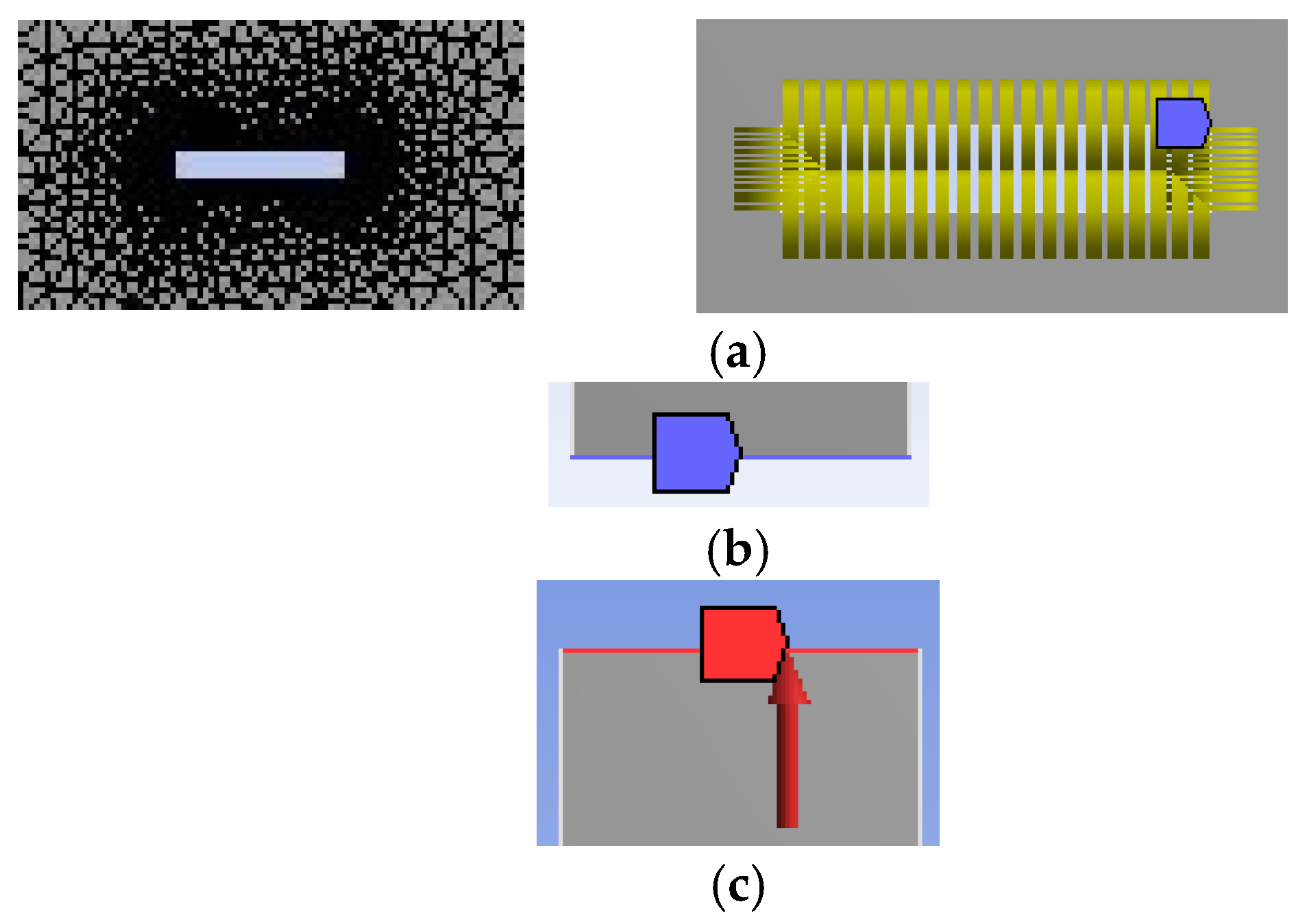
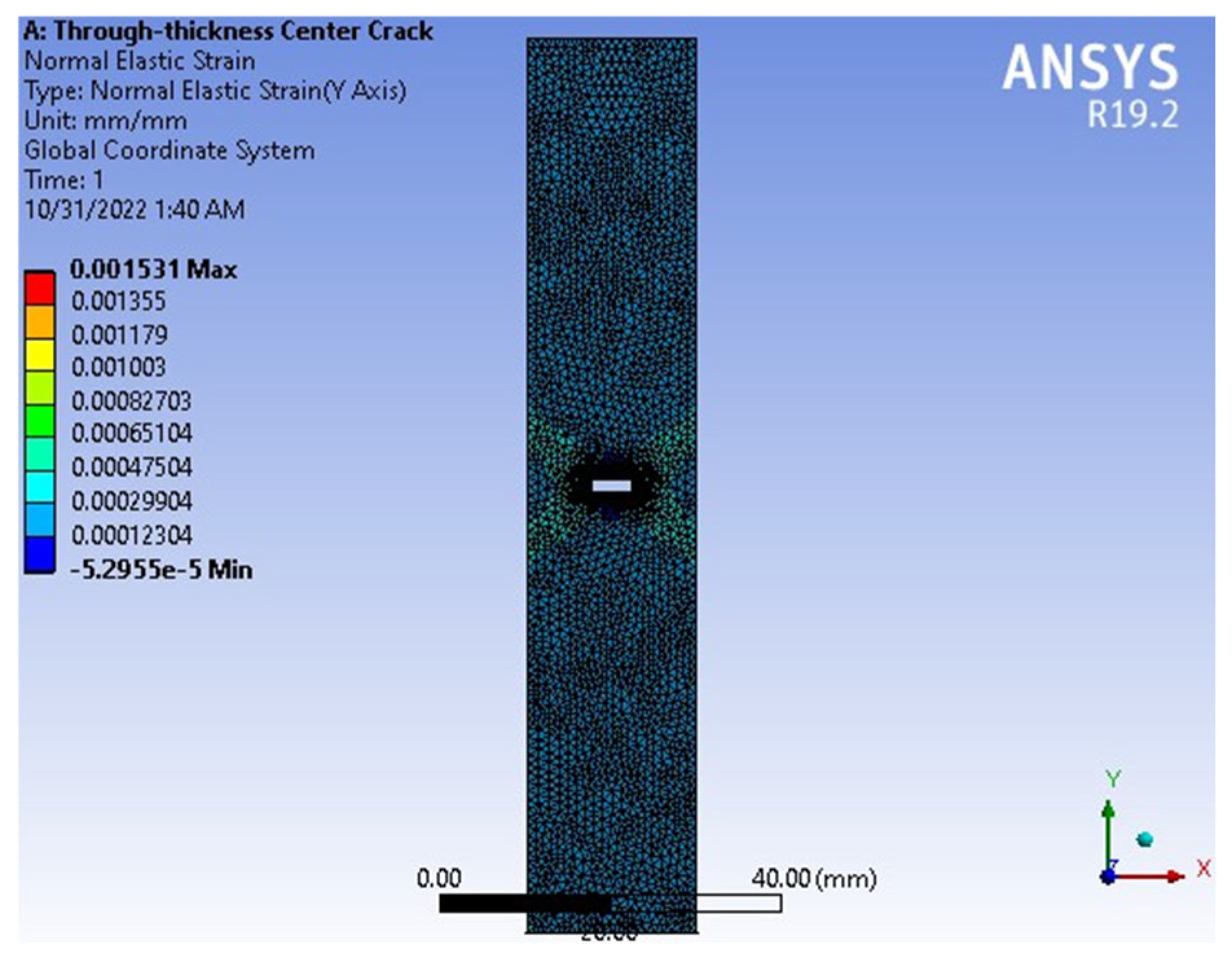
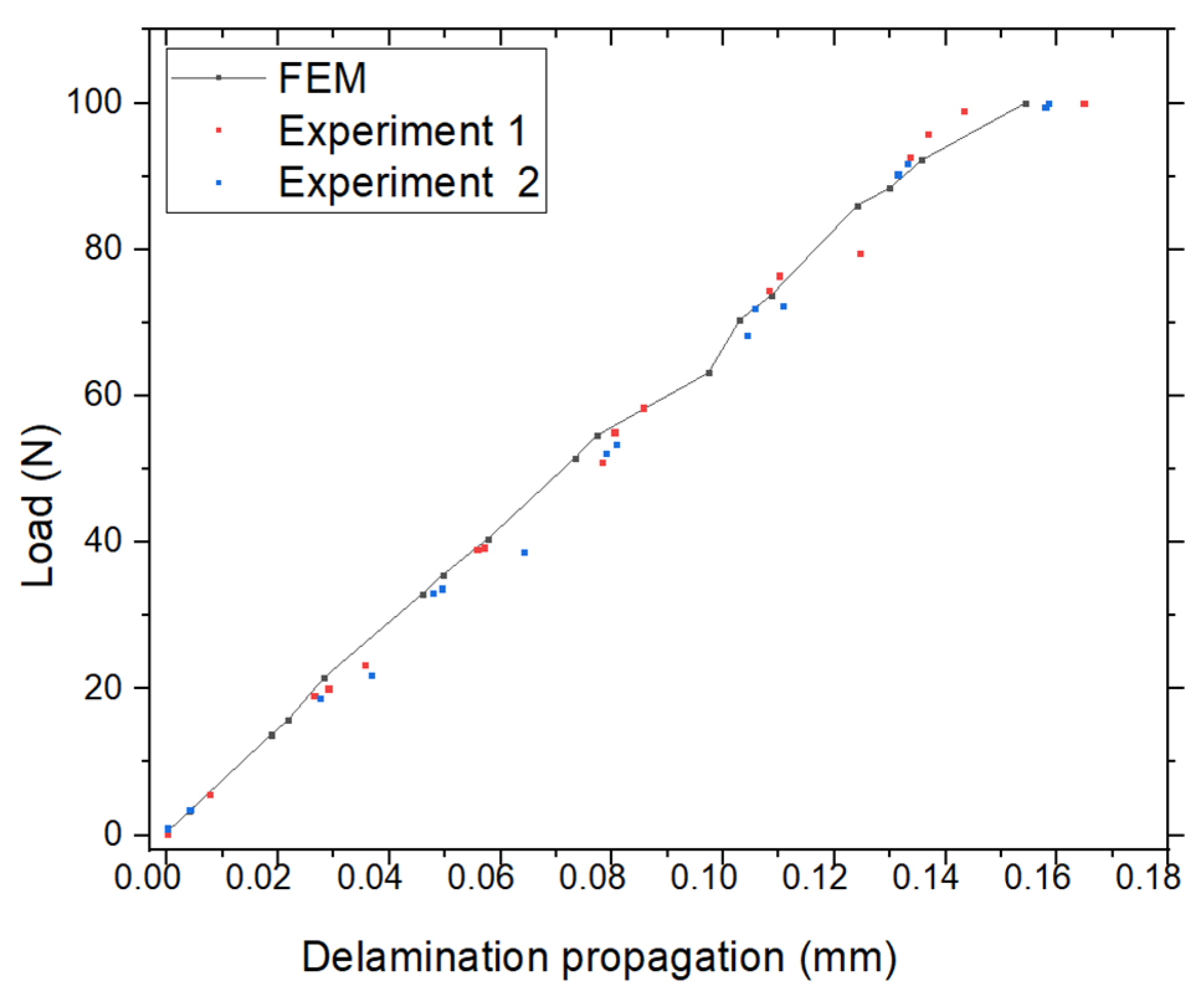
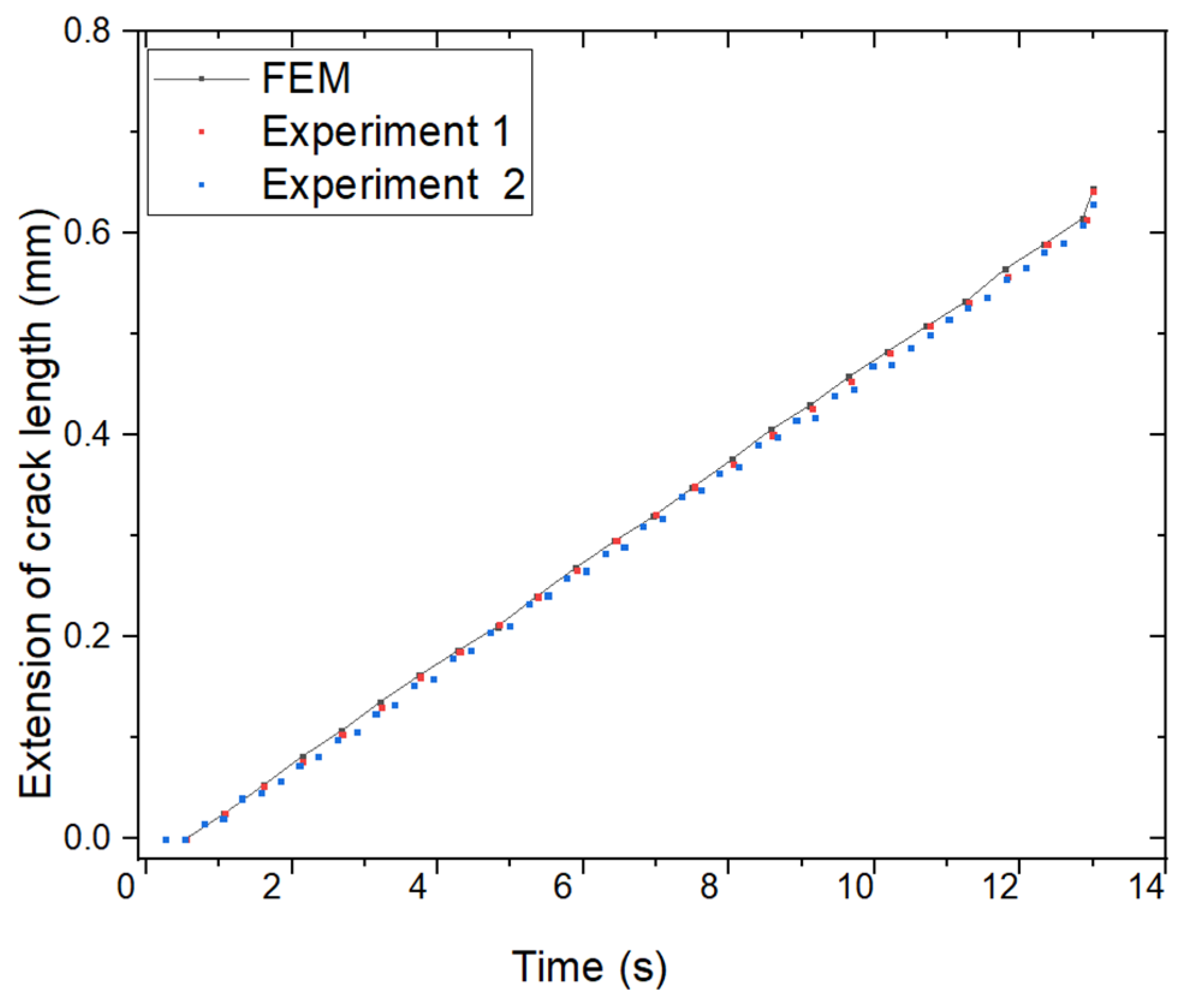
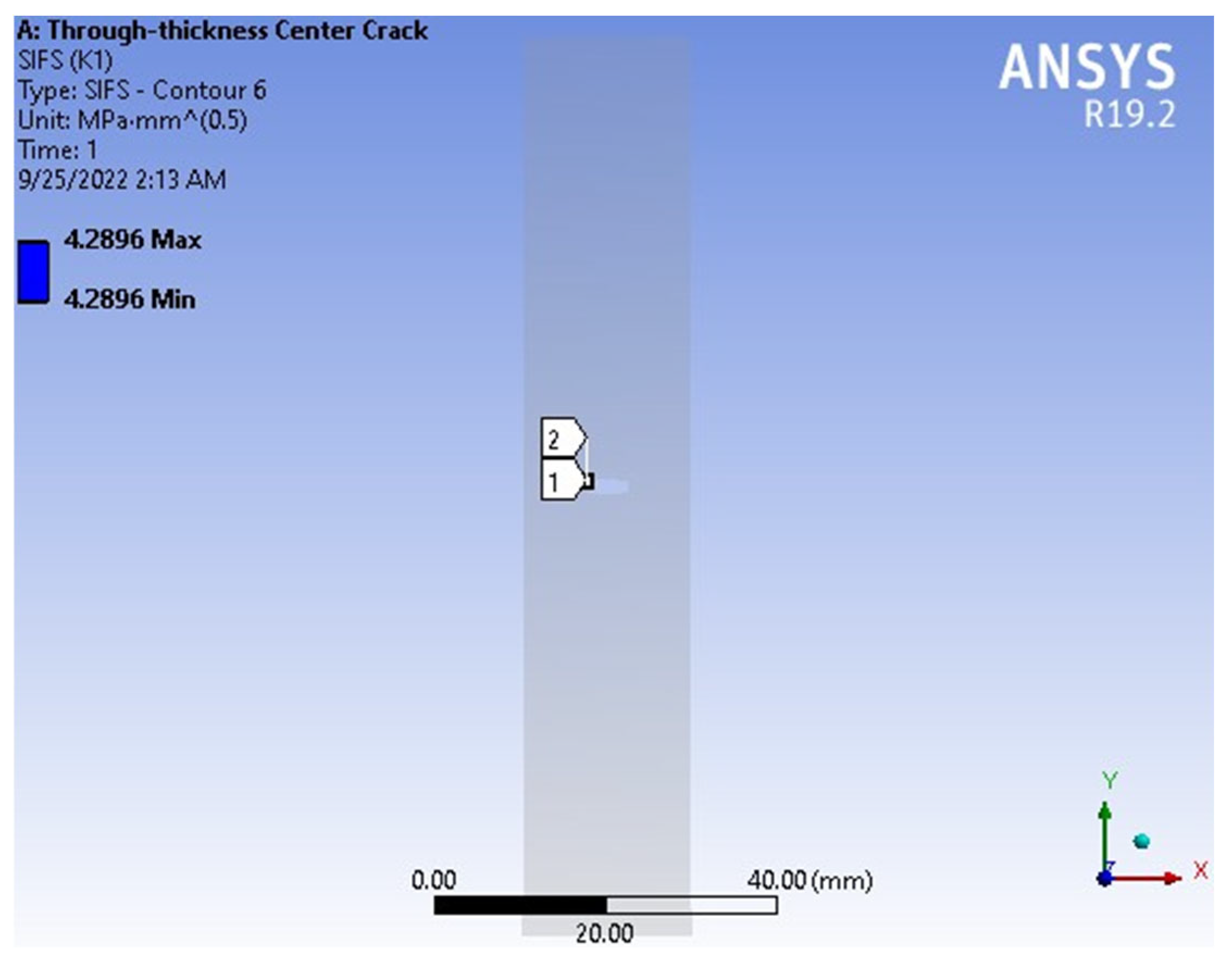
3. A Results and Discussions: A FGM Plate with the Through-Thickness Center Crack
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mutnbak, M.; Abbadi, A.; Mousa, S.; Abd-Elhady, A.A.; Sallam, H.E.M.; Reda, R.M. Effects of specimen geometry and size on mode I and mixed mode fracture behavior of high strength fiber reinforced concrete. Sci. Rep. 2025, 15, 15286. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.-D.; Huang, S.-C. Use of XTFEM based on the consecutive interpolation procedure of quadrilateral element to calculate J-integral and SIFs of an FGM plate. Theor. Appl. Fract. Mech. 2023, 127, 103985. [Google Scholar] [CrossRef]
- Nguyen, H.-D. Using Finite Element Method to Calculate Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate Based on Energy Methods. Int. J. Mech. Energy Eng. Appl. Sci. 2025, 17, 10345. [Google Scholar]
- Nguyen, H.-D.; Huang, S.-C. Using the Extended Finite Element Method to Integrate the Level-Set Method to Simulate the Stress Concentration Factor at the Circular Holes Near the Material Boundary of a Functionally-Graded Material Plate. J. Mater. Res. Technol. 2022, 21, 4658–4673. [Google Scholar] [CrossRef]
- Ma, L.; Wu, L.-Z.; Guo, L.-C.; Zhou, Z.-G. Dynamic behavior of a finite crack in the functionally graded materials. Mech. Mater. 2005, 37, 1153–1165. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar] [CrossRef]
- Nguyen, H.-D. Analysis for Stress Concentration Factor at the Circular Holes Near Materials Border by Extended Finite Element Method. In Proceedings of the 4th International Online Conference on Materials, Online, 3–5 November 2025. [Google Scholar]
- Nguyen, H.D.; Huang, S.-C. Applying Quarter-Point Singular Element in Finite Element Method to Calculate J-Integral and Stress Intensity Factors of a Rectangular Isotropic FGM Plate. Materials 2025, 27, 12085. [Google Scholar]
- Sladek, J.; Sladek, V.; Zhang, C. An advanced numerical method for computing elastodynamic fracture parameters in functionally graded materials. Comput. Mater. Sci. 2005, 32, 532–543. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. Extend Finite Element Method for A Plate with Two Holes and Multiple Cracks. In Proceedings of the Taiwan International Conference on Ocean Governance, Kaohsiung, China, 23 September 2021. [Google Scholar]
- Nguyen, H.-D.; Huang, S.-C. Extended Finite Element Method for Modeling Arbitrary Discontinuities with Center Edge Crack in Finite Dimensional Plate under Tension and Shear. In Proceedings of the International Conference on Advanced Technology Innovation, Okinawa, Japan, 1 September 2020. [Google Scholar]
- Sérgio, E.R.; Gonzáles, G.L.G.; Gonzáles, G.L.G.; Vasco-Olmo, J.M.; Antunes, F.V.; Prates, P.; Díaz, F.A.; Neto, D.M. A comparison between FEM predictions and DIC results of crack tip displacement field in AA2024-T3 CT specimens. Eng. Fract. Mech. 2025, 318, 110964. [Google Scholar] [CrossRef]
- Monfared, M.; Ayatollahi, M. Dynamic stress intensity factors of multiple cracks in an orthotropic strip with FGM coating. Eng. Fract. Mech. 2013, 109, 45–57. [Google Scholar] [CrossRef]
- Sih, G.C.; Cha, B.C.K. A fracture criterion for three-dimensional crack problems. Eng. Fract. Mech. 1974, 6, 699–723. [Google Scholar] [CrossRef]
- Nguyen, H.D. Using the eXtended Finite Element Method (XFEM) to Simulate Own Frequency under External Influences of a Closed System based on Dynamic Compensation Method. J. Int. Multidiscip. Res. 2025, 27, 985. [Google Scholar]
- Erdogan, F.; Sih, G.C. On the Crack Extension in Plates Under Plane Loading and Transverse Shea. J. Basic Eng. Dec. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Gao, X.W.; Zhang, C.; Sladek, J.; Sladek, V. Fracture analysis of functionally graded materials by a BEM. Compos. Sci. Technol. 2007, 68, 1209–1215. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. Designing and Calculating the Nonlinear Elastic Characteristic of Longitudinal–Transverse Transducers of an Ultrasonic Medical Instrument Based on the Method of Successive Loadings. Materials 2022, 15, 4002. [Google Scholar] [CrossRef]
- Nguyen, H.-D. Extended Finite Element Approach for Simulating Arbitrary Openings in Functionally Graded Plates. Int. J. Mech. Energy Eng. Appl. Sci. 2025, 17, 885. [Google Scholar]
- Hussain, M.A.; Pu, S.L.; Underwood, J. Strain energy release rate for a crack under combined mode-I and -II. Natl. Symp. Fract. Mech. 1974, 560, 2–28. [Google Scholar]
- Nguyen, H.D. Application of the eXtended Finite Element Method for Simulating Random Holes in Functionally Graded Plates. Mater. Proc. 2025, 27, 975. [Google Scholar]
- Kim, J.-H.; Paulino, G.H. Finite element evaluation of mixed mode stress intensity factors in functionally graded materials. Int. J. Numer. Meth. Eng. 2002, 53, 1903–1935. [Google Scholar] [CrossRef]
- Wu, C.; He, P.; Li, Z. Extension of J integral to dynamic fracture of functional graded material and numerical analysis. Comput. Struct. 2002, 80, 411–416. [Google Scholar]
- Song, S.H.; Paulino, G.H. Dynamic stress intensity factors for homogeneous and smoothly heterogeneous materials using the interaction integral method. Int. J.Solids Struct. 2006, 43, 4830–4866. [Google Scholar] [CrossRef]
- Dai, M.-J.; Xie, M.-Y. A novel inverse extended finite element method for structural health monitoring of cracked structures. Ocean. Eng. 2025, 325, 120786. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. Rubber’s crack of a platen in papermaking machines at a crack tip of hyperelastic materials with finite element method. In Proceedings of the IEEE 7th International Conference on Applied System Innovation, Chiayi, China, 24–25 September 2021. [Google Scholar]
- Bayesteh, H.; Mohammadi, S. FEM fracture analysis of orthotropic functionally graded materials. Compos. Part B 2013, 44, 8–25. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. Calculating Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate by Finite Element Method Based on Energy Methods. Materials 2025, 67, 8885. [Google Scholar]
- Singh, I.V.; Mishra, B.K.; Bhattacharya, S. FEM simulation of cracks, holes and inclusions in functionally graded materials. Int. J. Mech. Mater. Des. 2011, 7, 199–218. [Google Scholar] [CrossRef]
- Nestor, P. Fracture Mechanics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Nguyen, H.-D.; Huang, S.-C. The Uniaxial Stress Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials 2021, 14, 7534. [Google Scholar] [CrossRef]
- Nguyen, H.-D. Using Matlab to Study of the Response of the System to Oscillatory Influences be an Oscillatory Effect on the Resting Antenna. Int. J. Multidiscip. Res. Growth Eval. 2025, 27, 885. [Google Scholar]
- Rice, J.R. A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Eshelby, J.D. Calculation of Energy Release Rate. In Prospects of Fracture Mechanics; Sih, G.C., Von Elst, H.C., Broek, D., Eds.; Noordhoff: Groningen, The Netherlands, 1974; pp. 69–84. [Google Scholar]
- Riveros, G.A.; Gopalaratnam, V.S. Post-cracking behavior of reinforced concrete deep beams: A numerical fracture investigation of concrete strength and beam size. ASCE Struct. J. 2005, 47, 3885. [Google Scholar]






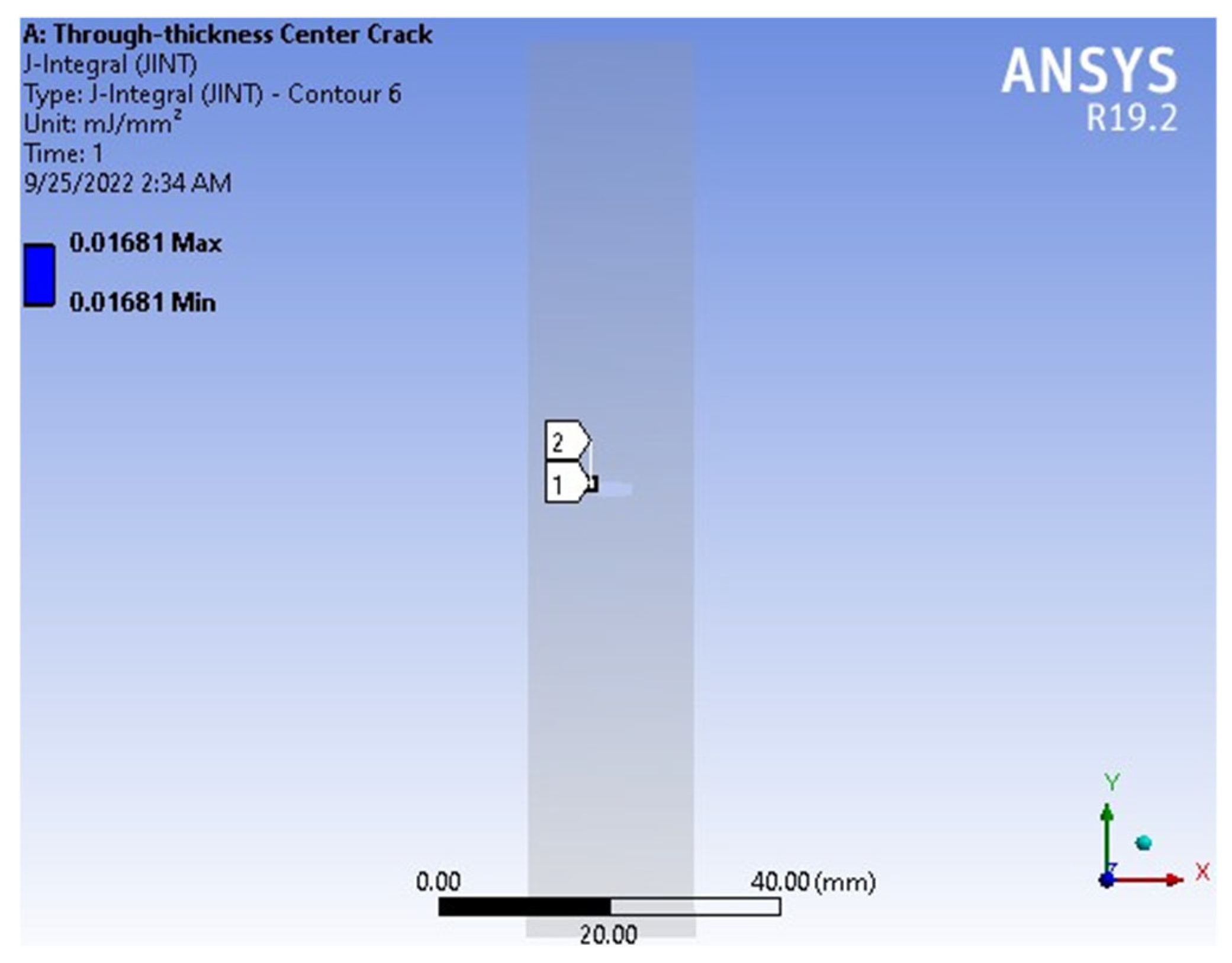
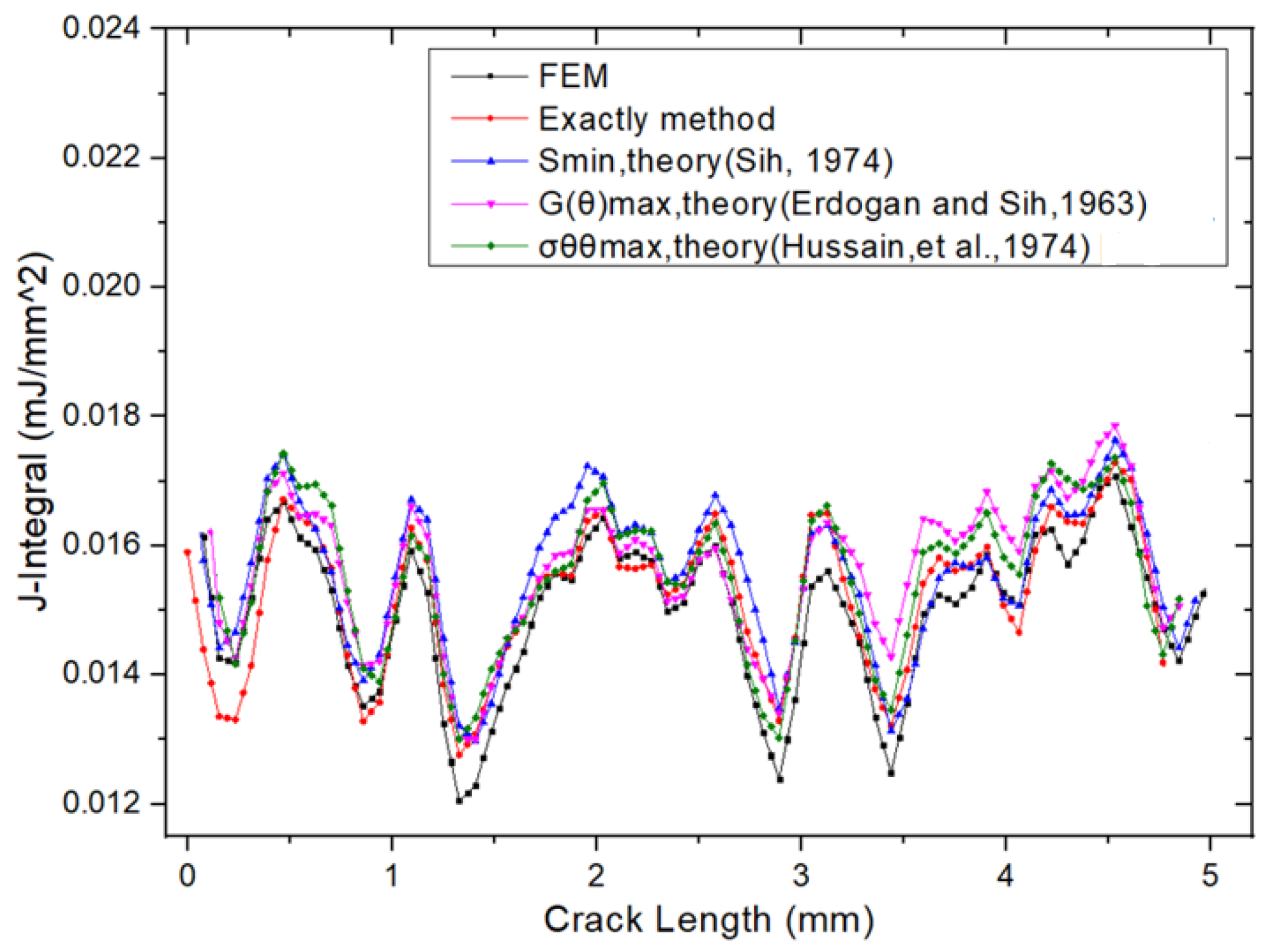
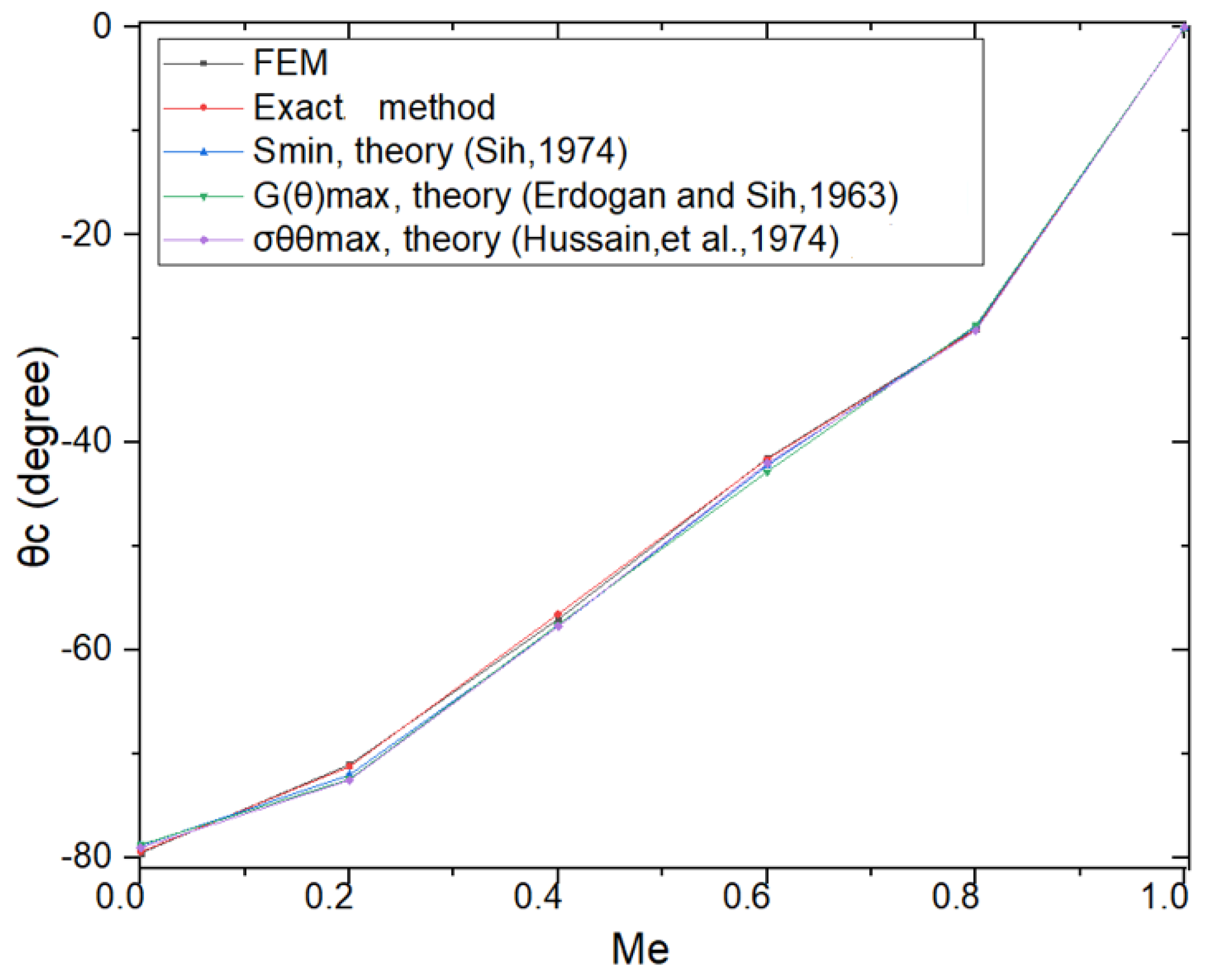

| FEM | Exper. | Error (%) | |||
|---|---|---|---|---|---|
| Exper. 1 | Exper. 2 | Exper. 1 | Exper. 2 | ||
| Displacement (mm) | 0.15882 | 0.16335 | 0.17032 | 5.55 | 6.42 |
| Strain (mm/mm) | 0.001531 | 0.0014833 | 0.001579 | 3.12 | 3.13 |
| Exact (MPa·) | 4.2152 |
| FEM (MPa·) | 4.2896 |
| Error (%) | 1.77 |
| FEM mJ/mm2 | 0.01760 |
| Exact mJ/mm2 | 0.01681 |
| Error (%) | 4.49 |
| (Degree) | ||
|---|---|---|
| Exact | 0.32 | −64.6 |
| FEM | 0.31 | −64.5 |
| Error (%) | 3.12 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.-D.; Huang, S.-C. Calculating Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate by Finite Element Method Based on Energy Methods. Materials 2025, 18, 2698. https://doi.org/10.3390/ma18122698
Nguyen H-D, Huang S-C. Calculating Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate by Finite Element Method Based on Energy Methods. Materials. 2025; 18(12):2698. https://doi.org/10.3390/ma18122698
Chicago/Turabian StyleNguyen, Huu-Dien, and Shyh-Chour Huang. 2025. "Calculating Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate by Finite Element Method Based on Energy Methods" Materials 18, no. 12: 2698. https://doi.org/10.3390/ma18122698
APA StyleNguyen, H.-D., & Huang, S.-C. (2025). Calculating Strain Energy Release Rate, Stress Intensity Factor and Crack Propagation of an FGM Plate by Finite Element Method Based on Energy Methods. Materials, 18(12), 2698. https://doi.org/10.3390/ma18122698






