Electronic Correlations in Altermagnet MnTe in Hexagonal Crystal Structure
Abstract
1. Introduction
2. Methods and Crystal Structure
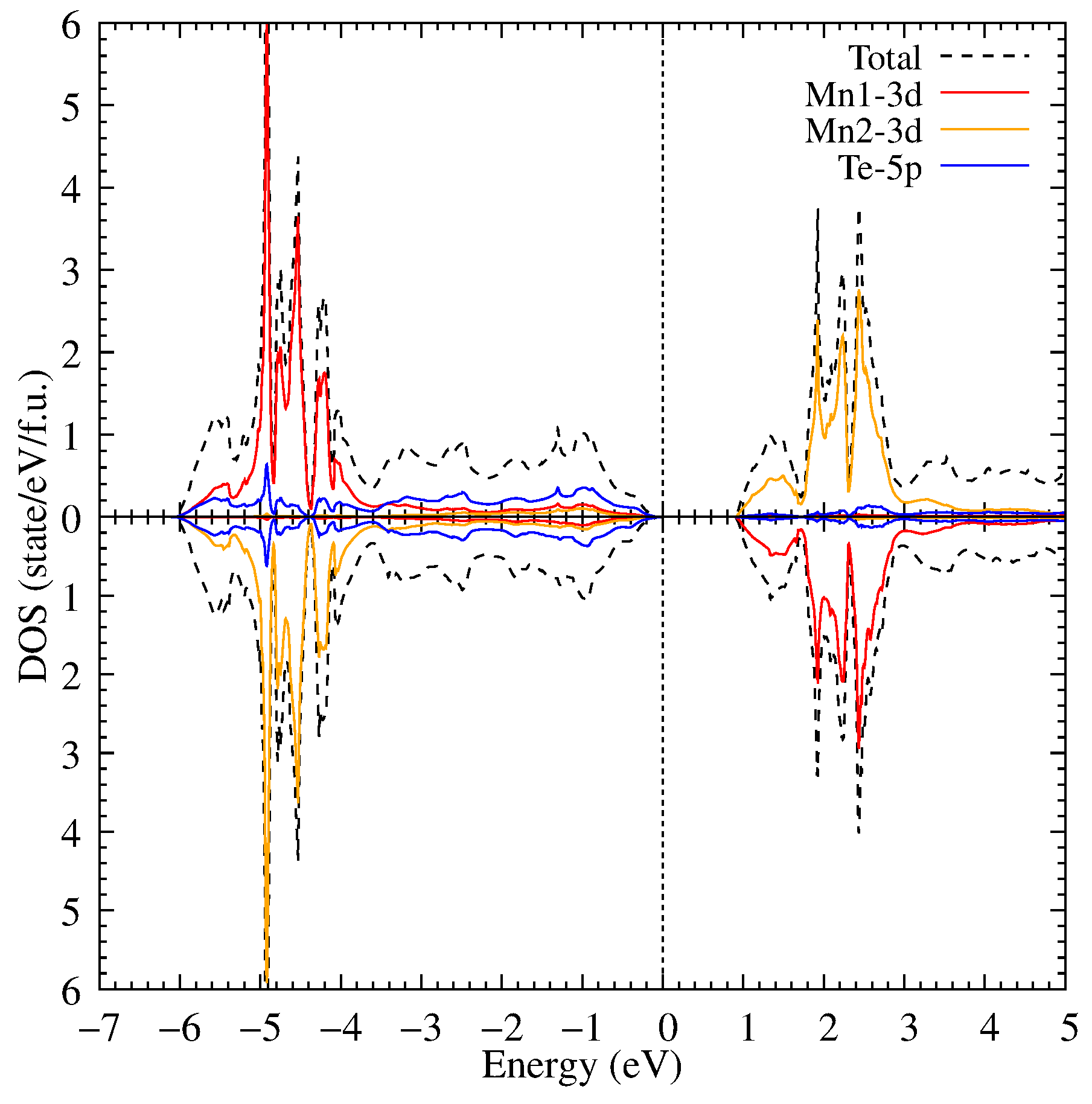
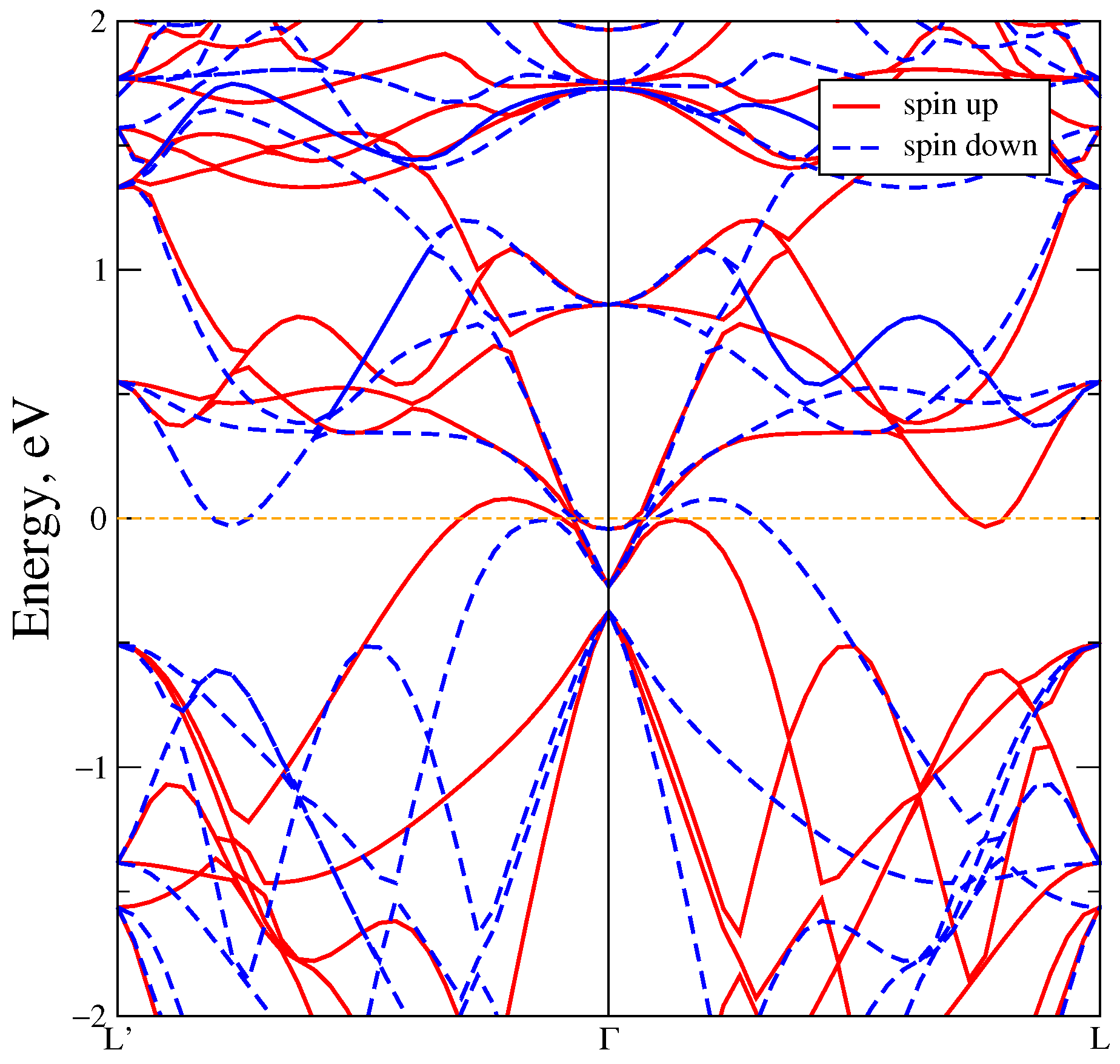
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TMC | Transition metal chalcogenides |
| DFT | Density functional theory |
| RS | Rock salt |
| SOC | Spin-orbit coupling |
| LSDA | Local spin-density approximation |
| GGA | Generalized gradient approximation |
References
- Amin, O.J.; Dal Din, A.; Golias, E.; Niu, Y.; Zakharov, A.; Fromage, S.C.; Fields, C.J.B.; Heywood, S.L.; Cousins, R.B.; Maccherozzi, F.; et al. Nanoscale imaging and control of altermagnetism in MnTe. Nature 2024, 636, 348–353. [Google Scholar] [CrossRef] [PubMed]
- Krempaský, J.; Šmejkal, L.; D’Souza, S.W.; Hajlaoui, M.; Springholz, G.; Uhlířová, K.; Alarab, F.; Constantinou, P.C.; Strocov, V.; Usanov, D.; et al. Altermagnetic lifting of Kramers spin degeneracy. Nature 2024, 626, 517–522. [Google Scholar] [CrossRef] [PubMed]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Emerging Research Landscape of Altermagnetism. Phys. Rev. X 2022, 12, 040501. [Google Scholar] [CrossRef]
- Gonzalez Betancourt, R.D.; Zubáč, J.; Geishendorf, K.; Ritzinger, P.; Růžičková, B.; Kotte, T.; Železný, J.; Olejník, K.; Springholz, G.; Büchner, B.; et al. Anisotropic magnetoresistance in altermagnetic MnTe. Npj Spintron. 2024, 2, 45. [Google Scholar] [CrossRef]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Beyond Conventional Ferromagnetism and Antiferromagnetism: A Phase with Nonrelativistic Spin and Crystal Rotation Symmetry. Phys. Rev. X 2022, 12, 031042. [Google Scholar] [CrossRef]
- McClarty, P.A.; Rau, J.G. Landau Theory of Altermagnetism. Phys. Rev. Lett. 2024, 132, 176702. [Google Scholar] [CrossRef]
- Chowde Gowda, C.; Chandravanshi, D.; Tromer, R.M.; Malya, A.; Chattopadhyay, K.; Galvão, D.S.; Tiwary, C.S. Tuning the band gap of manganese telluride quantum dots (MnTe QDs) for photocatalysis. Appl. Phys. A 2024, 130, 299. [Google Scholar] [CrossRef]
- Raju Baral, A.M.; Abeykoon, M.; Campbell, B.J.; Frandsen, B.A. Giant Spontaneous Magnetostriction in MnTe Driven by a Novel Magnetostructural Coupling Mechanism. Adv. Funct. Mater. 2023, 33, 2305247. [Google Scholar] [CrossRef]
- Šmejkal, L.; González-Hernández, R.; Jungwirth, T.; Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 2020, 6, eaaz8809. [Google Scholar] [CrossRef]
- González-Hernández, R.; Šmejkal, L.; Výborný, K.; Yahagi, Y.; Sinova, J.; Jungwirth, T.; Železný, J. Efficient Electrical Spin Splitter Based on Nonrelativistic Collinear Antiferromagnetism. Phys. Rev. Lett. 2021, 126, 127701. [Google Scholar] [CrossRef]
- López-Moreno, S.; Romero, A.H.; Mejía-López, J.; Munoz, A.; Roshchin, I.V. First-principles study of electronic, vibrational, elastic, and magnetic properties of FeF as a function of pressure. Phys. Rev. B 2012, 85, 134110. [Google Scholar] [CrossRef]
- Yuan, L.-D.; Wang, Z.; Luo, J.-W.; Rashba, E.I.; Zunger, A. Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets. Phys. Rev. B 2020, 102, 014422. [Google Scholar] [CrossRef]
- Iguchi, S.; Kobayashi, H.; Ikemoto, Y.; Furukawa, T.; Itoh, H.; Iwai, S.; Moriwaki, T.; Sasaki, T. Magnetooptical spectra of an organic antiferromagnet as a candidate for an altermagnet. Phys. Rev. Res. 2025, in press. [Google Scholar] [CrossRef]
- Woods-Robinson, R.; Han, Y.; Zhang, H.; Ablekim, T.; Khan, I.; Persson, K.A.; Zakutayev, A. Wide Band Gap Chalcogenide Semiconductors. Chem. Rev. 2020, 120, 4007. [Google Scholar] [CrossRef]
- Osumi, T.; Souma, S.; Aoyama, T.; Yamauchi, K.; Honma, A.; Nakayama, K.; Takahashi, T.; Ohgushi, K.; Sato, T. Observation of a giant band splitting in altermagnetic MnTe. Phys. Rev. B 2024, 109, 115102. [Google Scholar] [CrossRef]
- Barik, R.; Ingole, P.P. Challenges and prospects of metal sulfide materials for supercapacitors. Curr. Opin. Electrochem. 2020, 21, 327–334. [Google Scholar] [CrossRef]
- Huang, Z.F.; Song, J.; Li, K.; Tahir, M.; Wang, Y.T.; Pan, L.; Wang, L.; Zhang, X.; Zou, J.J. Hollow Cobalt-Based Bimetallic Sulfide Polyhedra for Efficient All-pH-Value Electrochemical and Photocatalytic Hydrogen Evolution. J. Am. Chem. Soc. 2016, 138, 1359. [Google Scholar] [CrossRef]
- Caetano, R.; Freire, H. Orbital selectivity versus Pomeranchuk instability in the iron–chalcogenide superconductors: A two-loop renormalization group study. Ann. Phys. 2019, 405, 308–324. [Google Scholar] [CrossRef]
- Dyachenko, A.A.; Lukoyanov, A.V.; Shorikov, A.O.; Anisimov, V.I. Magnetically driven phase transitions with a large volume collapse in MnSe under pressure: A DFT+DMFT study. Phys. Rev. B 2018, 98, 085139. [Google Scholar] [CrossRef]
- Chernov, E.D.; Lukoyanov, A.V. Metal-insulator transition in MnS. Phys. Scr. 2025, 100, 035903. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, L.; Wen, T.; Yang, L.; Gou, H.; Xiao, Y.; Chow, P.; Pravica, M.; Yang, W.; Zhao, Y. Giant Pressure-Driven Lattice Collapse Coupled with Intermetallic Bonding and Spin-State Transition in Manganese Chalcogenides. Angew. Chem. Int. Ed. 2016, 55, 10350. [Google Scholar] [CrossRef]
- Allen, J.W.; Lucovsky, G.; Mikkelsen, J.C., Jr. Optical properties and electronic structure of crossroads material MnTe. Solid State Commun. 1977, 24, 367–370. [Google Scholar] [CrossRef]
- Mimasaka, M.; Sakamoto, I.; Murata, K.; Fujii, Y.; Onodera, A. Pressure-induced phase transitions of MnTe. J. Phys. C Solid State Phys. 1987, 20, 4689–4694. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, S.C.; Zou, Y.; Chen, H.; Liu, Y.; Li, W.; Chen, J.; Zhu, J.; Wu, L.; Wang, S.; et al. Concurrent pressure-induced spin-state transitions and Jahn–Teller distortions in MnTe. Chem. Mater. 2022, 34, 3931–3940. [Google Scholar] [CrossRef]
- Xiao, G.; Yang, X.; Zhang, X.; Wang, K.; Huang, X.; Ding, Z.; Ma, Y.; Zou, G.; Zou, B. A Protocol to fabricate nanostructured new phase: B31-Type MnS synthesized under high pressure. J. Am. Chem. Soc. 2015, 137, 10297–10303. [Google Scholar] [CrossRef]
- Kriegner, D.; Reichlova, H.; Grenzer, J.; Schmidt, W.; Ressouche, E.; Godinho, J.; Wagner, T.; Martin, S.Y.; Shick, A.B.; Volobuev, V.V.; et al. Magnetic anisotropy in antiferromagnetic hexagonal MnTe. Phys. Rev. B 2017, 96, 214418. [Google Scholar] [CrossRef]
- Sattigeri, R.M.; Cuono, G.; Autieri, C. Altermagnetic surface states: Towards the observation and utilization of altermagnetism in thin films, interfaces and topological materials. Nanoscale 2023, 15, 16998. [Google Scholar] [CrossRef] [PubMed]
- Zulkifal, S.; Wang, Z.; Zhang, X.; Siddique, S.; Yu, Y.; Wang, C.; Gong, Y.; Li, S.; Li, D.; Zhang, Y.; et al. Multiple Valence Bands Convergence and Localized Lattice Engineering Lead to Superhigh Thermoelectric Figure of Merit in MnTe. Adv. Sci. 2023, 10, 2206342. [Google Scholar] [CrossRef]
- Devaraj, N.; Bose, A.; Narayan, A. Interplay of altermagnetism and pressure in hexagonal and orthorhombic MnTe. Phys. Rev. Mater. 2024, 8, 104407. [Google Scholar] [CrossRef]
- Faria Junior, P.E.; de Mare, K.A.; Zollner, K.; Ahn, K.; Erlingsson, S.I.; van Schilfgaarde, M.; Výborný, K. Sensitivity of the MnTe valence band to the orientation of magnetic moments. Phys. Rev. B 2023, 107, L100417. [Google Scholar] [CrossRef]
- Deng, H.; Lou, X.; Lu, W.; Zhang, J.; Li, D.; Li, S.; Zhang, Q.; Zhang, X.; Chen, X.; Zhang, D.; et al. High-performance eco-friendly MnTe thermoelectrics through introducing SnTe nanocrystals and manipulating band structure. Nano Energy 2021, 81, 105649. [Google Scholar] [CrossRef]
- Rooj, S.; Chakraborty, J.; Ganguli, N. Hexagonal MnTe with Antiferromagnetic Spin Splitting and Hidden Rashba–Dresselhaus Interaction for Antiferromagnetic Spintronics. Adv. Phys. Res. 2024, 3, 2300050. [Google Scholar] [CrossRef]
- Makovetskii, G.; Galyas, A.; Severin, G.; Yanushkevich, K.I. Synthesis of Solid Solutions of Cr1-xMnxTe (0 ≤ x ≤ 1). Inorg. Mater. 1996, 32, 846. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Kuneš, J.; Lukoyanov, A.V.; Anisimov, V.I.; Scalettar, R.T.; Pickett, W.E. Collapse of magnetic moment drives the Mott transition in MnO. Nat. Mater. 2008, 7, 198–202. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Sandratskii, L.M.; Egorov, R.F.; Berdyshev, A.A. Energy Band Structure and Electronic Properties of NiAs Type Compounds. II. Antiferromagnetic Manganese Telluride. Phys. Status Solidi 1981, 104, 103–107. [Google Scholar] [CrossRef]
- Xiong, W.; Wang, Z.; Zhang, X.; Wang, C.; Yin, L.; Gong, Y.; Zhang, Q.; Li, S.; Liu, Q.; Wang, P.; et al. Lattice Distortions and Multiple Valence Band Convergence Contributing to High Thermoelectric Performance in MnTe. Small 2022, 19, 2206058. [Google Scholar] [CrossRef]
- Sato, H.; Mihara, T.; Furuta, A.; Tamura, M.; Mimura, K.; Happo, N.; Taniguchi, M.; Ueda, Y. Chemical trend of occupied and unoccupied Mn 3d states in Mn Y (Y= S, Se, Te). Phys. Rev. B 1997, 56, 7222. [Google Scholar] [CrossRef]
- Krause, M.; Bechstedt, F. Structural and Magnetic Properties of MnTe Phases from Ab Initio Calculations. J. Supercond. Nov. Magn. 2013, 26, 1963–1972. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chernov, E.D.; Lukoyanov, A.V. Electronic Correlations in Altermagnet MnTe in Hexagonal Crystal Structure. Materials 2025, 18, 2637. https://doi.org/10.3390/ma18112637
Chernov ED, Lukoyanov AV. Electronic Correlations in Altermagnet MnTe in Hexagonal Crystal Structure. Materials. 2025; 18(11):2637. https://doi.org/10.3390/ma18112637
Chicago/Turabian StyleChernov, Evgenii D., and Alexey V. Lukoyanov. 2025. "Electronic Correlations in Altermagnet MnTe in Hexagonal Crystal Structure" Materials 18, no. 11: 2637. https://doi.org/10.3390/ma18112637
APA StyleChernov, E. D., & Lukoyanov, A. V. (2025). Electronic Correlations in Altermagnet MnTe in Hexagonal Crystal Structure. Materials, 18(11), 2637. https://doi.org/10.3390/ma18112637








