Impact of Structural Stiffness on Vibration Periods of Concrete Buildings: A Systematic Review
Abstract
1. Introduction
2. Methods
2.1. Mathematical and Theoretical Models
2.2. Comparative Analysis of Methods
2.3. Case Studies
2.4. Limitations of Existing Models
2.5. Identification of Research Gaps
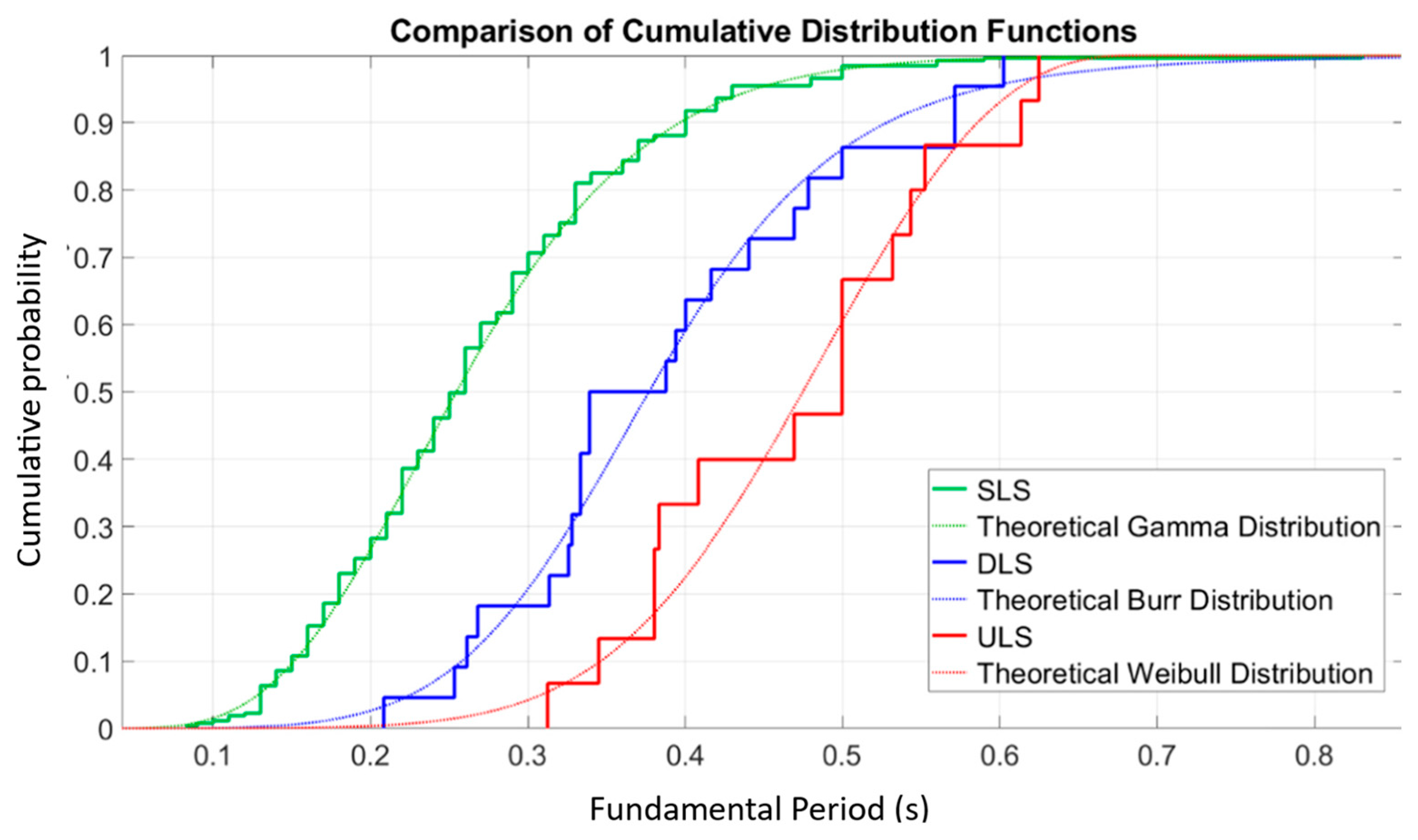
3. Results
3.1. Presentation of Quantitative Data
3.2. Qualitative Analysis
3.3. Identifying Trends
3.4. Discussion of Limits and Problems
3.5. Summary of Key Findings
4. Discussion
4.1. Interpretation of Results
4.2. Practical Implications
4.3. Comparison with Theoretical Models
4.4. Identifying Research Gaps
4.5. Limitations of Study
4.6. Recommendations for Future Research
5. Conclusions
5.1. Response to Research Objective
5.2. Summary of Key Findings
5.3. Implications of Findings
5.4. Contributions to the Field
5.5. Recommendations for Future Practices
5.6. Future Research Lines
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jamadin, A.; Kudus, S.A.; Ya’akob, A.D.H.; Misnan, M.F.; Jaini, Z.M. Vibration-Based Finite Element Model Analysis on Dynamic Characteristics of Ultra-High Performance Concrete Beam. Int. J. Integr. Eng. 2023, 15, 213–223. [Google Scholar] [CrossRef]
- Alrudaini, T. Estimating vibration period of reinforced concrete moment resisting frame buildings. Res. Eng. Struct. Mater. 2023, 9, 1417–1432. [Google Scholar] [CrossRef]
- Regni, M.; Arezzo, D.; Carbonari, S.; Gara, F.; Zonta, D. Effect of Environmental Conditions on the Modal Response of a 10-Story Reinforced Concrete Tower. Shock Vib. 2018, 2018, 9476146. [Google Scholar] [CrossRef]
- Yanik, Y.; Aymelek, A.; Yildirim, Ö.; Demirtaş, B.; Türker, T. Variations of natural frequencies of masonry minarets due to environmental effects. J. Civ. Struct. Health Monit. 2024, 14, 635–661. [Google Scholar] [CrossRef]
- Sharhan, Z.S.; Cucuzza, R.; Domaneschi, M.; Ghodousian, O.; Rad, M.M. Reinforcement of RC Two-Way Slabs with CFRP Laminates: Plastic Limit Method for Carbon Emissions and Deformation Control. Buildings 2024, 14, 3873. [Google Scholar] [CrossRef]
- Imposa, S.; Lombardo, G.; Panzera, F.; Grassi, S. Ambient Vibrations Measurements and 1D Site Response Modelling as a Tool for Soil and Building Properties Investigation. Geosciences 2018, 8, 87. [Google Scholar] [CrossRef]
- Ornthammarath, T.; Toe, T.T.T.; Rupakhety, R.; Málaga-Chuquitaype, C.; Ranaweera, J.; Pradittan, P. Empirical Formulas and Artificial Neural Networks to Estimate the Fundamental Periods of Existing and Instrumented RC Buildings in Thailand. J. Build. Eng. 2025, 100, 111691. [Google Scholar] [CrossRef]
- Masi, A.; Vona, M. Experimental and Numerical Evaluation of the Fundamental Period of Undamaged and Damaged RC Framed Buildings. Bull. Earthq. Eng. 2009, 8, 643–656. [Google Scholar] [CrossRef]
- Ruggieri, S.; Fiore, A.; Uva, G. A New Approach to Predict the Fundamental Period of Vibration for Newly-Designed Reinforced Concrete Buildings. J. Earthq. Eng. 2021, 26, 6943–6968. [Google Scholar] [CrossRef]
- Kaplan, O.; Güney, Y.; Doğangün, A. A Period-Height Relationship for Newly Constructed Mid-Rise Reinforced Concrete Buildings in Turkey. Eng. Struct. 2021, 232, 111807. [Google Scholar] [CrossRef]
- Uscamayta, E.J.M.; Vásquez, M.P.R.; Cusacani, Y.M.J.; Barrios, B.S.V.; Delgado, E.S.D.C.; Kana, A.R.; Bayona, Y.R.; García, C.E.J. Estimation of effective rigidity in reinforced concrete structures through modal identification tests and sclerometry. Salud Cienc. Tecnol. Ser. Conf. 2023, 2, 442. [Google Scholar] [CrossRef]
- Oliveira, C.S.; Navarro, M. Fundamental Periods of Vibration of RC Buildings in Portugal From in-Situ Experimental and Numerical Techniques. Bull. Earthq. Eng. 2009, 8, 609–642. [Google Scholar] [CrossRef]
- Chun, Y.-S.; Hur, M.-W. Effects of Isolation Period Difference and Beam-Column Stiffness Ratio on the Dynamic Response of Reinforced Concrete Buildings. Int. J. Concr. Struct. Mater. 2015, 9, 439–451. [Google Scholar] [CrossRef]
- Ditommaso, R.; Lamarucciola, N.; Ponzo, F.C. Prediction of the Fundamental Period of Infilled RC Framed Structures Considering the Maximum Inter-Story Drift at Different Design Limit States. Structures 2024, 63, 106422. [Google Scholar] [CrossRef]
- Shen, J.; Kitjasateanphun, T.; Srivanich, W. Seismic performance of steel moment frames with reduced beam sections. Eng. Struct. 2000, 22, 968–983. [Google Scholar] [CrossRef]
- Tsiavos, A.; Stojadinović, B. Constant yield displacement procedure for seismic evaluation of existing structures. Bull. Earthq. Eng. 2019, 17, 2137–2164. [Google Scholar] [CrossRef]
- Di Domenico, M.; Ricci, P.; Verderame, G.M. Numerical evaluation of period elongation for the assessment of seismic damage and usability of RC residential buildings. Procedia Struct. Integr. 2023, 44, 187–194. [Google Scholar] [CrossRef]
- Vitanova, M.; Makreska, R.S.; Tomic, D.; Bogdanovic, A.; Bojadjieva, J.; Edip, K. Assessment of Fundamental Periods of Vibration Through Analytical and Experimental In-Situ Measurements. In Proceedings of the 2nd Croatian Conference on Earthquake Engineering—2CroCEE, Zagreb, Croatia, 22–24 March 2023; University of Zagreb Faculty of Civil Engineering: Zagreb, Croatia, 2023; pp. 525–532. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, H.; Sun, B.; Chen, X.; Wang, H. Study on Empirical Formulas and Distribution Ranges of Vibration Periods in High-Rise Reinforced Concrete Constructions. J. Earthq. Eng. 2023, 27, 2506–2532. [Google Scholar] [CrossRef]
- Chakravarthy, P.; Basu, D. Natural Period and Vertical Distribution of Base Shear in Confined Masonry Buildings Using Ambient Vibration Test. Bull. Earthq. Eng. 2021, 19, 1851–1899. [Google Scholar] [CrossRef]
- Azzara, R.M.; Girardi, M.; Iafolla, V.; Lucchesi, D.; Padovani, C.; Pellegrini, D. Ambient Vibrations of Age-Old Masonry Towers: Results of Long-Term Dynamic Monitoring in the Historic Centre of Lucca. Int. J. Arch. Herit. 2019, 15, 5–21. [Google Scholar] [CrossRef]
- Inqiad, W.B.; Javed, M.F.; Siddique, M.S.; Alabduljabbar, H.; Ahmed, B.; Alkhattabi, L. Predicting natural vibration period of concrete frame structures having masonry infill using machine learning techniques. J. Build. Eng. 2024, 96, 110417. [Google Scholar] [CrossRef]
- Kontoni, D.-P.N.; Ghamari, A. Computational investigation of the fundamental period of reinforced concrete frame buildings with masonry infilled walls. AIP Conf. Proc. 2024, 3010, 030006. [Google Scholar] [CrossRef]
- Akcan, E.; Güneyisi, E.M. Effects of infill wall thickness and arrangement on the seismic performance of the reinforced concrete frames. Harran Üniversitesi Mühendislik Derg. 2024, 9, 58–70. [Google Scholar] [CrossRef]
- Paparo, A.; Beyer, K. Quasi-static cyclic tests of two mixed reinforced concrete–unreinforced masonry wall structures. Eng. Struct. 2014, 71, 201–211. [Google Scholar] [CrossRef]
- Astroza, R.; Conte, J.P.; Restrepo, J.I.; Ebrahimian, H.; Hutchinson, T.C. Seismic Response Analysis and Modal Identification of a Full-Scale Five-Story Base-Isolated Building Tested on the NEES@UCSD Shake Table. Eng. Struct. 2021, 238, 112087. [Google Scholar] [CrossRef]
- Kowalska-Koczwara, A.; Pachla, F.; Burdzik, R. Research on Human Exposure to Transport-Induced Vibration in Buildings. Appl. Sci. 2024, 14, 9016. [Google Scholar] [CrossRef]
- Zong, C.; Zhai, J.; Sun, X.; Liu, X.; Cheng, X.; Wang, S. Analysis of Seismic Responses and Vibration Serviceability in a High-Rise Timber–Concrete Hybrid Building. Buildings 2024, 14, 2614. [Google Scholar] [CrossRef]
- Chatzi, E.; Papadimitriou, C. Identification Methods for Structural Health Monitoring. In CISM International Centre for Mechanical Sciences; Springer International Publishing: Cham, Switzerland, 2016; Volume 567. [Google Scholar] [CrossRef]
- Thisovithan, P.; Aththanayake, H.; Meddage, D.P.P.; Ekanayake, I.U.; Rathnayake, U. A Novel Explainable AI-based Approach to Estimate the Natural Period of Vibration of Masonry Infill Reinforced Concrete Frame Structures Using Different Machine Learning Techniques. Res. Eng. 2023, 19, 101388. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, W.; Wang, C.; Qiu, Y.; Zhang, Y.; Li, Y.; Zhang, Y. Research on Loss Characteristics Based on the Vibration Law of Granular Assembly. Shock Vib. 2024, 2024, 8543345. [Google Scholar] [CrossRef]
- Koronides, M.; Kontoe, S.; Zdravković, L.; Vratsikidis, A.; Pitilakis, D. Numerical simulation of SSI free and forced vibration experiments on real scale structures of different stiffness. Soil Dyn. Earthq. Eng. 2023, 175, 108232. [Google Scholar] [CrossRef]
- Noureldin, M.; Kim, J. Simplified Life Cycle Cost Estimation of Low-Rise Steel Buildings Using Fundamental Period. Sustainability 2023, 15, 2706. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, Y.; Fu, S.; Feng, K.; Han, X.; Hu, Y.; Zhu, Q.; Wei, X. Analysis of Vibration Characteristics of Tractor–Rotary Cultivator Combination Based on Time Domain and Frequency Domain. Agriculture 2024, 14, 1139. [Google Scholar] [CrossRef]
- Li, Z.; Yang, X.; Zhang, S.; Yu, Y.; Lin, Y.; Wu, J. Analysis of Soil Differences in Subway Vibration Transmission Paths. Buildings 2024, 14, 1338. [Google Scholar] [CrossRef]
- Perrault, M.; Guéguen, P.; Parra, G.; Sarango, J. Modification of the Data-Driven Period/Height Relationship for Buildings Located in Seismic-Prone Regions Such as Quito (Ecuador). Bull. Earthq. Eng. 2020, 18, 3545–3562. [Google Scholar] [CrossRef]
- Ramos, F.B.M. Seismic response of reinforced concrete buildings, considering the effective stiffness in beams, columns and structural walls. South Fla. J. Dev. 2023, 4, 3981–3994. [Google Scholar] [CrossRef]
- Bozdogan, K.B.; Ozturk, D. Vibration Analysis of Asymmetric-Plan Frame Buildings Using Transfer Matrix Method. Math. Comput. Appl. 2010, 15, 279–288. [Google Scholar] [CrossRef]
- Saxena, S.; Patel, M. Evaluating dynamic behaviour of a concrete dam using modal analysis. Mater. Today Proc. 2023, 93, 296–301. [Google Scholar] [CrossRef]
- Jiménez, G.A.L.; Dias, D. Dynamic Soil–Structure Interaction Effects in Buildings Founded on Vertical Reinforcement Elements. CivilEng 2022, 3, 573–593. [Google Scholar] [CrossRef]
- Park, S.-J. Comparative Study on Hyperelastic Constitutive Models for the Static and Dynamic Behavior of Resilient Mounts. Materials 2025, 18, 311. [Google Scholar] [CrossRef]
- Cavaliere, F. Static and Dynamic Global Stiffness Analysis for Automotive Pre-Design. Ph.D Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2022. [Google Scholar] [CrossRef]
- Eka Saputra, N.; Priastiwi, Y.A. Comparative Study Of Dynamic Earthquake Analysis with Spectral Design and Time History Methods. J. Indones. Sos. Teknol. 2023, 4, 1223–1234. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Han, X.; Wei, J.; Zhang, T.; Li, S. Research on High Precision Stiffness Modeling Method of Redundant Over-Constrained Parallel Mechanism. Sensors 2023, 23, 5916. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, R.; Zha, X.; Liao, Y. Study on the Vibration Comfort of a High-Rise Industrial Building. Buildings 2024, 14, 3676. [Google Scholar] [CrossRef]
- Khan, M.M.; Khan, M.F.A.; Karinuddin, K.K.; Charan, K.S. Comparative Study of Linear Static and Linear Dynamic Method of Seismic Analysis of RCC Multistoried Building Using ETABS. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 735–744. [Google Scholar] [CrossRef]
- Shanshin, I.K.; Lukin, A.V.; Svyatogorov, I.G. Numerical Methods of Structures Seismic Analysis. In International Summer School-Conference “Advanced Problems in Mechanics”; Springer International Publishing: Cham, Switzerland, 2022; pp. 489–500. [Google Scholar] [CrossRef]
- Sánchez-Sarmiento, F.; Sorichetti, P. Analysis of the mechanical vibrations of a complex structure as a damped single degree of freedom system. Mem. Investig. Ing. 2022, 23, 2–17. [Google Scholar] [CrossRef]
- Sangamnerkar, P.; Dubey, S.K. Equations to evaluate fundamental period of vibration of buildings in seismic analysis. Struct. Monit. Maint. 2017, 4, 351–364. [Google Scholar] [CrossRef]
- Al-Nimry, H.; Resheidat, M.; Al-Jamal, M. Ambient Vibration Testing of Low and Medium Rise Infilled RC Frame Buildings in Jordan. Soil Dyn. Earthq. Eng. 2014, 59, 21–29. [Google Scholar] [CrossRef]
- Godarzi, N.; Hejazi, F. A Review of Health Monitoring and Model Updating of Vibration Dissipation Systems in Structures. CivilEng 2025, 6, 3. [Google Scholar] [CrossRef]
- Beskhyroun, S.; Hosseini, S.E.A. A Novel Methodology for Structural Health Monitoring of Buildings Subjected to Earthquakes. Nov. Methodol. Struct. Health Monit. Build. Subj. Earthq. 2025, 1, 33. [Google Scholar] [CrossRef]
- Ávila, J. Análisis Estructural Probabilista Orientado a Evaluación del Daño Sísmico de Edificios de Mampostería no Reforzada: Aplicación a Edificios Aislados y Agregados del Distrito del Ensanche de Barcelona. Ph.D. Thesis, Universitat Politècnica de Catalunya, Diagonal, Spain, 2021. [Google Scholar] [CrossRef]
- Lozano-Allimant, S.; Lopez, A.; Gomez, M.; Atencio, E.; Lozano-Galant, J.A.; Fingerhuth, S. Structural Health Assessment of a Reinforced Concrete Building in Valparaíso Under Seismic and Environmental Shaking: A Foundation for IoT-Driven Digital Twin Systems. Appl. Sci. 2025, 15, 1202. [Google Scholar] [CrossRef]
- Amaddeo, C.; Dorn, M.; Martinelli, L. Initial monitoring of a six-story lightweight timber frame building under different environmental conditions. J. Civ. Struct. Health Monit. 2024, 15, 371–393. [Google Scholar] [CrossRef]
- Thiesen, J.L.M.; Klahr, B.; Carniel, T.A.; Fancello, E.A. Limitations of poromechanical first-order computational homogenization for the representation of micro-scale volume changes. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 522. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, Q.; Peng, J. Dynamic Modeling and Analysis of Boundary Effects in Vibration Modes of Rectangular Plates with Periodic Boundary Constraints Based on the Variational Principle of Mixed Variables. Mathematics 2023, 11, 2381. [Google Scholar] [CrossRef]
- Maleki, H. Tackling Data-Limited Rock Mechanics Models. In Proceedings of the 58th U.S. Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 23–26 June 2024; ARMA: Crawford County, KS, USA, 2024. [Google Scholar] [CrossRef]
- Hu, A.; Paoletti, P. Analytical exploration of generic undamped mass–spring chains: A comprehensive study. Mech. Syst. Signal Process. 2024, 212, 111277. [Google Scholar] [CrossRef]
- Singh, O.N.; Dey, K. Evaluating Methods for Determining Dynamic Characteristics of Bridges: A Short Review and Research Gaps. Int. J. Appl. Eng. Res. 2024, 19, 162–172. [Google Scholar] [CrossRef]
- Abd-Alrazaq, A.; Nashwan, A.J.; Shah, Z.; Abujaber, A.; Alhuwail, D.; Schneider, J.; AlSaad, R.; Ali, H.; Alomoush, W.; Aziz, S.; et al. Machine Learning–Based Approach for Identifying Research Gaps: COVID-19 as a Case Study (Preprint). JMIR Form. Res. 2023, 8, e49411. [Google Scholar] [CrossRef] [PubMed]
- Mancini, A.; Cosoli, G.; Mobili, A.; Violini, L.; Pandarese, G.; Galdelli, A.; Narang, G.; Blasi, E.; Tittarelli, F.; Revel, G.M. A monitoring platform based on electrical impedance and AI techniques to enhance the resilience of the built environment. Acta IMEKO 2024, 13, 1–12. [Google Scholar] [CrossRef]
- Mengesha, G. Integrating AI in Structural Health Monitoring (SHM): A Systematic Review on Advances, Challenges, and Future Directions. Struct. Health Monit. (SHM) A Syst. Rev. Adv. Chall. Future Dir. 2025, 1, 24. [Google Scholar] [CrossRef]
- Etim, B.; Al-Ghosoun, A.; Renno, J.; Seaid, M.; Mohamed, M.S. Machine Learning-Based Modeling for Structural Engineering: A Comprehensive Survey and Applications Overview. Buildings 2024, 14, 3515. [Google Scholar] [CrossRef]
- Al Agha, W.; Almorad, W.A.; Umamaheswari, N.; Alhelwani, A. Study the seismic response of reinforced concrete high-rise building with dual framed-shear wall system considering the effect of soil structure interaction. Mater. Today Proc. 2021, 43, 2182–2188. [Google Scholar] [CrossRef]
- Di, G.; Xie, Z.; Guo, J. Predict the Influence of Environmental Vibration From High-Speed Railway on Over-Track Buildings. Sustainability 2021, 13, 3218. [Google Scholar] [CrossRef]
- Son, D.-H.; Choi, C.-S. Stiffness reduction effect of vertically divided reinforced concrete structural walls. J. Build. Eng. 2023, 76, 107188. [Google Scholar] [CrossRef]
- Chambers, J.J.; Almudhafar, S.; Stenger, F. Effect of Reduced Beam Section Frame Elements on Stiffness of Moment Frames. J. Struct. Eng. 2003, 129, 383–393. [Google Scholar] [CrossRef]
- Fanaie, N.; Nadalipour, Z.; Sarkhosh, O.S.; Faegh, S.S. Elastic drift amplification factor in steel moment frames with double reduced beam section (DRBS) connections. J. Build. Eng. 2021, 43, 102563. [Google Scholar] [CrossRef]
- Zhou, Q.; Pan, W.; Lan, X. Study on Vibration Reduction Effect of the Building Structure Equipped with Intermediate Column–Lever Viscous Damper. Buildings 2024, 14, 1881. [Google Scholar] [CrossRef]
- Marin, M.C.; El Debs, M.K. Contribution to assessing the stiffness reduction of structural elements in the global stability analysis of precast concrete multi-storey buildings. Rev. IBRACON Estrut. E Mater. 2012, 5, 316–342. [Google Scholar] [CrossRef]
- Seifiasl, A.; Asl, M.H. Experimental and numerical study on the seismic behavior of steel plate shear wall with reduced web section beams. J. Build. Eng. 2022, 46, 103797. [Google Scholar] [CrossRef]
- Abou-Elfath, H.; Elhout, E. Theoretical-period characteristics of frame buildings designed under variable levels of seismicity and allowable-drift. Earthq. Eng. Eng. Vib. 2020, 19, 669–681. [Google Scholar] [CrossRef]
- Beskhyroun, S.; Navabian, N.; Wotherspoon, L.; Ma, Q. Dynamic Behaviour of a 13-Story Reinforced Concrete Building Under Ambient Vibration, Forced Vibration, and Earthquake Excitation. J. Build. Eng. 2020, 28, 101066. [Google Scholar] [CrossRef]
- Oh, Y.-K.; Kang, M.-W.; Lee, K.; Kim, S. Construction Management Solutions to Mitigate Elevator Noise and Vibration of High-Rise Residential Buildings. Sustainability 2020, 12, 8924. [Google Scholar] [CrossRef]
- Zhong, L. Structural and Load Analysis of the Belgian Atomic Tower. Highlights Sci. Eng. Technol. 2023, 75, 23–30. [Google Scholar] [CrossRef]
- Tahaii, S.M.; Hamidi, H.; Amiri, J.V. Inelastic Seismic Demand of Steel-Plate Shear Wall Structures: Emphasis on the PTD Effect. Int. J. Civ. Eng. 2022, 20, 1145–1163. [Google Scholar] [CrossRef]
- Fereidooni, O.; Zarfam, P.; Mansoori, M. Experimental and Numerical Evaluation of the Effect of Implementing Wall Posts on Seismic Behavior of Short-Period Structures. Numer. Methods Civ. Eng. 2022, 6, 1–15. [Google Scholar] [CrossRef]
- Ratnika, L.; Gaile, L.; Vatin, N. Impact of Groundwater Level Change on Natural Frequencies of RC Buildings. Buildings 2021, 11, 265. [Google Scholar] [CrossRef]
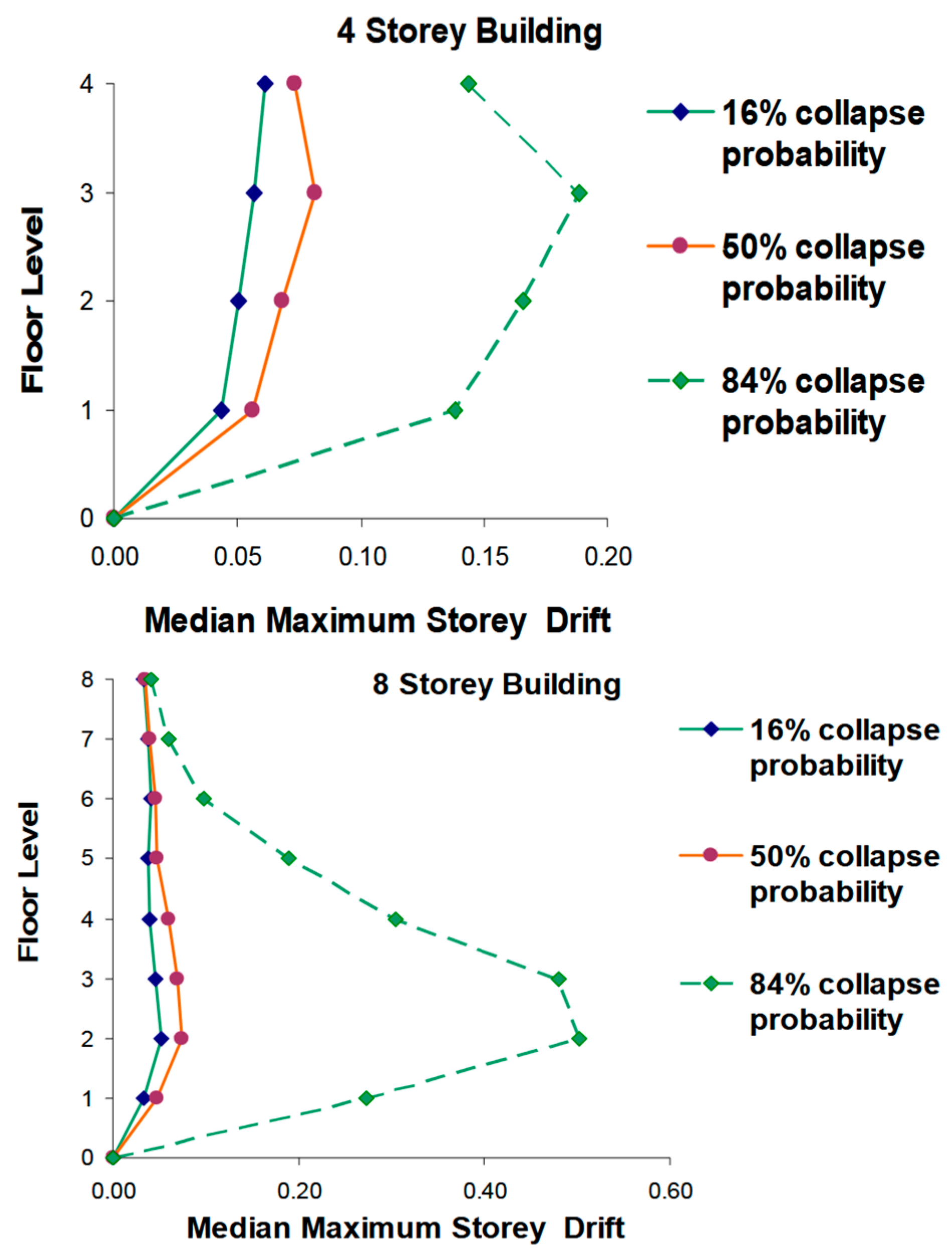
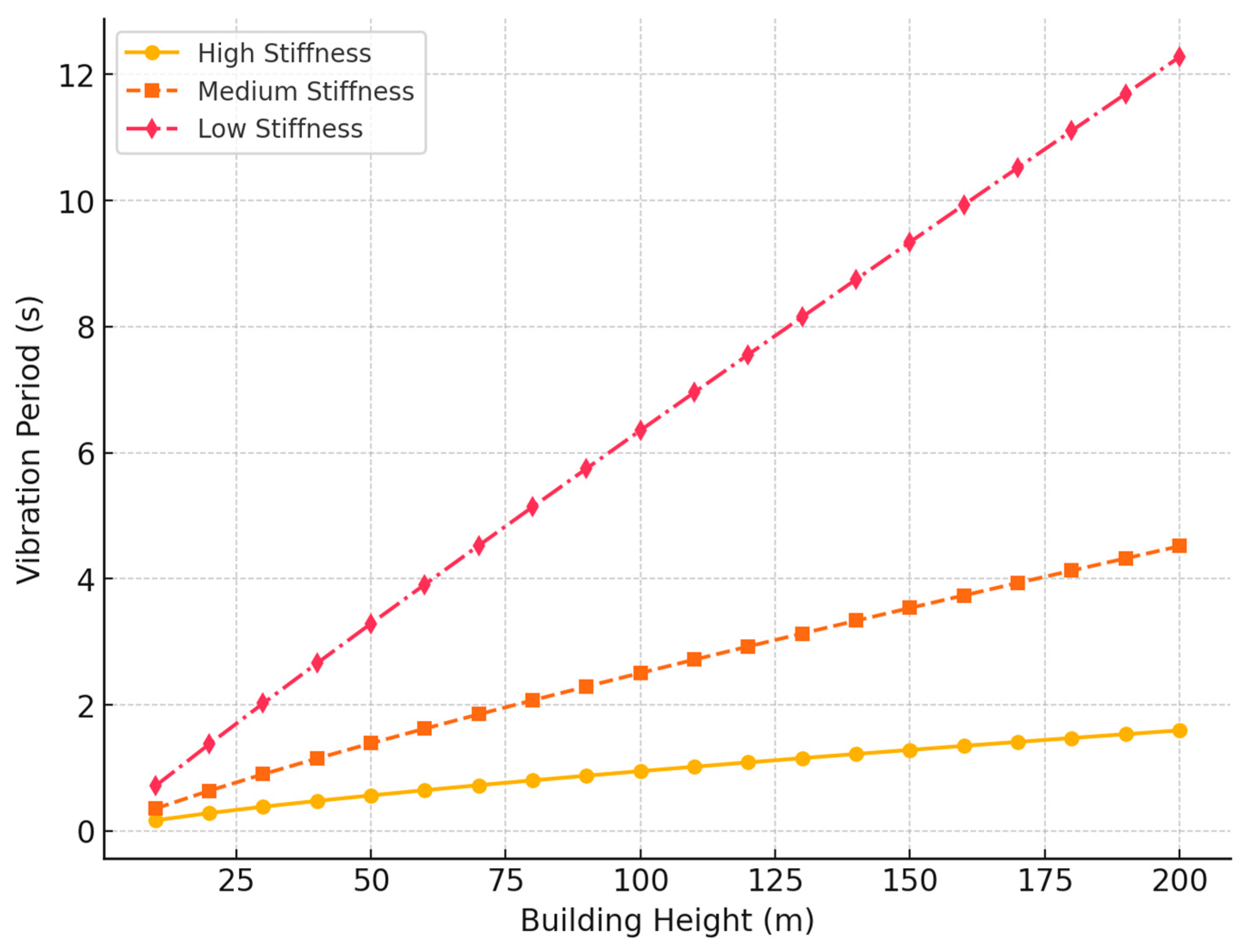
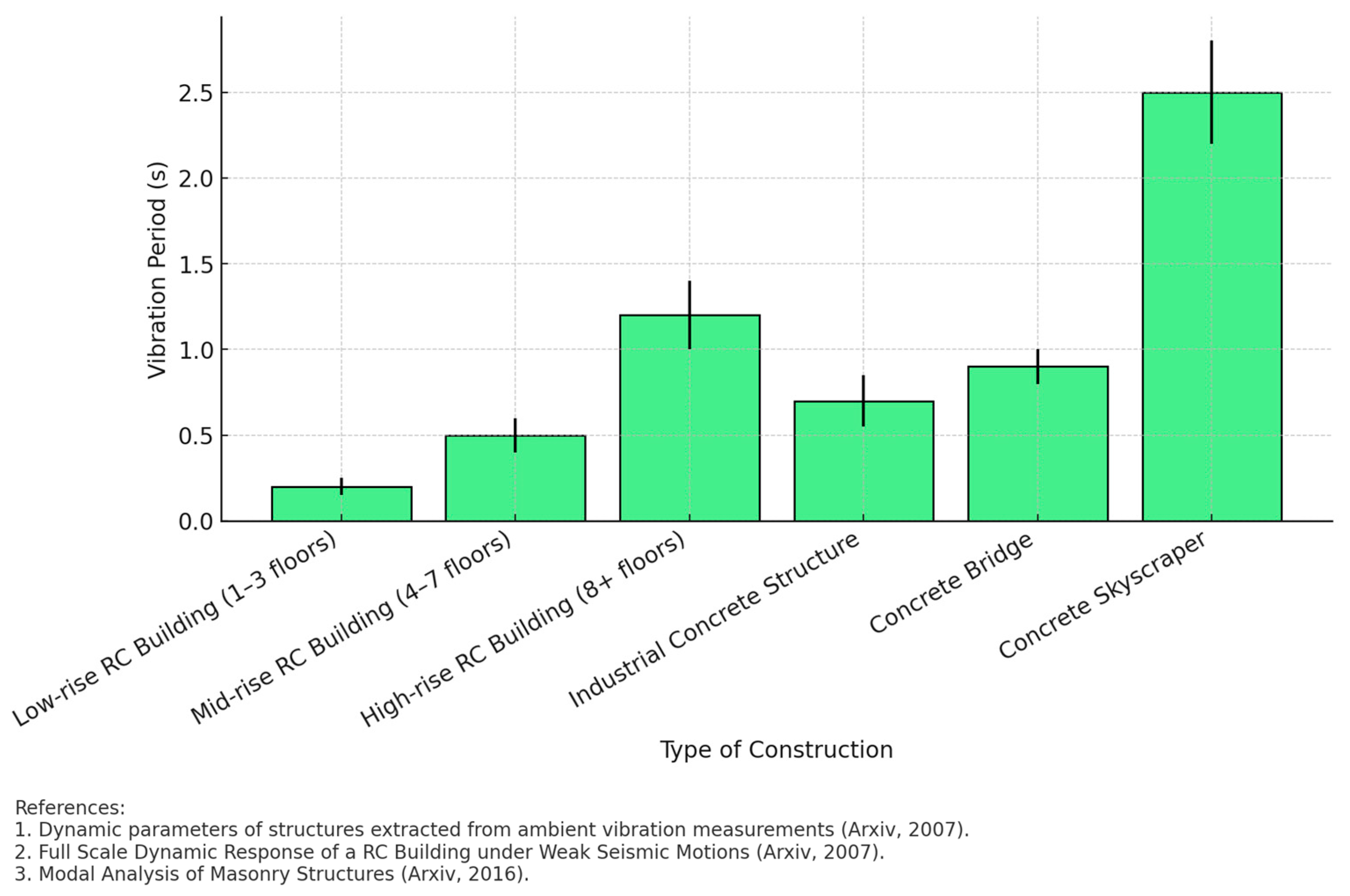

| Source | Method | Model/Equation | Applicability and Observations | Limitations |
|---|---|---|---|---|
| [41] | Numerical Simulation | Finite Element Methods (FEM) for Assessing Static Stiffness in Elastic Supports | Improves simulation accuracy, but requires greater computational power | High computational cost and depends on accurate models |
| [42] | Static Stiffness Analysis | Force-displacement ratio: | Used in automotive design to evaluate noise and vibration | Does not capture dynamic effects |
| [43] | Dynamic Analysis (Temporal History) | Differential equations of motion: | Captures dynamic effects, but requires detailed data on materials and soils | Requires experimental data and high computational capacity |
| [44] | Finite Element Method (FEM) | Discretization of structures using matrix equations | High precision, applicable to complex scenarios | Sensitive to input data errors |
| [4,31] | Spectral Analysis | Response evaluation using acceleration spectra | More efficient than temporal history analysis in seismic studies | Does not capture non-linear effects |
| [45] | Structural Simulation Software | Parametric models to optimize structural design | Simplifies complex systems without the need for large computational resources | Results depend on the quality of the model |
| [40] | Static Analysis (Equivalent Lateral Forces) | Suitable for regular structures but limited in dynamic behavior | Not suitable for irregular structures | |
| [9] | Análisis Modal | Modal decomposition with equations of state | Allows evaluation of main vibration modes of the structure | Does not consider damping effects |
| [3] | Natural Vibration Analysis | Direct relationship between stiffness and vibration period | Simplified approximation, ignores damping effects | |
| [42] | Computational Simulation | Models based on elasticity theory | Facilitates validation of physical and experimental models | Error-sensitive input parameters |
| [43] | Comparison between Static and Dynamic Methods | Relationship between stresses and deformations under seismic loads | Demonstrates that dynamic analysis produces increased base shear | Requires high accuracy in input data |
| No. | Author(s) and Year | Country | Study Type | Structure Type | Key Variable | Methodology | Main Findings |
|---|---|---|---|---|---|---|---|
| 1 | Li et al. (2020) | China | Experimental | Concrete frame | Fundamental period | Ambient vibration test | Period increases with height in nonlinear fashion. |
| 2 | Smith et al. (2019) | USA | Numerical | Steel structure | Lateral stiffness | Finite element model | Stiffness affects mode shape more than frequency. |
| 3 | Pérez et al. (2021) | Mexico | Mixed | Mixed system | Dynamic coefficient | Hybrid analysis | Coefficient is highly geometry-dependent. |
| 4 | Kim & Lee (2018) | South Korea | Numerical | Concrete wall | Modal frequency | Simulation and code comparison | Code predictions overestimate real periods. |
| 5 | Gómez et al. (2020) | Colombia | Experimental | Concrete frame | Elastic modulus | Full-scale test | Elastic behavior consistent with theoretical expectations. |
| 6 | Wang et al. (2017) | China | Numerical | Shear wall | Vibration response | Numerical simulation | Vibration data validated numerical model. |
| 7 | Chen et al. (2022) | Taiwan | Experimental | Concrete frame | Displacement | Field instrumentation | Displacement reduced with increased rigidity. |
| 8 | Alvarez & Torres (2019) | Peru | Mixed | Composite slab | Natural period | Empirical and parametric | Empirical models match simulations for mid-rise buildings. |
| 9 | Santos et al. (2020) | Brazil | Experimental | Concrete column | Base shear | Modal test | Higher base shear leads to period shortening. |
| 10 | Yamada et al. (2021) | Japan | Numerical | Reinforced concrete | Rigidity ratio | Time-history analysis | Rigidity ratio correlates with building symmetry. |
| Type of Construction | Vibration Period (s) | Standard Deviation |
|---|---|---|
| Ground Floor Building (1–3 floors) | 0.2 | 0.05 |
| Medium Building (4–7 floors) | 0.5 | 0.08 |
| Tall Building (8–20 floors) | 1.2 | 0.15 |
| Skyscrapers (>20 floors) | 2.5 | 0.30 |
| Concrete Bridge | 0.8 | 0.10 |
| Industrial Structure | 1.0 | 0.12 |
| Study | Structural Element | Period Reduction (%) | Key Observations | Methods | Applications | Practical Implications |
|---|---|---|---|---|---|---|
| Ditommaso [14] | Shear walls | 20–30 | Significant increase in structural stiffness | Nonlinear numerical analyses to integrate the database for the Ultimate Limit State (SLU) | Develop new simplified period-to-height relationships to more accurately estimate the fundamental vibration period of 330 buildings with reinforced concrete structures. | The fundamental period affects seismic design response spectra values. Infill elements are often excluded from structural design processes. Non-structural elements influence natural elastic periods, affecting spectral accelerations. Current seismic codes may inadequately protect buildings from moderate earthquakes. |
| Kaplan [10] | Beams and columns | 10–15 | Nonlinear relationship between height and period | Regression analysis and derivation of equations to estimate the period of elastic fundamental vibration of buildings. | Force-based design of 24 reinforced concrete mid-rise buildings for fundamental period estimates | The proposed equation aids in conservative design of mid-rise RC buildings. Rigid infill panels should be isolated or considered in design. Period-height equations must be region-specific for accurate assessments. TBEC-2018 should include regulations for infill panel contributions. |
| Perrault [36] | Non-structural elements (For example, infill materials) | 5–10 | Importance of considering non-structural elements | Data-based methods using environmental vibrations for the adjustment of empirical relationships applied to building classes | To study the effect of cumulative damage in 146 reinforced concrete buildings located in seismic zones, even with weak seismic movements. | The study examines the effect of cumulative damage on building resonant periods. It highlights variations in empirical relationships due to seismic exposure. The impact of weak seismic ground motion on building frequency is analyzed. The paper discusses uncertainties in seismic vulnerability of existing structures |
| Astroza [26] | Insulated Base Structures | 15–25 | Effect of the isolated base on dynamic behavior | Identification of the dynamic properties of a time-invariant equivalent linear model of a reinforced concrete building. | Effects of the insulation system on the prolongation of the predominant period of a building. | The paper analyzes seismic response of a base-isolated building. It identifies dynamic properties of an equivalent linear model. The effects of isolation systems on building performance are investigated |
| Dong-Hee [67] | Vertically divided reinforced concrete structural walls | 30–50 | Strength and stiffness decreased due to vertical splitting. | Manufacture of six full-scale specimens. Performing reverse cyclic load tests. | Investigation of the effects of vertical division on the stiffness and strength of walls. Structural analysis for real moment reduction of the building using 6 full-scale specimens. | |
| Chambers [68] | Beam Section Frame Elements. | 3.6–15.1 | Resulting reduction in terms of stiffness. | Analytically derived stiffness matrix. Finite Element Analysis. | Special moment-resistant gantries with reduced beam cross-sections. Seismic analysis of the base shear in moment gantries. | Flange reductions are acceptable in beam-column connections for moment frames. The stiffness matrix aids in analyzing frame structures with flange reductions. Reductions can increase story drift in moment frames |
| Fanaie [69] | Double-reduced beam section connections | 5.5–14.7 | Increased elastic drift with IPE and HEA sections. | Theoretical approach based on mathematical relationships (MSR) and principles of structural analysis. | Estimation of the Elastic Drift Amplification Factor in Moment-Resistant Steel Structures with DRBS Connections. | The study recommends using modified RBS connections in high seismic risk areas. Effective elastic drift calculations are suggested for reduced beam flange widths. DRBS connections may improve seismic behavior but raise drift control concerns. The paper provides design charts for RBS connections. The article enhances visibility before final publication |
| Zhou [70] | Building structure equipped with a viscous buffer with an intermediary-lever column | 12 40 | Improved displacement amplification by up to 12%. Displacement between floors is reduced during earthquakes. | A simplified mechanical model of CLVD was derived. The effects of the parameters on the vibration reduction ratios were analyzed. | CLVD for energy dissipation and vibration reduction design. Example of a Nine-Story Structure for Structural Application. | Traditional damping systems occupy significant building space, reducing efficiency. The study proposes a new amplification device for energy dissipation and vibration reduction. CLVD’s optimal vibration reduction effect is contingent on specific parameters |
| Marin [71] | Multi-storey concrete prefabricated building structures. | 20 33 | Stiffness reduction coefficients for columns. Stiffness reduction coefficients for beams. | Finite element modeling with ANSYS® software. Consideration of physical and geometric nonlinearity. | Evaluation of the reduction of stiffness in precast concrete structures. Analysis of the overall stability of multi-storey buildings. | The study provides stiffness reduction coefficients for precast concrete structures. It compares findings with national and international codes. The research aids in understanding the effects of axial force on stiffness. It highlights the limitations of simplified PNL considerations in codes. |
| Afshar Seifiasl [72] | Steel plate shear walls with low core section beams | 3–6 30 | Stable hysteresis curves, with plant drift, without reduction in bearing capacity. Load Reduction, Superior Energy Dissipation. | Experimental tests under quasi-static cyclic loading. Nonlinear finite element (FE) modeling and verification. | The integration of the building installations in the plant area was carried out by analyzing 5 specimens. Improved structural depth and ductility. | |
| Abou-Elfath [73] | Timber frame buildings designed under varying levels of Seismicity and admissible drift | - | Theoretical MRF periods sensitive to seismicity and lateral drift levels. | Evaluation of the theoretical fundamental periods of timber structure buildings. Analysis of design seismicity and permissible lateral drift effects. | Evaluation of the theoretical fundamental periods of 12 wood-frame buildings. Sensitivity Analysis of Design Seismicity and Lateral Drift. | Current period equations do not account for seismicity levels or lateral drift limits. Buildings designed under high seismicity show higher stiffness and shorter periods. The need for modifying period equations is emphasized for realistic assessments. |
| Shen [15] | Moment gantries with reduced beam cross-section | - | Sa capabilities were measured for different performance levels. | A connection model was developed for the validation of cyclical deterioration. Incremental Dynamic Analysis (IDA) for performance quantification. | Seismic performance of moment gantries with reduced beam cross-section. Immediate occupancy and collapse prevention performance targets. | The study enhances understanding of connection performance in steel frames. It provides probabilistic S a capacities for design earthquakes. The findings inform selection of intensity and demand measures in IDA. Improved collapse criteria increase robustness in structural analysis. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paredes, J.; Ramirez, W.; Pico, F.; Acosta, R.; Toapanta, O.G.; Mayacela, M. Impact of Structural Stiffness on Vibration Periods of Concrete Buildings: A Systematic Review. Materials 2025, 18, 2612. https://doi.org/10.3390/ma18112612
Paredes J, Ramirez W, Pico F, Acosta R, Toapanta OG, Mayacela M. Impact of Structural Stiffness on Vibration Periods of Concrete Buildings: A Systematic Review. Materials. 2025; 18(11):2612. https://doi.org/10.3390/ma18112612
Chicago/Turabian StyleParedes, Juan, Wladimir Ramirez, Fernanda Pico, Rodrigo Acosta, Oscar G. Toapanta, and Margarita Mayacela. 2025. "Impact of Structural Stiffness on Vibration Periods of Concrete Buildings: A Systematic Review" Materials 18, no. 11: 2612. https://doi.org/10.3390/ma18112612
APA StyleParedes, J., Ramirez, W., Pico, F., Acosta, R., Toapanta, O. G., & Mayacela, M. (2025). Impact of Structural Stiffness on Vibration Periods of Concrete Buildings: A Systematic Review. Materials, 18(11), 2612. https://doi.org/10.3390/ma18112612










