Computational Investigation of an All-sp3 Hybridized Superstable Carbon Allotrope with Large Band Gap
Abstract
1. Introduction
2. Computational Method
3. Results and Discussion
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balaban, A.T. Carbon and its nets. Comput. Math. Appl. 1989, 17, 397–416. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Lv, J.; Zhu, C.; Li, Q.; Zhang, M.; Li, Q.; Ma, Y. First-principles structural design of superhard materials. J. Chem. Phys. 2013, 138, 114101. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.T.; Chen, C.F.; Wang, E.G.; Kawazoe, Y. A New Carbon Allotrope with Six-Fold Helical Chains in all-sp2 Bonding Networks. Sci. Rep. 2014, 4, 04339. [Google Scholar] [CrossRef]
- Wang, J.T.; Mizuseki, C.F.C.H.; Kawazoe, Y. New carbon allotropes in sp+sp3 bonding networks consisting of C8 cubes. Phys. Chem. Chem. Phys. 2018, 20, 7962–7967. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, X.Y.; Gan, L.Y.; Cao, Y.; Li, B.S.; Wu, X.; Wang, R. Symmetry-guaranteed ideal Weyl semimetallic phase in face-centered orthogonal C6. Phys. Rev. B 2020, 101, 235119. [Google Scholar] [CrossRef]
- Wang, J.T.; Weng, H.; Chen, C.F. Topological nodal line semimetals in graphene network structures. Adv. Phys-X 2019, 4, 1625724. [Google Scholar] [CrossRef]
- Weng, H.; Liang, Y.; Xu, Q.; Yu, R.; Fang, Z.; Dai, X.; Kawazoe, Y. Topological node-line semimetal in three-dimensional graphene networks. Phys. Rev. B 2015, 92, 045108. [Google Scholar] [CrossRef]
- Wang, J.T.; Weng, H.; Nie, S.; Fang, Z.; Kawazoe, Y.; Chen, C.F. Body-centered orthorhombic C16: A novel topological node-line semimetal. Phys. Rev. Lett. 2016, 116, 195501. [Google Scholar] [CrossRef]
- Cheng, Y.; Feng, X.; Cao, X.T.; Wen, B.; Wang, Q.; Kawazoe, Y.; Jena, P. Body-centered tetragonal C16: A novel topological node-line semimetallic carbon composed of tetrarings. Small 2017, 13, 1602894. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Y.; Yang, S.A.; Pan, H.; Zhang, F.; Cohen, M.L.; Zhang, S.B. Nanostructured carbon allotropes with Weyl-like loops and points. Nano Lett. 2015, 15, 6974–6978. [Google Scholar] [CrossRef]
- Wang, J.T.; Chen, C.; Kawazoe, Y. Topological nodal line semimetal in an orthorhombic graphene network structure. Phys. Rev. B 2018, 97, 245147. [Google Scholar] [CrossRef]
- Li, Z.Z.; Chen, J.; Nie, S.; Xu, L.F.; Mizuseki, H.; Weng, H.; Wang, J.T. Orthorhombic carbon oC24: A novel topological nodal line semimetal. Carbon 2018, 133, 39–43. [Google Scholar] [CrossRef]
- Wang, J.T.; Qian, Y.; Weng, H.; Wang, E.G.; Chen, C.F. Three-dimensional crystalline modification of graphene in all-sp2 hexagonal lattices with or without topological nodal lines. J. Phys. Chem. Lett. 2019, 10, 2515–2521. [Google Scholar] [CrossRef]
- Bu, K.; Wang, J.T.; Weng, H.; Chen, C.F. Topological semimetal in an sp2-sp3 hybridized carbon network with nodal rings. Phys. Rev. B 2020, 101, 205104. [Google Scholar] [CrossRef]
- Bu, K.; Qian, Y.; Wang, J.T.; Weng, H. Hybrid Nodal Chain in an Orthorhombic Graphene Network. Phys. Rev. B 2021, 103, L081108. [Google Scholar] [CrossRef]
- Tao, Y.; Bu, K.; Wang, J.T. Orthorhombic C32: A topological semimetal with nodal ring. Phys. Lett. A 2022, 451, 128397. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wang, Q.; Kawazoe, Y.; Jena, P. A new 3D Dirac nodal-line semi-metallic graphene monolith for lithium ion battery anode materials. J. Mater. Chem. A 2018, 6, 13816–13824. [Google Scholar] [CrossRef]
- Ni, D.; Shen, Y.; Sun, W.; Wang, Q. Design of 3D topological nodal-net porous carbon for sodium-ion battery anodes. J. Mater. Chem. A 2022, 10, 7754–7763. [Google Scholar] [CrossRef]
- Zhao, Z.; Hang, Y.; Zhang, Z.; Guo, W. Topological hybrid nodal-loop semimetal in a carbon allotrope constructed by interconnected Riemann surfaces. Phys. Rev. B 2019, 100, 115420. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Z.; Guo, W. A family of all sp2-bonded carbon allotropes of topological semimetals with strain-robust nodal-lines. J. Mater. Chem. C 2020, 8, 1548–1555. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1984, 318, 162–163. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1981, 354, 56–58. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Yin, M.T. Si-III (BC-8) crystal phase of Si and C: Structural properties, phase stabilities, and phase transitions. Phys. Rev. B 1984, 30, 1773. [Google Scholar] [CrossRef]
- Johnston, L.R.; Hoffmann, R. Superdense Carbon, C8: Supercubane or Analogue of γ-Si? J. Am. Chem. Soc. 1989, 111, 810–819. [Google Scholar] [CrossRef]
- Knudson, M.D.; Desjarlais, M.P.; Dolan, D.H. Shock-wave exploration of the high-pressure phases of carbon. Science 2008, 322, 1822–1825. [Google Scholar] [CrossRef] [PubMed]
- Vora, H.; Moravec, T.J. Structural investigation of thin films of diamondlike carbon. J. Appl. Phys. 1981, 52, 6151–6157. [Google Scholar] [CrossRef]
- Mao, W.L.; Mao, H.K.; Eng, P.J.; Trainor, T.P.; Newville, M.; Kao, C.C.; Heinz, D.L.; Shu, J.; Meng, Y.; Hemley, R.J. Bonding changes in compressed superhard graphite. Science 2003, 202, 425–427. [Google Scholar] [CrossRef]
- Chen, P.W.; Huang, F.L.; Yun, S.R. Characterization of the condensed carbon in detonation soot. Carbon 2003, 41, 2093–2099. [Google Scholar] [CrossRef]
- Pantea, D.; Brochu, S.; Thiboutot, S.; Ampleman, G.; Scholz, G. A morphological investigation of soot produced by the detonation of munitions. Chemosphere 2006, 65, 821–831. [Google Scholar] [CrossRef]
- Kirai, H.; Kondo, K.I. Modified Phases of Diamond Formed Under Shock Compression and Rapid Quenching. Science 1991, 253, 772–774. [Google Scholar]
- Wen, B.; Li, T.; Dong, C.; Zhang, X.; Yao, S.; Cao, Z.; Wang, D.; Ji, S.; Jin, J. Preparation of diamond nanocrystals from catalysed carbon black in a high magnetic field. J. Phys. Condens. Matter 2003, 15, 8049. [Google Scholar] [CrossRef]
- Wen, B.; Li, T.; Dong, C.; Zhang, X.; Yao, S.; Cao, Z.; Wang, D.; Ji, S.; Jin, J. Study of the stability of n-diamond. J. Phys. Condens. Matter 2004, 16, 2991. [Google Scholar] [CrossRef]
- Wen, B.; Li, T.; Dong, C.; Zhang, X.; Yao, S.; Cao, Z.; Wang, D.; Ji, S.; Jin, J. Formation mechanism of diamond nanocrystal from catalysed carbon black. J. Phys. Condens. Matter 2004, 16, 6891. [Google Scholar] [CrossRef]
- Wen, B.; Zhao, J.; Li, T.; Dong, C.; Jin, J. n-diamond from catalysed carbon nanotubes: Synthesis and crystal structure. J. Phys. Condens. Matter 2005, 17, L513. [Google Scholar] [CrossRef]
- Wen, B.; Li, T.; Dong, C.; Jin, J. Transformation mechanism from carbon nanotubes to n-diamond. J. Mater. Res. 2005, 20, 1485–1489. [Google Scholar] [CrossRef]
- Wen, B.; Zhao, J.; Li, T.; Dong, C. n-diamond: An intermediate state between rhombohedral graphite and diamond? New J. Phys. 2006, 8, 62. [Google Scholar] [CrossRef]
- Hou, L.; Cui, X.; Guan, B.; Wang, S.; Li, R.; Liu, Y.; Zhu, D.; Zheng, J. Synthesis of a monolayer fullerene network. Nature 2022, 606, 507–510. [Google Scholar] [CrossRef]
- Pan, F.; Ni, K.; Xu, T.; Chen, H.; Wang, Y.; Gong, K.; Liu, C.; Li, X.; Lin, M.L.; Li, S.; et al. Long-range ordered porous carbons produced from C60. Nature 2023, 614, 95–101. [Google Scholar] [CrossRef]
- Wang, J.T.; Chen, C.F.; Kawazoe, Y. New cubic carbon phase via graphitic sheet rumpling. Phys. Rev. B 2012, 85, 214104. [Google Scholar] [CrossRef]
- Li, Z.Z.; Lian, C.S.; Xu, J.; Xu, L.F.; Wang, J.T.; Chen, C.F. Computational prediction of body-centered cubic carbon in an all-sp3 six-member ring configuration. Phys. Rev. B 2015, 91, 214106. [Google Scholar] [CrossRef]
- Li, Z.Z.; Wang, J.T.; Mizuseki, H.; Chen, C.F. Computational discovery of a new rhombohedral diamond phase. Phys. Rev. B 2018, 98, 094107. [Google Scholar] [CrossRef]
- Bu, K.; Li, Z.Z.; Wang, J.T. Computational prediction of a simple cubic carbon allotrope consisting of C12 clusters. J. Chem. Phys. 2017, 147, 064512. [Google Scholar] [CrossRef] [PubMed]
- Bu, K.; Wang, J.T.; Li, Z.Z.; Mizuseki, H.; Kawazoe, Y. A superhard orthorhombic carbon with all six-membered-ring in sp3 bonding networks. Phys. Lett. A 2019, 383, 2809–2812. [Google Scholar] [CrossRef]
- Li, Q.; Ma, Y.; Oganov, A.R.; Wang, H.; Wang, H.; Xu, Y.; Cui, T.; Mao, H.K.; Zou, G. Superhard Monoclinic Polymorph of Carbon. Phys. Rev. Lett. 2009, 102, 175506. [Google Scholar] [CrossRef]
- Umemoto, K.; Wentzcovitch, M.R.; Saito, S.; Miyake, T. Body-Centered Tetragonal C4: A Viable sp3 Carbon Allotrope. Phys. Rev. Lett. 2010, 104, 125504. [Google Scholar] [CrossRef]
- Wang, J.T.; Chen, C.F.; Kawazoe, Y. Low-Temperature Phase Transformation from Graphite to sp3 Orthorhombic Carbon. Phys. Rev. Lett. 2011, 106, 075501. [Google Scholar] [CrossRef]
- Amsler, M.; Flores-Livas, J.A.; Lehtovaara, L.; Balima, F.; Ghasemi, S.A.; Machon, D.; Pailhès, S.; Willand, A.; Caliste, D.; Botti, S.; et al. Crystal Structure of Cold Compressed Graphite. Phys. Rev. Lett. 2012, 108, 065501. [Google Scholar] [CrossRef]
- Sheng, X.L.; Yan, Q.B.; Ye, F.; Zheng, Q.R.; Su, G. T-Carbon: A Novel Carbon Allotrope. Phys. Rev. Lett. 2011, 106, 155703. [Google Scholar] [CrossRef]
- Samara Carbon Allotrope Database. Available online: http://sacada.sctms.ru (accessed on 22 May 2025).
- Hoffmann, R.; Kabanov, A.A.; Golov, A.A.; Proserpio, D.M. Homo Citans and Carbon Allotropes: For an Ethics of Citation. Angew. Chem. Int. Ed. 2016, 55, 10962–10976. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, R.; Zhu, X.; Pan, A.; Han, C.; Li, X.; Zhao, D.; Ma, C.; Wang, W.; Su, H.; et al. Pseudo-topotactic conversion of carbon nanotubes to T-carbon nanowires under picosecond laser irradiation in methanol. Nat. Commun. 2017, 8, 683. [Google Scholar] [CrossRef] [PubMed]
- Wells, A.F. The geometrical basis of crystal chemistry. Part 1. Acta Crystallogr. 1954, 7, 535–544. [Google Scholar] [CrossRef]
- He, C.; Shi, X.; Clark, S.J.; Li, J.; Pickard, C.J.; Ouyang, T.; Zhang, C.; Tang, C.; Zhong, J. Complex Low Energy Tetrahedral Polymorphs of Group IV Elements from First Principles. Phys. Rev. Lett. 2018, 121, 175701. [Google Scholar] [CrossRef]
- Shi, X.; Li, S.; Li, J.; Ouyang, T.; Zhang, C.; Tang, C.; He, C.; Zhong, J. High-Throughput Screening of Two-Dimensional Planar sp2 Carbon Space Associated with a Labeled Quotient Graph. J. Phys. Chem. Lett. 2021, 12, 11511–11519. [Google Scholar] [CrossRef]
- Calderon, H.A.; Estrada-Guel, I.; Alvarez-Ramírez, F.; Hadjiev, V.G.; Hernandez, F.C.R. Morphed graphene nanostructures: Experimental evidence for existence. Carbon 2016, 102, 288–296. [Google Scholar] [CrossRef]
- Kresse, G.; Furthüller, J. Effcient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Armiento, R.; Mattsson, A.E. Functional designed to include surface effects in self-consistent density functional theory. Phys. Rev. B 2005, 72, 085108. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Occelli, F.; Loubeyre, P.; LeToullec, R. Properties of diamond under hydrostatic pressures up to 140 GPa. Nat. Mater. 2002, 2, 151–154. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar]

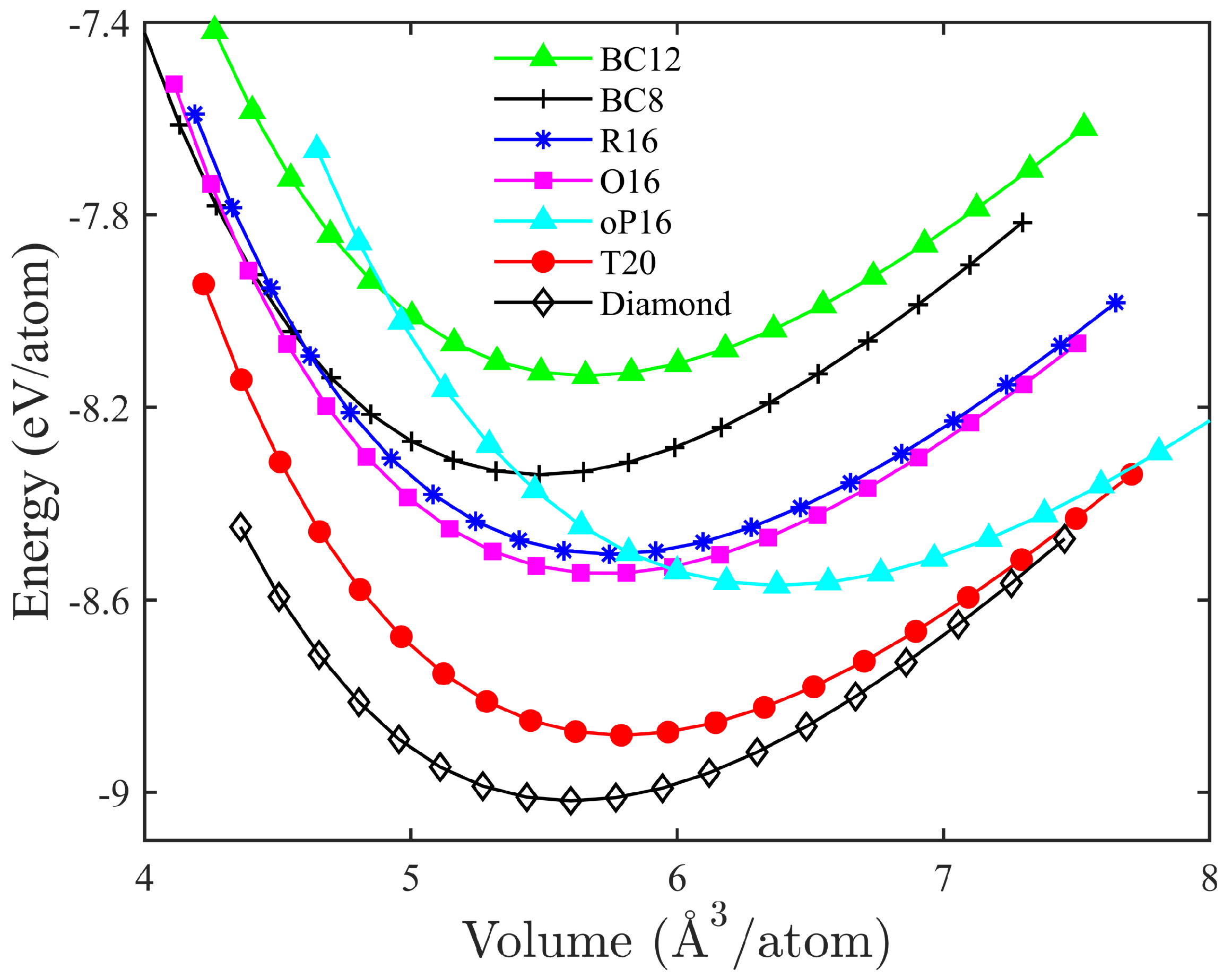
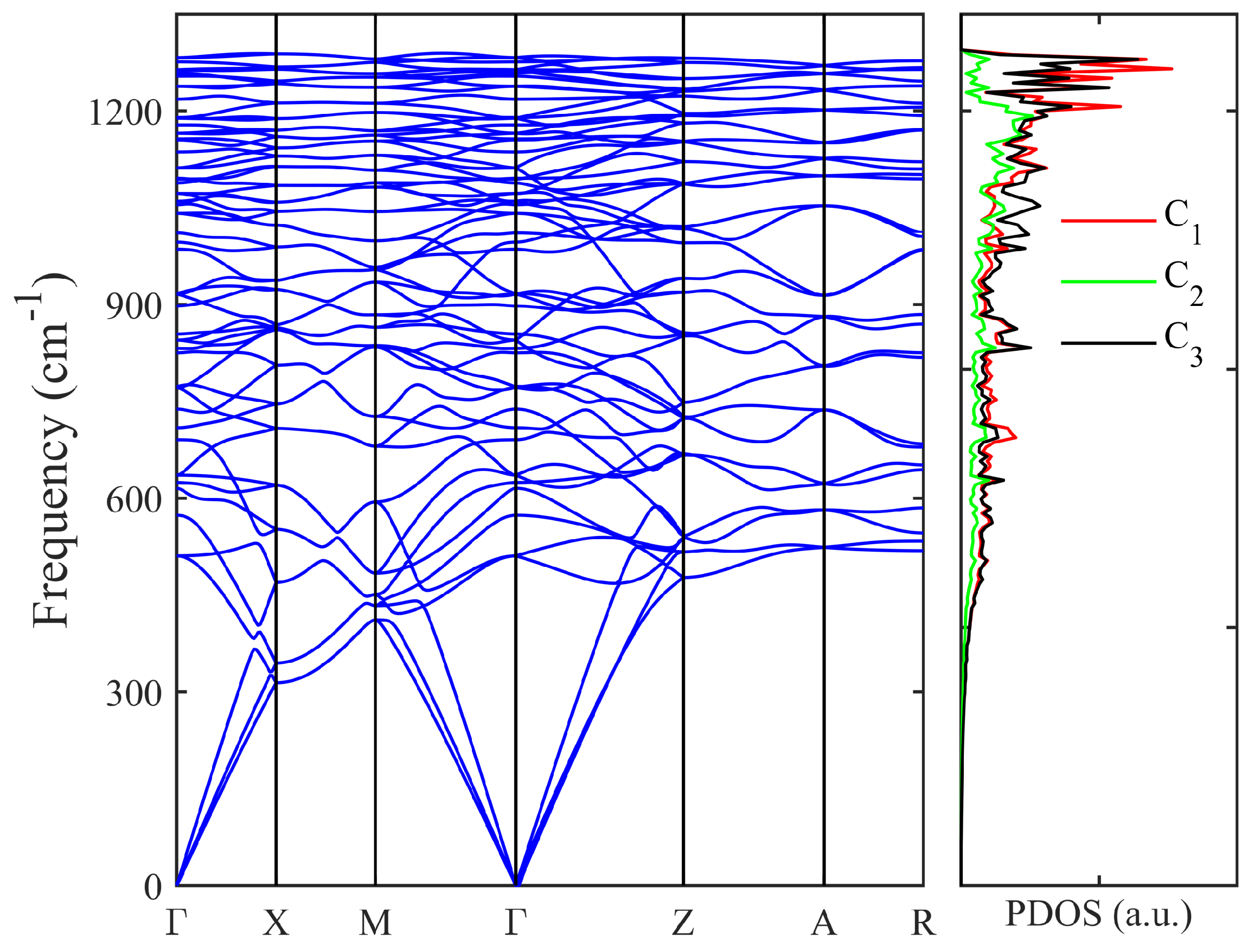
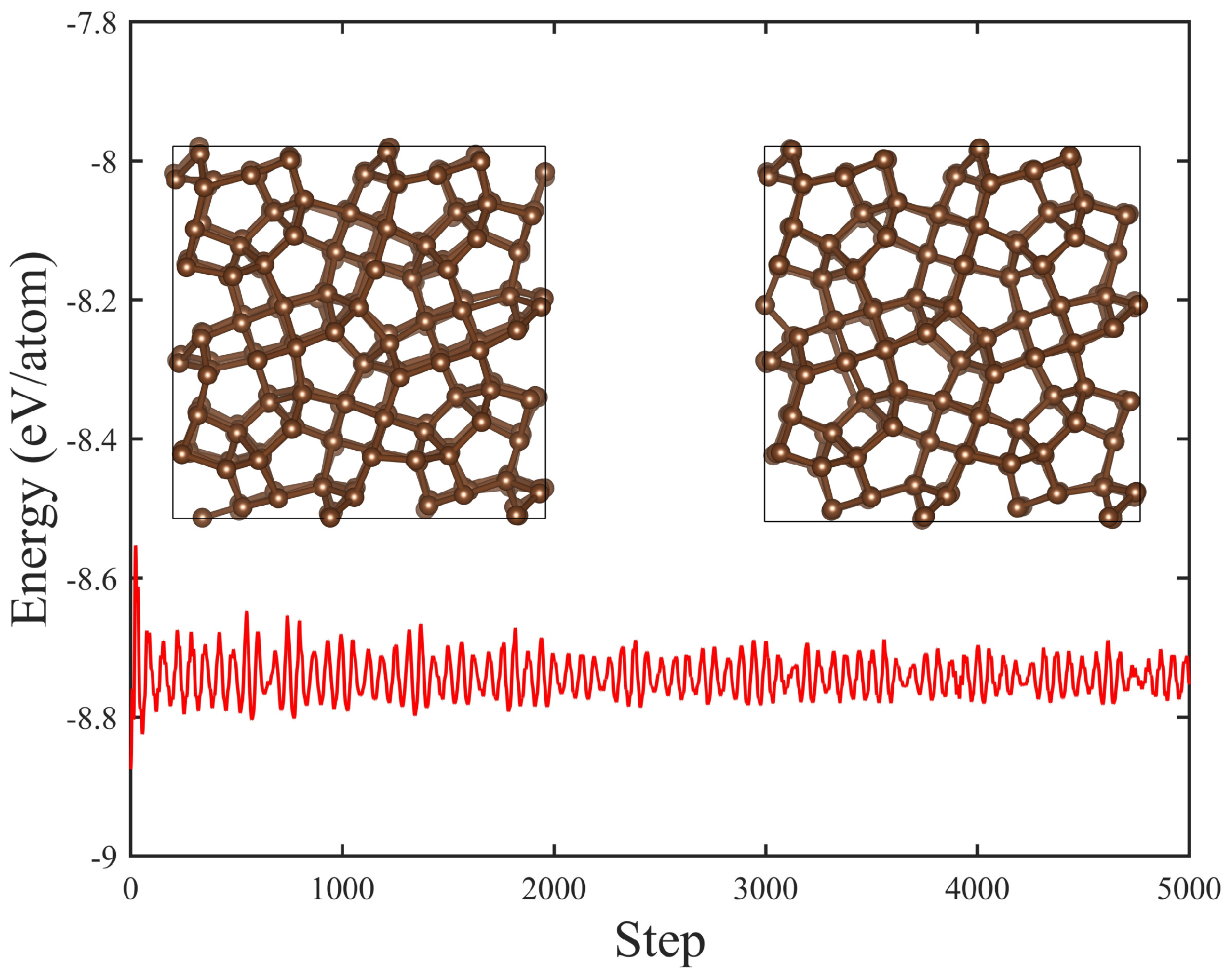
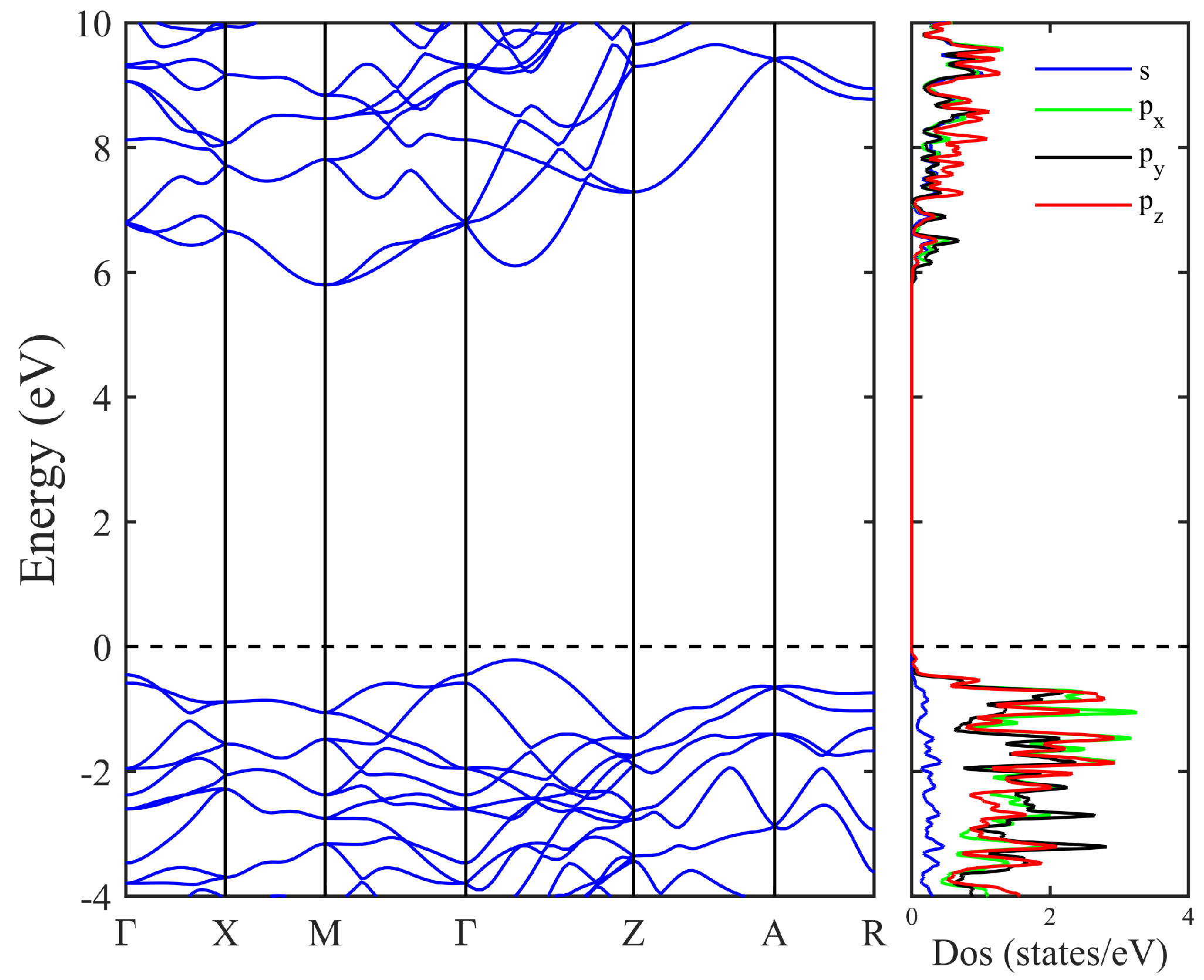

| Structure | Space Group | Method | a (Å) | b (Å) | c (Å) | (°) | () | (Å) | (eV) | (eV) | (GPa) | (GPa) | () |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diamond | AM05 | 3.552 | 5.60 | 1.538 | −9.018 | 5.36 | 451 | 93.5 | 3.45 | ||||
| Exp [66] | 3.567 | 5.67 | 1.544 | 5.47 | 446 | 96 | 3.52 | ||||||
| BC12 | AM05 [41] | 5.139 | 5.66 | 1.574 | −8.134 | 2.98 | 429 | 76.7 | 3.41 | ||||
| BC8 | AM05 [41] | 4.443 | 5.48 | 1.617 | −8.340 | 3.58 | 407 | 82.5 | 3.53 | ||||
| R16 | AM05 | 4.514 | 90.88 | 5.75 | 1.466–1.755 | −8.505 | 4.45 | 386 | 91 | 3.36 | |||
| O16 | AM05 | 4.405 | 4.740 | 4.384 | 5.72 | 1.493–1.730 | −8.546 | 4.23 | 418 | 85 | 3.38 | ||
| oP16 | AM05 | 4.646 | 4.277 | 5.133 | 6.37 | 1.353–1.691 | −8.570 | Semimetal | 370 | 56 | 3.03 | ||
| T20 | AM05 | 5.801 | 3.441 | 5.79 | 1.524–1.569 | −8.881 | 5.80 | 422 | 83.5 | 3.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, X.; Bu, K.; Zhang, C.; Sun, Y. Computational Investigation of an All-sp3 Hybridized Superstable Carbon Allotrope with Large Band Gap. Materials 2025, 18, 2533. https://doi.org/10.3390/ma18112533
Ju X, Bu K, Zhang C, Sun Y. Computational Investigation of an All-sp3 Hybridized Superstable Carbon Allotrope with Large Band Gap. Materials. 2025; 18(11):2533. https://doi.org/10.3390/ma18112533
Chicago/Turabian StyleJu, Xiaoshi, Kun Bu, Chunxiao Zhang, and Yuping Sun. 2025. "Computational Investigation of an All-sp3 Hybridized Superstable Carbon Allotrope with Large Band Gap" Materials 18, no. 11: 2533. https://doi.org/10.3390/ma18112533
APA StyleJu, X., Bu, K., Zhang, C., & Sun, Y. (2025). Computational Investigation of an All-sp3 Hybridized Superstable Carbon Allotrope with Large Band Gap. Materials, 18(11), 2533. https://doi.org/10.3390/ma18112533






