Monitored and Predicted Data for a Diesel Fuel Hydrotreating Reactor
Abstract
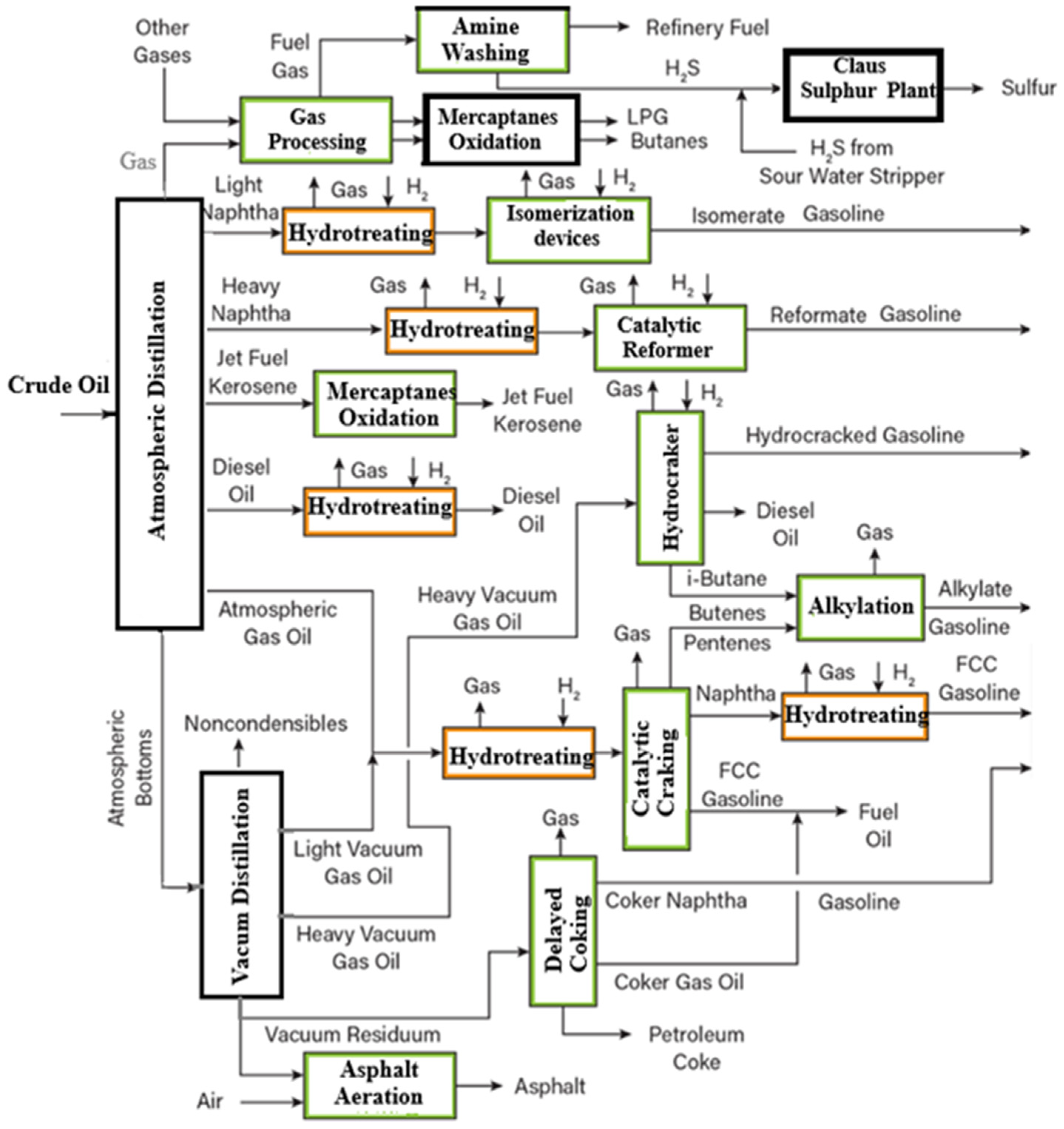
1. Introduction
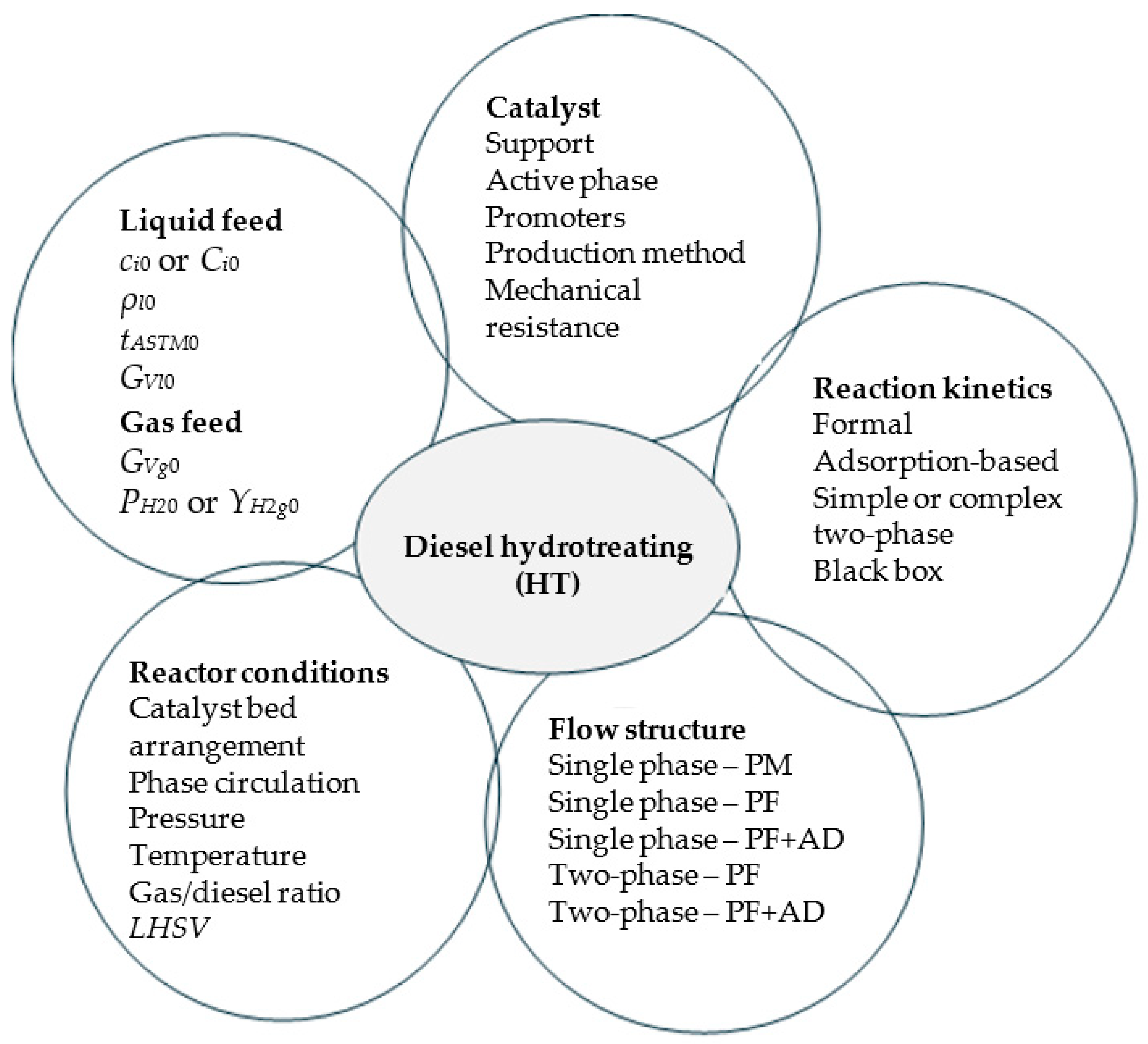
2. Materials and Methods
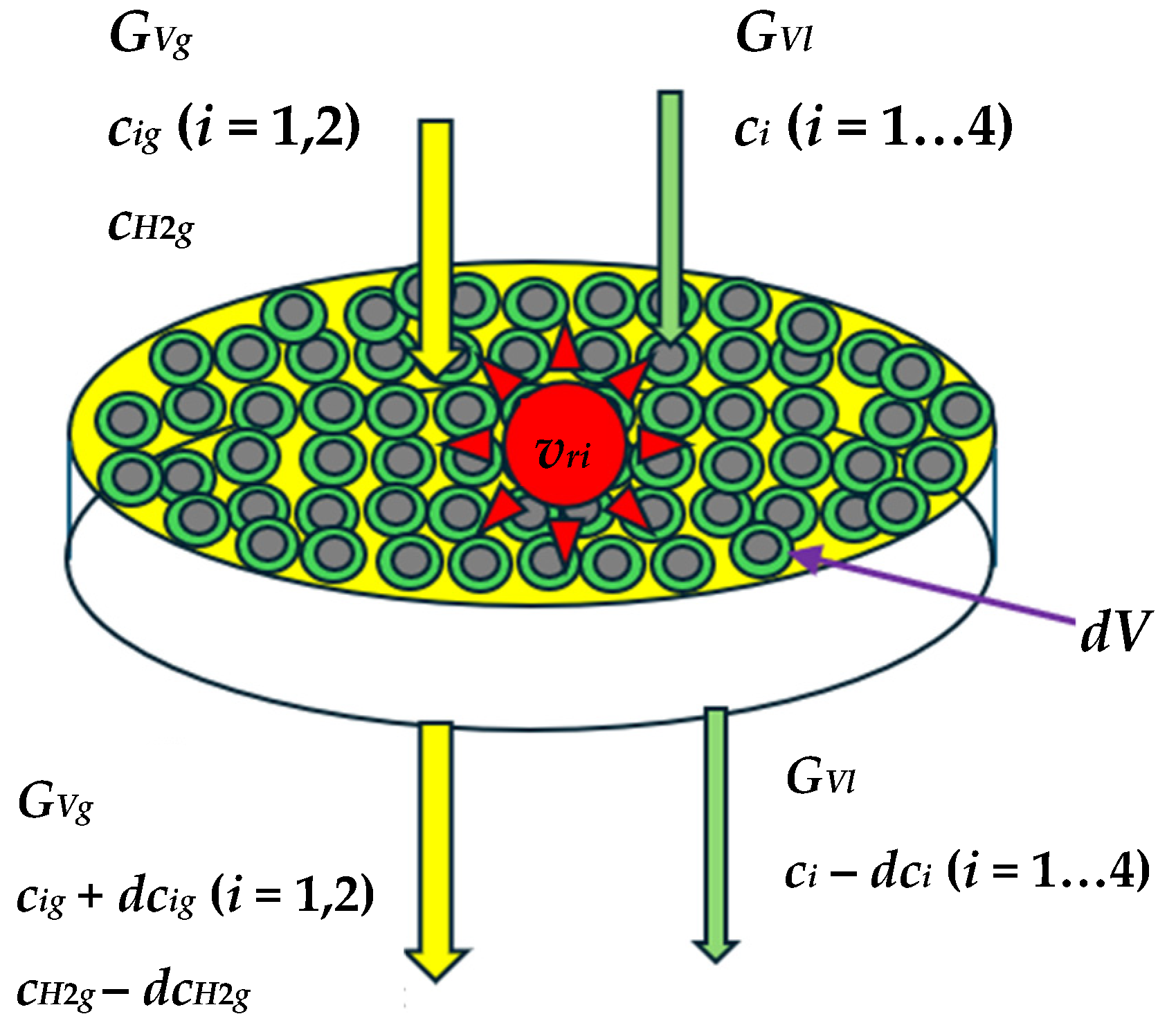
2.1. Modelling
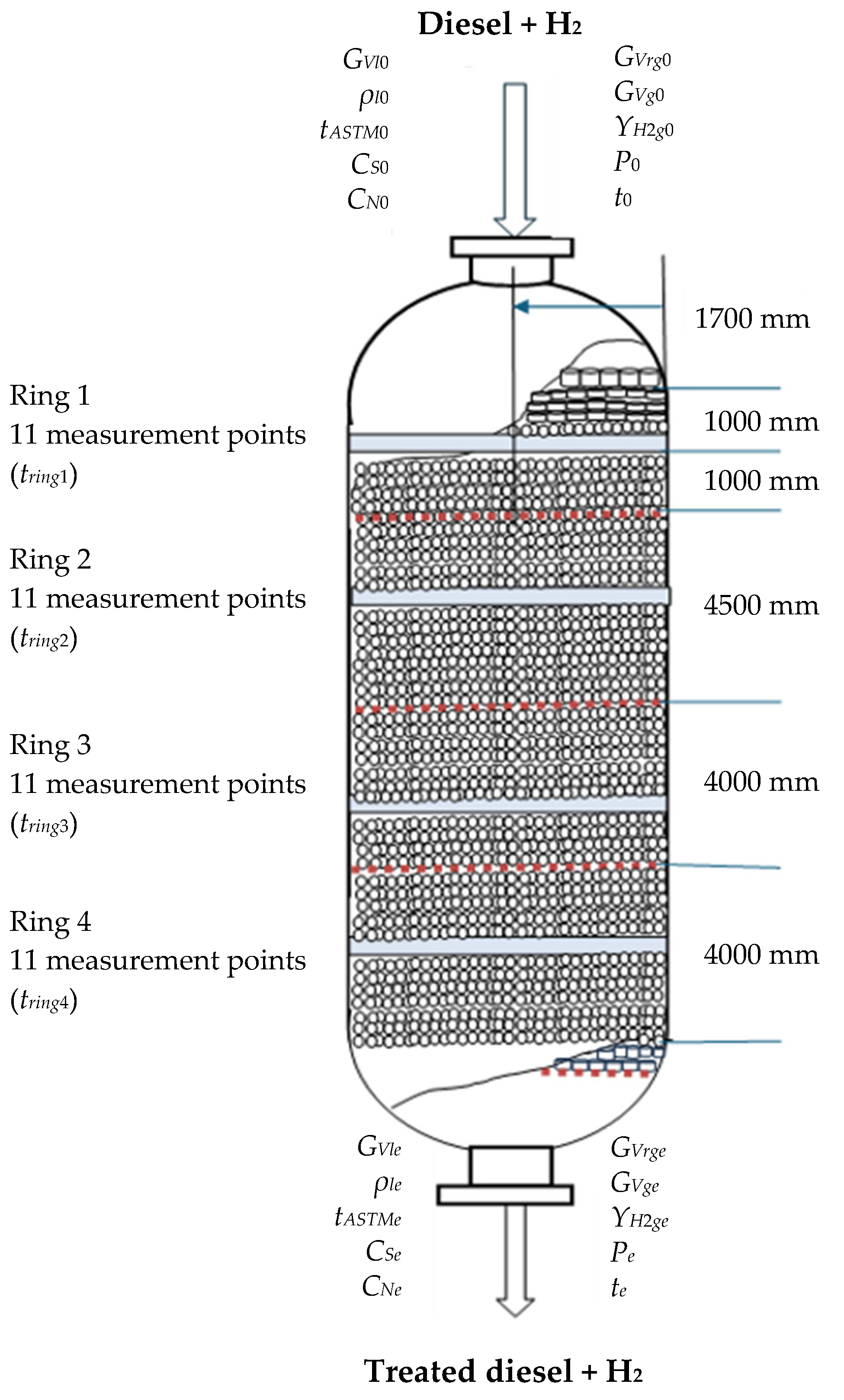
2.2. Experimental
2.3. Data Processing
3. Results and Discussion
3.1. Monitored and Predicted Dynamics of Sulfur and Nitrogen Compound Concentrations in Diesel Fuel at the Reactor Outlet
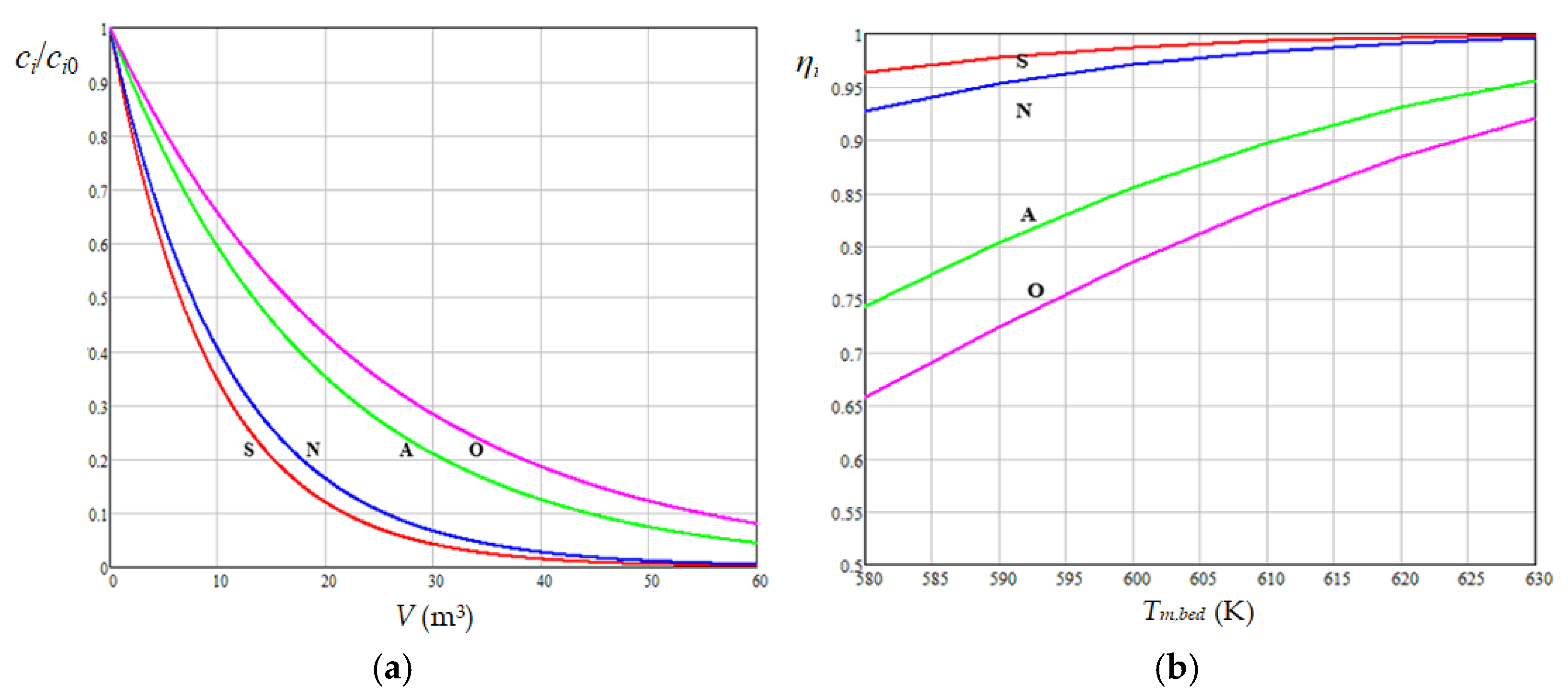
3.2. Predicted Dynamics of Compound Concentrations in Diesel Fuel at Different Levels of Process Factors
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ci | mass concentration of Si species in the liquid phase, kg/m3 |
| cH2g | mass concentration of hydrogen in the gas phase, kg/m3 |
| cig | mass concentration of Si species in the gas phase, kg/m3 |
| Ci | mass percentage of Si species in the liquid phase, wt% |
| Ehi | activation energy for hydrogenation reaction of Si species, kJ/mol |
| GVg | volumetric flow rate of gas phase, m3/h |
| GVl | volumetric flow rate of liquid phase, m3/h |
| GVrg | volumetric flow rate of recycled gas phase, m3/h |
| kdhi | dehydrogenation reaction rate constant of Si species, h−1 |
| khi | hydrogenation reaction rate constant of Si species, h−1 |
| khi0 | pre-exponential factor of Si species in the Arrhenius Equation (13), h−1 |
| LHSV | liquid hourly space velocity, h−1 |
| ni | reaction order of Si species |
| P | pressure, Pa |
| PH2 | partial pressure of hydrogen in the gas phase, Pa |
| rgl | gas/diesel volumetric ratio |
| R | universal gas constant, kJ/(molK) |
| t | temperature, °C |
| tASTM | diesel ASTM 50% distillation temperature, °C |
| T | absolute temperature, K |
| vri | reaction rate of Si species, kg/(m3h) |
| V | catalyst volume, m3 |
| YH2g | molar percentage of hydrogen in the gas phase (H2 purity), mol% |
| α1 | stoichiometric ratio between H2S and sulfur compounds |
| α2 | stoichiometric ratio between NH3 and nitrogen compounds |
| β1 | stoichiometric ratio between H2 and sulfur compounds |
| β2 | stoichiometric ratio between H2 and nitrogen compounds |
| β3 | stoichiometric ratio between H2 and aromatic compounds |
| β4 | stoichiometric ratio between H2 and olefins |
| ηi | hydrogenation degree of Si species |
| ρl | density of liquid phase, kg/m3 |
| τ | time, h |
| τLHSV | residence time of the liquid phase in the catalyst bed (1/LHSV), h |
| Subscripts | |
| e | exit from the reactor |
| g | gas |
| i | compound species; i = 1 (or S) for sulfur compounds; i = 2 (or N) for nitrogen compounds; i = 3 (or A) for aromatic compounds; i = 4 (or O) for olefins |
| l | liquid |
| m | mean |
| rg | recycled gas |
| 0 | reactor inlet (V = 0) |
References
- Ancheyta, J.; Speight, J.G. Hydroprocessing of Heavy Oils and Residual; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Gary, H.J.; Handwerk, H.J.; Kaiser, M.J.; Geddes, D. Petroleum Refining: Technology and Economics, 5th ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Mochida, I.; Choi, K.H. An Overview of Hydrodesulfurization and Hydrodenitrogenation. J. Jpn. Pet. Inst. 2004, 47, 145–163. [Google Scholar] [CrossRef]
- Directorate-General Environment. The Costs and Benefits of Lowering the Sulphur Content of Petrol & Diesel to Less than 10 ppm; European Commission: Brussels, Belgium, 2001. [Google Scholar]
- ASTM D975-22a; Standard Specification for Diesel Fuel. ASTM International: West Conshohocken, PA, USA, 2022.
- Fahim, M.A.; Al-Sahhaf, T.A.; Elkilani, A. Fundamentals of Petroleum Refining, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Speight, J.G. Hydrotreating and Hydrocracking Processes in Refining Technology, 1st ed.; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Babich, I.V.; Moulijn, J.A. Science and Technology of Novel Processes for Deep Desulfurization of Oil Refinery Streams: A Review. Fuel 2003, 82, 607–631. [Google Scholar] [CrossRef]
- Moonen, R.; Alles, J.; Ras, E.J.; Harvey, C.; Moulijn, J.A. Performance Testing of Hydrodesulfurization Catalysts Using a Single-Pellet-String Reactor. Chem. Eng. Technol. 2017, 40, 2025–2034. [Google Scholar] [CrossRef]
- Froment, G.F.; Depauw, G.A.; Vanrysselberghe, V. Kinetic Modelling and Reactor Simulation in Hydrodesulfurization of Oil Fractions. Ind. Eng. Chem. Res. 1994, 33, 2975–2988. [Google Scholar] [CrossRef]
- Song, C. An Overview of New Approaches to Deep Desulfurization for Ultra-Clean Gasoline, Diesel Fuel and Jet Fuel. Catal. Today 2003, 86, 211–263. [Google Scholar] [CrossRef]
- Whitehurst, D.D.; Isoda, T.; Mochida, I. Present State of the Art and Future Challenges in the Hydrodesulfurization of Sulfur Compounds. Adv. Catal. 1998, 42, 345–471. [Google Scholar]
- McKetta, J.J. (Ed.) Petroleum Processing Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Stanislaus, A.; Marafi, A.; Rana, M.S. Recent Advances in the Science and Technology of Ultra Low Sulfur Diesel (ULSD) Production. Catal. Today 2010, 153, 1–68. [Google Scholar]
- Mapiour, M.; Sundaramurthy, V.; Dalai, A.K.; Adjaye, J. Effects of the Operating Variables on Hydrotreating of Heavy Gas Oil: Experimental, Modeling, and Kinetic Studies. Fuel 2010, 89, 2536–2543. [Google Scholar] [CrossRef]
- Bej, S.K.; Dalai, A.K.; Adjaye, J. Comparison of Hydrodenitrogenation of Basic and Nonbasic Nitrogen compounds Present in Oil Sands Derived Heavy Gas Oil. Energy Fuels 2001, 15, 377–383. [Google Scholar] [CrossRef]
- Dufresne, P.; Bigeard, P.H.; Billon, A. New Developments in Hydrocracking: Low Pressure High-Conversion Hydrocracking. Catal. Today 1987, 1, 367–384. [Google Scholar] [CrossRef]
- Topsøe, H. The role of Co–Mo–S Type Structures in Hydrotreating Catalysts. Appl. Catal. A Gen. 2007, 322, 3–8. [Google Scholar] [CrossRef]
- Vasudevan, P.T.; Fierro, J.L.G. A Review of Deep Hydrodesulfurization Catalysis. Catal. Rev.-Sci. Eng. 1996, 38, 161–188. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Xie, B.; Wang, J.; Yu, Y. Insights into the High Activity of Hydrotreating Catalysts for Heavy Gas Oil. Catalysts 2025, 15, 90. [Google Scholar] [CrossRef]
- Weng, X.; Cao, L.; Zhang, G.; Chen, F.; Zhao, L.; Zhang, Y.; Gao, J.; Xu, C. Ultradeep Hydrodesulfurization of Diesel: Mechanisms, Catalyst Design Strategies, and Challenges. Ind. Eng. Chem. Res. 2020, 59, 21261–21274. [Google Scholar] [CrossRef]
- Dobre, T.; Pârvulescu, O.C.; Stoica-Guzun, A.; Stroescu, M.; Jipa, I.; Al Janabi, A.A. Heat and Mass Transfer in Fixed Bed Drying of Non-Deformable Porous Particles. Int. J. Heat Mass Transf. 2016, 103, 478–485. [Google Scholar] [CrossRef]
- Dobre, T.; Sanchez-Marcano, J. Chemical Engineering: Modelling, Simulation and Similitude; Wiley VCH: Weinheim, Germany, 2007. [Google Scholar]
- Chowdhury, R.; Pedernera, E.; Reimert, R. Trickle-Bed Reactor Model for Desulfurization and Dearomatization of Diesel. AIChE J. 2002, 48, 126–135. [Google Scholar] [CrossRef]
- Da Rocha Novaes, L.; de Resende, N.S.; Salim, V.M.M.; Secchi, A.R. Modeling, Simulation and Kinetic Parameter Estimation for Diesel Hydrotreating. Fuel 2017, 209, 184–193. [Google Scholar] [CrossRef]
- Da Silva, J.I.S.; Secchi, A.R. An Approach to Optimize Costs During Ultra-Low Hydrodesulfurization of a Blend Consisting of Different Oil Streams. Braz. J. Chem. Eng. 2018, 35, 1293–1304. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Y.; Wang, W.; Zhang, Q.; Jia, L. Simulation of Hydrotreating of Light Cycle Oil with a System Dynamics Model. Appl. Catal. A Gen. 2008, 339, 209–220. [Google Scholar] [CrossRef]
- Mederos, F.S.; Ancheyta, J. Mathematical Modeling and Simulation of Hydrotreating Reactors: Cocurrent versus Countercurrent Operations. Appl. Cat. A Gen. 2007, 332, 8–21. [Google Scholar] [CrossRef]
- Mederos, F.S.; Ancheyta, J.; Elizalde, I. Dynamic Modeling and Simulation of Hydrotreating of Gas Oil Obtained from Heavy Crude Oil. Appl. Cat. A Gen. 2012, 425–426, 13–27. [Google Scholar] [CrossRef]
- Murali, C.; Voolapalli, R.K.; Ravichander, N.; Gokak, D.T.; Choudary, N.V. Trickle Bed Reactor Model to Simulate the Performance of Commercial Diesel Hydrotreating Unit. Fuel 2007, 86, 1176–1184. [Google Scholar] [CrossRef]
- Ancheyta, J.; Angeles, M.J.; Macías, M.J.; Marroquin, G.; Morales, R. Changes in Apparent Reaction Order and Activation Energy in the Hydrodesulfurization of Real Feedstocks. Energy Fuels 2002, 16, 189–193. [Google Scholar] [CrossRef]
- Boahene, P.E.; Soni, K.K.; Dalai, A.K.; Adjaye, J. Hydroprocessing of Heavy Gas Oils Using FeW/SBA-15 Catalysts: Experimentals, Optimization of Metals Loading, and Kinetics Study. Catal. Today 2013, 207, 101–111. [Google Scholar] [CrossRef]
- Botchewey, C.; Dalai, A.K.; Adjaye, J. Two-Stage Hydrotreating of Athabasca Heavy gas Oil with Interstage Hydrogen Sulphide Removal: Effect of Process Conditions and Kinetic Analysis. Ind. Eng. Chem. Res. 2004, 43, 5854–5861. [Google Scholar] [CrossRef]
- Ferdous, D.; Dalai, A.K.; Adjaye, J. Hydrodenitrogenation and Hydrodesulfurization of Heavy Gas Oil Using NiMo/Al2O3 Catalyst Containing Boron: Experimental and Kinetic Studies. Ind. Eng. Chem. Res. 2006, 45, 544–552. [Google Scholar] [CrossRef]
- Girgis, M.J.; Gates, B.C. Reactivities, Reaction Networks, and Kinetics in High-Pressure Catalytic Hydroprocessing. Ind. Eng. Chem. Res. 1991, 30, 2021–2058. [Google Scholar] [CrossRef]
- Glišiæ, S.B.; Orloviæ, A.M. The Influence of Hydrodearomatisation Reaction Kinetics on the Modelling of Sulphur and Aromatics Removal from Diesel Fuel in an Industrial Hydrotreating Process. Energies 2021, 14, 4616. [Google Scholar] [CrossRef]
- Krivtcova, N.I.; Tataurshikov, A.A.; Ivanchina, E.D.; Krivtsov, E.B. Mathematical Modelling of Diesel Fuel Hydrodesulfurization Kinetics. Procedia Chem. 2015, 15, 180–186. [Google Scholar] [CrossRef]
- Marín, C.; Escobar, J.; Galván, E.; Murrieta, F.; Zárate, R.; Cortés, V. NiMo Supported on Faujasite-modified Al2O3 as Catalysts for the Hydrotreatment of a Light Cycle Oil/Straight Run Gas Oil Mixture. Can. J. Chem. Eng. 2002, 80, 903–910. [Google Scholar] [CrossRef]
- Owusu-Boakye, A.; Dalai, A.K.; Ferdous, D.; Adjaye, J. Experimental and Kinetics Studies of Aromatic Hydrogenation in a Two-Stage Hydrotreating Process using NiMo/Al2O3 and NiW/Al2O3 Catalysts. Can. J. Chem. Eng. 2006, 84, 572–580. [Google Scholar] [CrossRef]
- Pătrășcioiu, C.; Bohaltea, I. Modelling and Simulation of Gasoline Hydrofining Process. Chem. Bull. Politeh. Univ. Timiş. 2006, 51, 39–42. [Google Scholar]
- Petraş, L.; Koncsag, C.; Pârvulescu, O.; Deleanu, I.; Răducanu, C.; Dobre, T. A Simple Model for Gasoline Hydrofining. Bull. Rom. Chem. Eng. Soc. 2022, 9, 134–139. [Google Scholar]
- Petrova, D.; Lyubimenko, V.; Ivanov, E.; Gushchin, P.; Kolesnikov, I. Energy Basics of Catalytic Hydrodesulfurization of Diesel Fuels. Catalysts 2022, 12, 1301. [Google Scholar] [CrossRef]
- Ríos, J.J.; Leal, E.; Trejo, F.; Ancheyta, J. Kinetic Models of Deep Hydrotreating Reactions to Produce Ultralow Sulfur Diesel. Energy Fuels 2023, 37, 11216–11247. [Google Scholar] [CrossRef]
- Samoilov, N.A. Mathematical Modeling and Optimization of Diesel-Fuel Hydrotreatment. Theor. Found. Chem. Eng. 2021, 55, 91–100. [Google Scholar] [CrossRef]
- Tataurshikov, A.; Ivanchina, E.; Krivtcova, N.; Krivtsov, E.; Syskina, A. Mathematical Modeling of Diesel Fuel Hydrotreating. IOP Conf. Ser. Earth Environ. Sci. 2015, 27, 012046. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, W.; Wu, G.; Xin, F.; Qin, K.; Lu, Y.; Zhang, L.; Li, M. Kinetics toward Mechanism and Real Operation for Ultra-Deep Hydrodesulfurization and Hydrodenitrogenation of Diesel. AIChE J. 2021, 67, 17188. [Google Scholar] [CrossRef]
- Da Rocha Novaes, L.; Secchi, A.R.; Salim, V.M.M.; Resende, N.S. Enhancement of Hydrotreating Process Evaluation: Correlation between Feedstock Properties, In-Line Monitoring and Catalyst Deactivation. Catal. Today 2022, 394–396, 390–402. [Google Scholar] [CrossRef]
- Li, L.; Min, Y.C.; Weiyu, D.; Jin, S.; Yunhai, Y.; Shicai, L.; Rong, G. Reaction Kinetics of MoCo/Al2O3-Meso-ZSM-5 Catalyst for Ultra-Deep Hydrodesulfurization of Diesel Fuel. J. Pet. Sci. Technol. 2020, 10, 2–11. [Google Scholar]
- Tang, X.; Li, S.; Yue, C.; He, J.; Hou, J. Lumping Kinetics of Hydrodesulfurization and Hydrodenitrogenation of the Middle Distillate from Chinese Shale Oil. Oil Shale 2013, 30, 517–535. [Google Scholar] [CrossRef]
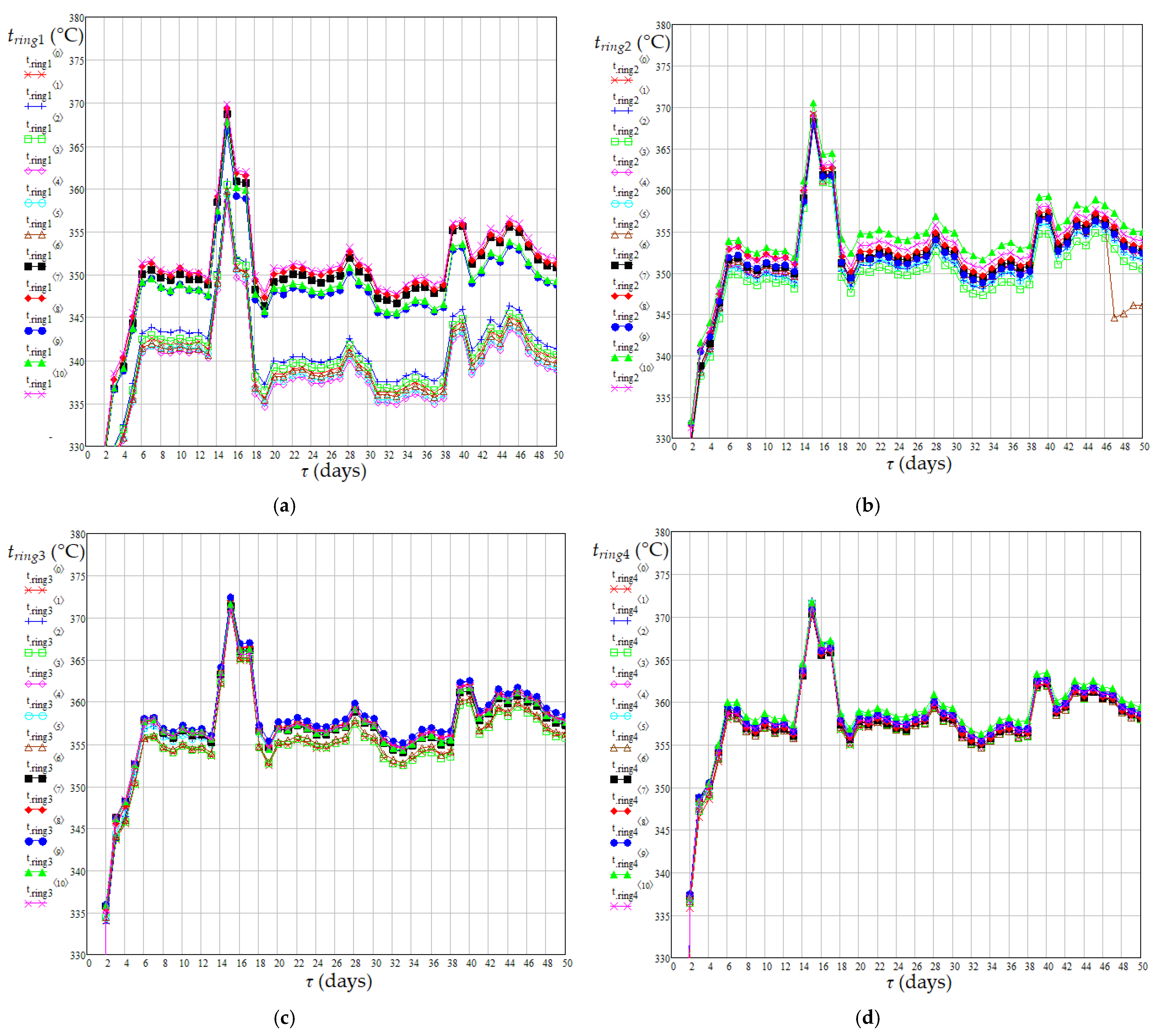
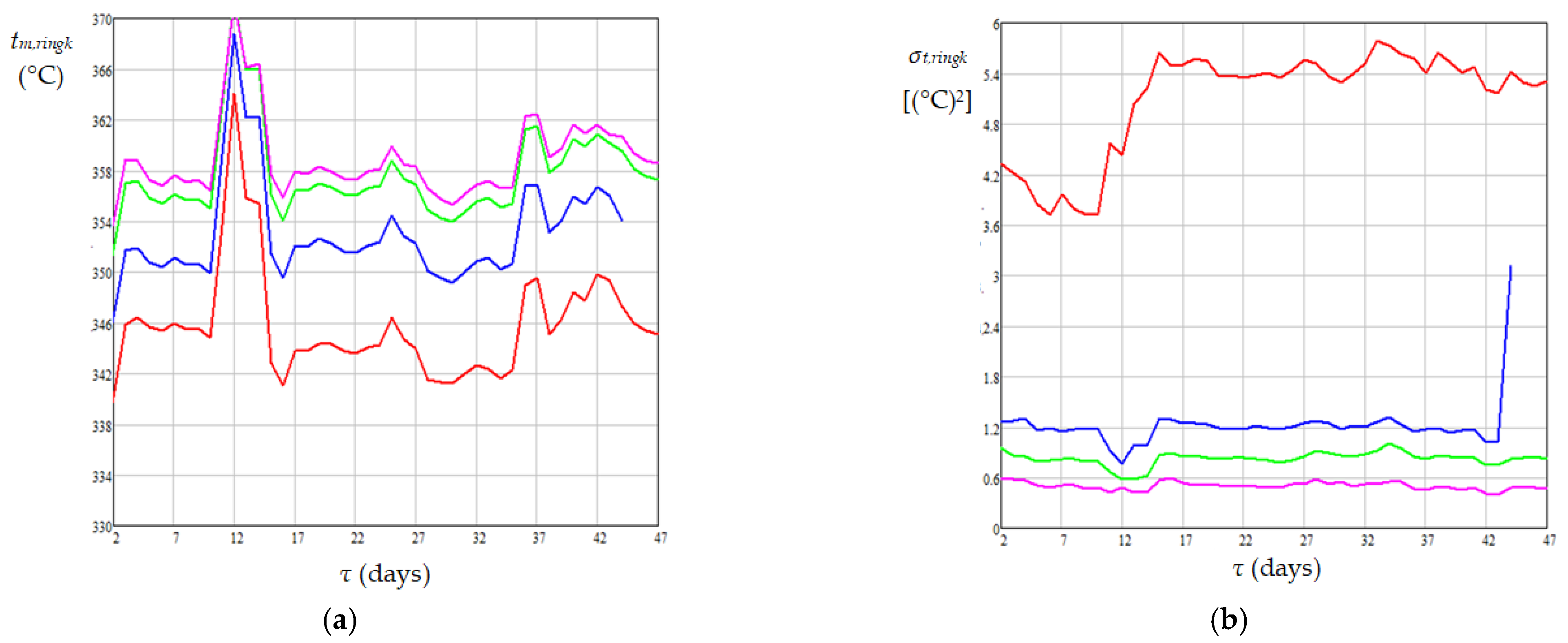

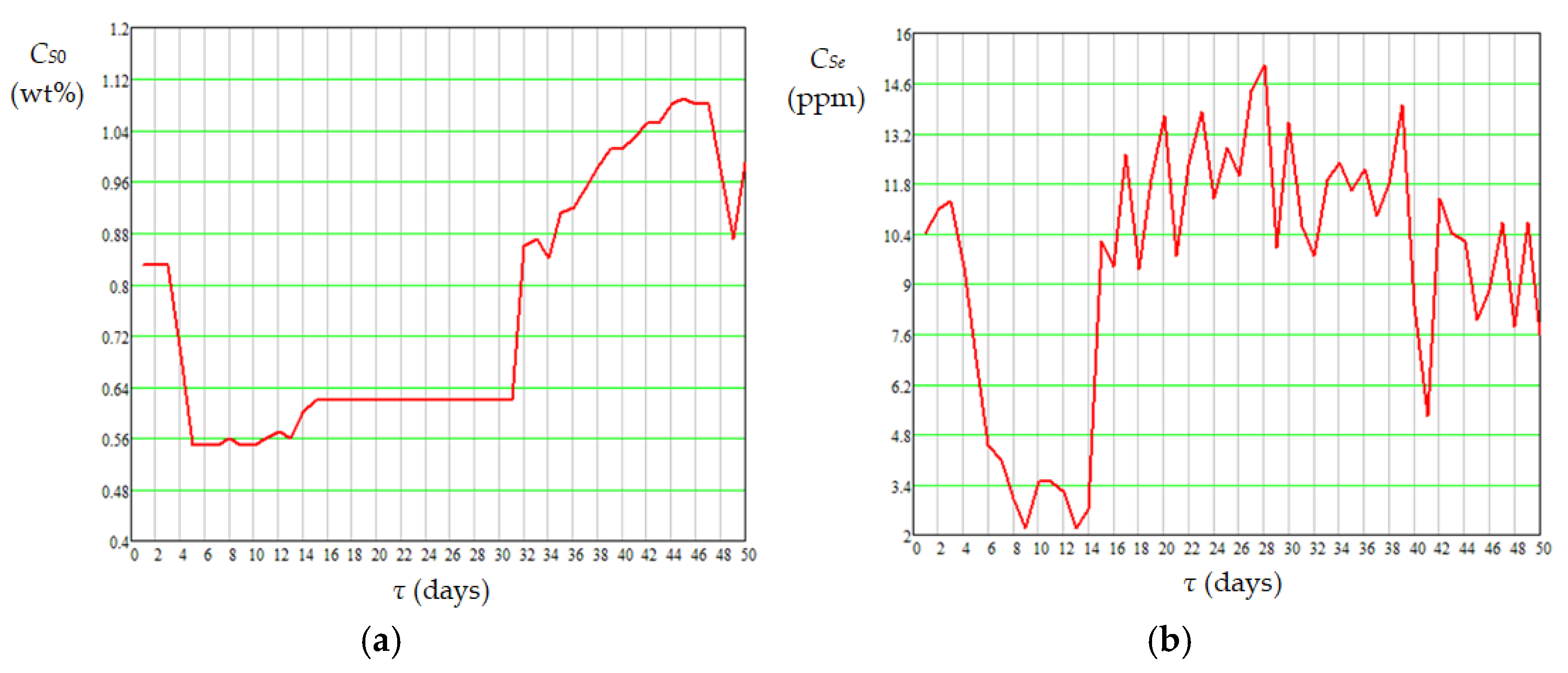
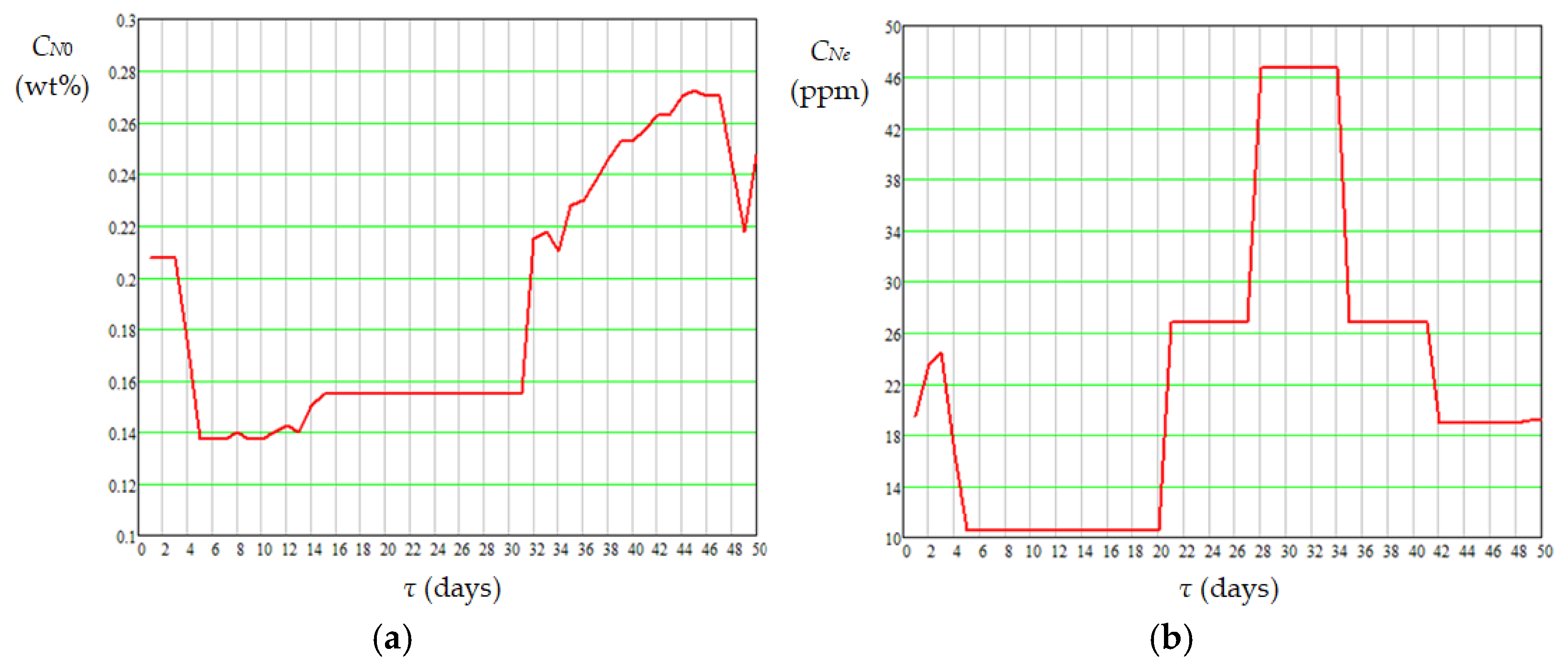

| Case | Pressure (MPa) | Temperature (°C) | H2 Purity (mol%) | Gas/Diesel Ratio (m3/m3) | Catalyst Type | Ref. |
|---|---|---|---|---|---|---|
| Light diesel | 1.5–3.5 | 260–340 | 86–96 | 350–1000 | CoMoS or NiMoS | [10,11,12] |
| Heavy diesel | 3.1–6.2 | 330–410 | 88–96 | 400–1100 | CoMoS or NiMoS | [13,14] |
| Day | GVl (m3/h) | tm,bed (°C) | CS0 (wt%) | CSe (wt%) |
|---|---|---|---|---|
| 1 | 20.1 | 335 | 0.83 | 1.04·10−3 |
| 2 | 65.3 | 348 | 0.83 | 1.11·10−3 |
| 3 | 90.9 | 353 | 0.69 | 1.13·10−3 |
| 4 | 84.6 | 354 | 0.55 | 0.93·10−3 |
| .......... | .......... | .......... | .......... | .......... |
| 47 | 101.8 | 355 | 0.98 | 0.78·10−3 |
| 48 | 99.6 | 354 | 0.87 | 1.07·10−3 |
| 49 | 98.6 | 352 | 0.99 | 0.76·10−3 |
| 50 | 84.7 | 355 | 0.96 | 1.44·10−3 |
| EhS (kJ/mol) | 52 | 54 | 56 | 58 | 60 | 62 | 64 | |
|---|---|---|---|---|---|---|---|---|
| khS0 (h−1) | ||||||||
| 3.6·105 | 4.272·103 | 3.669·103 | 4.076·103 | 3.871·105 | 6.235·106 | 4.066·107 | 1.470·108 | |
| 3.8·105 | 4.278·103 | 3.891·103 | 2.140·103 | 2.354·105 | 4.499·106 | 3.254·107 | 1.261·108 | |
| 4.0·105 | 4.282·103 | 4.035·103 | 1.702·103 | 1.419·105 | 3.245·106 | 2.604·107 | 1.082·108 | |
| 4.2·105 | 4.283·103 | 4.127·103 | 1.881·103 | 8.464·104 | 2.340·106 | 2.084·107 | 9.291·107 | |
| 4.4·105 | 4.284·103 | 4.185·103 | 2.267·103 | 4.983·104 | 1.686·106 | 1.669·107 | 7.977·107 | |
| 4.6·105 | 4.285·103 | 4.222·103 | 2.678·103 | 2.887·104 | 1.214·106 | 1.336·107 | 6.849·107 | |
| 4.8·105 | 4.285·103 | 4.245·103 | 3.045·103 | 1.645·104 | 8.725·105 | 1.070·107 | 5.881·107 | |
| 5.0·105 | 4.285·103 | 4.260·103 | 3.346·103 | 9.253·103 | 6.262·105 | 8.568·106 | 5.051·107 | |
| nS | khS0 (h−1) | EhS (kJ/mol) | nN | khN0 (h−1) | EhN (kJ/mol) |
|---|---|---|---|---|---|
| 1 | 8.189·104 | 47.75 | 1 | 6.515·104 | 47.24 |
| 0.914 | 1.192·105 | 62.91 | 0.908 | 1.562·105 | 66.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petraş, L.E.; Dobre, T.; Şerbănescu, N.; Pop, F.D.; Pârvulescu, O.C. Monitored and Predicted Data for a Diesel Fuel Hydrotreating Reactor. Materials 2025, 18, 2481. https://doi.org/10.3390/ma18112481
Petraş LE, Dobre T, Şerbănescu N, Pop FD, Pârvulescu OC. Monitored and Predicted Data for a Diesel Fuel Hydrotreating Reactor. Materials. 2025; 18(11):2481. https://doi.org/10.3390/ma18112481
Chicago/Turabian StylePetraş, Laura Elisabeta, Tănase Dobre, Nela Şerbănescu, Florian Daniel Pop, and Oana Cristina Pârvulescu. 2025. "Monitored and Predicted Data for a Diesel Fuel Hydrotreating Reactor" Materials 18, no. 11: 2481. https://doi.org/10.3390/ma18112481
APA StylePetraş, L. E., Dobre, T., Şerbănescu, N., Pop, F. D., & Pârvulescu, O. C. (2025). Monitored and Predicted Data for a Diesel Fuel Hydrotreating Reactor. Materials, 18(11), 2481. https://doi.org/10.3390/ma18112481








