Sensitivity Analysis in the Problem of the Impact of an External Heat Impulse on Oxygen Distribution in Biological Tissue
Abstract
1. Introduction
2. Materials and Methods
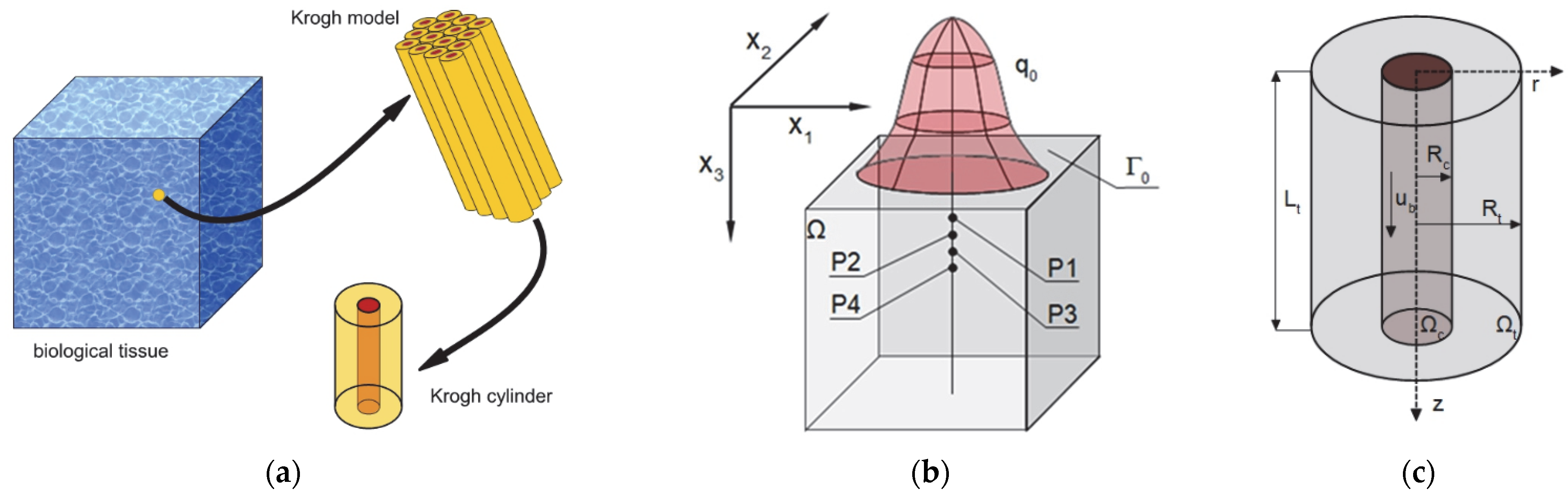
2.1. Governing Equations
2.2. Sensitivity Analysis of the Oxygen Distribution Model
- Krogh coefficient Kt and oxygen demand M0 (radial direction model, (2));
- Mass transfer coefficient k (radial and axial directions models, (2) and (3));
- Oxygen carrying a capacity of blood κb and blood velocity in capillary ub (axial direction model, (3));
- The Hill coefficient n and the oxygen pressure corresponding to 50% hemoglobin saturation P50 (Hill oxygen dissociation curve, (4)).
- Radial direction model: (15), (19), and (18);
- Axial direction model: (25) and (26);
- Inverted oxygen dissociation curve: (28).
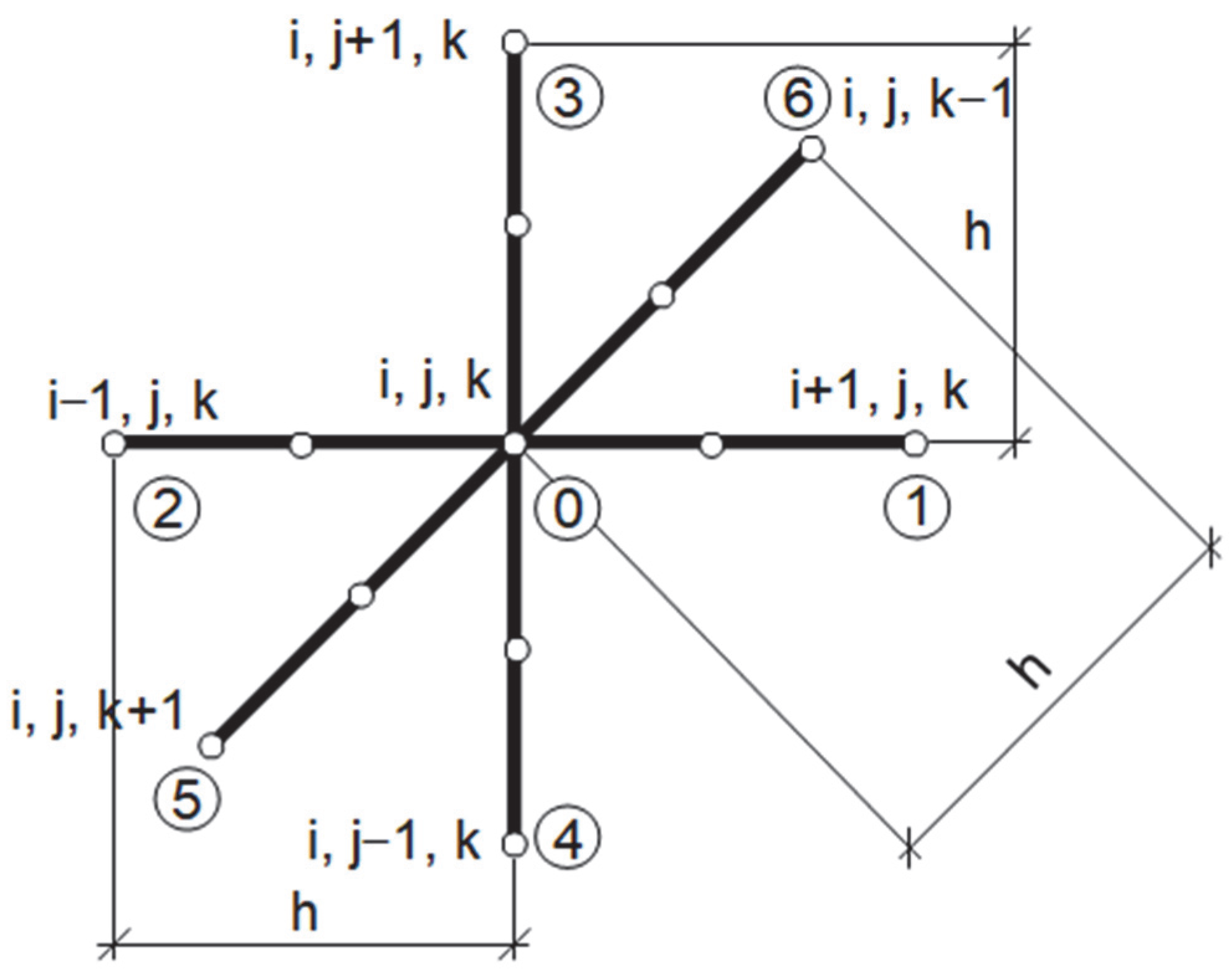
2.3. Methods of Solution
3. Results and Discussion
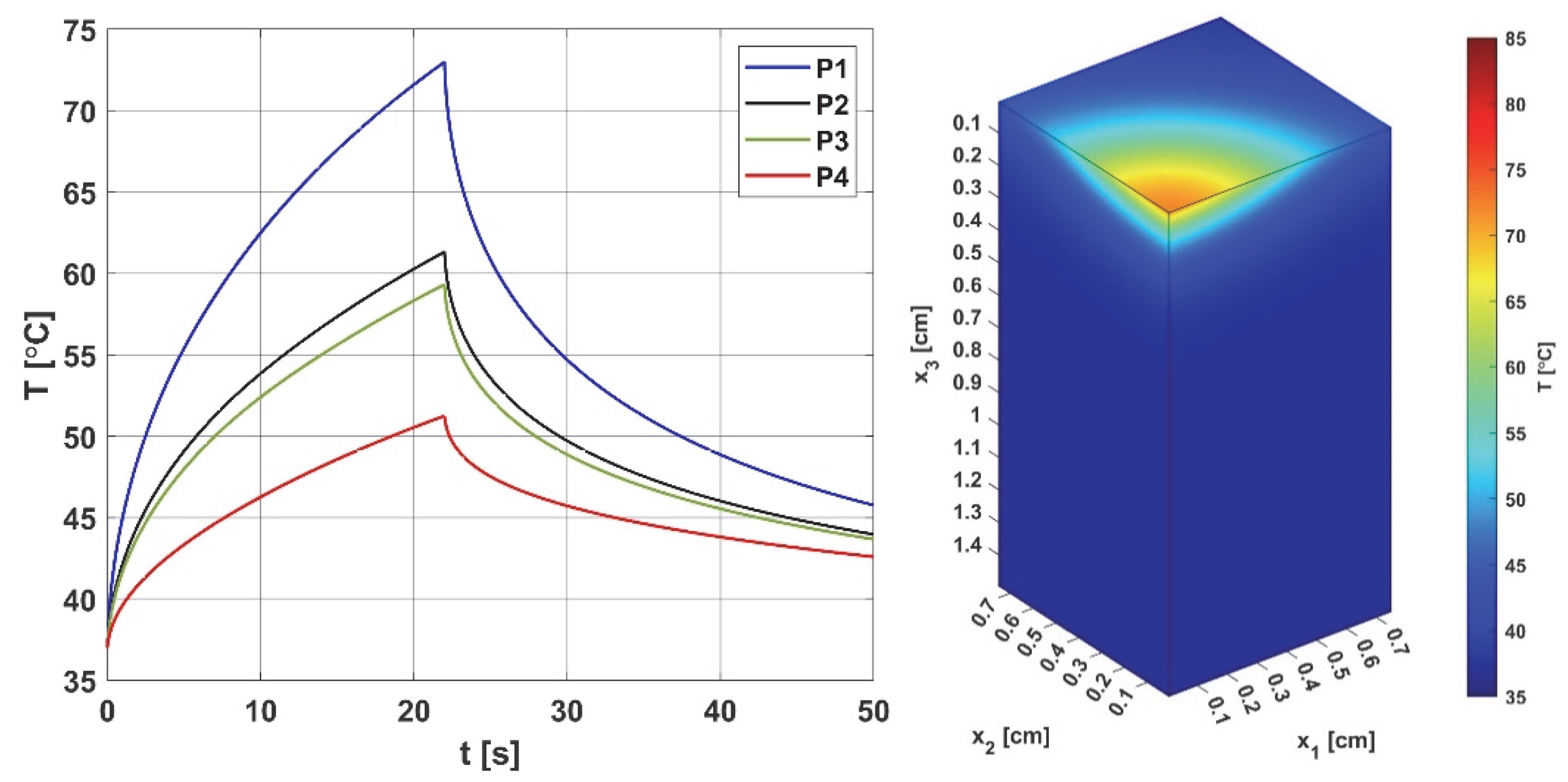
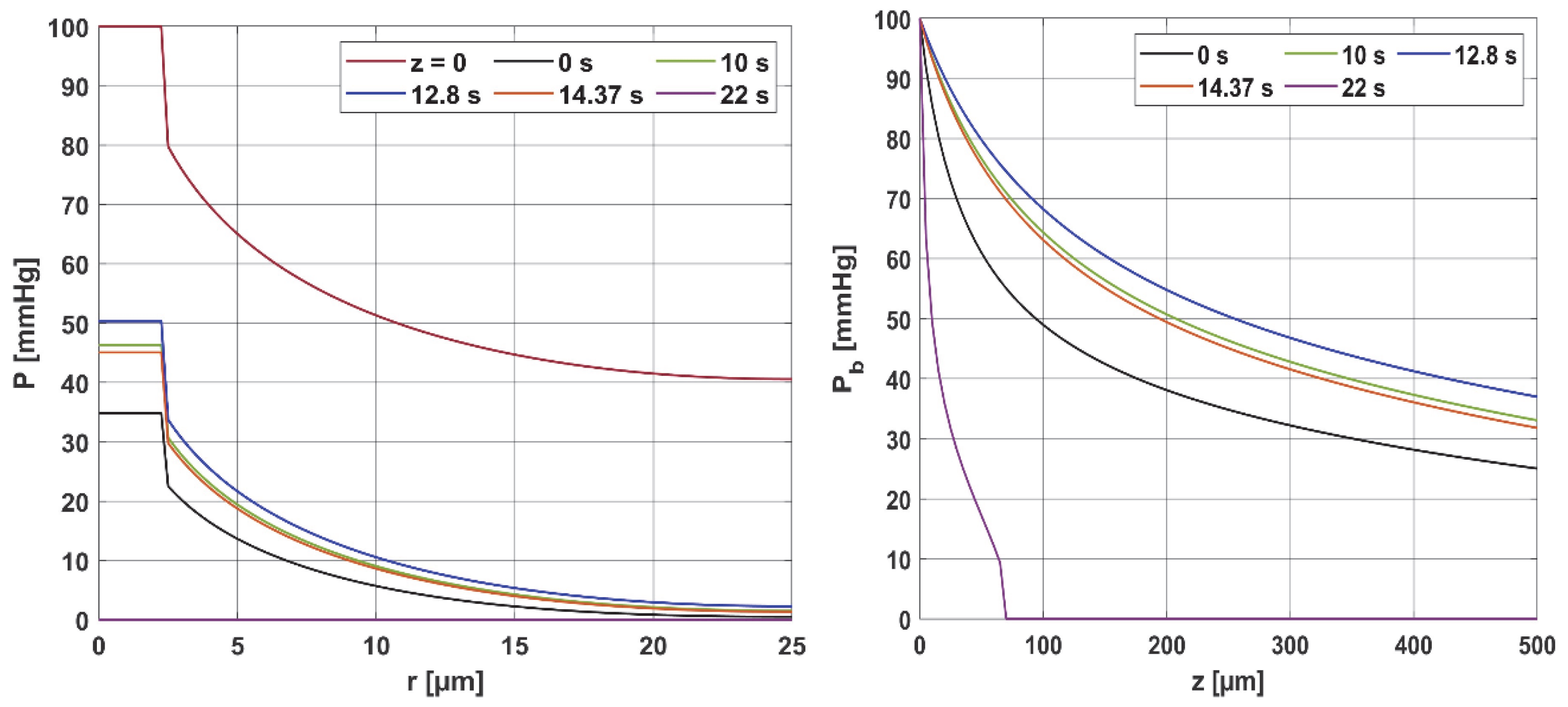
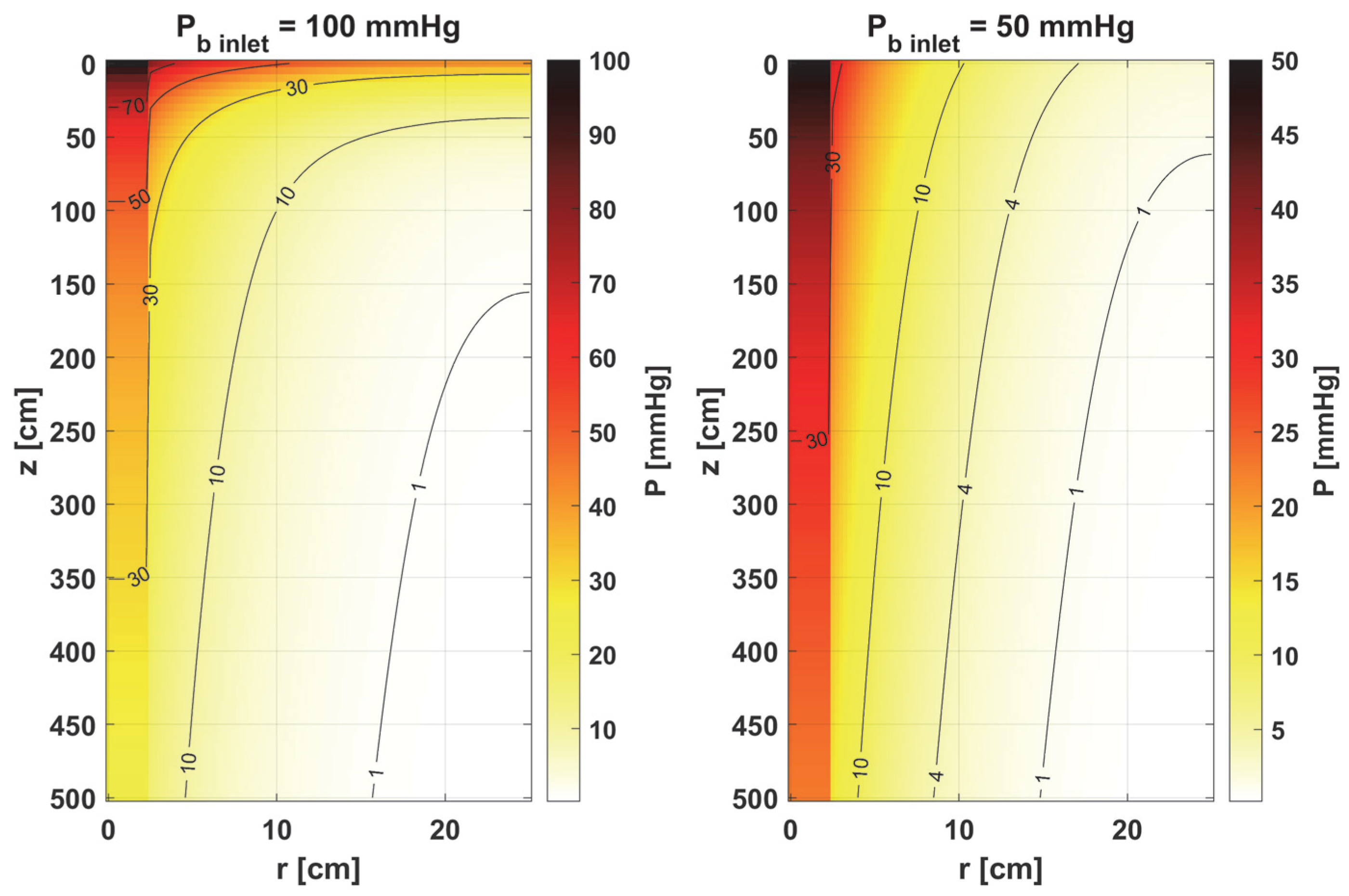
3.1. Bioheat Transfer and Oxygen Distribution
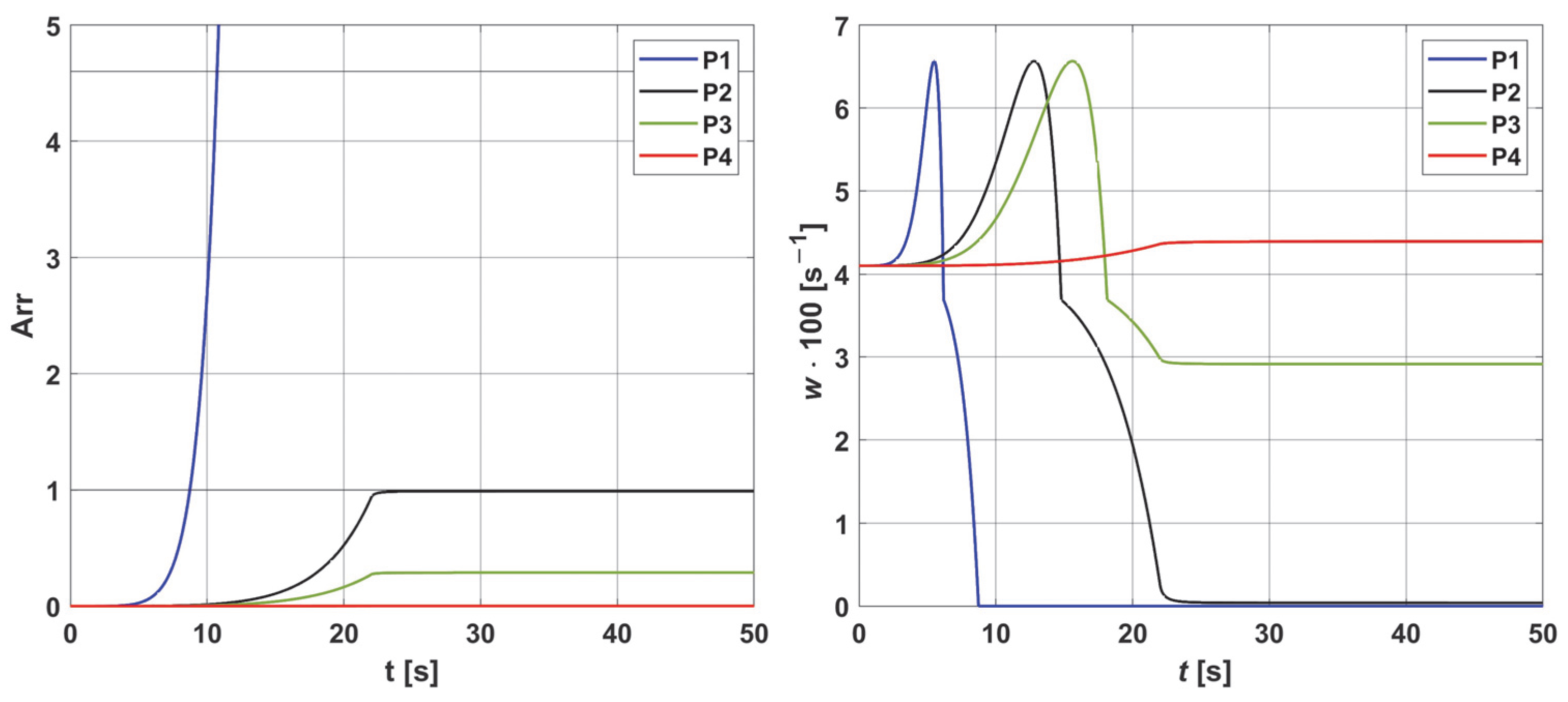
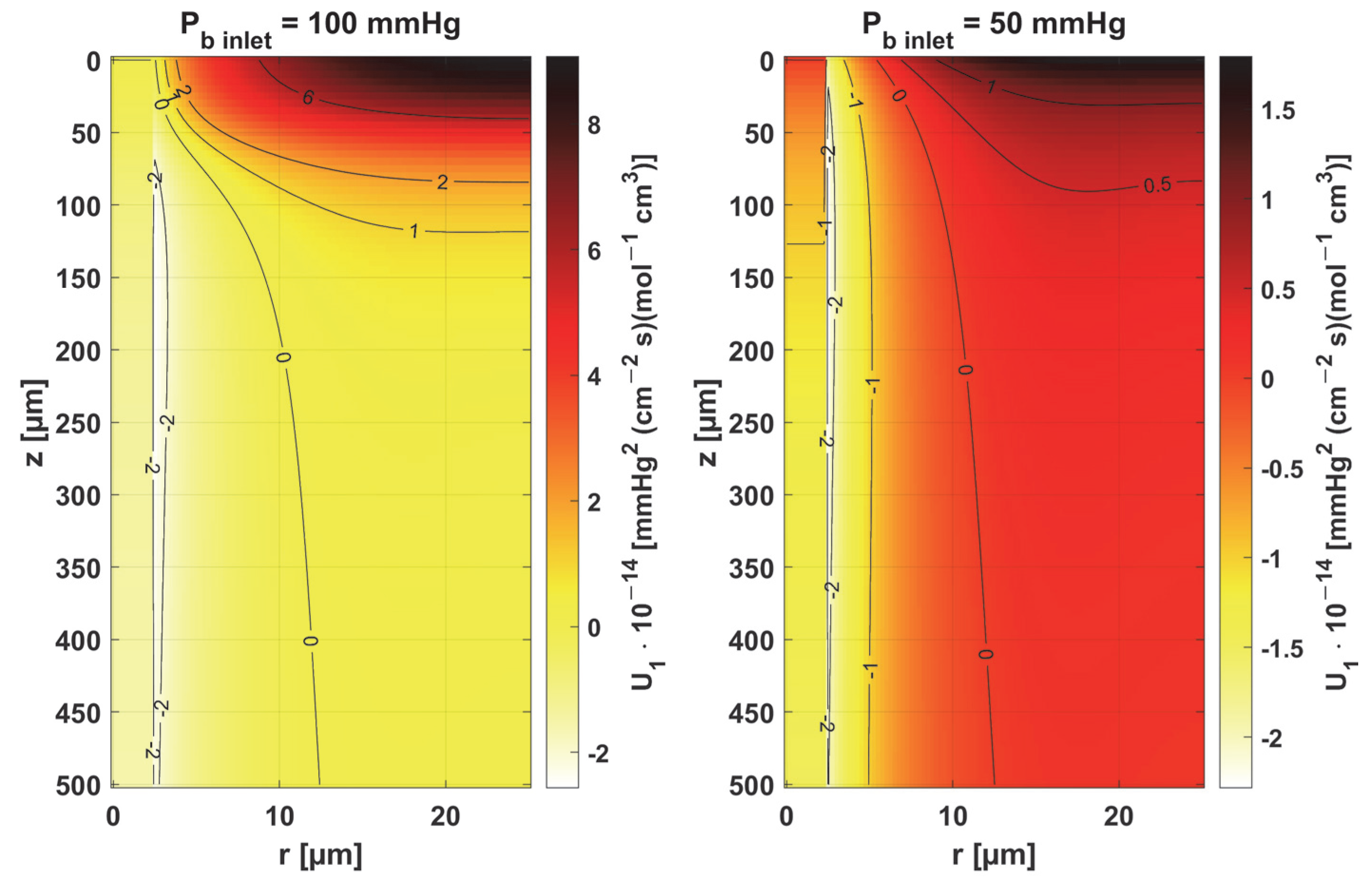
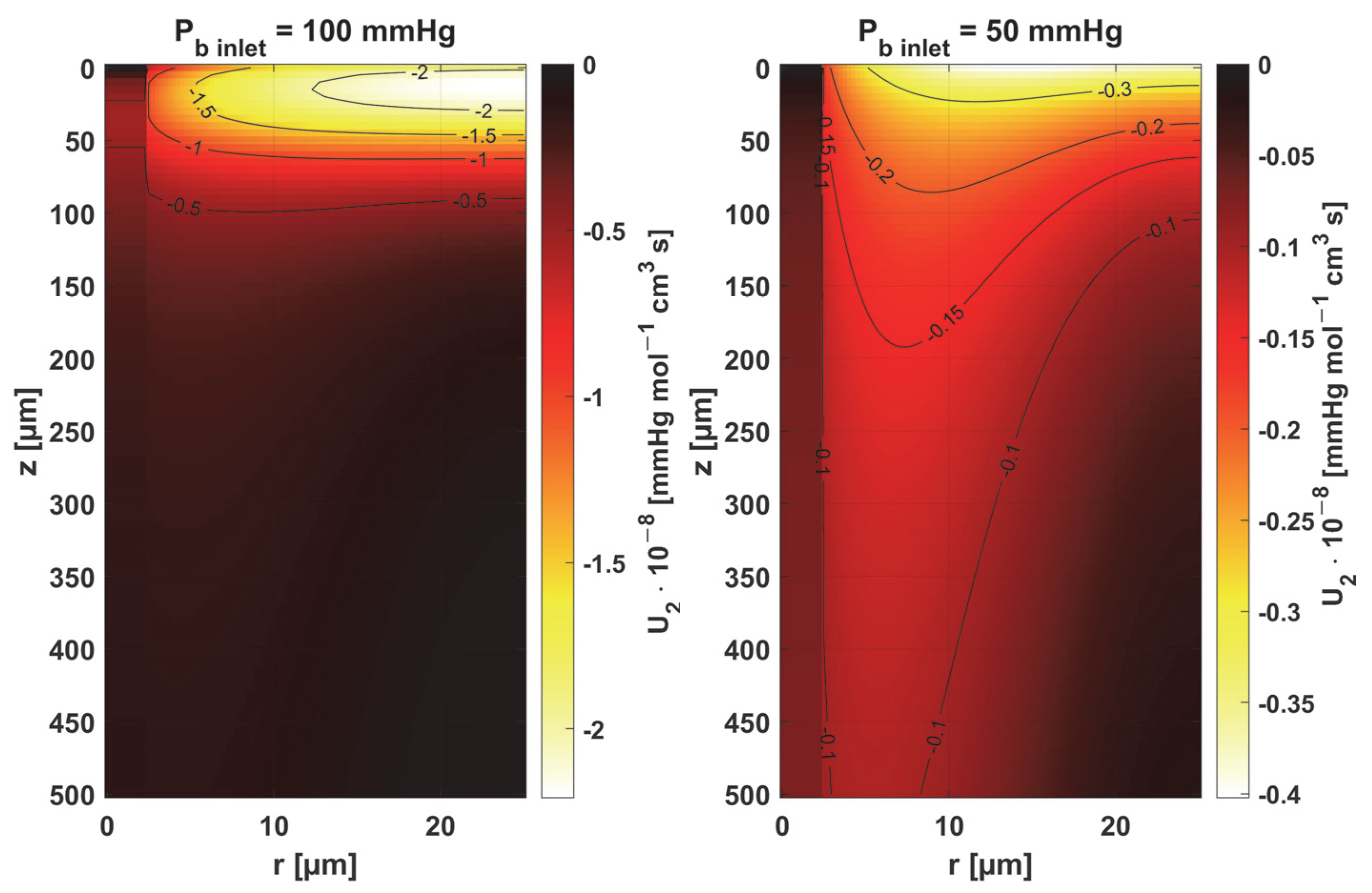
3.2. Sensitivity Analysis
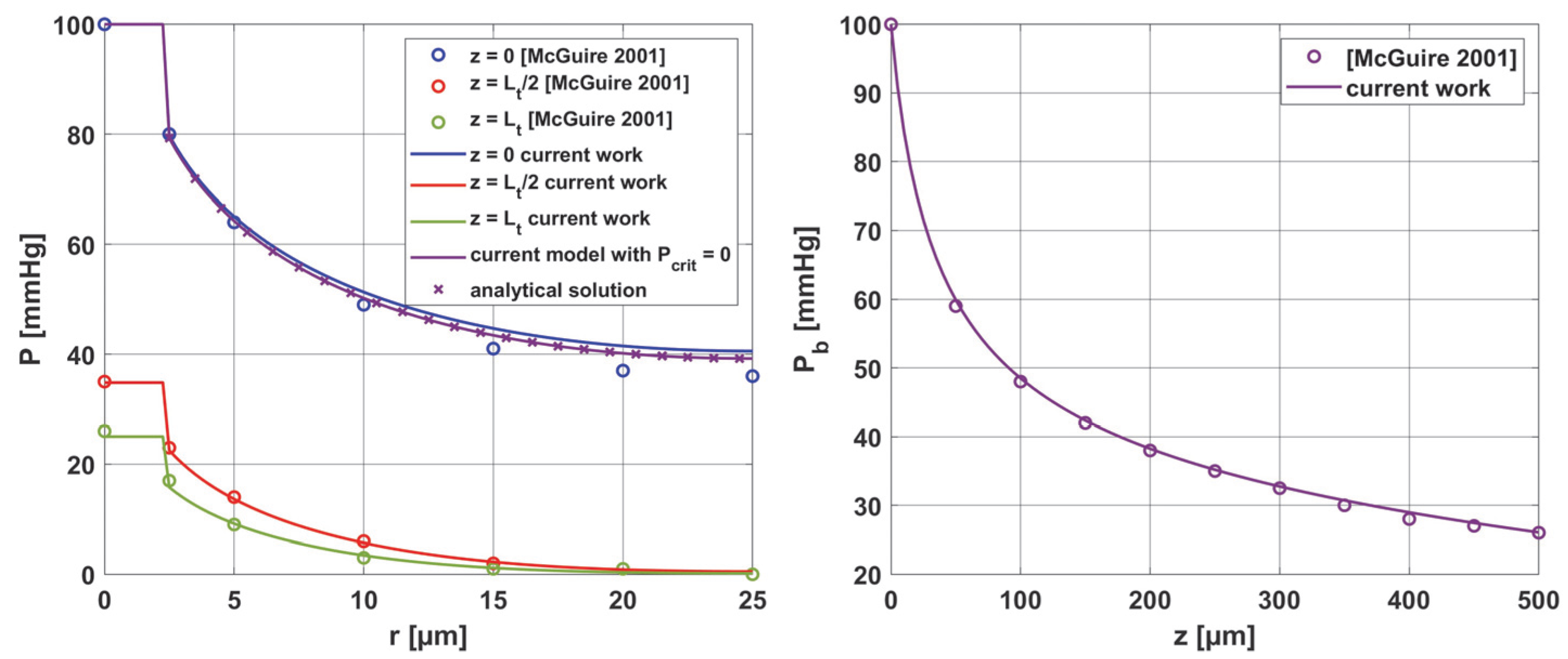
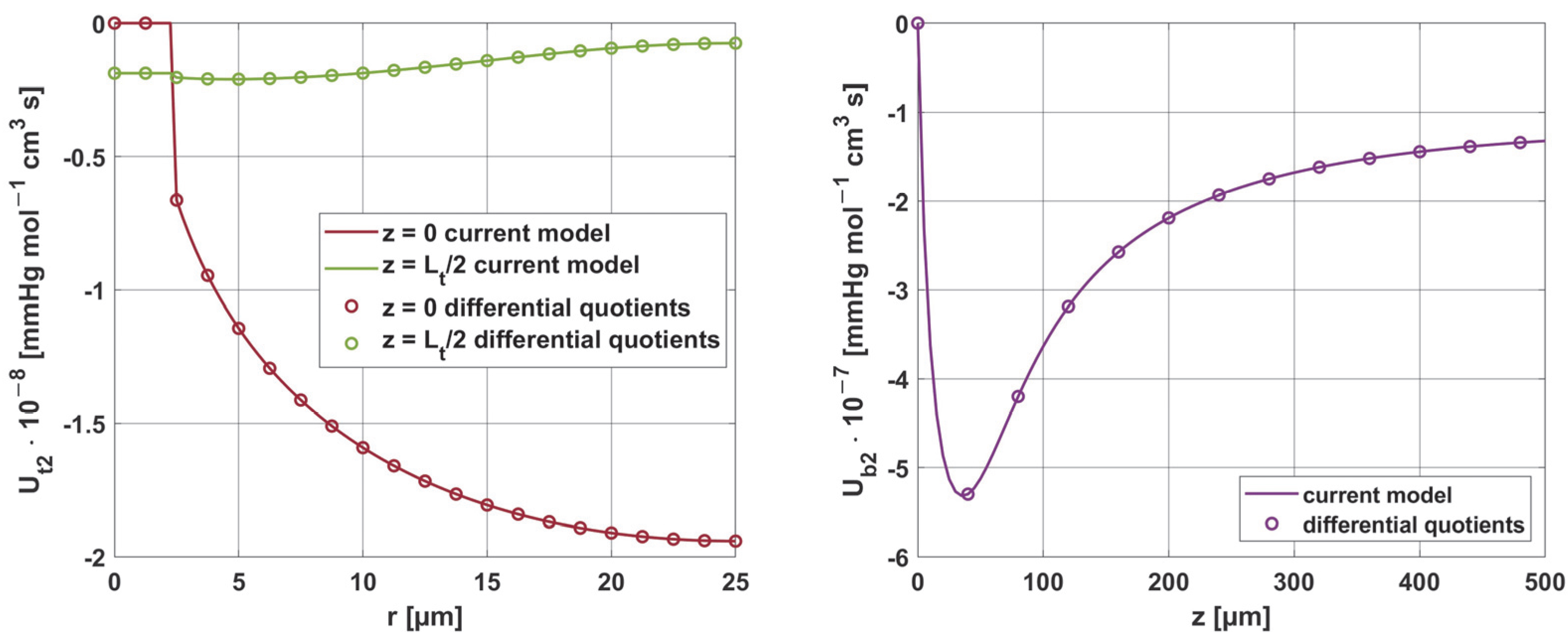
3.3. Results Verification
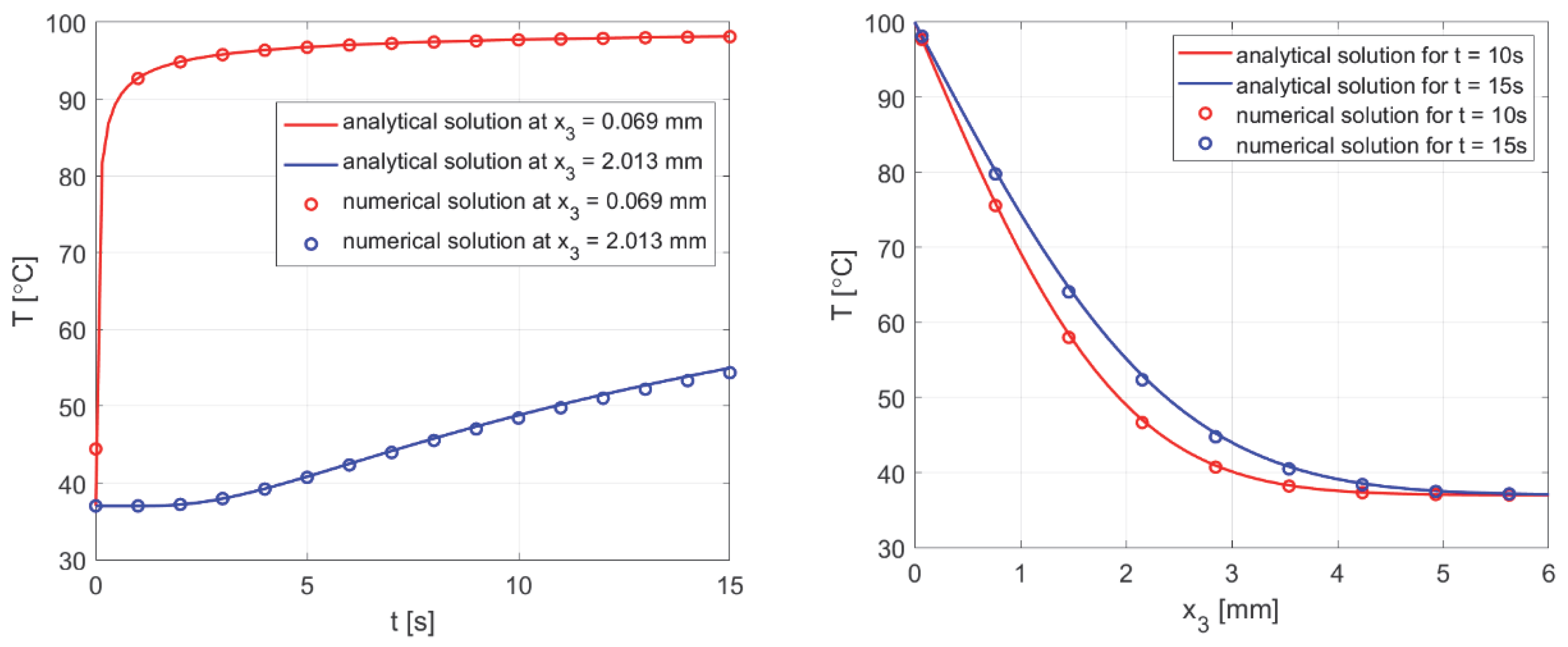
3.3.1. Bioheat Transfer
3.3.2. Oxygen Model
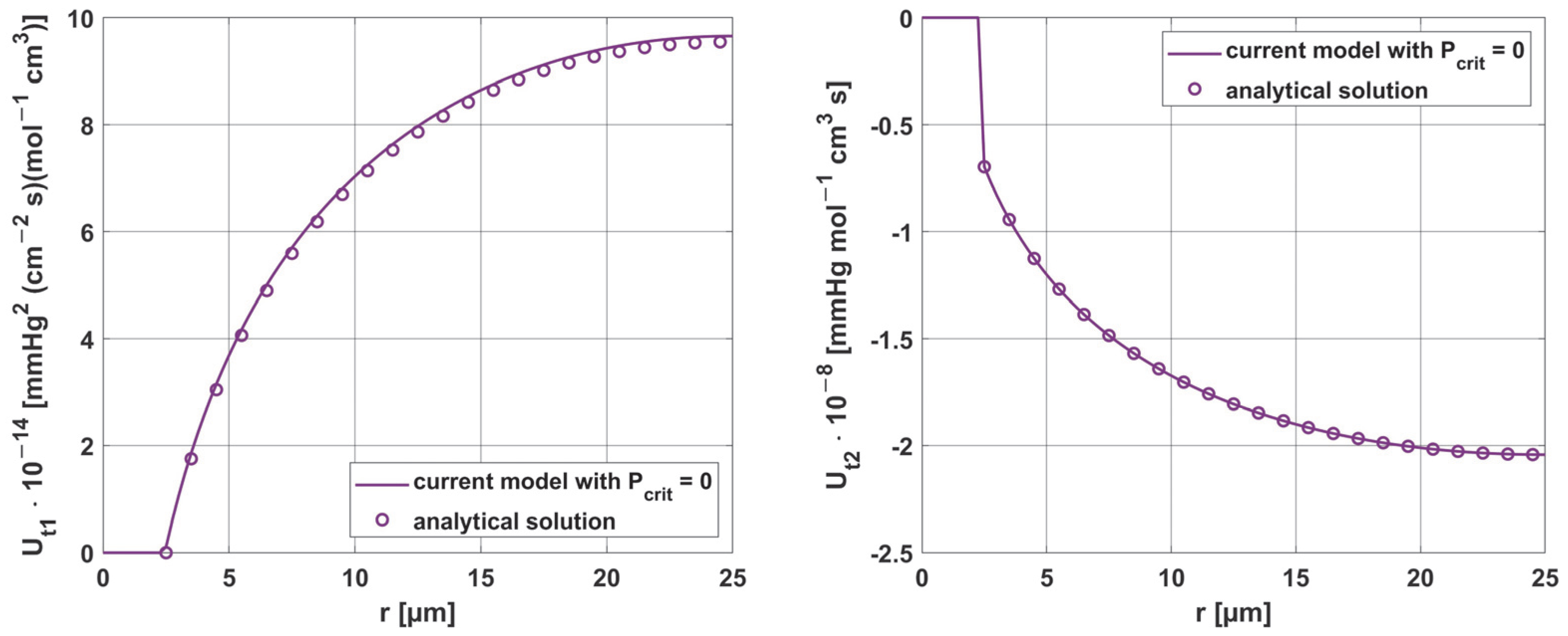
3.3.3. Sensitivity Analysis
4. Conclusions
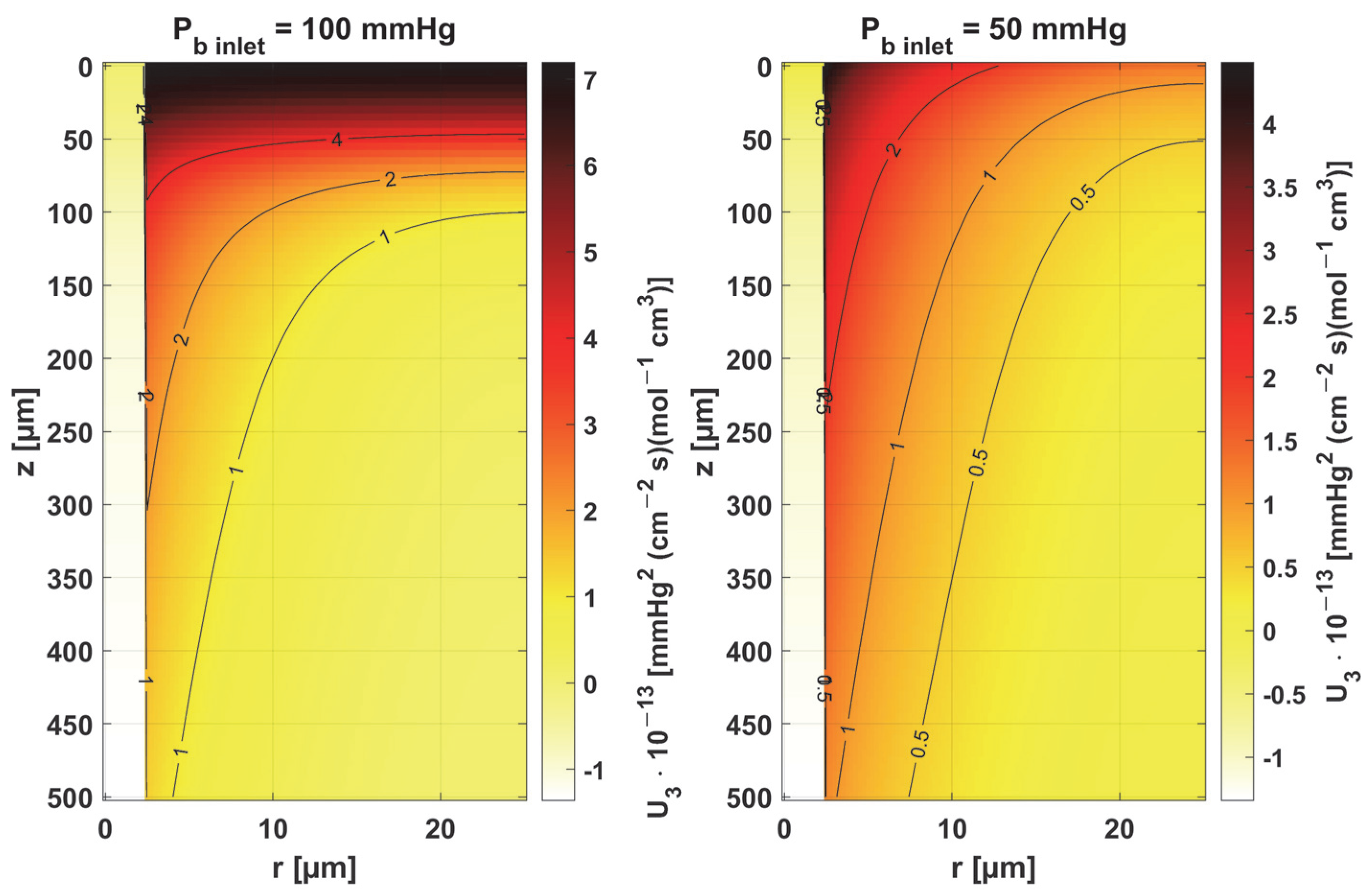
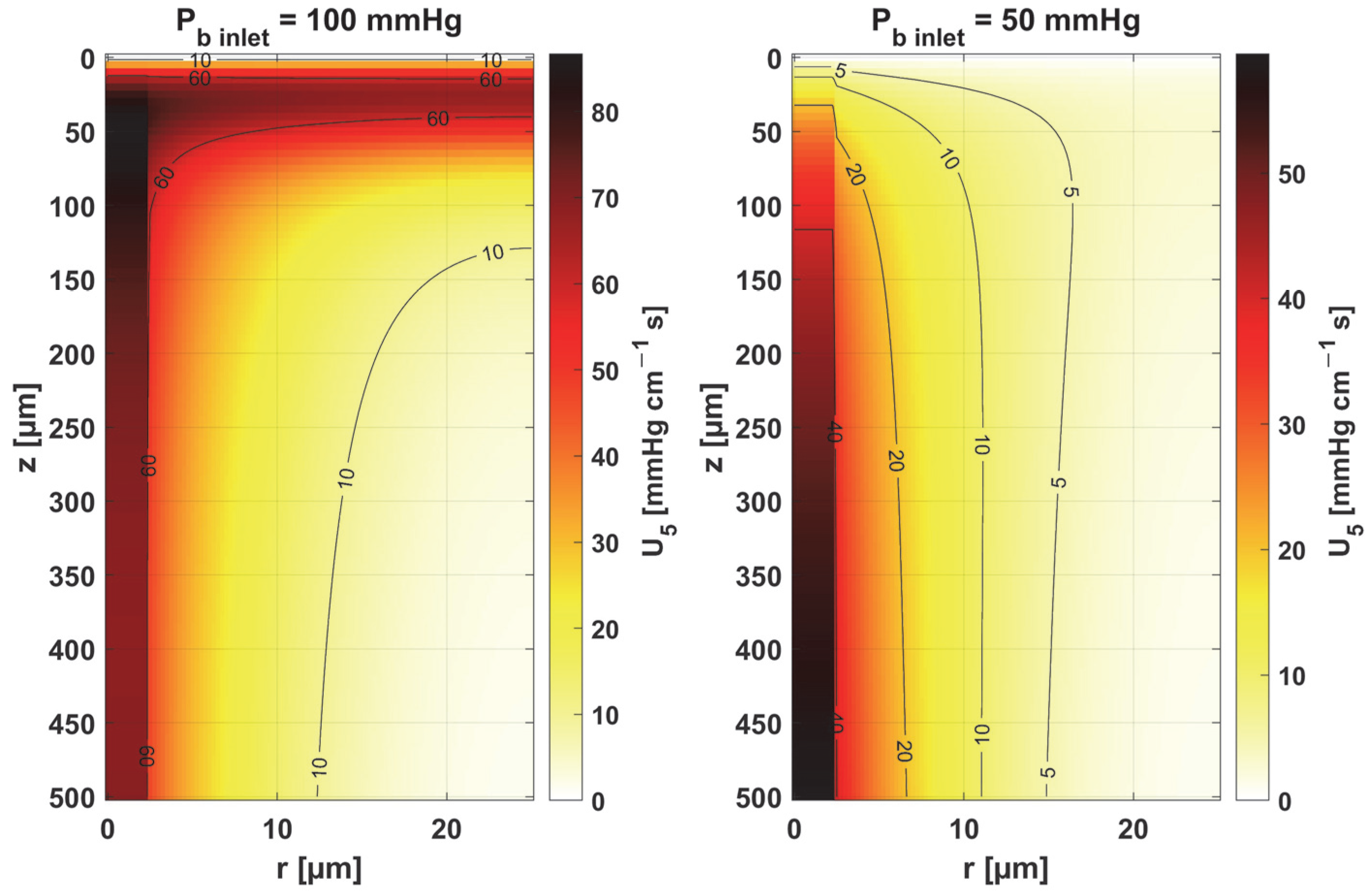
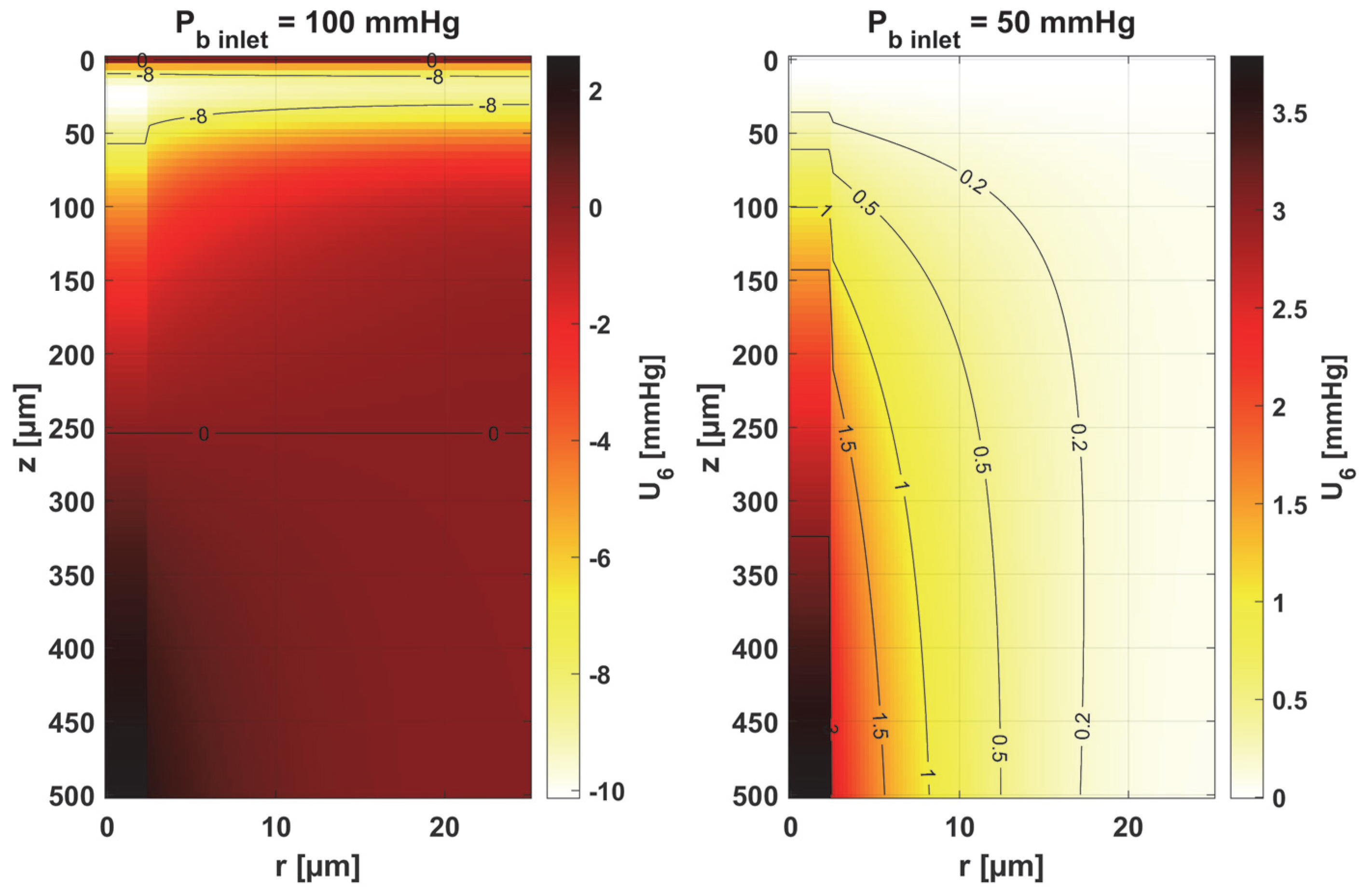
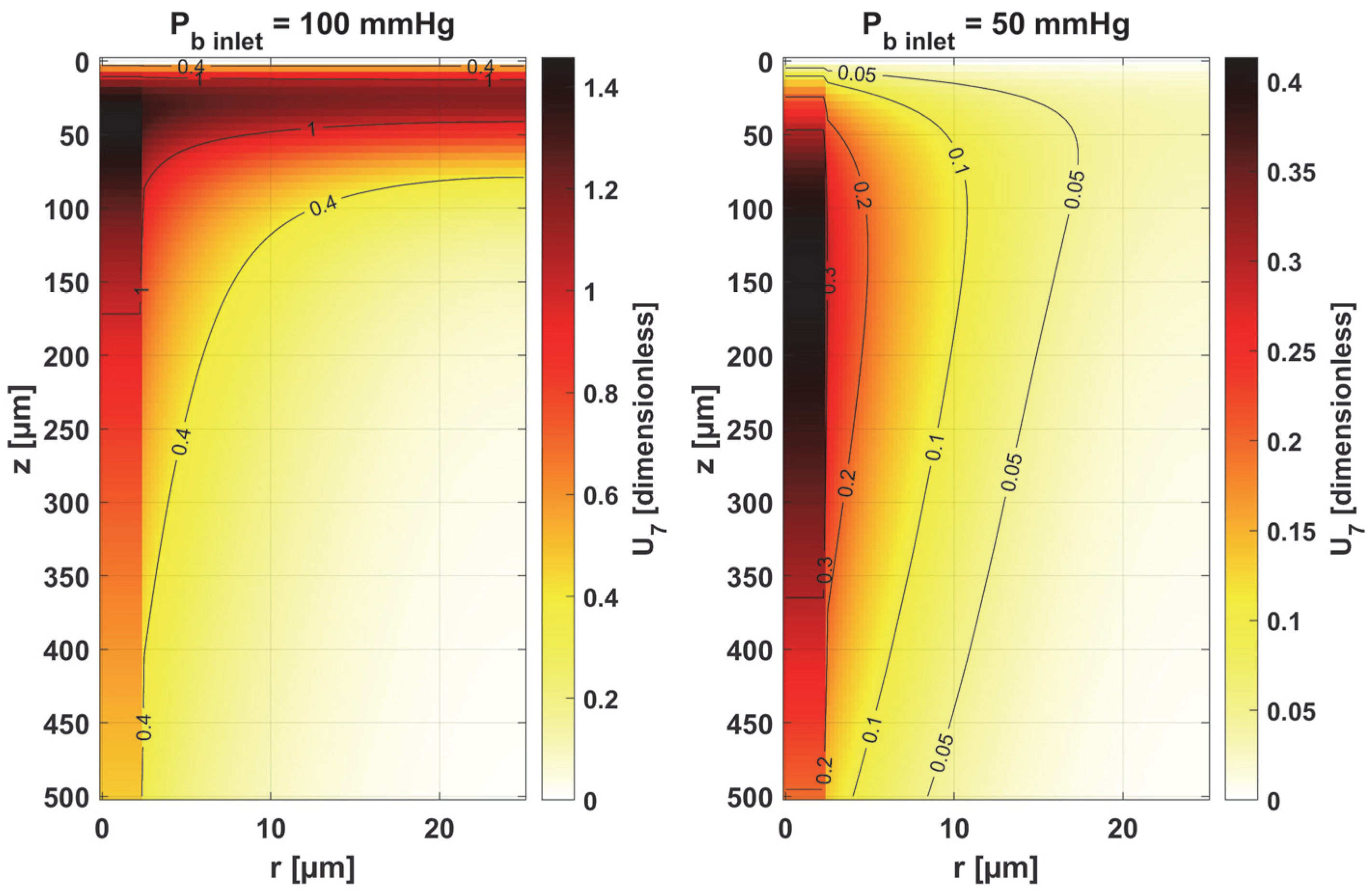
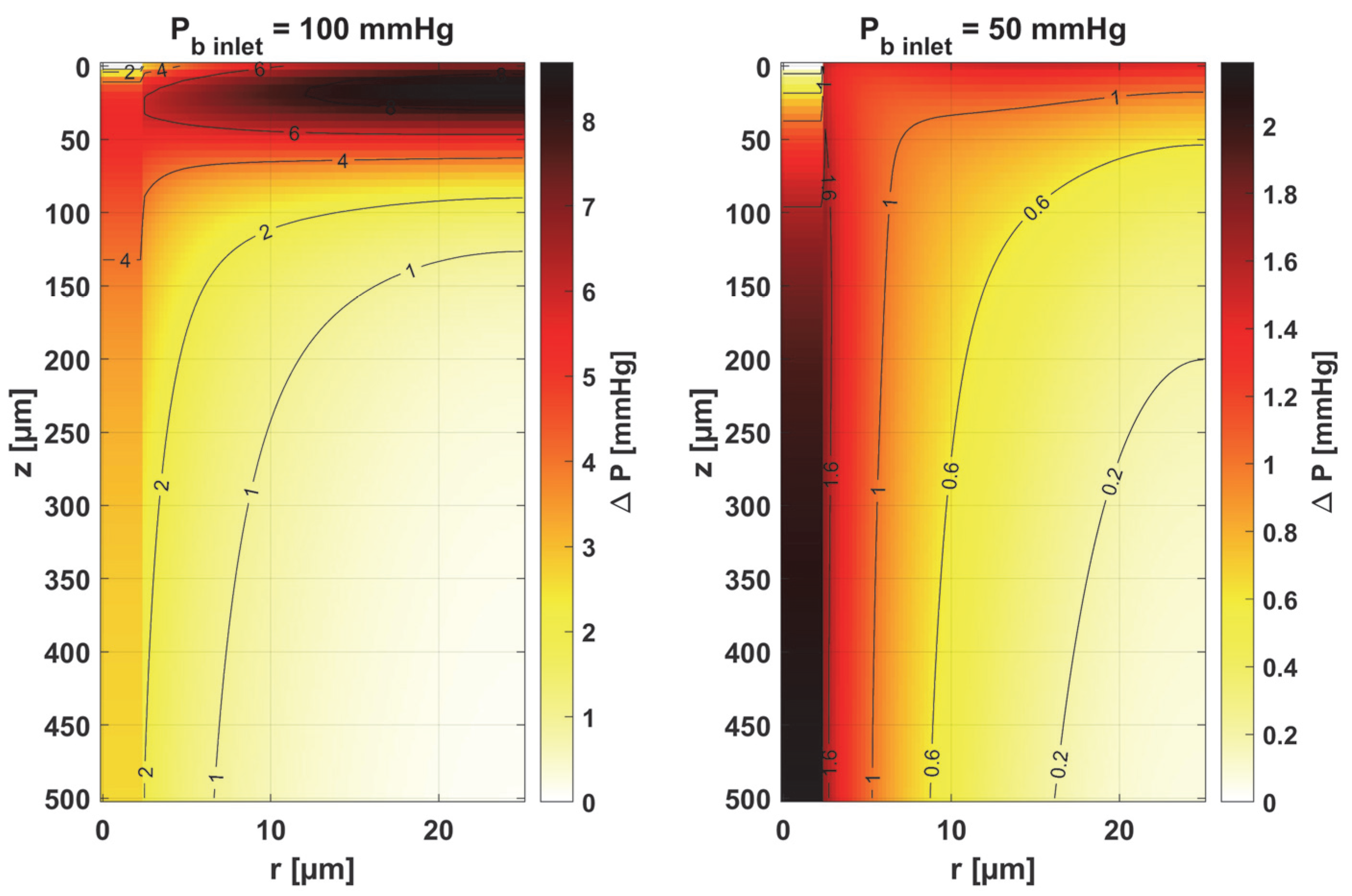
- Sensitivity functions were determined for the seven parameters present in the oxygen distribution model, for the normothermic state, as well as for two different values of the partial pressure at the capillary inlet corresponding to healthy and cancerous tissue (Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14).
- The maximum increment values for each parameter were determined, assuming a 10% change in the parameter values (Table 1).
- The most important features of the results are the following:
- The sensitivity functions for each parameter have completely different distributions for the case of the two Pb inlet values considered.
- For tumor tissue (Pb inlet = 50 mmHg), for each parameter and collectively, smaller increments were observed than for healthy tissue (Pb inlet = 100 mmHg).
- For healthy tissue, the largest absolute values of increments were recorded for the parameters Kt, M0, and P50, i.e., related to the radial direction model and ODC, while for cancer tissue, the largest increments values were quite close to each other and had different coordinates than for healthy tissue.
- In the case of blood-related parameters and ODC, for tumor tissue, the maximum increment points were located closer to the capillary outlet, indicating the importance of these parameters for hypoxic tissue.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassanpour, S.; Saboonchi, A. Modeling of Heat Transfer in a Vascular Tissue-like Medium during an Interstitial Hyperthermia Process. J. Therm. Biol. 2016, 62, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Afrin, N.; Zhou, J.; Zhang, Y.; Tzou, D.Y.; Chen, J.K. Numerical Simulation of Thermal Damage to Living Biological Tissues Induced by Laser Irradiation Based on a Generalized Dual Phase Lag Model. Numer. Heat Transf. Appl. Part A Appl. 2012, 61, 483–501. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Kumar, D.; Rai, K.N.; Singh, J. Analysis of Thermal Injuries Using Classical Fourier and DPL Models for Multi-Layer of Skin under Different Boundary Conditions. Int. J. Biomath. 2021, 14, 2150040. [Google Scholar] [CrossRef]
- Oden, J.T.; Diller, K.R.; Bajaj, C.; Browne, J.C.; Hazle, J.; Babuška, I.; Bass, J.; Biduat, L.; Demkowicz, L.; Elliott, A.; et al. Dynamic Data-Driven Finite Element Models for Laser Treatment of Cancer. Numer. Methods Partial Differ. Equ. 2007, 23, 904–922. [Google Scholar] [CrossRef]
- Abraham, J.P.; Sparrow, E.M. A Thermal-Ablation Bioheat Model Including Liquid-to-Vapor Phase Change, Pressure- and Necrosis-Dependent Perfusion, and Moisture-Dependent Properties. Int. J. Heat Mass Transf. 2007, 50, 2537–2544. [Google Scholar] [CrossRef]
- He, Y.; Shirazaki, M.; Liu, H.; Himeno, R.; Sun, Z. A Numerical Coupling Model to Analyze the Blood Flow, Temperature, and Oxygen Transport in Human Breast Tumor under Laser Irradiation. Comput. Biol. Med. 2006, 36, 1336–1350. [Google Scholar] [CrossRef]
- Jasiński, M. Numerical Analysis of Thermal Damage and Oxygen Distribution in Laser Irradiated Tissue. J. Appl. Math. Comput. Mech. 2022, 21, 51–62. [Google Scholar] [CrossRef]
- Secomb, T.W.; Alberding, J.P.; Hsu, R.; Dewhirst, M.W.; Pries, A.R. Angiogenesis: An Adaptive Dynamic Biological Patterning Problem. PLoS Comput. Biol. 2013, 9, e1002983. [Google Scholar] [CrossRef]
- Fry, B.C.; Roy, T.K.; Secomb, T.W. Capillary Recruitment in a Theoretical Model for Blood Flow Regulation in Heterogeneous Microvessel Networks. Physiol. Rep. 2013, 1, e00050. [Google Scholar] [CrossRef]
- Zhu, T.C.; Liu, B.; Penjweini, R. Study of Tissue Oxygen Supply Rate in a Macroscopic Photodynamic Therapy Singlet Oxygen Model. J. Biomed. Opt. 2015, 20, 038001. [Google Scholar] [CrossRef]
- Whiteley, J.P.; Gavaghan, D.J.; Hahn, C.E.W. Mathematical Modelling of Oxygen Transport to Tissue. J. Math. Biol. 2002, 44, 503–522. [Google Scholar] [CrossRef] [PubMed]
- Goldman, D. Theoretical Models of Microvascular Oxygen Transport to Tissue. Microcirculation 2008, 15, 795–811. [Google Scholar] [CrossRef] [PubMed]
- Jasiński, M.; Zadoń, M. Modeling of the Influence of Elevated Temperature on Oxygen Distribution in Soft Tissue. Eng. Trans. 2023, 71, 287–306. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I. Finite Element Analyses of Nonlinear DPL Bioheat Model in Spherical Tissues Using Experimental Data. Mech. Based Des. Struct. Mach. 2022, 50, 1287–1297. [Google Scholar] [CrossRef]
- Majchrzak, E.; Turchan, Ł.; Dziatkiewicz, J. Modeling of Skin Tissue Heating Using the Generalized Dual Phase-Lag Equation. Arch. Mech. 2015, 67, 417–437. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A.; Anukool, W. Nonlocal Thermal Effects on Biological Tissues and Tumors. Therm. Sci. Eng. Prog. 2022, 34, 101424. [Google Scholar] [CrossRef]
- Paruch, M. Mathematical Modeling of Breast Tumor Destruction Using Fast Heating during Radiofrequency Ablation. Materials 2020, 13, 455–458. [Google Scholar] [CrossRef]
- Mochnacki, B.; Ciesielski, M. Sensitivity of Transient Temperature Field in Domain of Forearm Insulated by Protective Clothing with Respect to Perturbations of External Boundary Heat Flux. Bull. Polish Acad. Sci. Tech. Sci. 2016, 64, 591–598. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Fractal Pennes and Cattaneo–Vernotte Bioheat Equations from Product-like Fractal Geometry and Their Implications on Cells in the Presence of Tumour Growth. J. R. Soc. Interface 2021, 18, 20210564. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Kumar, D.; Rai, K.N.; Singh, J. Numerical Simulation of the Skin Tissue Subjected to Hyperthermia Treatment Using a Nonlinear DPL Model. Therm. Sci. Eng. Prog. 2022, 34, 101394. [Google Scholar] [CrossRef]
- Majchrzak, E.; Stryczyński, M. Dual-Phase Lag Model of Heat Transfer between Blood Vessel and Biological Tissue. Math. Biosci. Eng. MBE 2021, 18, 1573–1589. [Google Scholar] [CrossRef] [PubMed]
- Akula, S.C.; Maniyeri, R. Numerical Simulation of Bioheat Transfer: A Comparative Study on Hyperbolic and Parabolic Heat Conduction. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 62. [Google Scholar] [CrossRef]
- Alzahrani, F.; Abbas, I. A Numerical Solution of Nonlinear DPL Bioheat Model in Biological Tissue Due to Laser Irradiations. Indian J. Phys. 2022, 96, 377–383. [Google Scholar] [CrossRef]
- Dombrovsky, L.A. Laser-Induced Thermal Treatment of Superficial Human Tumors: An Advanced Heating Strategy and Non-Arrhenius Law for Living Tissues. Front. Therm. Eng. 2022, 1, 807083. [Google Scholar] [CrossRef]
- Korczak, A.; Jasiński, M. Modelling of Biological Tissue Damage Process with Application of Interval Arithmetic. J. Theor. Appl. Mech. 2019, 57, 249–261. [Google Scholar] [CrossRef]
- Piasecka-Belkhayat, A.; Skorupa, A. Numerical Study of Heat and Mass Transfer during Cryopreservation Process with Application of Directed Interval Arithmetic. Materials 2021, 14, 2966. [Google Scholar] [CrossRef]
- Varma, A.; Morbidelli, M.; Wu, H. Parametric Sensitivity in Chemical Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Laporte, E.; Le Tallec, P. Numerical Methods in Sensitivity Analysis and Shape Optimization; Modeling and Simulation in Science, Engineering and Technology; Birkhäuser: Boston, MA, USA, 2003; ISBN 978-1-4612-6598-6. [Google Scholar]
- Cacuci, D.G. Sensitivity & Uncertainty Analysis, Volume 1: Theory; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003; ISBN 9780429210099. [Google Scholar]
- Susnjara, A.; Poljak, D.; Rezo, F.; Matkovic, J. Stochastic Sensitivity Analysis of Bioheat Transfer Equation. In Proceedings of the 2019 URSI International Symposium on Electromagnetic Theory (EMTS), San Diego, CA, USA, 27–31 May 2019. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Wang, H.; Qin, Q.H. Meshless Method with Operator Splitting Technique for Transient Nonlinear Bioheat Transfer in Two-Dimensional Skin Tissues. Int. J. Mol. Sci. 2015, 16, 2001–2019. [Google Scholar] [CrossRef]
- Majchrzak, E.; Kałuża, G. Sensitivity Analysis of Temperature in Heated Soft Tissues with Respect to Time Delays. Contin. Mech. Thermodyn. 2021, 34, 587–599. [Google Scholar] [CrossRef]
- Alosaimi, M.; Lesnic, D.; Niesen, J. Reconstruction of the Thermal Properties in a Wave-Type Model of Bio-Heat Transfer. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 5143–5167. [Google Scholar] [CrossRef]
- Pirtini Çetingül, M.; Herman, C. A Heat Transfer Model of Skin Tissue for the Detection of Lesions: Sensitivity Analysis. Phys. Med. Biol. 2010, 55, 5933–5951. [Google Scholar] [CrossRef]
- Ehsan, S.M.; George, S.C. Nonsteady State Oxygen Transport in Engineered Tissue: Implications for Design. Tissue Eng. Part A 2013, 19, 1433. [Google Scholar] [CrossRef] [PubMed]
- Vitullo, P.; Cicci, L.; Possenti, L.; Coclite, A.; Costantino, M.L.; Zunino, P. Sensitivity Analysis of a Multi-Physics Model for the Vascular Microenvironment. Int. J. Numer. Method. Biomed. Eng. 2023, 39, e3752. [Google Scholar] [CrossRef] [PubMed]
- McGuire, B.J.; Secomb, T.W. A Theoretical Model for Oxygen Transport in Skeletal Muscle under Conditions of High Oxygen Demand. J. Appl. Physiol. 2001, 91, 2255–2265. [Google Scholar] [CrossRef]
- Hlastala, M.P.; Woodson, R.D.; Wranne, B. Influence of Temperature on Hemoglobin-Ligand Interaction in Whole Blood. J. Appl. Physiol. 1977, 43, 545–550. [Google Scholar] [CrossRef]
- Majchrzak, E.; Kałuża, G. Sensitivity Analysis of Biological Tissue Freezing Process with Respect to the Radius of Spherical Cryoprobe. J. Theor. Appl. Mech. 2006, 44, 381–392. [Google Scholar]
- Davies, C.R.; Harasaki, H.; Saidel, G.M. Sensitivity Analysis of One-Dimensional Heat Transfer in Tissue With Temperature-Dependent Perfusion. J. Biomech. Eng. 1997, 119, 77–80. [Google Scholar] [CrossRef]
- Majchrzak, E.; Turchan, L.; Jasiński, M. Identification of Laser Intensity Assuring the Destruction of Target Region of Biological Tissue Using the Gradient Method and Generalized Dual-Phase Lag Equation. Iran. J. Sci. Technol.—Trans. Mech. Eng. 2019, 43, 539–548. [Google Scholar] [CrossRef]
- Keskin, A.Ü. Boundary Value Problems for Engineers; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Attili, B.S.; Syam, M.I. Efficient Shooting Method for Solving Two Point Boundary Value Problems. Chaos Solitons Fractals 2008, 35, 895–903. [Google Scholar] [CrossRef]
- Ha, S.N. A Nonlinear Shooting Method for Two-Point Boundary Value Problems. Comput. Math. Appl. 2001, 42, 1411–1420. [Google Scholar] [CrossRef]
- Majchrzak, E.; Jasiński, M. Numerical Estimation of Burn Degree of Skin Tissue Using the Sensitivity Analysis Methods. Acta Bioeng. Biomech. 2003, 5, 93–108. [Google Scholar]
- Woyke, S.; Brugger, H.; Ströhle, M.; Haller, T.; Gatterer, H.; Dal Cappello, T.; Strapazzon, G. Effects of Carbon Dioxide and Temperature on the Oxygen-Hemoglobin Dissociation Curve of Human Blood: Implications for Avalanche Victims. Front. Med. 2021, 8, 808025. [Google Scholar] [CrossRef] [PubMed]
- Dash, R.K.; Korman, B.; Bassingthwaighte, J.B. Simple Accurate Mathematical Models of Blood HbO2 and HbCO2 Dissociation Curves at Varied Physiological Conditions: Evaluation and Comparison with Other Models. Eur. J. Appl. Physiol. 2016, 116, 97–113. [Google Scholar] [CrossRef] [PubMed]
- Jasiński, M.; Zadoń, M. Modeling of Photochemical and Photothermal Effects in Soft Tissue Subjected to Laser Irradiation. Comput. Assist. Methods Eng. Sci. 2023, 31, 29–50. [Google Scholar] [CrossRef]
- Wise, D.L.; Houghton, G. Solubilities and Diffusivities of Oxygen in Hemolyzed Human Blood Solutions. Biophys. J. 1969, 9, 36–53. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Abbas, I.A.; Singh, J. Numerical Simulation of Thermal Response for Non-Linear Multi-Layer Skin Model Subjected to Heating and Cooling. Therm. Sci. Eng. Prog. 2023, 40, 101790. [Google Scholar] [CrossRef]



| Pb inlet = 100 mmHg | Pb inlet = 50 mmHg | |||||
|---|---|---|---|---|---|---|
| Parameter | Us × Δ ps [mmHg] | r [µm] | z [µm] | Us × Δ ps [mmHg] | r [µm] | z [µm] |
| Kt | 3.8086 | 25 | 0 | −0.9587 | 2.5 | 115 |
| M0 | −6.5718 | 25 | 15 | −1.1972 | 14 | 0 |
| k | 2.0083 | 2.5 | 0 | 1.2516 | 2.5 | 0 |
| ub | 1.7771 | 1.25 | 50 | 1.2201 | 1.25 | 500 |
| κb | 1.7771 | 1.25 | 50 | 1.2201 | 1.25 | 500 |
| n | −2.6057 | 1.25 | 25 | 0.9736 | 1.25 | 500 |
| P50 | 3.9371 | 1.25 | 40 | 1.1161 | 1.25 | 145 |
| All parameters | 8.6856 | 25 | 15 | 2.1871 | 1.25 | 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiński, M.; Zadoń, M. Sensitivity Analysis in the Problem of the Impact of an External Heat Impulse on Oxygen Distribution in Biological Tissue. Materials 2025, 18, 2425. https://doi.org/10.3390/ma18112425
Jasiński M, Zadoń M. Sensitivity Analysis in the Problem of the Impact of an External Heat Impulse on Oxygen Distribution in Biological Tissue. Materials. 2025; 18(11):2425. https://doi.org/10.3390/ma18112425
Chicago/Turabian StyleJasiński, Marek, and Maria Zadoń. 2025. "Sensitivity Analysis in the Problem of the Impact of an External Heat Impulse on Oxygen Distribution in Biological Tissue" Materials 18, no. 11: 2425. https://doi.org/10.3390/ma18112425
APA StyleJasiński, M., & Zadoń, M. (2025). Sensitivity Analysis in the Problem of the Impact of an External Heat Impulse on Oxygen Distribution in Biological Tissue. Materials, 18(11), 2425. https://doi.org/10.3390/ma18112425





