Microstructure Evolution of Cement Paste Based on a Continuous Hydration Model for Irregular Polyhedral Particles
Abstract
1. Introduction
2. Microstructure of Particle Packing in Cement Paste
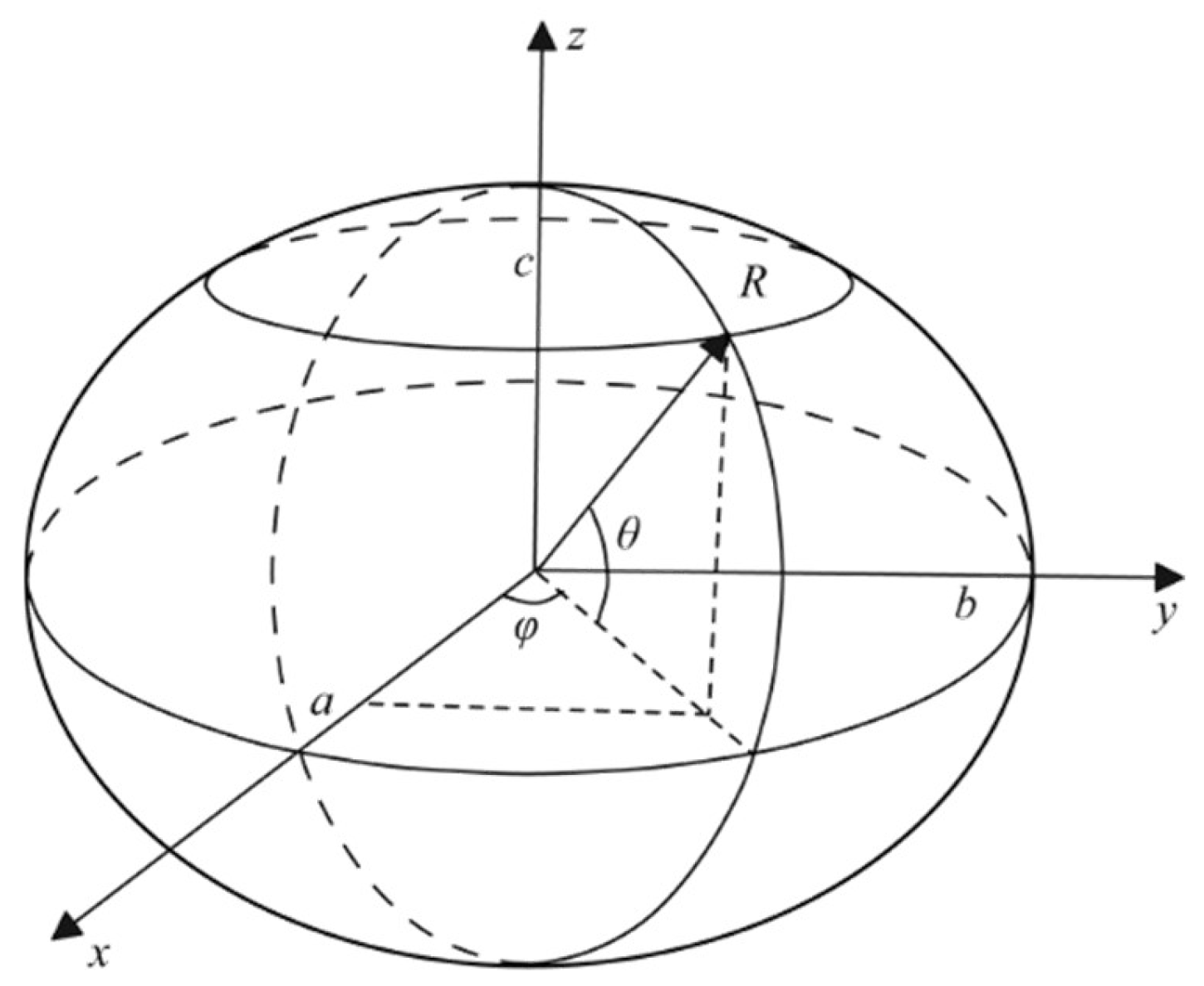
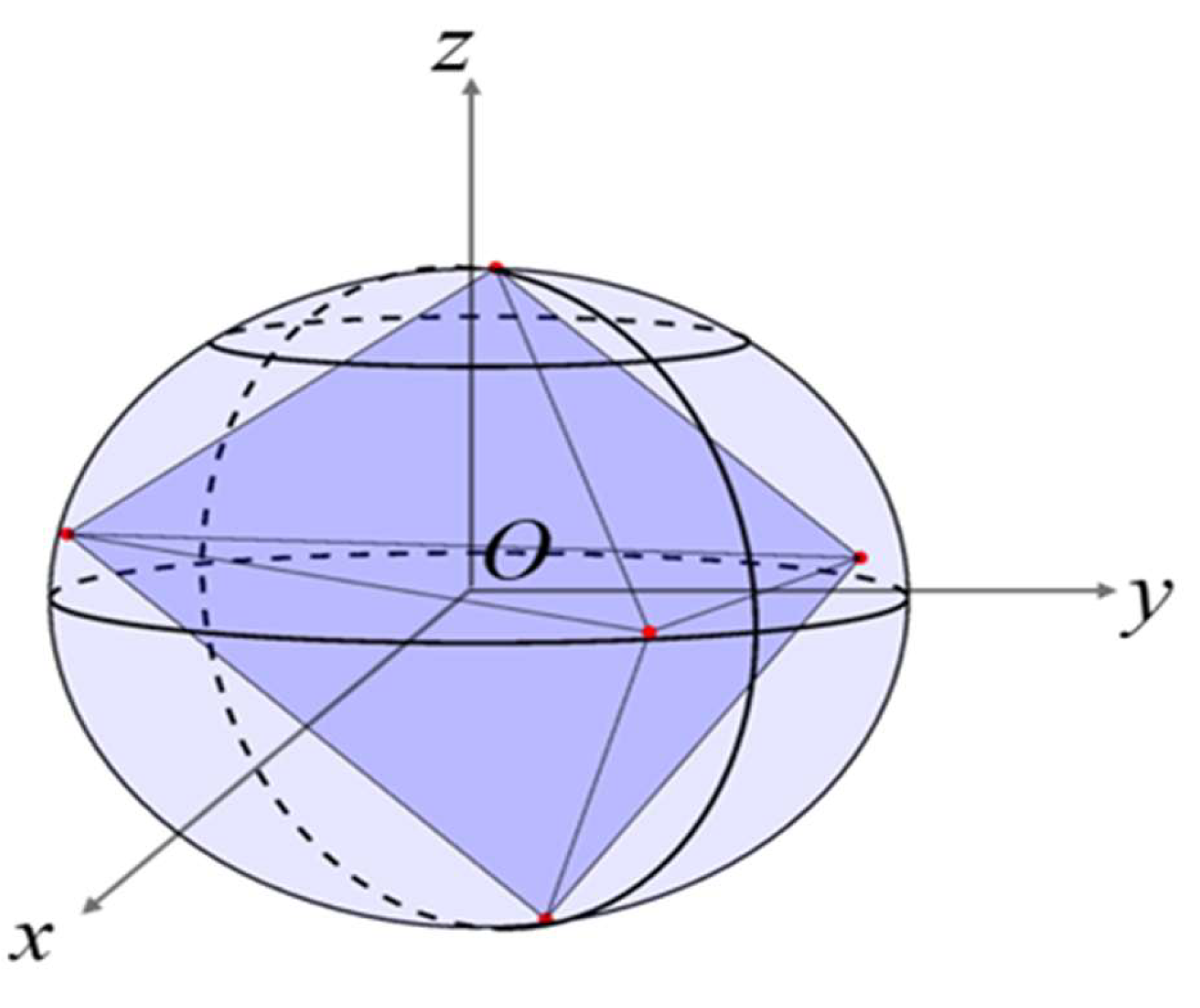
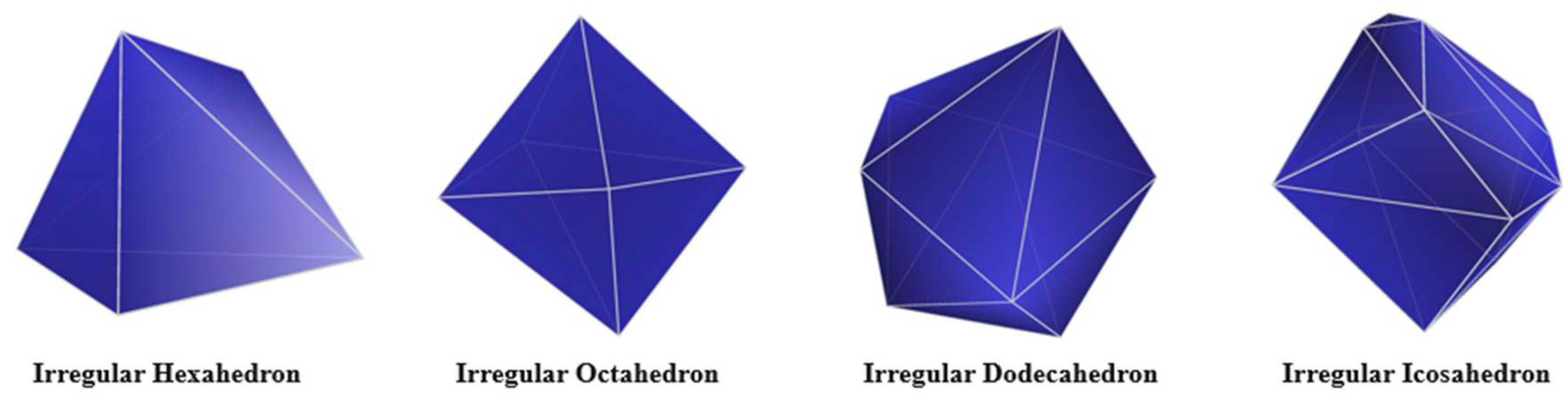
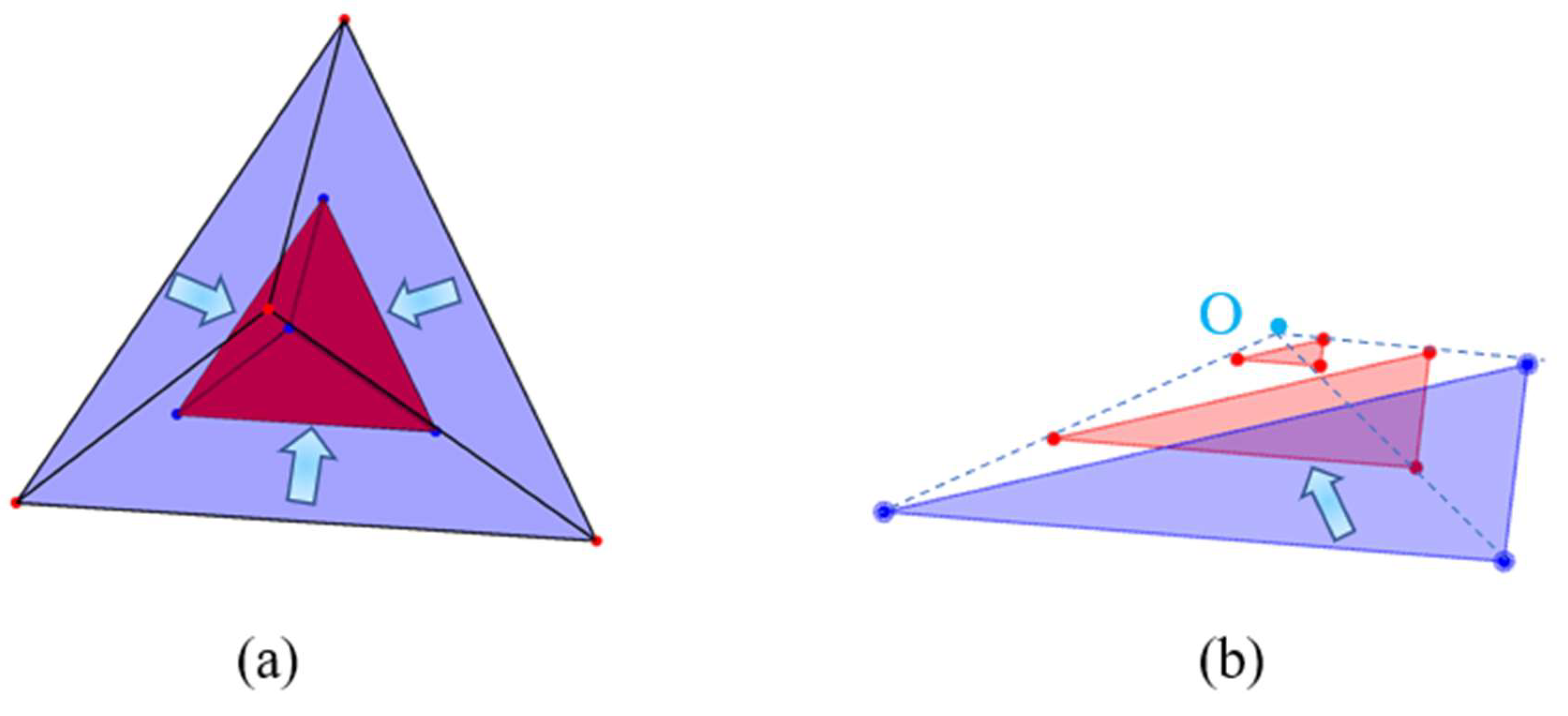
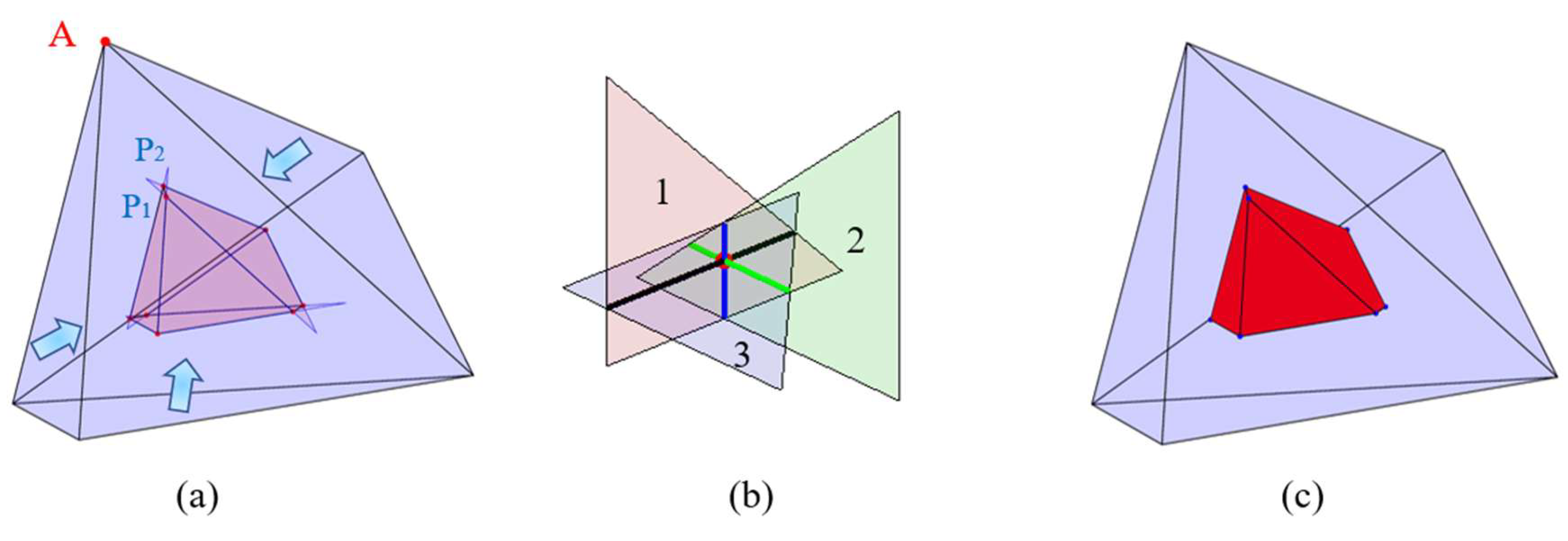
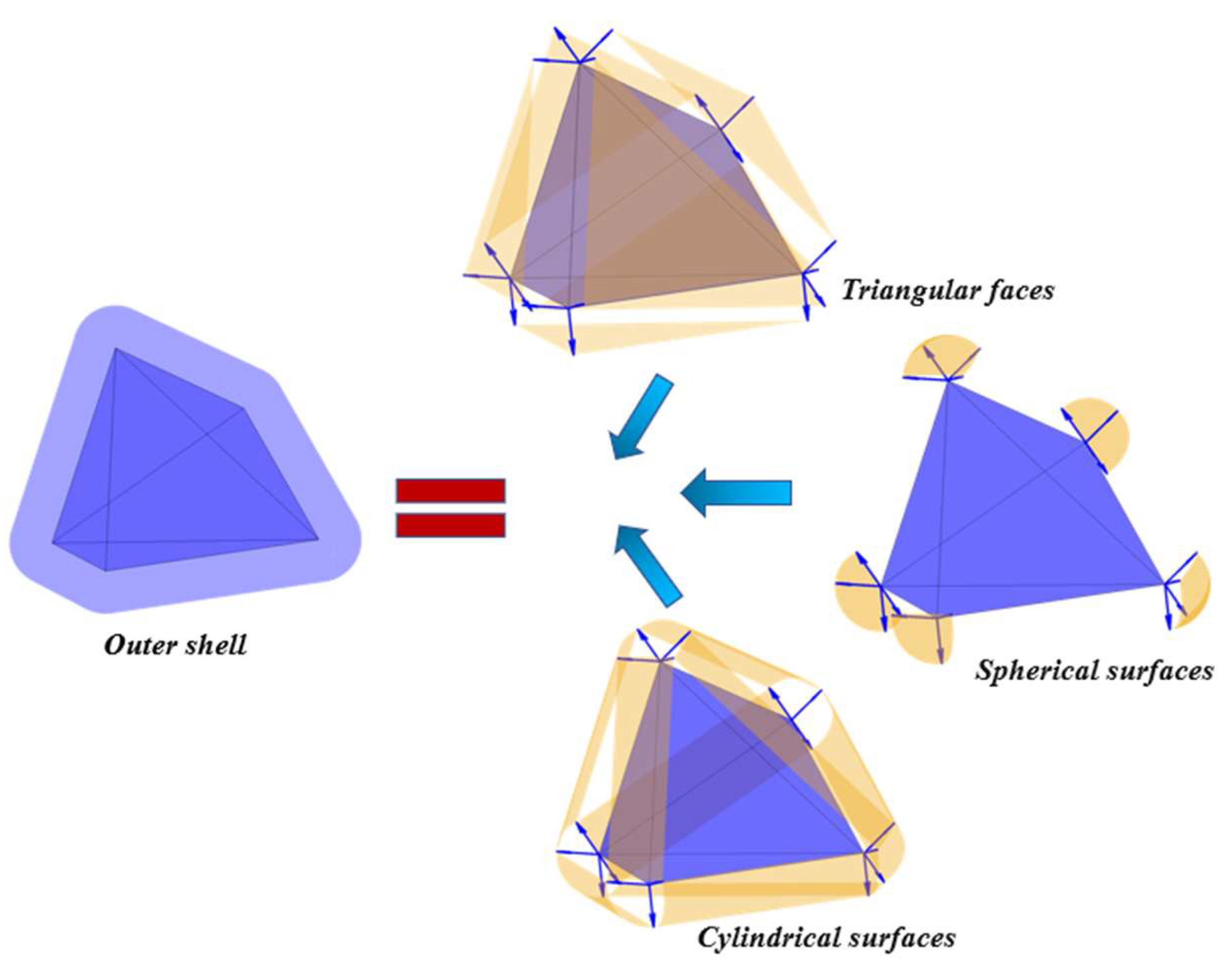
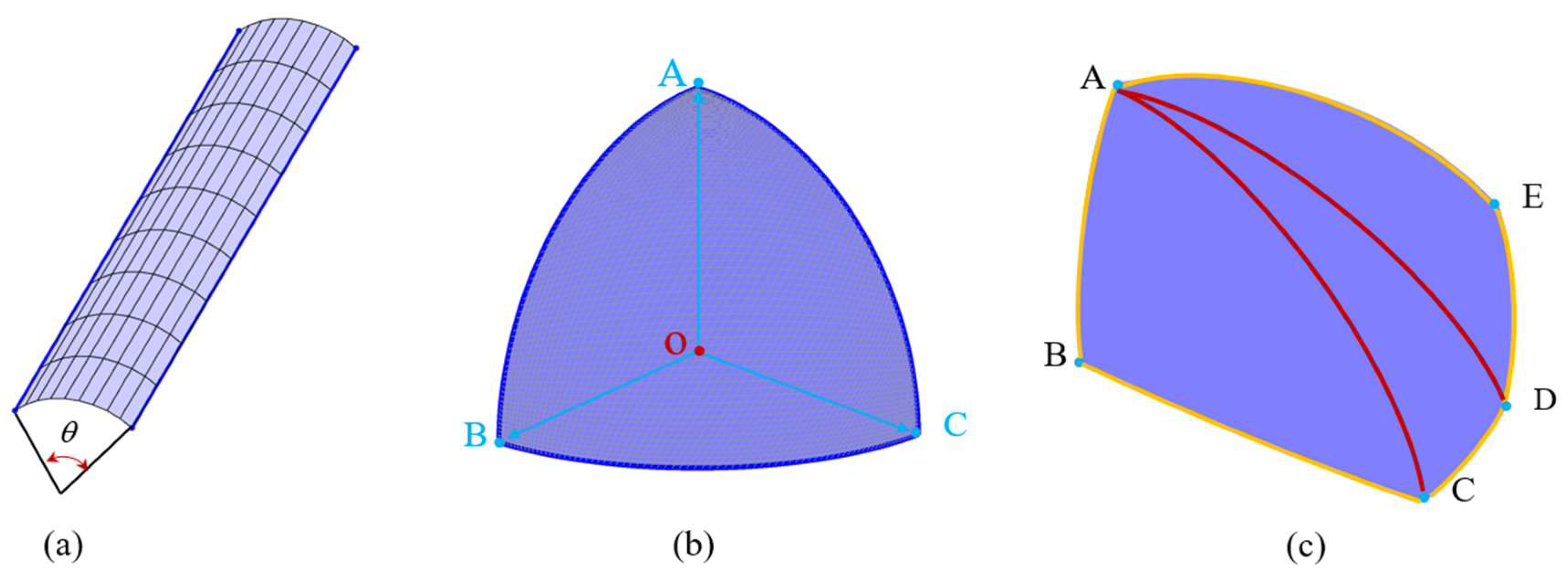
2.1. Construction of an Individual Cement Particle
2.2. Fresh State of Cement Paste
3. Simulation of Hydration Process and Microstructure of Cement Pastes
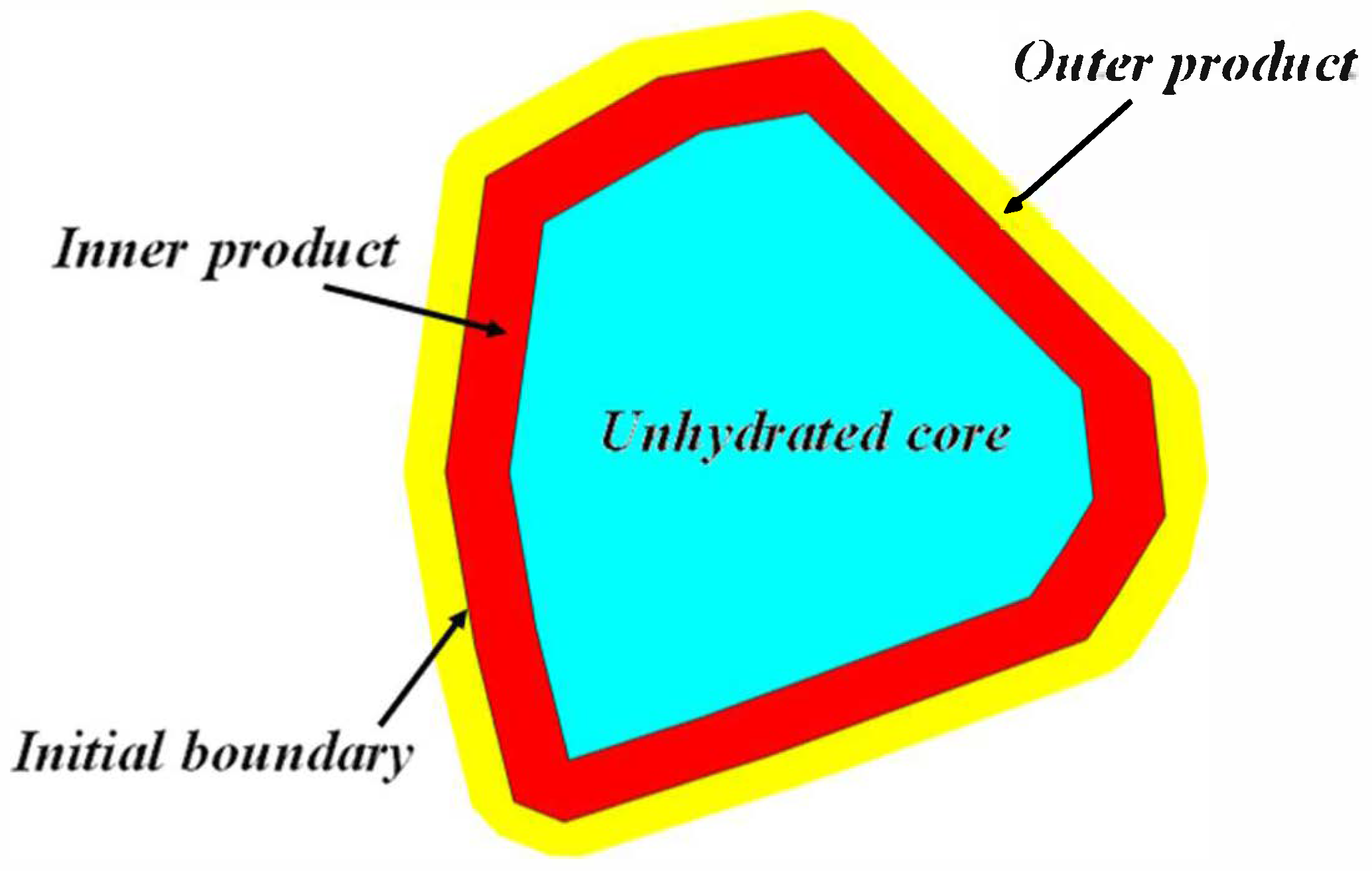
3.1. Hydration Mechanism of an Individual Irregular Polyhedral Particles
3.2. Simulation Mechanism of Hydration of Cement Paste Under Multiple Sized Particle
3.3. Hydration Simulation Process of Multi-Sized Irregular Polyhedral Cement Paste
4. Discussion
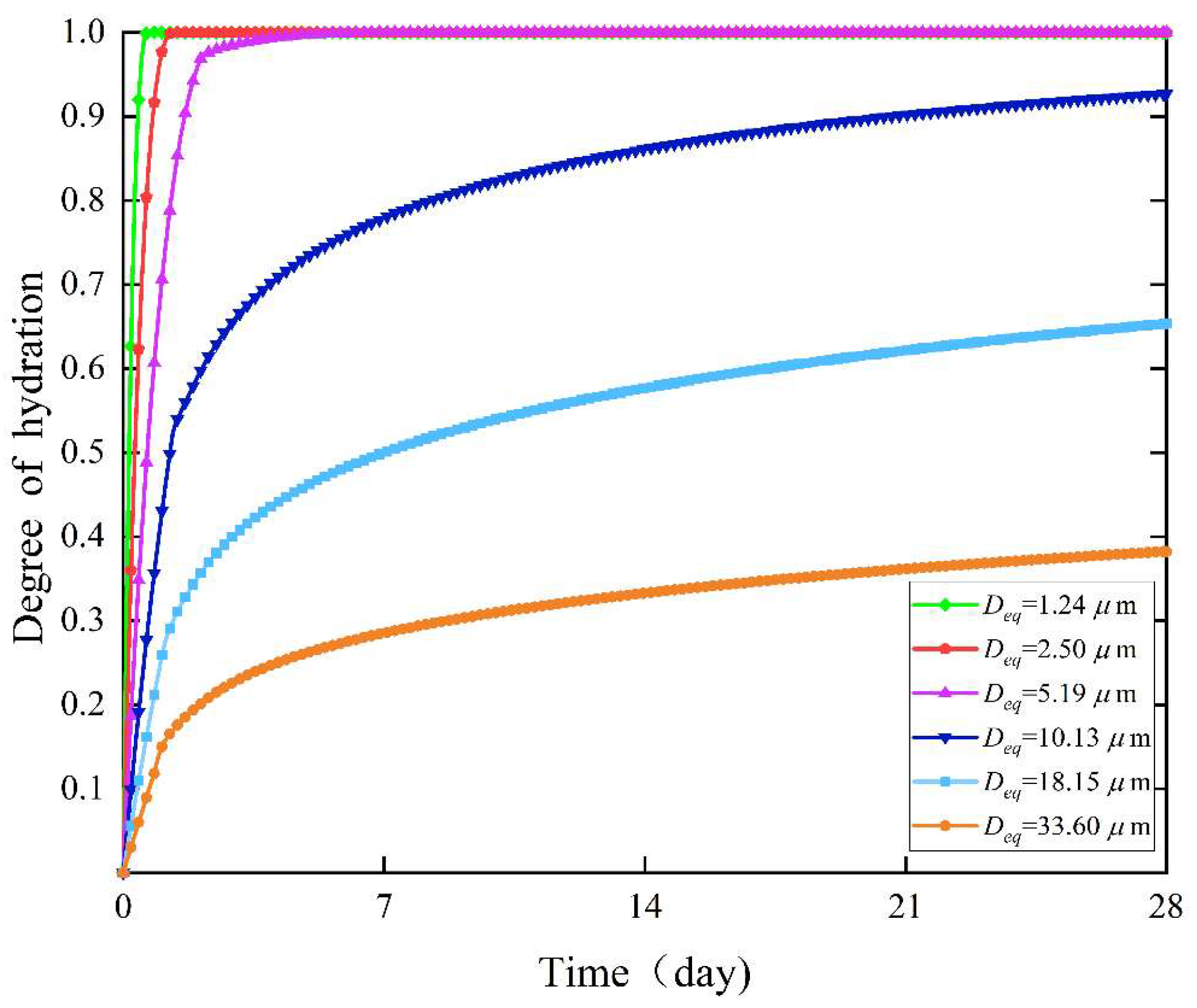
4.1. Effect of Particle Specific Surface Area on the Degree of Hydration
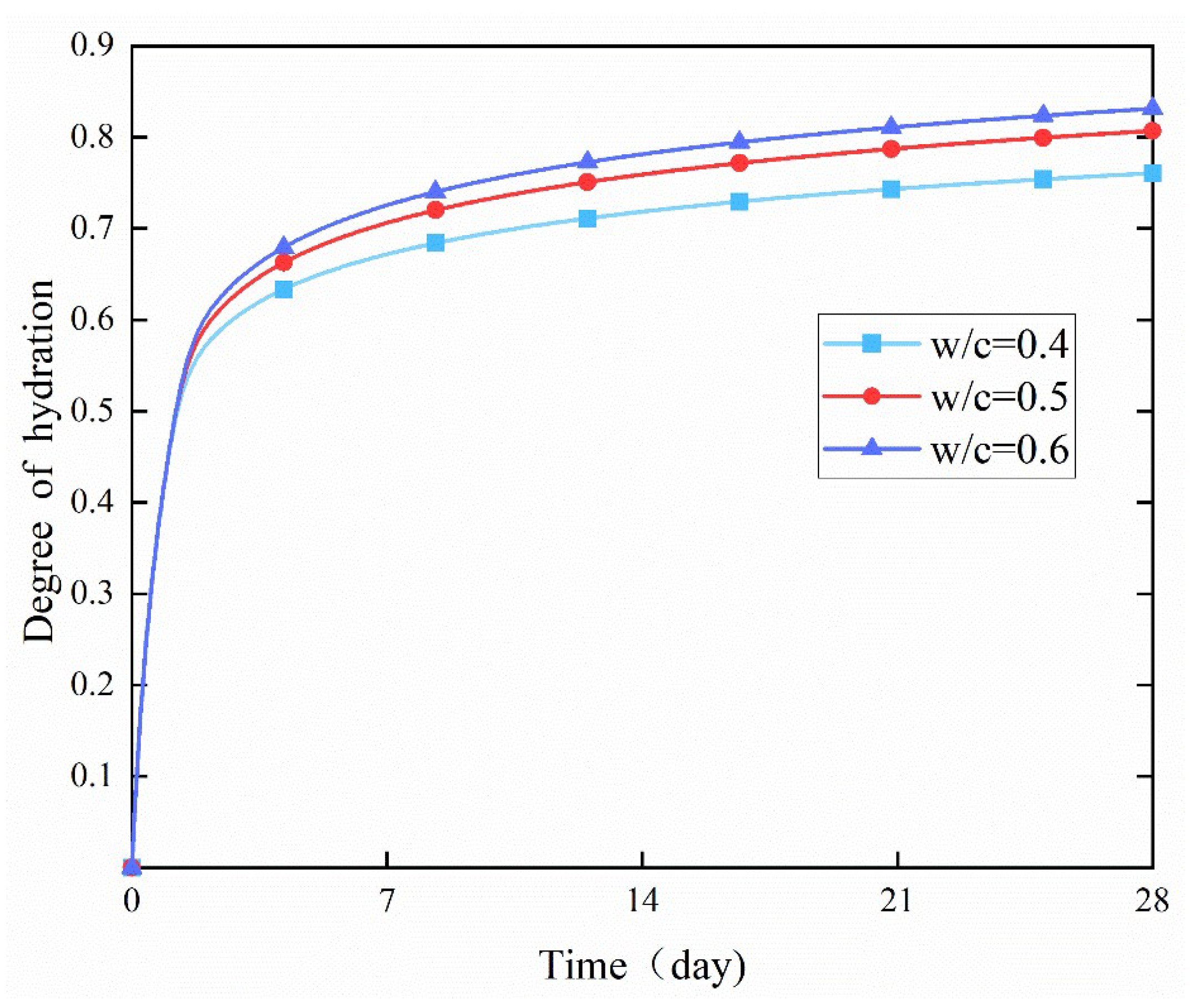
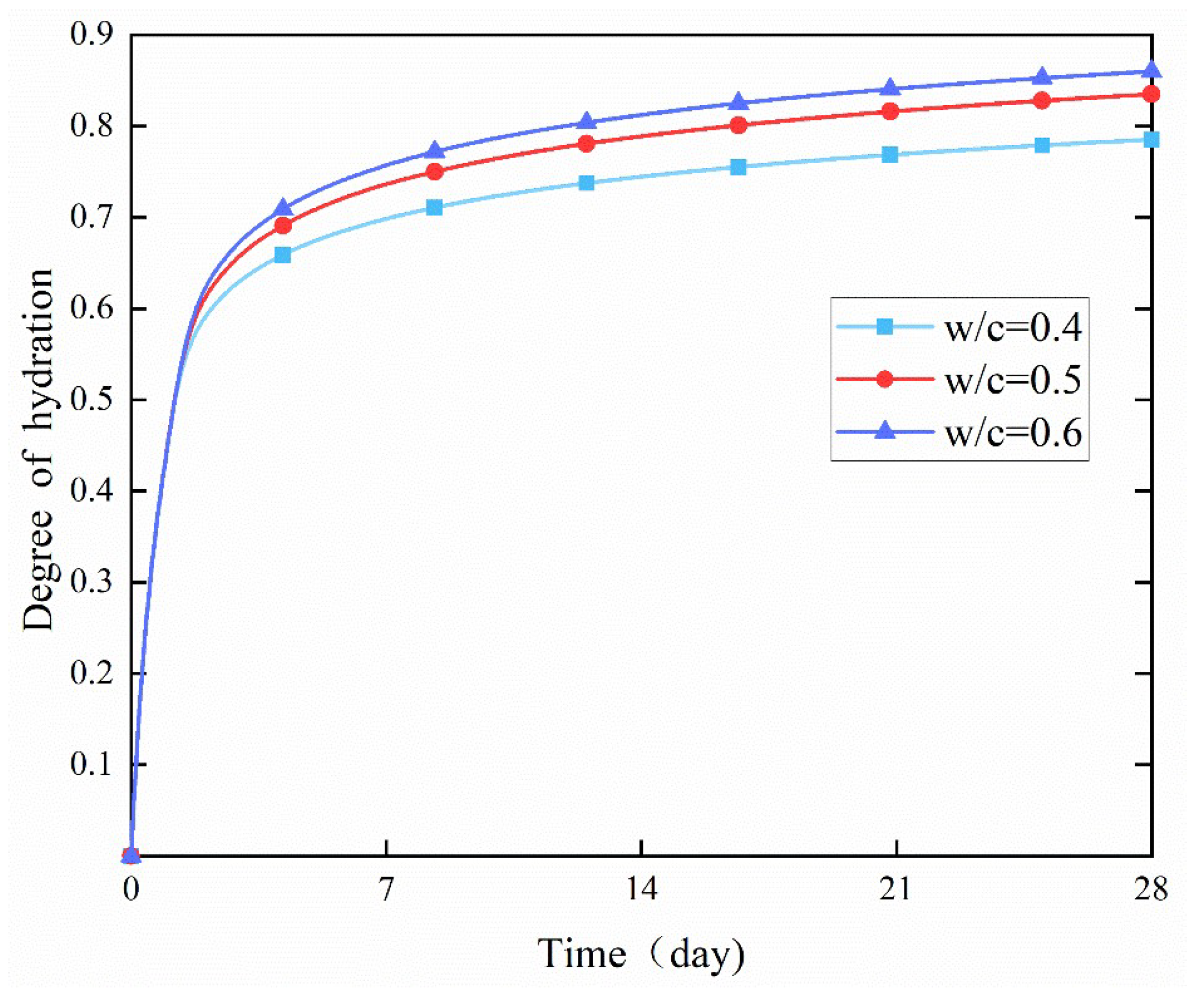
4.2. Effect of w/c Ratio
4.3. Effect of Curing Temperature
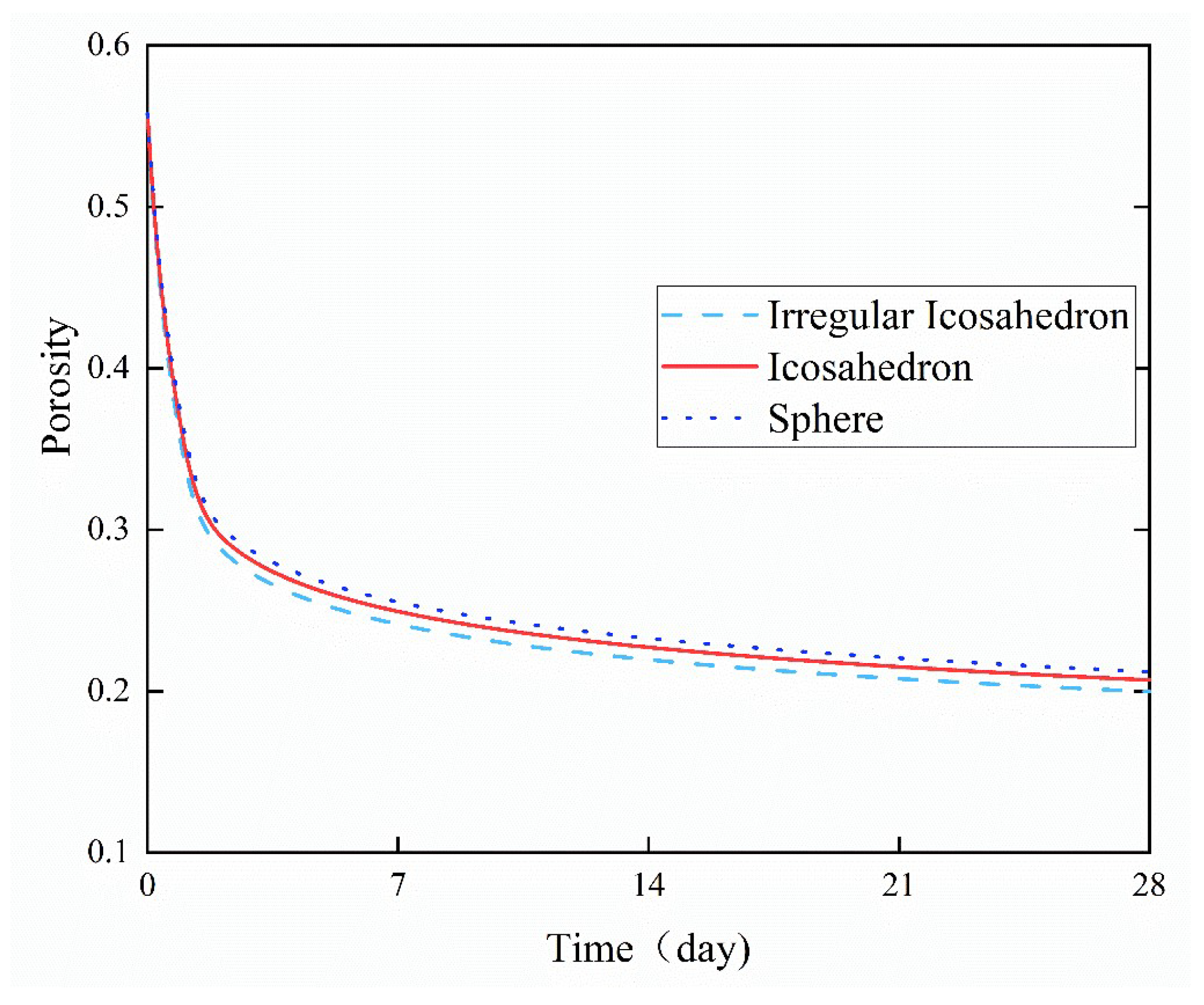
4.4. Porosity
5. Conclusions
- (1)
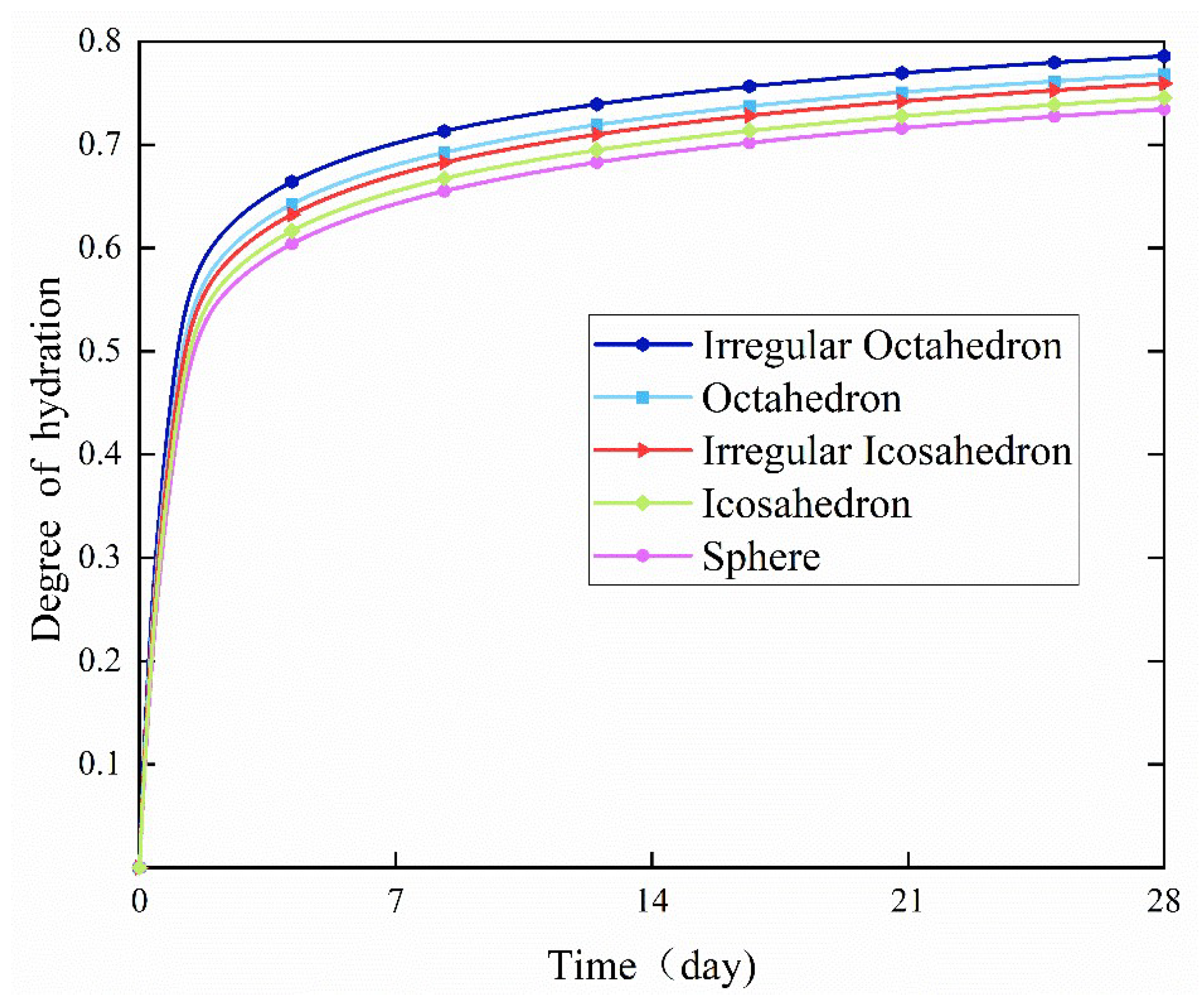
- The degree of hydration grew quickly within 48 h of the start of hydration, and there was no apparent difference in the degree of hydration between the various particle forms. After the first 48 h, the rate of hydration decreased, and changes in the level of hydration under various particle shapes gradually slowed.
- (2)
- The specific surface area of irregular octahedral particles was higher than that of spherical particles, regular octahedral particles, regular icosahedral particles, and irregular icosahedral particles. Results showed that irregular polyhedral particles had a greater specific surface area than regular polyhedral particles when the number of faces was equal. The specific surface area of irregular polyhedral particles increased with the number of faces. Furthermore, the rate of hydration increased with the specific surface area. The primary reason for this is that a higher specific surface area improves interaction with water, which makes it easier for water to enter the particles’ core and accelerates the hydration reaction.
- (3)
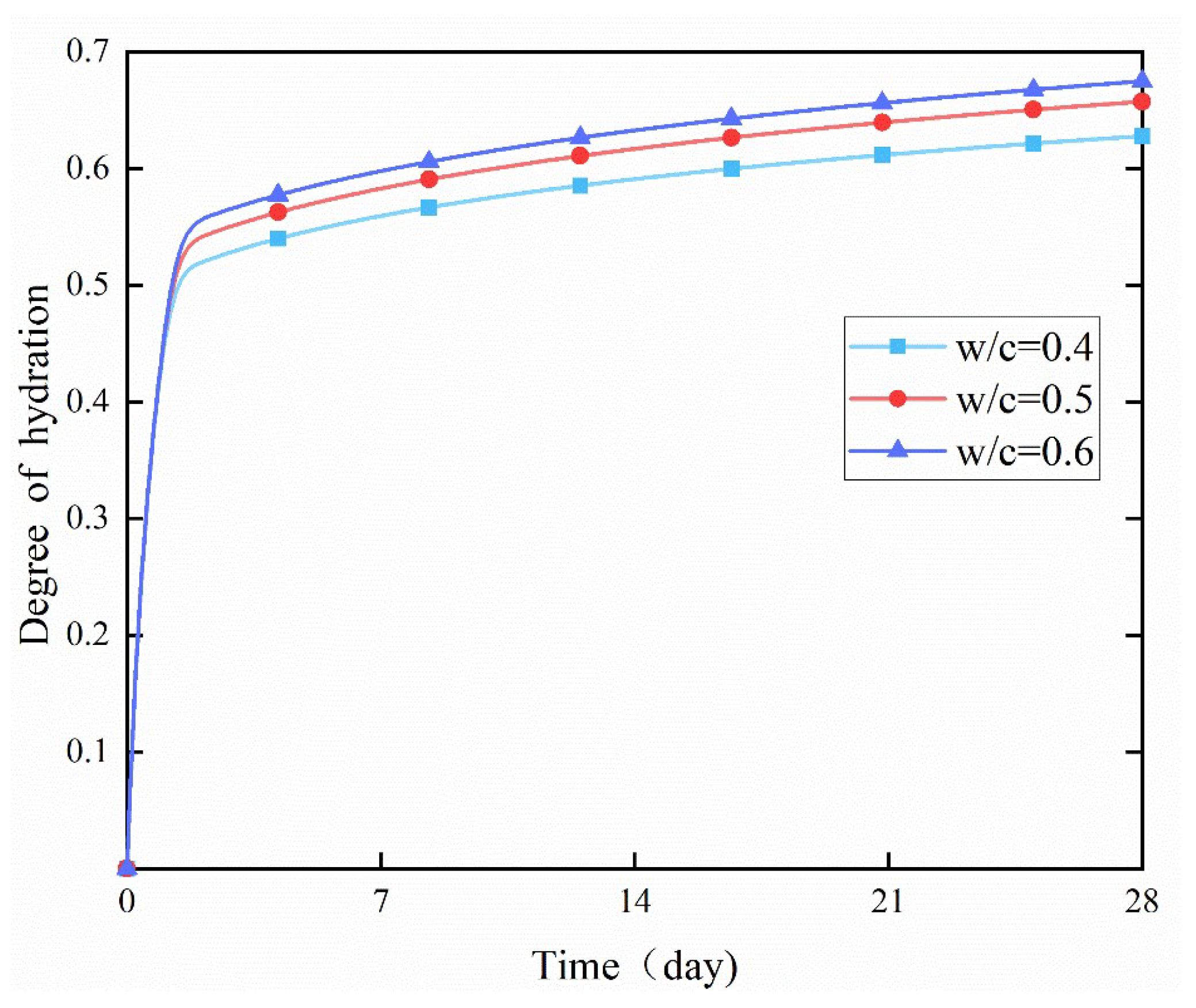
- In the early stage, different water-to-cement (w/c) ratios had no obvious effect on the degree of hydration. However, in the later stage, the degree of hydration increased significantly with the increase of the w/c ratio. This was because a higher w/c ratio allowed more water to react with cement particles per unit volume, thereby increasing the hydration rate.
- (4)
- An increase in the curing temperature of the surrounding environment also promoted the acceleration of the hydration rate of cement, while low temperatures had a more obvious inhibitory effect on the hydration reaction. When the curing temperature rose to 20 °C, the growth rate of the early-stage hydration reaction slowed down.
- (5)
- Among the three particle shapes, irregular icosahedral particles had the highest specific surface area, and their porosity decreased the fastest, followed by icosahedral particles and spherical particles. The porosity of the cement paste decreased rapidly in a short period of time after hydration began, but at a slower rate as hydration proceeded.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Gao, Y.F.; He, J.; Zhou, Y.D.; Geng, W.J. An experimental investigation of wind erosion resistance of desert sand cemented by soybean-urease induced carbonate precipitation. Geoderma 2023, 429, 116231. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Fu, W.G. Sponge effect of aerated concrete on phosphorus adsorption-desorption from agricultural drainage water in rainfall. Soil Water Res. 2020, 15, 220–227. [Google Scholar] [CrossRef]
- Bentz, D.P.; Garboczi, E.J. Digitised simulation model for microstructural development. Ceram. Trans. 1990, 16, 211–226. [Google Scholar]
- Bentz, D.P. Three-dimensional computer simulation of Portland cement hydration and microstructure development. J. Am. Ceram. Soc. 1997, 80, 3–21. [Google Scholar] [CrossRef]
- Bullard, J.W.; Garboczi, E.J. A model investigation of the influence of particle shape on portland cement hydration. Cem. Concr. Res. 2006, 36, 1007–1015. [Google Scholar] [CrossRef]
- Liu, C.; Huang, R.; Zhang, Y.S.; Liu, Z.Y.; Zhang, M.Z. Modelling of irregular-shaped cement particles and microstructural development of Portland cement. Constr. Build. Mater. 2018, 168, 362–378. [Google Scholar] [CrossRef]
- Van Breugel, K. Simulation of Hydration and Formation of Structure in Hardening Cement-Based Materials. Ph.D. Thesis, Delft Universirty of Technology, Delft, The Netherlands, 1993. [Google Scholar]
- Van Breugel, K. Numerical simulation of hydration and microstructural development in hardening cement-based materials (I) theory. Cem. Concr. Res. 1995, 25, 319–331. [Google Scholar] [CrossRef]
- Navi, P.; Pignat, C. Simulation of cement hydration and the connectivity of the capillary pore space. Adv. Cem. Based Mater. 1996, 4, 58–67. [Google Scholar] [CrossRef]
- Navi, P.; Pignat, C. Three-dimensional characterization of the pore structure of a simulated cement paste. Cem. Concr. Res. 1999, 29, 507–514. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, W.; Chen, H.; Tan, Z. Evolution of microstructures of cement paste via continuous-based hydration model of non-spherical cement particles. Compos. Part B Eng. 2020, 185, 107795. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, Z.; Yang, Z. A continuous hydration model for cement paste with realistic CT image-based particles and simulation of microstructural evolution. Cem. Concr. Res. 2024, 184, 107607. [Google Scholar] [CrossRef]
- Chen, Z.W.; Gao, Y.; Zhang, J.; Liu, Q.F.; Wang, H.L.; Zheng, J.J. Numerical modeling of microstructure development and chloride diffusion coefficient of cement paste with ellipsoidal particles. Constr. Build. Mater. 2023, 408, 133819. [Google Scholar] [CrossRef]
- Liu, L.; Sun, W.; Ye, G.; Chen, H.; Qian, Z. Estimation of the ionic diffusivity of virtual cement paste by random walk algorithm. Constr. Build. Mater. 2012, 28, 405–413. [Google Scholar] [CrossRef]
- Pintér, F.; Gosselin, C. The origin, composition and early age hydration mechanisms of Austrian natural Portland cement. Cem. Concr. Res. 2018, 110, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Liew, K. Multiscale simulation of mechanical properties and microstructure of CNT-reinforced cement-based composites. Comput. Methods Appl. Mech. Eng. 2017, 319, 393–413. [Google Scholar] [CrossRef]
- Luo, Y.W.; Wu, T.Q.; Zhu, X.P. The deformation space of delaunay triangulations of the sphere. Pac. J. Math. 2023, 323, 115–127. [Google Scholar] [CrossRef]
- OuYang, D.; Feng, H.Y. Reconstruction of 2D polygonal curves and 3D triangular surfaces via clustering of Delaunay circles/spheres. Comput.-Aided Des. 2011, 43, 839–847. [Google Scholar] [CrossRef]
- Brasselet, J.P.; Thuy, N.T.B. An elementary proof of Euler’s formula using Cauchy’s method. Topol. Its Appl. 2021, 293, 107558. [Google Scholar] [CrossRef]
- Bentz, D.P.; Garboczi, E.J.; Haecker, C.J.; Jensen, O.M. Effects of cement particle size distribution on performance properties of Portland cement-based materials. Cem. Concr. Res. 1999, 29, 1663–1671. [Google Scholar] [CrossRef]
- He, H.; Guo, Z.; Stroeven, P.; Stroeven, M.; Sluys, L.J. Self-healing capacity of concrete-computer simulation study of unhydrated cement structure. Image Anal. Stereol. 2007, 26, 137–143. [Google Scholar] [CrossRef]
- Ouyang, Q.; Yang, Y.C.; Park, B.; Kang, R.; Wu, J.Z.; Chen, Q.S.; Guo, Z.M.; Li, H.H. A novel hyperspectral microscope imaging technology for rapid evaluation of particle size distribution in matcha. J. Food Eng. 2020, 272, 109782. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, W.; Chen, H.; Wang, Y.; Gou, X.; Liu, L.; Gu, Y. Diffusivity of cement paste via a continuum-based microstructure and hydration model: Influence of cement grain shape. Cem. Concr. Compos. 2021, 118, 103920. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Z.; Liu, L.; Sun, W.; Miao, C. Aggregate shape effect on the overestimation of ITZ thickness: Quantitative analysis of Platonic particles. Powder Technol. 2016, 289, 1–17. [Google Scholar] [CrossRef]
- Tan, Z.; De Schutter, G.; Ye, G.; Gao, Y.; Machiels, L. Influence of particle size on the early hydration of slag particle activated by Ca(OH)2 solution. Constr. Build. Mater. 2014, 52, 488–493. [Google Scholar] [CrossRef]
- Gao, Y.; De Schutter, G.; Ye, G.; Yu, Z.; Tan, Z.; Wu, K. A microscopic study on ternary blended cement based composites. Constr. Build. Mater. 2013, 46, 28–38. [Google Scholar] [CrossRef]
- Lin, F.; Meyer, C. Hydration kinetics modeling of Portland cement considering the effects of curing temperature and applied pressure. Cem. Concr. Res. 2009, 39, 255–265. [Google Scholar] [CrossRef]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press, Inc.: London, UK, 1982. [Google Scholar]
- Xu, W.; Chen, H.; Duan, Q.; Chen, W. Strategy for interfacial overlapping degree in multiphase materials with complex convex particles. Powder Technol. 2015, 283, 455–461. [Google Scholar] [CrossRef]
- Santaló, L.A. Integral Geometry and Geometric Probability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhu, Z.; Chen, H. Aggregate shape effect on the overestimation of interface thickness for spheroidal particles. Powder Technol. 2017, 313, 218–230. [Google Scholar] [CrossRef]
- Hilliard, J. The calculation of the mean caliper diameter of a body for use in the analysis of the number of particles per unit volume, Stereology. In Proceedings of the Second International Congress for Stereology, Chicago, IL, USA, 8–13 April 1967; pp. 211–215. [Google Scholar]
- Xu, W.; Zhu, Z.; Zhang, D. Continuum percolation-based tortuosity and thermal conductivity of soft superball systems: Shape dependence from octahedra via spheres to cubes. Soft Matter 2018, 14, 8684–8691. [Google Scholar] [CrossRef]
- de Graaf, J.; Filion, L.; Marechal, M.; van Roij, R.; Dijkstra, M. Crystal-structure prediction via the Floppy-Box Monte Carlo algorithm: Method and application to hard (non) convex particles. J. Chem. Phys. 2012, 137, 214101. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, W.; Chen, H. The fraction of overlapping interphase around 2D and 3D polydisperse non-spherical particles: Theoretical and numerical models. Comput. Methods Appl. Mech. Eng. 2019, 345, 728–747. [Google Scholar] [CrossRef]
- Ye, G. Experimental Study and Numerical Simulation of the Development of the Microstructure and Permeability of Cementious Materials. Ph.D. Thesis, Delft Universirty of Technology, Delft, The Netherlands, 2003. [Google Scholar]
- Garboczi, E.J.; Bullard, J.W. 3D analytical mathematical models of random star-shape particles via a combination of X-ray computed microtomography and spherical harmonic analysis. Adv. Powder Technol. 2017, 28, 325–339. [Google Scholar] [CrossRef]
- Xu, W.; Jiao, Y. Theoretical framework for percolation threshold, tortuosity and transport properties of porous materials containing 3D non-spherical pores. Int. J. Eng. Sci. 2019, 134, 31–46. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, D.; Lan, P.; Jiao, Y. Multiple-inclusion model for the transport properties of porous composites considering coupled effects of pores and interphase around spheroidal particles. Int. J. Mech. Sci. 2019, 150, 610–616. [Google Scholar] [CrossRef]
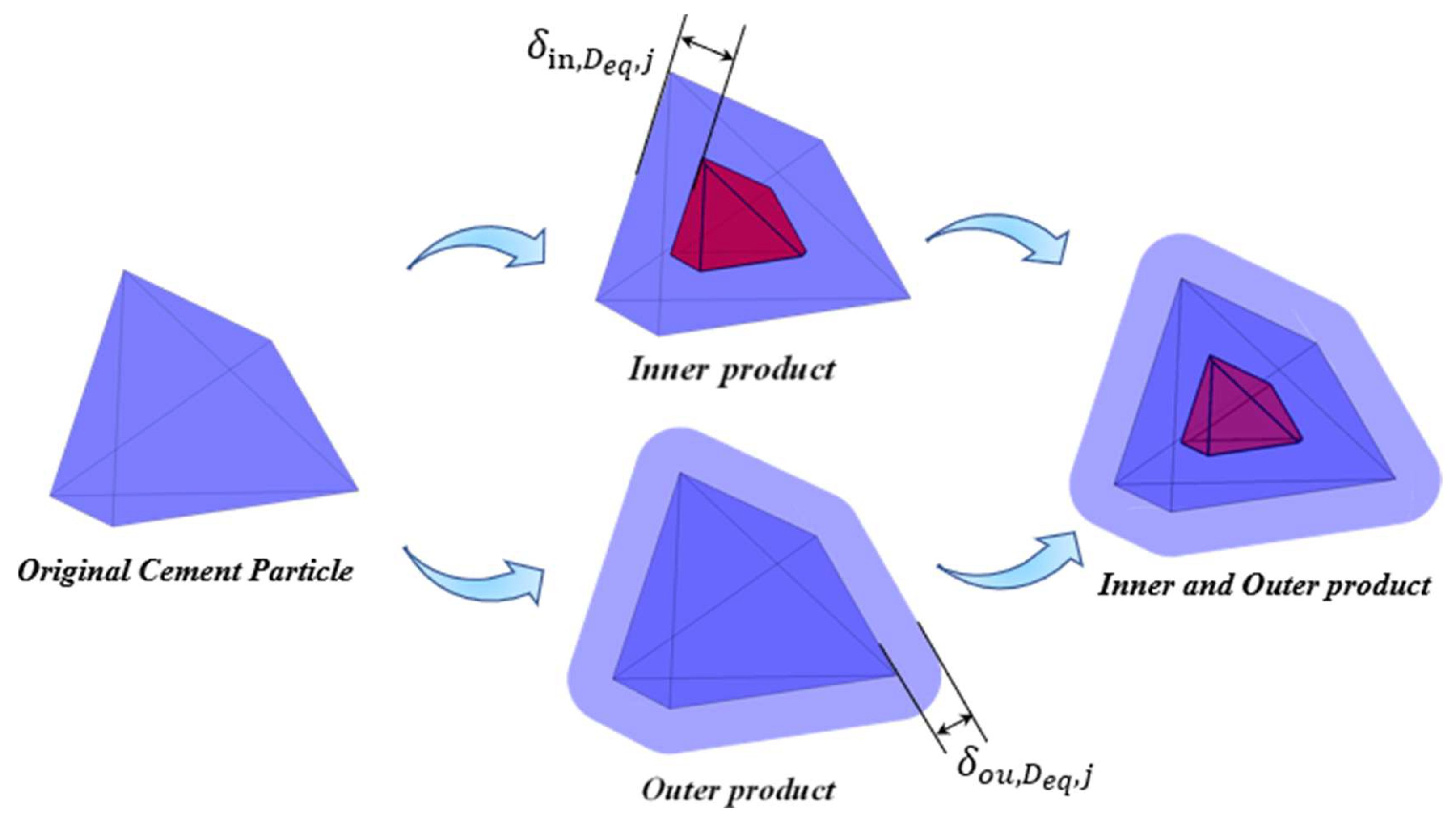
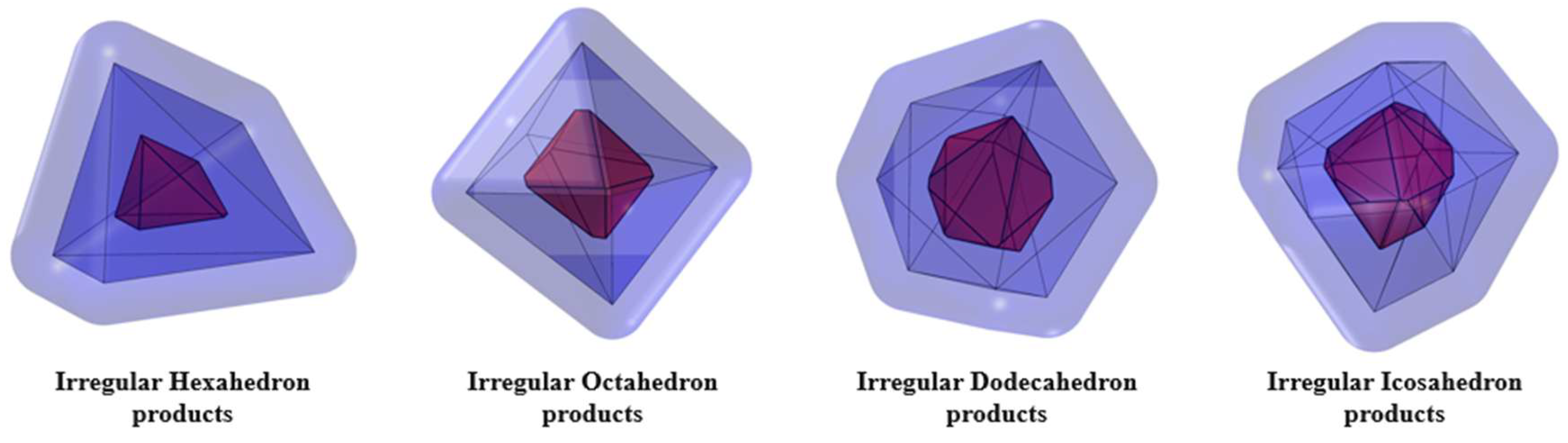
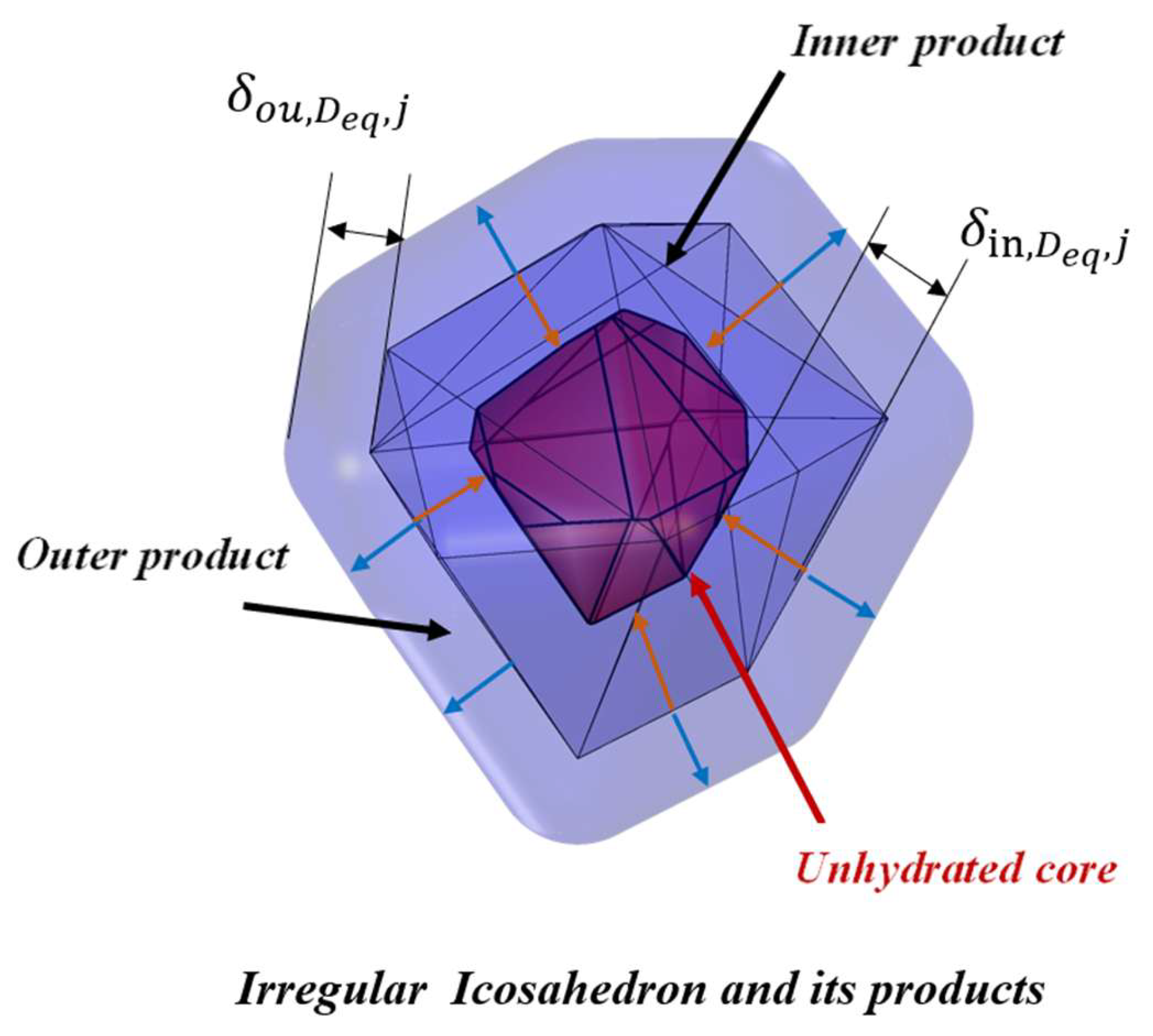
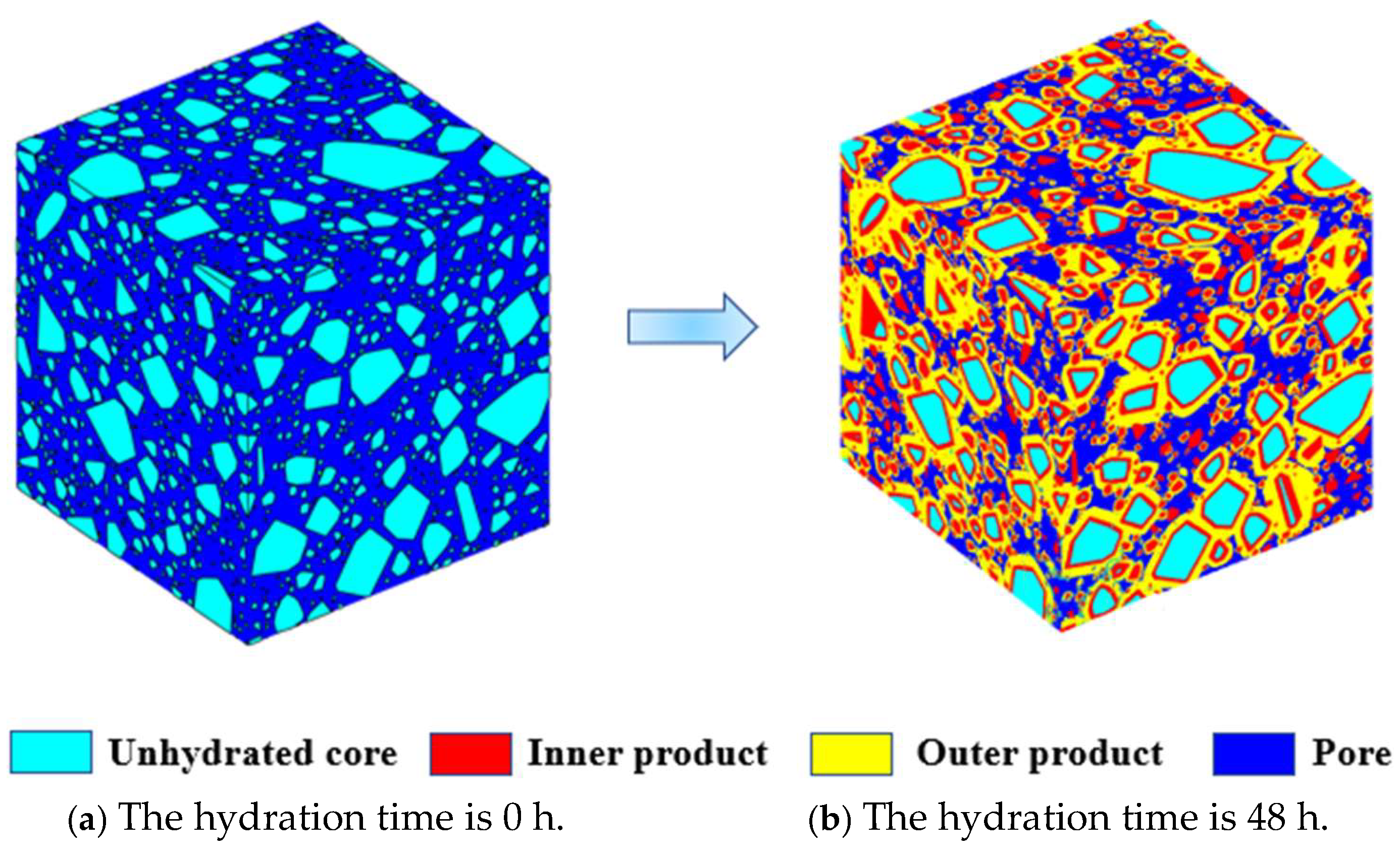
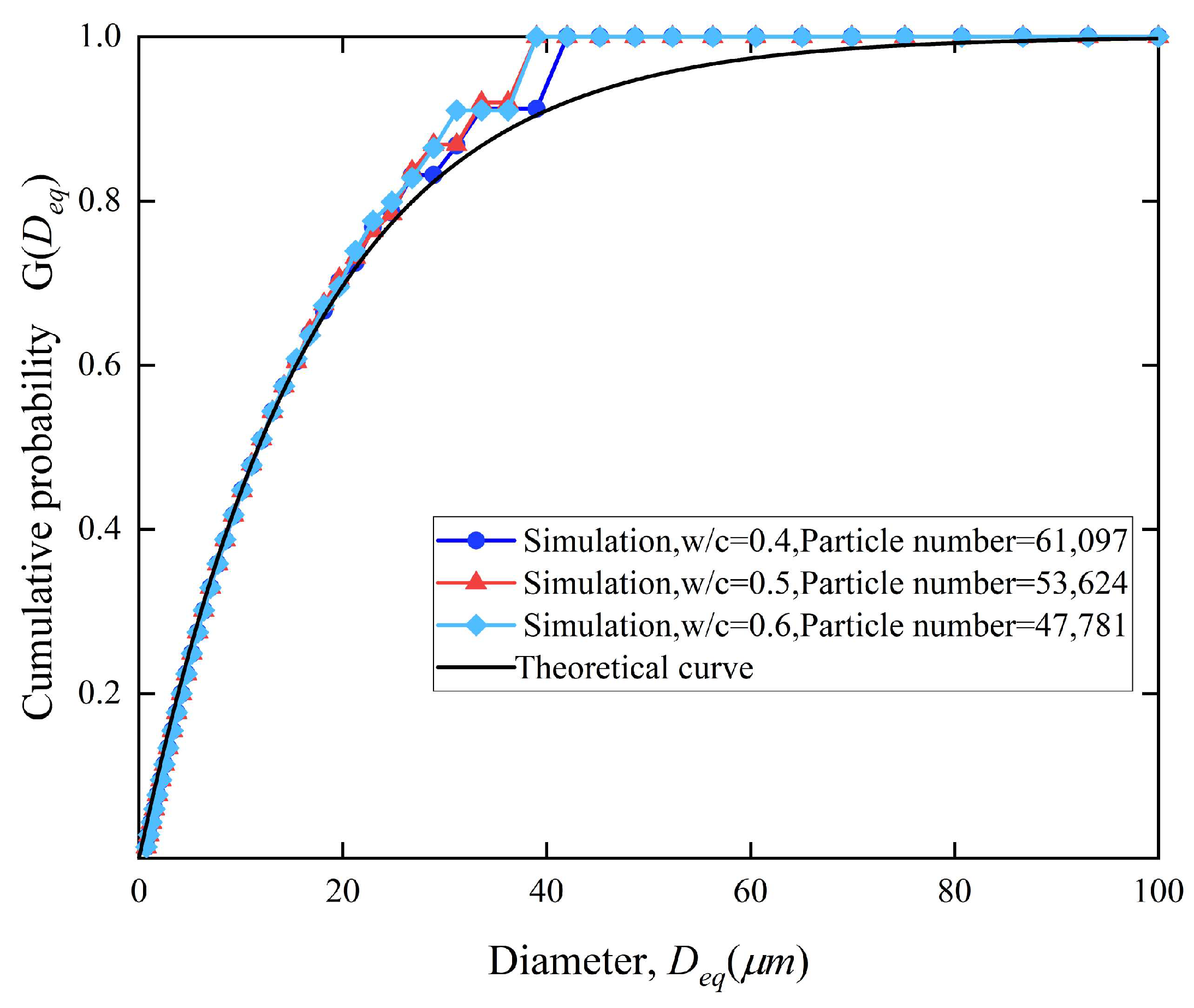

| Interval Sequence Number | Diameter | Interval Range |
|---|---|---|
| 0 | Deq,0 (Deq_min) | [Deq,0, Deq,1] |
| 1 | Deq,1 | [Deq,1, Deq,2] |
| … | … | … |
| i | Deq,i | [Deq,i−1, Deq,i] |
| … | … | … |
| M | Deq,M (Deq_max) | [Deq,M−1, Deq,M] |
| Phases | Weight (%) |
|---|---|
| C3S | 63 |
| C2S | 13 |
| C3A | 8 |
| C4AF | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Zhu, Z.; Li, Y.; Chen, H. Microstructure Evolution of Cement Paste Based on a Continuous Hydration Model for Irregular Polyhedral Particles. Materials 2025, 18, 2414. https://doi.org/10.3390/ma18112414
Huang H, Zhu Z, Li Y, Chen H. Microstructure Evolution of Cement Paste Based on a Continuous Hydration Model for Irregular Polyhedral Particles. Materials. 2025; 18(11):2414. https://doi.org/10.3390/ma18112414
Chicago/Turabian StyleHuang, Hong, Zhigang Zhu, Yichen Li, and Huisu Chen. 2025. "Microstructure Evolution of Cement Paste Based on a Continuous Hydration Model for Irregular Polyhedral Particles" Materials 18, no. 11: 2414. https://doi.org/10.3390/ma18112414
APA StyleHuang, H., Zhu, Z., Li, Y., & Chen, H. (2025). Microstructure Evolution of Cement Paste Based on a Continuous Hydration Model for Irregular Polyhedral Particles. Materials, 18(11), 2414. https://doi.org/10.3390/ma18112414





