Design of Bi-Material Triangle Curved Beam Honeycomb Metamaterial with Tunable Poisson’s Ratio, Thermal Expansion, and Band Gap Characteristics
Highlights
- A novel bi-material triangular curved beam metamaterial is proposed;
- Tunable Poisson’s ratio and thermal expansion are achieved via geometric control;
- Multi-bandgap characteristics validated through transmission curve analysis;
- Vibration modes reveal mechanisms behind wide and tunable phononic bandgaps.
Abstract
1. Introduction
2. Structural Design and Method
2.1. Design of Structure
2.2. Numerical Simulation
3. Results and Discussion
3.1. Parameter Analysis of the Effective PR
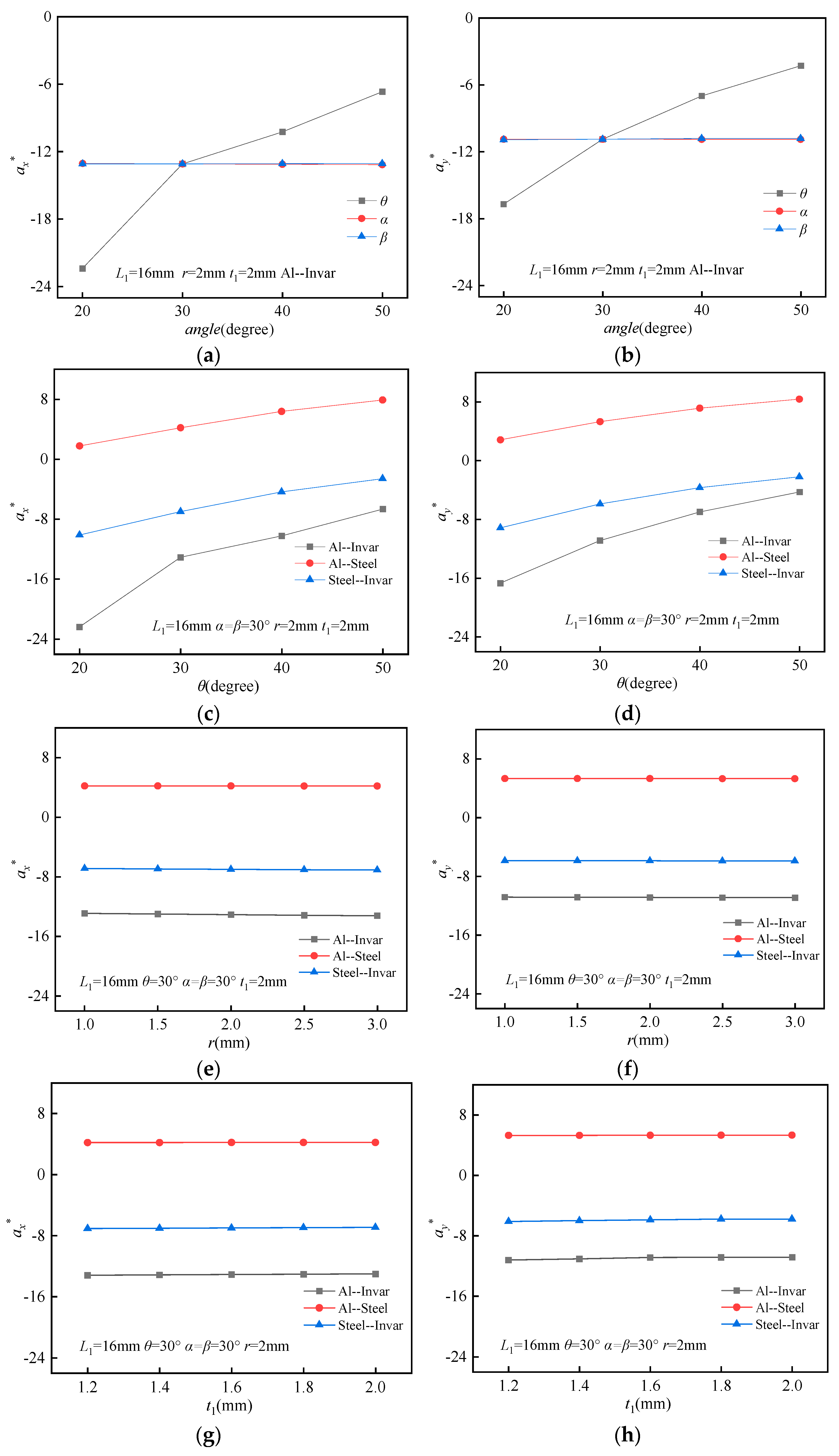
3.2. Parameter Analysis of the Effective CTE
3.3. Parameter Analysis of Bandgap Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.; Alavi, A.H. Mechanical Metamaterials and Beyond. Nat. Commun. 2023, 14, 6004. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical Metamaterials Associated with Stiffness, Rigidity and Compressibility: A Brief Review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Fraternali, F.; Paulino, G.H. Mechanics research communications special issue on advances in mechanical metamaterials and smart structures. Mech. Res. Commun. 2020, 107, 103531. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, L.; Wei, S.; Zhang, Z.; Choi, S.-K.; Song, B.; Shi, Y. A Review of Additive Manufacturing of Metamaterials and Developing Trends. Mater. Today 2021, 50, 303–328. [Google Scholar] [CrossRef]
- Huang, C.; Chen, L. Negative Poisson’s Ratio in Modern Functional Materials. Adv. Mater. 2016, 28, 8079–8096. [Google Scholar] [CrossRef]
- Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing Auxetic Materials from the Mechanics Point of View: A Structural Review on the Negative Poisson’s Ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y. Low Frequency Bandgap and High Stiffness of Innovative Auxetic Metamaterial with Negative Thermal Expansion. Thin-Walled Struct. 2024, 201, 112010. [Google Scholar] [CrossRef]
- Peng, X.-L.; Bargmann, S. Tunable Auxeticity and Isotropic Negative Thermal Expansion in Three-Dimensional Lattice Structures of Cubic Symmetry. Extreme Mech. Lett. 2021, 43, 101201. [Google Scholar] [CrossRef]
- Ha, C.S.; Hestekin, E.; Li, J.; Plesha, M.E.; Lakes, R.S. Controllable Thermal Expansion of Large Magnitude in Chiral Negative Poisson’s Ratio Lattices. Phys. Status Solidi B 2015, 252, 1431–1434. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Zhou, S.; Shao, J.; Wu, X. Novel Negative Poisson’s Ratio Lattice Structures with Enhanced Stiffness and Energy Absorption Capacity. Materials 2018, 11, 1095. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.-Y.; Liu, H.-T.; An, M.-R. Crushing Behaviors of Novel Diabolo Shaped Honeycombs with Enhanced Energy Absorption Performance. Int. J. Mech. Sci. 2022, 229, 107492. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Hu, W.; He, C.; Wu, W.; Ma, Y. Bandgap and Wave Attenuation Mechanisms of Innovative Reentrant and Anti-Chiral Hybrid Auxetic Metastructure. Extreme Mech. Lett. 2019, 28, 58–68. [Google Scholar] [CrossRef]
- Goh, H.; Kallivokas, L.F. Inverse Band Gap Design of Elastic Metamaterials for P and SV Wave Control. Comput. Methods Appl. Mech. Eng. 2020, 370, 113263. [Google Scholar] [CrossRef]
- Han, D.; Zhang, G.; Zhao, J.; Yao, H.; Liu, H. Study on Band Gap and Sound Insulation Characteristics of an Adjustable Helmholtz Resonator. Appl. Sci. 2022, 12, 4512. [Google Scholar] [CrossRef]
- Quinteros, L.; Meruane, V.; Lenz Cardoso, E.; Ruiz, R.O. Phononic Bandgap Optimization in Sandwich Panels Using Cellular Truss Cores. Materials 2021, 14, 5236. [Google Scholar] [CrossRef] [PubMed]
- Fu, M.H.; Xu, O.T.; Hu, L.L.; Yu, T.X. Nonlinear Shear Modulus of Re-Entrant Hexagonal Honeycombs under Large Deformation. Int. J. Solids Struct. 2016, 80, 284–296. [Google Scholar] [CrossRef]
- Hughes, T.P.; Marmier, A.; Evans, K.E. Auxetic Frameworks Inspired by Cubic Crystals. Int. J. Solids Struct. 2010, 47, 1469–1476. [Google Scholar] [CrossRef]
- Bouakba, M.; Bezazi, A.; Scarpa, F. FE Analysis of the In-Plane Mechanical Properties of a Novel Voronoi-Type Lattice with Positive and Negative Poisson’s Ratio Configurations. Int. J. Solids Struct. 2012, 49, 2450–2459. [Google Scholar] [CrossRef]
- Hu, L.L.; Luo, Z.R.; Yin, Q.Y. Negative Poisson’s Ratio Effect of Re-Entrant Anti-Trichiral Honeycombs under Large Deformation. Thin Wall. Struct. 2019, 141, 283–292. [Google Scholar] [CrossRef]
- Xu, F.; Yu, K.; Hua, L. In-Plane Dynamic Response and Multi-Objective Optimization of Negative Poisson’s Ratio (NPR) Honeycomb Structures with Sinusoidal Curve. Compos. Struct. 2021, 269, 114018. [Google Scholar] [CrossRef]
- Meng, F.; Chen, S.; Zhang, W.; Ou, P.; Zhang, J.; Chen, C.; Song, J. Negative Poisson’s Ratio in Graphene Miura Origami. Mech. Mater. 2021, 155, 103774. [Google Scholar] [CrossRef]
- Fu, M.; Liu, F.; Hu, L. A novel category of 3D chiral material with negative Poisson’s ratio. Compos. Sci. Technol. 2018, 160, 111–118. [Google Scholar] [CrossRef]
- Miller, W.; Mackenzie, D.S.; Smith, C.W.; Evans, K.E. A Generalised Scale-Independent Mechanism for Tailoring of Thermal Expansivity: Positive and Negative. Mech. Mater. 2008, 40, 351–361. [Google Scholar] [CrossRef]
- Wei, K.; Peng, Y.; Qu, Z.; Pei, Y.; Fang, D. A Cellular Metastructure Incorporating Coupled Negative Thermal Expansion and Negative Poisson’s Ratio. Int. J. Solids Struct. 2018, 150, 255–267. [Google Scholar] [CrossRef]
- Nanda, A.; Karami, M.A. Tunable Bandgaps in a Deployable Metamaterial. J. Sound Vib. 2018, 424, 120–136. [Google Scholar] [CrossRef]
- Wen, G.; Ou, H.; Liu, J. Ultra-Wide Band Gap in a Two-Dimensional Phononic Crystal with Hexagonal Lattices. Mater. Today Commun. 2020, 24, 100977. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, M.; Liu, Y.; Pei, D.; Chen, M.; Wang, Y. Band Gaps and Vibration Isolation of a Three-Dimensional Metamaterial with a Star Structure. Materials 2020, 13, 3812. [Google Scholar] [CrossRef]
- Liu, K.-J.; Liu, H.-T.; Li, J. Thermal Expansion and Bandgap Properties of Bi-Material Triangle Re-Entrant Honeycomb with Adjustable Poisson’s Ratio. Int. J. Mech. Sci. 2023, 242, 108015. [Google Scholar] [CrossRef]
- Zhang, X.; Ye, H.; Wei, N.; Tao, R.; Luo, Z. Design Optimization of Multifunctional Metamaterials with Tunable Thermal Expansion and Phononic Bandgap. Mater. Des. 2021, 209, 109990. [Google Scholar] [CrossRef]
- Ai, L.; Gao, X.-L. Metamaterials with Negative Poisson’s Ratio and Non-Positive Thermal Expansion. Compos. Struct. 2017, 162, 70–84. [Google Scholar] [CrossRef]
- Lv, S.; Xu, W.; Bai, L.; Qi, W.; Wang, W. Thermal Tuning of Band Gap Properties in Planar Stretch-Dominated Lattices with Tailorable Coefficient of Thermal Expansion. Appl. Phys. A 2021, 127, 425. [Google Scholar] [CrossRef]












| Material | Young’s Modulus E (GPa) | Poisson’s Ratio v | Density ρ (kg/m3) | CTE α (ppm/°C) |
|---|---|---|---|---|
| Al | 71 | 0.3 | 2810 | 24.0 |
| Steel | 206 | 0.3 | 7800 | 13.0 |
| Invar | 144 | 0.29 | 8050 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cheng, Y.; Zhao, H.; Zhang, H. Design of Bi-Material Triangle Curved Beam Honeycomb Metamaterial with Tunable Poisson’s Ratio, Thermal Expansion, and Band Gap Characteristics. Materials 2025, 18, 2408. https://doi.org/10.3390/ma18102408
Wang Z, Cheng Y, Zhao H, Zhang H. Design of Bi-Material Triangle Curved Beam Honeycomb Metamaterial with Tunable Poisson’s Ratio, Thermal Expansion, and Band Gap Characteristics. Materials. 2025; 18(10):2408. https://doi.org/10.3390/ma18102408
Chicago/Turabian StyleWang, Zelong, Yong Cheng, Huichuan Zhao, and Han Zhang. 2025. "Design of Bi-Material Triangle Curved Beam Honeycomb Metamaterial with Tunable Poisson’s Ratio, Thermal Expansion, and Band Gap Characteristics" Materials 18, no. 10: 2408. https://doi.org/10.3390/ma18102408
APA StyleWang, Z., Cheng, Y., Zhao, H., & Zhang, H. (2025). Design of Bi-Material Triangle Curved Beam Honeycomb Metamaterial with Tunable Poisson’s Ratio, Thermal Expansion, and Band Gap Characteristics. Materials, 18(10), 2408. https://doi.org/10.3390/ma18102408





