Monolayer TiAlTe3: A Perfect Room-Temperature Valleytronic Semiconductor
Abstract
1. Introduction
2. Computational Details
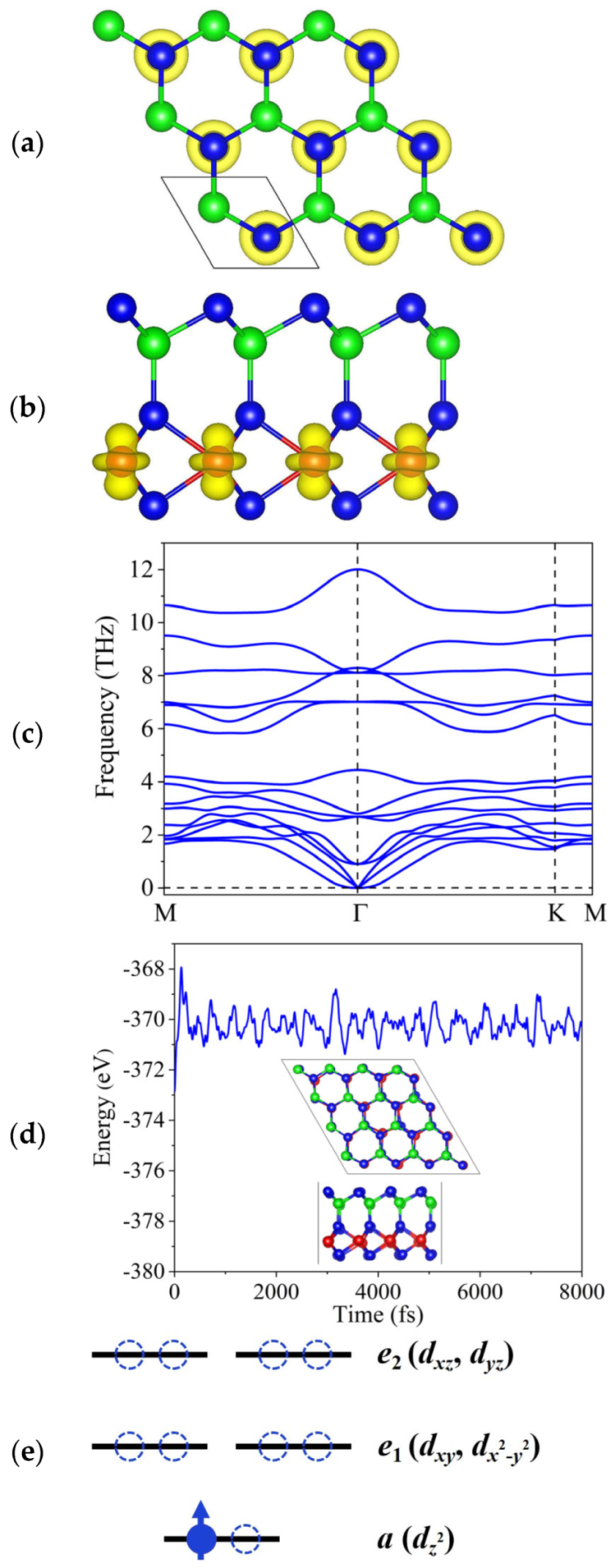
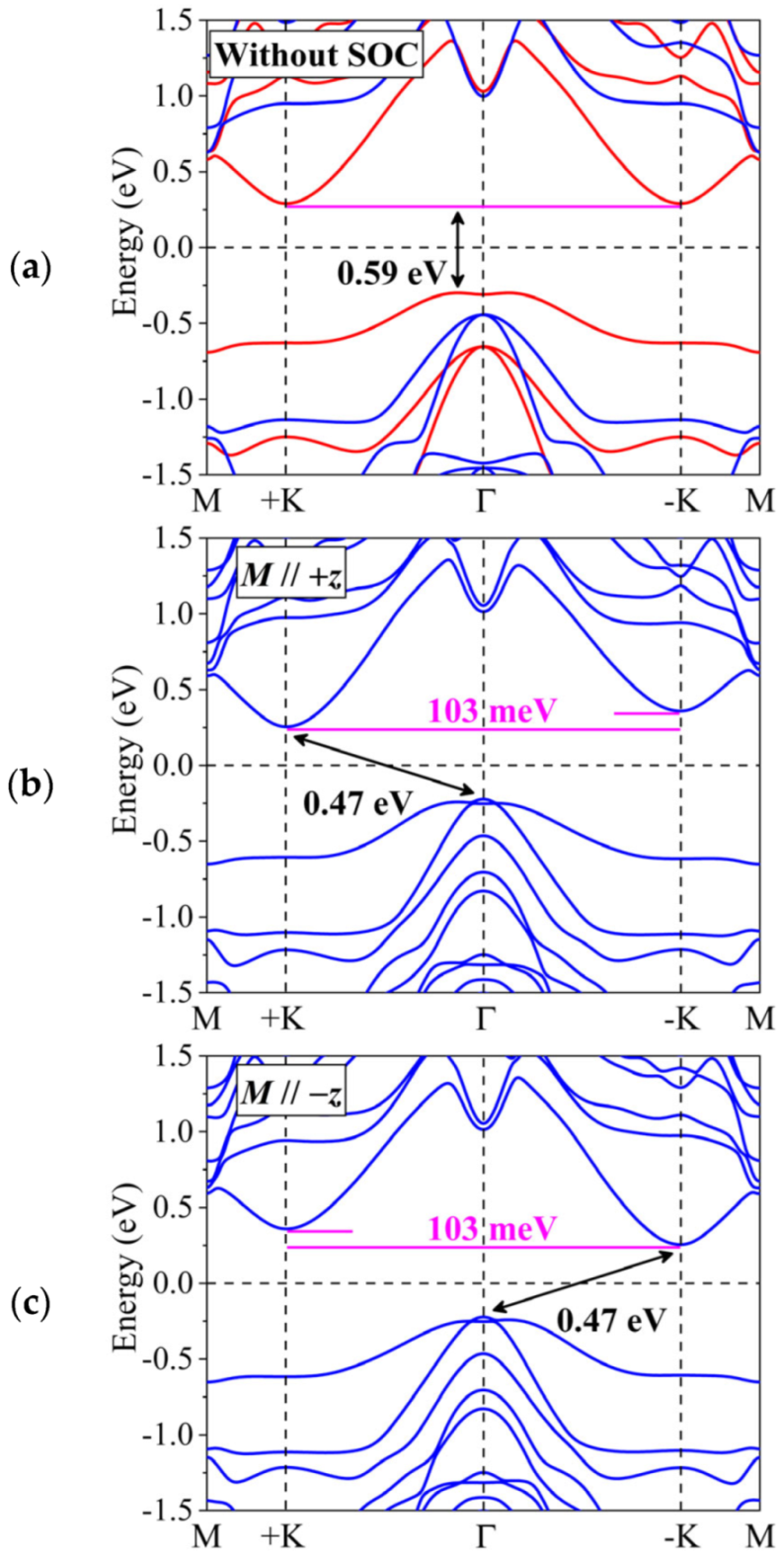
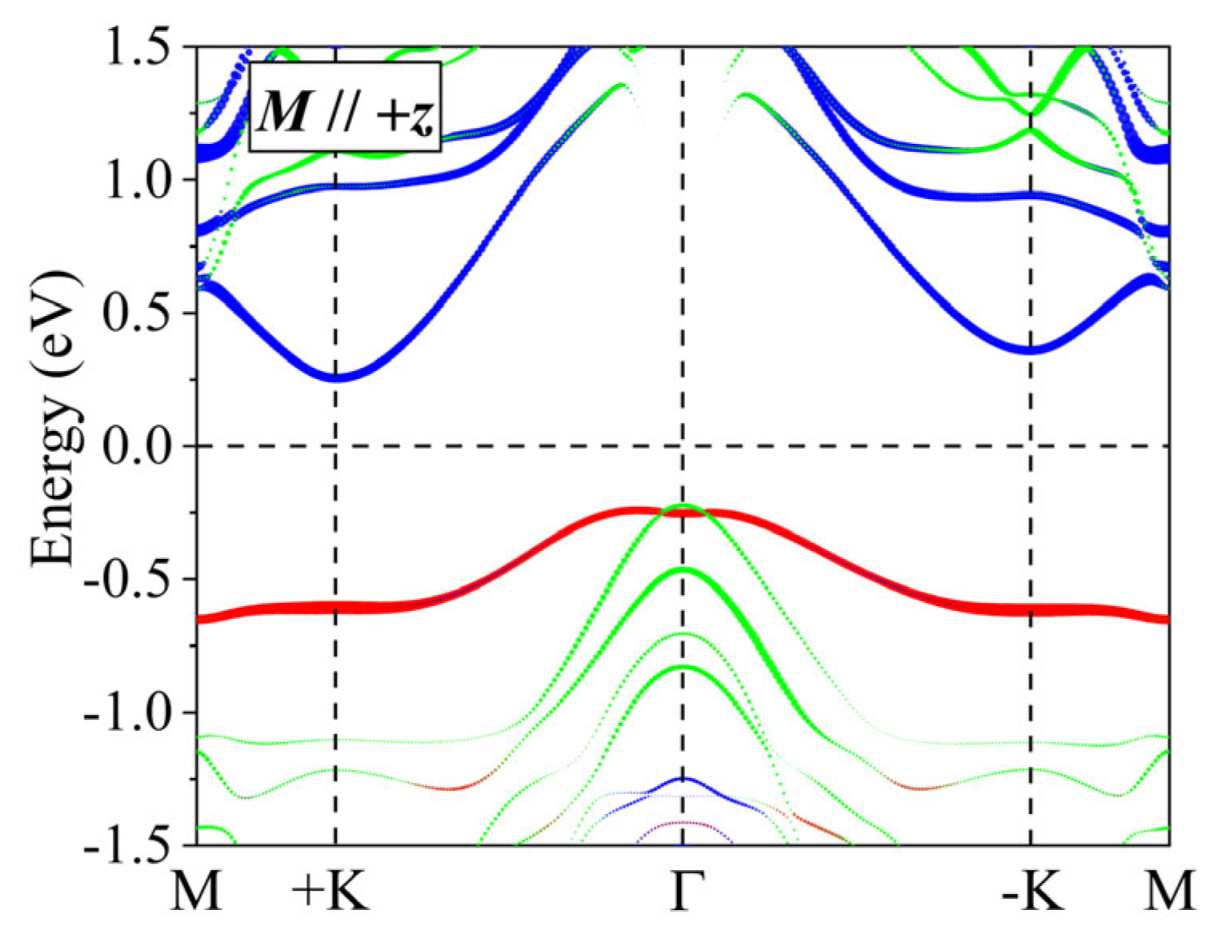
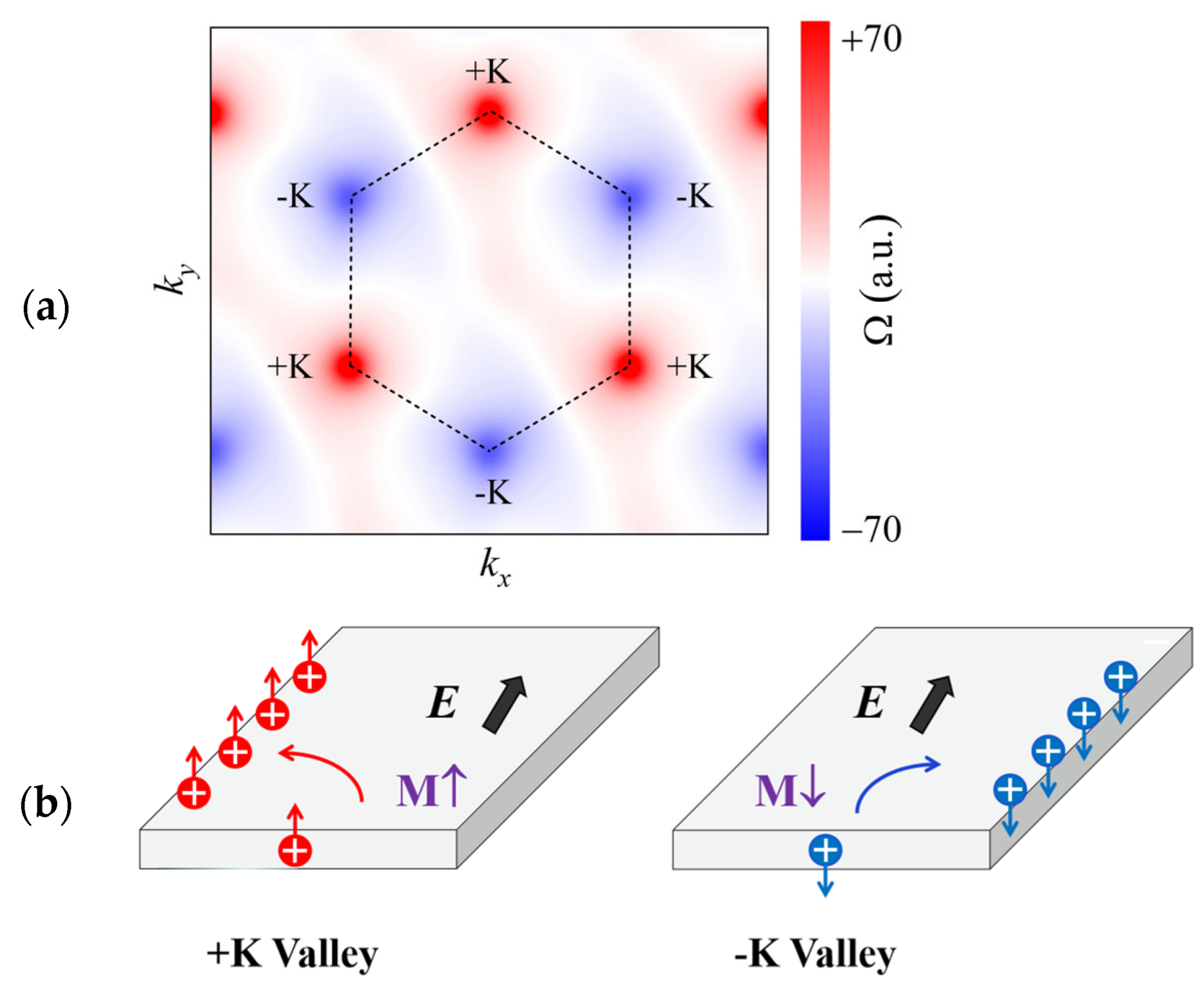
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rycerz, A.; Tworzydło, J.; Beenakker, C. Valley filter and valley valve in graphene. Nat. Phys. 2007, 3, 172–175. [Google Scholar] [CrossRef]
- Mak, K.F.; Xiao, D.; Shan, J. Light-valley interactions in 2D semiconductors. Nat. Photonics 2018, 12, 451–460. [Google Scholar] [CrossRef]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnar, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- Vitale, S.A.; Nezich, D.; Varghese, J.O.; Kim, P.; Gedik, N.; Jarillo-Herrero, P.; Xiao, D.; Rothschild, M. Valleytronics: Opportunities, challenges, and paths forward. Small 2018, 14, 1801483. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef]
- Xiao, D.; Yao, W.; Niu, Q. Valley-contrasting physics in graphene: Magnetic moment and topological transport. Phys. Rev. Lett. 2007, 99, 236809. [Google Scholar] [CrossRef]
- Pacchioni, G. Valleytronics with a twist. Nat. Rev. Mater. 2020, 5, 480. [Google Scholar] [CrossRef]
- Yao, W.; Xiao, D.; Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 2008, 77, 235406. [Google Scholar] [CrossRef]
- Zeng, H.; Dai, J.; Yao, W.; Xiao, D.; Cui, X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 2012, 7, 490–493. [Google Scholar] [CrossRef]
- MacNeill, D.; Heikes, C.; Mak, K.F.; Anderson, Z.; Kormanyos, A.; Zolyomi, V.; Park, J.; Ralph, D.C. Breaking of Valley Degeneracy by Magnetic Field in Monolayer MoSe2. Phys. Rev. Lett. 2015, 114, 037401. [Google Scholar] [CrossRef] [PubMed]
- Norden, T.; Zhao, C.; Zhang, P.; Sabirianov, R.; Petrou, A.; Zeng, H. Giant valley splitting in monolayer WS2 by magnetic proximity effect. Nat. Commun. 2019, 10, 4163. [Google Scholar] [CrossRef] [PubMed]
- Peng, R.; Ma, Y.; Zhang, S.; Huang, B.; Dai, Y. Valley Polarization in Janus Single-Layer MoSSe via Magnetic Doping. J. Phys. Chem. Lett. 2018, 9, 3612–3617. [Google Scholar] [CrossRef] [PubMed]
- Tong, W.Y.; Gong, S.J.; Wan, X.; Duan, C.G. Concepts of ferrovalley material and anomalous valley Hall effect. Nat. Commun. 2016, 7, 13612. [Google Scholar] [CrossRef]
- Jia, K.; Dong, X.J.; Li, S.S.; Ji, W.X.; Zhang, C.W. Spontaneous valley polarization and valley-nonequilibrium quantum anomalous Hall effect in Janus monolayer ScBrI. Nanoscale 2023, 15, 8395–8405. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.S.; Ji, W.X.; Zhang, C.W. Valley-dependent topological phase transition and quantum anomalous valley Hall effect in single-layer RuClBr. Phys. Rev. B 2022, 105, 195112. [Google Scholar] [CrossRef]
- Jia, K.; Dong, X.J.; Li, S.S.; Ji, W.X.; Zhang, C.W. Tunable abundant valley Hall effect and chiral spin-valley locking in Janus monolayer VCGeN4. Nanoscale 2024, 16, 8639–8649. [Google Scholar] [CrossRef]
- Cheng, H.X.; Zhou, J.; Ji, W.; Zhang, Y.N.; Feng, Y.P. Two-dimensional intrinsic ferrovalley GdI2 with large valley polarization. Phys. Rev. B 2021, 103, 125121. [Google Scholar] [CrossRef]
- Jiang, P.; Kang, L.; Li, Y.L.; Zheng, X.; Zeng, Z.; Sanvito, S. Prediction of the two-dimensional Janus ferrovalley material LaBrI. Phys. Rev. B 2021, 104, 035430. [Google Scholar] [CrossRef]
- Sheng, K.; Chen, Q.; Yuan, H.K.; Wang, Z.Y. Monolayer CeI2: An intrinsic room-temperature ferrovalley semiconductor. Phys. Rev. B 2022, 105, 075304. [Google Scholar] [CrossRef]
- Zhang, S.J.; Zhang, C.W.; Zhang, S.F.; Ji, W.X.; Li, P.; Wang, P.J.; Li, S.S.; Yan, S.S. Intrinsic Dirac half-metal and quantum anomalous Hall phase in a hexagonal metal-oxide lattice. Phys. Rev. B 2017, 96, 205433. [Google Scholar] [CrossRef]
- Wu, B.; Song, Y.L.; Ji, W.X.; Wang, P.J.; Zhang, S.F.; Zhang, C.W. Quantum anomalous Hall effect in an antiferromagnetic monolayer of MoO. Phys. Rev. B 2023, 107, 214419. [Google Scholar] [CrossRef]
- Lou, W.H.; Liu, G.; Ma, X.G.; Yang, C.L.; Feng, L.X.; Liu, Y.; Gao, X.C. Enhancing photocatalytic water splitting via GeC/SGaSnP Z-scheme heterojunctions with built-in electric fields. J. Mater. Chem. A 2025, 13, 4356–4366. [Google Scholar] [CrossRef]
- Lou, W.H.; Gao, J.M.; Liu, G.; Ali, A.; Jia, B.N.; Guan, X.N.; Ma, X.G. Enhancing hydrogen evolution reaction performance through defect engineering in WTeX (X = S, Se) monolayers: A first-principles study. Int. J. Hydrog. Energy 2024, 87, 620–629. [Google Scholar] [CrossRef]
- Hong, Y.L.; Liu, Z.; Wang, L.; Zhou, T.; Ma, W.; Xu, C.; Feng, S.; Chen, L.; Chen, M.L.; Sun, D.M.; et al. Chemical vapor deposition of layered two-dimensional MoSi2N4 materials. Science 2020, 369, 670–674. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Lei, B.; Cao, Y.; Qi, J.; Peng, H.; Wang, Q.; Huang, L.; Lu, H.; Lin, X.; Wang, Y.L.; et al. Epitaxial fabrication of two-dimensional TiTe2 monolayer on Au(111) substrate with Te as buffer layer. Chin. Phys. B 2019, 28, 056801. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Yekta, Y.; Hadipour, H.; Şaşıoğlu, E.; Friedrich, C.; Jafari, S.A.; Blügel, S.; Mertig, I. Strength of effective Coulomb interaction in two-dimensional transition-metal halides MX2 and MX3 (M = Ti, V, Cr, Mn, Fe, Co, Ni; X = Cl, Br, I). Phys. Rev. Mater. 2021, 5, 034001. [Google Scholar] [CrossRef]
- Sheng, K.; Zhang, B.; Wang, Z.Y. Valley Polarization in a TwoDimensional High-Temperature Semiconducting TiInTe3 Honeycomb Ferromagnet. Acta Mater. 2024, 262, 119461. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, L.F.; Moreo, A.; Dagotto, E. Theoretical study of the crystal and electronic properties of α-RuI3. Phys. Rev. B 2022, 105, 085107. [Google Scholar] [CrossRef]
- Bucher, D.; Pierce, L.C.T.; McCammon, J.A.; Markwick, P.R.L. On the use of accelerated molecular dynamics to enhance configurational sampling in ab initio simulations. J. Chem. Theory Comput. 2011, 7, 890–897. [Google Scholar] [CrossRef]
- Wu, X.; Vanderbilt, D.; Hamann, D.R. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Phys. Rev. B 2005, 72, 035105. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, S.; Kholmanov, I.; Dong, L.; Er, D.; Chen, W.; Guo, H.; Jin, Z.; Shenoy, V.B.; Shi, L.; et al. Janus Monolayer Transition-Metal Dichalcogenides. ACS Nano 2017, 11, 8192–8198. [Google Scholar] [CrossRef]
- Andrew, R.C.; Mapasha, R.E.; Ukpong, A.M.; Chetty, N. Mechanical properties of graphene and boronitrene. Phys. Rev. B 2012, 85, 125428. [Google Scholar] [CrossRef]
- Goodenough, B. Theory of the role of covalence in the Perovskite-type manganites [La, M(II)] MnO3. Phys. Rev. 1955, 100, 564. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Anderson, P.W. New approach to the theory of superexchange interactions. Phys. Rev. 1959, 115, 2. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one-or two-dimensionalisotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; Mcguire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, K.; Zhang, C.-W.; Wang, Z.-R.; Wang, P.-J. Monolayer TiAlTe3: A Perfect Room-Temperature Valleytronic Semiconductor. Materials 2025, 18, 2396. https://doi.org/10.3390/ma18102396
Jia K, Zhang C-W, Wang Z-R, Wang P-J. Monolayer TiAlTe3: A Perfect Room-Temperature Valleytronic Semiconductor. Materials. 2025; 18(10):2396. https://doi.org/10.3390/ma18102396
Chicago/Turabian StyleJia, Kang, Chang-Wen Zhang, Zi-Ran Wang, and Pei-Ji Wang. 2025. "Monolayer TiAlTe3: A Perfect Room-Temperature Valleytronic Semiconductor" Materials 18, no. 10: 2396. https://doi.org/10.3390/ma18102396
APA StyleJia, K., Zhang, C.-W., Wang, Z.-R., & Wang, P.-J. (2025). Monolayer TiAlTe3: A Perfect Room-Temperature Valleytronic Semiconductor. Materials, 18(10), 2396. https://doi.org/10.3390/ma18102396




