Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas
Abstract
1. Introduction
2. Experimental Database
3. Finite Element Modeling and Validation
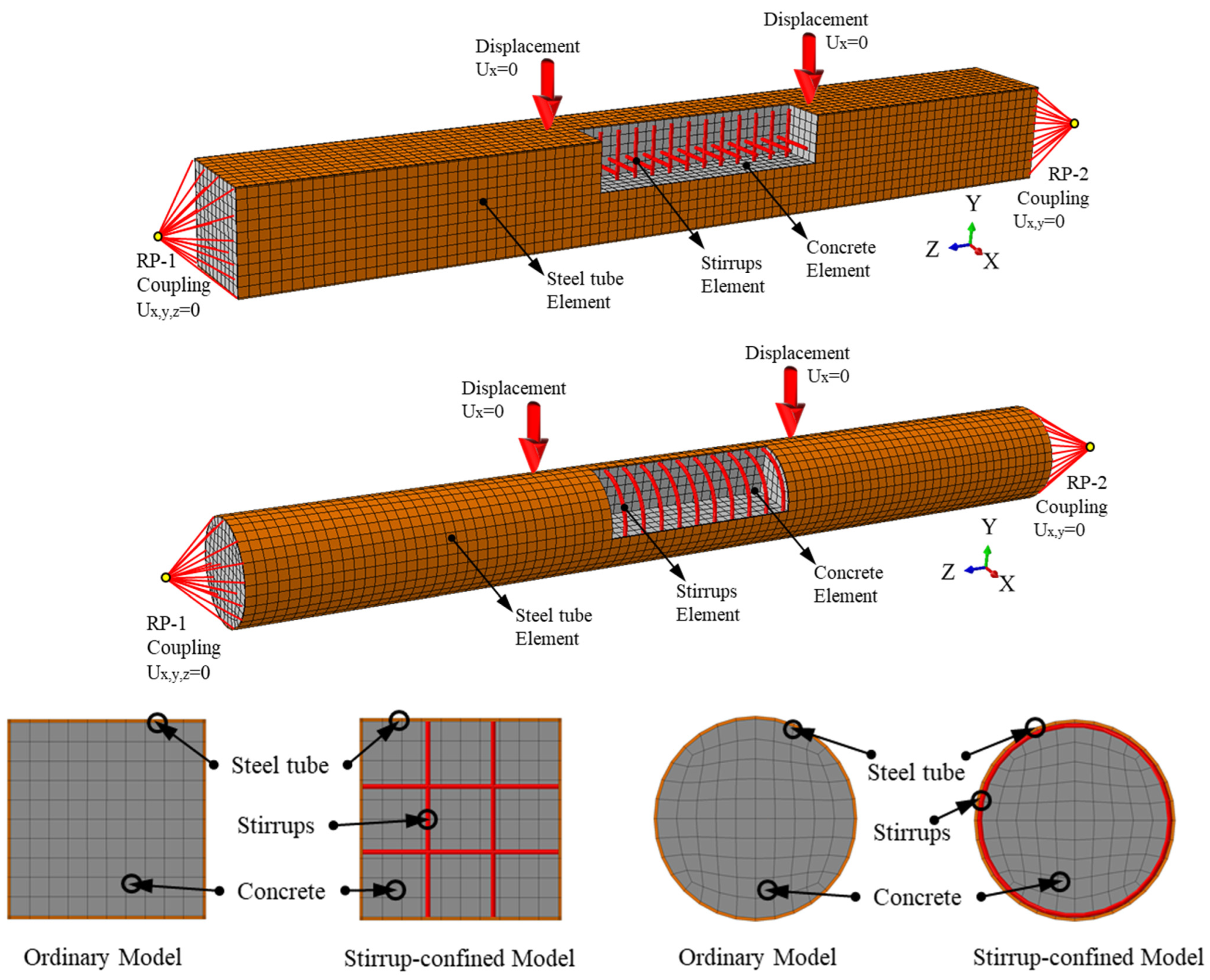
3.1. Finite Element Model Establishment
3.1.1. Element Type, Instruction, Mesh, and Boundary Conditions
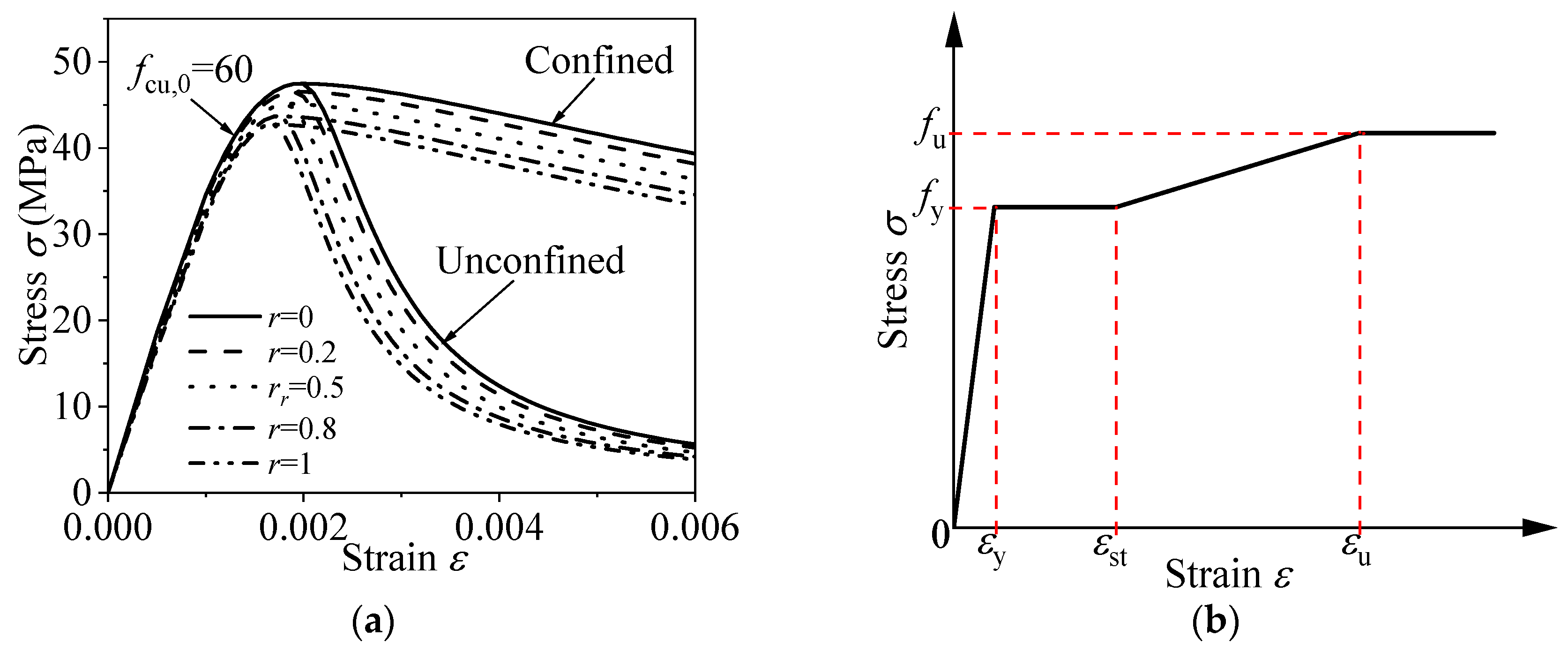
3.1.2. Material Constitutive Models
- (1)
- Desert sand concrete
- (2)
- Steel
3.2. Finite Element Model Validation
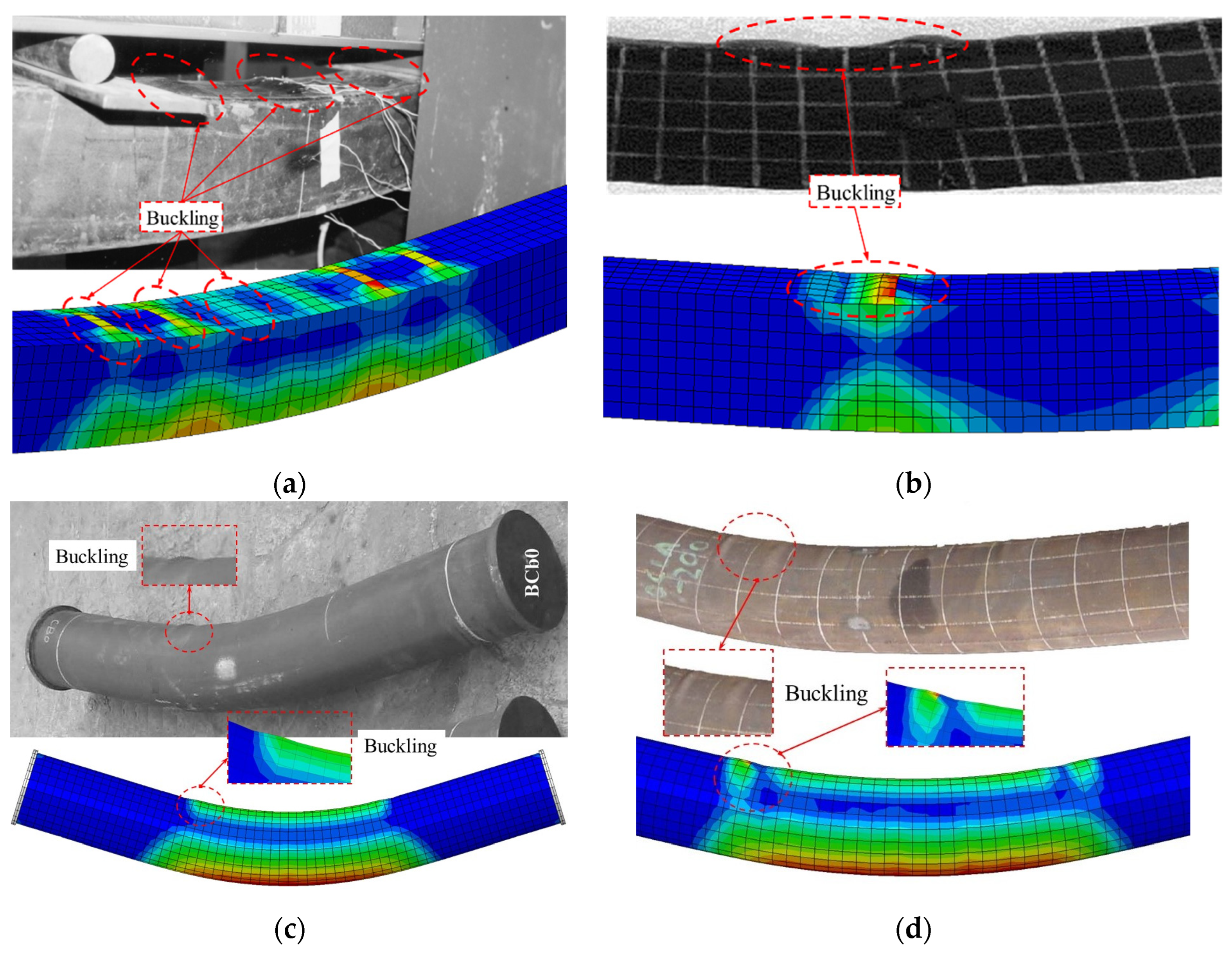
3.2.1. Failure Mode
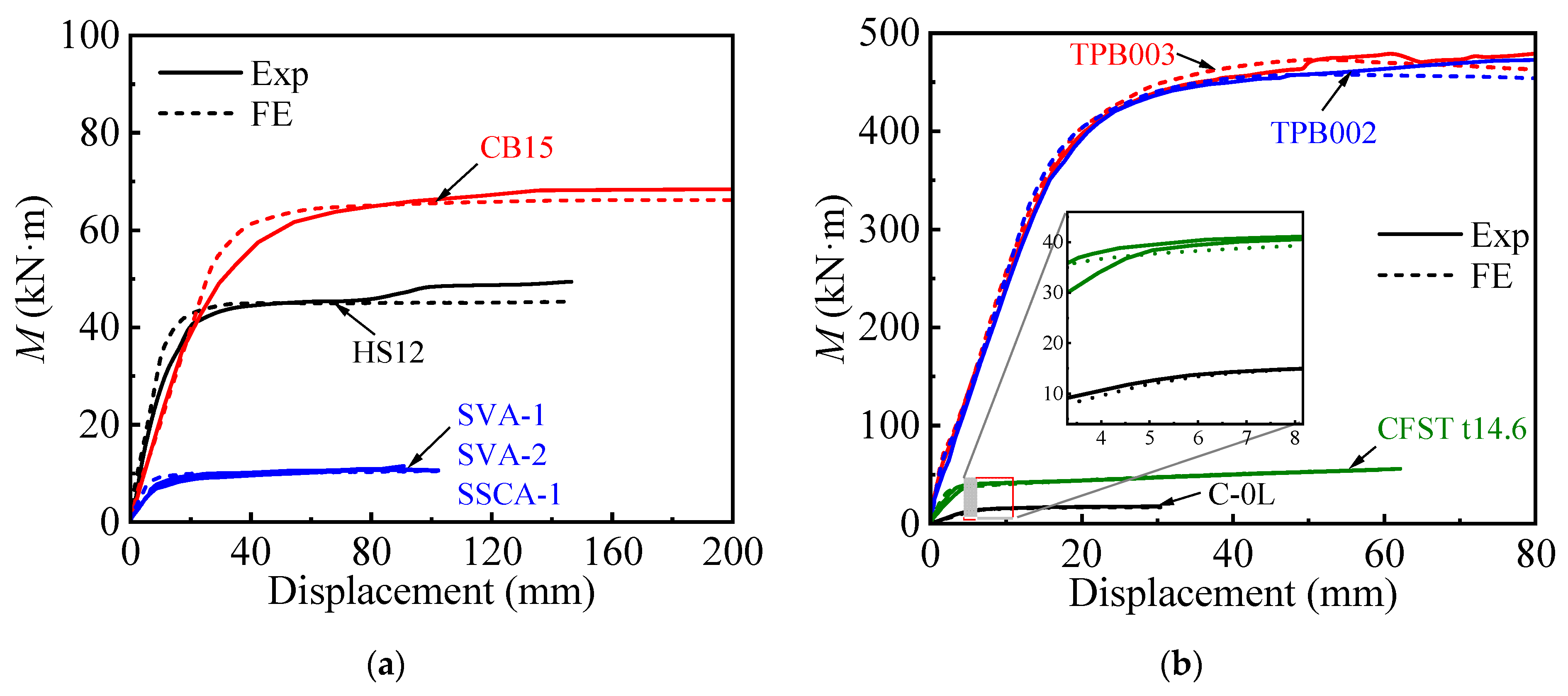
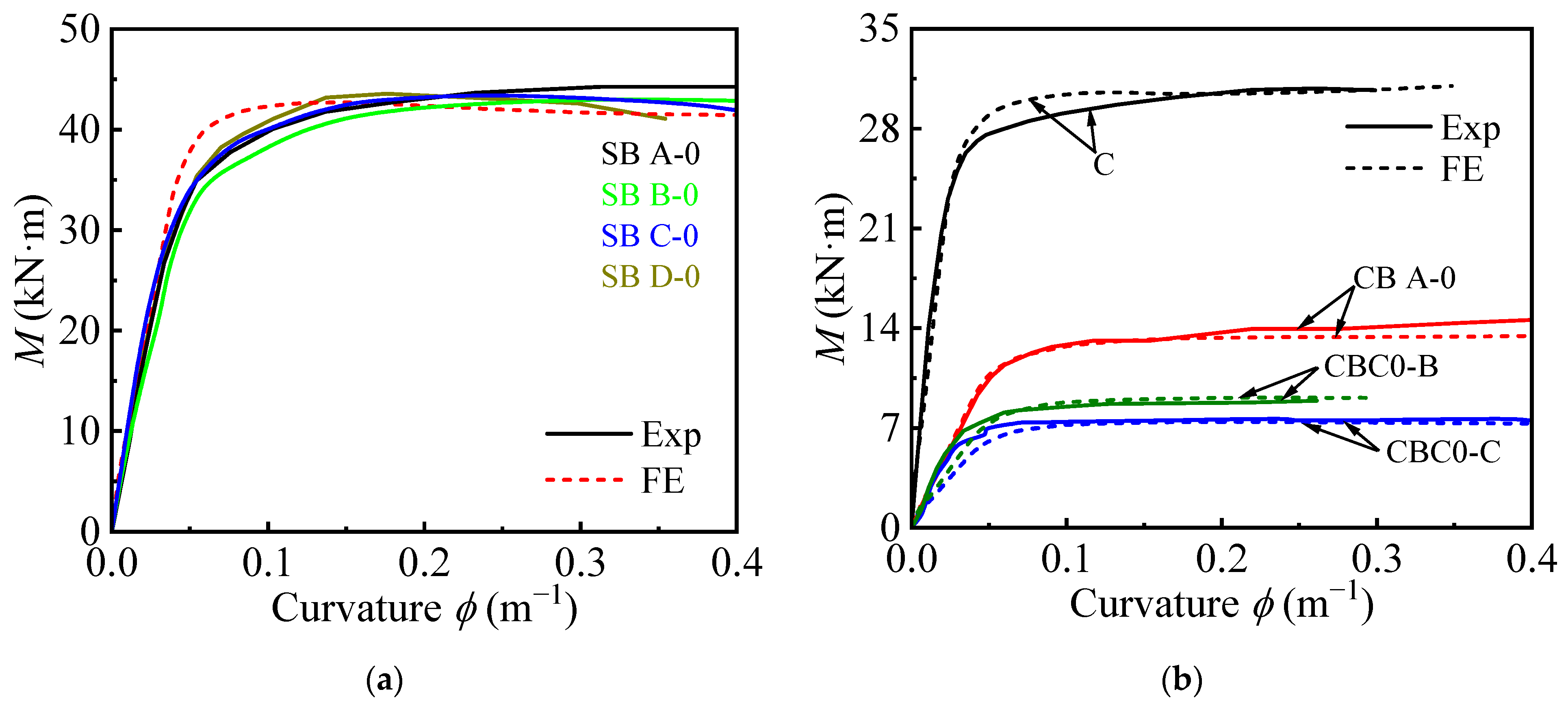
3.2.2. Moment-Displacement and Moment-Curvature Curves
4. Finite Element Results and Analysis
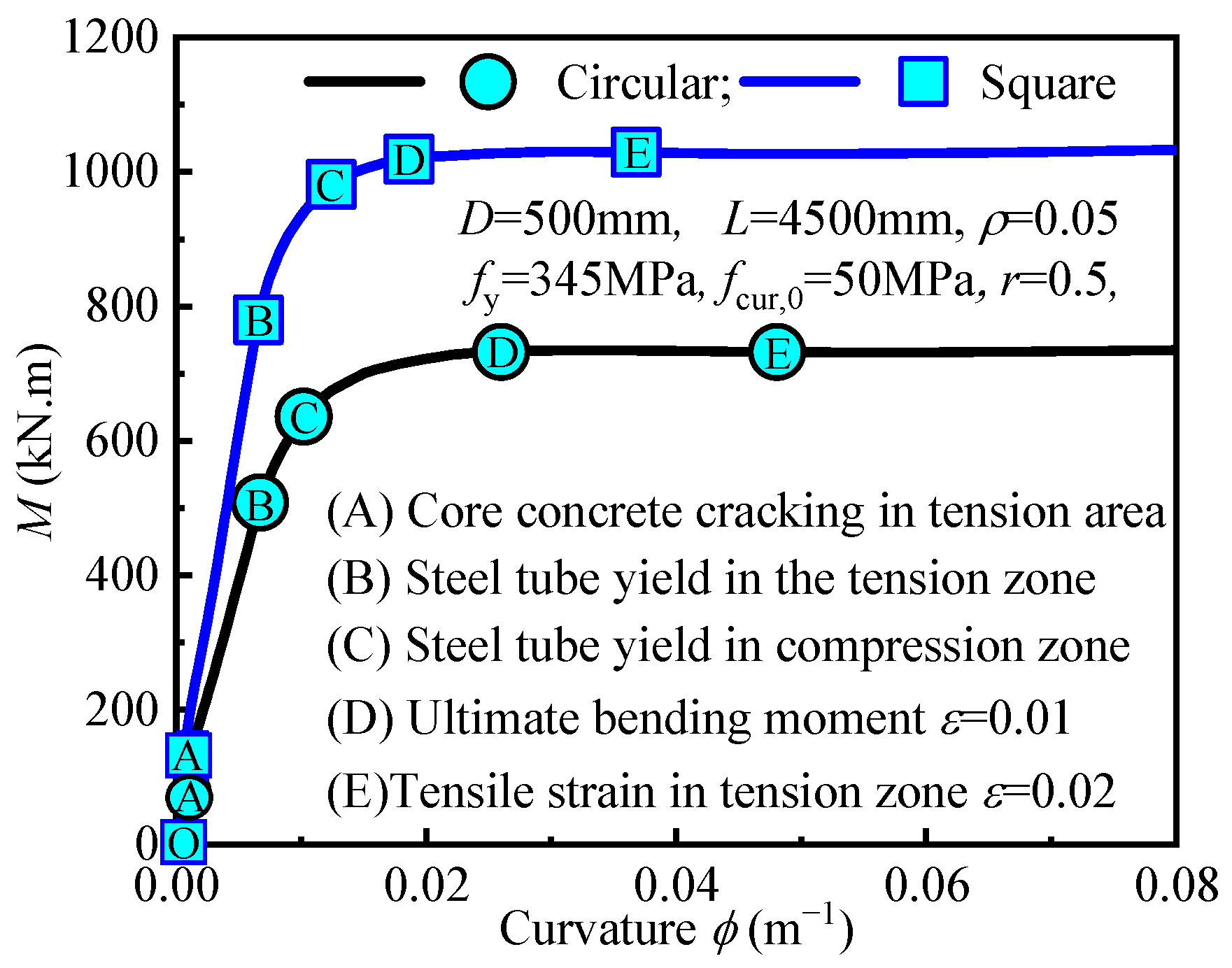
4.1. Full Curve Analysis
4.2. Analysis of Factors Influencing Bending Moment and Flexural Stiffness
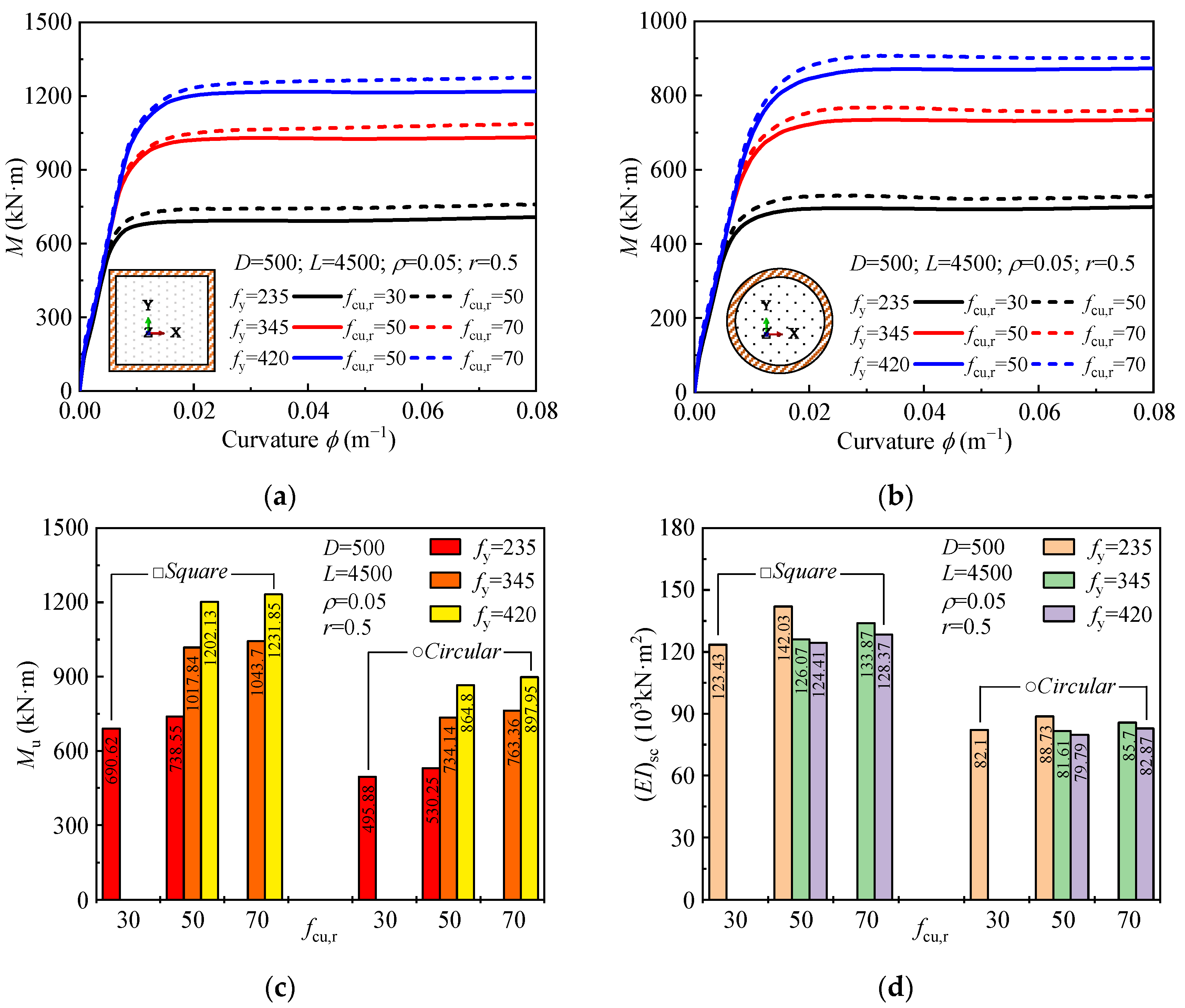
4.2.1. Material Strength
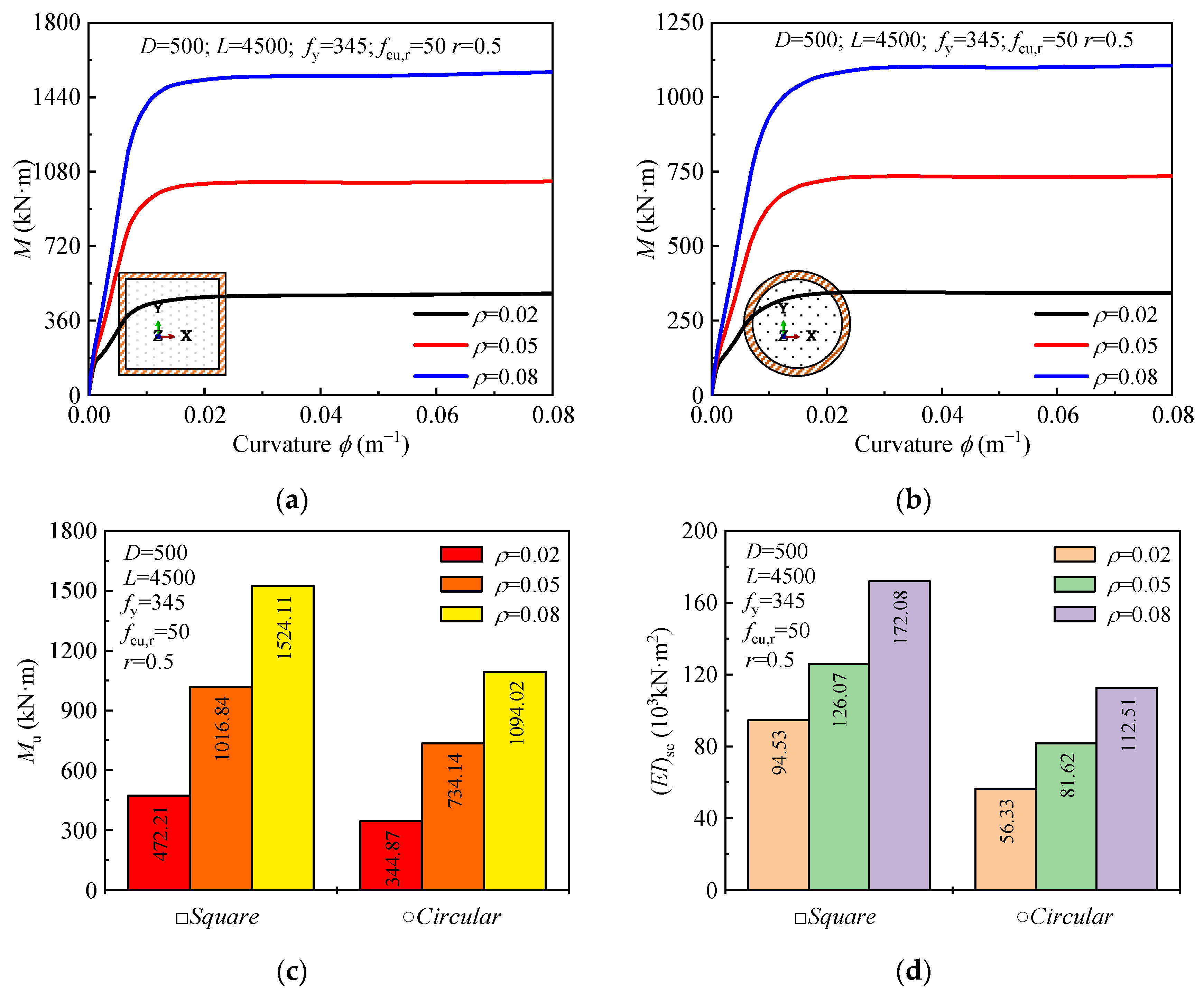
4.2.2. Steel Ratio
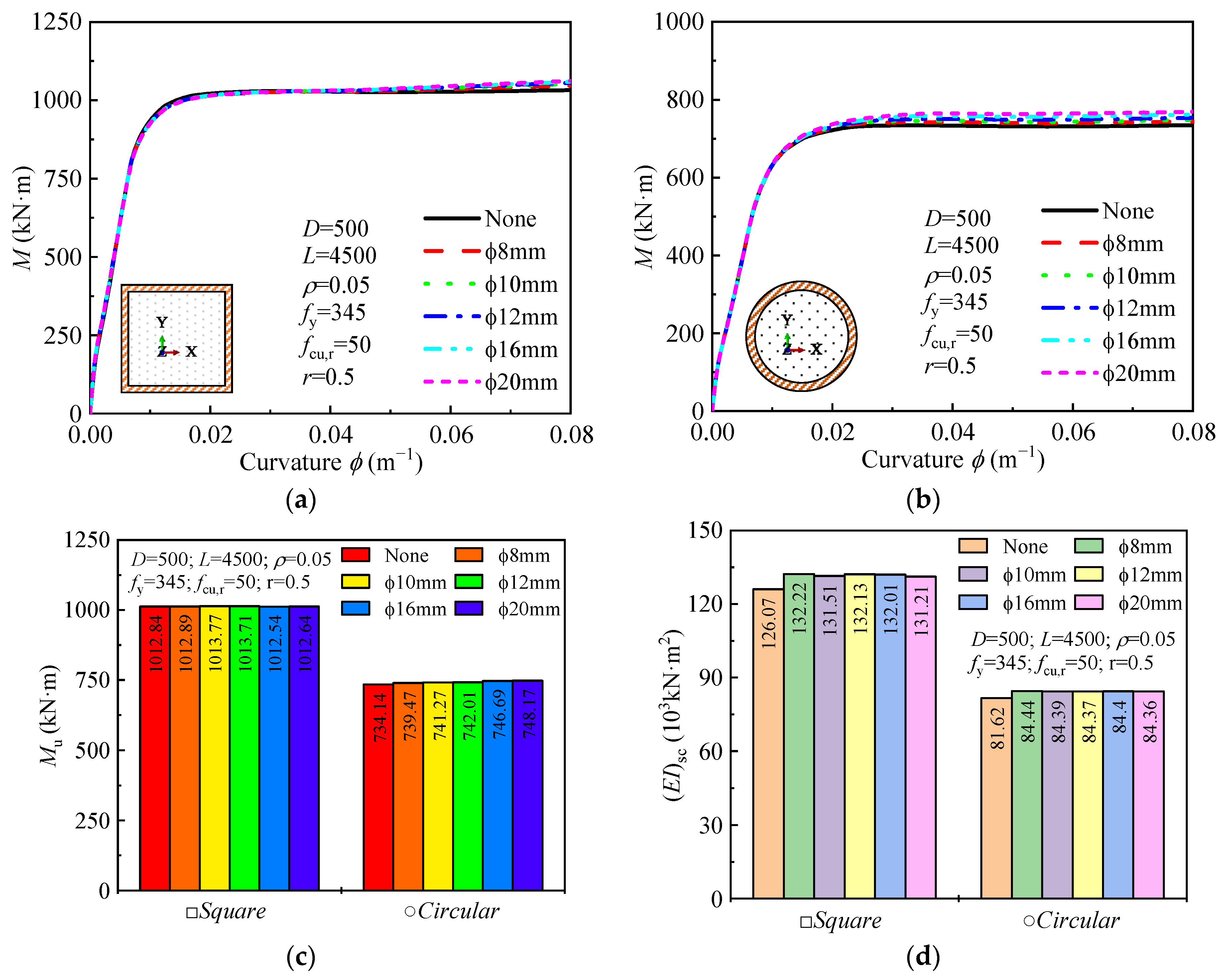
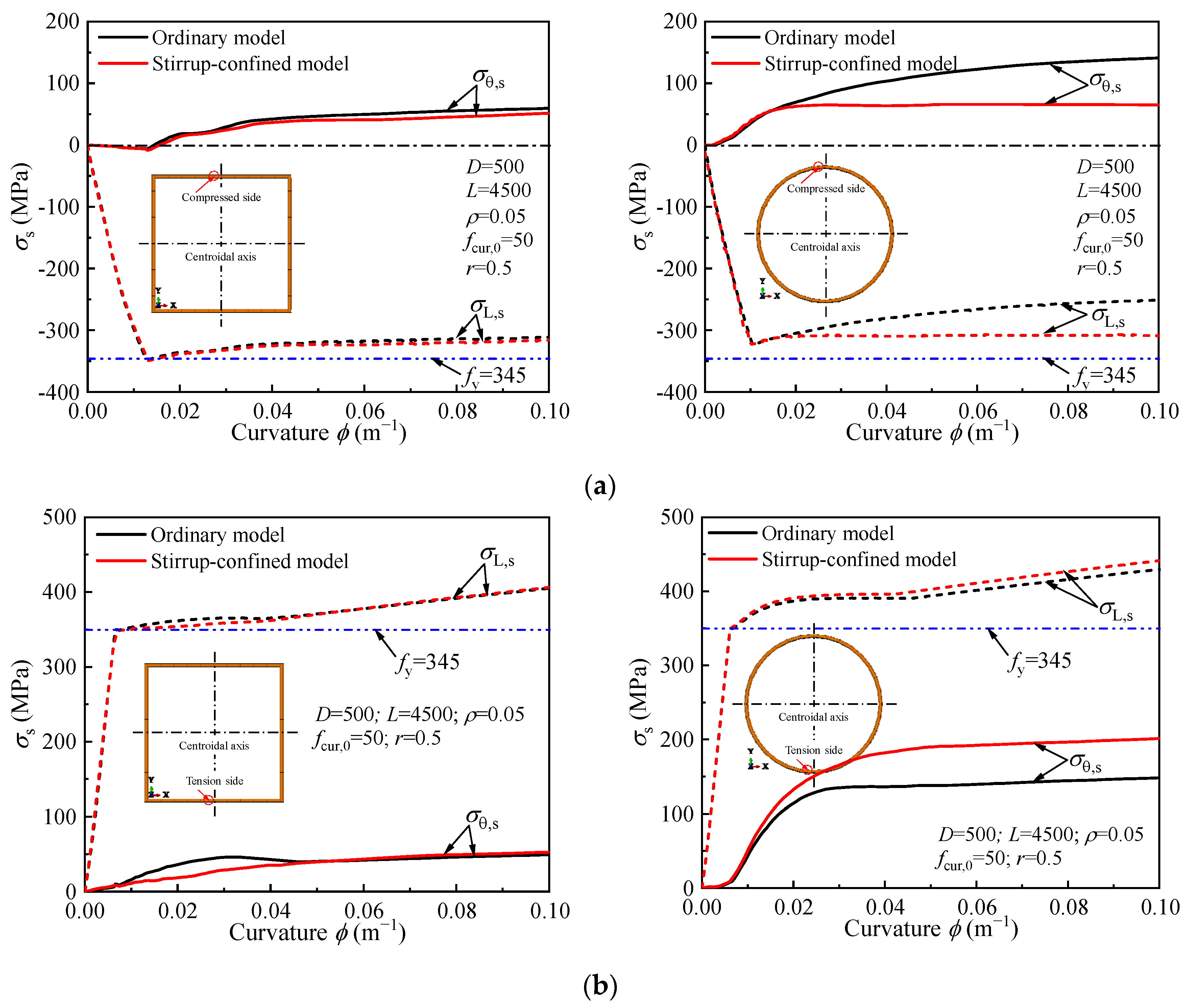
4.2.3. Stirrup Confinement
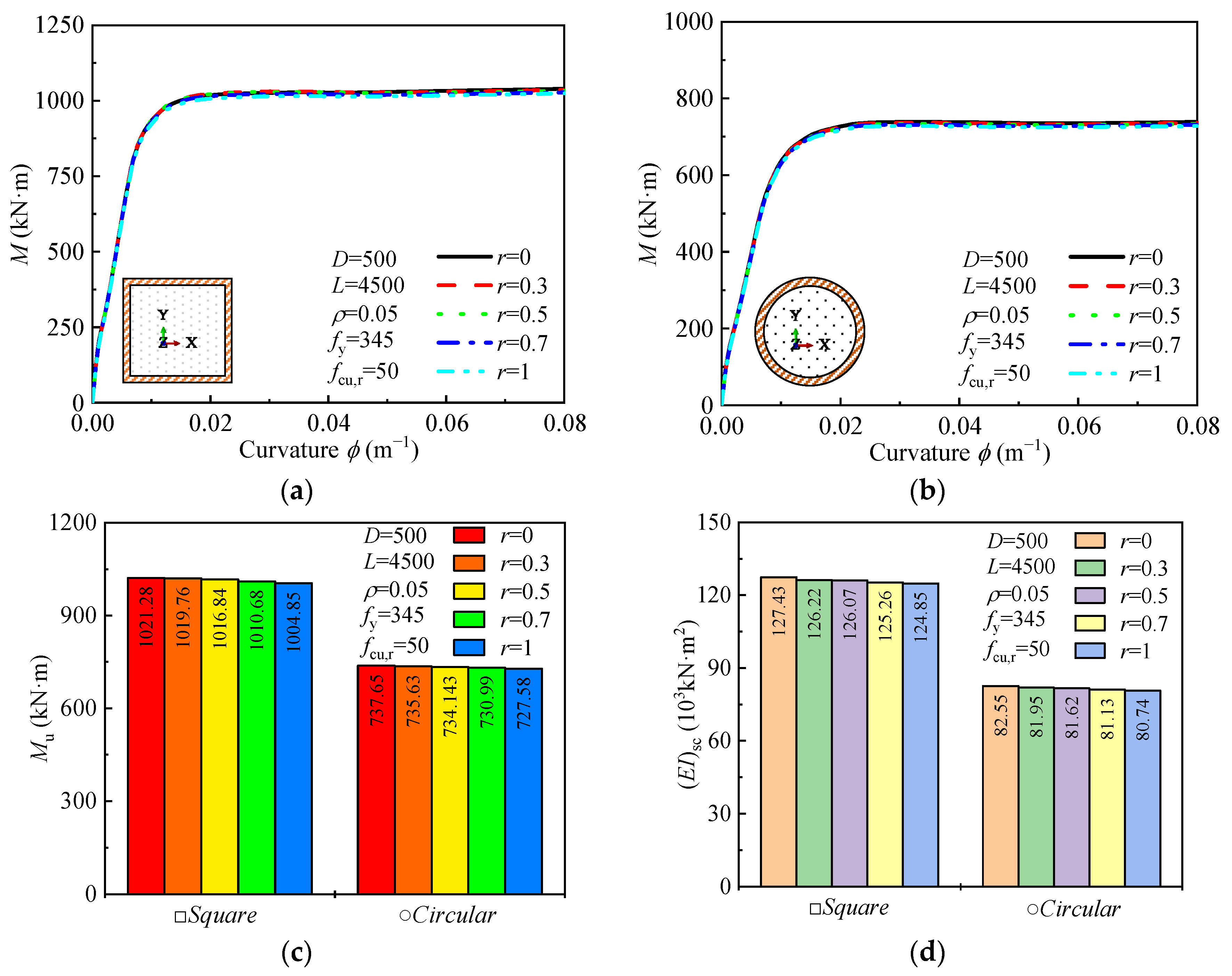
4.2.4. Desert Sand Replacement Ratio
4.3. Failure Analysis
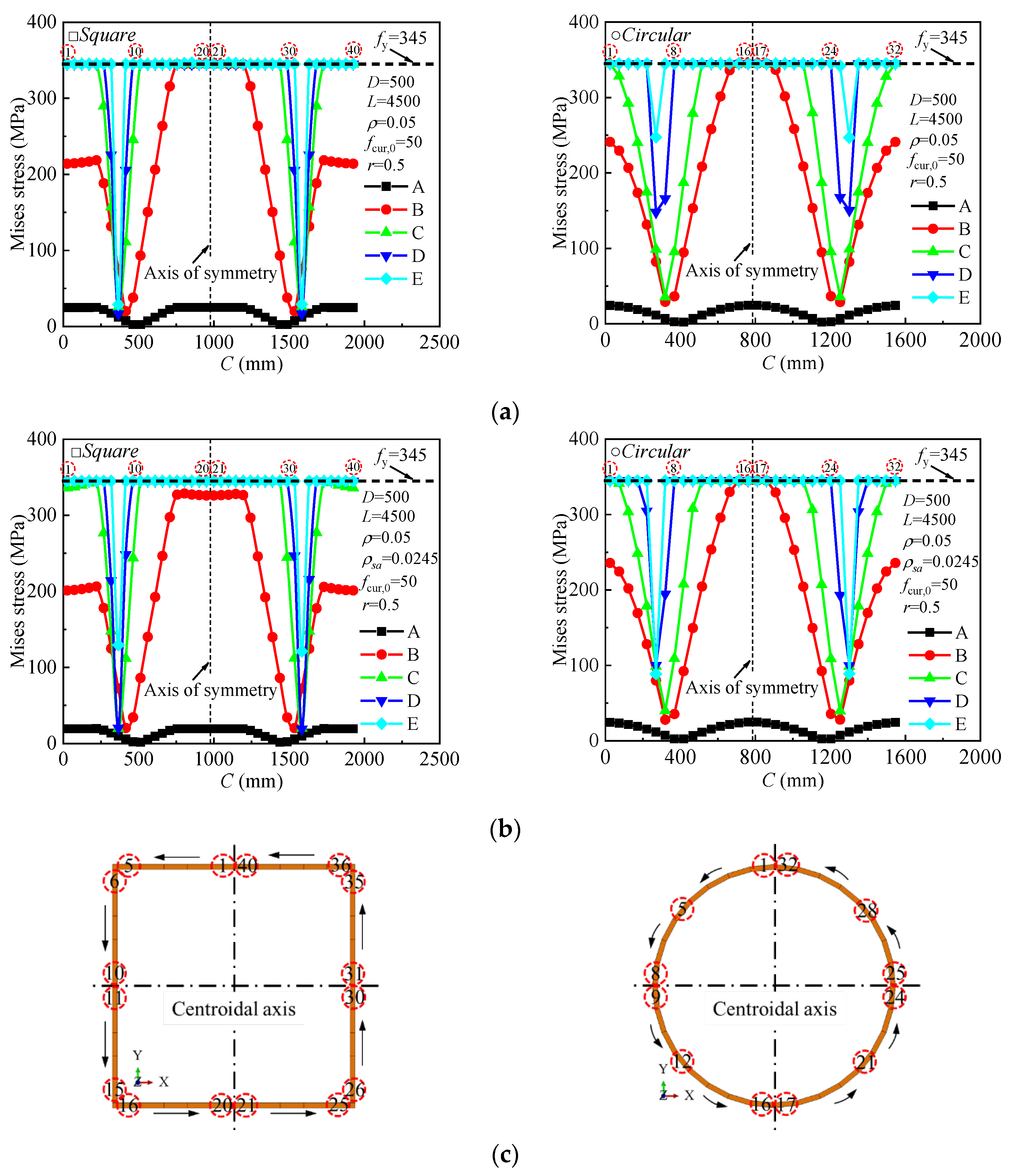
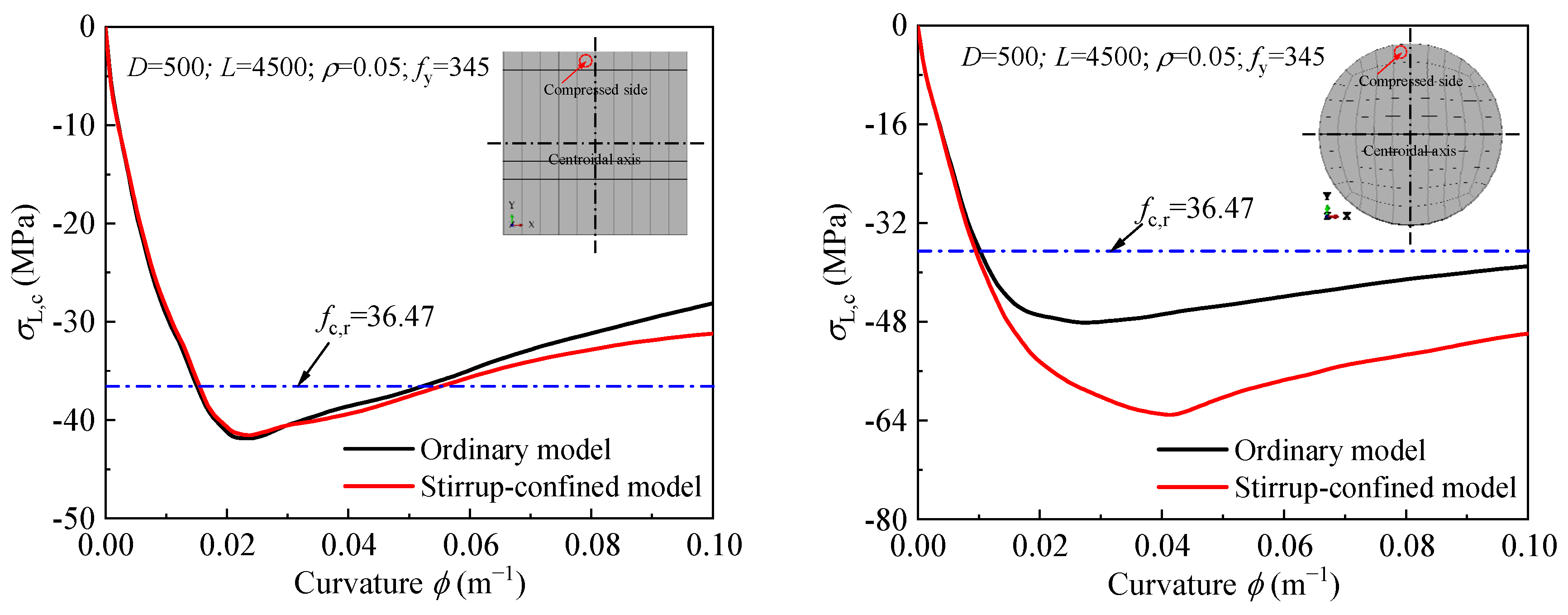
4.4. Stress Distribution Analysis at Different Loading Stages
5. Prediction Design Formulas
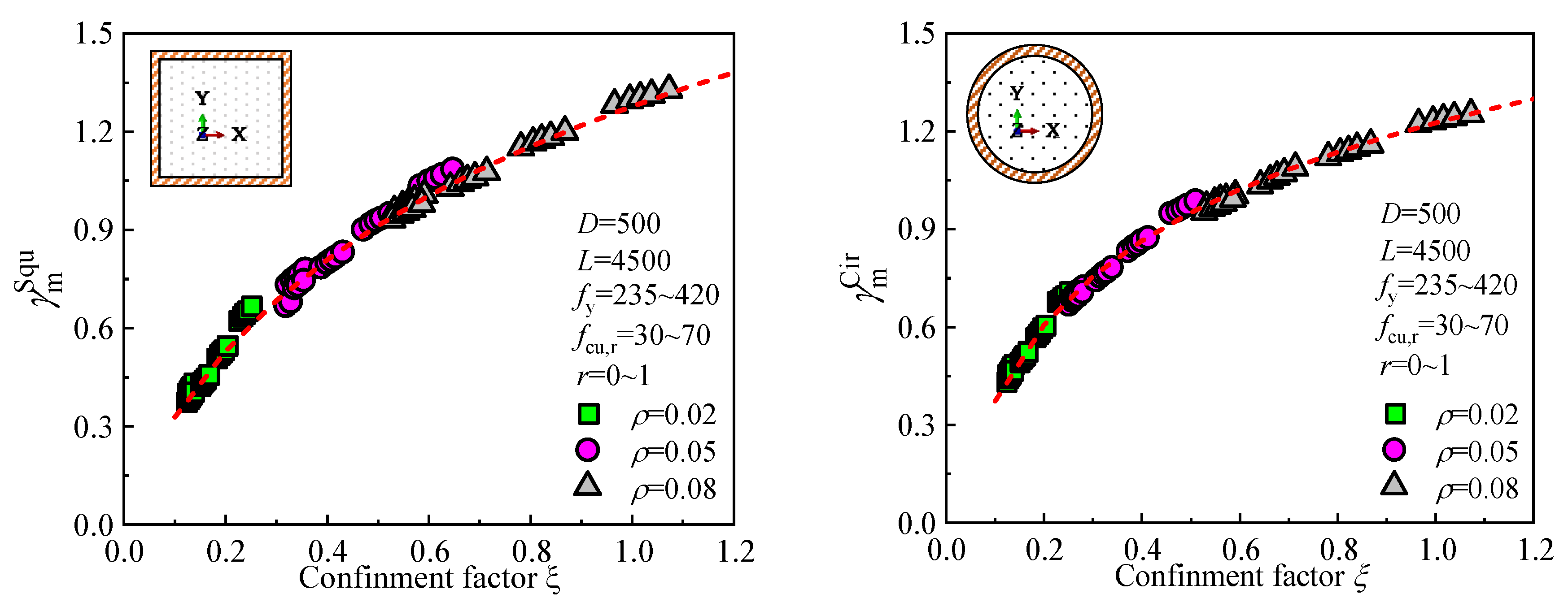
5.1. Ultimate Bending Moment
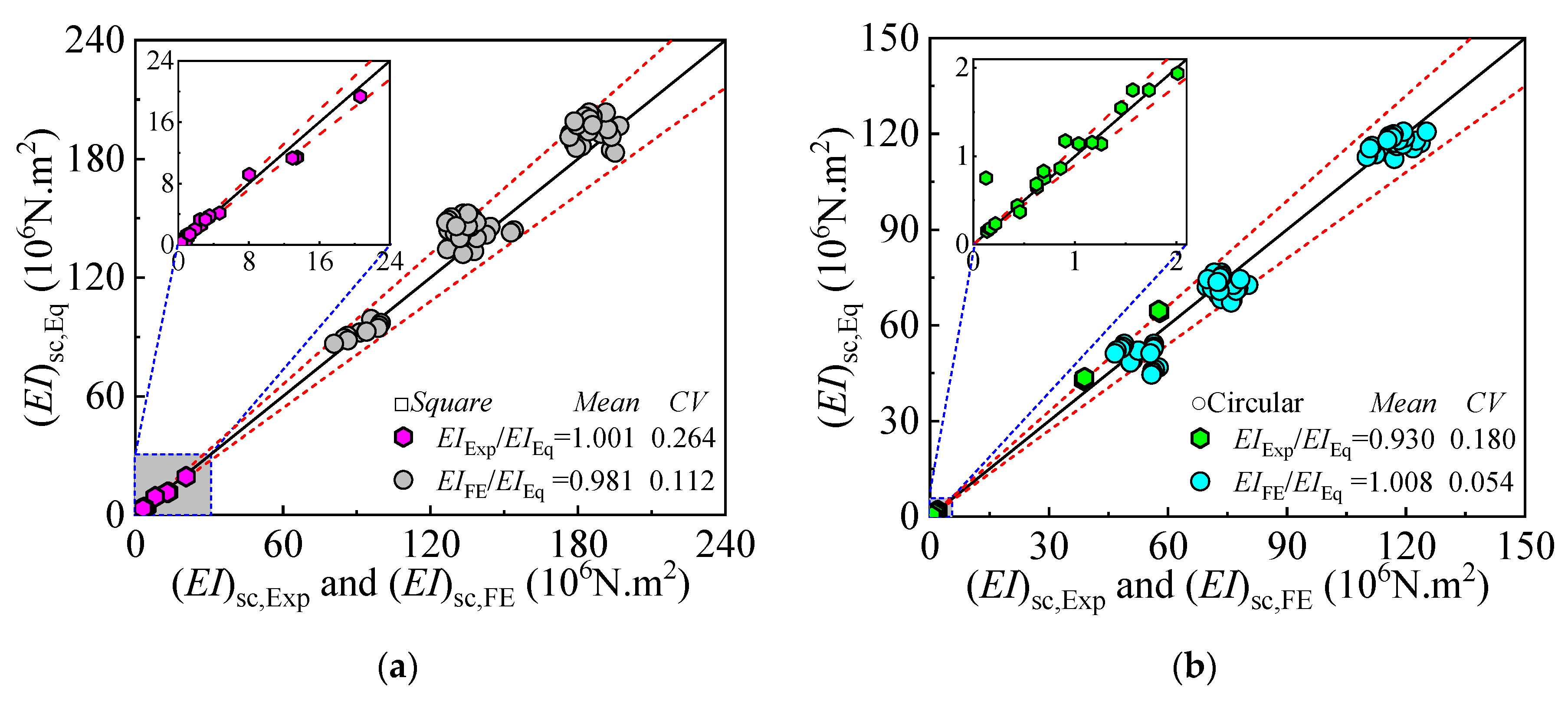
5.2. Flexural Stiffness
6. Conclusions
- The ABAQUS-based finite element model accurately predicted the failure modes and moment-curvature relationships for both square and circular sections. The model demonstrated strong agreement with experimental results, successfully capturing the three-stage bending response.
- Steel yield strength significantly influenced the ultimate bending moment, with increases of up to 38.5% as the steel yield strength rose from 235 MPa to 420 MPa. The steel ratio also played a crucial role, with a 115% and 113% increase in moment capacity for square and circular sections, respectively. While stirrup confinement had minimal effect on bending capacity, it helped control crack propagation. Desert sand replacement had a negligible impact on capacity, confirming its feasibility as a sustainable material for concrete production.
- Square sections exhibited localized buckling due to stress concentrations at the corners, whereas circular sections showed more uniform stress distribution and greater ductility. The neutral axis shifted more abruptly in square sections compared to the smoother transition observed in circular sections.
- New formulas for predicting ultimate bending moment and flexural stiffness were developed, incorporating confinement effects and stiffness reduction factors. These formulas demonstrated superior accuracy compared to existing design codes (AIJ, AISC, GB50936-2014), with low coefficients of variation, thus enhancing the reliability of DS-CFST design.
- This research provides valuable tools for designing DS-CFST members, highlighting the potential of desert sand as a sustainable construction material. Future research could explore long-term durability, cyclic loading performance, and the optimization of stirrup confinement strategies to further enhance seismic resistance and overall performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a | Shear span |
| Ac | Cross-sectional area of concrete |
| As | Cross-sectional area of the steel tube |
| AIJ | Architectural Institute of Japan |
| AISC | American Institute of Steel Construction |
| CFST | Concrete-filled steel tubular |
| D | Outer dimension of the steel tube; diameter for circular, side length for square sections |
| DS | Desert sand |
| Ec | Elastic modulus of concert |
| Es | Elastic modulus of steel |
| (EI)sc | Steel-concrete composite flexural stiffness |
| FEM | Finite element model |
| fc | Axial compressive strength of concrete |
| fy | Yield strength of the steel tube |
| fcu | Concrete cube strength |
| kz | Concrete flexural stiffness reduction factor considering concrete cracking |
| Mu | Ultimate bending moment |
| Mue | Experimental measured ultimate bending moment |
| Mu,FE | Finite element computed ultimate bending moment |
| Mu,eq | Formula calculated ultimate bending moment |
| L | Length of the member |
| r | Replacement ratio |
| t | thickness of the steel tube |
| l0 | clear span |
| ϕ | Midspan curvature |
| ϕ | stirrup diameter |
| ε | strain |
| ρ | Steel ratio in the steel tube |
| ρsa | equivalent stirrup ratios |
| σ | stress |
| σθ,s | Hoop stress |
| σL,s | Longitudinal stress |
References
- Macfarlane, M.; Mitchell, P. Scoping and assessment of the environmental and social impacts of river mining in Jamaica. Chemistry 2003, 8, 4980–4991. [Google Scholar]
- Pilkey, O.H.; Young, R.S.; Kelley, J.; Griffith, A.D. Mining of Coastal Sand: A Critical Environmental and Economic Problem for Morocco; White Paper; Western Carolina University: Cullowhee, NC, USA, 2007. [Google Scholar]
- Kazmi, S.M.S.; Munir, M.J.; Wu, Y.F. Development of sustainable high-performance desert sand concrete: Engineering and environmental impacts of compression casting. Resour. Conserv. Recycl. 2025, 212, 108002. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Bani-Hani, K.A.; Malkawi, D.A.H.; Albatayneh, O. Suitability of sustainable sand for concrete manufacturing—A complete review of recycled and desert sand substitution. Results Eng. 2024, 23, 102478. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Albatayneh, O.; Bani-Hani, K.A.; Malkawi, A.I.H. Performance of modified desert sand concrete: An experimental case study. Case Stud. Constr. Mater. 2024, 21, e03465. [Google Scholar] [CrossRef]
- Al-Harthy, A.S.; Halim, M.A.; Taha, R.; Al-Jabri, K.S. The properties of concrete made with fine dune sand. Constr. Build. Mater. 2007, 21, 1803–1808. [Google Scholar] [CrossRef]
- Hamada, H.M.; Abed, F.; Al-Sadoon, Z.A.; Elnassar, Z.; Hassan, A. The use of treated desert sand in sustainable concrete: A mechanical and microstructure study. J. Build. Eng. 2023, 79, 107843. [Google Scholar] [CrossRef]
- Gong, L.; Zhao, X.H.; Bu, Y.Z.; Xu, T.L.; Yu, X.B.; Liang, Y.T. Research on frost resistance of desert sand machine-made sand blended concrete and life prediction. Structures 2024, 70, 107875. [Google Scholar] [CrossRef]
- Li, Z.Q.; Gan, D. Cyclic behavior and strength evaluation of RC columns with dune sand. J. Build. Eng. 2022, 47, 103801. [Google Scholar] [CrossRef]
- Wang, W.H.; Han, L.H.; Li, W.; Jia, Y.H. Behavior of concrete-filled steel tubular stub columns and beams using dune sand as part of fine aggregate. Constr. Build. Mater. 2014, 51, 352–363. [Google Scholar] [CrossRef]
- Sadat, S.I.; Ding, F.X.; Lyu, F.; Wang, E.; Sun, H.; Akhunzada, K.; Lessani, N. Axial compression behavior and reliable design approach of rectangular dune sand concrete-filled steel tube stub columns. Dev. Built Environ. 2024, 18, 100437. [Google Scholar] [CrossRef]
- Sadat, S.I.; Ding, F.X.; Wang, M.; Lyu, F.; Akhunzada, K.; Xu, H.; Hui, B. Behavior and Reliable Design Methods of Axial Compressed Dune Sand Concrete-Filled Circular Steel Tube Columns. Appl. Sci. 2024, 14, 6939. [Google Scholar] [CrossRef]
- Li, Z.Q.; Zhang, R.C.; Zhou, Y.; Ji, F. Axial compressive properties analysis and strength evaluation of reinforced concrete short columns with dune sand. Structures 2025, 73, 108472. [Google Scholar] [CrossRef]
- Li, Z.Q.; Yang, S.; Luo, Y. Experimental evaluation of the effort of dune sand replacement levels on flexural behaviour of reinforced beam. J. Asian Archit. Build. Eng. 2020, 19, 480–489. [Google Scholar] [CrossRef]
- Li, Z.Q.; Ma, R.; Li, G. Experimental Study on the Shear Strength of Dune Sand Concrete Beams. Adv. Civ. Eng. 2020, 2020, 8062691. [Google Scholar] [CrossRef]
- Li, Z.Q.; Zhai, D.; Li, J. Seismic behavior of the dune sand concrete beam-column joints under cyclic loading. Structures 2022, 40, 1014–1024. [Google Scholar] [CrossRef]
- Ding, F.X.; Luo, S.; Sadat, S.I.; Sun, H.; Lyu, F. Analysis of the seismic response and vulnerability of square stirrup-confined concrete-filled steel tube columns. Eng. Struct. 2025, 333, 120167. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Q.Y.; Ding, F.X.; Wang, L.P.; Lyu, F.; Sadat, S.I. Seismic behavior of thin-walled stirrup-confined circular concrete-filled steel tube piers: Experimental, numerical, and restoring force model analysis. Soil Dyn. Earthq. Eng. 2024, 176, 108310. [Google Scholar] [CrossRef]
- Ding, F.X.; Sadat, S.I.; Lyu, F.; Yin, Y. Flexural performance of rectangular CFST composite T-beams: Experimental, numerical, and theoretical investigation. J. Constr. Steel Res. 2024, 213, 108356. [Google Scholar] [CrossRef]
- Ding, F.X.; Zhang, T.; Wang, L.P.; Fu, L. Behavior of concrete-filled round-ended steel tubes under bending. Steel Compos. Struct. 2017, 25, 457–472. [Google Scholar] [CrossRef]
- Ding, F.X.; Zhang, T.; Wang, L.P.; Fu, L. Further analysis on the flexural behavior of concrete-filled round-ended steel tubes. Steel Compos. Struct. 2019, 30, 149–169. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, Y.Z.; Ding, F.X.; Liu, X.M.; Yu, Z.W. Experimental and numerical investigation on the flexural behavior of concrete-filled elliptical steel tube (CFET). J. Build. Eng. 2021, 41, 102412. [Google Scholar] [CrossRef]
- Wang, R.; Li, X.; Zhao, H.; Wang, Y.H.; Lam, D.; Wang, W.D. Flexural behaviour of round-ended CFST members: Testing, numerical analysis, and design. J. Constr. Steel Res. 2024, 218, 108678. [Google Scholar] [CrossRef]
- Abed, F.; Abdelmageed, Y.; Alhoubi, Y. Effect of different cross-sections and concrete types on the flexural behavior of CFSTs. Compos. Struct. 2021, 276, 114570. [Google Scholar] [CrossRef]
- Han, L.H. Flexural behaviour of concrete-filled steel tubes. J. Constr. Steel Res. 2004, 60, 313–337. [Google Scholar] [CrossRef]
- Wang, R.; Han, L.H.; Nie, J.G.; Zhao, X.L. Flexural performance of rectangular CFST members. Thin-Walled Struct. 2014, 79, 154–165. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Piluso, V.; Todisco, P. Experimental and analytical study on the behaviour of circular concrete filled steel tubes in cyclic bending. Eng. Struct. 2024, 304, 117610. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Piluso, V.; Todisco, P. Finite element analysis of concrete filled steel tubes subjected to cyclic bending. Eng. Struct. 2024, 314, 118364. [Google Scholar] [CrossRef]
- Lu, Y.Q.; Kennedy, D.L. The flexural behaviour of concrete-filled hollow structural sections. Can. J. Civ. Eng. 1994, 21, 111–130. [Google Scholar] [CrossRef]
- Uy, B. Strength of concrete filled steel box columns incorporating local buckling. J. Struct. Eng. 2000, 126, 341–352. [Google Scholar] [CrossRef]
- Han, L.H.; Lu, H.; Yao, G.H.; Liao, F.Y. Further study on the flexural behaviour of concrete-filled steel tubes. J. Constr. Steel Res. 2006, 62, 554–565. [Google Scholar] [CrossRef]
- Yang, Y.F.; Han, L.H. Compressive and flexural behaviour of recycled aggregate concrete filled steel tubes (RACFST) under short-term loadings. Steel Compos. Struct. 2006, 6, 257. [Google Scholar] [CrossRef]
- Soundararajan, A.; Shanmugasundaram, K. Flexural behaviour of concrete-filled steel hollow sections beams. J. Civ. Eng. Manag. 2008, 14, 107–114. [Google Scholar] [CrossRef]
- Wang, Q.L.; Li, J.; Shao, Y.B.; Zhao, W.J. Flexural performances of square concrete filled CFRP-steel tubes (S-CF-CFRP-ST). Adv. Struct. Eng. 2015, 18, 1319–1344. [Google Scholar] [CrossRef]
- Elchalakani, M.; Zhao, X.L.; Grzebieta, R.H. Concrete-filled circular steel tubes subjected to pure bending. J. Constr. Steel Res. 2001, 57, 1141–1168. [Google Scholar] [CrossRef]
- Wu, Y.X.; Yu, Q. Test on pure bending mechanical performance of steel tube confined high–prerformance concrete. J. Harbin Inst. Technol. 2005, 37, 276–279. [Google Scholar]
- Wheeler, A.; Bridge, R. The behaviour of circular concrete-filled thin-walled steel tubes in flexure. In Composite Construction in Steel and Concrete V; ASCE Library: Reston, VA, USA, 2006; pp. 412–423. [Google Scholar]
- Chitawadagi, M.V.; Narasimhan, M.C. Strength deformation behaviour of circular concrete filled steel tubes subjected to pure bending. J. Constr. Steel Res. 2009, 65, 1836–1845. [Google Scholar] [CrossRef]
- Wang, Q.L.; Shao, Y.B. Flexural performance of circular concrete filled CFRP-steel tubes. Adv. Steel Constr. 2015, 11, 127–149. [Google Scholar]
- Al Zand, A.W.; Badaruzzaman, W.H.W.; Mutalib, A.A.; Hilo, S.J. The enhanced performance of CFST beams using different strengthening schemes involving unidirectional CFRP sheets: An experimental study. Eng. Struct. 2016, 128, 184–198. [Google Scholar] [CrossRef]
- Abed, F.H.; Abdelmageed, Y.I.; Ilgun, A.K. Flexural response of concrete-filled seamless steel tubes. J. Constr. Steel Res. 2018, 149, 53–63. [Google Scholar] [CrossRef]
- Al Zand, A.W.; Badaruzzaman, W.H.W.; Mutalib, A.A.; Hilo, S.J. Flexural behavior of CFST beams partially strengthened with unidirectional CFRP sheets: Experimental and theoretical study. J. Compos. Constr. 2018, 22, 04018018. [Google Scholar] [CrossRef]
- Ou, J.; Shao, Y.; Huang, C.; Chen, Y.; Bi, X. Flexural behavior of circular concrete filled steel tubular members strengthened by CFRP sheets. Structures 2023, 55, 201–214. [Google Scholar] [CrossRef]
- Ding, F.X.; Cao, Z.Y.; Lyu, F.; Huang, S.J.; Hu, M.W.; Lin, Q.T. Practical design equations of the axial compressive capacity of circular CFST stub columns based on finite element model analysis incorporating constitutive models for high-strength materials. Case Stud. Constr. Mater. 2022, 16, e01115. [Google Scholar] [CrossRef]
- Sadat, S.I.; Ding, F.X.; Lyu, F.; Lessani, N.; Liu, X.Y.; Yang, J. Unified prediction models for mechanical properties and stress-strain relationship of dune sand concrete. Comput. Concr. 2023, 32, 595–606. [Google Scholar] [CrossRef]
- Ding, F.X.; Wu, X.; Xiang, P.; Yu, Z.W. New Damage Ratio Strength Criterion for Concrete and Lightweight Aggregate Concrete. ACI Struct. J. 2021, 118, 165–178. [Google Scholar] [CrossRef]
- AIJ. Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures; Architectural Institute of Japan: Tokyo, Japan, 1997. [Google Scholar]
- AISC-LRFD99; Load and Resistance Factor Design Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 1999.
- GB50936-2014; Technical Code for Concrete Filled Steel Tubular Structures. China Architecture & Building Press: Beijing, China, 2014.





| Specimen Label | Ref. | D/mm | t/mm | l0/mm | a/mm | fcu/MPa | fy/MPa | Mue/kN·m | Mu,FE/kN·m | Mue/Mu,FE |
|---|---|---|---|---|---|---|---|---|---|---|
| CB12 | [29] | 152 | 4.8 | 1975 | 235 | 58.8 | 389 | 73.6 | 71.52 | 1.03 |
| CB13 | 152 | 4.8 | 8430 | 463 | 53.5 | 389 | 75.1 | 72.01 | 1.04 | |
| CB15 | 152 | 4.8 | 3040 | 768 | 51.5 | 389 | 71.3 | 72.90 | 0.98 | |
| CB22 | 152 | 9.5 | 1976 | 236 | 58.6 | 432 | 146.5 | 119.51 | 1.23 | |
| HS6 | [30] | 126 | 3 | 1800 | 600 | 62.5 | 300 | 27.9 | 27.99 | 1.00 |
| HS12 | 126 | 3 | 2250 | 750 | 62.5 | 300 | 42.4 | 44.53 | 0.95 | |
| NS6 | 186 | 3 | 2700 | 900 | 40.0 | 300 | 62.6 | 56.64 | 1.11 | |
| NS12 | 246 | 3 | 3600 | 1200 | 47.5 | 300 | 103.5 | 105.23 | 0.98 | |
| NS18 | 306 | 3 | 4500 | 1500 | 47.5 | 300 | 153 | 155.38 | 0.98 | |
| RB1-1 | [25] | 120 | 3.84 | 1000 | 250 | 27.3 | 330.1 | 29.34 | 28.45 | 1.03 |
| RB2-1 | 120 | 3.84 | 1000 | 250 | 35.2 | 330.1 | 30.16 | 29.06 | 1.04 | |
| RB2-2 | 120 | 3.84 | 1000 | 250 | 35.2 | 330.1 | 32.25 | 29.06 | 1.11 | |
| RB2-3 | 120 | 3.84 | 1000 | 250 | 35.2 | 330.1 | 31.69 | 29.06 | 1.09 | |
| RB3-1 | 120 | 5.86 | 1000 | 250 | 31.3 | 321.1 | 40.9 | 39.88 | 1.03 | |
| RB3-2 | 120 | 5.86 | 1000 | 250 | 31.3 | 321.1 | 41.54 | 39.88 | 1.04 | |
| RB4-1 | 120 | 5.86 | 1000 | 250 | 40.0 | 321.1 | 41.43 | 40.61 | 1.02 | |
| RB4-2 | 120 | 5.86 | 1000 | 250 | 40.0 | 321.1 | 42.61 | 40.61 | 1.05 | |
| BSb0 | [31] | 150 | 2.94 | 1000 | 250 | 42.7 | 344.1 | 34.9 | 36.80 | 0.95 |
| SVA-1 | [32] | 100 | 1.9 | 1400 | 350 | 81.3 | 282 | 10.83 | 9.94 | 1.09 |
| SVA-2 | 100 | 1.9 | 1400 | 350 | 81.3 | 282 | 9.96 | 9.94 | 1.00 | |
| SSCA-1 | 100 | 1.9 | 1400 | 350 | 81.3 | 282 | 10.33 | 9.94 | 1.04 | |
| SVB-1 | 200 | 1.9 | 1400 | 350 | 81.3 | 282 | 42.3 | 48.69 | 0.87 | |
| SVB-2 | 200 | 1.9 | 1400 | 350 | 81.3 | 282 | 54.3 | 48.69 | 1.12 | |
| SSCB-1 | 200 | 1.9 | 1400 | 350 | 81.3 | 282 | 56.7 | 48.69 | 1.16 | |
| SB1-1 | [32] | 140 | 3 | 840 | 210 | 51.5 | 235 | 31.9 | 27.02 | 1.18 |
| SB1-2 | 140 | 3 | 840 | 210 | 51.5 | 235 | 27.5 | 27.02 | 1.02 | |
| SB2-1 | 140 | 3 | 1680 | 420 | 51.5 | 235 | 29.4 | 28.64 | 1.03 | |
| SB4-1 | 180 | 3 | 900 | 225 | 62.6 | 235 | 37.6 | 43.22 | 0.87 | |
| SB4-2 | 180 | 3 | 900 | 225 | 62.6 | 235 | 43.1 | 43.22 | 1.00 | |
| SB5-1 | 180 | 3 | 1800 | 450 | 62.6 | 235 | 37.9 | 43.02 | 0.88 | |
| NMC-1 | [33] | 72 | 3.2 | 1000 | 333 | 32.5 | 345 | 10.06 | 10.07 | 1.00 |
| NMC-2 | 72 | 3.2 | 1000 | 333 | 32.5 | 345 | 9.57 | 10.07 | 0.95 | |
| NMC-3 | 72 | 3.2 | 1000 | 333 | 32.5 | 345 | 10.4 | 10.07 | 1.03 | |
| FAC-1 | 72 | 3.2 | 1000 | 333 | 32.5 | 345 | 9.9 | 10.07 | 0.98 | |
| FAC-2 | 72 | 3.2 | 1000 | 333 | 32.5 | 345 | 10.07 | 10.07 | 1.00 | |
| FAC-3 | 72 | 3.2 | 1000 | 333 | 32.5 | 345 | 10.4 | 10.07 | 1.03 | |
| SB A-0 | [34] | 140 | 3.5 | 1200 | 400 | 33.0 | 300 | 42 | 41.05 | 1.02 |
| SB B-0 | 140 | 3.5 | 1200 | 400 | 39.4 | 300 | 42.4 | 41.09 | 1.03 | |
| SB C-0 | 140 | 3.5 | 1200 | 400 | 49.0 | 300 | 43.4 | 41.55 | 1.04 | |
| SB D-0 | 140 | 3.5 | 1200 | 400 | 59.7 | 300 | 43.2 | 42.54 | 1.02 | |
| Mean | 1.026 | |||||||||
| CV | 0.072 |
| Specimen Label | Ref. | D/mm | t/mm | l0/mm | a/mm | fcu/MPa | fy/MPa | Mue /kN·m | Mu,FE/kN·m | Mue/Mu,FE |
|---|---|---|---|---|---|---|---|---|---|---|
| CBC0-C | [35] | 109.9 | 1 | 1400 | 300 | 29.25 | 400 | 7.64 | 7.00 | 1.091 |
| CBC0-B | 110.4 | 1.25 | 1400 | 300 | 29.25 | 400 | 9.08 | 8.60 | 1.056 | |
| CBC0-A | 110.9 | 1.5 | 1400 | 300 | 29.25 | 400 | 11.72 | 10.18 | 1.152 | |
| CBC1 | 101.83 | 2.53 | 1400 | 300 | 29.25 | 365 | 11.33 | 10.71 | 1.058 | |
| CBC2 | 88.64 | 2.79 | 1400 | 300 | 29.25 | 432 | 10.94 | 10.03 | 1.091 | |
| CBC3 | 76.32 | 2.45 | 1400 | 300 | 29.25 | 415 | 6.84 | 6.52 | 1.049 | |
| CBC4 | 89.26 | 3.35 | 1400 | 300 | 29.25 | 412 | 11.25 | 11.81 | 0.952 | |
| CBC5 | 60.65 | 2.44 | 1400 | 300 | 29.25 | 433 | 3.97 | 3.96 | 1.003 | |
| CBC6 | 76.19 | 3.24 | 1400 | 300 | 29.25 | 456 | 9.87 | 8.55 | 1.154 | |
| CBC7 | 60.67 | 3.01 | 1400 | 300 | 29.25 | 408 | 5 | 4.68 | 1.068 | |
| CBC8 | 33.66 | 1.98 | 1400 | 300 | 29.25 | 442 | 0.93 | 0.97 | 0.955 | |
| CBC9 | 33.78 | 2.63 | 1400 | 300 | 29.25 | 460 | 1.2 | 1.26 | 0.950 | |
| C1 | [36] | 180 | 1.48 | 1200 | 300 | 64 | 307 | 25.1 | 22.27 | 1.127 |
| C2 | 180 | 1.48 | 1200 | 300 | 64 | 307 | 18.8 | 22.27 | 0.844 | |
| TPB002 | [37] | 406 | 6.4 | 3800 | 1300 | 50 | 350 | 489 | 463.42 | 1.055 |
| TPB003 | 406 | 6.4 | 3800 | 1300 | 62.5 | 350 | 489 | 475.30 | 1.029 | |
| TPB005 | 456 | 6.4 | 3800 | 1300 | 60 | 350 | 630 | 604.00 | 1.043 | |
| TPB006 | 456 | 6.4 | 3800 | 1300 | 66 | 350 | 647 | 620.39 | 1.043 | |
| BCb0 | [32] | 165 | 2.57 | 100 | 250 | 42.7 | 343.1 | 29.4 | 30.43 | 0.966 |
| CVA-1 | [25] | 100 | 1.9 | 1400 | 350 | 81.3 | 282 | 3.5 | 7.156 | 1.284 |
| CVA-2 | 100 | 1.9 | 1400 | 350 | 81.3 | 282 | 3.5 | 7.156 | 1.024 | |
| CSCA-1 | 100 | 1.9 | 1400 | 350 | 81.3 | 282 | 3.5 | 7.156 | 1.082 | |
| CVB-1 | 200 | 1.9 | 1400 | 350 | 81.3 | 282 | 1.75 | 33.355 | 0.971 | |
| CVB-2 | 200 | 1.9 | 1400 | 350 | 81.3 | 282 | 1.75 | 33.355 | 1.016 | |
| CSCB-1 | 200 | 1.9 | 1400 | 350 | 81.3 | 282 | 1.75 | 33.355 | 1.097 | |
| CB1-1 | 140 | 3 | 840 | 210 | 51.5 | 235 | 1.5 | 18.856 | 1.050 | |
| CB1-2 | 140 | 3 | 840 | 210 | 51.5 | 235 | 1.5 | 18.856 | 1.146 | |
| CB2-1 | 140 | 3 | 1680 | 420 | 51.5 | 235 | 3 | 18.625 | 1.154 | |
| CB4-1 | 180 | 3 | 900 | 225 | 62.6 | 235 | 33.9 | 31.18 | 1.087 | |
| CB4-2 | 180 | 3 | 900 | 225 | 62.6 | 235 | 34.9 | 31.18 | 1.119 | |
| CB5-1 | 180 | 3 | 1800 | 450 | 62.6 | 235 | 32.2 | 31.79 | 1.013 | |
| D1t1M20 | [38] | 44.45 | 1.25 | 900 | 300 | 26.84 | 250 | 0.74 | 0.78 | 0.949 |
| D1t2M30 | 44.45 | 1.6 | 900 | 300 | 40.06 | 250 | 1.16 | 1.24 | 0.935 | |
| D1t3M40 | 44.45 | 2 | 900 | 300 | 48.32 | 250 | 1.46 | 1.49 | 0.980 | |
| D2t1M30 | 57.15 | 1.25 | 900 | 300 | 40.06 | 250 | 1.57 | 1.42 | 1.106 | |
| D2t2M40 | 57.15 | 1.6 | 900 | 300 | 48.32 | 250 | 2.03 | 2.11 | 0.962 | |
| D2t3M20 | 57.15 | 2 | 900 | 300 | 26.84 | 250 | 2.25 | 2.27 | 0.991 | |
| D3t1M40 | 63.5 | 1.25 | 900 | 300 | 48.32 | 250 | 2.03 | 2.08 | 0.976 | |
| D3t2M20 | 63.5 | 1.6 | 900 | 300 | 26.84 | 250 | 2.18 | 2.22 | 0.982 | |
| D3t3M30 | 63.5 | 2 | 900 | 300 | 40.06 | 250 | 3.16 | 3.19 | 0.991 | |
| CB A-0 | [39] | 89 | 4.5 | 1200 | 400 | 60.7 | 204 | 12.5 | 12.27 | 1.018 |
| CB B-0 | 108 | 4.5 | 1200 | 400 | 60.7 | 269 | 18.5 | 19.16 | 0.966 | |
| CB C-0 | 133 | 4.5 | 1200 | 400 | 60.7 | 333 | 32.7 | 31.97 | 1.023 | |
| CB D-0 | 159 | 4.5 | 1200 | 400 | 60.7 | 333 | 51.5 | 48.60 | 1.060 | |
| CS | [40] | 135 | 3 | 1850 | 620 | 30.2 | 353.3 | 18.5 | 21.89 | 0.845 |
| CFST17.5 | [41] | 114 | 6.5 | 1000 | 300 | 49.25 | 245 | 21.8 | 21.11 | 1.033 |
| CFST13.5 | 114 | 8.5 | 1000 | 300 | 49.25 | 245 | 29.78 | 28.95 | 1.029 | |
| CFST7.82 | 114 | 14.6 | 1000 | 300 | 49.25 | 245 | 41.53 | 41.97 | 0.990 | |
| C | [42] | 165 | 2.7 | 1700 | 620 | 31.5 | 346 | 30.9 | 30.20 | 1.023 |
| C-0L | [43] | 114 | 2.9 | 1200 | 400 | 40.6 | 364.1 | 17.1 | 16.03 | 1.067 |
| Mean | 1.033 | |||||||||
| CV | 0.076 | |||||||||
| Condition | x | y | fc(r)orft(r) | εc(r) or εt(r) | An(r) | Bn(r) | αn(r) |
|---|---|---|---|---|---|---|---|
| Compression n = c | ε/εc(r) | σ/fc(r) | 0.15 | ||||
| Tension n = t | ε/εt(r) | σ/ft(r) | 0.8 |
| Parameter Name | Value |
|---|---|
| Desert sand concrete elastic modulus, Ec | (1−0.1r)9500fcu1/3 |
| Poisson’s ratio | 0.2 |
| Dilation angle | 40° |
| Eccentricity e | 0.1 |
| Ratio of biaxial to uniaxial compressive strength, fb0/fc0 | 1.331 |
| Viscosity parameter, K | 0.0005 |
| Section Type | D/mm | L/mm | ρ | ρsa | fcu/MPa | fy/MPa | r |
|---|---|---|---|---|---|---|---|
| Square Circular | 500 | 4500 | 0.02, 0.05, 0.08 | 0 | 30~70 | 235~420 | 0~1 |
| 0.05 | 0.004~0.0245 |
| Ref. | Section Shape | Mu,Ex/Mu,Eq | Mu,EF/Mu,Eq | Mean | CV | ||
|---|---|---|---|---|---|---|---|
| Mean | CV | Mean | CV | ||||
| This study | Square | 0.982 | 0.089 | 1.003 | 0.047 | 0.993 | 0.068 |
| Circular | 1.005 | 0.066 | 0.997 | 0.019 | 1.001 | 0.043 | |
| AIJ | Square | 1.324 | 0.123 | 1.451 | 0.149 | 1.388 | 0.136 |
| Circular | 1.474 | 0.130 | 1.455 | 0.096 | 1.465 | 0.113 | |
| AISC-LFRD | Square | 1.510 | 0.128 | 1.613 | 0.149 | 1.562 | 0.139 |
| Circular | 1.638 | 0.130 | 1.616 | 0.096 | 1.627 | 0.113 | |
| GB 50936 | Square | 1.090 | 0.117 | 0.991 | 0.058 | 1.041 | 0.088 |
| Circular | 1.164 | 0.161 | 1.120 | 0.034 | 1.142 | 0.098 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.-C.; Ding, F.-X.; Sadat, S.I.; Lyu, F.; Huang, X.-Y.; Gao, R.; Yu, T.; Liu, Y.-L. Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas. Materials 2025, 18, 2371. https://doi.org/10.3390/ma18102371
Zhang C-C, Ding F-X, Sadat SI, Lyu F, Huang X-Y, Gao R, Yu T, Liu Y-L. Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas. Materials. 2025; 18(10):2371. https://doi.org/10.3390/ma18102371
Chicago/Turabian StyleZhang, Chao-Cheng, Fa-Xing Ding, Said Ikram Sadat, Fei Lyu, Xin-Yu Huang, Rui Gao, Tao Yu, and Yu-Lin Liu. 2025. "Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas" Materials 18, no. 10: 2371. https://doi.org/10.3390/ma18102371
APA StyleZhang, C.-C., Ding, F.-X., Sadat, S. I., Lyu, F., Huang, X.-Y., Gao, R., Yu, T., & Liu, Y.-L. (2025). Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas. Materials, 18(10), 2371. https://doi.org/10.3390/ma18102371







