Simulation Prediction and Experimental Research on Surface Morphology of Ball Head Milling Processing
Abstract
1. Introduction
2. Materials and Methods
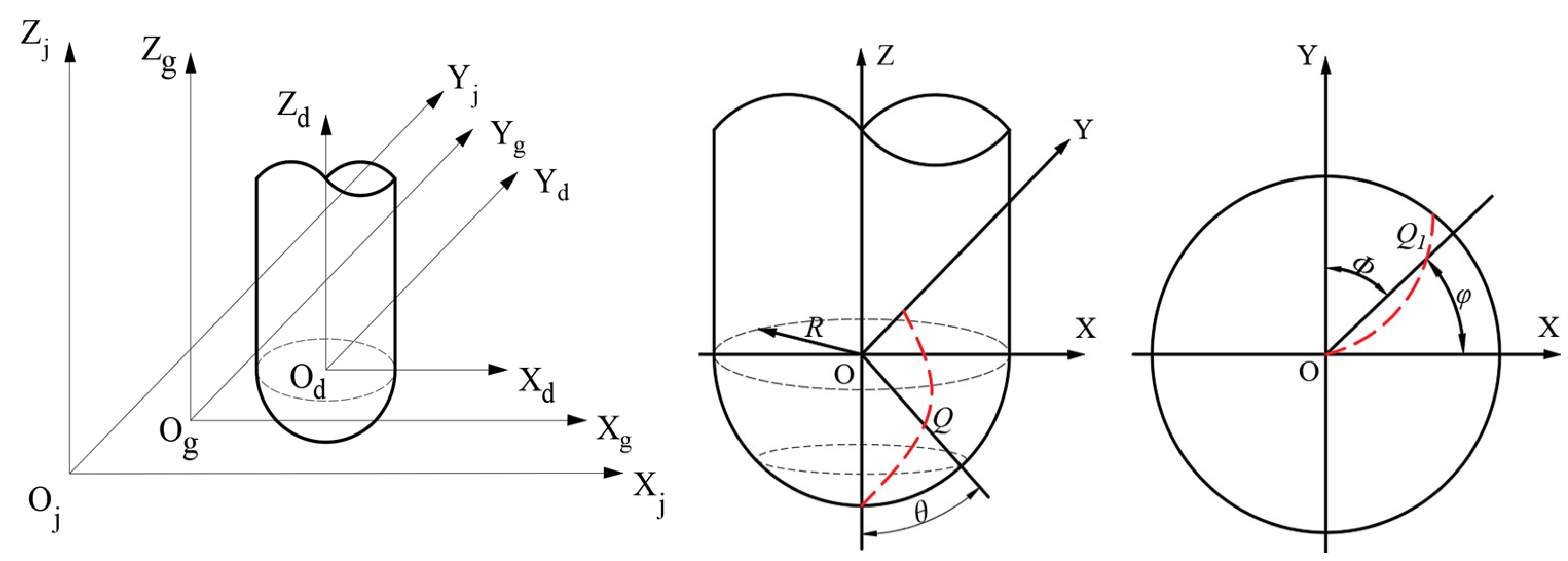
2.1. Establishing a Mathematical Model for the Cutting Edge in Ball-Head Milling
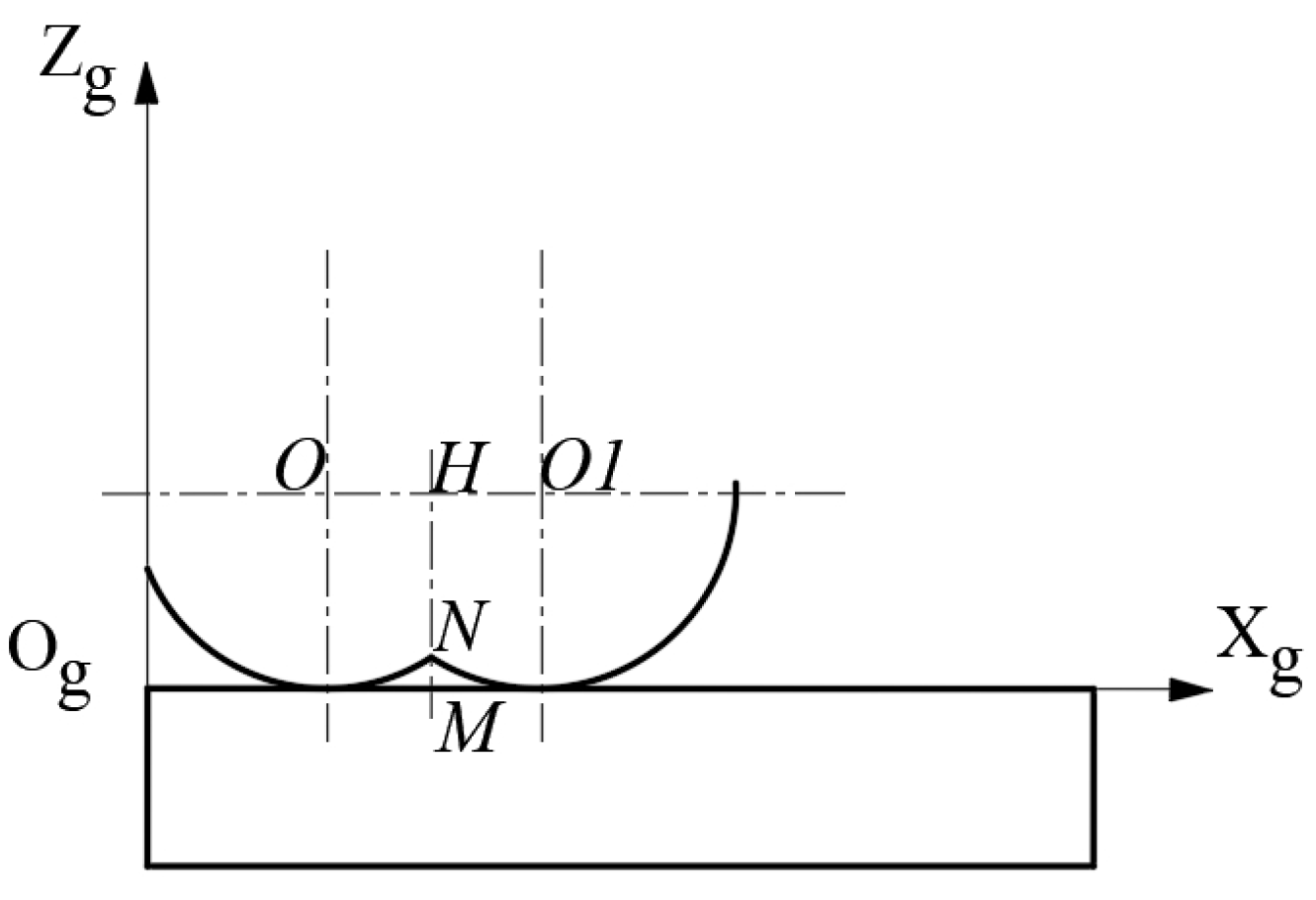
2.2. Calculation Model for Residual Height of Milling Surface Morphology
2.3. Multi Factor Modeling of Ball End Milling Cutter Motion Trajectory
2.3.1. Modeling of the Influence of Tool Vibration on Cutting Edge Motion Trajectory
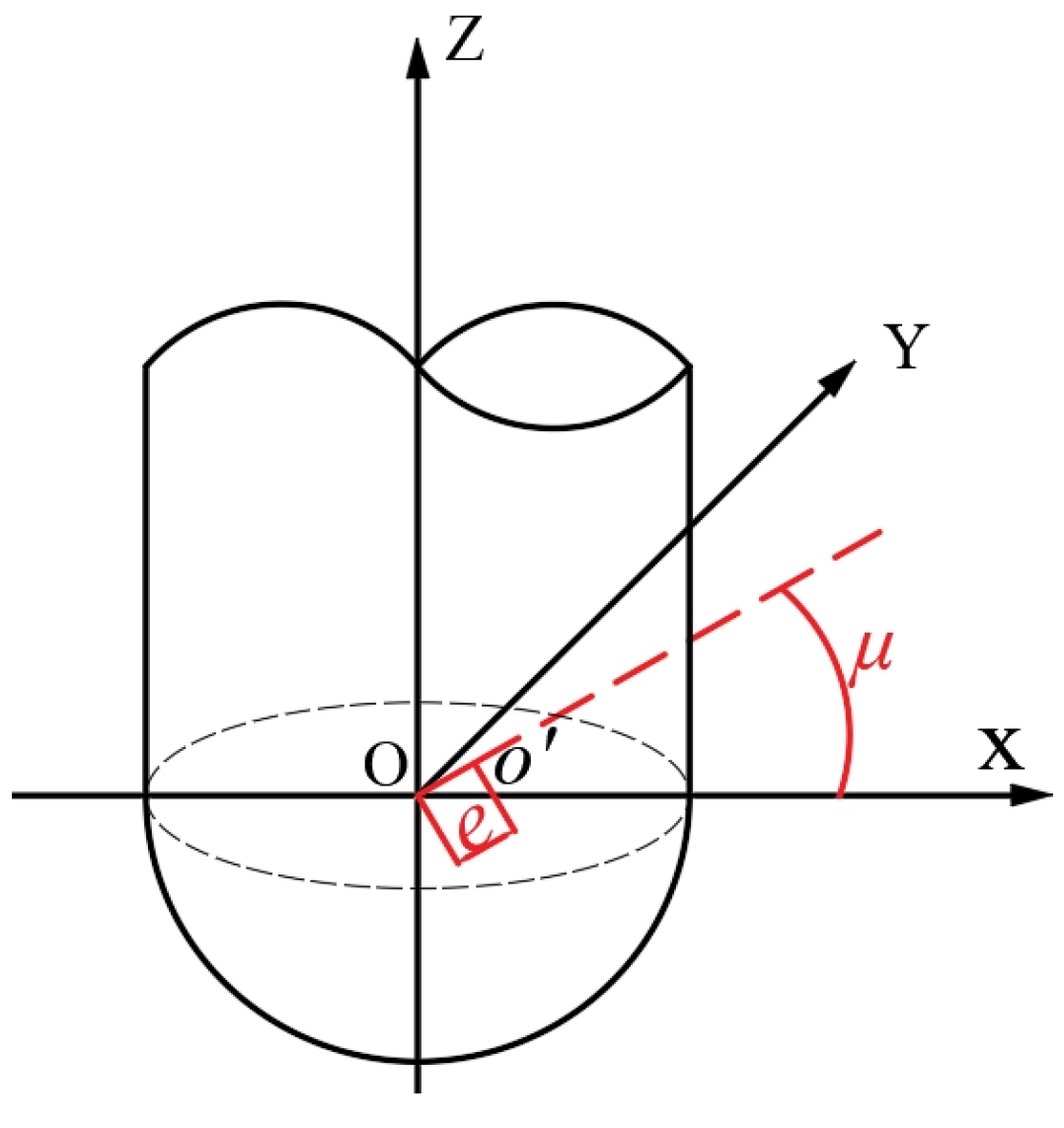
2.3.2. Modeling of the Influence of Tool Eccentricity on Cutting Edge Motion Trajectory
2.3.3. Modeling of the Influence of Tool Deformation on Cutting Edge Motion Trajectory
2.4. Modeling Method for Surface Morphology
2.5. Materials and Experiments
3. Simulation Analysis of the Influence of Processing Parameters on Milling Surface Morphology
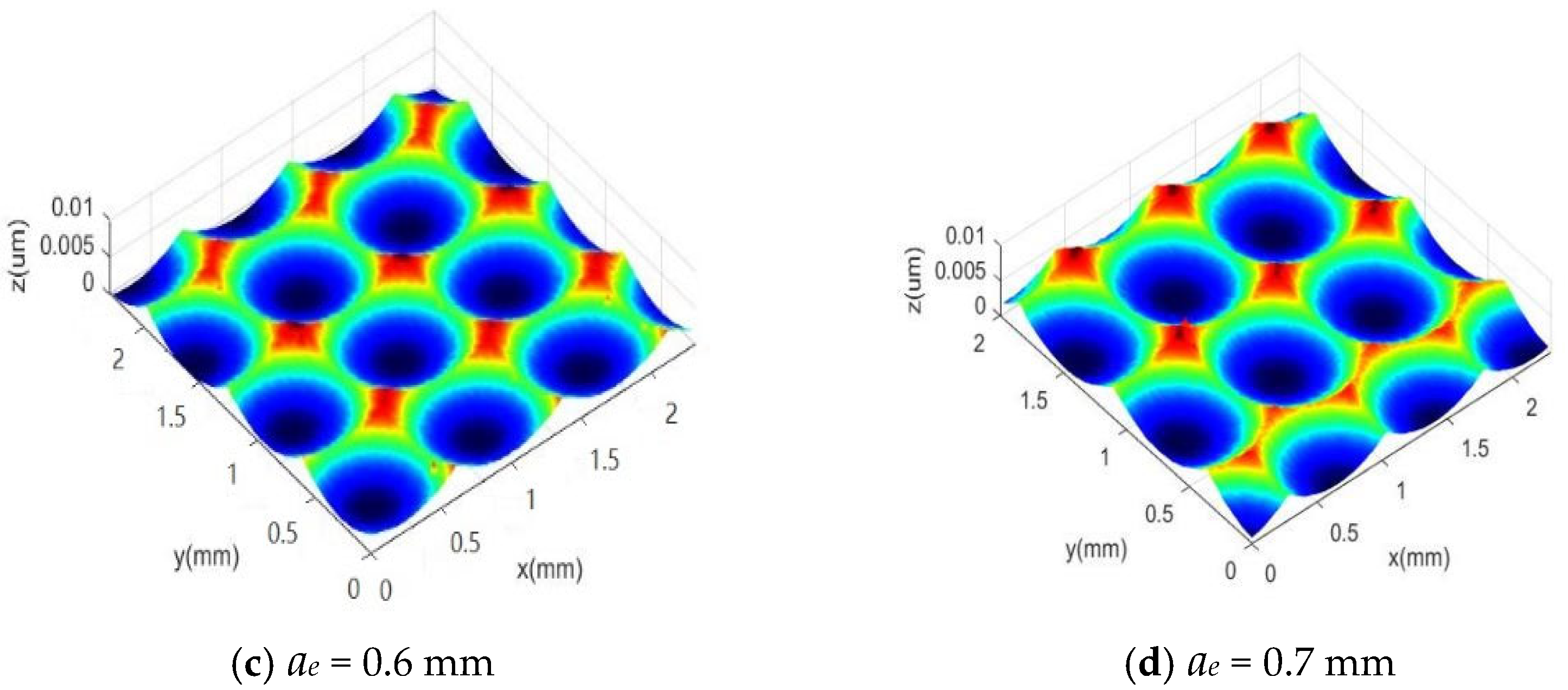
3.1. Simulation Study on the Influence of Line Spacing on Surface Morphology
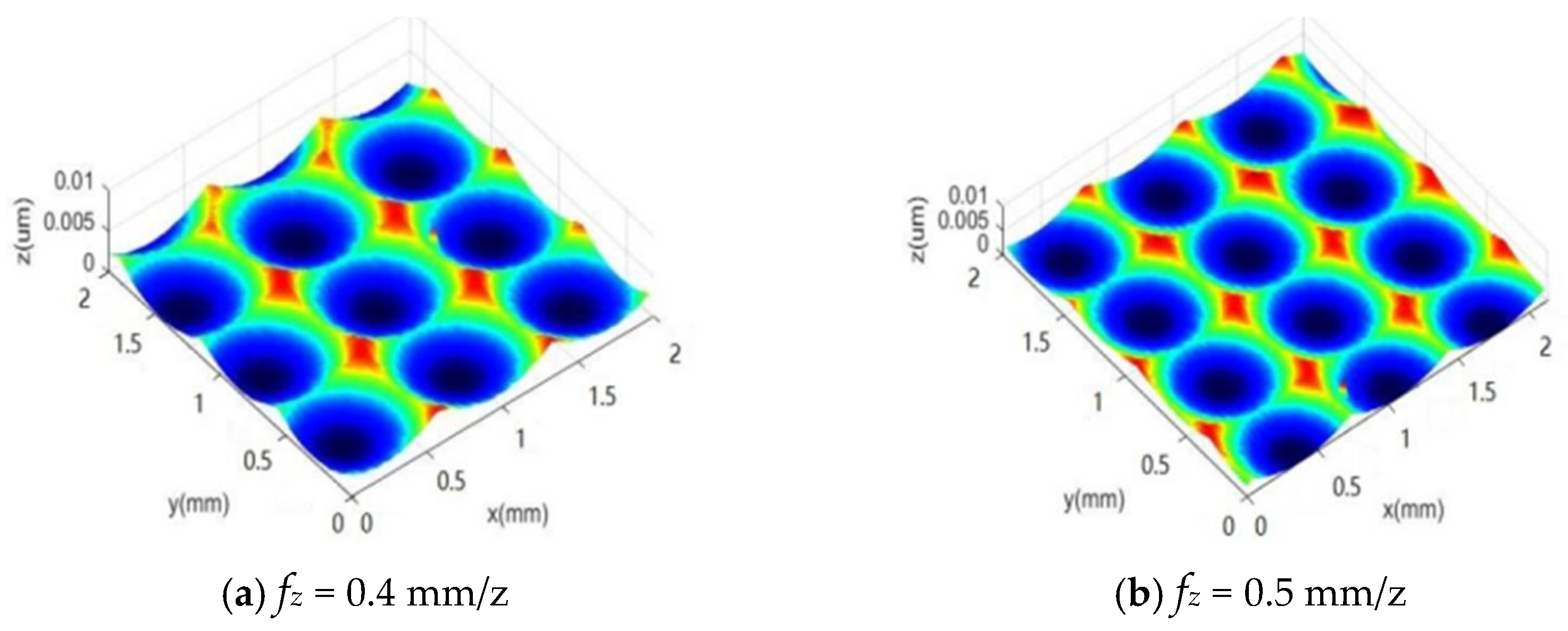
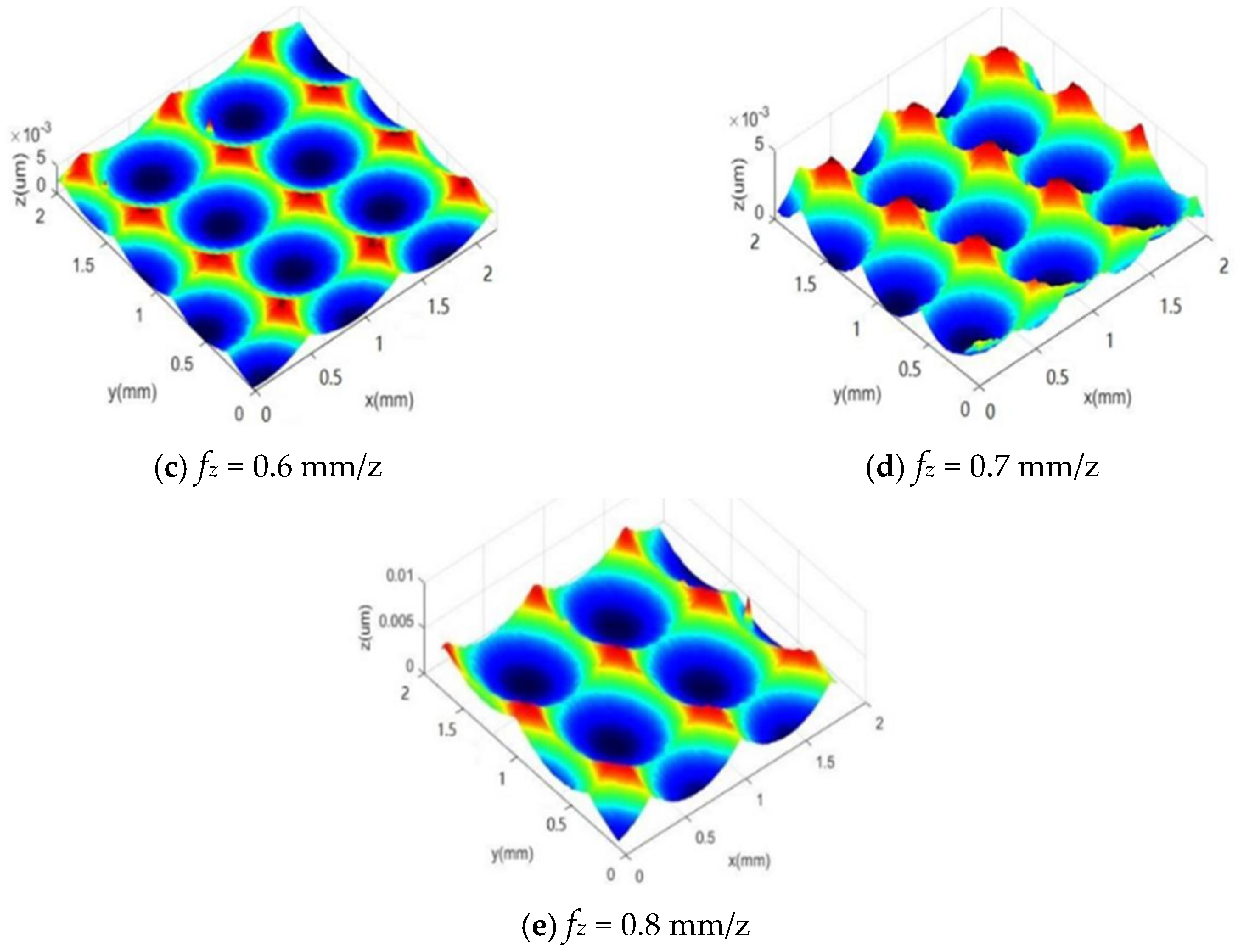
3.2. Simulation Study on the Influence of Feed per Tooth on Surface Morphology
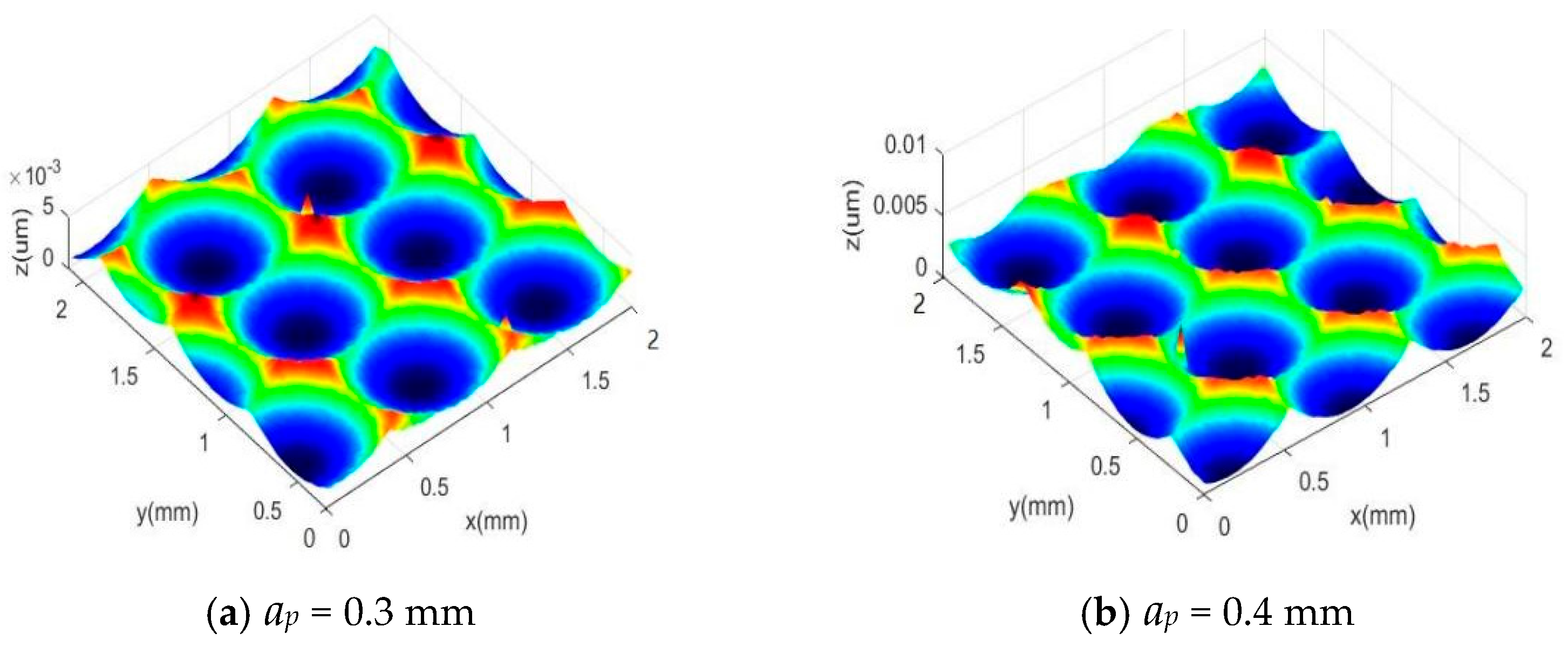
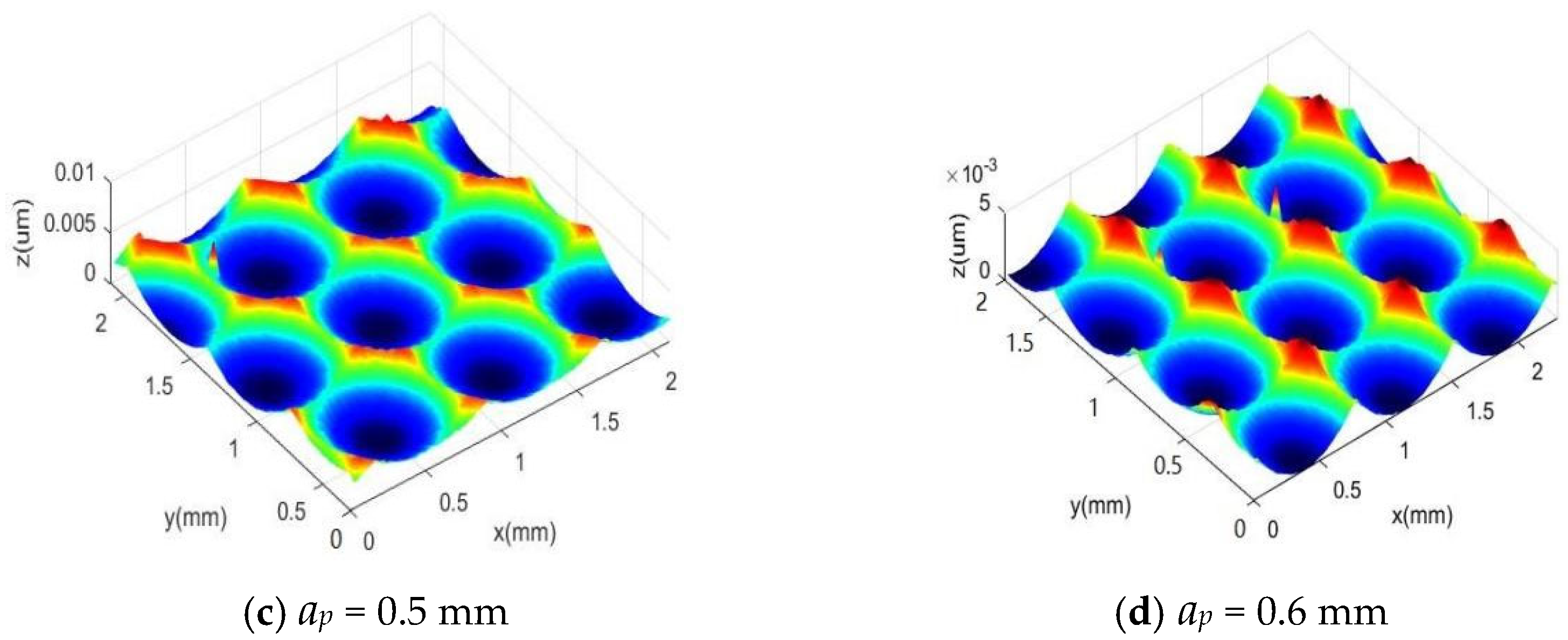
3.3. Simulation Study on the Influence of Cutting Depth on Surface Morphology
3.4. Simulation Study on the Influence of Phase Difference on Surface Morphology
4. Experimental Study on Surface Morphology of High-Speed Ball Head Milling Processing
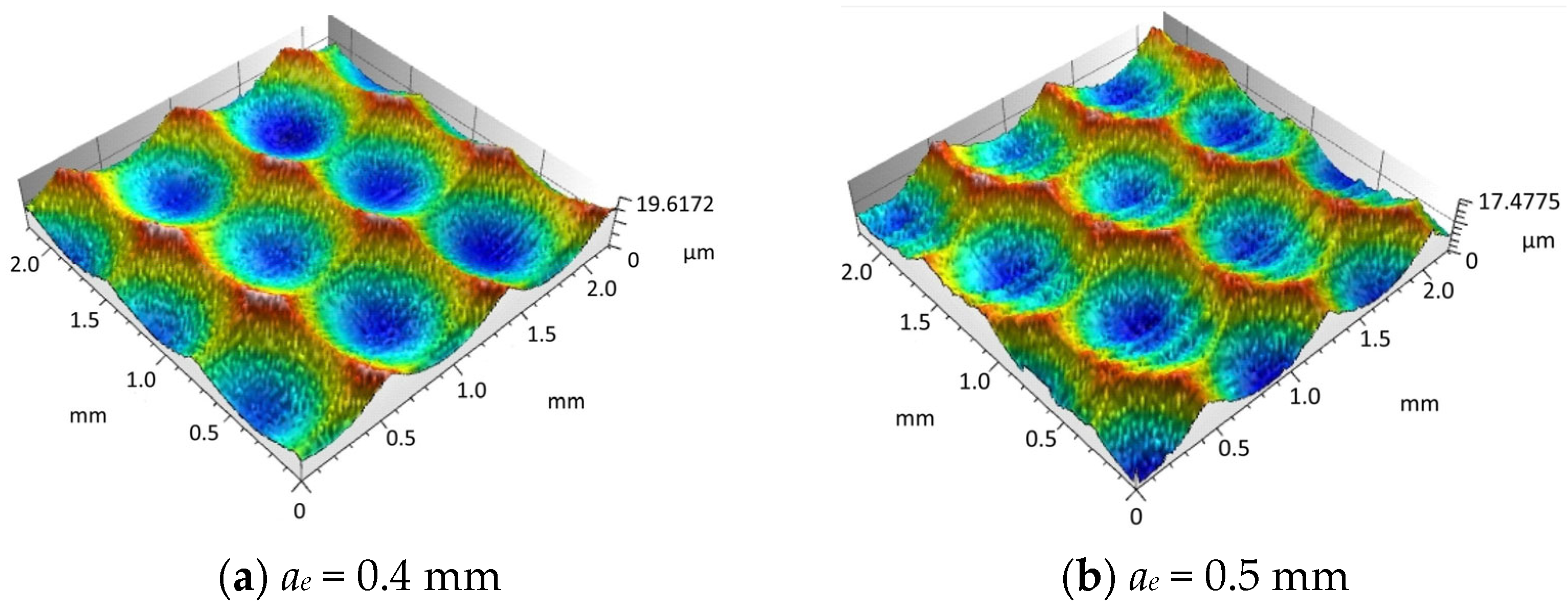
4.1. Experimental Study on the Influence of Line Spacing on Surface Morphology
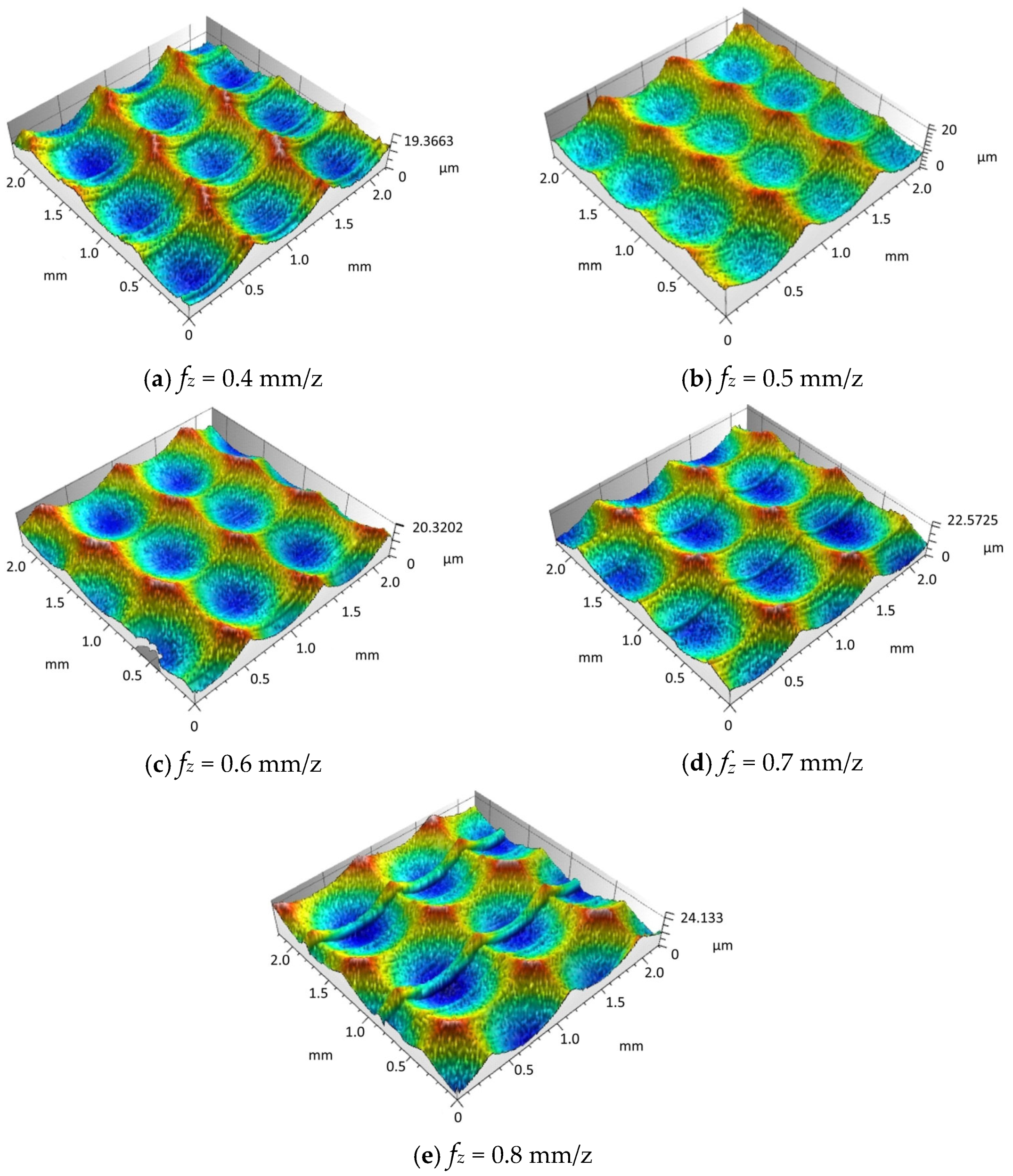
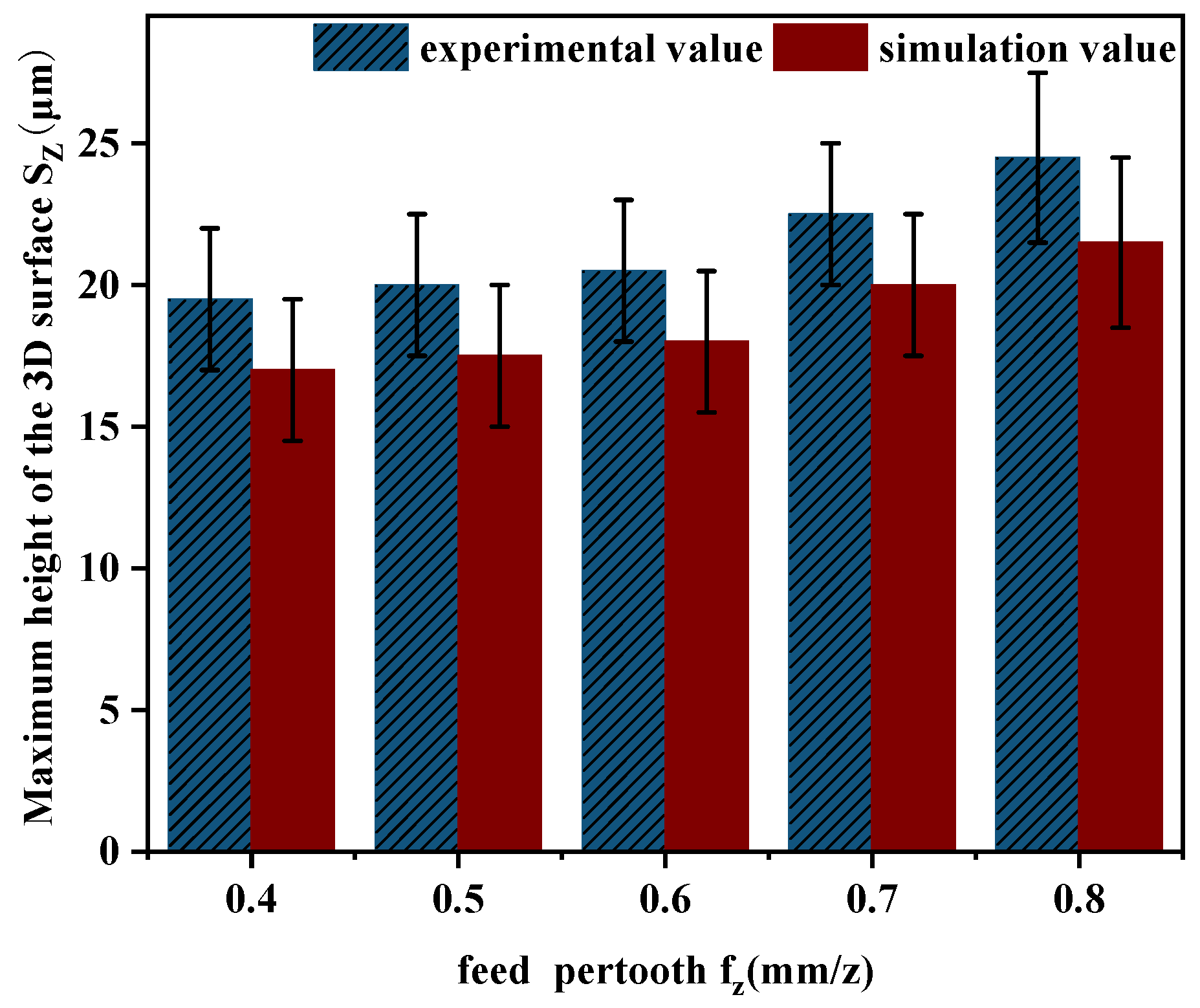
4.2. Effect of Feed per Tooth on Surface Morphology
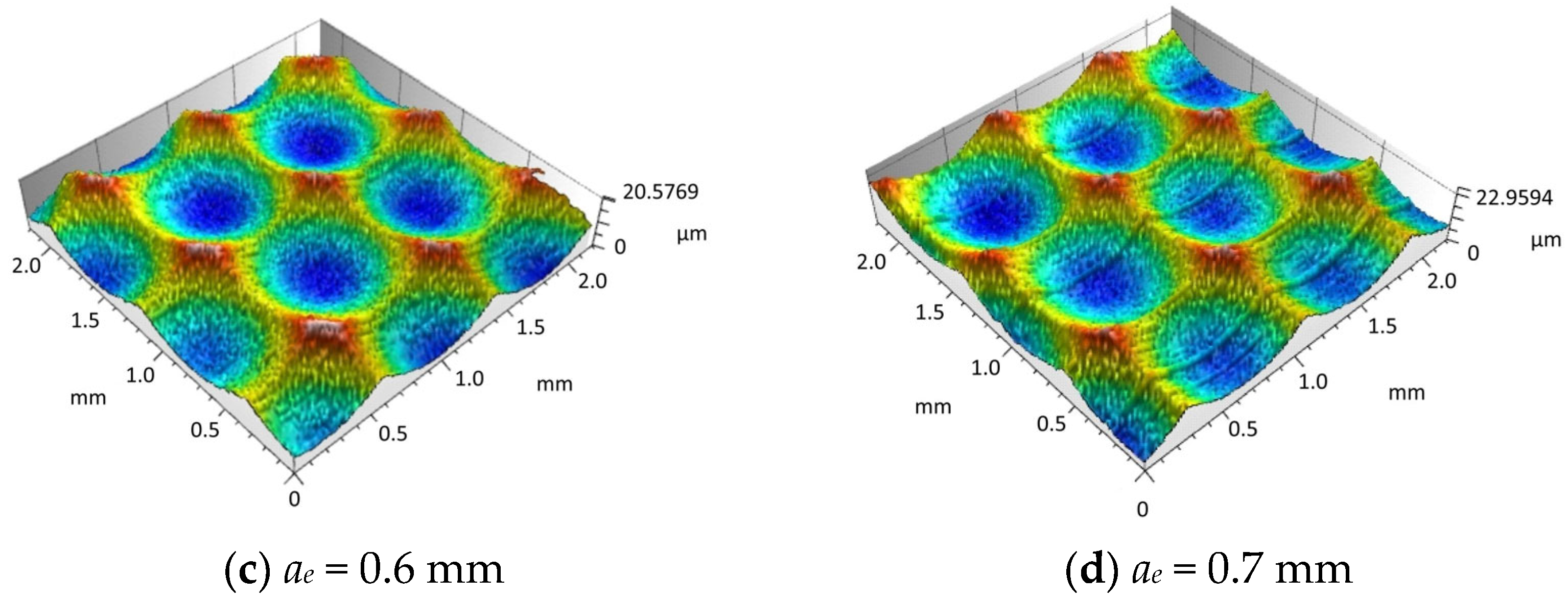
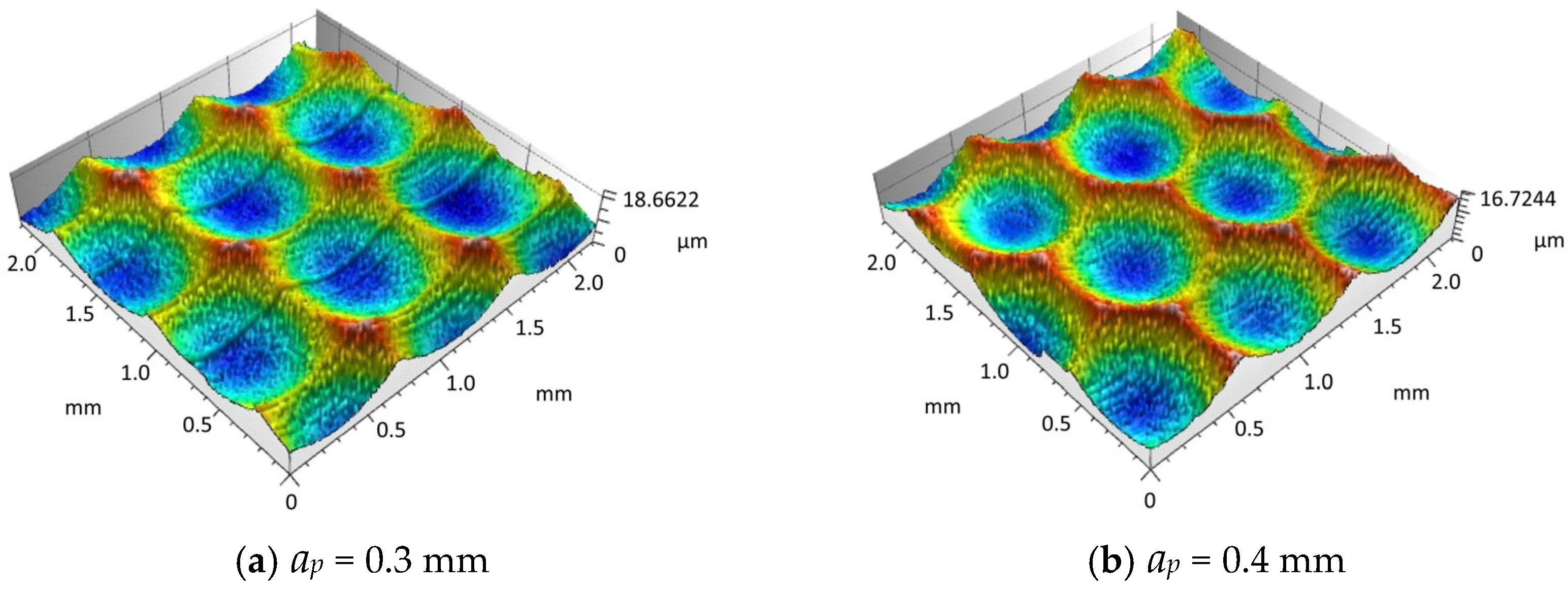
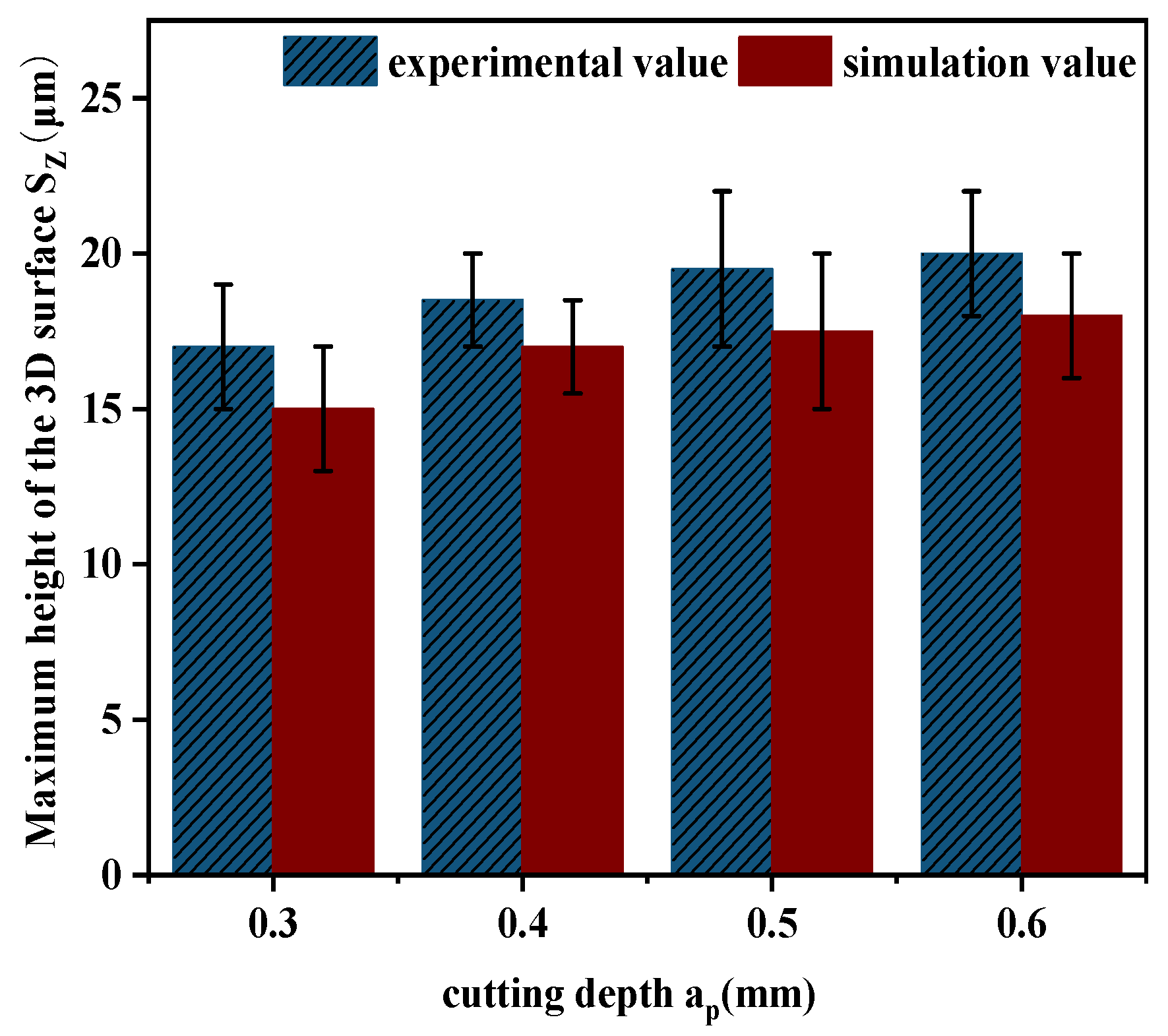
4.3. The Influence of Cutting Depth on Surface Morphology
4.4. The Influence of Phase Angle on Surface Morphology
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ae | line spacing (radial distance between adjacent cutter paths) |
| ap | cutting depth (axial depth of material removal) |
| fz | feed per tooth (distance advanced per cutter tooth) |
| phase difference (Δφ) | phase difference between adjacent cutter teeth (in degrees) |
| residual height | uncut material height between adjacent scallop tracks |
References
- Du, K.; Li, J.; Pei, Y. Research on hard turning machinability of quenched ultra-high strength steel 45CrNiMoVA. J. Ordnance Eng. 2023, 44, 773–782. [Google Scholar]
- Qin, J.; Xu, X.; Liu, P. Experimental study on surface roughness and residual stress of quenched H13 steel by high-speed milling. Light Ind. Mach. 2019, 37, 46–51. [Google Scholar]
- Guillemot, N.; Lartigue, C.; Billardon, R.; Mawussi, B.K. Prediction of the endurance limit taking account of the microgeometry after finishing milling. Int. J. Interact. Des. Manuf. 2010, 4, 239–249. [Google Scholar] [CrossRef]
- Quinsat, Y.; Lavernhe, S.; Lartigue, C. Surface topography in ball end milling process: Description of a 3D surface roughness parameter. Mater. Process Technol. 2008, 195, 135–143. [Google Scholar] [CrossRef]
- Quinsat, Y.; Lavernhe, S.; Lartigue, C. Characterization of 3D surface topography in 5-axis milling. Wear 2011, 27, 590–595. [Google Scholar] [CrossRef]
- Zhuo, Y.; Han, Z.; An, D.; Jin, H. Surface topography prediction in peripheral milling of thin-walled parts considering cutting vibration and material removal effect. Int. J. Mech. Sci. 2021, 211, 106797. [Google Scholar] [CrossRef]
- Urbikain, G.; Trejo, D.O.; Luo, M.; Lacalle, L.; Elías-Zuiga, A. Surface roughness prediction with new barrel-shape mills considering runout: Modelling and validation. Measurement 2021, 173, 108670. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Vivancos-Calvet, J.; Dominguez-Fernandez, A. Surface topography in ball-end milling processes as a function of feed per tooth and radial depth of cut. Int. J. Mach. Tools Manuf. 2012, 53, 151–159. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Li, Z. The influence of milling process parameters on the surface roughness characteristics of tin bismuth alloy and experimental analysis. Equip. Environ. Eng. 2019, 16, 43–47. [Google Scholar]
- Wang, L.; Ge, S.; Si, H.; Yuan, X.; Duan, F. Roughness control method for five-axis flank milling based on the analysis of surface topography. Int. Mech. Sci. 2020, 169, 105337. [Google Scholar] [CrossRef]
- Zhang, W.; Hua, B.; Zhang, L.; Si, B. Modeling and simulation of surface topography in secondary milling with ellipsoid end milling cutter. Int. J. Interact. Des. Manuf. 2024, 18, 5043–5056. [Google Scholar] [CrossRef]
- Wei, J.; Hou, X.; Sun, C. Modeling and simulation of surface topography in five-axis ball end milling. J. Phys. Conf. Ser. 2021, 1820, 012049. [Google Scholar] [CrossRef]
- Sylvain, S.; Quinsat, Y.; Lartigue, C. Model for the prediction of 3D surface topography in 5-axis milling. Int. J. Adv. Manuf. Technol. 2010, 51, 915–924. [Google Scholar]
- Gao, H.; Yue, C.; Liu, X.; Nan, Y. Simulation of surface topography considering cut-in impact and tool flank wear. Appl. Sci. 2019, 9, 732. [Google Scholar] [CrossRef]
- Lei, Z.; Zheng, M.; Zhang, W.; Li, K. Influence and prediction of tool wear on workpiece surface roughness based on milling topography analysis. Adv. Manuf. Technol. 2022, 122, 1883–1896. [Google Scholar]
- Liu, H.; Dong, Y.; Li, Y.; Li, P.; Yang, Z.; Landers, R.G. Geometrical simulation and analysis of ball-end milling surface topography. Int. J. Adv. Manuf. Technol. 2019, 102, 1885–1900. [Google Scholar]
- Layegh, S.E.; Lazoglu, I. 3D surface topography analysis in 5-axis ball-end milling. CIRP Annals 2017, 66, 133–136. [Google Scholar] [CrossRef]
- Felhő, C.; Karpuschewski, B.; Kundrák, J. Surface roughness modelling in face milling. Procedia Cirp 2015, 31, 136–141. [Google Scholar] [CrossRef]
- Yu, Y.; Lin, C.; Hu, Y. Study on simulation and experiment of non-circular gear surface topography in ball end milling. Adv. Manuf. Technol. 2021, 114, 1913–1923. [Google Scholar] [CrossRef]
- Jin, X.; Yu, F.; Wang, X.; Li, Y.; Zhu, Q. Surface topography model of ultra-high strength steel AF1410 based on dynamic characteristics of milling system. Processes 2023, 11, 641. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Wang, Y.; Zhang, W. Surface forming mechanism and process in laser milling of 7075 aluminum alloy with inclination. In Proceedings of the 24th National Laser Conference & Fifteenth National Conference on Laser Technology and Optoelectronics, Shanghai, China, 17–20 October 2020. [Google Scholar]
- Lu, X.; Sun, X.; Hou, P.; Xue, L.; Liang, S.Y. Surface topography simulation and roughness prediction of micro-milling single crystal copper. Int. J. Nanomanuf. 2021, 17, 139–153. [Google Scholar] [CrossRef]
- Meng, S. Simulation and Experimental Study on High-Speed Milling Morphology of Cr12MoV Die Steel. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2020. [Google Scholar]
- Sun, M.; Wang, L. Research on the dynamic model of ball end milling cutter and its milling stability. Mach. Tools Hydraul. 2012, 40, 52–54. [Google Scholar]
- Yang, D.; Liu, Z. Surface plastic deformation and surface topography prediction in peripheral milling with variable pitch end mill. Int. J. Mach. Tools Manuf. 2015, 91, 43–53. [Google Scholar] [CrossRef]
- Mei, W. Research on Dynamic Modeling and Simulation System Design of High-Speed Milling Process. Master’s Thesis, North China University, Beijing, China, 2011. [Google Scholar]
- Cui, Y.; Zheng, M.; Zhang, W.; Wang, B.; Sun, Y.; Wang, W. Study on Fatigue Characteristics of Bionic Functional Surface of Hardened Steel. Materials 2020, 13, 4130. [Google Scholar] [CrossRef]










| Element | C | Cr | Mo | V | Mn |
|---|---|---|---|---|---|
| content | 1.45–1.70 | 11.00–12.50 | 0.4–0.6 | 0.15~0.30 | ≤0.40 |
| element | Si | Ni | Cu | S | P |
| content | ≤0.40 | ≤0.25 | ≤0.30 | ≤0.030 | ≤0.030 |
| Serial Number | Line Spacing ae (mm) | Feed per Tooth fz (mm/z) | Cutting Depth ap (mm) | Spindle Speed n (r/min) |
|---|---|---|---|---|
| a | 0.4 | 0.4 | 0.3 | 10,000 |
| b | 0.5 | 0.5 | 0.4 | |
| c | 0.6 | 0.6 | 0.5 | |
| d | 0.7 | 0.7 | 0.6 | |
| e | - | 0.8 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Li, X.; Zheng, M.; Mu, H.; Liu, C.; Wang, D.; Yan, B.; Li, Q.; Jiang, H.; Wang, F.; et al. Simulation Prediction and Experimental Research on Surface Morphology of Ball Head Milling Processing. Materials 2025, 18, 2355. https://doi.org/10.3390/ma18102355
Cui Y, Li X, Zheng M, Mu H, Liu C, Wang D, Yan B, Li Q, Jiang H, Wang F, et al. Simulation Prediction and Experimental Research on Surface Morphology of Ball Head Milling Processing. Materials. 2025; 18(10):2355. https://doi.org/10.3390/ma18102355
Chicago/Turabian StyleCui, Youzheng, Xinmiao Li, Minli Zheng, Haijing Mu, Chengxin Liu, Dongyang Wang, Bingyang Yan, Qingwei Li, Hui Jiang, Fengjuan Wang, and et al. 2025. "Simulation Prediction and Experimental Research on Surface Morphology of Ball Head Milling Processing" Materials 18, no. 10: 2355. https://doi.org/10.3390/ma18102355
APA StyleCui, Y., Li, X., Zheng, M., Mu, H., Liu, C., Wang, D., Yan, B., Li, Q., Jiang, H., Wang, F., & Hu, Q. (2025). Simulation Prediction and Experimental Research on Surface Morphology of Ball Head Milling Processing. Materials, 18(10), 2355. https://doi.org/10.3390/ma18102355







