Simulation of the Thermodynamic Properties and Hydrophobicity of Polydimethylsiloxane Modified by Grafting Nano-SiO2 with Different Silane Coupling Agents
Abstract
1. Introduction
2. Modeling and Simulations
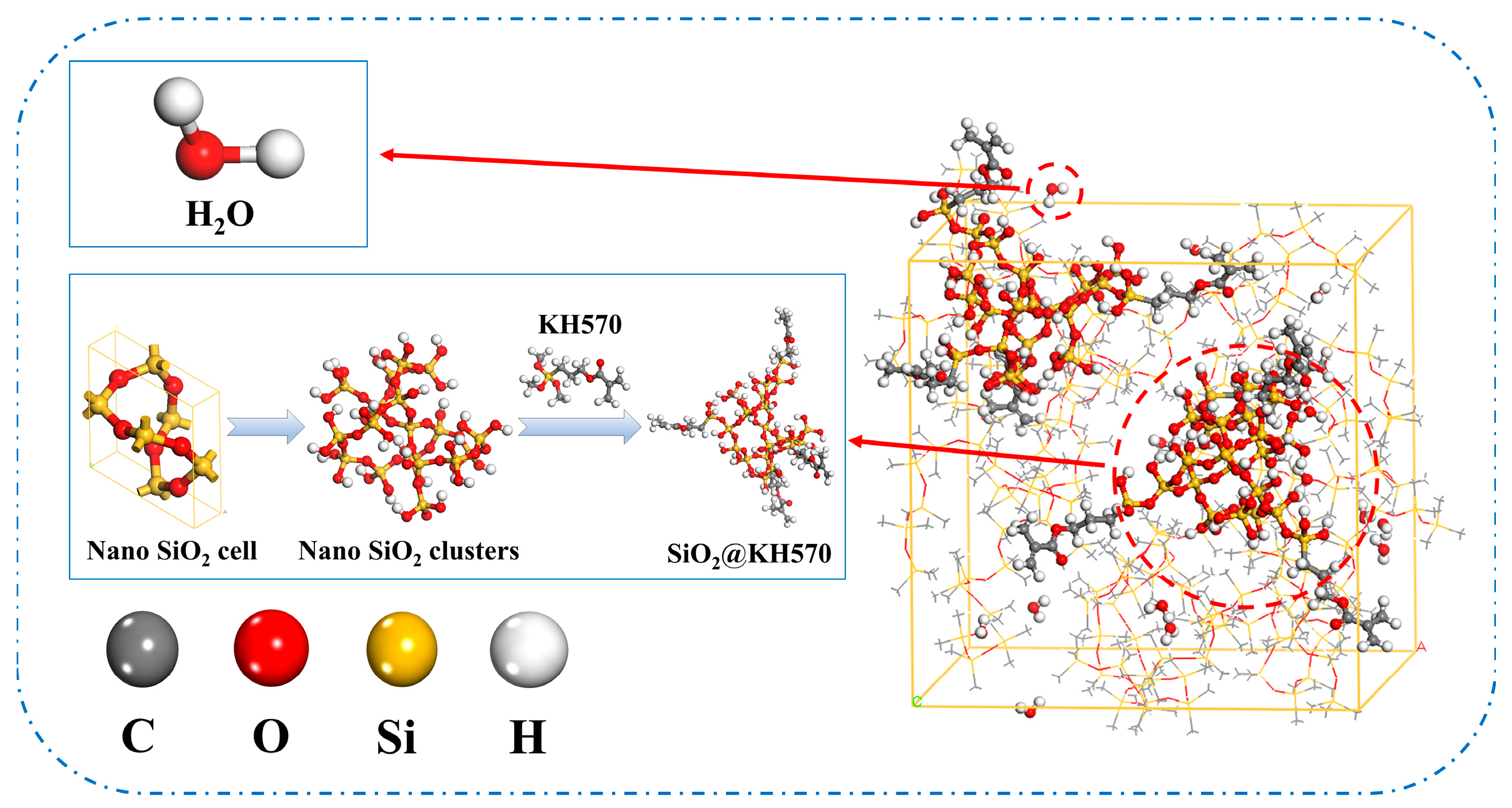
2.1. Molecular Model Establishment
- SiO2 nanoparticles with a 5 Å diameter were constructed and subjected to surface hydrogen termination. Subsequently, each nanoparticle was functionalized with four silane coupling agent molecules, achieving a grafting density of 12.5%. The modified nanostructures then underwent geometry optimization using the COMPASS force field.
- PDMS is a widely used hydrophobic material. Published reports indicate that in molecular simulations of polymeric systems, excessive polymer quantities or extended chain lengths can significantly prolong relaxation times. A degree of polymerization between 10 and 20 has been demonstrated to enable accurate simulations of composite material properties [22]. Consequently, this study adopts a polymerization degree of 10. Single-chain PDMS with this polymerization degree was subjected to geometry optimization using the COMPASS force field.
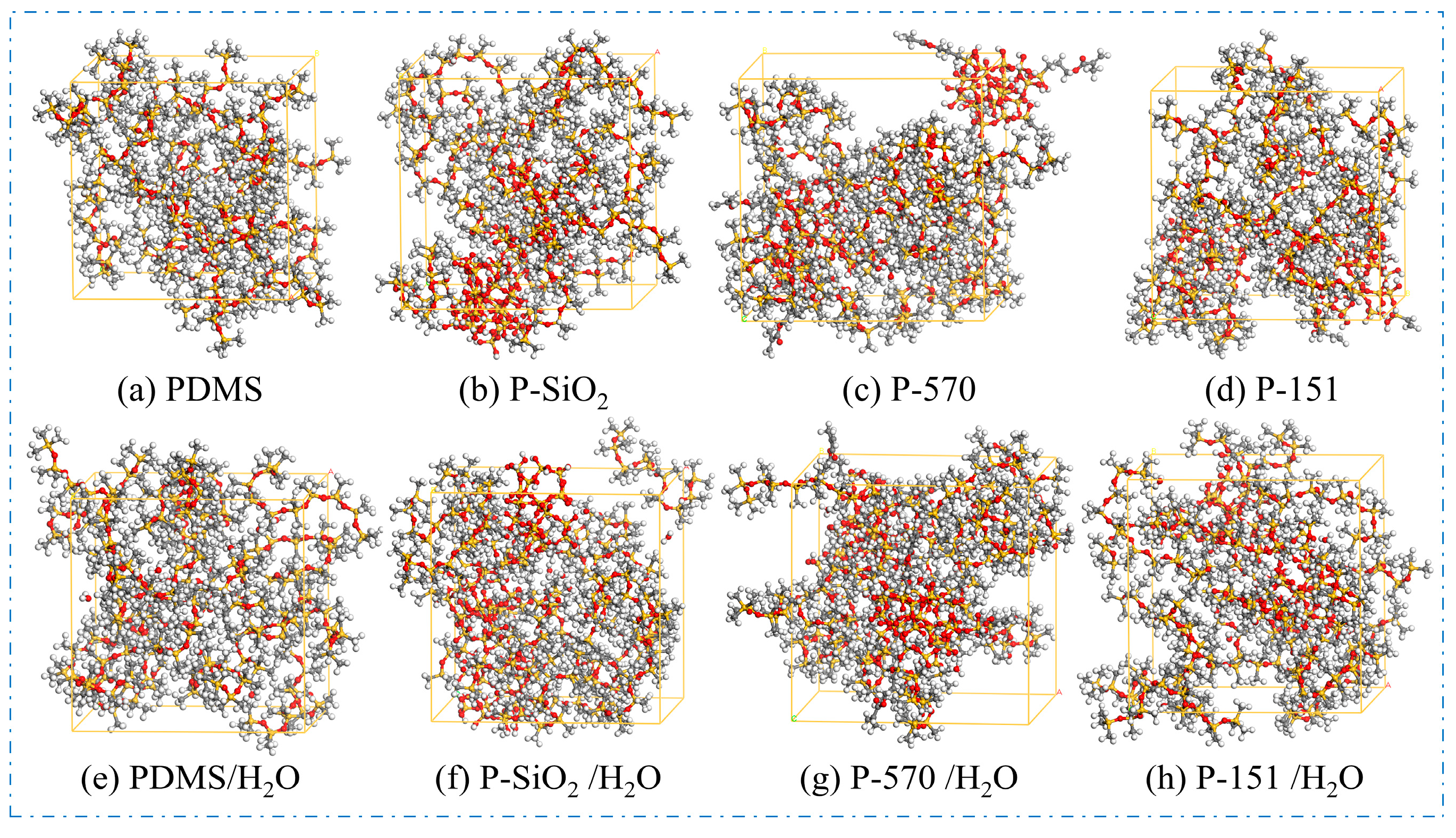
- Composite crystal cell models were constructed using the Amorphous Cell module. Eighteen PDMS molecular chains were combined with SiO2, SiO2@KH570, and SiO2@KH151 nanoparticles in the composite cell model with a controlled nanoparticle mass fraction of 30%, and the density was set to be 0.97 g/cm3. As shown in Figure 2, four anhydrous models and four water-containing models were constructed.
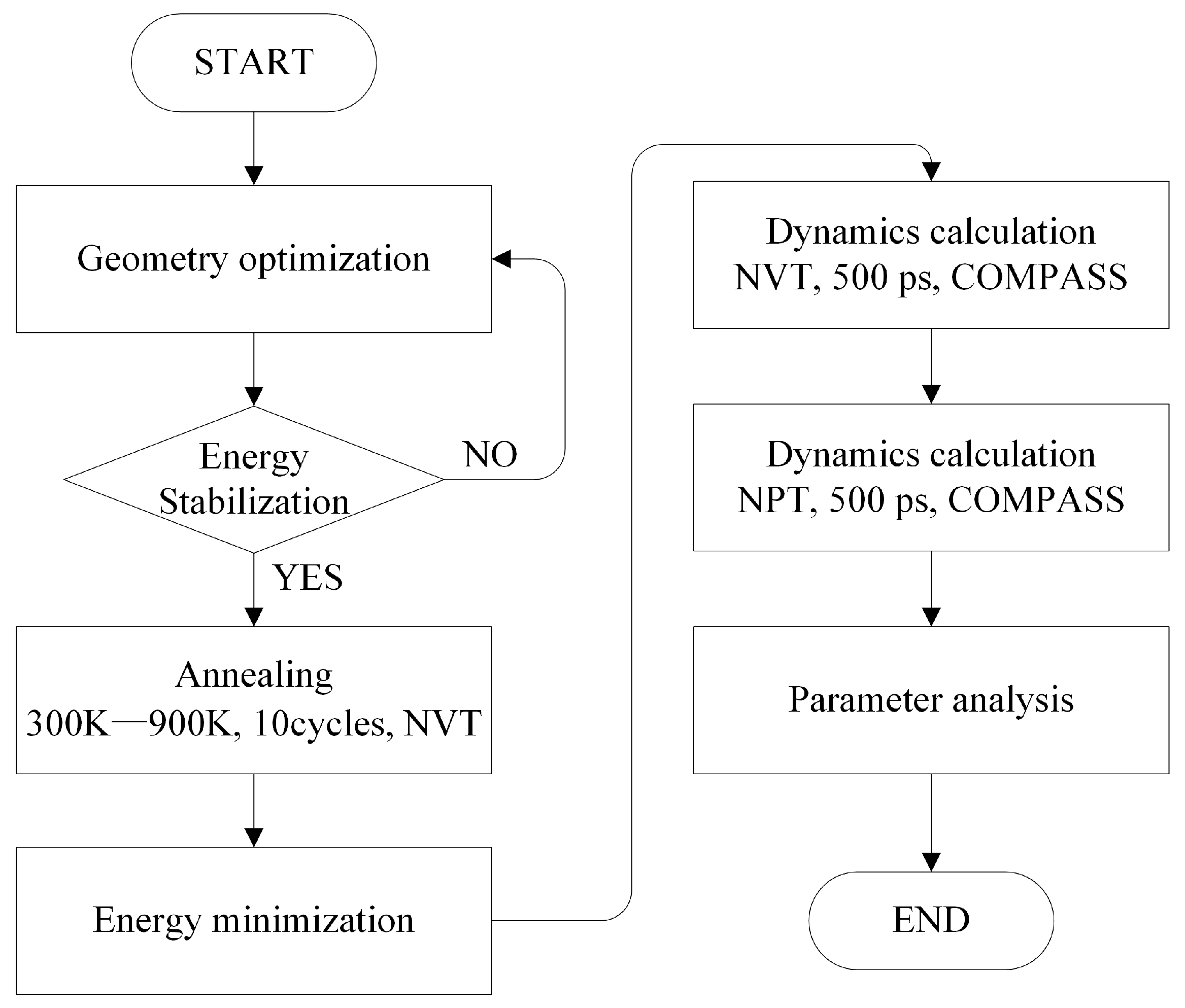
2.2. Simulation Details
3. Analysis of Thermodynamic Properties
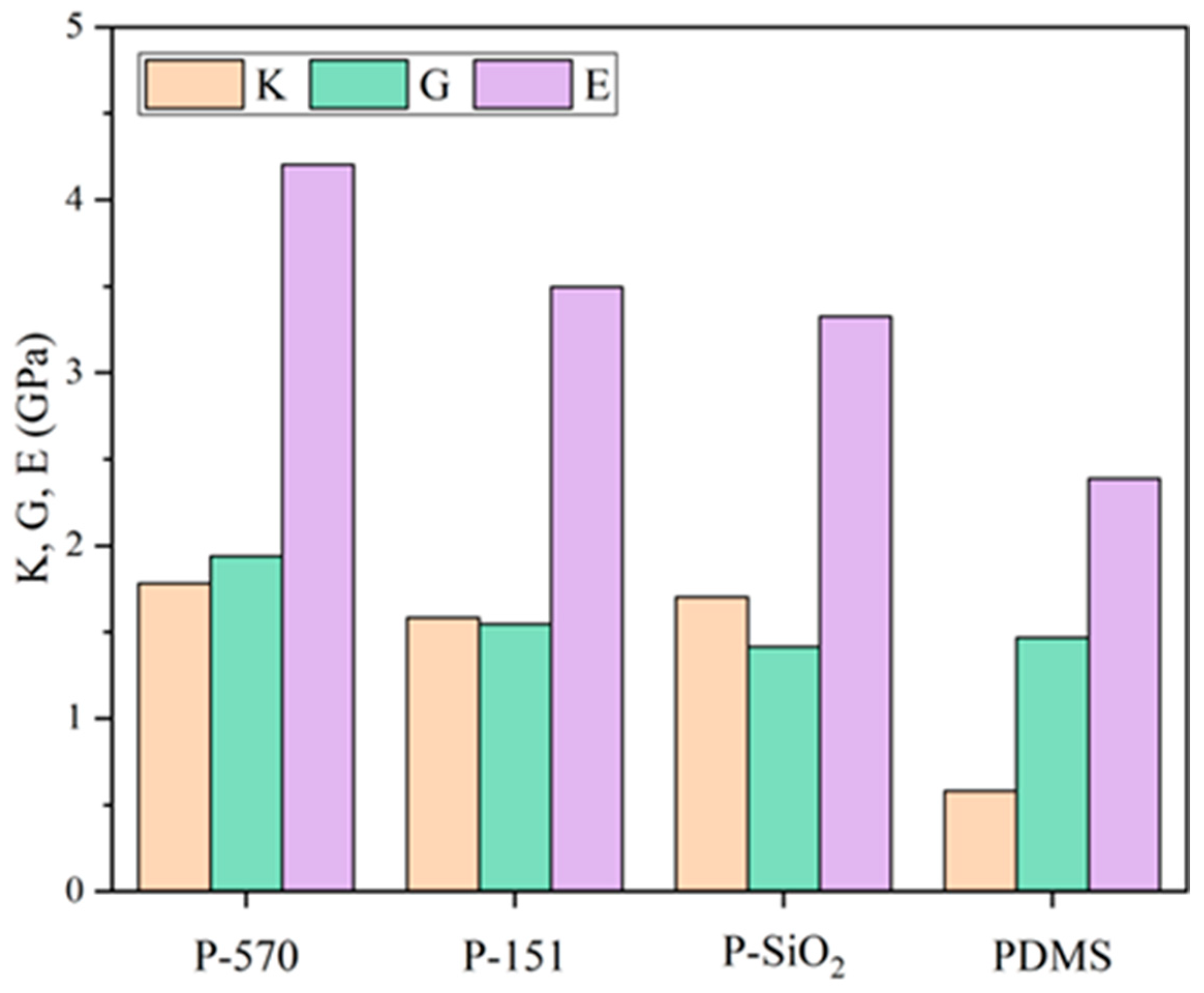
3.1. Mechanical Properties
3.2. Fractional Free Volume
3.3. Cohesive Energy Density
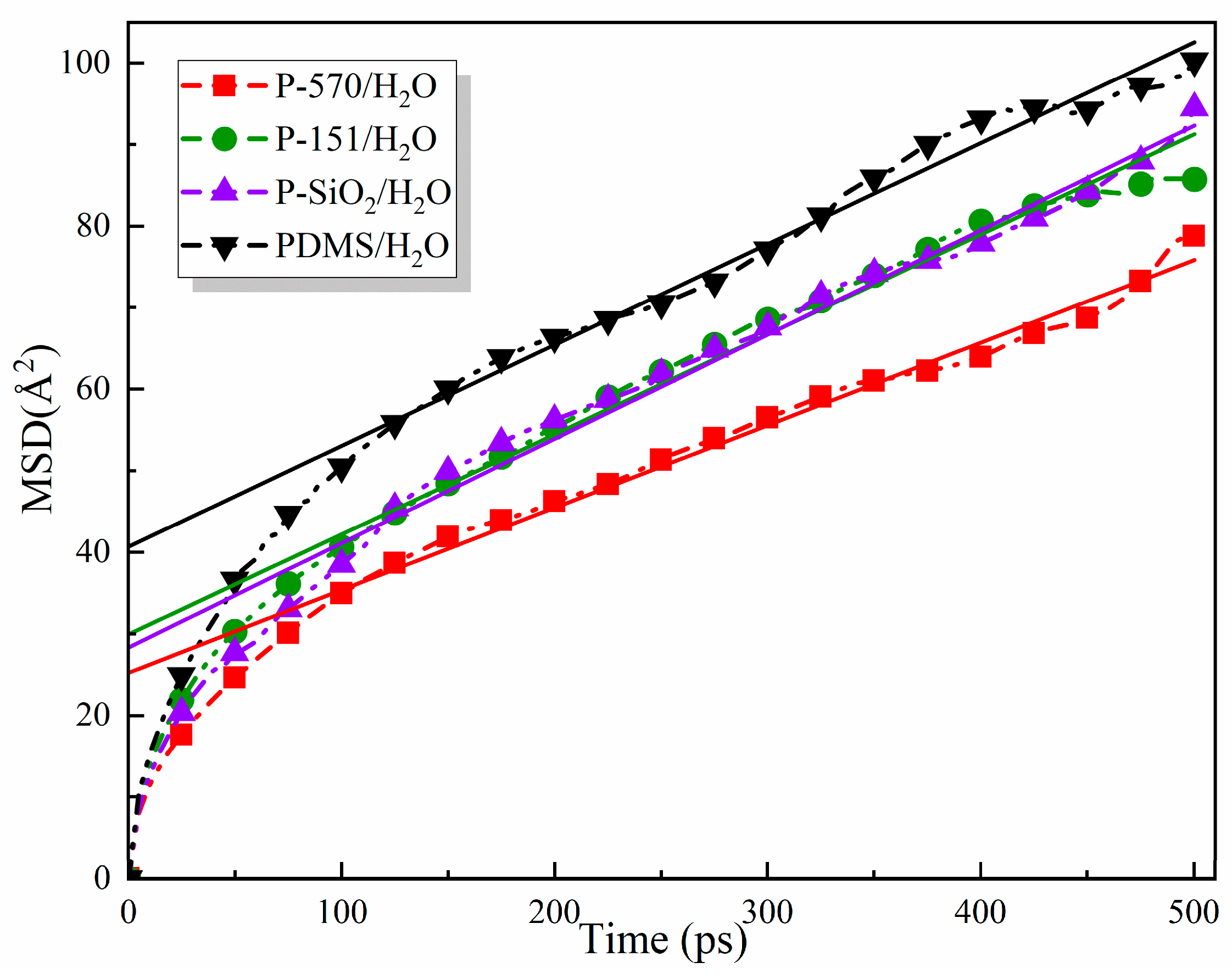
3.4. Mean Square Displacement
4. Hydrophobicity Analysis
4.1. Diffusion Coefficient
4.2. Interaction Energy
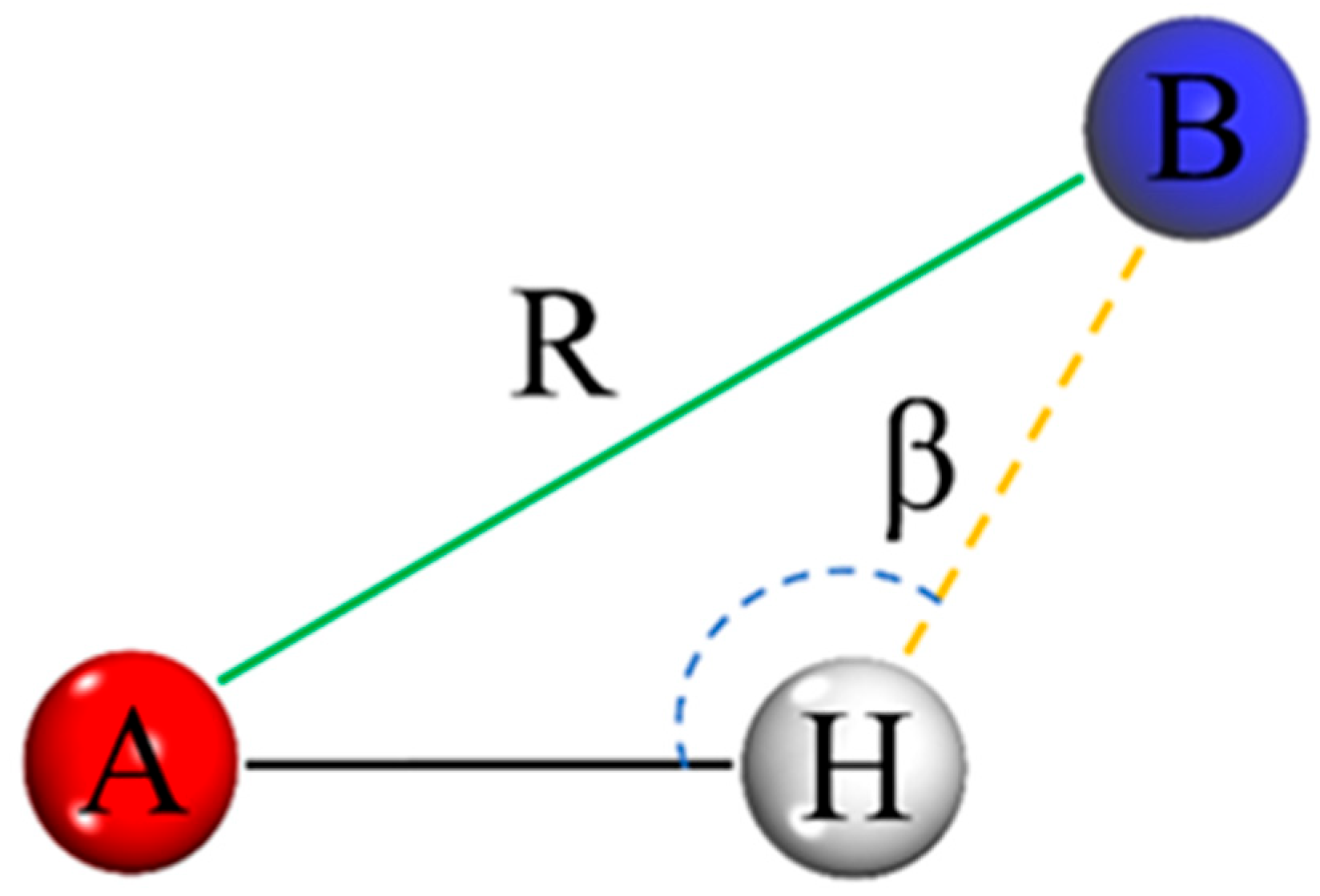
4.3. Hydrogen Bonding
4.4. Performance Comparison
5. Conclusions
- The grafting of silane coupling agents onto SiO2 nanoparticle surfaces effectively enhances interfacial bond strength, reduces FFV, inhibits chain movement, and mitigates agglomeration, promoting uniform stress distribution and significantly enhancing the composites’ thermomechanical properties. The parameters are manifested in the enhancement of mechanical modulus and cohesive energy density, as well as the decrease in FFV and MSD values.
- Silane coupling agent grafting on nano-SiO2 effectively reduces hydrogen bonds between the PDMS matrix material and water molecules, forming a uniform micro-nanostructure, lowering the diffusion coefficient, and decreasing interaction energy, thereby enhancing composite hydrophobicity.
- Grafting different silane coupling agents variably influenced the composites’ thermodynamic and hydrophobic properties. KH570 showed the best enhancement effect on the thermomechanical and hydrophobic properties of the composites, with its system exhibiting 4.5%, 37.0%, 26.5%, and 31.0% increases in elastic, shear, and bulk moduli and CED compared to the pure SiO2 composite model at 343 K simulation. Meanwhile, the FFV, MSD, diffusion coefficient, interaction energy, and hydrogen bonds decreased by 9.1%, 16.6%, 24.7%, 61.8%, and 35.3%, respectively. The reason is that the flexible long chain of KH570 not only occupies more free volume but also can become physically entangled with the PDMS molecular chain, which restricts the molecular chain movement. In addition, the flexible long chains can form a larger steric hindrance layer, which inhibits the formation of hydrogen bonds and constructs a low-energy surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hao, J.; Dai, X.Z.; Gao, J.; Yang, L.J.; Jian, Z.; Du, Y.Y.; Liao, R.J. Synergistic Enhancement Effect of Moisture and Aging on Frequency Dielectric Response of Oil-Immersed Cellulose Insulation and its Degree of Polymerization Evaluation Using Dielectric Modulus. Cellulose 2021, 28, 1–17. [Google Scholar] [CrossRef]
- Yuan, F.T.; Yan, Z.W.; Zhang, R.J.; Yang, Y.; Jian, S.K.; Tang, B. Research on Vibration Characteristic Analysis and Fault Diagnosis Method of Oil-Immersed Transformer Based on Multi-Physics Coupling. IEEJ Trans. Electr. Electron. Eng. 2024, 19, 1621–1630. [Google Scholar] [CrossRef]
- Contreras, J.E.; Rodriguez, J.; Gaytan, C.; Greaves, B.; Prevost, T. Thermal Aging Performance of Cellulose Insulation in Natural Ester Liquid. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1357–1362. [Google Scholar] [CrossRef]
- Zhao, X.; Li, L.X.; Li, B.C.; Zhang, J.P.; Wang, A.Q. Durable Superhydrophobic/Superoleophilic PDMS Sponges and their Applications in Selective Oil Absorption and in Plugging Oil Leakages. J. Mater. Chem. A 2014, 2, 18281–18287. [Google Scholar] [CrossRef]
- Chen, W.H.; Chen, P.C.; Wang, S.C.; Yeh, J.T.; Huang, C.Y.; Chen, K.N. UV-Curable PDMS-Containing PU System for Hydrophobic Textile Surface Treatment. J. Polym. Res. 2009, 16, 601–610. [Google Scholar] [CrossRef]
- Deng, L.C.; Wang, Z.W.; Wu, J.Z.; Gu, X.S.; Yu, H.; Li, Y.; Cao, Y.R.; Luo, F.; Liu, X.H.; Chen, Q. A Superhydrophobic Fe3O4@MSN-PDMS Based Composite Coating with Icephobicity, Long-Term Durability and Self-Healing Property for Anti-/De-Icing. Compos. Sci. Technol. 2025, 259, 110937. [Google Scholar] [CrossRef]
- Wen, N.; Miao, X.R.; Yang, X.J.; Long, M.Y.; Deng, W.S.; Zhou, Q.N.; Deng, W.L. An Alternative Fabrication of Underoil Superhydrophobic or Underwater Superoleophobic Stainless Steel Meshes for Oil-Water Separation: Originating from One-Step Vapor Deposition of Polydimethylsiloxane. Sep. Purif. Technol. 2018, 204, 116–126. [Google Scholar] [CrossRef]
- Stanton, M.M.; Ducker, R.E.; MacDonald, J.C.; Lambert, C.R.; McGimpsey, W.G. Super-Hydrophobic, Highly Adhesive, Polydimethylsiloxane (PDMS) Surfaces. J. Colloid. Interface Sci. 2012, 367, 502–508. [Google Scholar] [CrossRef]
- Xie, D.L.; An, Z.L.; Xiao, H.H.; Zheng, F.H.; Lei, Q.Q.; Zhang, Y.W. Highly Hydrophobic and Partially Conductive Polydimethylsiloxane Surface Produced by Direct Fluorination and Subsequent Annealing. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2968–2977. [Google Scholar] [CrossRef]
- Akbasak, T.; Kodal, M.; Mert, O.; Özkoç, G. Novel and Eco-Friendly Hydrophobic Treatment of Cotton and Polyester Fabrics Based-On Octavinyl and Aminopropylisobutyl Polyhedral Oligomeric. Polymer 2023, 268, 125723. [Google Scholar] [CrossRef]
- Divandari, M.; Arcifa, A.; Ayer, M.A.; Letondor, C.; Spencer, N.D. Applying an Oleophobic/Hydrophobic Fluorinated Polymer Monolayer Coating from Aqueous Solutions. Langmuir 2021, 37, 4387–4394. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.C.; Yu, W.; Zhang, L.Y.; Yin, J.S.; Wang, J.K.; Xie, H.Q. Thermal Conductivity and Mechanical Properties of Low-Density Silicone Rubber Filled with Al2O3 and Graphene Nanoplatelets. J. Therm. Sci. Eng. Appl. 2018, 10, 011014. [Google Scholar] [CrossRef]
- Chen, D.; Chen, F.; Zhang, H.; Yin, X.; Liu, X.; Zhou, Y. Preparation and Characterization of Novel Addition Cured Polydimethylsiloxane Nanocomposites Using Nano-Silica Sol as Reinforcing Filler. Polym. Int. 2015, 64, 1741–1746. [Google Scholar] [CrossRef]
- Senses, E.; Akcora, P. An Interface-Driven Stiffening Mechanism in Polymer Nanocomposites. Macromolecules 2013, 46, 1868–1874. [Google Scholar] [CrossRef]
- Kango, S.; Kalia, S.; Celli, A.; Njuguna, J.; Habibi, Y.; Kumar, R. Surface Modification of Inorganic Nanoparticles for Development of Organic–Inorganic Nanocomposites—A Review. Prog. Polym. Sci. 2013, 38, 1232–1261. [Google Scholar] [CrossRef]
- Agrawal, N.; Low, P.S.; Tan, J.; Fong, E.; Lai, Y.K.; Chen, Z. Durable Easy-Cleaning and Antibacterial Cotton Fabrics Using Fluorine-Free Silane Coupling Agents and CuO Nanoparticles. Nano Mater. Sci. 2020, 2, 281–291. [Google Scholar] [CrossRef]
- Tang, J.J.; Yao, W.; Li, W.L.; Xu, J.; Jin, L.; Zhang, J.D.; Xu, Z.X. Study on a Novel Composite Coating Based on PDMS Doped with Modified Graphene Oxide. J. Coat. Technol. Res. 2018, 15, 375–383. [Google Scholar] [CrossRef]
- Chua, T.P.; Mariatti, M.; Azizan, A.; Rashid, A.A. Effects of Surface-Functionalized Multi-Walled Carbon Nanotubes on the Properties of Poly(Dimethyl Siloxane) Nanocomposites. Compos. Sci. Technol. 2010, 70, 671–677. [Google Scholar] [CrossRef]
- Xie, J.; Liu, Z.Q.; Tian, H.N.; Zhou, Z.; Xie, Q.; Lü, F.C.; Cheng, L. Influence of Water Penetration on Glass Fiber-Epoxy Resin Interface Under Electric Field: A DFT and Molecular Dynamics Study. J. Mol. Liq. 2023, 385, 122346. [Google Scholar] [CrossRef]
- Fukui, K.; Sumpter, B.G.; Barnes, M.D.; Noid, D.W. Molecular Dynamics Studies of the Structure and Properties of Polymer Nano-Particles. Comput. Theor. Polym. Sci. 1999, 9, 245–254. [Google Scholar] [CrossRef]
- Peng, X.; Su, Z.M.; Li, C.G.; Tang, C. High Mechanical and Thermal Performance of Insulating Paper Cellulose Modified with Appropriate H-BN Doping Amount: A Molecular Simulation Study. Adv. Eng. Mater. 2023, 25, 2200949. [Google Scholar] [CrossRef]
- Wang, X.B.; Tang, C.; Wang, Q.; Li, X.P.; Hao, J. Selection of Optimal Polymerization Degree and Force Field in the Molecular Dynamics Simulation of Insulating Paper Cellulose. Energies 2017, 10, 1377. [Google Scholar] [CrossRef]
- Berendsen, H.; Postma, J.; Van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular-Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Yadav, A.; Kumar, A.; Sharma, K.; Pandey, A.K. Influence of Various Functional Groups in Graphene on the Mechanical and Interfacial Properties of Epoxy Nanocomposites: A Review on Molecular Modeling and MD Simulations. Int. J. Comput. Mat. Sci. Eng. 2022, 11, 2250001. [Google Scholar] [CrossRef]
- Alian, A.R.; Kundalwal, S.I.; Meguid, S.A. Interfacial and Mechanical Properties of Epoxy Nanocomposites Using Different Multiscale Modeling Schemes. Compos. Struct. 2015, 131, 545–555. [Google Scholar] [CrossRef]
- Alentiev, A.Y.; Yampolskii, Y.P.; Shantarovich, V.P.; Nemser, S.M.; Plate, N.A. High Transport Parameters and Free Volume of Perfluorodioxole Copolymers. J. Membr. Sci. 1997, 126, 123–132. [Google Scholar] [CrossRef]
- Zhao, J.H.; Jiang, J.W.; Jia, Y.; Guo, W.L.; Rabczuk, T. A Theoretical Analysis of Cohesive Energy Between Carbon Nanotubes, Graphene and Substrates. Carbon 2013, 57, 108–119. [Google Scholar] [CrossRef]
- Ozaki, H.; Narita, T.; Koga, T.; Indei, T. Theoretical Analysis of Critical Flowable Physical Gel Cross-Linked by Metal Ions and Polyacrylamide-Derivative Associating Polymers Containing Imidazole Groups. Polymers 2017, 9, 256. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, S.L.; Tian, S.; Wei, X.J.; Peng, T.F. Molecular Simulations of Adsorption and Thermal Energy Storage of Mixed R1234Ze/UIO-66 Nanoparticle Nanofluid. J. Nanomater. 2019, 2019, 5154173. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Qin, J.S.; Peng, X.; Qiu, Q.P.; Tang, C. A New Type of Nano APTES-HBN Modified Palm Oil as Natural Ester Insulating Oil with Upgraded Thermal Aging Characteristics. Renew. Energy 2022, 200, 743–750. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Langan, P.; Chanzy, H. Crystal Structure and Hydrogen-Bonding System in Cellulose 1β From Synchrotron X-Ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. [Google Scholar] [CrossRef] [PubMed]


| Model | Parameter | Temperature | ||
|---|---|---|---|---|
| 323 K | 343 K | 363 K | ||
| PDMS | VF/Å3 | 6499.96 | 6872.70 | 7230.11 |
| VO/Å3 | 17,726.93 | 17,649.50 | 17,606.21 | |
| FFV/% | 26.83 | 28.03 | 29.11 | |
| P-SiO2 | VF/Å3 | 6059.03 | 7634.04 | 8115.44 |
| VO/Å3 | 20,823.32 | 20,494.44 | 20,846.63 | |
| FFV/% | 22.54 | 27.14 | 28.02 | |
| P-570 | VF/Å3 | 6515.75 | 7094.46 | 7985.02 |
| VO/Å3 | 21,695.82 | 21,677.88 | 21,333.76 | |
| FFV/% | 23.10 | 24.66 | 27.24 | |
| P-151 | VF/Å3 | 6200.29 | 7041.56 | 7606.01 |
| VO/Å3 | 19,661.20 | 19,571.17 | 19,497.76 | |
| FFV/% | 23.97 | 26.46 | 28.06 | |
| Model | Diffusion Coefficient (10−8 cm2/s) | ||
|---|---|---|---|
| 303 K | 323 K | 343 K | |
| PDMS/H2O | 134.6 | 168.6 | 198.7 |
| P-SiO2/H2O | 116.6 | 168.2 | 204.0 |
| P-570/H2O | 110.2 | 124.8 | 153.7 |
| P-151/H2O | 111.8 | 136.9 | 177.1 |
| Model | Etotal (kJ·mol−1) | EH2O (kJ·mol−1) | Emixture (kJ·mol−1) | E (kJ·mol−1) |
|---|---|---|---|---|
| P-SiO2/H2O | −21,470.26 | −33.13 | −21,336.56 | −100.57 |
| P-570/H2O | −19,564.68 | −44.51 | −19,481.79 | −38.38 |
| P-151/H2O | −18,948.10 | −47.95 | −18,844.72 | −55.43 |
| Model | Number of Hydrogen Bonds | ||
|---|---|---|---|
| 303 K | 323 K | 343 K | |
| P-SiO2/H2O | 4149 | 3704 | 3436 |
| P-570/H2O | 2807 | 2554 | 2223 |
| P-151/H2O | 3519 | 3013 | 2834 |
| Case | Research Method | Strengths and Limitations |
|---|---|---|
| P-570 | Molecular dynamics simulation | Excellent thermomechanical performance and hydrophobicity. |
| PDMS [8] | Experiment, templating technique | Excellent hydrophobicity, unknown thermodynamic properties, templating technique is not suitable for the preparation of hydrophobic coatings for insulating paper. |
| Surface fluoridated PDMS [9] | Experiment, direct fluorination | High hydrophobicity, partially conductive, low surface energy, but the use of fluorine-based materials is harmful to the environment. |
| CuO@PDMS [18] | Experiment | Highly hydrophobic and antibacterial, high durability, but poor chemical stability and insulating properties of nano-CuO. |
| GO@PDMS [18] | Experiment | Excellent thermomechanical properties with erosion resistance, but more expensive and less insulating than nano-SiO2. |
| MWNT@PDMS [18] | Experiment | Excellent thermodynamic and electrical properties, but the cost of MWNTs is high, and the preparation process of functionalized modification is complicated. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Dai, W.; Yan, J.; Wang, Z.; Tang, C. Simulation of the Thermodynamic Properties and Hydrophobicity of Polydimethylsiloxane Modified by Grafting Nano-SiO2 with Different Silane Coupling Agents. Materials 2025, 18, 2323. https://doi.org/10.3390/ma18102323
Xie Y, Dai W, Yan J, Wang Z, Tang C. Simulation of the Thermodynamic Properties and Hydrophobicity of Polydimethylsiloxane Modified by Grafting Nano-SiO2 with Different Silane Coupling Agents. Materials. 2025; 18(10):2323. https://doi.org/10.3390/ma18102323
Chicago/Turabian StyleXie, Yuzhang, Weiju Dai, Jingyi Yan, Zuhao Wang, and Chao Tang. 2025. "Simulation of the Thermodynamic Properties and Hydrophobicity of Polydimethylsiloxane Modified by Grafting Nano-SiO2 with Different Silane Coupling Agents" Materials 18, no. 10: 2323. https://doi.org/10.3390/ma18102323
APA StyleXie, Y., Dai, W., Yan, J., Wang, Z., & Tang, C. (2025). Simulation of the Thermodynamic Properties and Hydrophobicity of Polydimethylsiloxane Modified by Grafting Nano-SiO2 with Different Silane Coupling Agents. Materials, 18(10), 2323. https://doi.org/10.3390/ma18102323






