Mechanical and Energy Evolution Characteristics of Fractured Sandstone Materials: A True Triaxial Experimental Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Equipment
2.2. Specimen Preparation
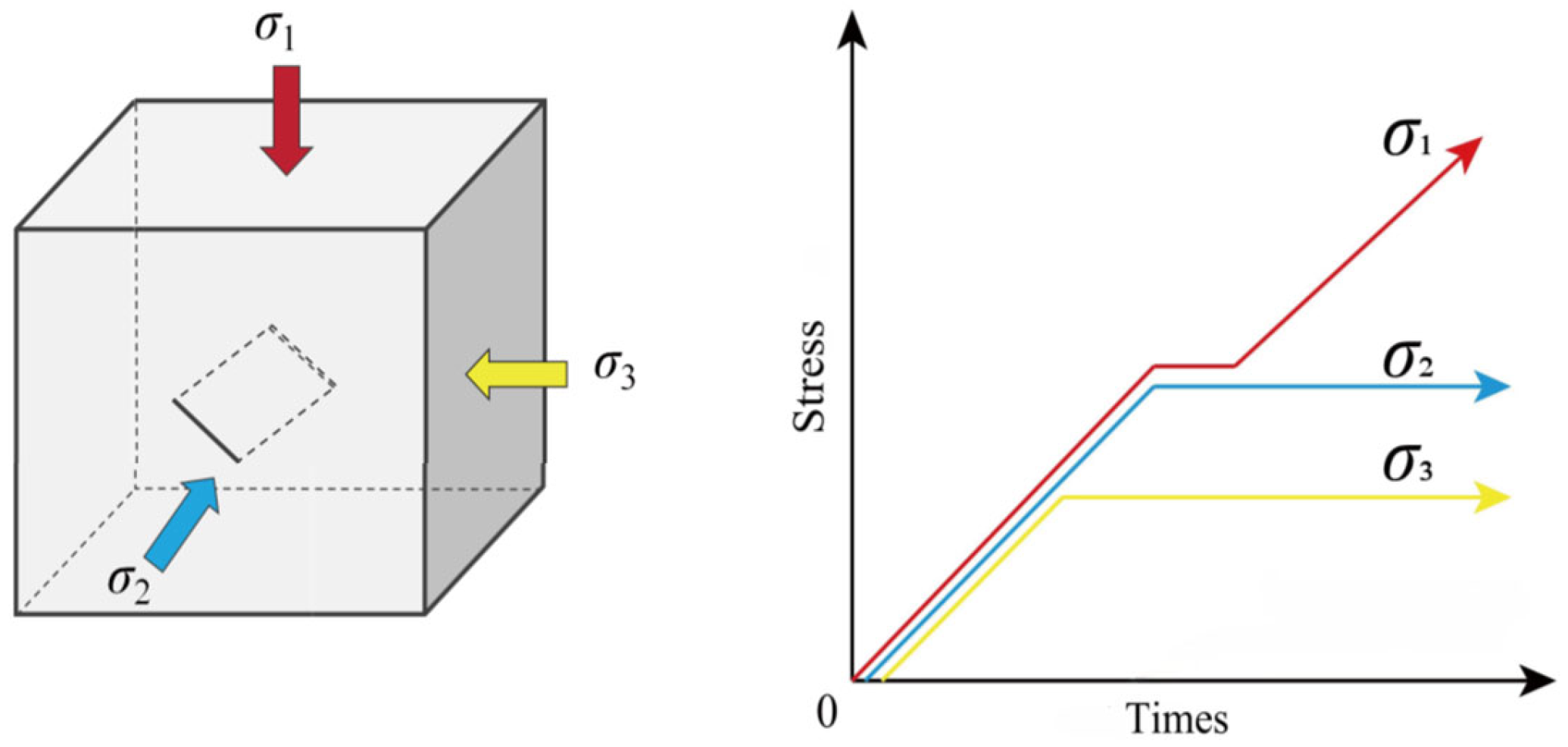
2.3. Stress Loading Procedure
- 1.
- Apply triaxial stress simultaneously using the force control mode (0.2 kN/s) until reaching hydrostatic stress conditions of σ1 = σ2 = σ3 = 15 MPa.
- 2.
- Maintain the minimum principal stress σ3 = 15 MPa constant, and use the force control mode (0.2 kN/s) to increase the intermediate principal stress σ2 and the maximum principal stress σ1 until σ1 = σ2 = 30 MPa.
- 3.
3. Experimental Results and Analysis
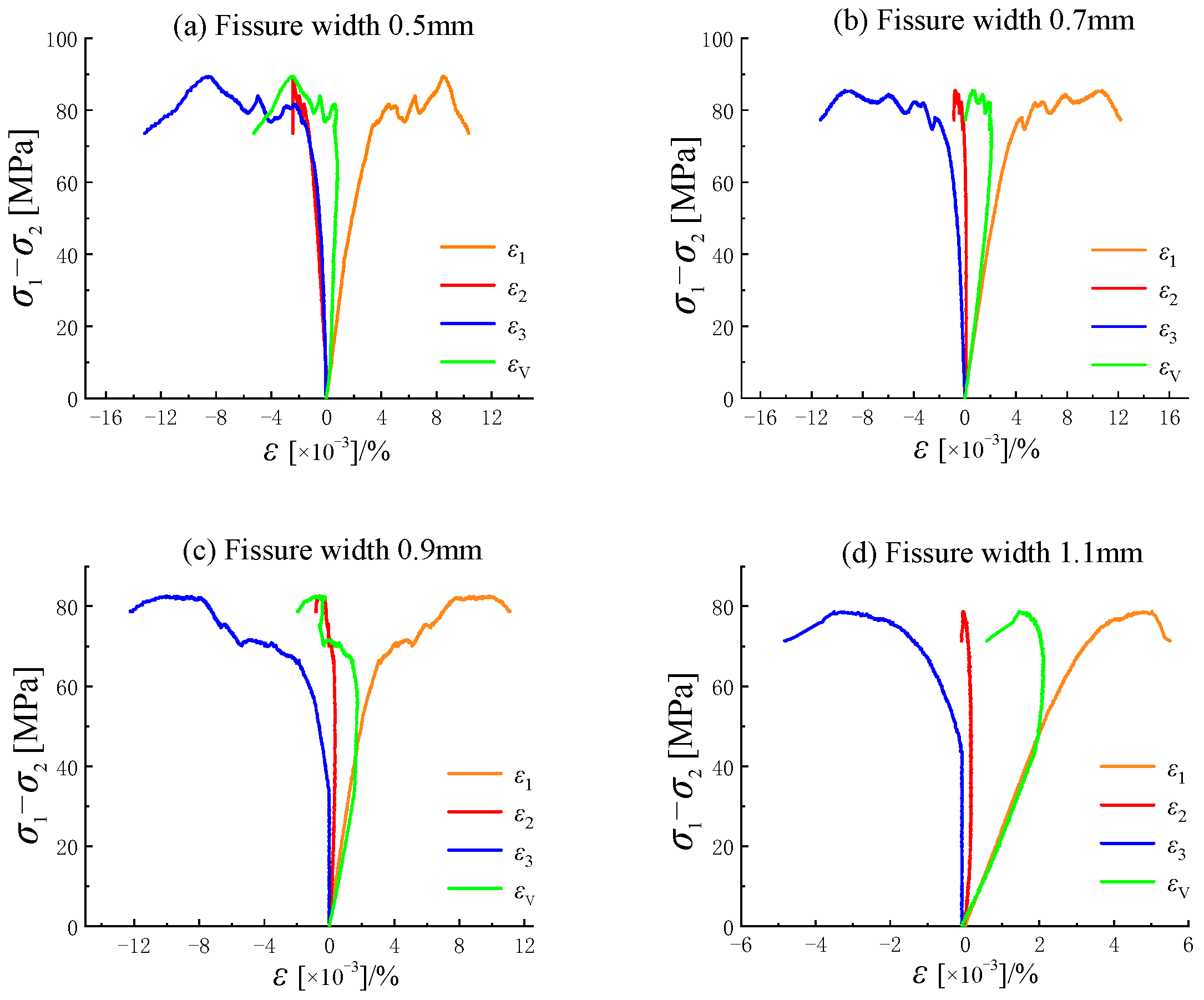
3.1. Stress–Strain Curve Analysis
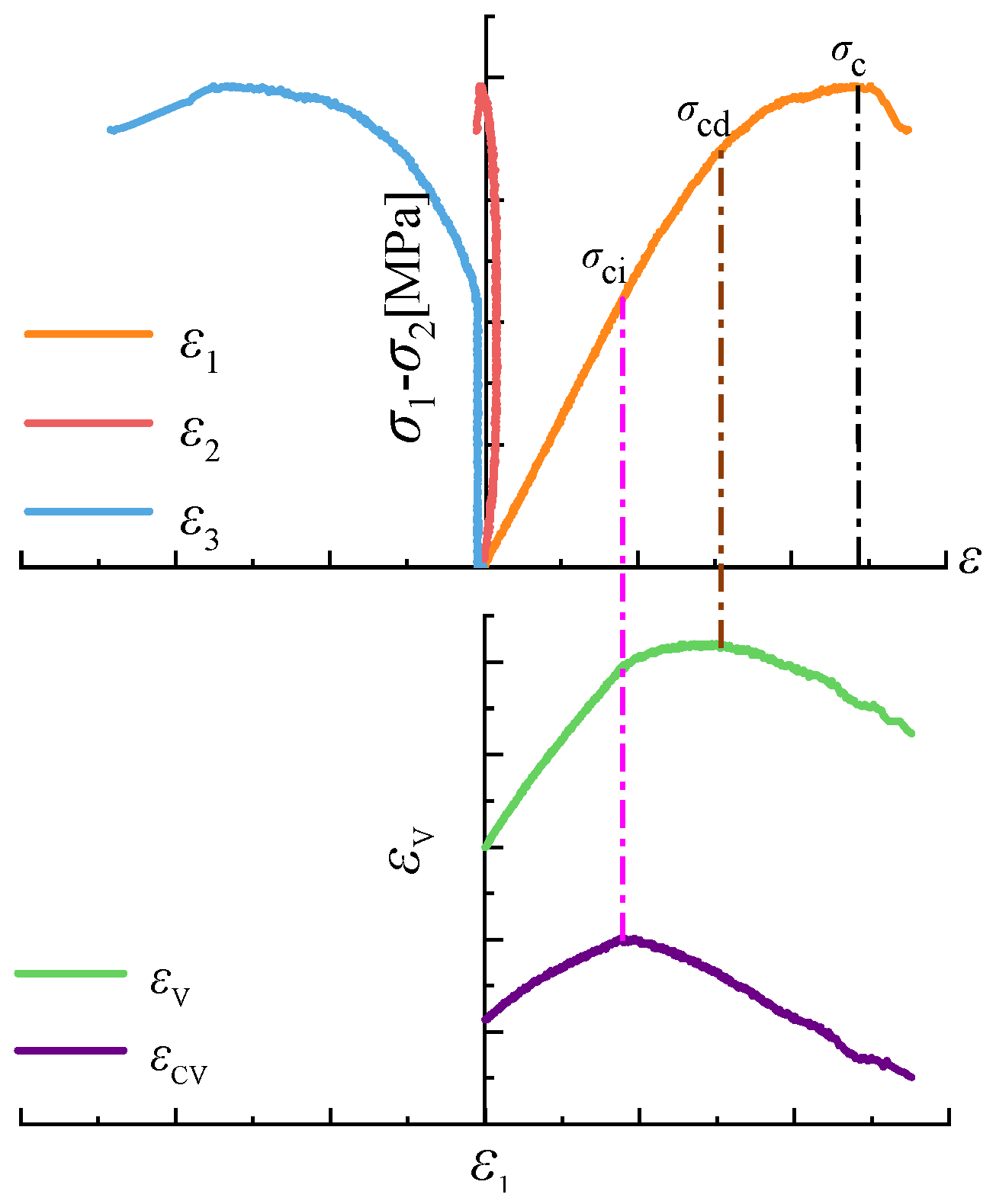
3.2. Determination of Rock Initiation and Damage Stresses
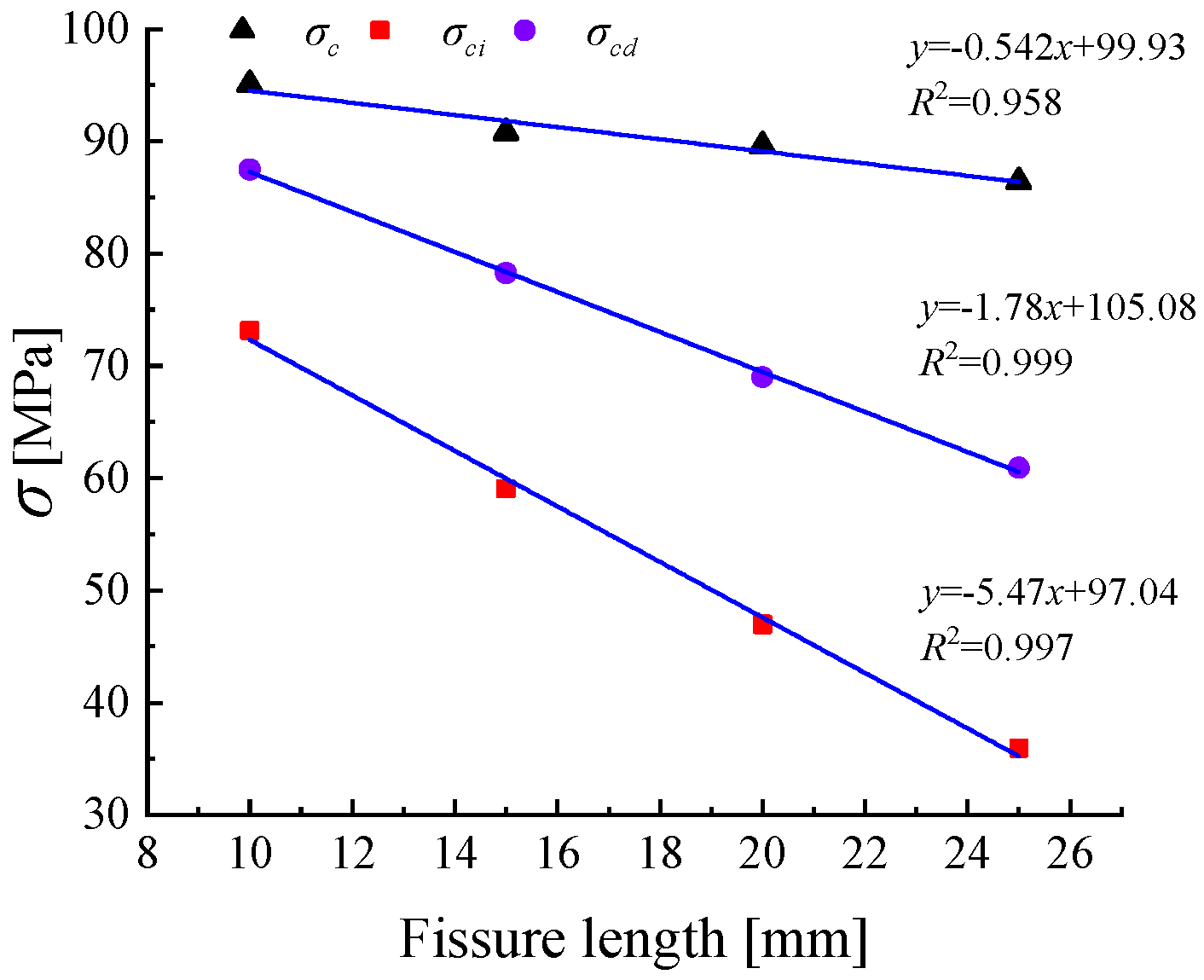
3.3. Analysis of Crack Initiation and Damage Stress of Sandstone with Different Crack Lengths
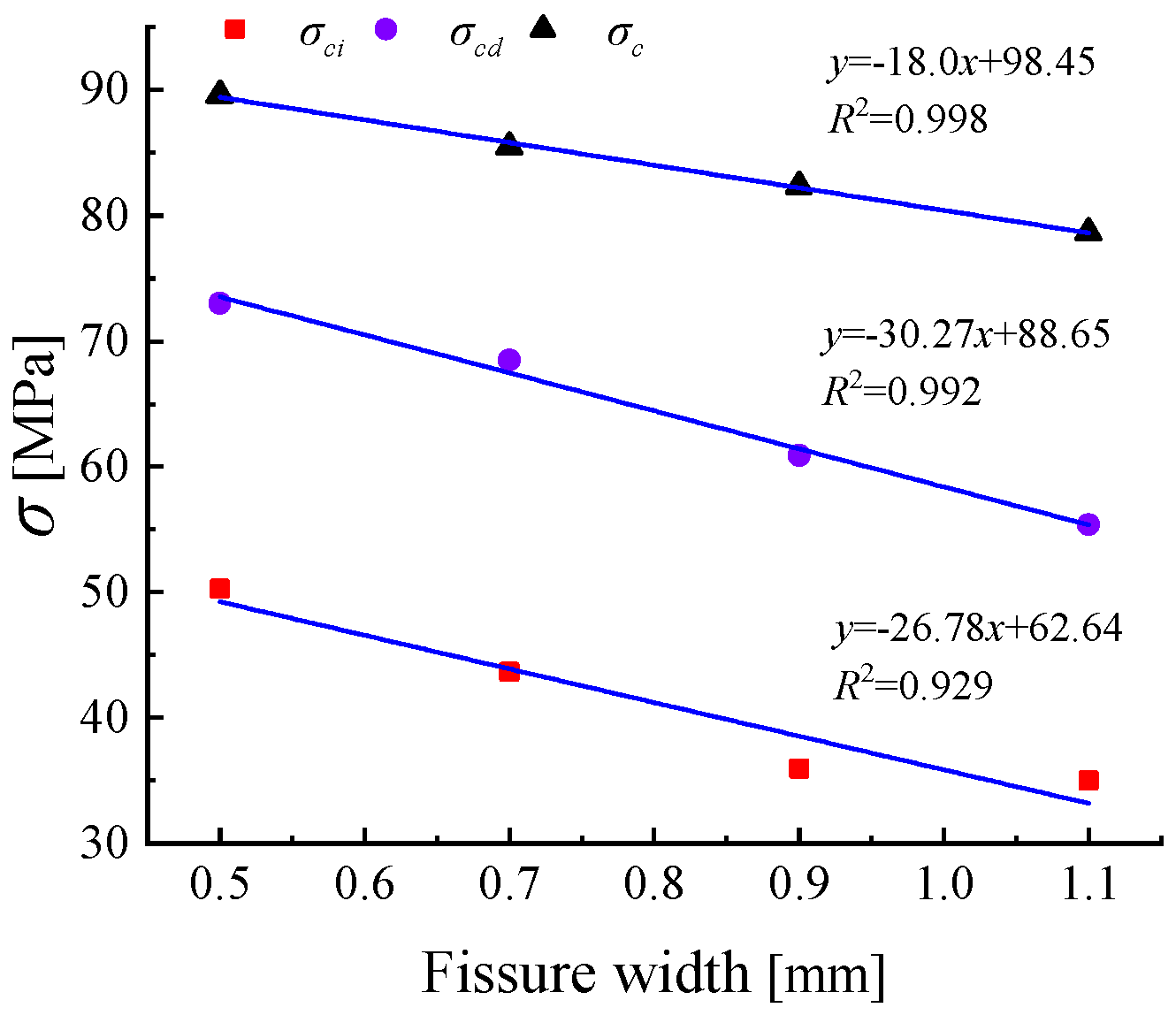
3.4. Analysis of Crack Initiation and Damage Stress of Sandstone with Different Crack Widths
4. Analysis of the Energy Evolution of Fractured Sandstones Under True Triaxial Stresses
4.1. Energy Evolution Characteristics of Sandstone with Different Fracture Lengths and Widths
4.2. Analysis of Rock Strength and Energy Evolution
5. Conclusions
- (1)
- Under true triaxial stress, the peak strength of sandstone decreases with the increase in fracture length and width. Similarly, the initiation stress and damage stress of fractured sandstone decrease as fracture length and width increase. Fractures act as prefabricated defects in sandstone specimens, and their increasing scale (length and width) reduces rock strength, accelerating the sandstone’s progression to the stages of fracture closure, crack initiation, and propagation.
- (2)
- As fracture width increases incrementally by 0.2 mm, the decrease in specimen strength exhibits a relatively clear pattern. However, the reduction in strength with increasing fracture length is less regular. The largest drop in peak strength occurs when fracture length increases from 10 mm to 15 mm. Fracture length has a stronger influence on the initiation stress and damage stress of sandstone than fracture width.
- (3)
- The total strain energy of sandstone decreases with the enlargement of internal fracture geometric dimensions. Significant energy dissipation occurs after the peak stress. The impact of fracture width on the energy storage limit of sandstone is less significant than that of fracture length.
- (4)
- Under true triaxial stresses, as fracture length and width increase, the damage to sandstone becomes more severe, the energy storage limit decreases, and the resistance to failure weakens. When the extent of damage to sandstone exceeds a certain threshold, the influence of fractures on resistance to failure and the energy storage limit under true triaxial stress reaches an upper limit.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| σ | stress |
| σ1 | maximum principal stress |
| σ2 | intermediate principal stress |
| σ3 | minimum principal stress |
| σc | peak stress |
| σci | cracking stress |
| σcd | damage stress |
| ε | strains |
| ε1 | maximum principal strain |
| ε2 | intermediate principal strain |
| ε3 | minimum principal strain |
| εv | volumetric strain |
| εcv | crack volume strain |
| εev | elastic volumetric strain |
| E | modulus of elasticity |
| μ | Poisson’s ratio |
| U | total strain energy |
| Ud | dissipative energy |
| Ue | elastic strain energy |
References
- Yuan, L. Progress in deep mining response and disaster prevention and control. J. Coal Sci. 2021, 46, 716–725. [Google Scholar] [CrossRef]
- Chen, J.M.; Ren, Q.W.; Tu, Y.C.; Wang, X.S.; Wu, J.X.; Gao, P.J.; Meng, Y.C.; Xu, M.L.; Huang, W.; Zhang, Z.S. Experimental research and theoretical application of petrophysics based on pore-fracture theory. Georeview 2023, 69, 585–587. [Google Scholar] [CrossRef]
- Sun, H.; Chen, S.; Jin, A.; Zhu, D. Uniaxial compressive strength characteristics and crack evolution law of fracture-containing rock specimens. J. Northeast. Univ. (Nat. Sci. Ed.) 2022, 43, 404–413. [Google Scholar]
- Xia, Z.; Zhang, X.; Yao, C.; Chen, H.; Yang, J.; Jiang, Q.; Zhou, C. Experiments on seepage characteristics of post-peak ruptured rocks during loading and unloading of peri-compression. J. Coal 2019, 44, 3379–3387. [Google Scholar] [CrossRef]
- Luo, D.; Lu, S.; Su, G.; Tao, H. Experimental study of true triaxial single-face airborne rockburst of granite containing prefabricated single fissure. Geotechnics 2023, 44, 75–87. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, K.; Zhou, W.; Yao, Y.; Xie, T. Uniaxial Compressive Damage Characteristics of Rock-like Materials with Prefabricated Conjugate Cracks. Appl. Sci. 2024, 14, 823. [Google Scholar] [CrossRef]
- Wang, B.; Yao, C.; Yang, J.; Jiang, S. Numerical Simulation of Macro-Meso Mechanical Behaviours of Sandstone Containing a Single Open Fissure under Uniaxial Compression. Eur. J. Environ. Civ. Eng. 2018, 22, s99–s113. [Google Scholar] [CrossRef]
- Guo, W.; Yu, F.; Tan, Y.; Zhao, T. Experimental Study on the Failure Mechanism of Layer-Crack Structure. Energy Sci. Eng. 2019, 7, 2351–2372. [Google Scholar] [CrossRef]
- Zhao, C.; Niu, J.; Zhang, Q.; Yu, S.; Morita, C. Numerical Simulations on Cracking Behavior of Rock-Like Specimens with Single Flaws under Conditions of Uniaxial and Biaxial Compressions. J. Mater. Civ. Eng. 2019, 31, 04019305. [Google Scholar] [CrossRef]
- Han, G.; Jing, H.; Jiang, Y.; Liu, R.; Su, H.; Wu, J. The Effect of Joint Dip Angle on the Mechanical Behavior of Infilled Jointed Rock Masses under Uniaxial and Biaxial Compressions. Processes 2018, 6, 49. [Google Scholar] [CrossRef]
- Takahashi, N.; Takahashi, M.; Park, H.; Fujii, Y.; Takemura, T. Deformation and Strength Characteristics of Kimachi Sandstone under Confined Compression and Extension Test Conditions. In True Triaxial Testing of Rocks; Kwasniewski, M., Li, X., Takahashi, M., Eds.; A.A. Balkema: Leiden, The Netherlands, 2012; Volume 4, pp. 203–209. [Google Scholar]
- Wang, B.; Li, T.; Zhu, Q.; Ran, J.; Du, Y.; Zhang, H. Study on the Creep Properties and Crack Propagation Behavior of Single-Fissure Sandstone Based on the Damage Bond Model. Theor. Appl. Fract. Mech. 2023, 124, 103805. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Tian, W.-L.; Liu, X.-R.; Huang, Y.-H.; Yang, J. An Experimental Study on Failure Mechanical Behavior and Cracking Mechanism of Rectangular Solid Sandstone Containing Two Non-Coplanar Fissures under Conventional Triaxial Compression. Theor. Appl. Fract. Mech. 2021, 114, 102975. [Google Scholar] [CrossRef]
- Zhang, L.; Cong, Y.; Meng, F.; Wang, Z.; Zhang, P.; Gao, S. Energy Evolution Analysis and Failure Criteria for Rock under Different Stress Paths. Acta Geotech. 2021, 16, 569–580. [Google Scholar] [CrossRef]
- Gong, H.; Luo, Y.; Xu, K.; Wang, X.; Tao, Y.; Li, X. Mechanical Characteristics of Failure and Rockburst Proneness of Fractured Granite from Shuangjiangkou Hydropower Station under Triaxial Loading and Unloading. Bull. Eng. Geol. Environ. 2023, 82, 256. [Google Scholar] [CrossRef]
- Majedi, M.R.; Afrazi, M.; Fakhimi, A. A Micromechanical Model for Simulation of Rock Failure Under High Strain Rate Loading. Int. J. Civ. Eng. 2021, 19, 501–515. [Google Scholar] [CrossRef]
- Afrazi, M.; Lin, Q.; Fakhimi, A. Physical and Numerical Evaluation of Mode II Fracture of Quasi-Brittle Materials. Int. J. Civ. Eng. 2022, 20, 993–1007. [Google Scholar] [CrossRef]
- Li, K.-S.; Chen, L.-X.; Zhao, Z.; Liu, C.-X. Experimental Investigation on Mechanical, Acoustic, and Fracture Behaviors and the Energy Evolution of Sandstone Containing Non-Penetrating Horizontal Fissures. Theor. Appl. Fract. Mech. 2023, 123, 103703. [Google Scholar] [CrossRef]
- Liu, H. Numerical simulation of rock fracture parameters under different fracturing conditions. Energy Technol. Manag. 2021, 46, 92–93+111. [Google Scholar]
- Zhao, G.; Liu, Z.; Meng, X.; Zhang, R.; Gu, Q.; Qi, M. Energy evolution of sandstone under true triaxial cyclic principal stress. Geotechnics 2023, 44, 1875–1890. [Google Scholar] [CrossRef]
- Li, C.; Xie, H.; Xie, L. Experiment and theory of shale initiation stress and crack damage stress. J. Coal 2017, 42, 969–976. [Google Scholar] [CrossRef]
- Yin, G.C.; Ma, B.; Liu, C.; Li, M.H.; Lu, J.; Yin, S.Y. Effects of loading and unloading rates on mechanical properties and energy characteristics of sandstone under true triaxial stress conditions. J. Coal 2019, 44, 454–462. [Google Scholar] [CrossRef]
- Yin, G.C.; Li, M.H.; Xu, J.; Wang, W.Z.; Li, W.P.; Li, S.; Song, Z.L.; Deng, B.C. Development and application of a multifunctional true three-axis fluid-solid coupling test system. J. Rock Mech. Eng. 2015, 34, 2436–2445. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, Y.; Song, M.; Karim, S.I. Strength Characteristics of Different Stress Spaces of Red Sandstone under Loading and Unloading Tests. Sci. Rep. 2024, 14, 17988. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, W.; Kong, R.; Guo, J. Mechanical Characterization of Deep Sandstone under True Three-Way Stress. J. Northeast. Univ. (Nat. Sci. Ed.) 2023, 44, 689–696. [Google Scholar]
- Liu, H.N.; Wang, J.M.; Wang, S.J. Experimental study on true triaxial modeling of columnar jointed rocks in Baihetan. Geotech. Mech. 2010, 31, 163–171. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, G.; Xu, D.; Huang, X.; Hu, Y.-Y.; Xia, Y.-L.; Zhang, D. Experimental characterization of deformation and damage of deeply buried hard rock under triaxial and cyclic loading and unloading stress paths. Geotechnics 2020, 41, 1521–1530. [Google Scholar] [CrossRef]
- Li, B.; Gong, J.; Long, Y.; Hu, H.; Cao, Y.-B. Experimental Investigations on Mechanical and Failure Behaviors of Transversely Isotropic Shale Containing Twin Fissures under True Triaxial Stresses. Arch. Appl. Mech. 2023, 93, 3205–3228. [Google Scholar] [CrossRef]
- Zhang, Y.; Jing, W.; Jing, L.; Jin, R.; Cheng, P. Numerical simulation of the effects of fissure inclination and length on rock strength and damage characteristics. Coal Technol. 2023, 42, 106–109. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, J.; Dai, Z.; Yi, T. Experimental Study on Mechanical Properties and Failure Modes of Low-Strength Rock Samples Containing Different Fissures under Uniaxial Compression. Eng. Fract. Mech. 2018, 197, 1–20. [Google Scholar] [CrossRef]
- Li, S.-C.; Kang, Y.-L.; Luo, P.-Y. Effect of stress on fracture width and permeability of coal rock. Coalf. Geol. Explor. 2009, 37, 29–32. [Google Scholar]





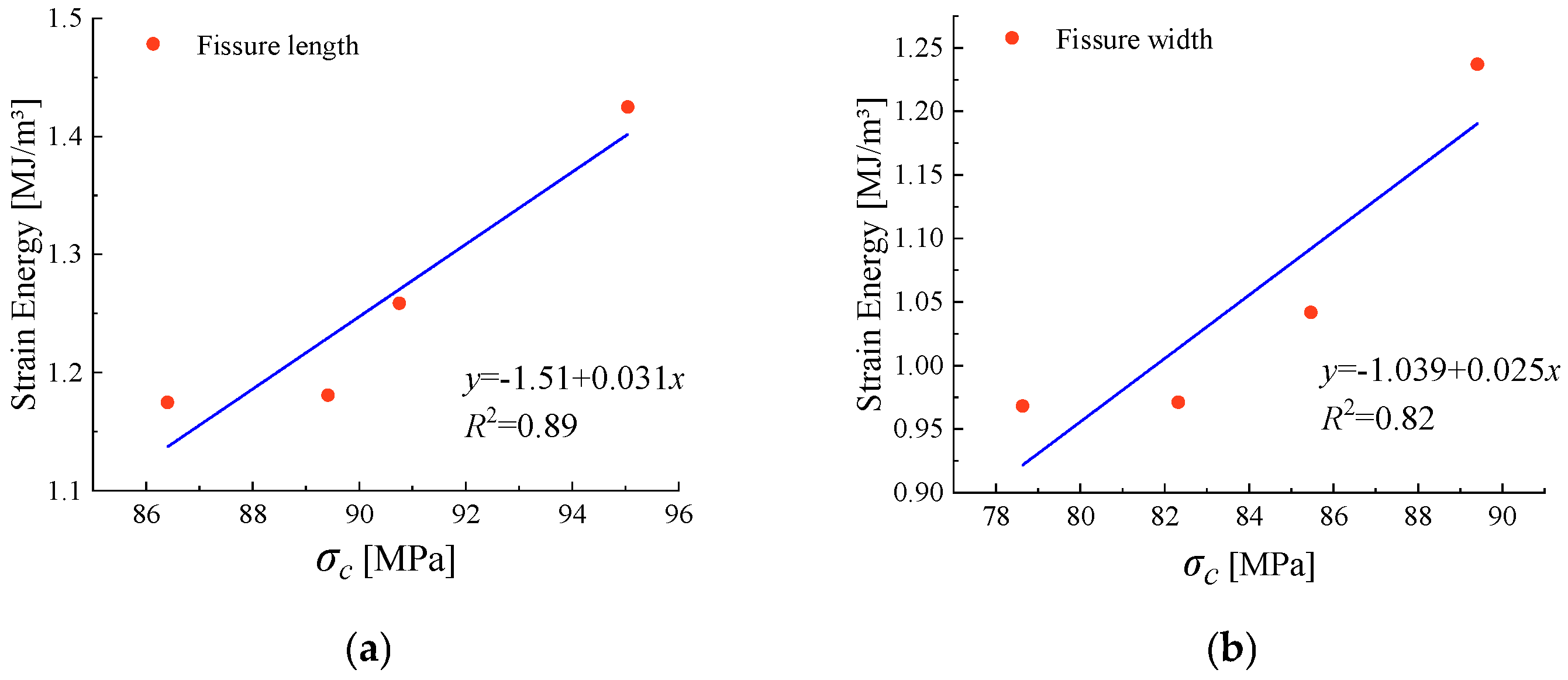
| Specimens | Fissure Length [mm] | Fissure Width [mm] | σ2 [MPa] | σ3 [MPa] |
|---|---|---|---|---|
| Sandstone 1 | 20 | 0.5 | 15 | 30 |
| Sandstone 2 | 20 | 0.7 | 15 | 30 |
| Sandstone 3 | 20 | 0.9 | 15 | 30 |
| Sandstone 4 | 20 | 1.1 | 15 | 30 |
| Sandstone 5 | 10 | 0.5 | 15 | 30 |
| Sandstone 6 | 15 | 0.5 | 15 | 30 |
| Sandstone 7 | 20 | 0.5 | 15 | 30 |
| Sandstone 8 | 25 | 0.5 | 15 | 30 |
| Fissure Length [mm] | [MPa] | [MPa] | [MPa] | E [GPa] | ||
|---|---|---|---|---|---|---|
| 10 | 73.15 | 87.50 | 95.04 | 76.97% | 92.07% | 31.23 |
| 15 | 59.02 | 78.25 | 90.75 | 65.04% | 86.23% | 29.41 |
| 20 | 46.95 | 68.98 | 89.59 | 52.41% | 77.00% | 23.88 |
| 25 | 35.96 | 60.90 | 86.40 | 41.62% | 70.49% | 18.27 |
| Fissure Width [mm] | [MPa] | [MPa] | [MPa] | E [GPa] | ||
|---|---|---|---|---|---|---|
| 0.5 | 50.28 | 73.02 | 89.59 | 56.12% | 81.50% | 29.41 |
| 0.7 | 43.65 | 68.48 | 85.47 | 51.07% | 80.12% | 23.16 |
| 0.9 | 35.96 | 60.90 | 82.32 | 43.68% | 74.00% | 20.85 |
| 1.1 | 34.99 | 55.37 | 78.63 | 44.50% | 70.42% | 19.87 |
| Fissure Length [mm] | [MPa] | Strain Energy [MJ/m3] | Fissure Width [mm] | [MPa] | Strain Energy [MJ/m3] | |
|---|---|---|---|---|---|---|
| 10 | 95.04 | 1.425 | 0.5 | 89.59 | 1.237 | |
| 15 | 90.75 | 1.256 | 0.7 | 85.47 | 1.041 | |
| 20 | 89.59 | 1.180 | 0.9 | 82.32 | 0.971 | |
| 25 | 86.40 | 1.174 | 1.1 | 78.63 | 0.968 | |
| maximum | 95.04 | 1.425 | 89.59 | 1.237 | ||
| minimum | 86.40 | 1.174 | 78.63 | 0.968 | ||
| average | 90.445 | 1.259 | 84.01 | 1.054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Lu, Y.; Huang, G.; Liang, Q.; Huang, X. Mechanical and Energy Evolution Characteristics of Fractured Sandstone Materials: A True Triaxial Experimental Study. Materials 2025, 18, 175. https://doi.org/10.3390/ma18010175
Sun G, Lu Y, Huang G, Liang Q, Huang X. Mechanical and Energy Evolution Characteristics of Fractured Sandstone Materials: A True Triaxial Experimental Study. Materials. 2025; 18(1):175. https://doi.org/10.3390/ma18010175
Chicago/Turabian StyleSun, Guowen, Yu Lu, Gun Huang, Qinming Liang, and Xinyu Huang. 2025. "Mechanical and Energy Evolution Characteristics of Fractured Sandstone Materials: A True Triaxial Experimental Study" Materials 18, no. 1: 175. https://doi.org/10.3390/ma18010175
APA StyleSun, G., Lu, Y., Huang, G., Liang, Q., & Huang, X. (2025). Mechanical and Energy Evolution Characteristics of Fractured Sandstone Materials: A True Triaxial Experimental Study. Materials, 18(1), 175. https://doi.org/10.3390/ma18010175





