Measurement and Analysis of the Vibration Responses of Piano Soundboards with Different Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Free-Plate Torsional Vibration Method
2.3. Vibration Frequencies of the Soundboards
2.4. Dynamic Modulus of Elasticity and Dynamic Shear Modulus
3. Results and Discussion
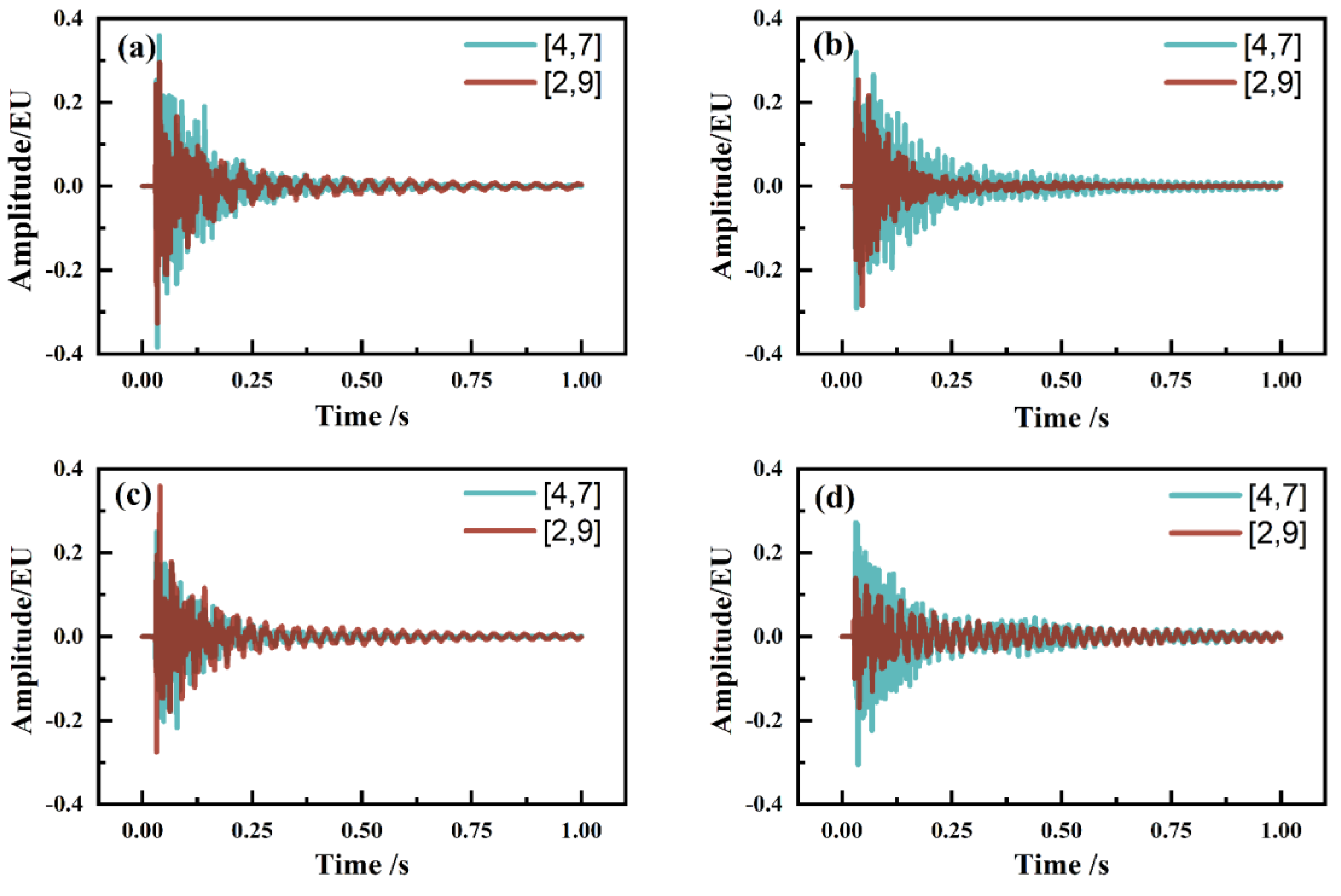
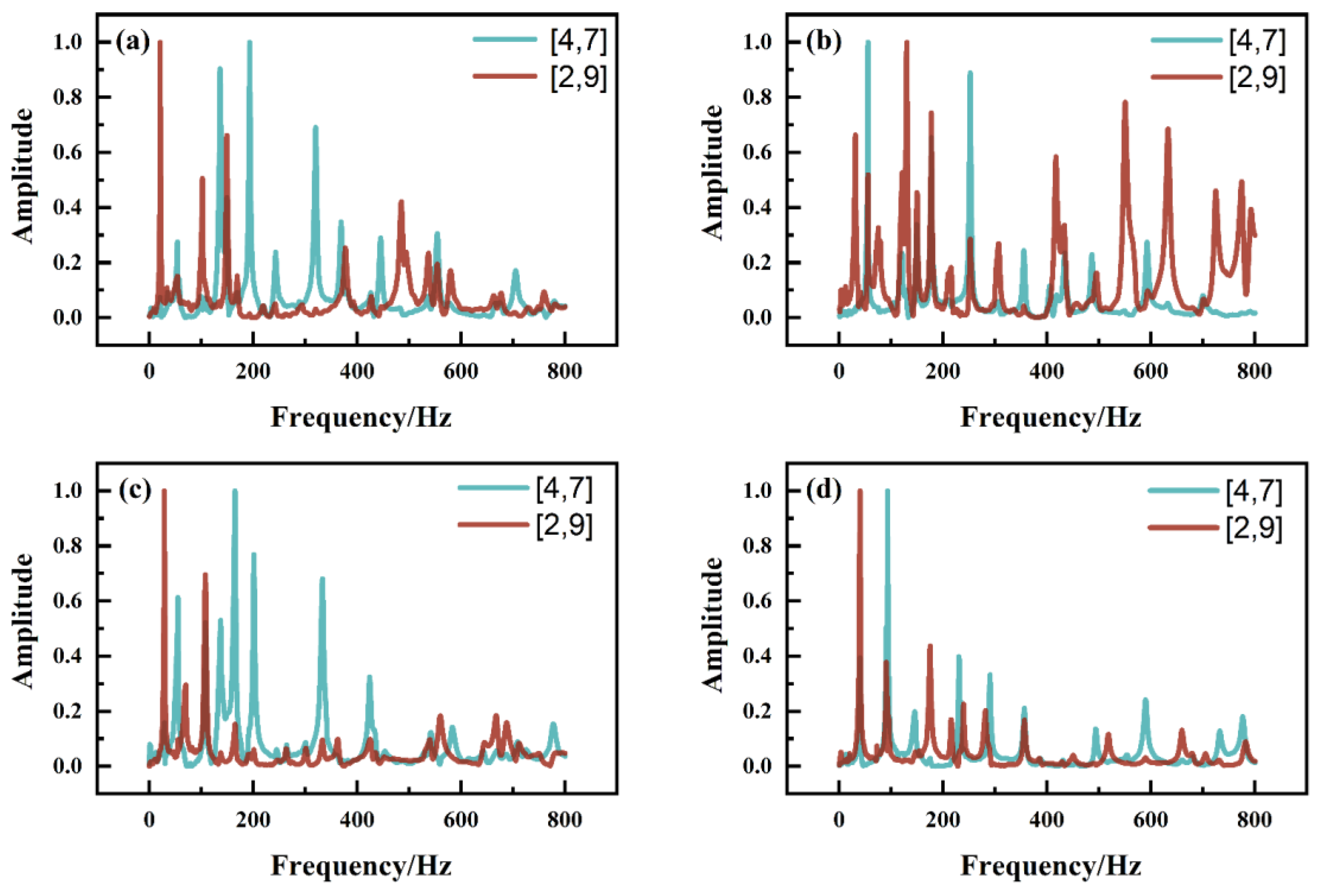
3.1. Multi-Point Excitation Test
3.2. Vibration Frequencies of the Four Piano Soundboards with Different Structures
3.3. Comparison of Results Obtained Using the Free-Vibration Frequency Method for Thin Wooden Plates and Those Obtained Using the Eulerian Free-Beam Method and the Free-Plate Torsional Vibration Method
4. Conclusions
- (1)
- Excitations at different points highlight the different modes of vibration of the soundboards. To obtain the (2,0)- and (0,2)-order frequencies, measurements can be made parallel to the grain direction of the panel. To obtain the (1,1)-order frequency, measurements can be made perpendicular to the grain direction of the panel.Different piano soundboards can be spliced differently. Furthermore, splicing results in complex texture angles, and in vibration modes that are less regular and symmetric than those of isotropic materials. It is thus more difficult to judge the vibration mode of a spliced soundboard.
- (2)
- EF and GF calculated using the free-vibration frequency method for a thin wooden plate are similar to EE calculated using the Euler free-beam method and GT calculated using the free-plate torsional vibration method. The obtained trends are the same. In the x-direction, the resistance to bending deformation decreases in the order of ExD > ExB > ExC > EXa. In the y-direction, the order is EyC > EyA > EyD > EyB. The resistance to torsional deformation decreases in the order of GD > GC > GA > GB. In practical applications, Euler’s free-beam method and the free-plate torsional vibration method can be used to conduct simple calculations for comparing and judging the mechanical properties and vibration characteristics of different soundboards.
- (3)
- This investigation delved into the impact of various soundboard structures on the vibrational responses and modal patterns of piano soundboards. The study has measurement orientations conductive to the expedited acquisition of (2,0), (0,2), and (1,1) modal frequencies. Furthermore, it deduced the elastic and shear moduli for rectangular soundboards, which can be conveniently computed using Euler–Bernoulli beam theory and the free-torsion method. Prospective research avenues may encompass examining the influence of core board angles on the soundboard’s vibrational dynamics, as well as making enhancements to the free-torsion method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, J.J.; Chaigne, A.; Acri, A. Operational Transfer Path Analysis of a Piano. Appl. Acoust. 2018, 140, 39–47. [Google Scholar] [CrossRef]
- Bucur, V. Handbook of Materials for String Musical Instruments; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-32078-6. [Google Scholar]
- Chen, Z.X.; Zhou, Y.D.; Zhou, F.; Fu, Z.Y.; Gao, X. Requirements for Wood Materials and Production Processin Piano Manufacturing. Chin. J. Wood Sci. Technol. 2021, 35, 6–11. [Google Scholar] [CrossRef]
- Squicciarini, G.; Valiente, P.M.; Thompson, D.J. Sound Power and Vibration Levels for Two Different Piano Soundboards. J. Phys. Conf. Ser. 2016, 744, 012091. [Google Scholar] [CrossRef]
- Gerhard, S.; Maierhofer, J.; Loidli, D.; Puchegger, S.; Stanzl-Tscheggi, S. Elastic constants of six wood species measured with the resonant beam technique. Wood Res. 2020, 65, 347–352. [Google Scholar] [CrossRef]
- Ray, T.; Kaljun, J.; Straže, A. Comparison of the Vibration Damping of the Wood Species Used for the Body of an Electric Guitar on the Vibration Response of Open-Strings. Materials 2021, 14, 5281. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.; Plath, N. Impact of Damping on Oscillation Patterns on the Plain Piano Soundboard. Acoustics 2022, 4, 1013–1027. [Google Scholar] [CrossRef]
- Lewandowski, M.; Foltynowicz, Z. Selected aspects of resonance properties of different woods and the construction of string instruments. Drewno 2022, 65, 132022. [Google Scholar] [CrossRef]
- Guiman, M.V.; Stanciu, M.D.; Roșca, I.C.; Georgescu, S.V.; Năstac, S.M.; Câmpean, M. Influence of the Grain Orientation of Wood upon Its Sound Absorption Properties. Materials 2023, 16, 5998. [Google Scholar] [CrossRef]
- Hossen, M.F.; Hamdan, S.; Rahman, M.R. Investigation of the Acoustic Properties of Chemically Impregnated Kayu Malam Wood Used for Musical Instrument. Adv. Mater. Sci. Eng. 2018, 2018, 7829613. [Google Scholar] [CrossRef]
- Corradi, R.; Miccoli, S.; Squicciarini, G.; Fazioli, P. Modal Analysis of a Grand Piano Soundboard at Successive Manufacturing Stages. Appl. Acoust. 2017, 125, 113–127. [Google Scholar] [CrossRef][Green Version]
- Berthaut, J.; Ichchou, M.N.; Jézéquel, L. Piano Soundboard: Structural Behavior, Numerical and Experimental Study in the Modal Range. Appl. Acoust. 2003, 64, 1113–1136. [Google Scholar] [CrossRef]
- Jenei-Kulcsár, D.; Fiala, P. Piano Soundboard Analysis at Radiated Sound. Period. Polytech. Electr. Eng. Comput. Sci. 2023, 67, 291–299. [Google Scholar] [CrossRef]
- Elie, B.; Cotte, B.; Boutillon, X. Physically-Based Sound Synthesis Software for Computer-Aided-Design of Piano Soundboards. ACTA Acust. 2022, 6, 30. [Google Scholar] [CrossRef]
- Salvi, D.; Gonzalez, S.; Antonacci, F.; Sarti, A. Modal Analysis of Free Archtop Guitar Top Plates. J. Acoust. Soc. Am. 2021, 150, 1505–1513. [Google Scholar] [CrossRef] [PubMed]
- Boutillon, X.; Ege, K. Vibroacoustics of the Piano Soundboard: Reduced Models, Mobility Synthesis, and Acoustical Radiation Regime. J. Sound Vib. 2013, 332, 4261–4279. [Google Scholar] [CrossRef][Green Version]
- Zhou, J.; Chui, Y.H.; Gong, M.; Hu, L. Comparative Study on Measurement of Elastic Constants of Wood-Based Panels Using Modal Testing: Choice of Boundary Conditions and Calculation Methods. J. Wood Sci. 2017, 63, 523–538. [Google Scholar] [CrossRef]
- Ege, K.; Boutillon, X.; Rébillat, M. Vibroacoustics of the Piano Soundboard: (Non)Linearity and Modal Properties in the Low and Mid-Frequency Ranges. J. Sound Vib. 2013, 332, 1288–1305, Erratum in J. Sound Vib. 2013, 75, 428–435.. [Google Scholar] [CrossRef]
- Opazo-Vega, A.; Rosales-Garcés, V.; Oyarzo-Vera, C. Non-Destructive Assessment of the Dynamic Elasticity Modulus of Eucalyptus Nitens Timber Boards. Materials 2021, 14, 269. [Google Scholar] [CrossRef]
- Ou, D.; Mak, C.M. Optimization of Natural Frequencies of a Plate Structure by Modifying Boundary Conditions. J. Acoust. Soc. Am. 2017, 142, EL56–EL62. [Google Scholar] [CrossRef] [PubMed]
- Trévisan, B.; Ege, K.; Laulagnet, B. A Modal Approach to Piano Soundboard Vibroacoustic Behavior. J. Acoust. Soc. Am. 2017, 141, 690–709. [Google Scholar] [CrossRef] [PubMed]
- Guan, C.; Zhang, H.; Wang, X.; Miao, H.; Zhou, L.; Liu, F. Experimental and Theoretical Modal Analysis of Full-Sized Wood Composite Panels Supported on Four Nodes. Materials 2017, 10, 683. [Google Scholar] [CrossRef]
- Yang, X.; Amano, T.; Ishimaru, Y.; Iida, I. Application of Modal Analysis by Transfer Function to Nondestructive Testing of Wood II: Modulus of Elasticity Evaluation of Sections of Differing Quality in a Wooden Beam by the Curvature of the Flexural Vibration Wave. J. Wood Sci. 2003, 49, 140–144. [Google Scholar] [CrossRef]
- Mania, P.; Fabisiak, E.; Skrodzka, E. Investigation of Modal Behaviour of Resonance Spruce Wood Samples (Picea abies L.). Arch. Acoust. 2017, 42, 23–28. [Google Scholar] [CrossRef][Green Version]
- Zhai, X.Y.; Miao, Y.Y.; Wang, X.Y.; Wan, K.; Yin, Y.X.; Liu, Z.B. Vibration and acoustic response characteristics of soundboard wood under axial compressive load. J. Vib. Shock. 2021, 40, 187–193. [Google Scholar] [CrossRef]
- Yin, Y.X.; Miao, Y.Y.Y.; Wan, K.; Wang, X.Y.; Zhai, X.Y.; Liu, Z.B. Analysis and evaluation of wood acoustic vibration signal based on Daubechies wavelet base. J. For. Eng. 2021, 6, 68–75. [Google Scholar] [CrossRef]
- Nop, P.; Tippner, J. Influence of Dimensions of Wooden Samples for Determination of Acoustic Parameters and Sound Timbre. Appl. Acoust. 2022, 196, 108895. [Google Scholar] [CrossRef]
- Yoshihara, H.; Maruta, M. Effect of Specimen Configuration and Orthotropy on the Young’s Modulus of Solid Wood Obtained from a Longitudinal Vibration Test. Holzforschung 2021, 75, 428–435. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, H.; Hunt, J.F.; Yan, H. Determining Shear Modulus of Thin Wood Composite Materials Using a Cantilever Beam Vibration Method. Constr. Build. Mater. 2016, 121, 285–289. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Z.Z.; Gu, L.L.; Liu, B.; Wang, Y.L.; Yang, Y. Torsional Vibration Shape Method of Free Plate for Testing Shear Modulus of Lumber. Sci. Silvae Sin. 2014, 50, 122–128. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, W.; Wang, Z.; Cao, Y. Strain Method for Synchronous Dynamic Measurement of Elastic, Shear Modulus and Poisson’s Ratio of Wood and Wood Composites. Constr. Build. Mater. 2018, 182, 608–619. [Google Scholar] [CrossRef]
- Guan, C.; Liu, J.; Zhang, H.; Wang, X.; Zhou, L. Evaluation of Modulus of Elasticity and Modulus of Rupture of Full-Size Wood Composite Panels Supported on Two Nodal-Lines Using a Vibration Technique. Constr. Build. Mater. 2019, 218, 64–72. [Google Scholar] [CrossRef]
- QB/T 2978-2008; Piano Sound Board. China Light Industry Press Ltd.: Beijing, China, 2008.
- Gurukiran, K.; Kumar Samal, P. Experimental Determination of Mode Shapes of a Plate Using Speaker as Excitation Device. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1189, 012029. [Google Scholar] [CrossRef]
- Nakao, T.; Okano, T.; Asano, I. Vibrational properties of a wooden plate. Mokuzai Gakkaishi 1985, 31, 793–800. [Google Scholar]
- Wang, Z.; Zhou, Y.H.; Shen, Z.Y.; He, Y.H. Applicability of Timoshenko Beam Iterative Method to Calculate Wood Elastic Modulus and Shear Modulus. Sci. Silvae Sin. 2022, 58, 173–181. [Google Scholar] [CrossRef]
- Chaigne, A.; Cotté, B.; Viggiano, R. Dynamical Properties of Piano Soundboards. J. Acoust. Soc. Am. 2013, 133, 2456–2466. [Google Scholar] [CrossRef]
- Rescalvo, F.J.; Timbolmas, C.; Bravo, R.; Gallego, A. Experimental and Numerical Analysis of Mixed I-214 Poplar/Pinus Sylvestris Laminated Timber Subjected to Bending Loadings. Materials 2020, 13, 3134. [Google Scholar] [CrossRef]
- Ghafouri, M.; Ghassabi, M.; Zarastvand, M.R.; Talebitooti, R. Sound Propagation of Three-Dimensional Sandwich Panels: Influence of Three-Dimensional Re-Entrant Auxetic Core. AIAA J. 2022, 60, 6374–6384. [Google Scholar] [CrossRef]
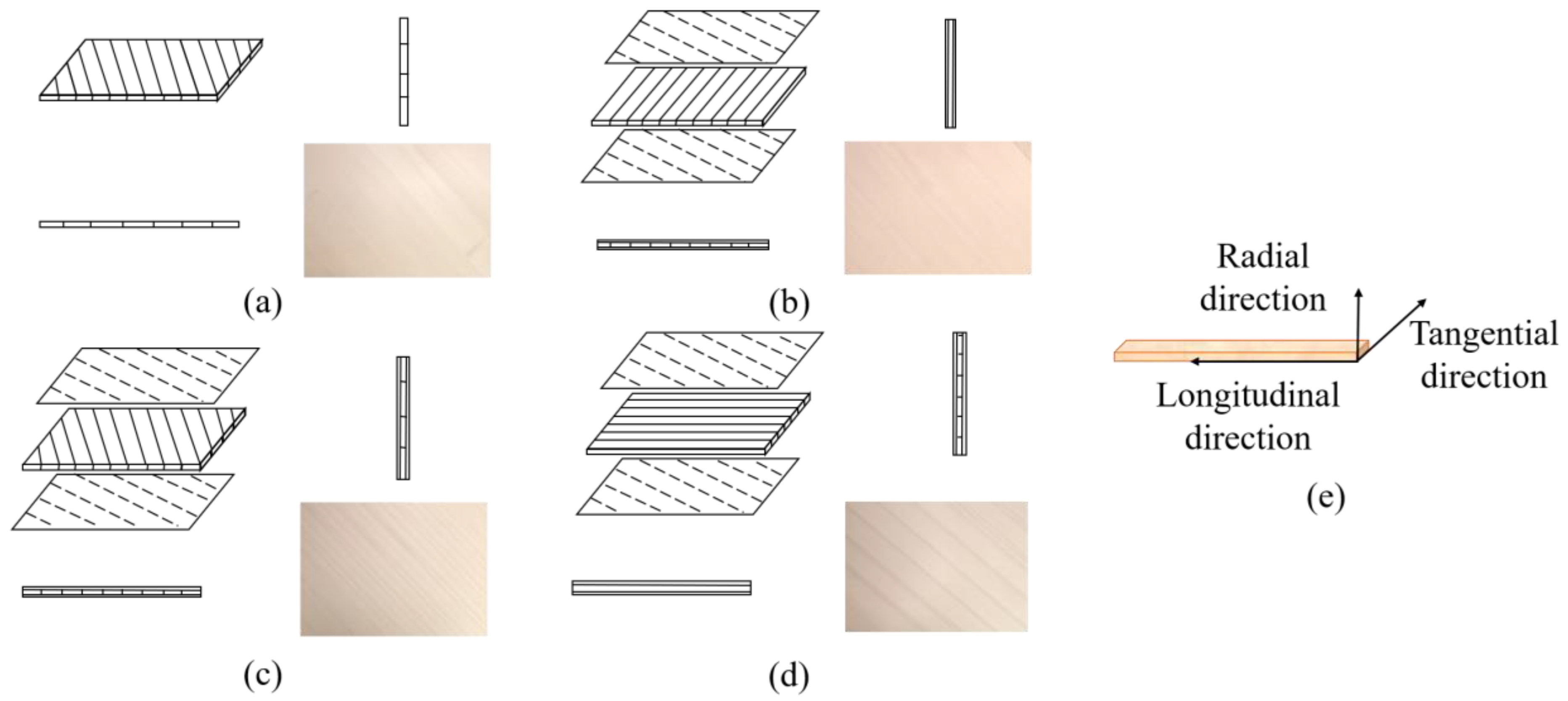
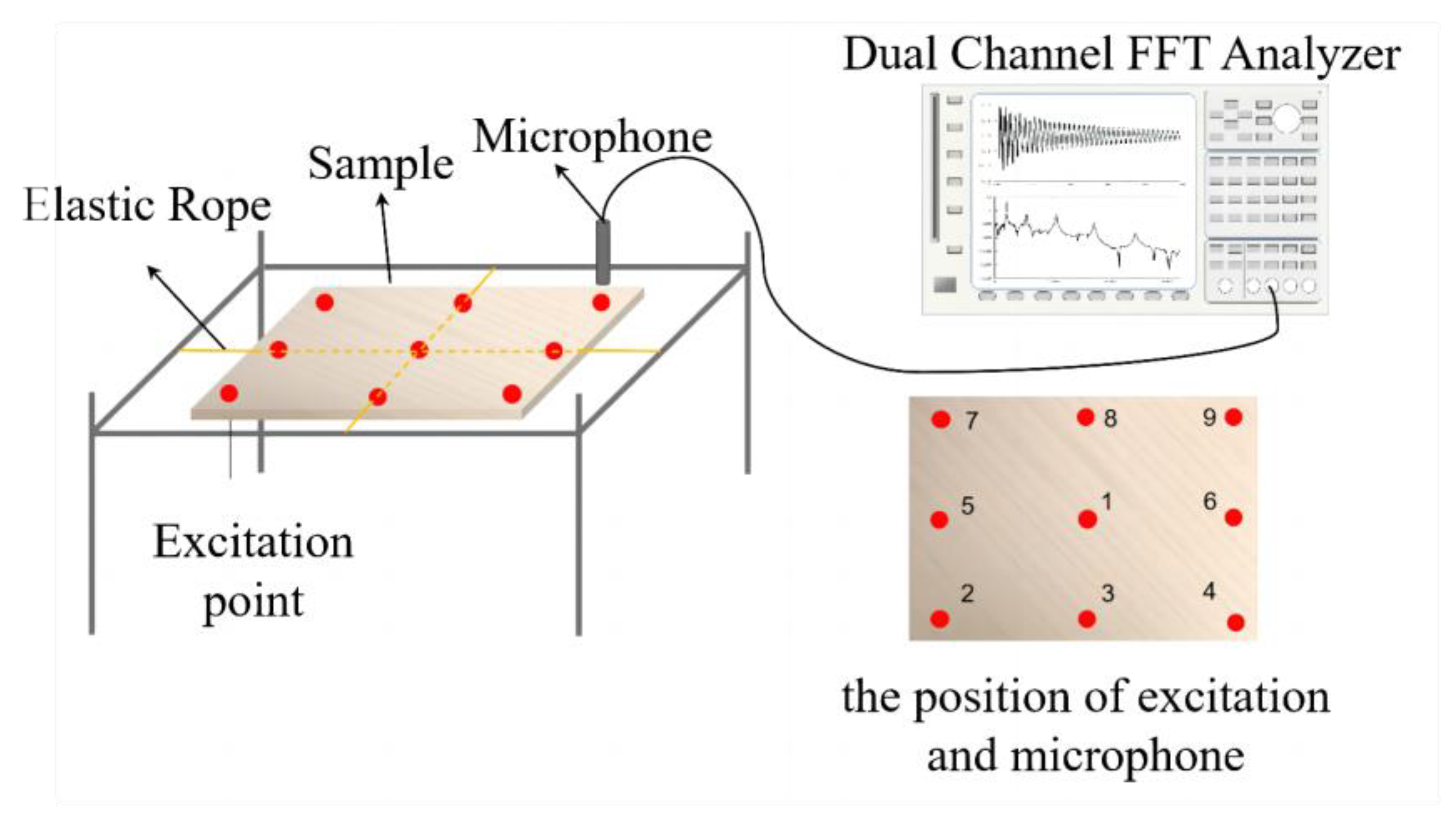
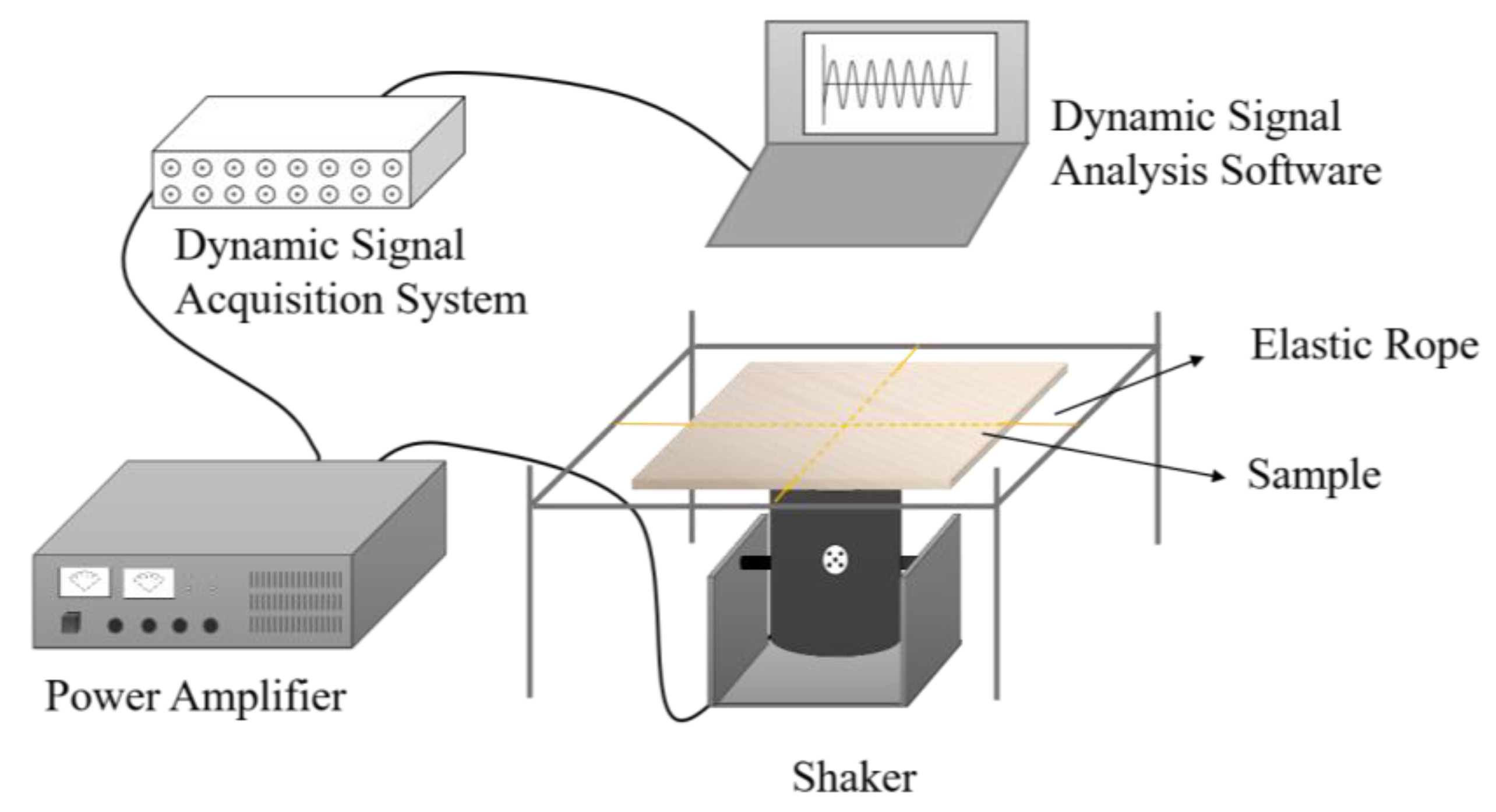

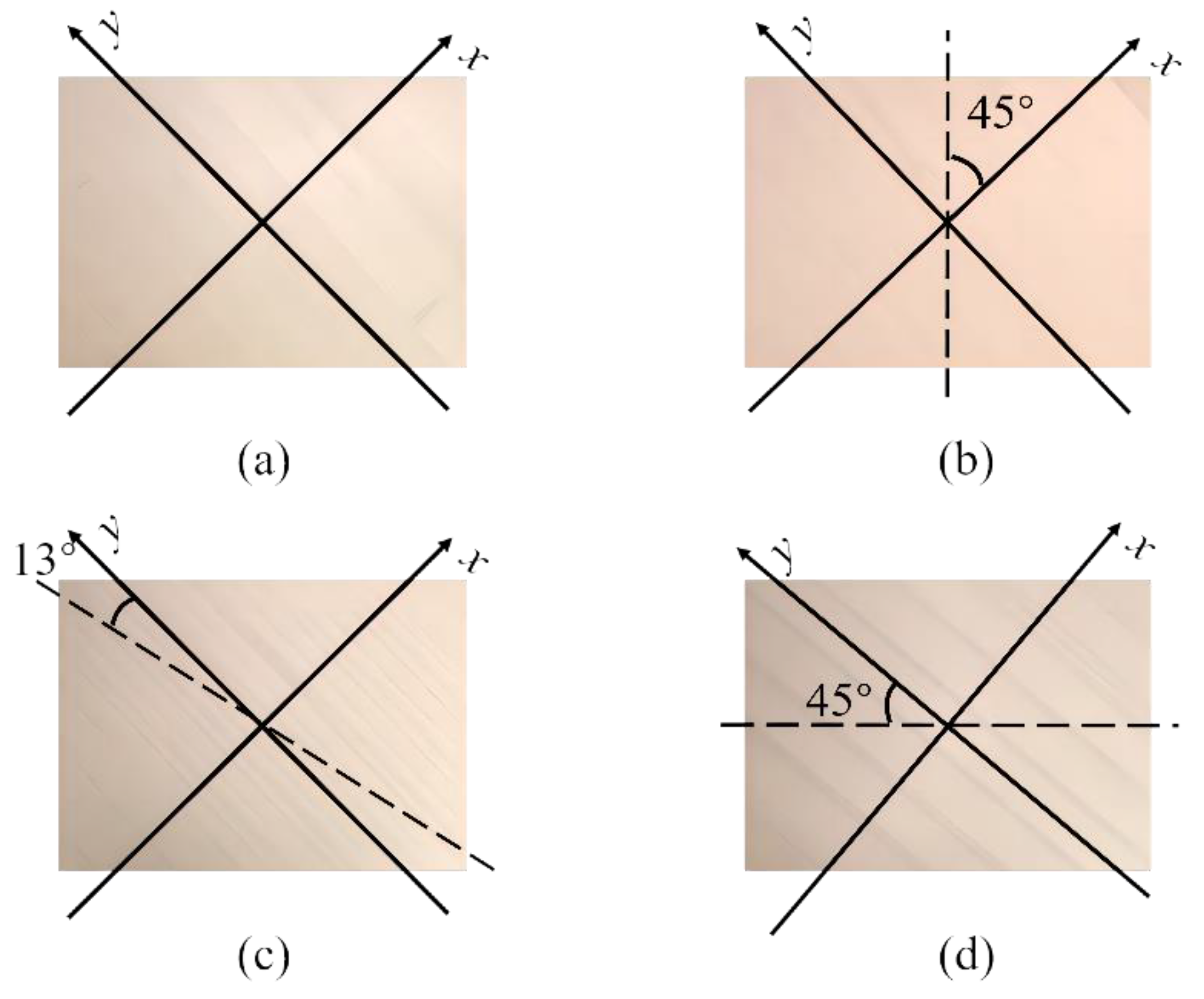
| Sample Group | Type | Core | Angles of the Surface Plate to the Cores | Dimensions (mm) | Density (kg·m−3) |
|---|---|---|---|---|---|
| A | tone-wood soundboard | — | 47° | 698.86 × 497.91 × 9.26 | 481.05 |
| B | laminate soundboard | vertical core | 90°/45° | 698.26 × 498.53 × 7.37 | 443.85 |
| C | laminate soundboard | incline core | 55°/42° | 698.51 × 498.22 × 8.21 | 447.79 |
| D | laminate soundboard | horizontal core | 180°/45° | 699.20 × 496.23 × 7.98 | 415.53 |
| (m,n) | α1 | α2 | α3 | α4 |
|---|---|---|---|---|
| (1,1) | 0 | 0 | 0 | 144 |
| (0,2) | 0 | 500.6 | 0 | 0 |
| (2,0) | 500.6 | 0 | 0 | 0 |
| (2,2) | 500.6 | 500.6 | 151.3 | 2448.3 |
| Sample Group | Excitation Point | Order of Vibration | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (2,0) | (1,1) | (0,2) | (2,2) | ||||||
| f/Hz | A | f/Hz | A | f/Hz | A | f/Hz | A | ||
| A | [2,9] | 20 | 0.543 | 55.3 | 0.102 | 105.3 | 0.143 | 134.8 | 0.057 |
| [4,7] | 20 | 0.042 | 53 | 0.201 | 111.7 | 0.027 | 134.9 | 0.651 | |
| B | [2,9] | 29.5 | 0.158 | 46.4 | 0.045 | 53.2 | 0.109 | 116.6 | 0.137 |
| [4,7] | 30.5 | 0.514 | 42.125 | 0.061 | 55.375 | 1.000 | 118.625 | 0.222 | |
| C | [2,9] | 29 | 0.583 | 55.5 | 0.049 | 110.1 | 0.342 | 139.1 | 0.036 |
| [4,7] | 29 | 0.136 | 55.2 | 0.485 | 110.6 | 0.146 | 138.9 | 0.331 | |
| D | [2,9] | 40 | 1.000 | 91 | 0.271 | 108 | 0.027 | 174.8 | 0.437 |
| [4,7] | 40 | 0.394 | 94 | 0.475 | 108 | 0.061 | 174.6 | 0.029 | |
| Sample Group | Ex (GPa) | ΔEx (GPa) | Ey (GPa) | ΔEy (GPa) | G (GPa) | ΔG (GPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| ExF | ExE | EyF | EyE | GF | GT | ||||
| A | 0.501 (8.7%) | 0.507 (8.7%) | −0.006 | 3.797 (12.6%) | 3.839 (12.6%) | −0.043 | 1.618 (9.3%) | 1.976 (9.3%) | −0.357 |
| B | 1.588 (3.6%) | 1.606 (3.6%) | −0.023 | 1.351 (7.5%) | 1.369 (10.2%) | −0.018 | 1.575 (12.3%) | 1.917 (12.3%) | −0.342 |
| C | 1.169 (5.8%) | 1.268 (12.7%) | −0.013 | 4.702 (11.3%) | 5.141 (18.6%) | −0.044 | 2.040 (10.9%) | 2.680 (17.8%) | −0.64 |
| D | 2.309 (0.6%) | 2.335 (0.6%) | −0.026 | 1.869 (1.4%) | 1.890 (1.4%) | −0.021 | 5.457 (4.2%) | 6.655 (4.3%) | −1.198 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Liang, Y.; Zhang, L.; Zhou, J.; Wang, R.; Liu, Z. Measurement and Analysis of the Vibration Responses of Piano Soundboards with Different Structures. Materials 2024, 17, 1004. https://doi.org/10.3390/ma17051004
He L, Liang Y, Zhang L, Zhou J, Wang R, Liu Z. Measurement and Analysis of the Vibration Responses of Piano Soundboards with Different Structures. Materials. 2024; 17(5):1004. https://doi.org/10.3390/ma17051004
Chicago/Turabian StyleHe, Lan, Yuwei Liang, Liang Zhang, Jing Zhou, Ruofan Wang, and Zhenbo Liu. 2024. "Measurement and Analysis of the Vibration Responses of Piano Soundboards with Different Structures" Materials 17, no. 5: 1004. https://doi.org/10.3390/ma17051004
APA StyleHe, L., Liang, Y., Zhang, L., Zhou, J., Wang, R., & Liu, Z. (2024). Measurement and Analysis of the Vibration Responses of Piano Soundboards with Different Structures. Materials, 17(5), 1004. https://doi.org/10.3390/ma17051004






