A Modified DF2016 Criterion for the Fracture Modeling from Shear to Equibiaxial Tension
Abstract
1. Introduction
2. A Modified DF2016 Fracture Criterion
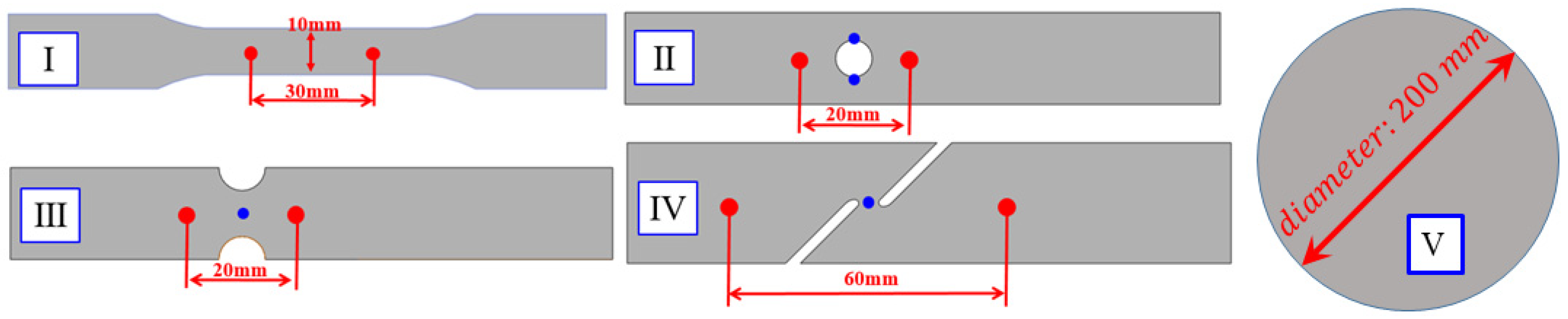
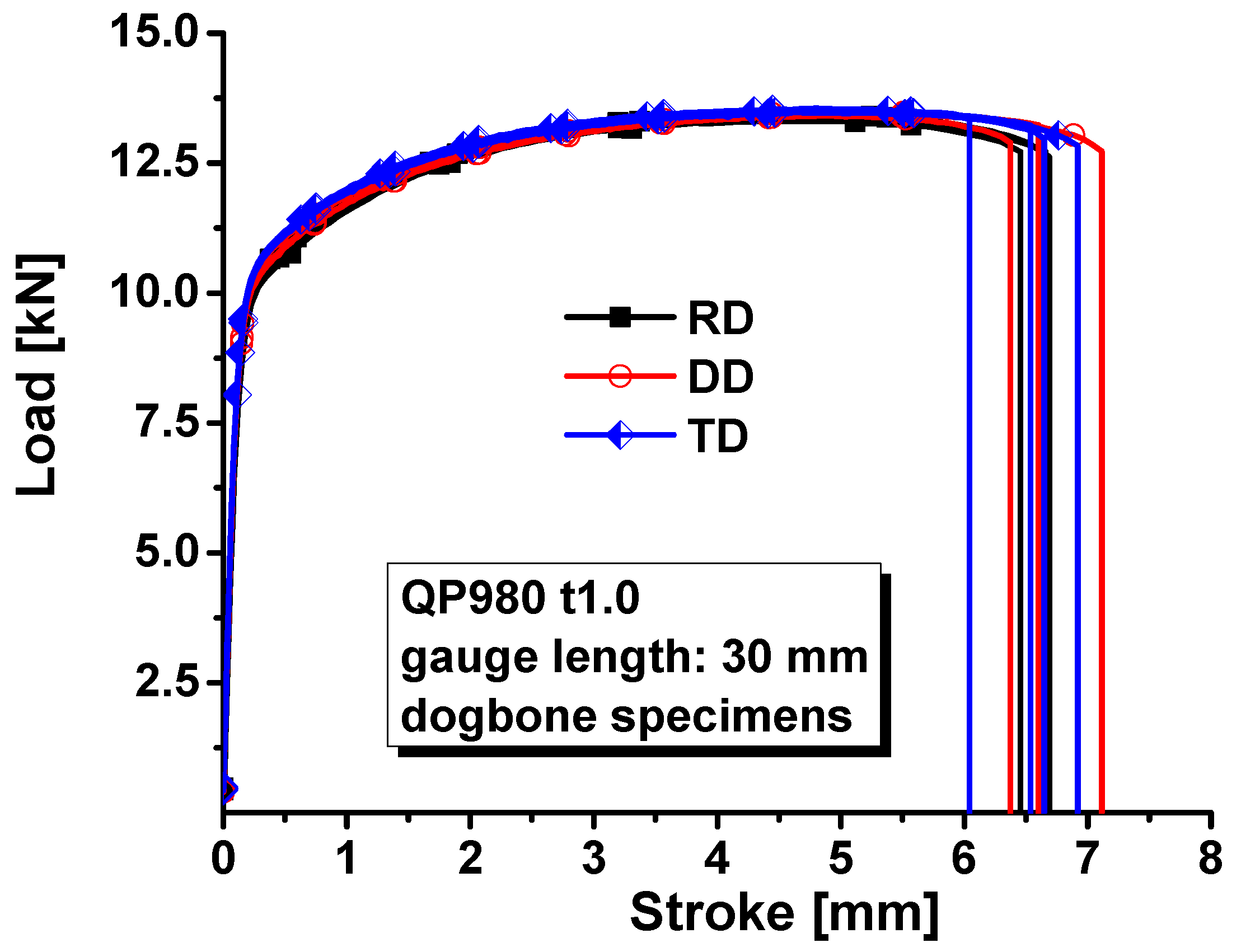
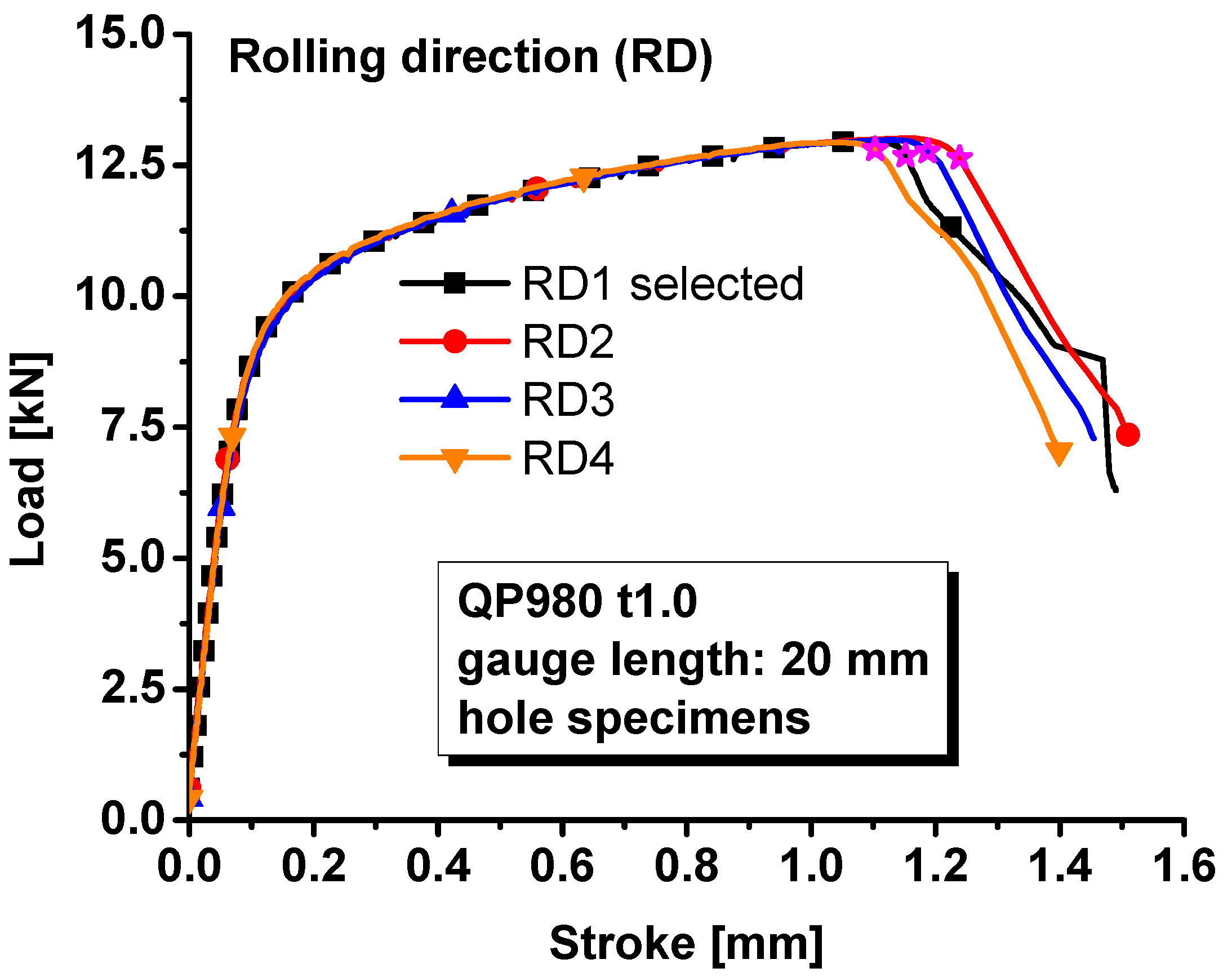
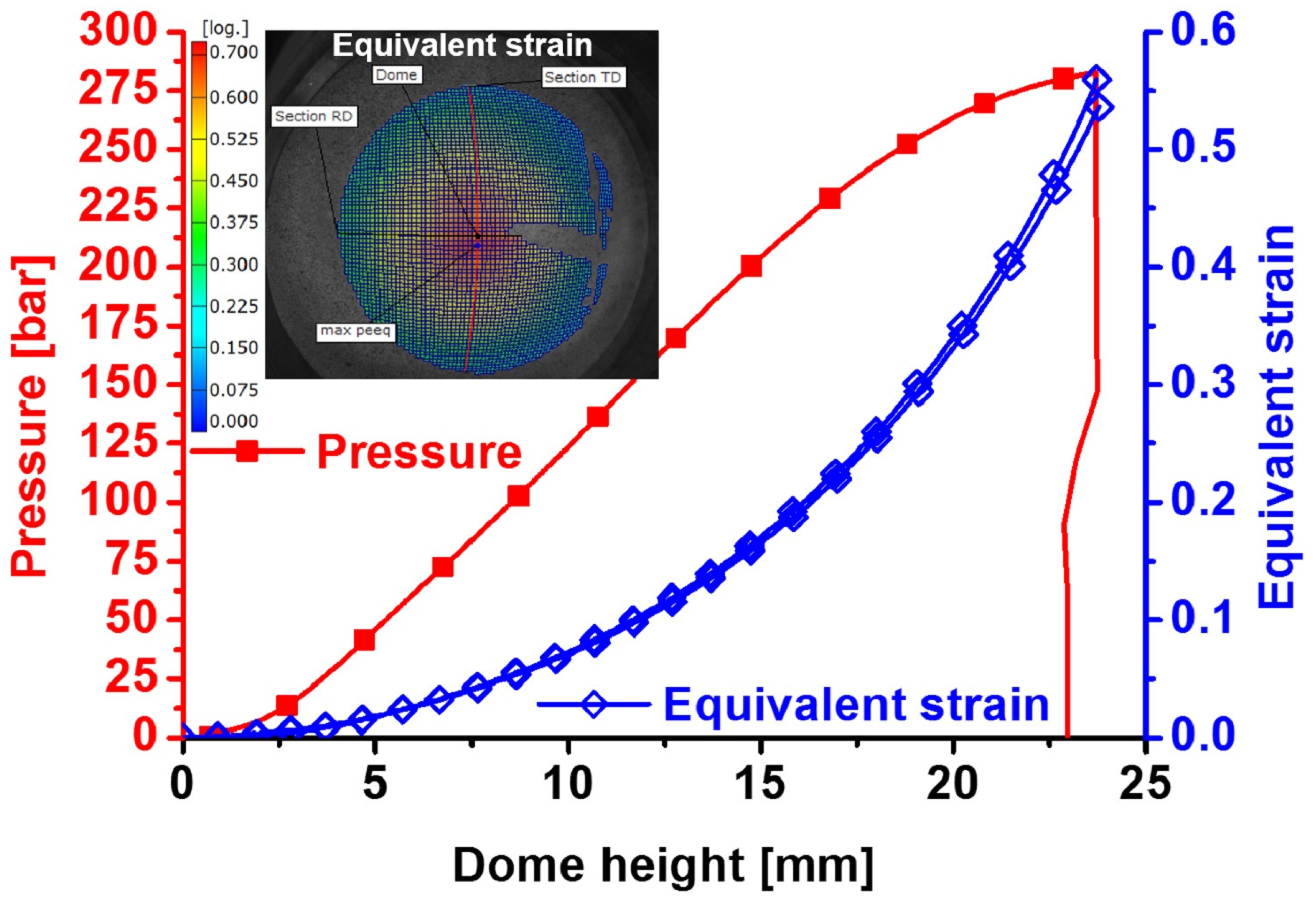
3. Materials and Experiments
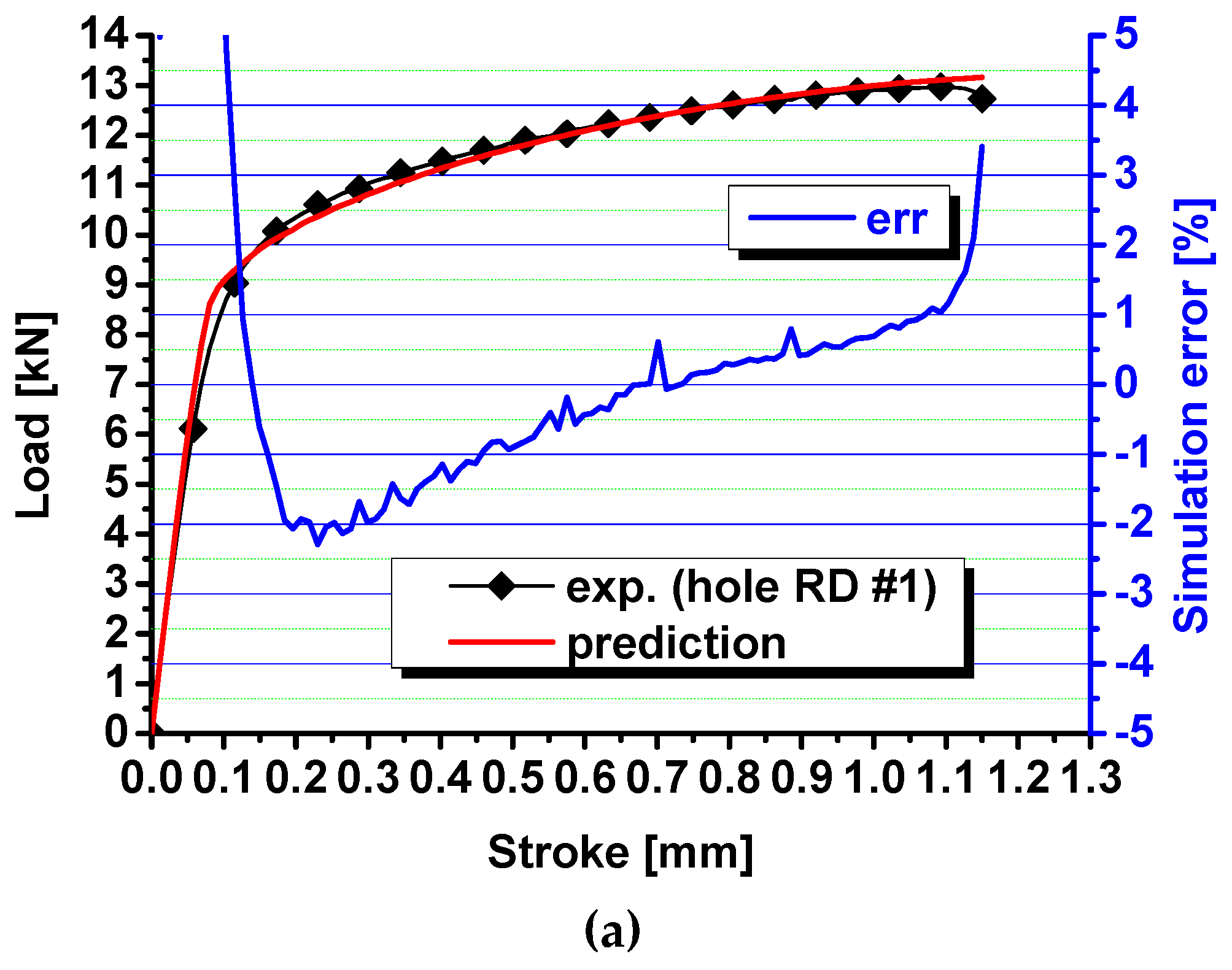
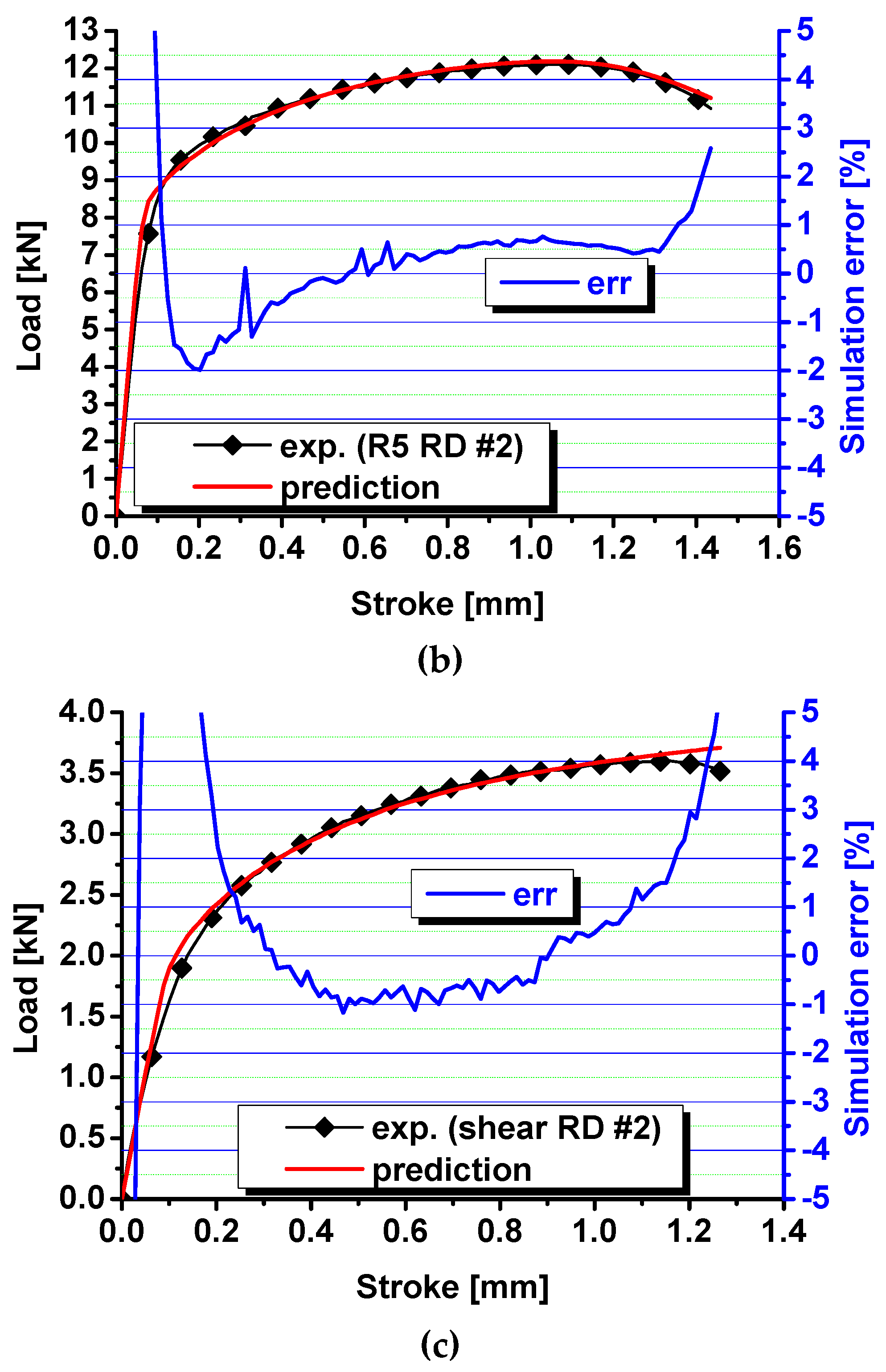
4. Plasticity Modeling
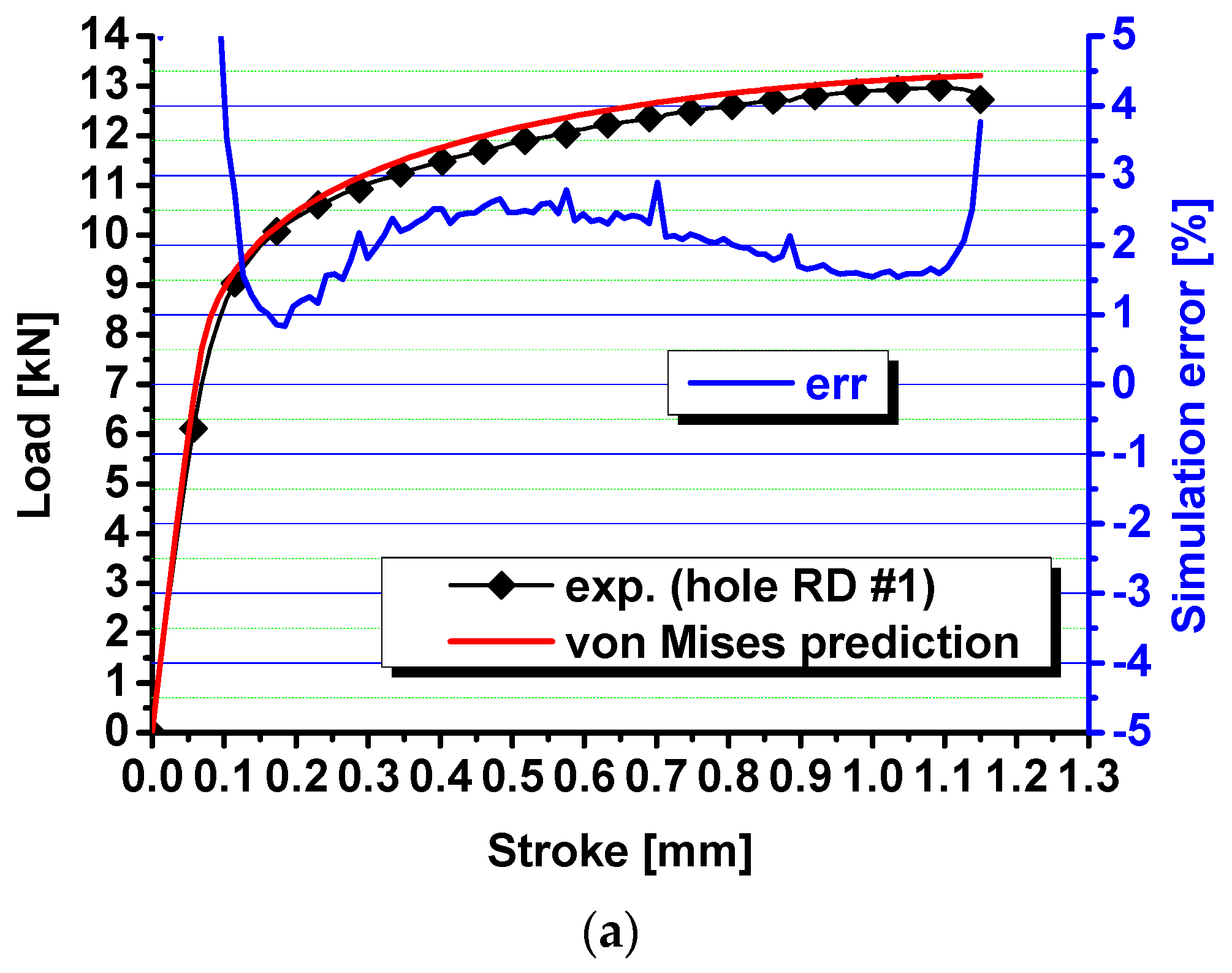
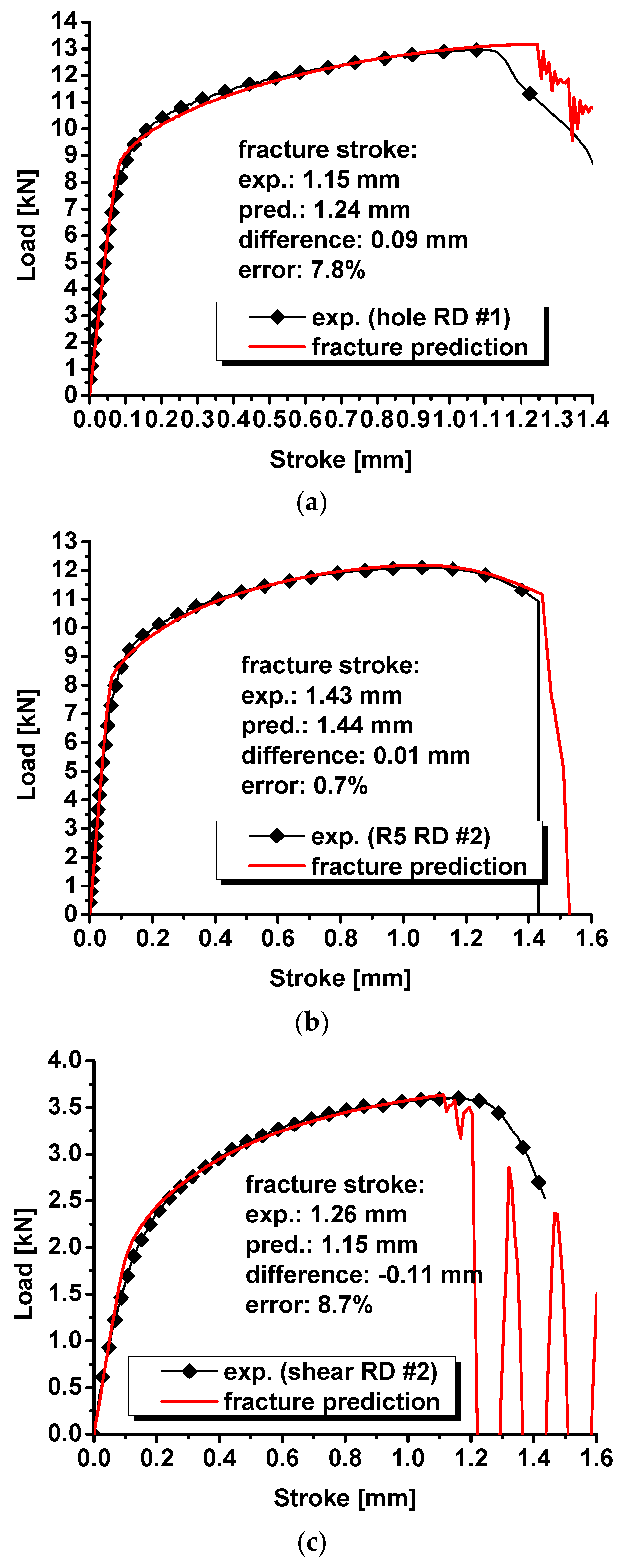
5. Fracture Modeling with the Modified DF2016 Criterion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
- Barlat, F.; Lian, K. Plastic behavior and stretchability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Barlat, F.; Lege, D.J.; Brem, J.C. A six-component yield function for anisotropic materials. Int. J. Plast. 1991, 7, 693–712. [Google Scholar] [CrossRef]
- Barlat, F.; Brem, J.C.; Yoon, J.W.; Chung, K.; Dick, R.; Lege, D.J.; Pourboghrat, F.; Choi, S.-H.; Chu, E. Plane stress yield function for aluminum alloy sheets—Part 1: Theory. Int. J. Plast. 2003, 19, 1297–1319. [Google Scholar] [CrossRef]
- Barlat, F.; Aretz, H.; Yoon, J.W.; Karabin, M.E.; Brem, J.C.; Dick, R.E. Linear transfomation-based anisotropic yield functions. Int. J. Plast. 2005, 21, 1009–1039. [Google Scholar] [CrossRef]
- Banabic, D.; Aretz, H.; Comşa, D.S.; Părăianu, L. An improved analytical description of orthotropy in metallic sheets. Int. J. Plast. 2005, 21, 493–512. [Google Scholar] [CrossRef]
- Aretz, H.; Barlat, F. New convex yield functions for orthotropic metal plasticity. Int. J. Non-Linear Mech. 2013, 51, 97–111. [Google Scholar] [CrossRef]
- Cazacu, O.; Plunkett, B.; Barlat, F. Orthotropic yield criterion for hexagonal closed packed metals. Int. J. Plast. 2006, 22, 1171–1194. [Google Scholar] [CrossRef]
- Cazacu, O. New yield criteria for isotropic and textured metallic materials. Int. J. Solids Struct. 2018, 139–140, 200–210. [Google Scholar] [CrossRef]
- Yoshida, F.; Hamasaki, H.; Uemori, T. A user-friendly 3D yield function to describe anisotropy of steel sheets. Int. J. Plast. 2013, 45, 119–139. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W. Anisotropic yield function based on stress invariants for BCC and FCC metals and its extension to ductile fracture criterion. Int. J. Plast. 2018, 101, 125–155. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. Anisotropic hardening and non-associated flow in proportional loading of sheet metals. Int. J. Plast. 2009, 25, 1777–1817. [Google Scholar] [CrossRef]
- Lee, E.-H.; Stoughton, T.B.; Yoon, J.W. A yield criterion through coupling of quadratic and non-quadratic functions for anisotropic hardening with non-associated flow rule. Int. J. Plast. 2017, 99, 120–143. [Google Scholar] [CrossRef]
- Park, N.S.; Stoughton, T.B.; Yoon, J.W. A criterion for general description of anisotropic hardening considering strength differential effect with non-associated flow rule. Int. J. Plast. 2019, 121, 76–100. [Google Scholar] [CrossRef]
- Hou, Y.; Min, J.; Stoughton, T.B.; Lin, J.; Carsley, J.E.; Carlson, B.E. A non-quadratic pressure-sensitive constitutive model under non-associated flow rule with anisotropic hardening: Modeling and validation. Int. J. Plast. 2020, 135, 102808. [Google Scholar] [CrossRef]
- Hou, Y.; Min, J.; Guo, N.; Shen, Y.; Lin, J. Evolving asymmetric yield surfaces of quenching and partitioning steels: Characterization and modeling. J. Mater. Process. Technol. 2021, 290, 116979. [Google Scholar] [CrossRef]
- Hou, Y.; Du, K.; El-Aty, A.A.; Lee, M.-G.; Min, J. Plastic anisotropy of sheet metals under plane strain loading: A novel non-associated constitutive model based on fourth-order polynomial functions. Mater. Des. 2022, 223, 111187. [Google Scholar] [CrossRef]
- Hou, Y.; Min, J.; Lin, J.; Lee, M.-G. Modeling stress anisotropy, strength differential, and anisotropic hardening by coupling quadratic and stress-invariant-based yield functions under non-associated flow rule. Mech. Mater. 2022, 174, 104458. [Google Scholar] [CrossRef]
- Hu, Q.; Yoon, J.W.; Manopulo, N.; Hora, P. A coupled yield criterion for anisotropic hardening with analytical description under associated flow rule: Modeling and validation. Int. J. Plast. 2021, 136, 102882. [Google Scholar] [CrossRef]
- Hu, Q.; Yoon, J.W. Analytical description of an asymmetric yield function (Yoon2014) by considering anisotropic hardening under non-associated flow rule. Int. J. Plast. 2021, 140, 102978. [Google Scholar] [CrossRef]
- Hu, Q.; Yoon, J.W.; Stoughton, T.B. Analytical determination of anisotropic parameters for Poly6 yield function. Int. J. Mech. Sci. 2021, 201, 106467. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, J.; Yoon, J.W. A new asymmetric yield criterion based on Yld 2000-2d under both associated and non-associated flow rules: Modeling and validation. Mech. Mater. 2022, 167, 104245. [Google Scholar] [CrossRef]
- Hu, Q.; Yoon, J.W.; Chen, J. Analytically described polynomial yield criterion by considering both plane strain and pure shear states. Int. J. Plast. 2023, 162, 103514. [Google Scholar] [CrossRef]
- Du, K.; Huang, S.; Hou, Y.; Wang, H.; Wang, Y.; Zheng, W.; Yuan, X. Characterization of the asymmetric evolving yield and flow of 6016-T4 aluminum alloy and DP490 steel. J. Mater. Sci. Technol. 2023, 133, 209–229. [Google Scholar] [CrossRef]
- Hu, Q.; Li, X.; Han, X.; Li, H.; Chen, J. A normalized stress invariant-based yield criterion: Modeling and validation. Int. J. Plast. 2017, 99, 248–273. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, C.; Zhang, S.; Yoon, J.W. A general yield function with differential and anisotropic hardening for strength modelling under various stress states with non-associated flow rule. Int. J. Plast. 2022, 158, 103414. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W. Lode-dependent anisotropic-asymmetric yield function for isotropic and anisotropic hardening of pressure-insensitive materials. Part I: Quadratic function under non-associated flow rule. Int. J. Plast. 2023, 166, 103647. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr–Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H.; Lim, S.; Pack, K. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals. Int. J. Solids Struct. 2012, 49, 3605–3615. [Google Scholar] [CrossRef]
- Lou, Y.; Chen, L.; Clausmeyer, T.; Tekkaya, A.E.; Yoon, J.W. Modeling of ductile fracture from shear to balanced biaxial tension for sheet metals. Int. J. Solids Struct. 2017, 112, 169–184. [Google Scholar] [CrossRef]
- Mu, L.; Jia, Z.; Ma, Z.; Shen, F.; Sun, Y.; Zang, Y. A theoretical prediction framework for the construction of a fracture forming limit curve accounting for fracture pattern transition. Int. J. Plast. 2020, 129, 102706. [Google Scholar] [CrossRef]
- Ganjiani, M.; Homayounfard, M. Development of a ductile failure model sensitive to stress triaxiality and Lode angle. Int. J. Solids Struct. 2021, 225, 111066. [Google Scholar] [CrossRef]
- Hu, Q.; Li, X.; Han, X.; Chen, J. A new shear and tension based ductile fracture criterion: Modeling and validation. Eur. J. Mech. A-Solid. 2017, 66, 370–386. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, K.; Jiang, Y.; Wan, M.; Meng, B. A new ductile failure criterion for micro/meso scale forming limit prediction of metal foils considering size effect and free surface roughening. Int. J. Plast. 2022, 157, 103406. [Google Scholar] [CrossRef]
- Zhang, T.; Yuan, H.; Yang, S. Fracture energy and tensile strength depending on stress triaxiality along a running crack front in three-dimensional cohesive modeling. Eng. Fract. Mech. 2020, 227, 106919. [Google Scholar] [CrossRef]
- Quach, H.; Kim, J.-J.; Nguyen, D.-T.; Kim, Y.-S. Uncoupled ductile fracture criterion considering secondary void band behaviors for failure prediction in sheet metal forming. Int. J. Mech. Sci. 2020, 169, 105297. [Google Scholar] [CrossRef]
- Shang, X.; Cui, Z.; Fu, M.W. A ductile fracture model considering stress state and Zener–Hollomon parameter for hot deformation of metallic materials. Int. J. Mech. Sci. 2018, 144, 800–812. [Google Scholar] [CrossRef]
- Weck, A.; Wilkinson, D. Experimental investigation of void coalescence in metallic sheets containing laser drilled holes. Acta Mater. 2008, 56, 1774–1784. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W.; Huh, H.; Chao, Q.; Song, J.H. Correlation of the maximum shear stress with micro-mechanisms of ductile fracture for metals with high strength-to-weight ratio. Int. J. Mech. Sci. 2018, 146, 583–601. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, H. A new approach for ductile fracture prediction on Al 2024-T351 alloy. Int. J. Plast. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. A new approach for failure criterion for sheet metals. Int. J. Plast. 2011, 27, 440–459. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S.J. Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracturev initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67–68, 40–55. [Google Scholar] [CrossRef]
- Lou, Y.; Wu, P.; Zhang, C.; Wang, J.; Li, X.; Chai, R.; Yoon, J.W. A stress-based shear fracture criterion considering the effect of stress triaxiality and Lode parameter. Int. J. Solids Struct. 2022, 256, 111993. [Google Scholar] [CrossRef]
- Beese, A.M.; Luo, M.; Li, Y.; Bai, Y.; Wierzbicki, T. Partially coupled anisotropic fracture model for aluminum sheets. Eng. Fract. Mech. 2010, 77, 1128–1152. [Google Scholar] [CrossRef]
- Luo, M.; Dunand, M.; Mohr, D. Experiments and modeling of anisotropic aluminum extrusions under multi-axial loading–Part II: Ductile fracture. Int. J. Plast. 2012, 32, 36–58. [Google Scholar] [CrossRef]
- Jia, Y.; Bai, Y. Ductile fracture prediction for metal sheets using all-strain-based anisotropic eMMC model. Int. J. Mech. Sci. 2016, 115, 516–531. [Google Scholar] [CrossRef]
- Lou, Y.; Yoon, J.W. Anisotropic ductile fracture criterion based on linear transformation. Int. J. Plast. 2017, 93, 3–25. [Google Scholar] [CrossRef]
- Park, S.-J.; Lee, K.S.; Nam, W.S.; Kim, K.H.; Park, B.J. Numerical Study on a Ductile Fracture Model in Pre-Cracked Tension Tests of SUS304L. Materials 2024, 17, 276. [Google Scholar] [CrossRef]
- Baral, M.; Ha, J.; Korkolis, Y.P. Plasticity and ductile fracture modeling of an Al–Si–Mg die-cast alloy. Int. J. Fract. 2019, 216, 101–121. [Google Scholar] [CrossRef]
- Bidadi, J.; Googarchin, H.S.; Akhavan-Safar, A.; Silva, L.F.M. Effects of Mode Mixity and Loading Rate on Fracture Behavior of Cracked Thin-Walled 304L Stainless Steel Sheets with Large Non-Linear Plastic Deformation. Materials 2023, 16, 7690. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.S.; Liu, H. Strain rate and temperature dependent fracture criteria for isotropic and anisotropic metals. Int. J. Plast. 2012, 37, 1–15. [Google Scholar] [CrossRef]
- Wcisli, W.; Lipiec, S. Voids development in metals: Numerical modelling. Materials 2023, 16, 4998. [Google Scholar] [CrossRef] [PubMed]
- Baral, M.; Korkolis, Y.P. Ductile fracture under proportional and non-proportional multiaxial loading. Int. J. Solids Struct. 2021, 210–211, 88–108. [Google Scholar] [CrossRef]
- Alrasheedi, N.H.; Ataya, S.; Seleman, M.M.E.-S.; Ahmed, M.M.Z. Tensile Deformation and Fracture of Unreinforced AZ91 and Reinforced AZ91-C at Temperatures up to 300 °C. Materials 2023, 16, 4785. [Google Scholar] [CrossRef] [PubMed]
- Ha, J.; Baral, M.; Korkolis, Y.P. Ductile fracture of an aluminum sheet under proportional loading. J. Mech. Phys. Solids 2019, 132, 103685. [Google Scholar] [CrossRef]
- Egidio, G.D.; Martini, C.; Borjesson, J.; Ghassemali, E.; Ceschini, L.; Morri, A. Influence of Microstructure on Fracture Mechanisms of the Heat-Treated AlSi10Mg Alloy Produced by Laser-Based Powder Bed Fusion. Materials 2023, 16, 2006. [Google Scholar] [CrossRef] [PubMed]
- Korkolis, Y.P.; Kyriakides, S. Path-dependent failure of inflated aluminum tubes. Int. J. Plast. 2009, 25, 2059–2080. [Google Scholar] [CrossRef]
- Torabi, A.R.; Mirzavand, M.; Saboori, B.; Cicero, S. Fracture Behavior of AA7075-AA6061 and AA7075-Cu Friction-Stir Welded Joints Containing Blunt V-Notches under Opening-Mode Loading. Materials 2023, 16, 1757. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling. Int. J. Plast. 2014, 56, 19–44. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Chen, Z.; Yang, N.; Lou, Y.; Clausmeyer, T.; Tekkaya, A.E.; Zhang, Q. Charaterization of plasticity and fracture of an QP1180 steel sheet. Procedia Manuf. 2020, 50, 529–534. [Google Scholar] [CrossRef]
- Lou, Y.; Chen, Z.; Zhang, C.; Jiang, N.; Yang, G. Charaterization of anisotropic hardening of AA3003-O. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1270, 012120. [Google Scholar] [CrossRef]







| K [GPa] | e0 | n | A [GPa] | B [GPa] | C | ||
|---|---|---|---|---|---|---|---|
| Swift | 1.6562 | 0.0014 | 0.1451 | \ | \ | \ | \ |
| Voce | \ | \ | \ | 1.2543 | 0.7393 | 21.5435 | \ |
| Swift–Voce | 1.6562 | 0.0014 | 0.1451 | 1.2543 | 0.7393 | 21.5435 | 1.0262 |
| pDrucker | Swift–Voce Hardening Law | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | K [GPa] | e0 | n | A [GPa] | B [GPa] | C | |
| 1.8769 | −0.02486 | 1.2692 | 1.796 | 0.0080 | 0.1862 | 1.4050 | 0.6993 | 15.2893 | 0.5 |
| C1 | C2 | C3 | C4 | C |
|---|---|---|---|---|
| 0.0654 | 1.1221 | 0.5361 | 4.542 | 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Yan, R.; Fang, X. A Modified DF2016 Criterion for the Fracture Modeling from Shear to Equibiaxial Tension. Materials 2024, 17, 958. https://doi.org/10.3390/ma17040958
Xu X, Yan R, Fang X. A Modified DF2016 Criterion for the Fracture Modeling from Shear to Equibiaxial Tension. Materials. 2024; 17(4):958. https://doi.org/10.3390/ma17040958
Chicago/Turabian StyleXu, Xiaona, Ruqiang Yan, and Xucheng Fang. 2024. "A Modified DF2016 Criterion for the Fracture Modeling from Shear to Equibiaxial Tension" Materials 17, no. 4: 958. https://doi.org/10.3390/ma17040958
APA StyleXu, X., Yan, R., & Fang, X. (2024). A Modified DF2016 Criterion for the Fracture Modeling from Shear to Equibiaxial Tension. Materials, 17(4), 958. https://doi.org/10.3390/ma17040958






