A New Approach for Predicting Strength Based on Temperature-Time History Using Two-Parameter Maturity ANN Models
Abstract
1. Introduction
| Maturity Estimation Model | |
|---|---|
| Nurse-Saul [9] | M = ∑(T − To)·Δt, |
| Rastrup [10] | te = ∑(T − To)·(Tr − To)·Δt |
| Hansen and Pedersen [8] | te = ∑exp(−E/R)[1/T − 1/Tr]·Δt |
| Carino et al. [11] | te = ∑exp{B(T − Tr)}·Δt |
| Strength Prediction Model | |
| Plowman [12] | S = a + b·log(M) |
| Lew and Reichard [13] | S = K/{1+K·a·[log(M − 30)] b} |
| Hansen and Pedersen [14,15] | S = Su·exp{−[τ/M]α} |
| Gompertz [16] | S = Su·exp(−a·e − b·logM) |
| ASTM C 1074 [17,18] | S = Su·k·(t − to)/{1 + k·(t − to)} |
- (a)
- Can the ANN method produce a model that accurately describes the relationship between mortar strength, temperature, and time?
- (b)
- Does incorporating two predictive parameters—heat of hydration (Q) and activation energy (Ea)—into the model improve its description of mortar strength development, both at early and late ages?
- (c)
- How can the ANN-based model, fc% = f(Q, E, T, t), be used to calculate the relative strength of mortar as it depends on variations in curing temperature and time?
2. Materials and Methods
2.1. Materials
- -
- Standard sand (0–2 mm grain size) in accordance with CEN PN-EN 196-1.
- -
- Six different cements: five Portland cements (CEM I) and one slag cement (CEM III/A).
- -
- A plasticiser.
2.2. Mixture Proportions and Sample Preparation
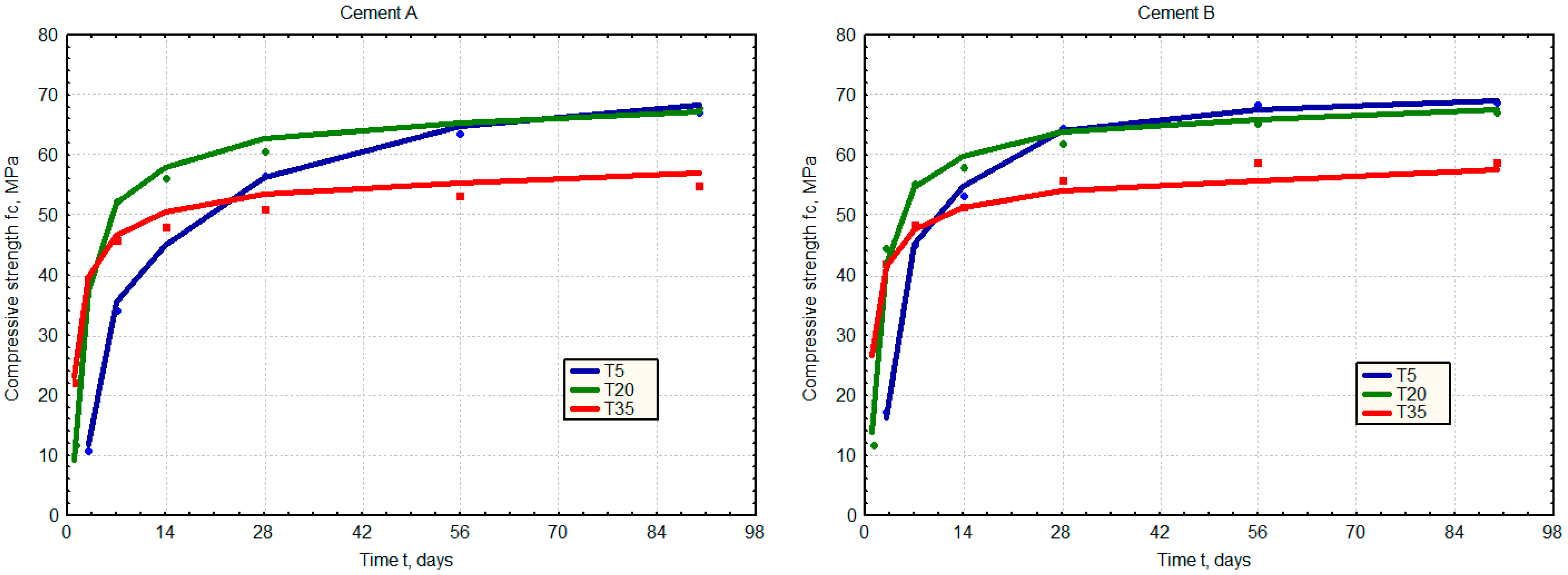
2.3. Compressive Strength
3. Results and Discussion
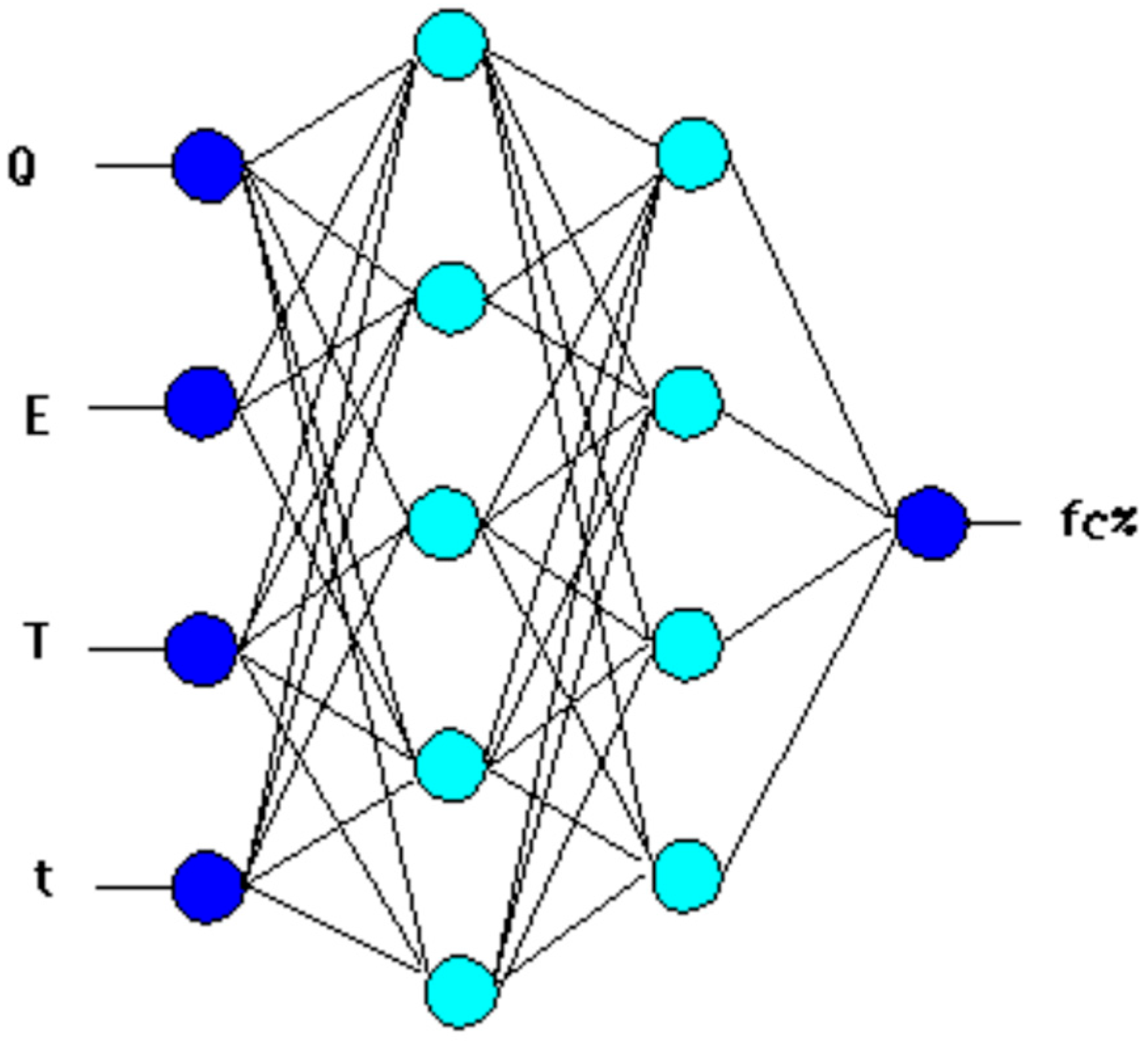
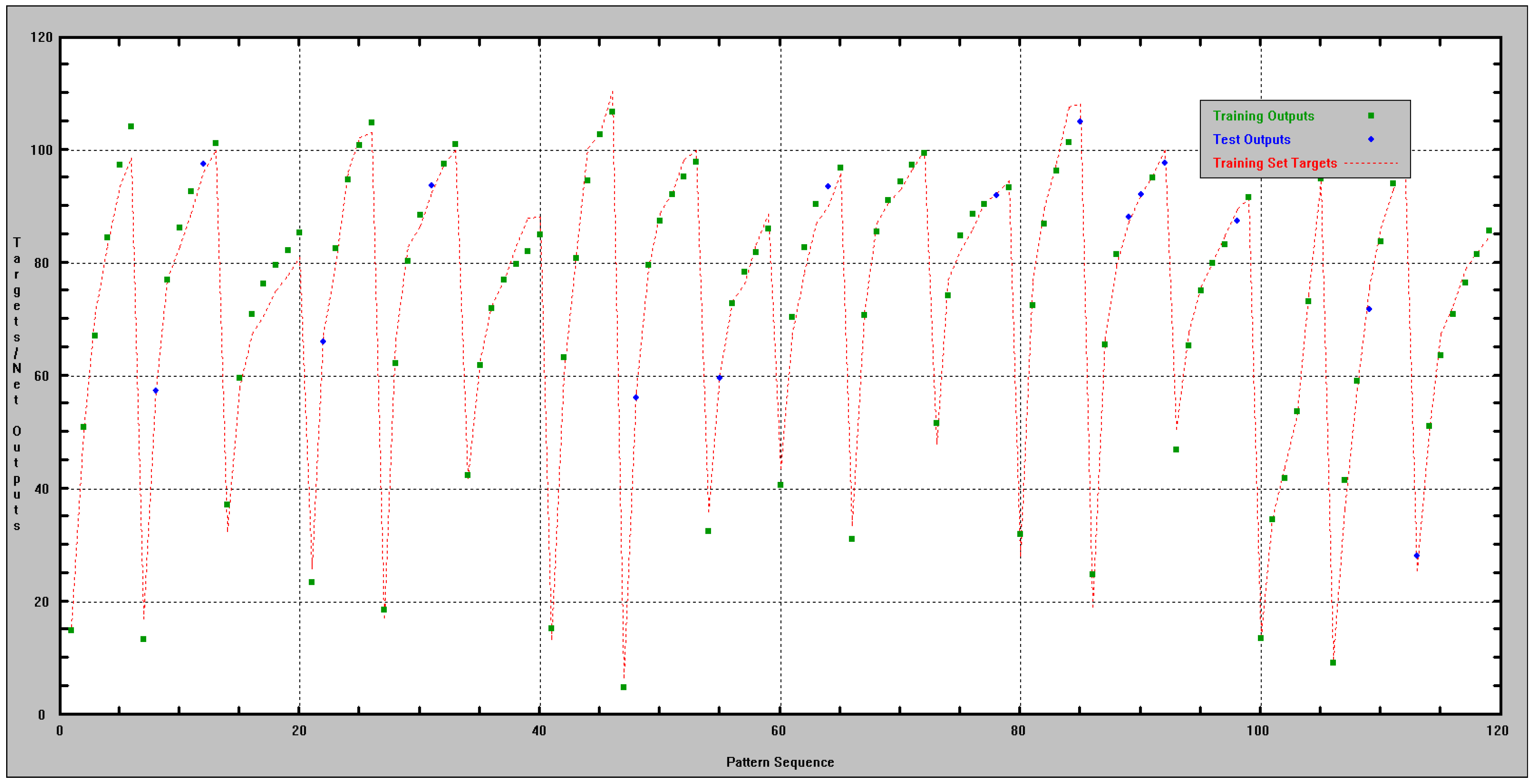
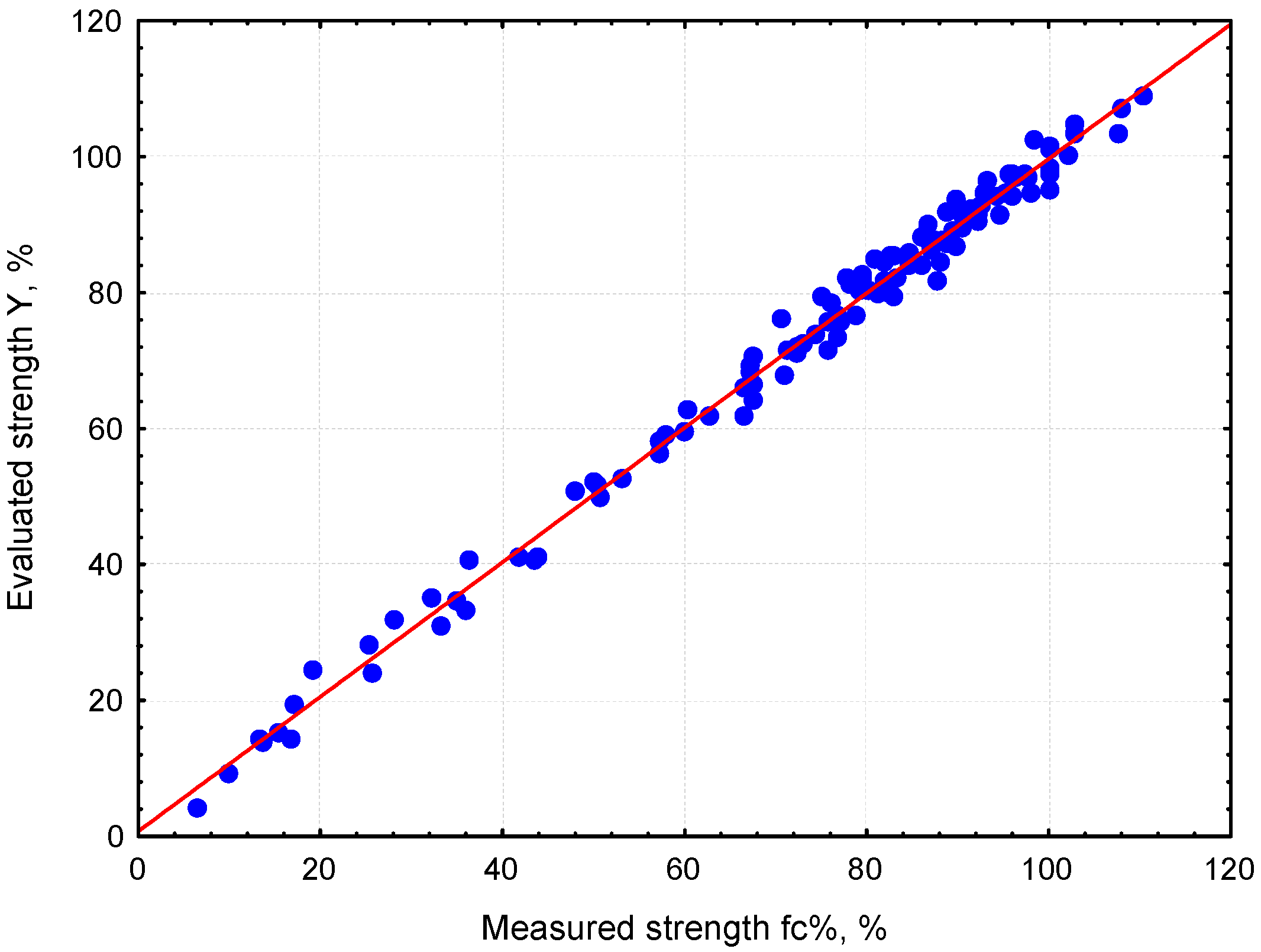
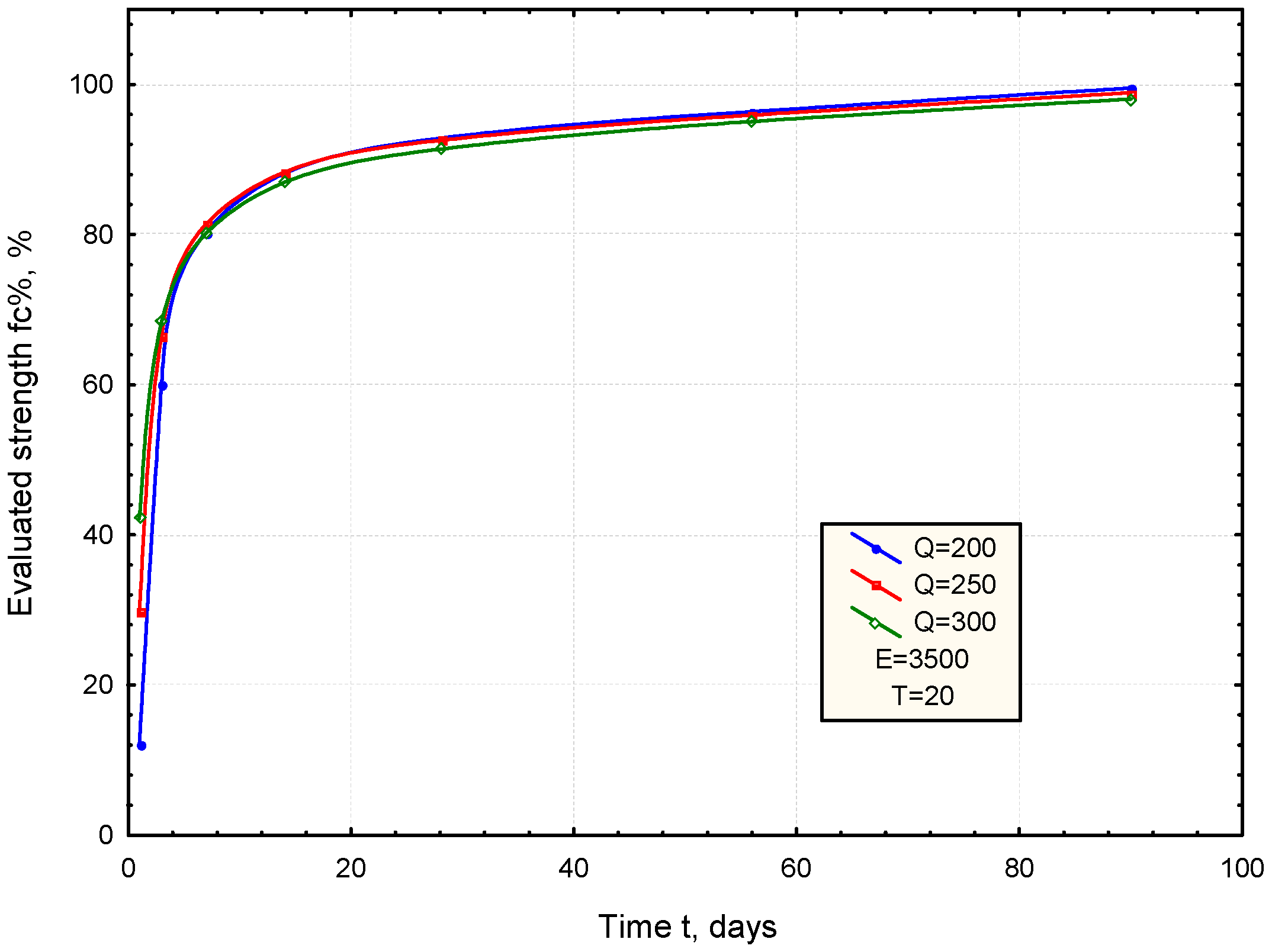
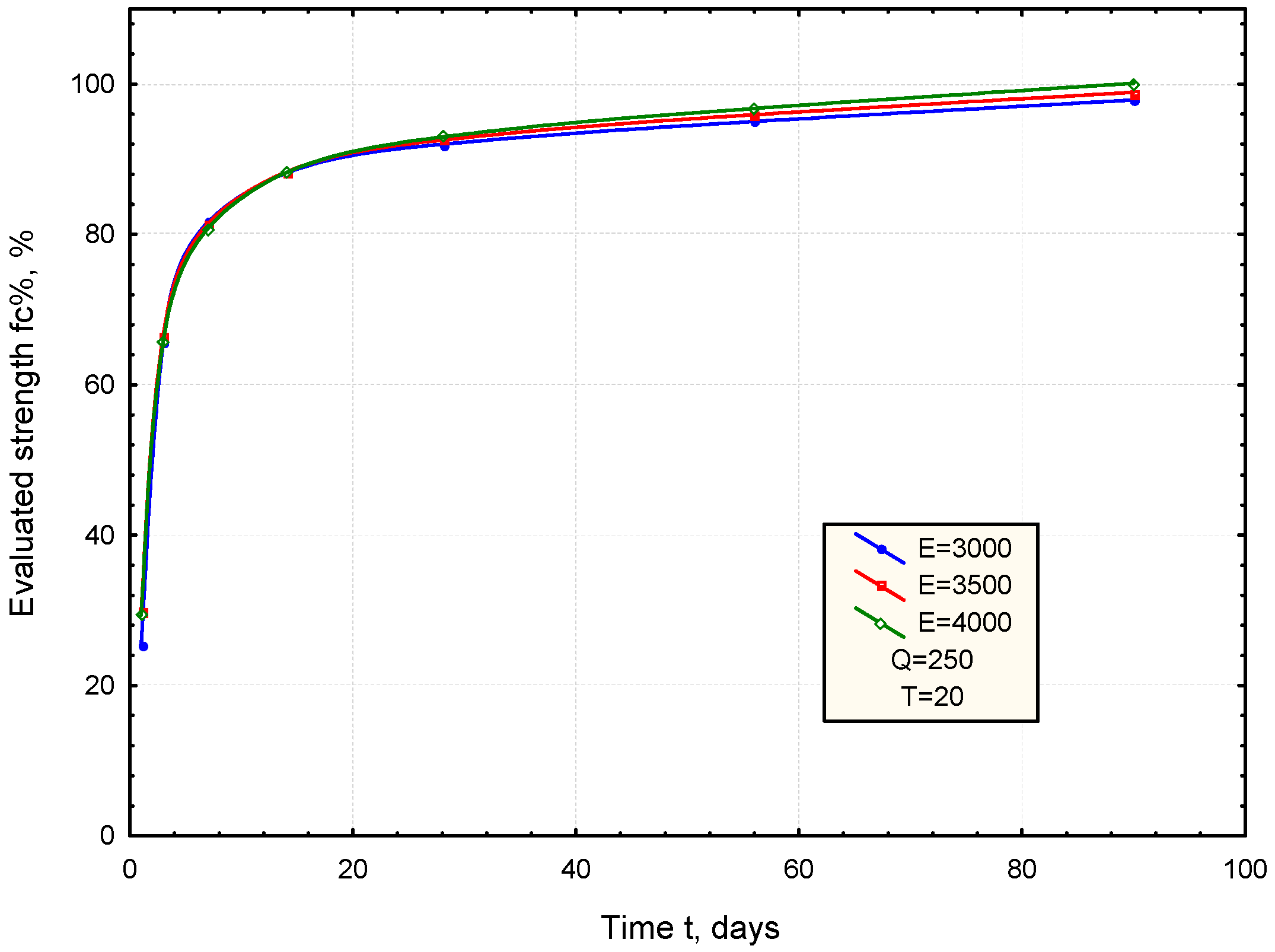
3.1. ANN Model for Prediction of Strength Development
- -
- Q: Hydration heat of the cement after 48 h, J/g,
- -
- E: Activation temperature of the cement, °C,
- -
- T: Temperature of the mortar, °C,
- -
- t: Curing time, days.
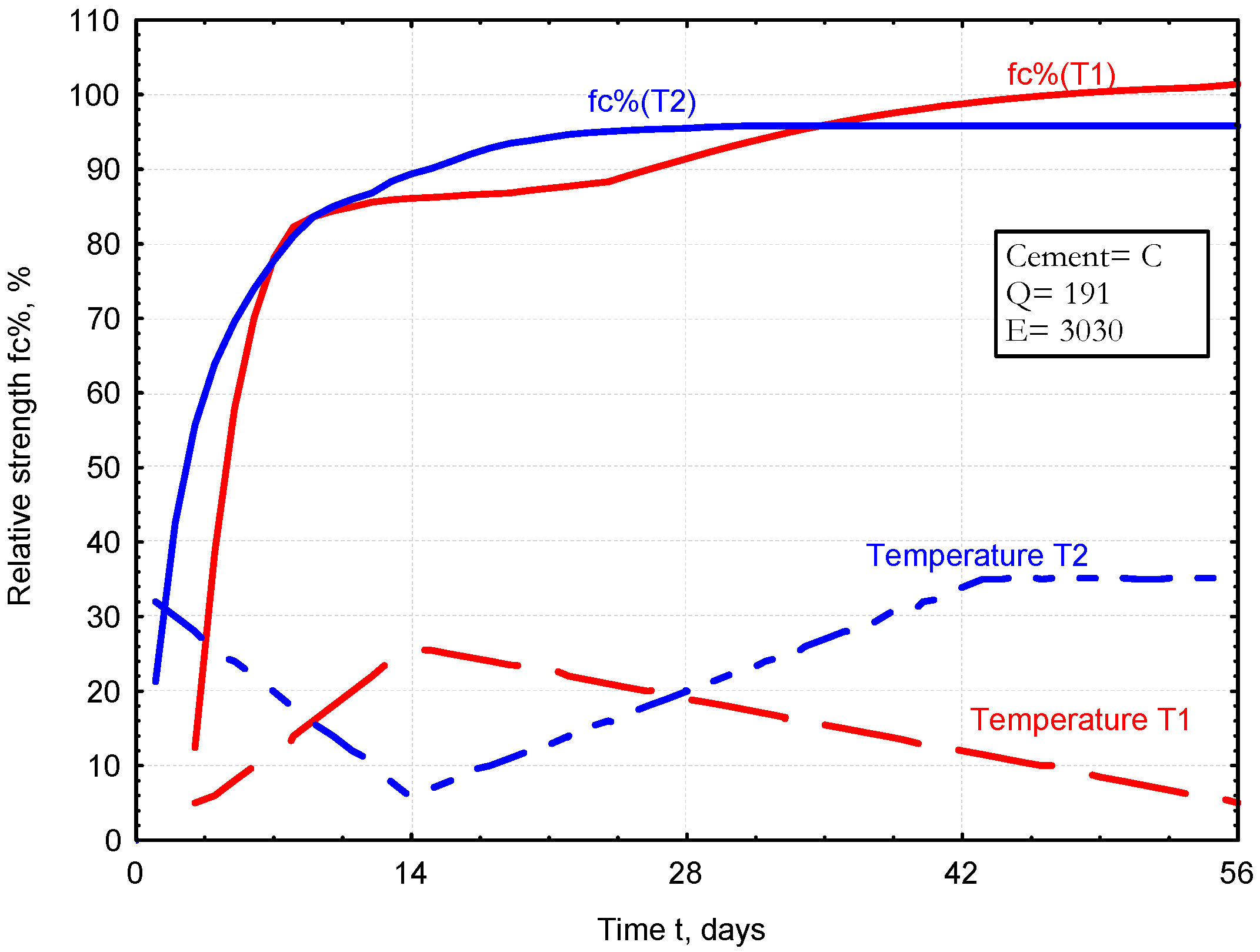
3.2. Application of the Developed ANN-fc% Network for Predicting Hardened Mortar Strength
- -
- Calculations are performed for a fixed time step dt.
- -
- Within the interval dt at a given temperature, the strength increment is dYi (%).
- -
- After time t = n × dt, the strength level is Y at the current temperature T1.
- -
- If the temperature changes to T2 in the next time step, the time at which the strength level Y is reached at this temperature must be calculated, along with the strength increment dY2.
- -
- In subsequent time steps, further strength increments dYi are calculated.
- -
- The increase in strength with changing temperature cannot be negative dY ≥ 0.
- -
- The final strength Y after a certain time t is the sum of the individual increments dYi, as shown in the lower right corner of the diagram.
- -
- The process is repeated until the final time is reached.

4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carino, N.J. The maturity method: Theory and application. ASTM J. Cem. Concr. Aggreg. 1984, 6, 61–73. [Google Scholar] [CrossRef]
- Jin, N.J.; Yeon, K.-S.; Min, S.-H.; Yeon, J. Using the Maturity Method in Predicting the Compressive Strength of Vinyl Ester Polymer Concrete at an Early Age. Adv. Mater. Sci. Eng. 2017, 12, 4546732. [Google Scholar] [CrossRef]
- Saul, A.G.A. Principles underlying the steam curing of concrete at atmospheric pressure. Mag. Concr. Res. 1951, 2, 127–140. [Google Scholar] [CrossRef]
- Rastrup, E. Heat of hydration in concrete. Mag. Concr. Res. 1954, 6, 79–92. [Google Scholar] [CrossRef]
- Carino, N.J.; Lew, H.S.; Volz, C.K. Early age temperature effects on concrete strength prediction by the maturity method. ACI J. Proc. 1983, 80, 93–101. [Google Scholar]
- Plowman, J.M. Maturity and the strength of concrete. Mag. Concr. Res. 1956, 8, 13–22. [Google Scholar] [CrossRef]
- Carino, N.J.; Lew, N.J. The maturity method: From theory to application. In Proceedings of the 2001 Structures Congress & Exposition, Washington, DC, USA, 21–23 May 2001. [Google Scholar]
- Hansen, P.F.; Pedersen, E.J. Maturity Computer for Controlled Curing and Hardening of Concrete; Nordisk Betong: Stockholm, Sweden, 1977; pp. 21–25. [Google Scholar]
- Lew, H.S.; Reichard, T.W. Prediction of strength of concrete from maturity. ACI Spec. Publ. 1978, 56, 229–248. [Google Scholar]
- Tank, R.C.; Carino, N.J. Rate constant functions for strength development of concrete. ACI Mater. J. 1991, 88, 74–83. [Google Scholar]
- Hansen, P.F.; Pedersen, E.J. Curing of concrete structures. CEB Inf. Bull. 1985, 166, 42. [Google Scholar]
- Benaicha, M.; Burtschell, Y.; Alaoui, A.H. Prediction of compressive strength at early age of concrete—Application of maturity. J. Build. Eng. 2016, 6, 119–125. [Google Scholar] [CrossRef]
- Ohama, Y.; Demura, K.; Lee, Y.S.; Yeon, K.S. Compressive strength prediction of polyester mortars by the maturity method. Proc. Int. Symp. Brittle Matrix Compos. 2000, 6, 439–448. [Google Scholar]
- Vazquez-Herrero, C.; Martinez-Lange, I.; Sanchez-Tembleque, F. A new procedure to ensure structural safety based on the maturity method and limit state theory. Constr. Build. Mater. 2012, 35, 383–398. [Google Scholar] [CrossRef]
- Wirquin, E.; Broda, M.; Duthoit, B. Determination of the apparent activation energy of one concrete by calorimetric and mechanical means Influence of a superplasticizer. Cem. Concr. Res. 2002, 32, 1207–1213. [Google Scholar] [CrossRef]
- D’Aloia, L.; Chavillard, G. Determination the “apparent” activation energy of concrete Ea- numerical simulations of the heat of hydration of cement. Cem. Concr. Res. 2002, 32, 1277–1289. [Google Scholar] [CrossRef]
- Venuant, M. Rev. Mat. Constr. 1961.
- Kurdowski, W.; Pichniarczyk, P. Problems with the Arrhenius equation in the evaluation of concrete maturity. Cem. Lime Concr. 2016, 21, 149–156. [Google Scholar]
- Yang, H.-M.; Kwon, S.-J.; Myung, N.V.; Singh, J.K.; Lee, H.-S.; Mandal, S. Evaluation of Strength Development in Concrete with Ground Granulated Blast Furnace Slag Using Apparent Activation Energy. Materials 2020, 13, 442. [Google Scholar] [CrossRef]
- Zhang, J.; Cusson, D.; Monteiro, P.; Harvey, J. New perspectives on maturity method and approach for high performance concrete applications. Cem. Concr. Res. 2008, 38, 1438–1446. [Google Scholar] [CrossRef]
- Ho, L.S.; Nakarai, K.; Eguchi, K.; Ogawa, Y. Difference in Strength Development between Cement-Treated Sand and Mortar with Various Cement Types and Curing Temperatures. Materials 2020, 13, 4999. [Google Scholar] [CrossRef]
- Abdel-Jawad, Y.A. The maturity method: Modifications to improve estimation of concrete strength at later ages. Constr. Build. Mater. 2006, 20, 893–900. [Google Scholar] [CrossRef]
- Yeh, I.-C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Eskandari-Naddaf, H.; Kazemi, R. ANN prediction of cement mortar compressive strength, influence of cement strength class. Constr. Build. Mater. 2017, 138, 1–11. [Google Scholar] [CrossRef]
- Getahun, M.A.; Shitote, S.M.; Gariy, Z.C.A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
- Silva, F.A.; Delgado, J.M.; Cavalcanti, R.S.; Azevedo, A.C.; Guimarães, A.S.; Lima, A.G. Use of Nondestructive Testing of Ultrasound and Artificial Neural Networks to Estimate Compressive Strength of Concrete. Buildings 2021, 11, 44. [Google Scholar] [CrossRef]
- Amiri, M.; Hatami, F. Prediction of mechanical and durability characteristics of concrete including slag and recycled aggregate concrete with artificial neural networks (ANNs). Constr. Build. Mater. 2022, 325, 126839. [Google Scholar] [CrossRef]
- Abellan-Garcia, J.; Pacheco-Bustos, C. ANN approach to evaluate the effects of supplementary cementitious materials on the compressive strength of recycled aggregate concrete. Constr. Build. Mater. 2023, 402, 132992. [Google Scholar] [CrossRef]
- ASTM C1074-11; Standard Practice for Estimating Concrete Strength by the Maturity Method. ASTM International: West Conshohocken, PA, USA, 2011.
- FIB Model Code 2010, First Complete Draft; International Federation for Structural Concrete: Lausanne, Switzerland, 2010; Volume 1.
- QNET’97—Neural Network Modeling for Windows 95/98/NT, Vesta Services Inc.: Winnetka, IL, USA, 1997.
- STATISTICA; Statistics Program Package, StatSoft PL: Kraków, Poland.
| Experimental Level | Items |
|---|---|
| W/C ratio | 0.45 |
| Cement | CEM I, CEM III Heat of hydration Q |
| Curing temperature, °C | 5, 20, 35 |
| Compressive strength, MPa | 1, 2, 3, 7, 14, 28, 56, 90 days Activation energy Ea->E |
| Cement | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|
| Class | CEM I 32.5R | CEM I 42.5R | CEM I 42.5R | CEM I 52.5R | CEM I 42.5R | CEM III/A 42.5 | |
| CaO | % | 62.4 | 63.3 | 62.8 | 63.5 | 63.2 | 52.5 |
| SiO2 | % | 21.3 | 19.8 | 19.0 | 19.4 | 21.9 | 27.7 |
| Al2O3 | % | 5.0 | 4.9 | 5.4 | 5.4 | 3.7 | 6.0 |
| Fe2O3 | % | 3.1 | 2.6 | 2.9 | 3.0 | 4.8 | 1.7 |
| SO3 | % | 2.7 | 2.6 | 3.2 | 3.3 | 2.5 | 2.7 |
| Na2O eq | % | 0.47 | 0.71 | 0.8 | 0.8 | 0.66 | 0.79 |
| Density | kg/dm3 | 3.05 | 3.10 | 3.11 | 3.12 | 3.14 | 2.96 |
| Blain suf. | m2/kg | 290 | 362 | 329 | 509 | 373 | 411 |
| Strength fc-2 | MPa | 15,2 | 29.2 | 26.1 | 41.1 | 29.9 | 21.5 |
| fc-28 | MPa | 47,3 | 56.2 | 56.7 | 65.4 | 55.1 | 53.2 |
| Cement | |||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | ||
| Activation temperature E | °C | 4450 | 4300 | 3030 | 2760 | 3100 | 4800 |
| Heat of hydration Q | J/g | 196 | 214 | 191 | 302 | 244 | 173 |
| Input/Output | Unit | Min | Max | |
|---|---|---|---|---|
| Q | J/g | X1 | 173 | 302 |
| E | °C | X2 | 2760 | 4800 |
| T | °C | X3 | 5 | 35 |
| t | days | X4 | 1 | 56 |
| fc | MPa | Y1 | 3.8 | 74.3 |
| fc% | % | Y2 | 6.6 | 110.3 |
| N | Max. Error | RMS Error | Correlation | |
|---|---|---|---|---|
| Training set | 104 | 6.03 | 0.0181 | 0.994 |
| Test set | 15 | 5.30 | 0. 0137 | 0.956 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wawrzeńczyk, J. A New Approach for Predicting Strength Based on Temperature-Time History Using Two-Parameter Maturity ANN Models. Materials 2024, 17, 6157. https://doi.org/10.3390/ma17246157
Wawrzeńczyk J. A New Approach for Predicting Strength Based on Temperature-Time History Using Two-Parameter Maturity ANN Models. Materials. 2024; 17(24):6157. https://doi.org/10.3390/ma17246157
Chicago/Turabian StyleWawrzeńczyk, Jerzy. 2024. "A New Approach for Predicting Strength Based on Temperature-Time History Using Two-Parameter Maturity ANN Models" Materials 17, no. 24: 6157. https://doi.org/10.3390/ma17246157
APA StyleWawrzeńczyk, J. (2024). A New Approach for Predicting Strength Based on Temperature-Time History Using Two-Parameter Maturity ANN Models. Materials, 17(24), 6157. https://doi.org/10.3390/ma17246157






