Third-Generation CALPHAD Modeling of Elemental Nb and Zr and Partial Re-Assessment of Their Binary Phase Diagram
Abstract
1. Introduction
2. Literature Review of Experimental and Assessed Data
2.1. Pure Nb
2.2. Pure Zr
2.3. The Nb-Zr System
3. Thermodynamic Model
3.1. Pure Elements
3.2. Solution Phases
3.3. Parameters Estimation and Optimization Procedures
| Element | Phase | (J mol−1) | (J mol−1 K−1) | (K) | (-) | (J mol−1 K−2) | (J mol−1 K-ν−1) |
| Nb | FCC_A1 | 31,070 (a) | −1.7 (b) | 211.85 | 4 | 2.9658 × 10−3 | 1.9255 × 10−13 |
| BCC_A2 (α) | 0 | - | 197.89 | 4 | 2.9658 × 10−3 | 1.9255 × 10−13 | |
| HCP_A3 | 28,658 (a) | −2.4 (b) | 217.88 | 4 | 2.9658 × 10−3 | 1.9255 × 10−13 | |
| amorphous | 17,568 | - | 197.88 | - | 4.6 × 10−3 (c) | - | |
| Zr | FCC_A1 | 3860 (a) | 0.9 (b) | 200.56 | 4 | 7.3793 × 10−3 | 4.8187 × 10−7 |
| BCC_A2 | 7719 (a) | - | 140.79 | 4 | 2.3062 × 10−3 | 3.0624 × 10−13 | |
| HCP_A3 (α) | 0 | - | 207.93 | 2 | 7.3793 × 10−3 | 4.8187 × 10−7 | |
| amorphous | 11,840 | - | 140.79 | - | 1.65 × 10−3 (c),(d) | - | |
| Element | Phase | (J mol−1) | (J mol−1 K−1) | (J mol−1 K) | |||
| Nb | liquid | 29,076 | 8.3144 | −1.0000 × 10−8 | |||
| Zr | liquid | 48,452 | 8.3144 | −9.6122 × 10−1 | |||
| Element | Phase | Parameter | Value | Element | Phase | Parameter | Value |
| Nb | gas | 7.1937 × 105 | Zr | gas | 5.9956 × 105 | ||
| −3.3777 × 101 | −7.9467 × 100 | ||||||
| 3.6289 × 101 | −1.0028 × 102 | ||||||
| 6.4223 × 10−3 | −6.6663 × 10−2 | ||||||
| −9.3483 × 10−7 | 5.6647 × 10−5 | ||||||
| 5.8594 × 10−11 | −3.5606 × 10−8 | ||||||
| −1.1731 × 10−15 | 1.5301 × 10−11 | ||||||
| 0 | −4.4752 × 10−15 | ||||||
| 0 | 8.7741 × 10−19 | ||||||
| 0 | −1.1042 × 10−22 | ||||||
| 0 | 8.0661 × 10−27 | ||||||
| 0 | −2.6006 × 10−31 | ||||||
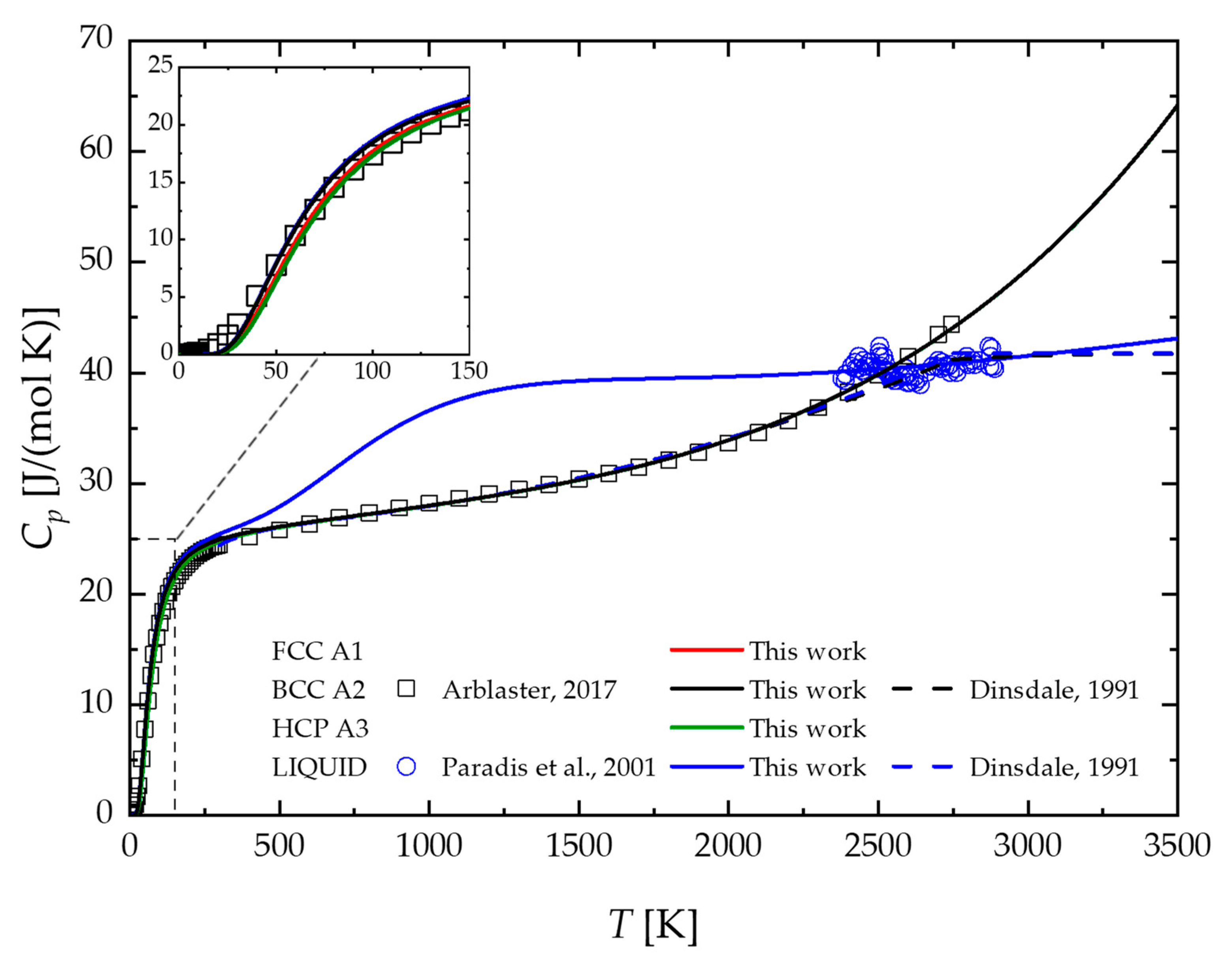
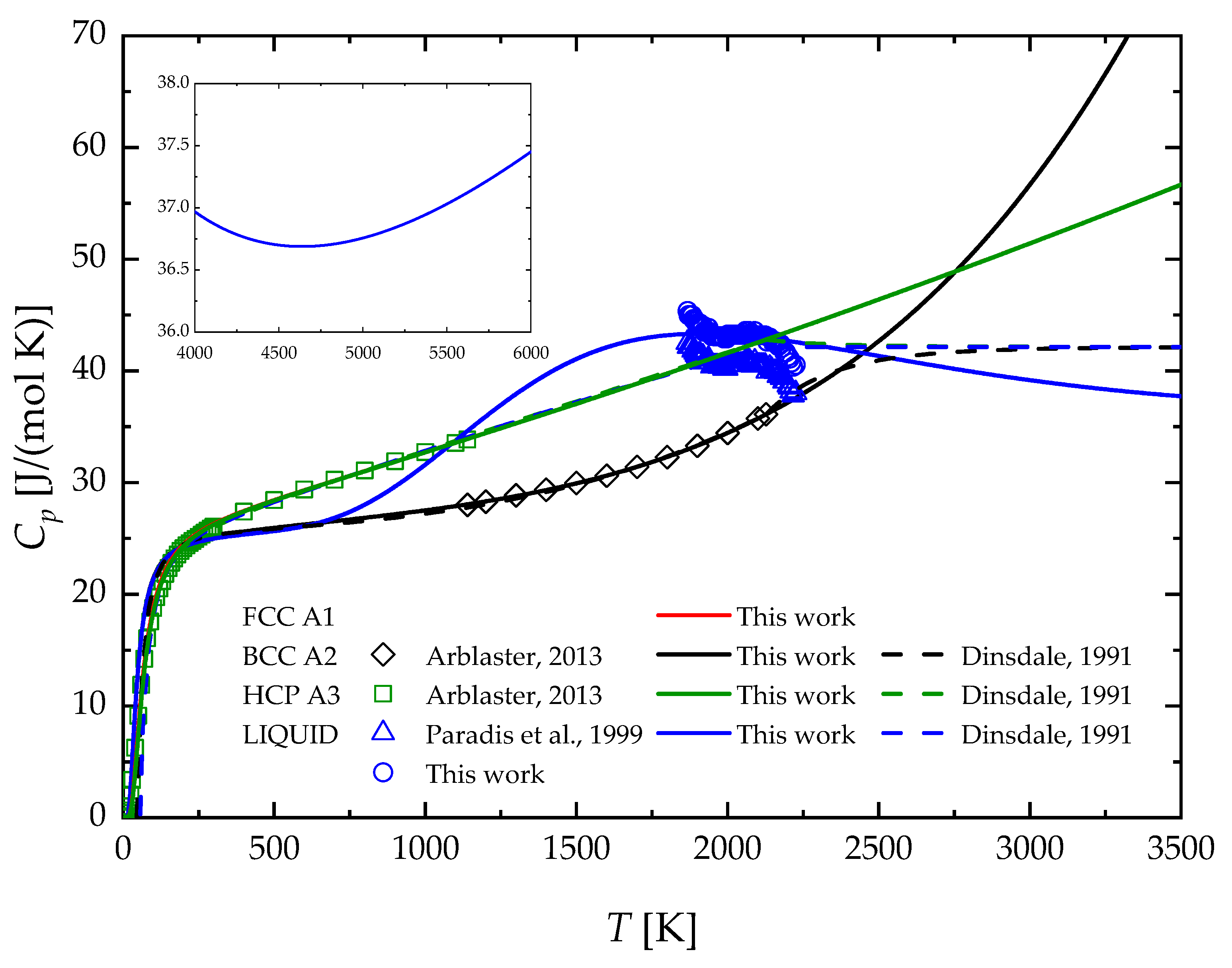
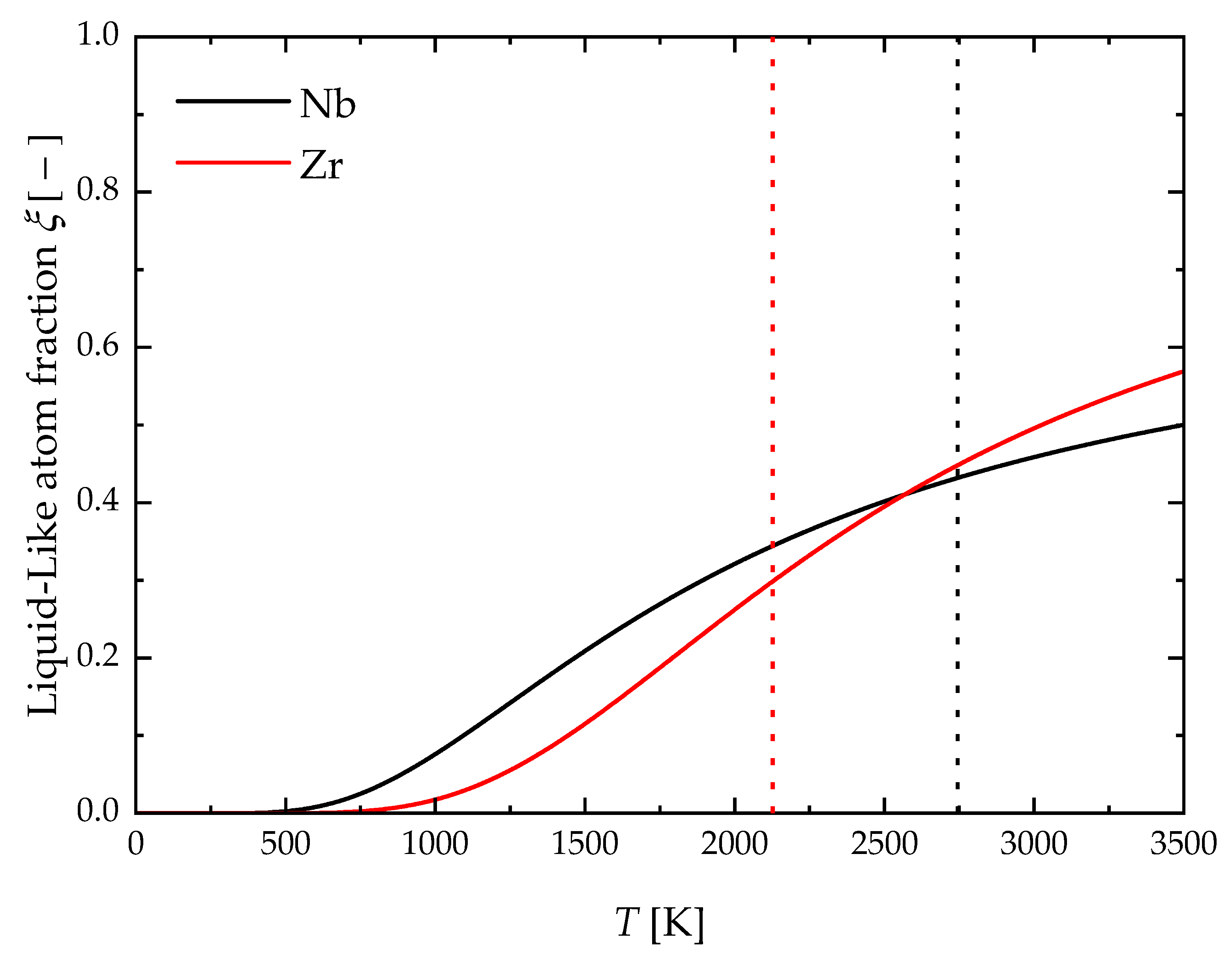
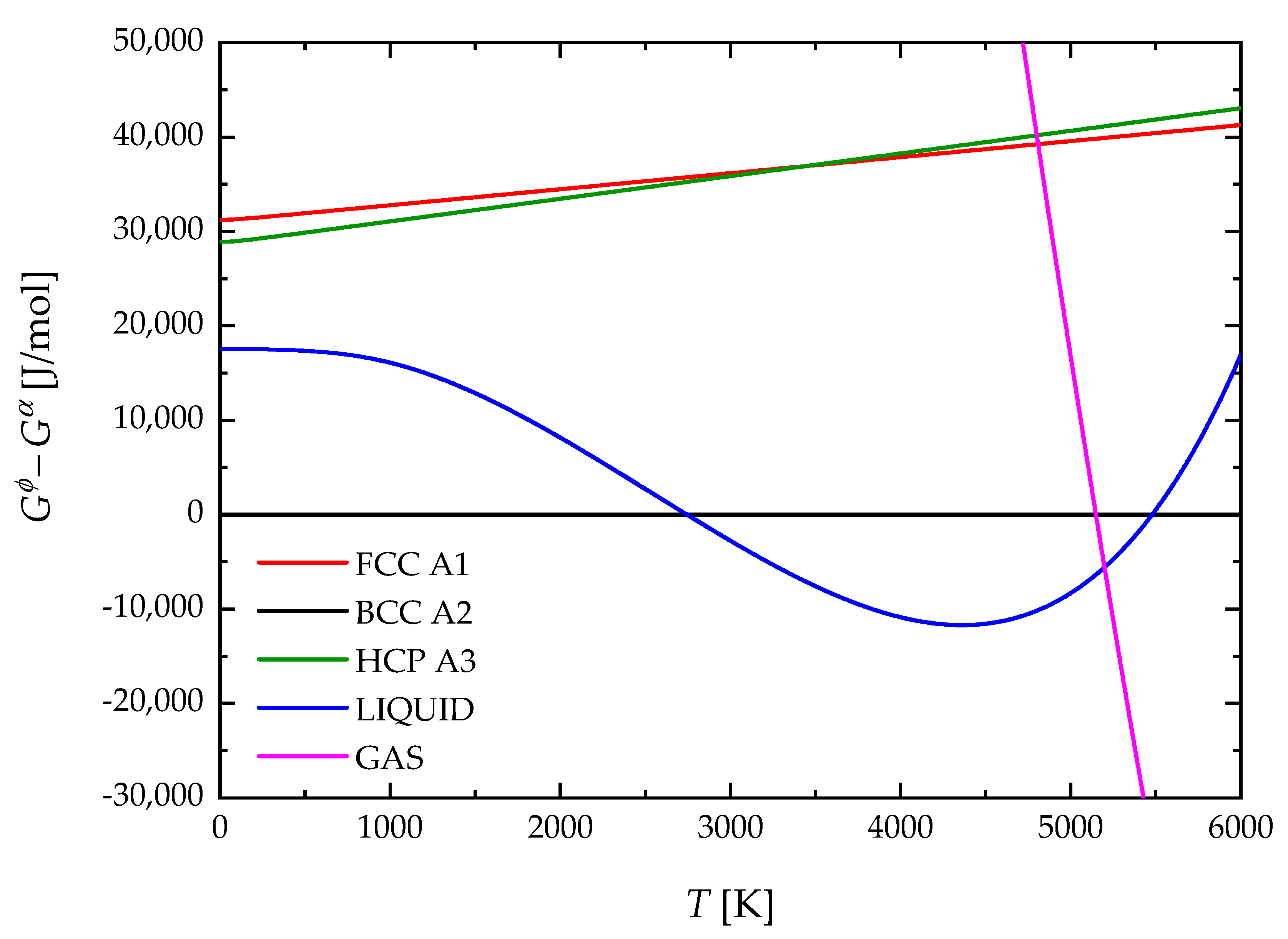
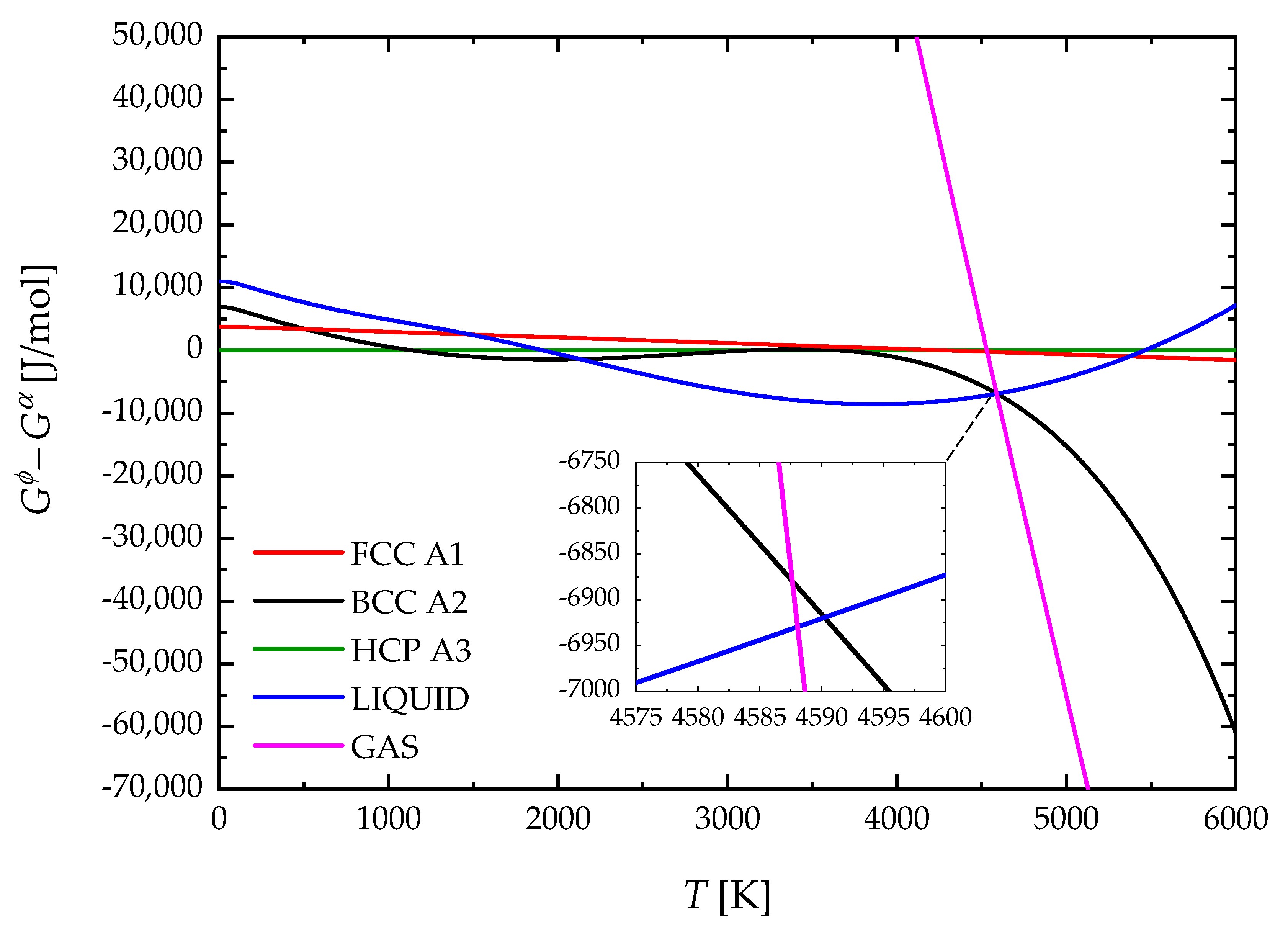
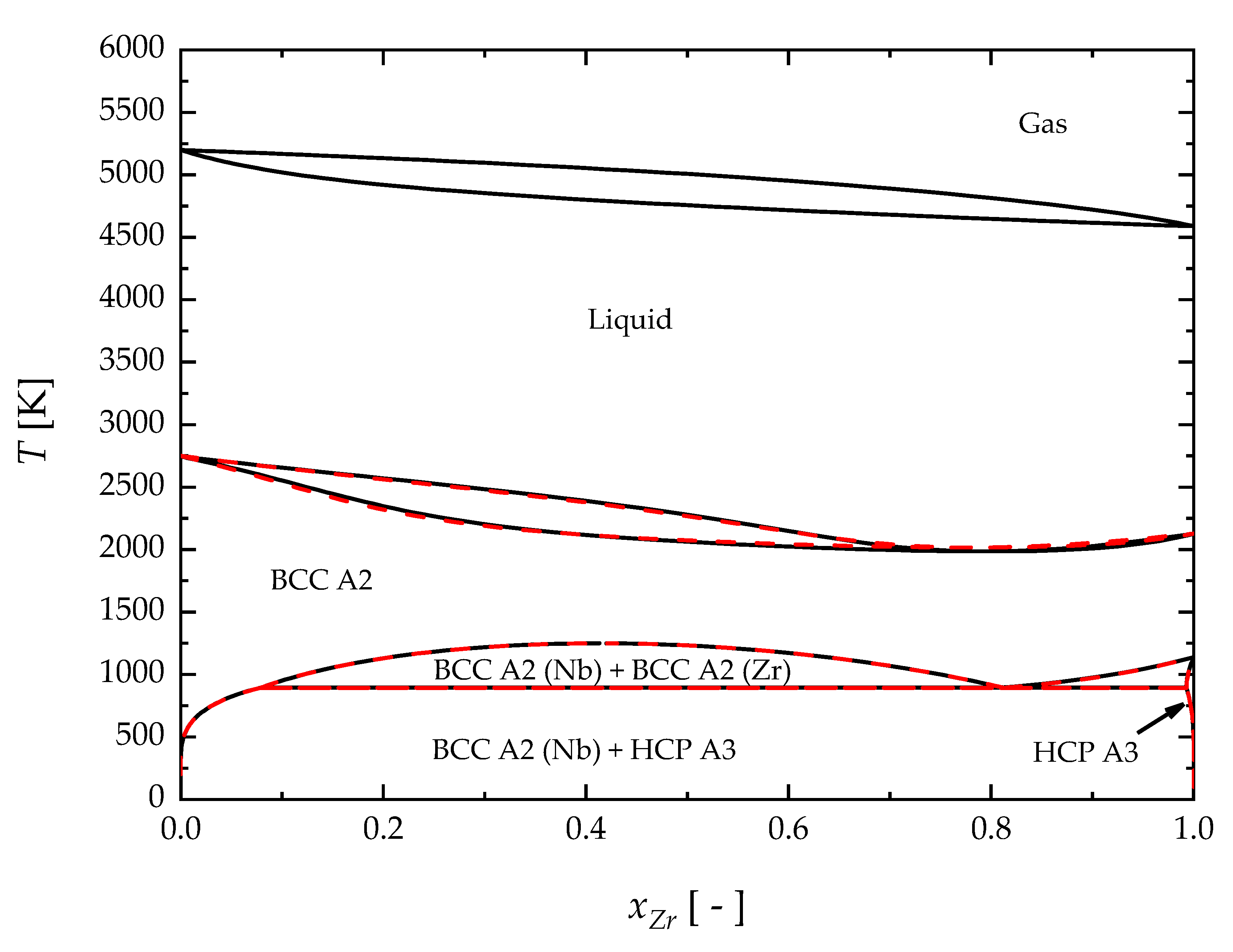
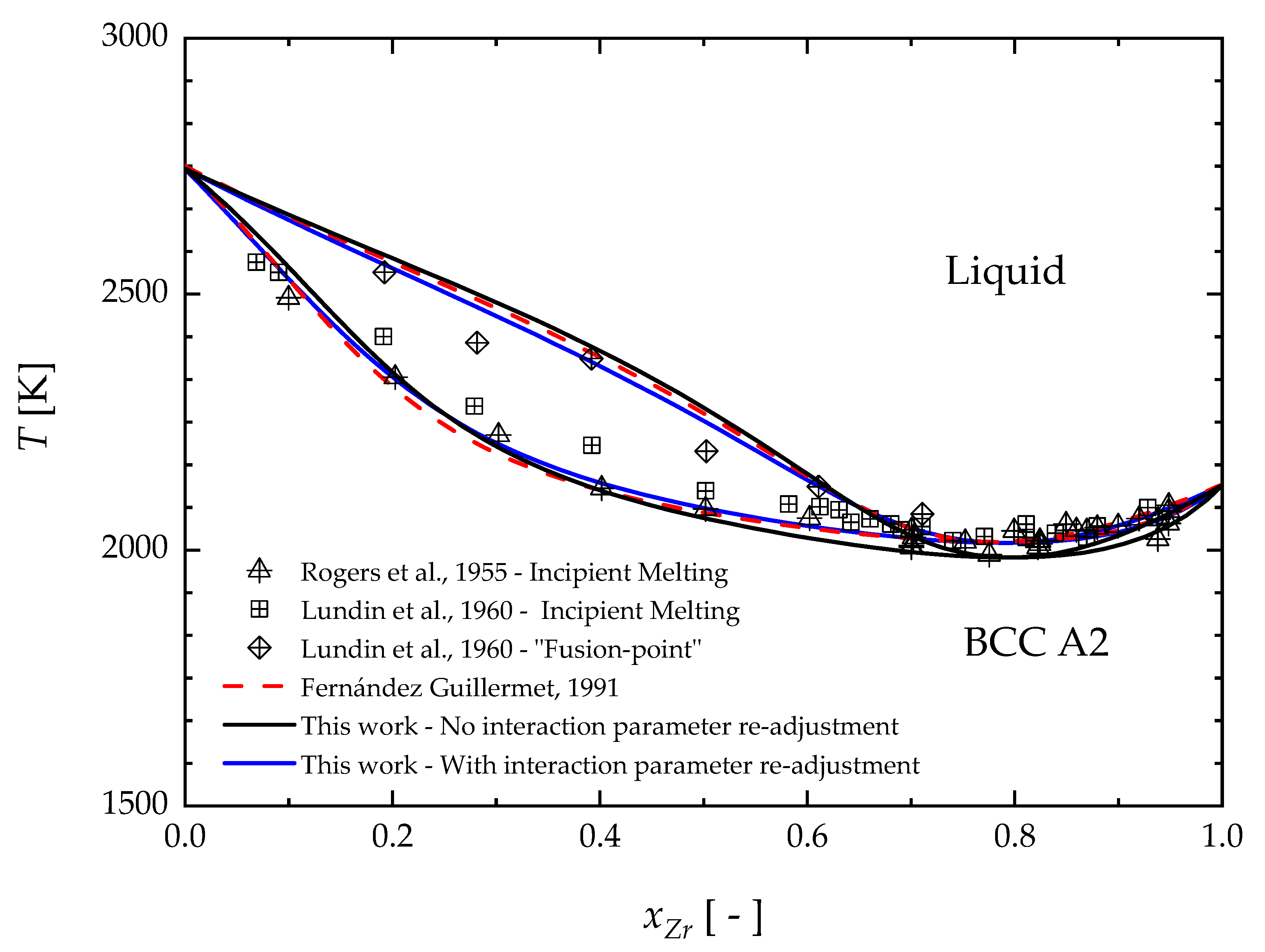
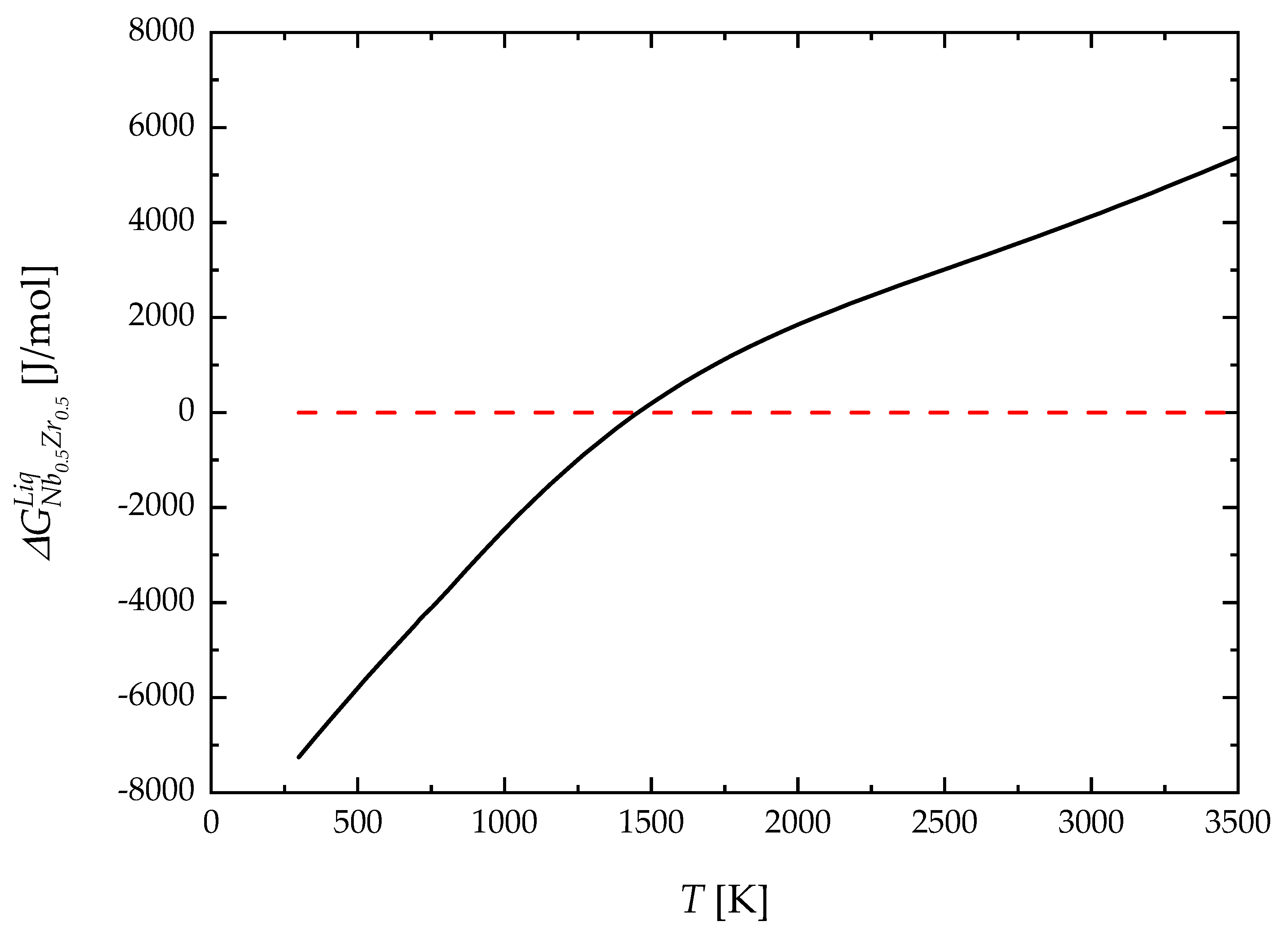
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiao, B.; Han, W.; Zhang, W.; Hu, Z.; Li, J. Preparation, deformation behavior and irradiation damage of refractory metal single crystals for nuclear applications: A Review. Materials 2024, 17, 3417. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, P.; Gabourel, A.; Firdosy, S.A.; Hofmann, D.C.; Moridi, A. Additive manufacturing of refractory metals and carbides for extreme environments: An overview. Sci. Technol. Weld. Join. 2024, 29, 99–115. [Google Scholar] [CrossRef]
- Cabrera, M.; Oropesa, Y.; Sanhueza, J.P.; Tuninetti, V.; Oñate, A. Multicomponent alloys design and mechanical response: From high entropy alloys to complex concentrated alloys. Mater. Sci. Eng. R Rep. 2024, 161, 100853. [Google Scholar] [CrossRef]
- Dube, T.C.; Zhang, J. Underpinning the relationship between synthesis and properties of high entropy ceramics: A comprehensive review on borides, carbides and oxides. J. Eur. Ceram. Soc. 2024, 44, 1335–1350. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, J.; Fu, H.; Xiong, Y.; Ma, S.; Xiang, X.; Xu, B.; Lu, W.; Zhang, Y.; Weber, W.J.; et al. Irradiation performance of high entropy ceramics: A comprehensive comparison with conventional ceramics and high entropy alloys. Prog. Mater. Sci. 2024, 143, 101250. [Google Scholar] [CrossRef]
- Deshmukh, A.A.; Ranganathan, R. Recent advances in modelling structure-property correlations in high-entropy alloys. J. Mater. Sci. Technol. 2025, 204, 127–151. [Google Scholar] [CrossRef]
- Dehury, R.K.; Kumar, R.; Joshi, Y.G.; Gupta, V. Elemental Influence on Oxidation Behaviour of Cantor-Based and Refractory High Entropy Alloys: A Critical Review. Adv. Eng. Mater. 2024, 26, 2302124. [Google Scholar] [CrossRef]
- Wang, B.; Yang, C.; Shu, D.; Sun, B. A Review of Irradiation-Tolerant Refractory High-Entropy Alloys. Metals 2024, 14, 45. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, Y.; Dou, Z.; Wang, J.; Huang, Z. Refractory high-entropy alloys fabricated by powder metallurgy: Progress, challenges and opportunities. J. Sci. Adv. Mater. Devices 2024, 9, 100688. [Google Scholar] [CrossRef]
- Ghassemali, E.; Conway, P.L.J. High-Throughput CALPHAD: A Powerful Tool Towards Accelerated Metallurgy. Front. Mater. 2022, 9, 889771. [Google Scholar] [CrossRef]
- Robin, I.K.; Gräning, T.; Yang, Y.; Haider, S.B.; Lass, E.A.; Katoh, Y.; Zinkle, S.J. Evaluation of Tungsten—Steel Solid-State Bonding: Options and the Role of CALPHAD to Screen Diffusion Bonding Interlayers. Metals 2023, 13, 1438. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, Y. The CALPHAD approach for HEAs: Challenges and opportunities. MRS Bull. 2022, 47, 158–167. [Google Scholar] [CrossRef]
- Khvan, A.V.; Uspenskaya, I.A.; Aristova, N.M.; Chen, Q.; Trimarchi, G.; Konstantinova, M.; Dinsdale, A.T. Description of the thermodynamic properties of pure gold in the solid and liquid states from 0 K. Calphad 2020, 68, 101724. [Google Scholar] [CrossRef]
- Li, Z.; Bigdeli, S.; Mao, H.; Chen, Q.; Selleby, M. Thermodynamic evaluation of pure Co for the third generation of thermodynamic databases. Phys. Status Solidi B 2017, 254, 1600231. [Google Scholar] [CrossRef]
- Li, Z.; Mao, H.; Selleby, M. Thermodynamic modeling of pure Co accounting two magnetic states for the Fcc phase. J. Phase Equilibria Diffus. 2018, 39, 502–509. [Google Scholar] [CrossRef]
- Hao, L.; Ruban, A.; Xiong, W. CALPHAD modeling based on Gibbs energy functions from zero kelvin and improved magnetic model: A case study on the Cr-Ni system. Calphad 2021, 73, 102268. [Google Scholar] [CrossRef]
- Zhang, E.; Xu, X.; Chen, Y.; Tang, Y. Third-generation thermodynamic descriptions for Ta-Cr and Ta-V binary systems. Materials 2022, 15, 2074. [Google Scholar] [CrossRef]
- Khvan, A.V.; Uspenskaya, I.A.; Aristova, N.M. Critical assessment of the data for pure Cu from 0 K, using two-state model fro the description of the liquid phase. Calphad 2024, 84, 102637. [Google Scholar] [CrossRef]
- Chen, Q.; Sundman, B. Modeling of thermodynamic properties for Bcc, Fcc, liquid, and amorphous iron. J. Phase Equilibria 2001, 22, 631–644. [Google Scholar] [CrossRef]
- Hu, B.; Sridar, S.; Hao, L.; Xiong, W. A new thermodynamic modeling of the Ti-V system including the metastable ω phase. Intermetallics 2020, 122, 106791. [Google Scholar] [CrossRef]
- Bigdeli, S.; Mao, H.; Selleby, M. On the third generation Calphad databases: An updated description of Mn. Physica Status Solidi B 2015, 252, 2199–2208. [Google Scholar] [CrossRef]
- Zhang, E.; Tang, Y.; Wen, M.; Obaied, A.; Roslyakova, I.; Zhang, L. On phase stability of Mo-Nb-Ta-W refractory high-entropy alloys. Int. J. Refract. Met. Hard Mater. 2022, 103, 105780. [Google Scholar] [CrossRef]
- He, Z.; Selleby, M. A third generation Calphad description of pure W. Mater. Chem. Phys. 2022, 276, 125445. [Google Scholar] [CrossRef]
- Dinsdale, A.; Zobac, O.; Kroupa, A.; Khvan, A. Use of third generation data for the elements to model the thermodynamics of binary alloy systems: Part 1—The critical assessment of data for the Al-Zn system. Calphad 2020, 68, 101723. [Google Scholar] [CrossRef]
- Pavlů, J.; Řehák, P.; Vřešt’ál, J.; Šob, M. Combined quantum-mechanical and Calphad approach to description of heat capacity of pure elements below room temperature. Calphad 2015, 51, 161–171. [Google Scholar] [CrossRef]
- Hu, B.; Jiang, Y.; Wang, J.; Yao, B.; Min, F.; Du, Y. Thermodynamic calculation of the T_0 curve and metastable phase diagrams of the Ti-M (M = Mo, V, Nb, Cr, Al) binary systems. Calphad 2018, 62, 75–82. [Google Scholar] [CrossRef]
- Jiang, Y.; Zomorodpoosh, S.; Roslyakova, I.; Zhang, L. Thermodynamic re-assessment of binary Cr-Nb system down to 0 K. Calphad 2018, 62, 109–118. [Google Scholar] [CrossRef]
- Vřešt’ál, J.; Štrof, J.; Pavlů, J. Extension of SGTE data for pure elements to zero Kelvin temperature—A case study. Calphad 2012, 37, 37–48. [Google Scholar] [CrossRef]
- Štrof, J.; Pavlů, J.; Wdowik, U.; Buršík, J.; Šob, M.; Vřešt’ál, J. Laves phases in the V-Zr system below room temperature: Stability analysis using ab initio results and phase diagram. Calphad 2014, 44, 62–69. [Google Scholar] [CrossRef]
- Arblaster, J.W. The thermodynamic properties of niobium. J. Phase Equilibria Diffus. 2017, 38, 707–722. [Google Scholar] [CrossRef]
- Kirillin, V.A.; Sheindlin, A.E.; Chekhovskoi, V.Y.; Zhukova, I.A. Experimental determination of the enthalpy of niobium in the temperature range 600–2600°K. High Temp. 1965, 3, 357–363. [Google Scholar]
- Sheindlin, A.E.; Berezin, B.Y.; Chekhovskoi, V.Y. Enthalpy of niobium in the solid and liquid state. High Temp. High Press. 1972, 4, 611–619. [Google Scholar]
- Betz, G.; Frohberg, M.G. The enthalpy of solid and liquid niobium. Scr. Metall. 1981, 15, 269–272. [Google Scholar] [CrossRef]
- Hultgren, R.; Desai, P.D.; Hawkins, D.T.; Gleiser, M.; Kelley, K.K.; Wagman, D.D. Selected Values of the Thermodynamic Properties of the Elements; American Society for Metals, Metals Park: Detroit, MI, USA, 1973. [Google Scholar]
- Paradis, P.F.; Ishikawa, T.; Yoda, S. Non-contact measurements of thermophysical properties of niobium at high temperature. J. Mater. Sci. 2001, 36, 5125–5130. [Google Scholar] [CrossRef]
- Bonnell, J.F. Oxford College Biographical Files, Series No. 0181972, Box: 1, Folder: 18; Oxford College Archives: Oxford, UK, 1972; Available online: https://archives.libraries.emory.edu/repositories/6/archival_objects/476659 (accessed on 17 June 2024).
- Schaefers, K.; Rösner-Kuhn, M.; Frohberg, M.G. Enthalpy measurements of undercooled melts by levitation calorimetry: The pure metals nickel, iron, vanadium and niobium. Mater. Sci. Eng. A 1995, 197, 83–90. [Google Scholar] [CrossRef]
- Arblaster, J.W. Thermodynamic properties of zirconium. Calphad 2013, 43, 32–39. [Google Scholar] [CrossRef]
- Paradis, P.F.; Rhim, W.K. Thermophysical properties of zirconium at high temperature. J. Mater. Res. 1999, 14, 3713–3719. [Google Scholar] [CrossRef]
- Sakata, K.; Watanabe, Y.; Okada, J.T.; Kumar, M.V.; Paradis, P.F.; Ishikawa, T. FT-IR emissivity measurements of Nb melt using an electrostatic levitation furnace. J. Chem. Thermodyn. 2015, 91, 116–120. [Google Scholar] [CrossRef]
- Kats, S.A.; Chekhovskoi, V.Y.; Kovalenko, M.D. Teplofiz. Vys. Temp. 1985, 23, 395–397. [Google Scholar]
- Vollmer, O.; Braun, M.; Kohlhaas, R. Die atomwärme des zirkons zwischen 300 und 1700 °K. Z. Naturforschung A 1967, 22, 833–834. [Google Scholar] [CrossRef]
- Rösner-Kuhn, M.; Drewes, K.; Franz, H.; Frohberg, M.G. Enthalpy measurements of the solid high-temperature β-phase of titanium and zirconium by levitation drop calorimetry. J. Alloys Compd. 2001, 316, 175–178. [Google Scholar] [CrossRef]
- Fernández Guillermet, A. Thermodynamic analysis of the stable phases in the Zr-Nb system and calculation of the phase diagram. Z. Fuer Met. 1991, 82, 478–487. [Google Scholar]
- Lafaye, P.; Toffolon-Masclet, C.; Crivello, J.C.; Joubert, J.M. Experimental investigations and thermodynamic modelling of the Cr–Nb–Sn–Zr system. Calphad 2019, 64, 43–54. [Google Scholar] [CrossRef]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 5, 317–425. [Google Scholar] [CrossRef]
- Chase, M.W.; Ansara, I.; Dinsdale, A.; Eriksson, G.; Grimvall, G.; Hoglund, L.; Yokokawa, H. Thermodynamic models and data for pure elements and other endmembers of solutions—Group 1: Heat capacity models for crystalline phases from 0 K to 6000 K. Calphad 1995, 19, 437–447. [Google Scholar] [CrossRef]
- Ågren, J.; Cheynet, B.; Clavaguera-Mora, M.T.; Hack, K.; Hertz, J.; Sommer, F.; Kattner, U. Thermodynamic models and data for pure elements and other endmembers of solutions: Group 2 extrapolation of the heat capacity in liquid and amorphous phases. Calphad 1995, 19, 449–480. [Google Scholar] [CrossRef]
- Rogers, D.W. Einstein’s Other Theory: The Planck-Bose-Einstein Theory of Heat Capacity; Princeton University Press: Princeton, NJ, USA, 2005; ISBN 0-691-11826-4. [Google Scholar]
- Khvan, A.V.; Dinsdale, A.T.; Uspenskaya, I.A.; Zhilin, M.; Babkina, T.; Phiri, A.M. A thermodynamic description of data for pure Pb from 0 K using the expanded Einstein model for the solid and the two-state model for the liquid phase. Calphad 2018, 60, 144–155. [Google Scholar] [CrossRef]
- Ågren, J. Thermodynamics of supercooled liquids and their glass transition. Phys. Chem. Liq. 1988, 18, 123–139. [Google Scholar] [CrossRef]
- Becker, C.A.; Ågren, J.; Baricco, M.; Chen, Q.; Decterov, S.A.; Kattner, U.R.; Perepezko, J.H.; Pottlacher, G.R.; Selleby, M. Thermodynamic modelling of liquids: CALPHAD approaches and contributions from statistical physics. Phys. Status Solidi B 2014, 251, 33–52. [Google Scholar] [CrossRef]
- Benigni, P. Interest of the regular 2-state model for the description of unary liquids: Presentation of the formalism. Calphad 2023, 83, 102627. [Google Scholar] [CrossRef]
- PANDAT, Version 2024; Software for Multicomponent Phase Diagram Calculation by Computherm LLC: Middleton, WI, USA, 2024. Available online: www.computherm.com (accessed on 17 June 2024).
- Cacciamani, G.; Chang, Y.A.; Grimvall, G.; Franke, P.; Kaufman, L.; Miodownik, P.; Sanchez, J.M.; Schalin, M.; Sigli, C. Workshop on thermodynamic modelling of solutions and alloys: Schloβ Ringberg, March 10-16, 1996. Calphad 1997, 21, 219–246. [Google Scholar] [CrossRef]
- Stewart, G.R. Measurement of low-temperature specific heat. Rev. Sci. Instrum. 1983, 54, 1–11. [Google Scholar] [CrossRef]
- Tari, A. The Specific Heat of Matter at Low Temperatures; Imperial College Press: London, UK, 2003. [Google Scholar] [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The Open Quantum Materials Database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. npj Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Zhdanov, K.R.; Rakhmenkulov, F.S. Influence of electron-phonon interaction on electronic heat capacity of Nb. Phys. Status Solidi B 1982, 111, 361–364. [Google Scholar] [CrossRef]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier Science B.V.: Berlin/Heidelberg, Germany, 1999; ISBN 978-0-444-82794-4. [Google Scholar] [CrossRef]
- Forsblom, M.; Grimvall, G. Heat capacity of liquid Al: Molecular dynamics simulations. Phys. Rev. B-Condens. Matter Mater. Phys. 2005, 72, 132204. [Google Scholar] [CrossRef]
- Hirschfelder, J.; Stevenson, D.; Eyring, H. A Theory of Liquid Structure. J. Chem. Phys. 1937, 5, 896–912. [Google Scholar] [CrossRef]
- He, Z.; Kaplan, B.; Mao, H.; Selleby, M. The third generation Calphad description of Al–C including revisions of pure Al and C. Calphad 2021, 72, 102250. [Google Scholar] [CrossRef]
- He, Z.; Selleby, M. A third generation Calphad description of W-C including a revision of liquid C. Calphad 2022, 78, 102449. [Google Scholar] [CrossRef]
- Sundman, B.; Kattner, U.R.; Hillert, M.; Selleby, M.; Ågren, J.; Bigdeli, S.; Chen, Q.; Dinsdale, A.; Hallstedt, B.; Khvan, A.; et al. A method for handling the extrapolation of solid crystalline phases to temperatures far above their melting point. Calphad 2020, 68, 101737. [Google Scholar] [CrossRef]
- Rogers, B.A.; Atkins, D.F. Zirconium-columbium diagram. JOM 1955, 7, 1034–1041. [Google Scholar] [CrossRef]
- Lundin, C.E.; Cox, R.H. The Determination of the Equilibrium Phase Diagram Zirconium-Niobium; TID-11919; US Atomic Energy Commission: Germantown, MD, USA, 1960. [Google Scholar]
- De Boer, F.R.; Boom, R.; Mattens, W.C.M.; Miedema, A.R.; Niessen, A.K. Cohesion in Metals. Transition Metal Alloys; North-Holland Physics Publishing: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Bakker, H. Enthalpies in Alloys: Miedema’s Semi-Empirical Model; Trans Tech Publications Ltd.: Wollerau, Switzerland, 1998. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traversari, G.; Casu, M.; Orrù, R.; Cincotti, A.; Concas, A.; Cao, G.; Locci, A.M. Third-Generation CALPHAD Modeling of Elemental Nb and Zr and Partial Re-Assessment of Their Binary Phase Diagram. Materials 2024, 17, 5978. https://doi.org/10.3390/ma17235978
Traversari G, Casu M, Orrù R, Cincotti A, Concas A, Cao G, Locci AM. Third-Generation CALPHAD Modeling of Elemental Nb and Zr and Partial Re-Assessment of Their Binary Phase Diagram. Materials. 2024; 17(23):5978. https://doi.org/10.3390/ma17235978
Chicago/Turabian StyleTraversari, Gabriele, Mariano Casu, Roberto Orrù, Alberto Cincotti, Alessandro Concas, Giacomo Cao, and Antonio Mario Locci. 2024. "Third-Generation CALPHAD Modeling of Elemental Nb and Zr and Partial Re-Assessment of Their Binary Phase Diagram" Materials 17, no. 23: 5978. https://doi.org/10.3390/ma17235978
APA StyleTraversari, G., Casu, M., Orrù, R., Cincotti, A., Concas, A., Cao, G., & Locci, A. M. (2024). Third-Generation CALPHAD Modeling of Elemental Nb and Zr and Partial Re-Assessment of Their Binary Phase Diagram. Materials, 17(23), 5978. https://doi.org/10.3390/ma17235978








