A Novel Simulation Model of Shielding Performance Based on the Anisotropic Magnetic Property of Magnetic Shields
Abstract
1. Introduction
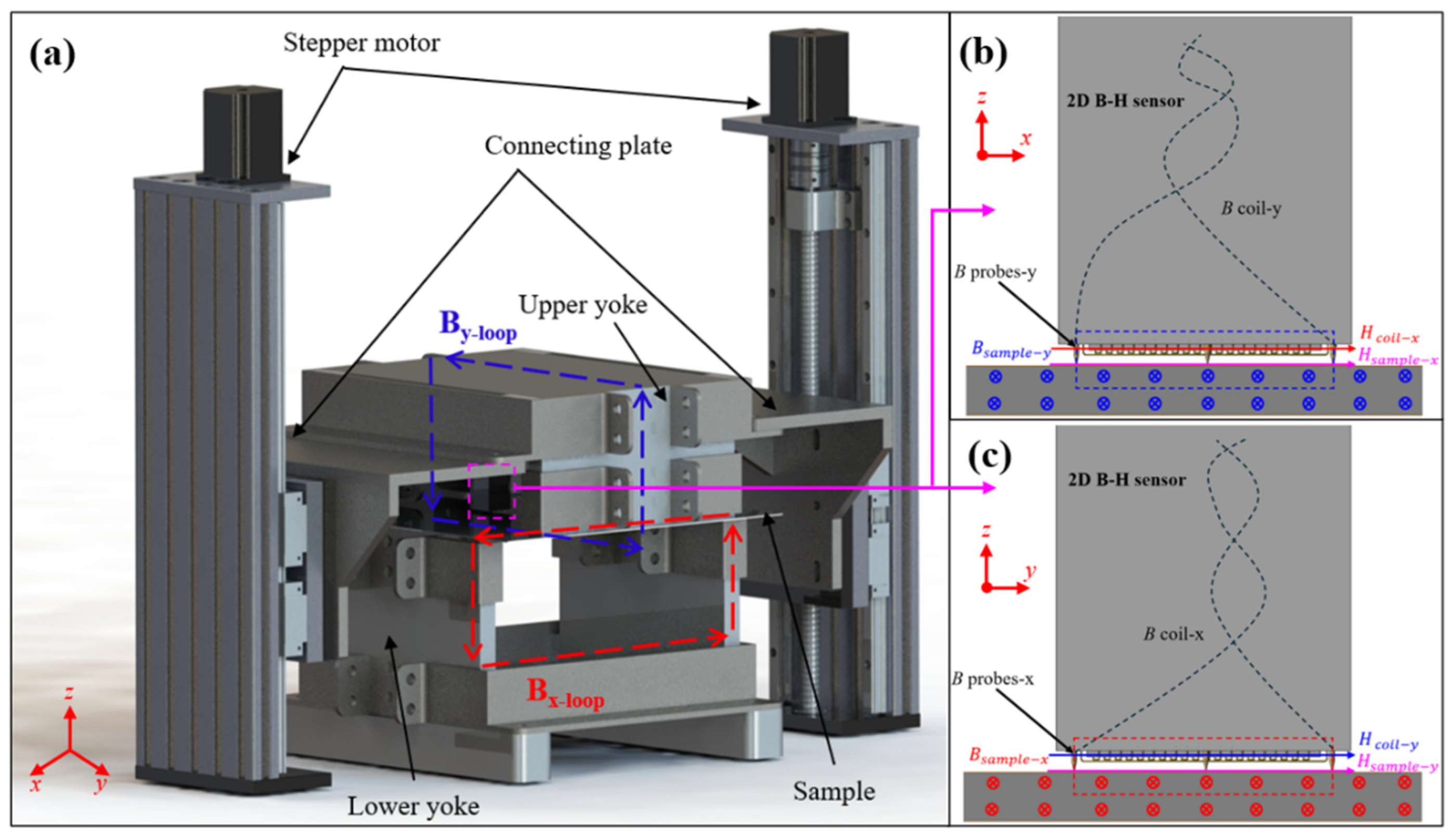
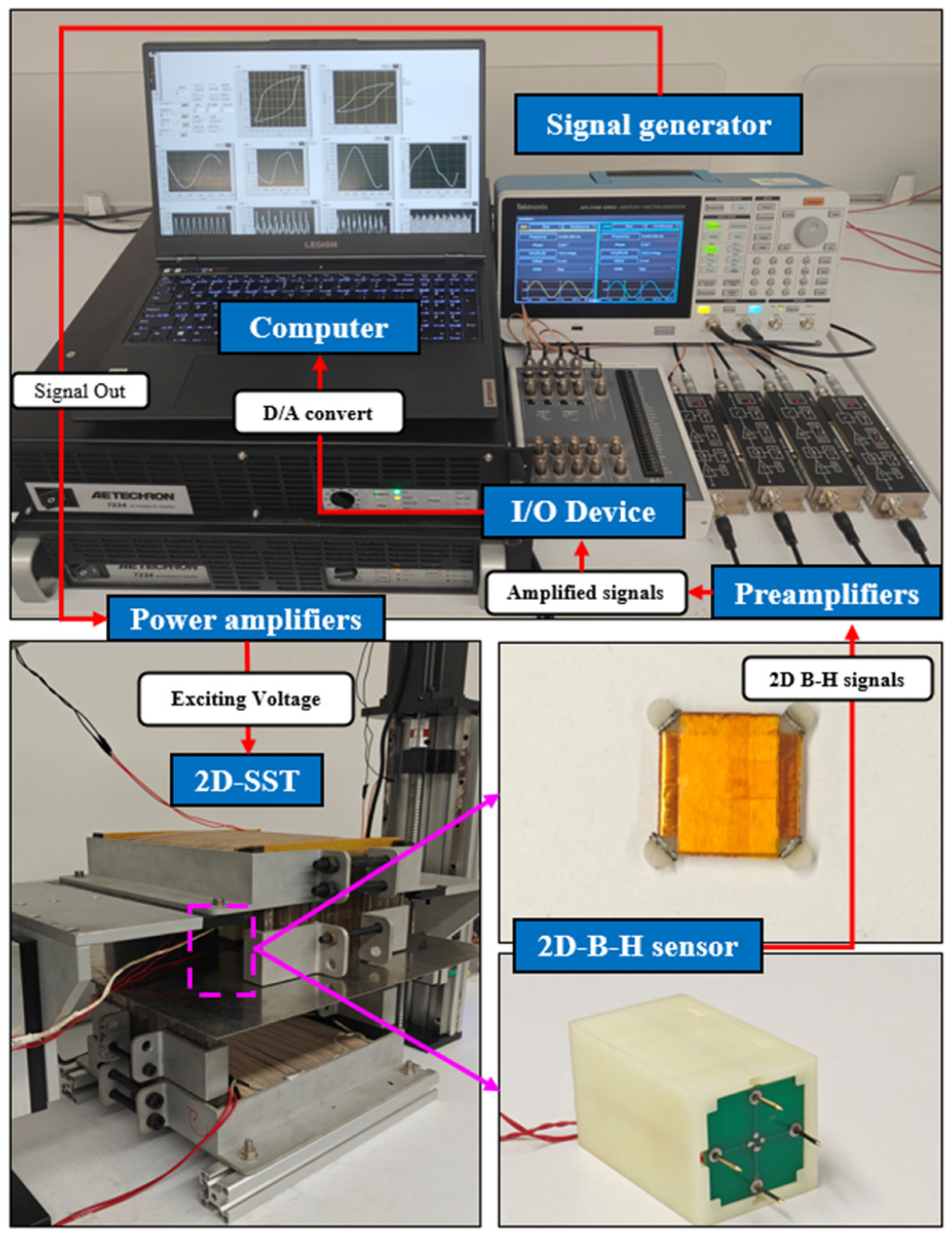
2. The Design and Application of 2D-SST
3. The Measurement and Analysis of Anisotropic Magnetic Properties
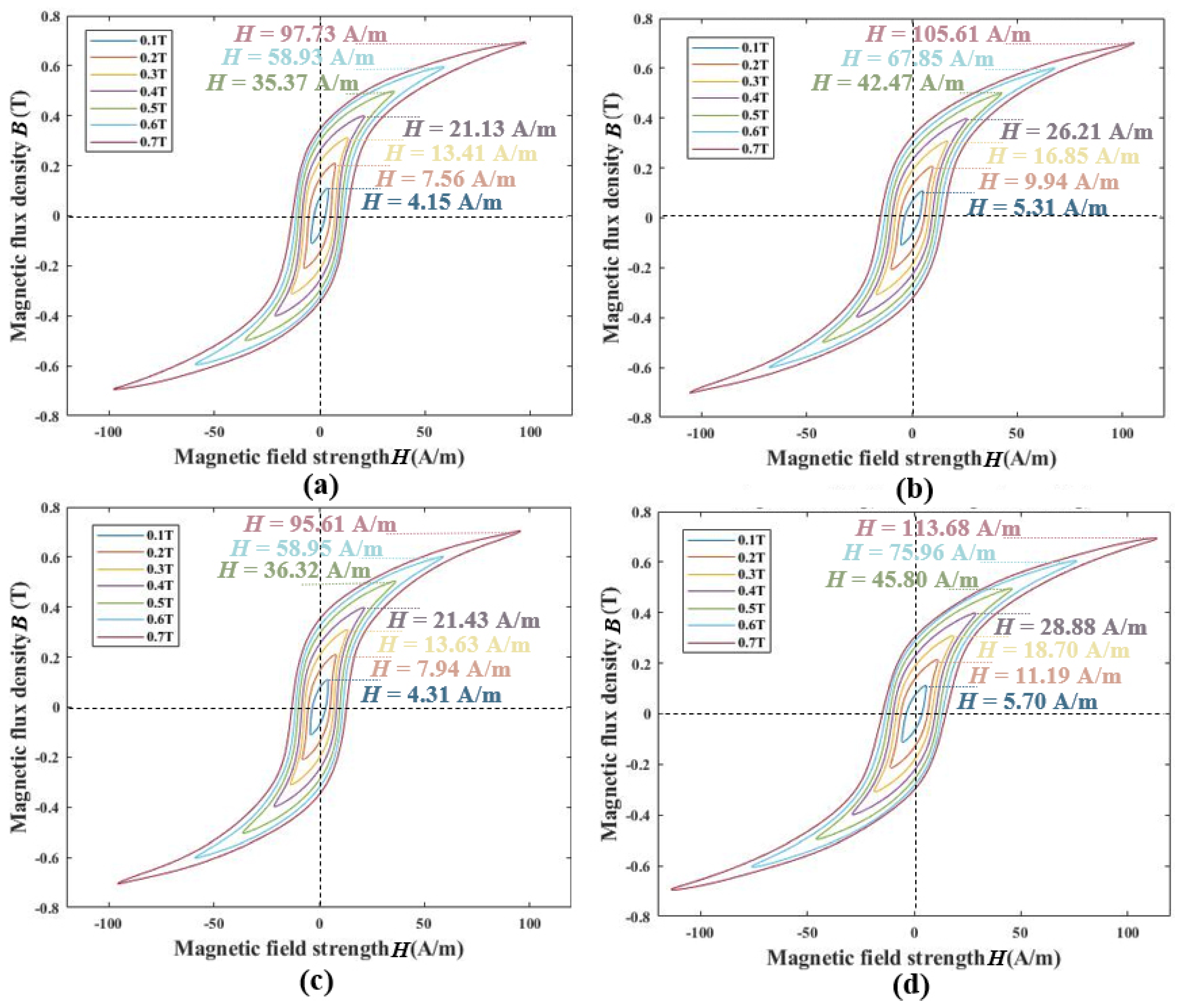
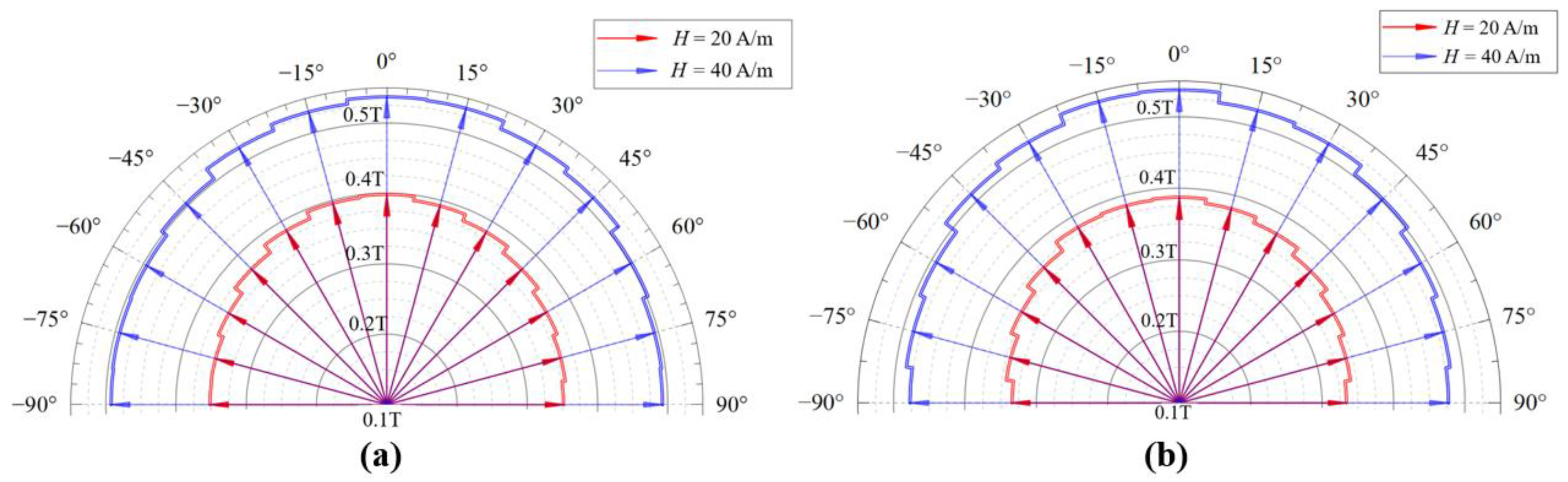
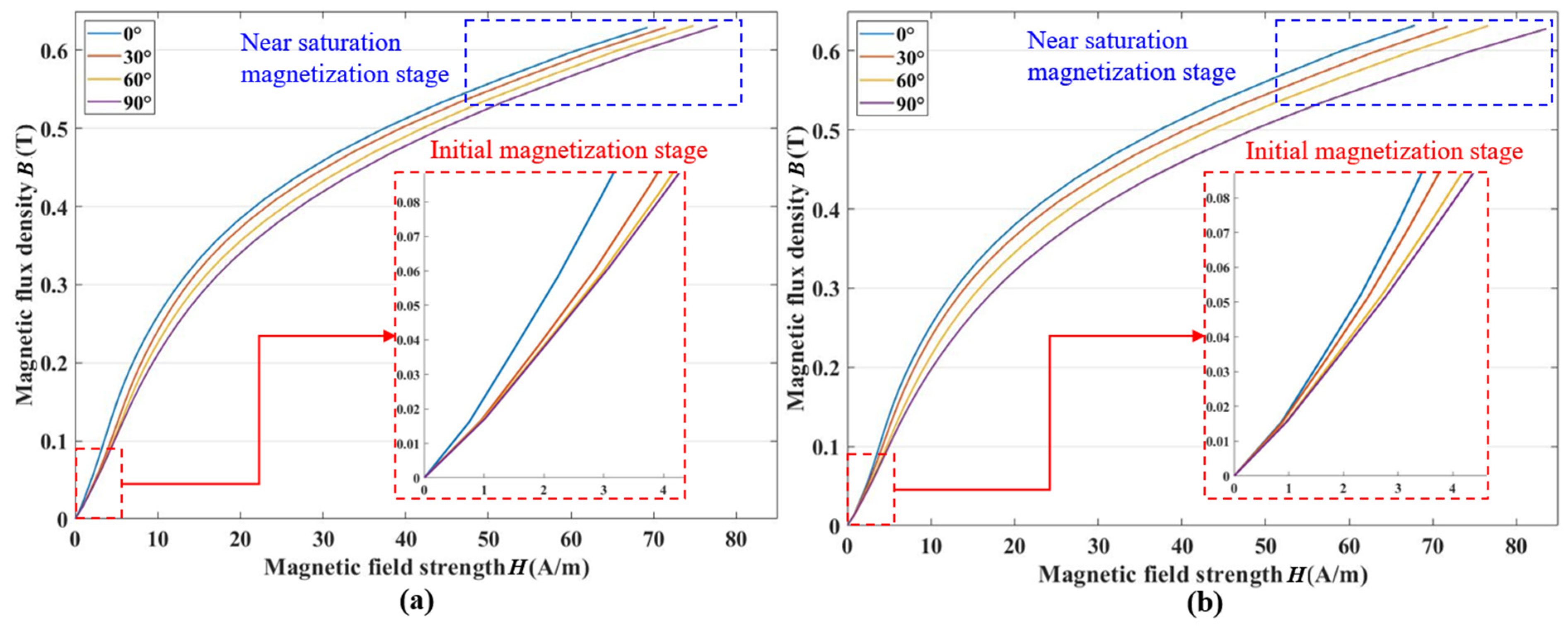
3.1. The Measured Anisotropic Magnetic Properties
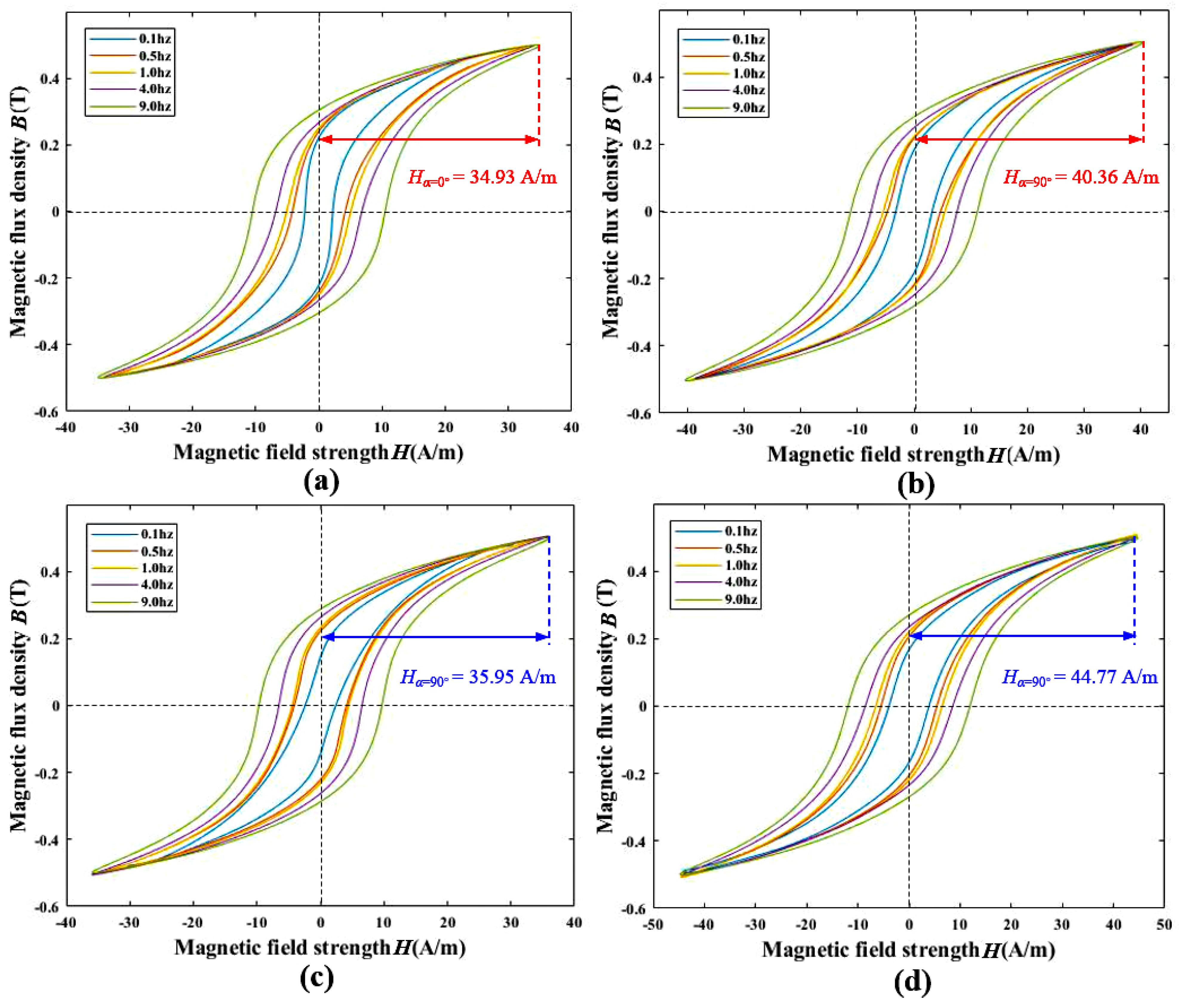
3.2. Measurement and Comparison of Permalloy Sheet
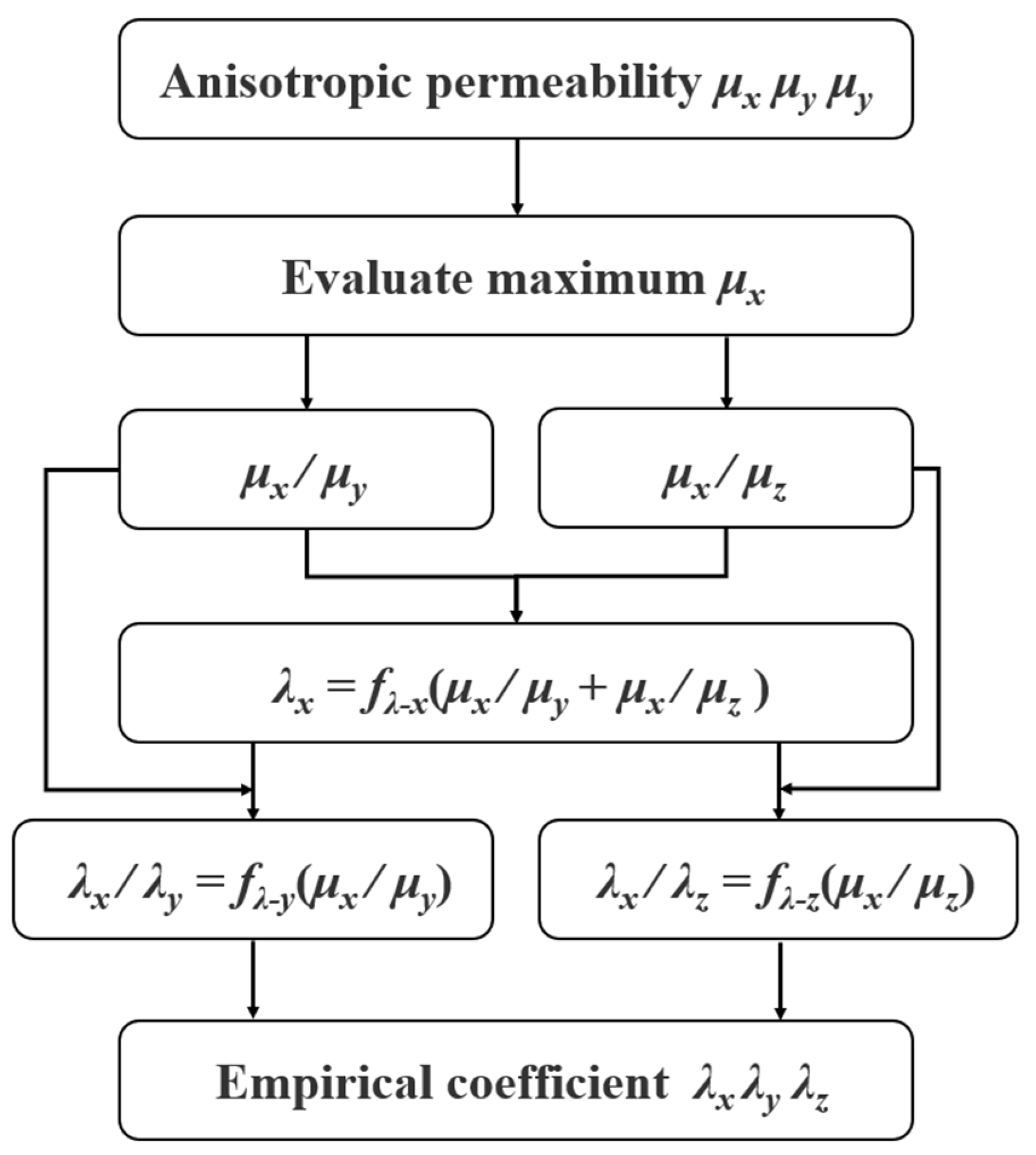
4. Analysis and Optimization of the Calculation for MSR Performance
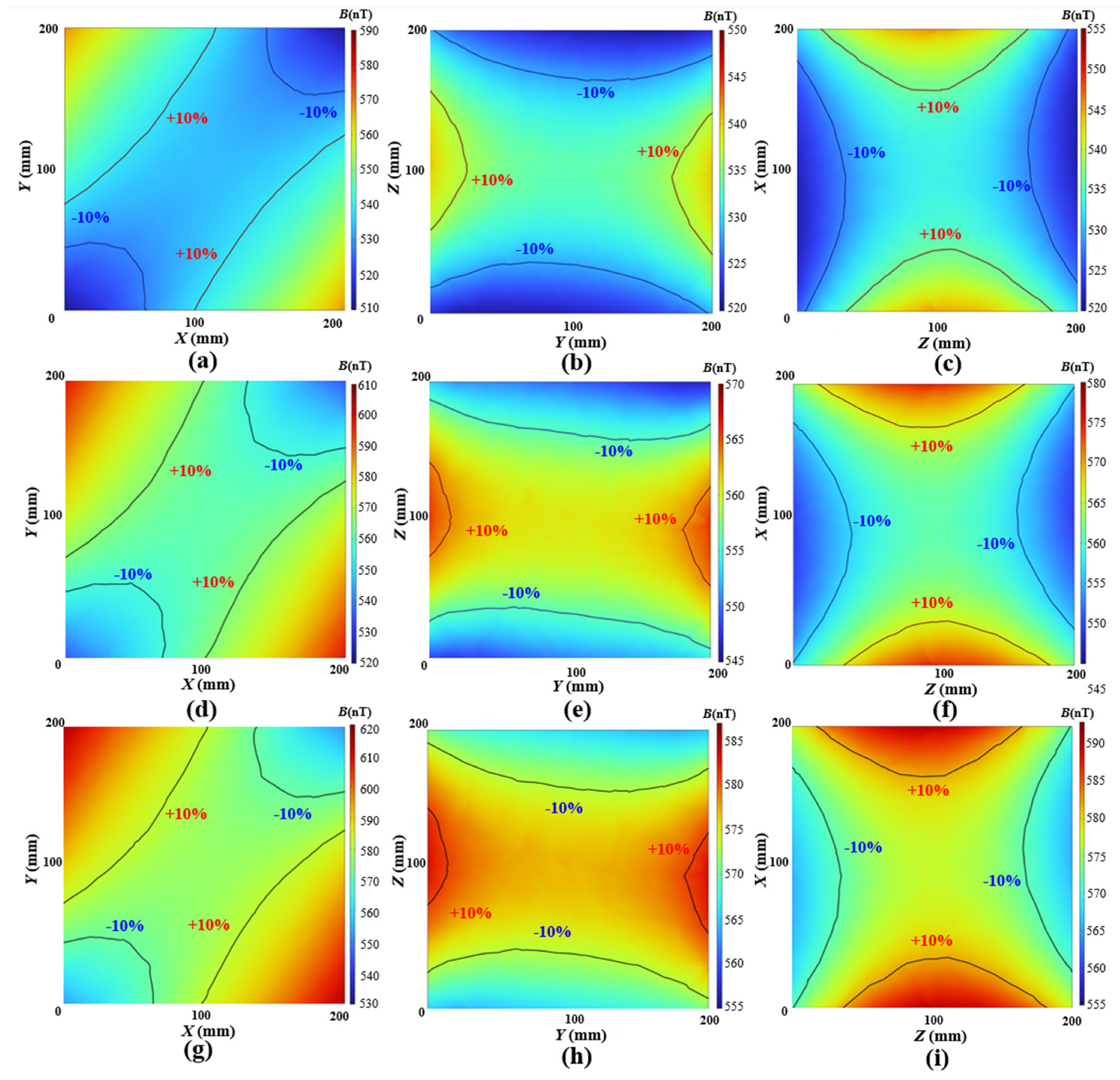
4.1. Simulation of Remanence and SF for MSR
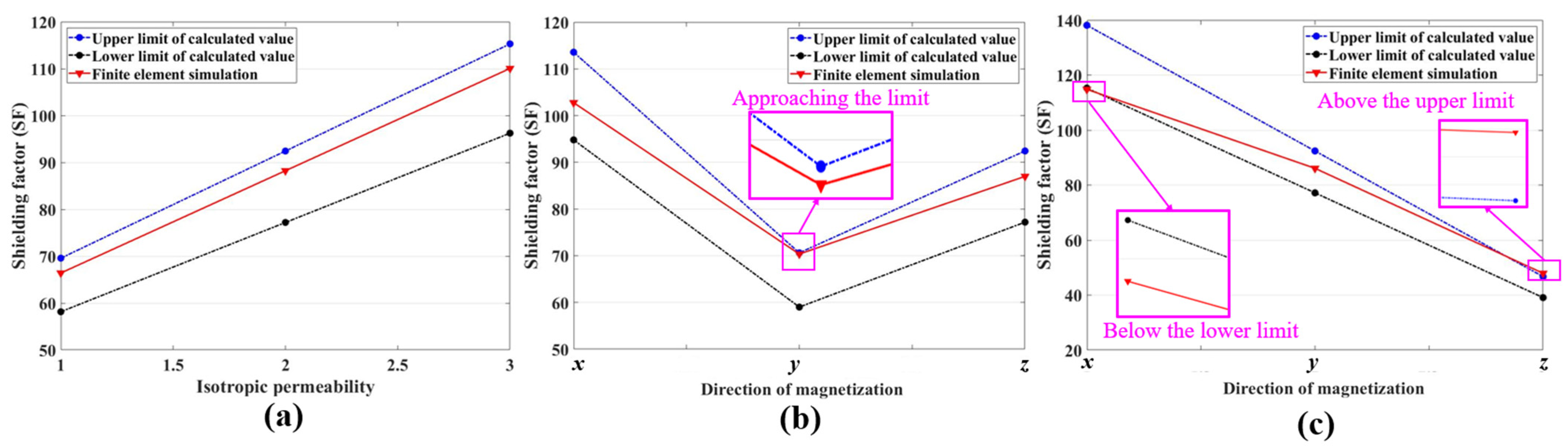
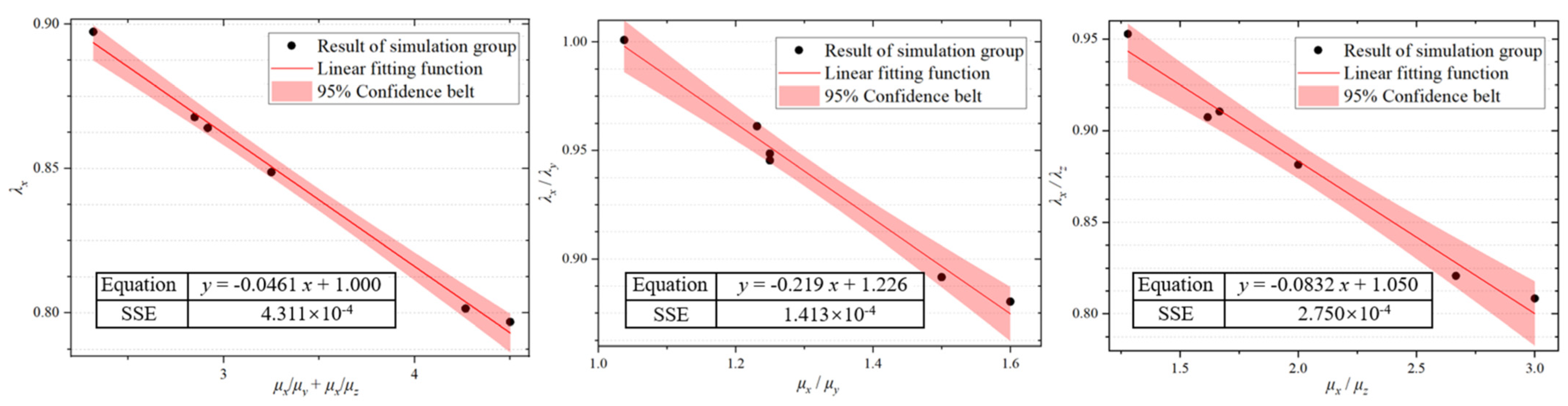
4.2. Analysis and Optimization of Theoretical Calculation for SF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Yang, J.; Cao, F.; Zhang, X.; Zheng, S. Enhancement of Magnetic Shielding Based on Low-Noise Materials, Magnetization Control, and Active Compensation: A Review. Materials 2024, 17, 5469. [Google Scholar] [CrossRef] [PubMed]
- Wan, J.; Zhang, Z.; Lin, J.; Li, Z.; Liu, H.; Li, Q.; Yang, S.; Wang, L. Simultaneously Enhancing Hole Extraction and Defect Passivation with More Conductive Hole-Selective Self-Assembled Molecules for Efficient Inverted Perovskite Solar Cells. J. Mater. Chem. C 2024, 12, 15644–15653. [Google Scholar] [CrossRef]
- Szeftel, J.; Sandeau, N.; Ghantous, M.A. Study of the Superconducting to Normal Transition. J. Supercond. Nov. Magn. 2020, 33, 1307–1316. [Google Scholar] [CrossRef]
- Kornack, T.W.; Ghosh, R.K.; Romalis, M.V. Nuclear Spin Gyroscope Based on an Atomic Comagnetometer. Phys. Rev. Lett. 2005, 95, 230801. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, Y.; Lin, S.; Cao, L.; Tang, J.; Lei, G.; Zhai, Y. Crosstalk Analysis and Suppression of Optically Pumped Magnetometer Array for Bio-Magnetic Field Measurement Systems. Measurement 2024, 237, 115223. [Google Scholar] [CrossRef]
- Wang, T.; Kimball, D.F.J.; Sushkov, A.O.; Aybas, D.; Blanchard, J.W.; Centers, G.; Kelley, S.R.O.; Wickenbrock, A.; Fang, J.; Budker, D. Application of Spin-Exchange Relaxation-Free Magnetometry to the Cosmic Axion Spin Precession Experiment. Phys. Dark Universe 2018, 19, 27–35. [Google Scholar] [CrossRef]
- Zhao, J.; Ding, M.; Lu, J.; Yang, K.; Ma, D.; Yao, H.; Han, B.; Liu, G. Determination of Spin Polarization in Spin-Exchange Relaxation-Free Atomic Magnetometer Using Transient Response. IEEE Trans. Instrum. Meas. 2020, 69, 845–852. [Google Scholar] [CrossRef]
- Tang, J.; Zhai, Y.; Zhou, B.; Han, B.; Liu, G. Dual-Axis Closed Loop of a Single-Beam Atomic Magnetometer: Toward High Bandwidth and High Sensitivity. IEEE Trans. Instrum. Meas. 2021, 70, 1504808. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Y.; Wang, Y.; Zhou, B.; Han, B.; Zhai, Y.; Liu, G. Enhancement of Bandwidth in Spin-Exchange Relaxation-Free (SERF) Magnetometers with Amplitude-Modulated Light. Appl. Phys. Lett. 2022, 120, 084001. [Google Scholar] [CrossRef]
- Fang, X.; Ma, D.; Zhao, T.; Fan, W.; Quan, W.; Xiao, Z.; Zhai, Y. Accurate and Fast Measurement of Alkali-Metal and Noble-Gas Atoms Spin Polarizability Based on Frequency Response in SERF Co-Magnetometer. Measurement 2023, 222, 113562. [Google Scholar] [CrossRef]
- Fang, X.; Wei, K.; Zhai, Y.; Zhao, T.; Chen, X.; Zhou, M.; Liu, Y.; Ma, D.; Xiao, Z. Analysis of Effects of Magnetic Field Gradient on Atomic Spin Polarization and Relaxation in Optically Pumped Atomic Magnetometers. Opt. Express 2022, 30, 3926. [Google Scholar] [CrossRef] [PubMed]
- Rea, M.; Holmes, N.; Hill, R.M.; Boto, E.; Leggett, J.; Edwards, L.J.; Woolger, D.; Dawson, E.; Shah, V.; Osborne, J.; et al. Precision Magnetic Field Modelling and Control for Wearable Magnetoencephalography. NeuroImage 2021, 241, 118401. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Savukov, I.; Newman, S. Magnetocardiography with a 16-Channel Fiber-Coupled Single-Cell Rb Optically Pumped Magnetometer. Appl. Phys. Lett. 2019, 114, 143702. [Google Scholar] [CrossRef]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving Magnetoencephalography towards Real-World Applications with a Wearable System. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef]
- Shahnas, H.; Arkani-Hamed, J. Viscous and Impact Demagnetization of Martian Crust. J. Geophys. Res. 2007, 112, 2005JE002424. [Google Scholar] [CrossRef]
- Yang, K.; Lu, J.; Wang, Z.; Sun, B.; Ma, Y.; Wang, Y.; Han, B. Minimizing Magnetic Fields of the Low-Noise MnZn Ferrite Magnetic Shield for Atomic Magnetometer. J. Phys. D Appl. Phys. 2022, 55, 015003. [Google Scholar] [CrossRef]
- Rikitake, T. Magnetic and Electromagnetic Shielding; Terra Scientific Publishing Company: Tokyo, Japan, 1987; ISBN 978-90-277-2406-9. [Google Scholar]
- Altarev, I.; Bales, M.; Beck, D.H.; Chupp, T.; Fierlinger, K.; Fierlinger, P.; Kuchler, F.; Lins, T.; Marino, M.G.; Niessen, B.; et al. A Large-Scale Magnetic Shield with 10^6 Damping at mHz Frequencies. J. Appl. Phys. 2015, 117, 183903. [Google Scholar] [CrossRef]
- Altarev, I.; Babcock, E.; Beck, D.; Burghoff, M.; Chesnevskaya, S.; Chupp, T.; Degenkolb, S.; Fan, I.; Fierlinger, P.; Frei, A.; et al. A Magnetically Shielded Room with Ultra Low Residual Field and Gradient. Rev. Sci. Instrum. 2014, 85, 075106. [Google Scholar] [CrossRef]
- Liyi, L.; Zhiyin, S.; Donghua, P.; Jiaxi, L.; Feng, Y. An Approach to Analyzing Magnetically Shielded Room Comprising Discontinuous Layers Considering Permeability in Low Magnetic Field. IEEE Trans. Magn. 2014, 50, 2008104. [Google Scholar] [CrossRef]
- Sun, Z.; Schnabel, A.; Burghoff, M.; Li, L. Calculation of an Optimized Design of Magnetic Shields with Integrated Demagnetization Coils. AIP Adv. 2016, 6, 075220. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Shi, M.; Yuan, S.; Wang, L.; Han, B. Modeling and Application of Magnetic Shaking for Improving Permeability and Performance of Magnetic Shields. IEEE Trans. Ind. Electron. 2024, 71, 8162–8172. [Google Scholar] [CrossRef]
- Shi, M.; Zhang, X.; Yang, J.; Ma, Y.; Zhang, L.; Tian, K.; Yuan, S. The SF and Remanence Evaluation of Magnetic Shields Based on SST for Low-Frequency and Degaussing Situation. J. Phys. D Appl. Phys. 2024, 57, 365003. [Google Scholar] [CrossRef]
- Dionne, G.F. Magnetic Oxides; Springer: Boston, MA, USA, 2009; ISBN 978-1-4419-0053-1. [Google Scholar]
- Crangle, J. The Magnetic Properties of Solids; The Structures and Properties of Solids, 6; Edward Arnold: London, UK, 1977; ISBN 978-0-7131-2573-3. [Google Scholar]
- Pfutzner, H.; Krismanic, G. The Needle Method for Induction Tests: Sources of Error. IEEE Trans. Magn. 2004, 40, 1610–1616. [Google Scholar] [CrossRef]
- Yue, S.; Moses, A.J.; Anderson, P.I.; Harrison, C.; Li, Y.; Yang, Q. Measurement and Analysis of the Non-Symmetry of Transverse Magnetisation and Resulting Loss in Grain-Oriented Steel Using a Modified RSST. J. Magn. Magn. Mater. 2022, 561, 169671. [Google Scholar] [CrossRef]
- Yang, J.; Shi, M.; Zhang, X.; Ma, Y.; Liu, Y.; Yuan, S.; Han, B. Demagnetization Parameters Evaluation of Magnetic Shields Based on Anhysteretic Magnetization Curve. Materials 2023, 16, 5238. [Google Scholar] [CrossRef]
- Shi, M.; Zhang, X.; Yang, J.; Yuan, S.; Wang, L. An Optimized Measurement Method for Magnetic Properties of Permalloy Sheet Under Demagnetization. IEEE Trans. Instrum. Meas. 2022, 71, 6003509. [Google Scholar] [CrossRef]
- Sun, J.; Ren, J.; Li, J.; Huang, Y. Measurement and Analysis of Magnetic Properties of Permalloy for Magnetic Shielding Devices under Different Temperature Environments. Materials 2023, 16, 3253. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Y.; Dou, Y.; Yue, S.; Li, Z. Magnetic Property Measurement of Ultra-Thin Silicon Steel with an Improved B–H Sensor. IEEE Trans. Magn. 2024, 60, 6000305. [Google Scholar] [CrossRef]
- Li, Y.; Gao, J.; Yue, S.; Dou, Y.; Yin, J. Effects of Simultaneous Loading of Temperature and Biaxial Stress on the 1&2D Magnetic Properties of Non-Oriented Electrical Steel Sheets. AIP Adv. 2024, 14, 015230. [Google Scholar] [CrossRef]


| Isotropy | Anisotropy | ||||
|---|---|---|---|---|---|
| μ = 25,000 | μ = 20,000 | μ = 15,000 | Argon Arc Welding | Laser Welding | |
| δxoy | 10.80% | 10.79% | 10.77% | 11.22% | 10.81% |
| δyoz | 3.91% | 3.91% | 3.90% | 3.57% | 3.59% |
| δzox | 4.65% | 4.64% | 4.64% | 4.66% | 4.45% |
| SFx | 110.05 | 88.23 | 66.41 | 102.75 | 89.70 |
| SFy | 110.04 | 88.22 | 66.41 | 70.36 | 73.76 |
| SFz | 109.05 | 87.43 | 65.81 | 86.99 | 86.39 |
| μx | μy | μz | λx | λy | λz |
|---|---|---|---|---|---|
| 10,000 | 8000 | 5000 | 0.849 | 0.898 | 0.963 |
| 30,000 | 20,000 | 10,000 | 0.797 | 0.894 | 0.986 |
| 50,000 | 40,000 | 30,000 | 0.864 | 0.911 | 0.950 |
| 80,000 | 50,000 | 30,000 | 0.801 | 0.910 | 0.976 |
| SFx | SFy | SFz | MSE | |
|---|---|---|---|---|
| Original model | 172.43 | 129.57 | 86.71 | 49.97 |
| Modified model | 162.21 | 130.45 | 92.22 | 0.13 |
| Finite element simulation | 161.74 | 130.58 | 92.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Shi, M.; Zhang, L.; Li, T.; Ling, X.; Yuan, S.; Wang, H.; Gao, Y. A Novel Simulation Model of Shielding Performance Based on the Anisotropic Magnetic Property of Magnetic Shields. Materials 2024, 17, 5906. https://doi.org/10.3390/ma17235906
Ma Y, Shi M, Zhang L, Li T, Ling X, Yuan S, Wang H, Gao Y. A Novel Simulation Model of Shielding Performance Based on the Anisotropic Magnetic Property of Magnetic Shields. Materials. 2024; 17(23):5906. https://doi.org/10.3390/ma17235906
Chicago/Turabian StyleMa, Yuzheng, Minxia Shi, Leran Zhang, Teng Li, Xuechen Ling, Shuai Yuan, Hanxing Wang, and Yi Gao. 2024. "A Novel Simulation Model of Shielding Performance Based on the Anisotropic Magnetic Property of Magnetic Shields" Materials 17, no. 23: 5906. https://doi.org/10.3390/ma17235906
APA StyleMa, Y., Shi, M., Zhang, L., Li, T., Ling, X., Yuan, S., Wang, H., & Gao, Y. (2024). A Novel Simulation Model of Shielding Performance Based on the Anisotropic Magnetic Property of Magnetic Shields. Materials, 17(23), 5906. https://doi.org/10.3390/ma17235906






