Photoluminescence Spectra of Helium Ion-Implanted Diamond
Abstract
1. Introduction
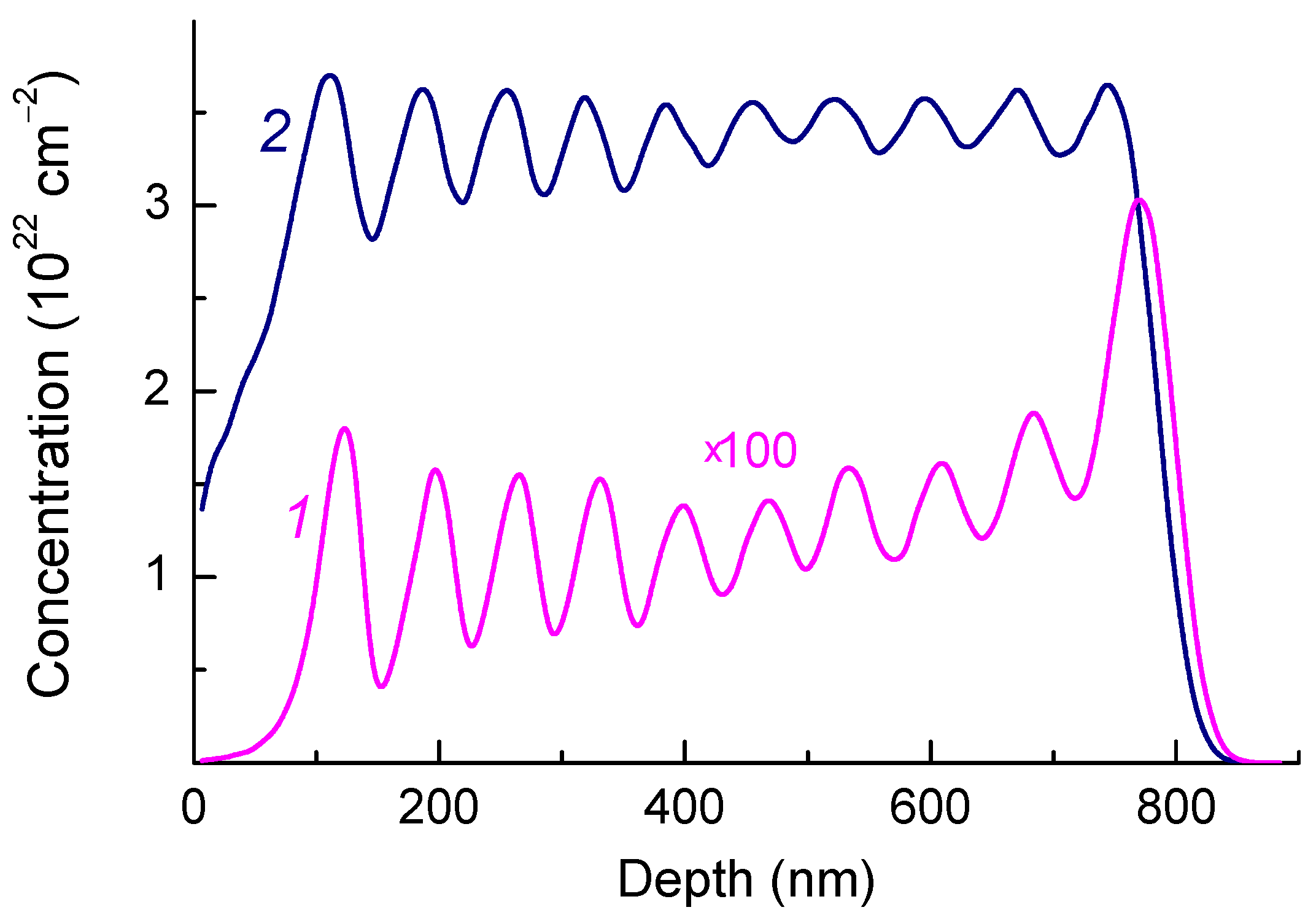
2. Materials and Methods
3. Results
3.1. Raman Spectra of [He]-Implanted Diamond
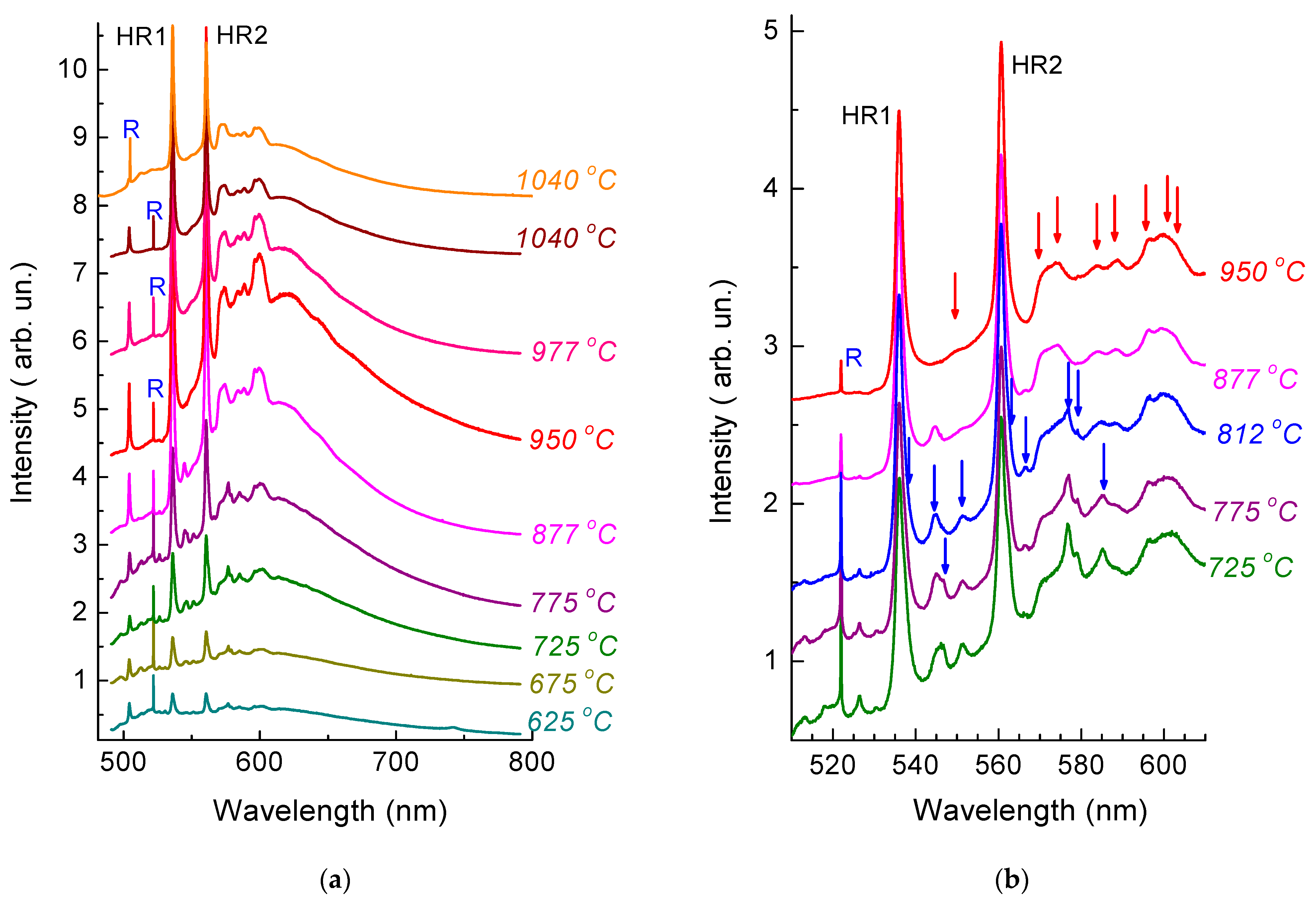
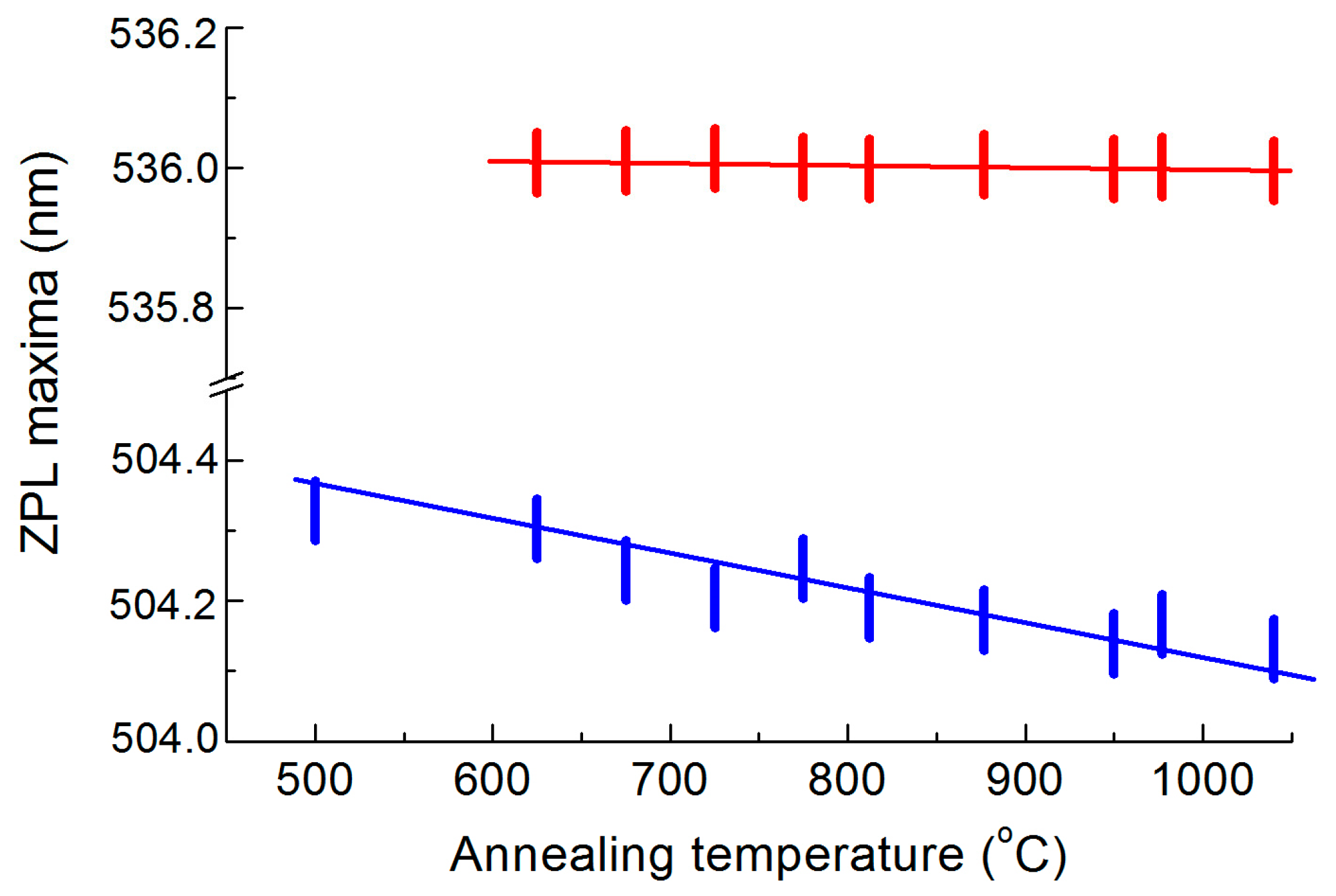
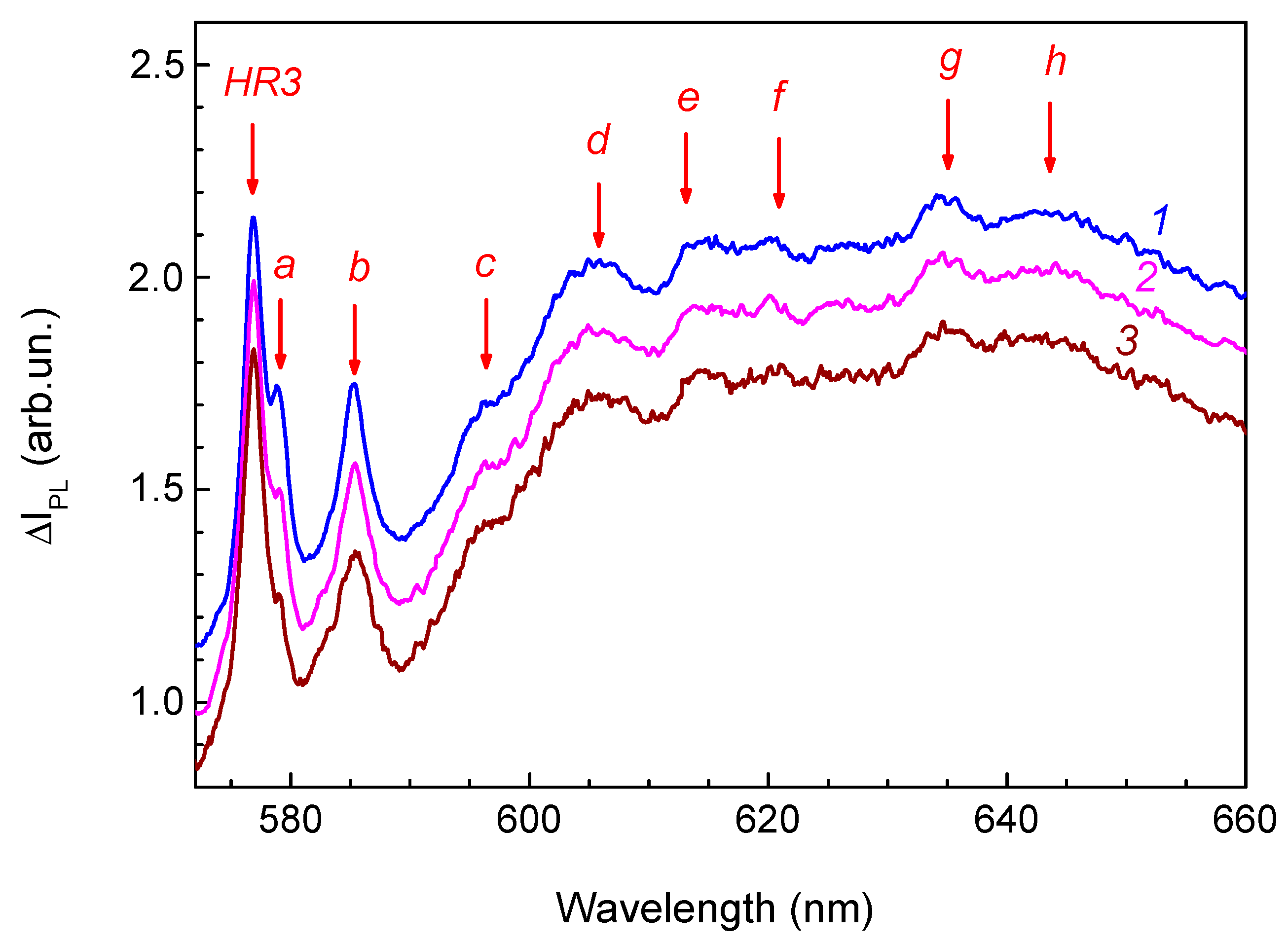
3.2. Transformations of PL Spectra with Annealing Temperature
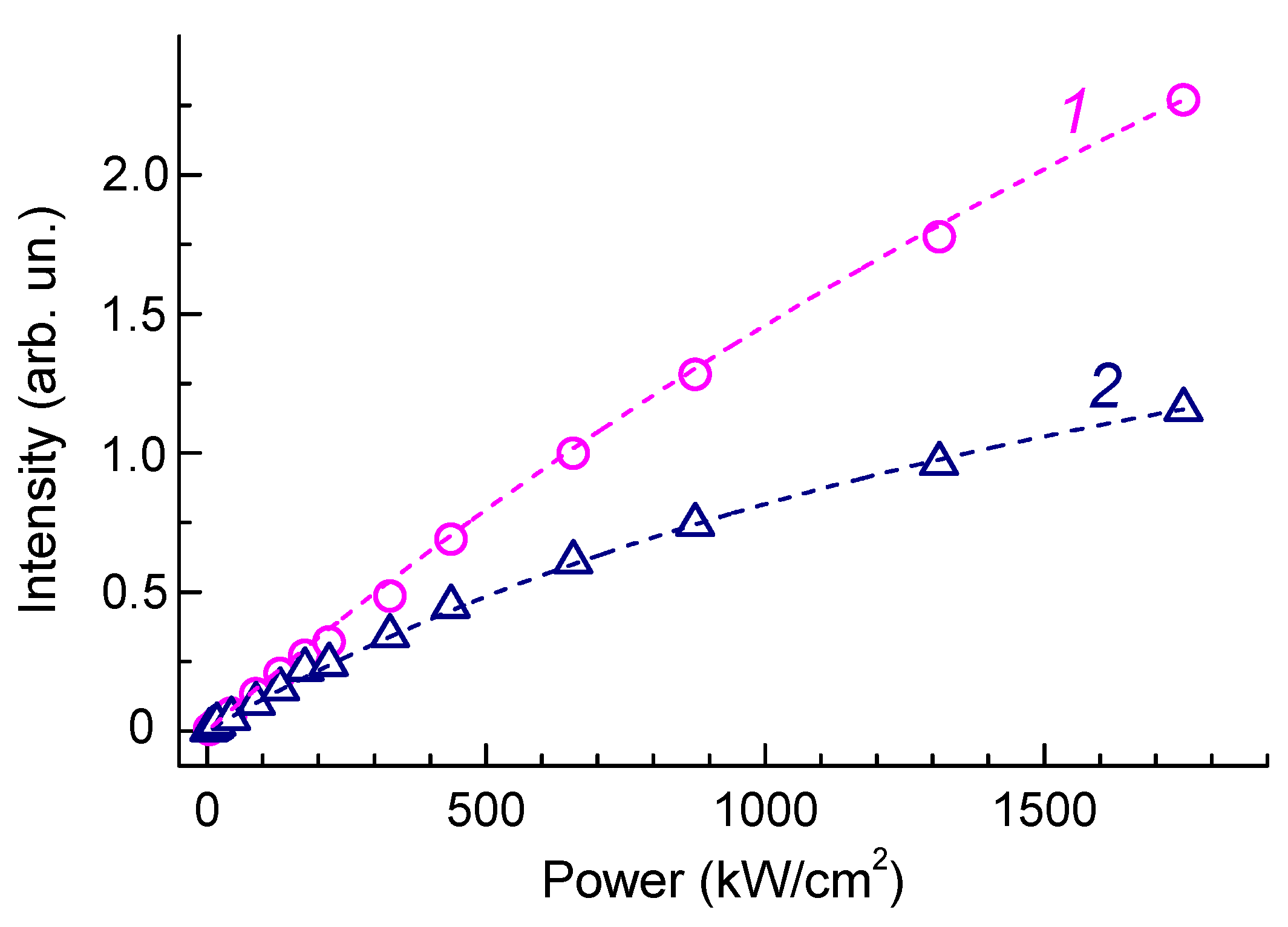
3.3. Photoluminescence Saturation Properties of HR1 and HR2 ZPLs
4. Discussion
4.1. Phonon Sidebands of HR1 and HR2 ZPLs
4.2. On the Interstitial Nature of He-Related Centers in Ion-Implanted Diamonds
4.3. Saturation Pump Power of HR1 and HR2 ZPLs
4.4. Transformations of Less Thermally Stable Helium-Related Centers in the PL Spectra
5. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pezzagna, S.; Meijer, J. Quantum computer based on color centers in diamond. Appl. Phys. Rev. 2021, 8, 011308. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Flatae, A.M.; Kambalathmana, H.; Sledz, F.; Hunold, L.; Soltani, N.; Reuschel, P.; Sciortino, S.; Gelli, N.; Massi, M.; et al. Creation of silicon-vacancy color centers in diamond by ion implantation. Front. Phys. 2021, 8, 601362. [Google Scholar] [CrossRef]
- Wang, L.; Wang, R.; Jia, G.; Bai, H.; Hao, J.; Zhang, Y.; Wang, K.; Wang, H.X. The luminescence study of GeV centers and damage in diamond induced by 300keV Ge ion implantation. Vacuum 2024, 222, 113074. [Google Scholar] [CrossRef]
- Nieto Hernández, E.; Redolfi, E.; Stella, C.; Andrini, G.; Corte, E.; Sachero, S.; Ditalia Tchernij, S.; Picariello, F.; Herzig, T.; Borzdov, Y.M.; et al. Efficiency Optimization of Ge-V Quantum Emitters in Single-Crystal Diamond upon Ion Implantation and HPHT Annealing. Adv. Quantum Technol. 2023, 6, 2300010. [Google Scholar] [CrossRef]
- Ju, Z.; Lin, J.; Shen, S.; Wu, B.; Wu, E. Preparations and applications of single color centers in diamond. Adv. Phys. 2021, 6, 1858721. [Google Scholar] [CrossRef]
- Mrózek, M.; Schabikowski, M.; Mitura-Nowak, M.; Lekki, J.; Marszałek, M.; Wojciechowski, A.M.; Gawlik, W. Nitrogen-vacancy color centers created by proton implantation in a diamond. Materials 2021, 14, 833. [Google Scholar] [CrossRef] [PubMed]
- Becker, J.N.; Neu, E. The silicon vacancy center in diamond. In Semiconductors and Semimetals; Nebel, C.E., Aharonovich, I., Mizuochi, N., Hatano, M., Eds.; Fraunhofer Institute for Applied Solid State Physics: Freiburg, Germany, 2020; Volume 103, pp. 201–235. [Google Scholar]
- Gippius, A.A.; Vavilov, V.S.; Zaitsev, A.M.; Zhakupbekov, B.S. Defects production and interaction in ion-implanted diamond. Physica B+C 1983, 116, 187–194. [Google Scholar] [CrossRef]
- Iwasaki, T.; Ishibashi, F.; Miyamoto, Y.; Doi, Y.; Kobayashi, S.; Miyazaki, T.; Tahara, K.; Jahnke, K.D.; Rogers, L.J.; Naydenov, B.; et al. Germanium-vacancy single color centers in diamond. Sci. Rep. 2015, 5, 12882. [Google Scholar] [CrossRef] [PubMed]
- Corte, E.; Sachero, S.; Ditalia Tchernij, S.; Lühmann, T.; Pezzagna, S.; Traina, P.; Degiovanni, I.P.; Moreva, E.; Olivero, P.; Meijer, J.; et al. Spectral emission dependence of tin-vacancy centers in diamond from thermal processing and chemical functionalization. Adv. Photon. Res. 2022, 3, 2100148. [Google Scholar] [CrossRef]
- Martinovich, V.A.; Turukhin, A.V.; Zaitsev, A.M.; Gorokhovsky, A.A. Photoluminescence spectra of xenon implanted natural diamonds. J. Luminesc. 2003, 102, 785–790. [Google Scholar] [CrossRef]
- Corte, E.; Andrini, G.; Nieto Hernández, E.; Pugliese, V.; Costa, Â.; Magchiels, G.; Moens, J.; Tunhuma, S.M.; Villarreal, R.; Pereira, L.M.C.; et al. Magnesium-vacancy optical centers in diamond. ACS Photon. 2022, 10, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Tkachev, V.D.; Zaitsev, A.M.; Tkachev, V.V. Chemical activity of noble gases in diamond. Phys. Status Solidi B 1985, 129, 129–133. [Google Scholar] [CrossRef]
- Forneris, J.; Battiato, A.; Monticone, D.G.; Picollo, F.; Amato, G.; Boarino, L.; Brida, G.; Degiovanni, I.P.; Enrico, E.; Genovese, M.; et al. Electroluminescence from a diamond device with ion-beam-micromachined buried graphitic electrodes. Nucl. Instrum. Methods Phys. Res. B 2015, 348, 187–190. [Google Scholar] [CrossRef]
- Forneris, J.; Tengattini, A.; Tchernij, S.D.; Picollo, F.; Battiato, A.; Traina, P.; Degiovanni, I.P.; Moreva, E.; Brida, G.; Grilj, V.; et al. Creation and characterization of He-related color centers in diamond. J. Luminesc. 2016, 179, 59–63. [Google Scholar] [CrossRef]
- Prestopino, G.; Marinelli, M.; Milani, E.; Verona, C.; Verona-Rinati, G.; Traina, P.; Moreva, E.; Degiovanni, I.P.; Genovese, M.S.; Ditalia Tchernij, S.; et al. Photo-physical properties of He-related color centers in diamond. Appl. Phys. Lett. 2017, 111, 111105. [Google Scholar] [CrossRef]
- Moreva, E.; Traina, P.; Forneris, J.; Tchernij, S.D.; Picollo, F.; Degiovanni, I.P.; Carabelli, V.V.; Olivero, P.; Genovese, M. Color centres in diamond from single photon sources to ODMR in cells. Proc. SPIE 2018, 10733, 1073304. [Google Scholar]
- Chen, M.; Best, J.P.; Shorubalko, I.; Michler, J.; Spolenak, R.; Wheeler, J.M. Influence of helium ion irradiation on the structure and strength of diamond. Carbon 2020, 158, 337–345. [Google Scholar] [CrossRef]
- Sumikura, H.; Hirama, K.; Nishiguchi, K.; Shinya, A.; Notomi, M. Highly nitrogen-vacancy doped diamond nanostructures fabricated by ion implantation and optimum annealing. APL Mater. 2020, 8, 031113. [Google Scholar] [CrossRef]
- McCloskey, D.; Fox, D.; O’Hara, N.; Usov, V.; Scanlan, D.; McEvoy, N.; Duesberg, G.S.; Cross, G.L.W.; Zhang, H.Z.; Donegan, J.F. Helium ion microscope generated nitrogen-vacancy centres in type Ib diamond. Appl. Phys. Lett. 2014, 104, 031109. [Google Scholar] [CrossRef]
- Ngambou, M.W.N.; Perrin, P.; Balasa, I.; Brinza, O.; Valentin, A.; Mille, V.; Bénédic, F.; Goldner, P.; Tallaire, A.; Achard, J. Optimizing ion implantation to create shallow NV centre ensembles in high-quality CVD diamond. Mater. Quantum Technol. 2022, 2, 045001. [Google Scholar] [CrossRef]
- Khmelnitskiy, R.A.; Zavedeev, E.V.; Khomich, A.V.; Gooskov, A.V.; Gippius, A.A. Blistering in diamond implanted with hydrogen ions. Vacuum 2005, 78, 273–279. [Google Scholar] [CrossRef]
- Goss, J.P.; Coomer, B.J.; Jones, R.; Shaw, T.D.; Briddon, P.R.; Rayson, M.; Öberg, S. Self-interstitial aggregation in diamond. Phys. Rev. B 2001, 63, 195208. [Google Scholar] [CrossRef]
- Tallaire, A.; Brinza, O.; De Feudis, M.; Ferrier, A.; Touati, N.; Binet, L.; Nicolas, L.; Delord, T.; Hetet, G.; Herzig, T.; et al. Synthesis of loose nanodiamonds containing nitrogen-vacancy centers for magnetic and thermal sensing. ACS Appl. Nano Mater. 2019, 2, 5952–5962. [Google Scholar] [CrossRef]
- Zaitsev, A.M. Optical Properties of Diamond: A Data Handbook; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Khmelnitsky, R.; Kovalchuk, O.; Gorevoy, A.; Danilov, P.; Pomazkin, D.; Kudryashov, S. Novel robust internal calibration procedure for precise FT-IR measurements of nitrogen impurities in diamonds. Chemosensors 2023, 11, 313. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter. Nucl. Instrum. Methods Phys. Res. B 2013, 268, 1818–1823. [Google Scholar] [CrossRef]
- Khmelnitsky, R.A.; Dravin, V.A.; Tal, A.A.; Zavedeev, E.V.; Khomich, A.A.; Khomich, A.V.; Alekseev, A.A.; Terentiev, S.A. Damage accumulation in diamond during ion implantation. J. Mater. Res. 2015, 30, 1583–1592. [Google Scholar] [CrossRef]
- Prins, J.F. Ballistic self-annealing during ion implantation. J. Phys. D Appl. Phys. 2001, 34, 3003–3010. [Google Scholar] [CrossRef]
- Kalish, R.; Reznik, A.; Prawer, S.; Saada, D.; Adler, J. Ion-implantation-induced defects in diamond and their annealing: Experiment and simulation. Phys. Status Solidi A 1999, 174, 83–99. [Google Scholar] [CrossRef]
- Orwa, J.O.; Nugent, K.W.; Jamieson, D.N.; Prawer, S. Raman investigation of damage caused by deep ion implantation in diamond. Phys. Rev. B 2000, 62, 5461–5472. [Google Scholar] [CrossRef]
- Khomich, A.A.; Khmelnitsky, R.A.; Khomich, A.V. Probing the nanostructure of neutron-irradiated diamond using Raman spectroscopy. Nanomaterials 2019, 10, 1166. [Google Scholar] [CrossRef]
- Khomich, A.V.; Khmelnitskiy, R.A.; Dravin, V.A.; Gippius, A.A.; Zavedeev, E.V.; Vlasov, I.I. Radiation damage in diamonds subjected to helium implantation. Phys. Solid State 2007, 49, 1661–1665. [Google Scholar] [CrossRef]
- Ashfold, M.N.; Goss, J.P.; Green, B.L.; May, P.W.; Newton, M.E.; Peaker, C.V. Nitrogen in diamond. Chem. Rev. 2020, 120, 5745–5794. [Google Scholar] [CrossRef] [PubMed]
- Khomich, A.A.; Averin, A.A.; Poklonskaya, O.N.; Bokova-Sirosh, S.N.; Dzeraviaha, A.N.; Khmelnitsky, R.A.; Vlasov, I.I.; Shenderova, O.; Poklonski, N.A.; Khomich, A.V. Features of the 1640 cm−1 band in the Raman spectra of radiation-damaged and nano-sized diamonds. J. Phys. Conf. Ser. 2019, 1400, 044017. [Google Scholar] [CrossRef]
- Liu, Y.H.; Zhang, J.L.; Wu, F.L.; Qi, M.; Hei, L.F.; Lv, F.X. The Raman Spectroscopy and XPS investigation of CVD diamond after fast-neutron irradiation. Mater. Today Com. 2020, 22, 100699. [Google Scholar] [CrossRef]
- Poklonski, N.A.; Khomich, A.A.; Svito, I.A.; Vyrko, S.A.; Poklonskaya, O.N.; Kovalev, A.I.; Kozlova, M.V.; Khmelnitskii, R.A.; Khomich, A.V. Magnetic and optical properties of natural diamonds with subcritical radiation damage induced by fast neutrons. Appl. Sci. 2023, 13, 6221. [Google Scholar] [CrossRef]
- Steeds, J.W.; Charles, S.; Davis, T.J.; Gilmore, A.; Hayes, J.; Pickard, D.; Butler, J.E. Creation and mobility of self-interstitials in diamond by use of a transmission electron microscope and their subsequent study by photoluminescence microscopy. Diam. Relat. Mater. 1999, 8, 94–100. [Google Scholar] [CrossRef]
- Dischler, B. Handbook of Spectral Lines in Diamond: Volume 1: Tables and Interpretations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dobrinets, I.A.; Vins, V.G.; Zaitsev, A.M. HPHT-Treated Diamonds; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hainschwang, T.; Notari, F.; Pamies, G. A defect study and classification of brown diamonds with deformation-related color. Minerals 2020, 10, 903. [Google Scholar] [CrossRef]
- Hainschwang, T.; Karampelas, S.; Fritsch, E.; Notari, F. Luminescence spectroscopy and microscopy applied to study gem materials: A case study of C centre containing diamonds. Miner. Petrol. 2013, 107, 393–413. [Google Scholar] [CrossRef]
- Khomich, A.A.; Khmelnitskii, R.A.; Poklonskaya, O.N.; Averin, A.A.; Bokova-Sirosh, S.N.; Poklonski, N.A.; Ralchenko, V.G.; Khomich, A.V. Photoluminescence Spectra of the 580-nm Center in Irradiated Diamonds. J. Appl. Spectrosc. 2019, 86, 597–605. [Google Scholar] [CrossRef]
- Dale, M.W. Colour Centres on Demand in Diamond. Ph.D. Thesis, University of Warwick, Warwick, UK, 2015. [Google Scholar]
- Poklonskaya, O.N.; Vyrko, S.A.; Khomich, A.A.; Averin, A.A.; Khomich, A.V.; Khmelnitsky, R.A.; Poklonski, N.A. Raman scattering in natural diamond crystals implanted with high-energy ions and irradiated with fast neutrons. J. Appl. Spectrosc. 2014, 81, 969–977. [Google Scholar] [CrossRef]
- Deslandes, A.; Guenette, M.C.; Belay, K.; Elliman, R.G.; Karatchevtseva, I.; Thomsen, L.; Riley, D.P.; Lumpkin, G.R. Diamond structure recovery during ion irradiation at elevated temperatures. Nucl. Instrum. Methods Phys. Res. B 2015, 365, 331–335. [Google Scholar] [CrossRef]
- Jia, G.; Zhang, Y.; Kong, X.; Huangfu, C.; Hao, J.; Wang, W.; Song, Z.; Wang, H.; Wang, K. The near surface damage and recovery of low nitrogen diamond implanted with MeV phosphorus ions. Appl. Surf. Sci. 2024, 661, 160080. [Google Scholar] [CrossRef]
- Steeds, J.W.; Kohn, S. Annealing of electron radiation damage in a wide range of Ib and IIa diamond samples. Diam. Relat. Mater. 2014, 50, 110–122. [Google Scholar] [CrossRef]
- Eaton-Magaña, S.; Ardon, T. Temperature effects on luminescence centers in natural type IIb diamonds. Diam. Relat. Mater. 2016, 69, 86–95. [Google Scholar] [CrossRef]
- Won, J.; Yagi, H.; Hatta, A.; Jiang, N.; Ito, T.; Sasaki, T.; Hiraki, A. Effects of remote hydrogen plasma treatment (RHPT) on ion-implanted CVD diamond. Diam. Relat. Mater. 1997, 6, 1041–1046. [Google Scholar] [CrossRef]
- Goss, J.P.; Eyre, R.J.; Briddon, P.R.; Mainwood, A. Density functional simulations of noble-gas impurities in diamond. Phys. Rev. B 2009, 80, 085204. [Google Scholar] [CrossRef]
- Zaitsev, A.M. Vibronic spectra of impurity-related optical centers in diamond. Phys. Rev. B 2000, 61, 12909. [Google Scholar] [CrossRef]
- Alsid, S.T.; Barry, J.F.; Pham, L.M.; Schloss, J.M.; O’Keeffe, M.F.; Cappellaro, P.; Braje, D.A. Photoluminescence decomposition analysis: A technique to characterize N-V creation in diamond. Phys. Rev. Appl. 2019, 12, 044003. [Google Scholar] [CrossRef]
- Klein, C.A.; Hartnett, T.M.; Robinson, C.J. Critical-point phonon frequencies of diamond. Phys. Rev. B 1992, 45, 12854. [Google Scholar] [CrossRef]
- Vogelgesang, R.; Alvarenga, A.D.; Kim, H.; Ramdas, A.K.; Rodriguez, S.; Grimsditch, M.; Anthony, T.R. Multiphonon Raman and infrared spectra of isotopically controlled diamond. Phys. Rev. B 1998, 58, 5408. [Google Scholar] [CrossRef]
- Dean, P.J. Bound excitons and donor-acceptor pairs in natural and synthetic diamond. Phys. Rev. 1965, 139, A588–A602. [Google Scholar] [CrossRef]
- Dean, P.J.; Jones, I.H. Recombination radiation from diamond. Phys. Rev. 1964, 133, A1698–A1705. [Google Scholar] [CrossRef]
- Mainwood, A. Modelling of interstitial-related defects in diamond. Diam. Relat. Mater. 1999, 8, 1560–1564. [Google Scholar] [CrossRef]
- Collins, A.T.; Davies, G.; Kanda, H.; Woods, G.S. Spectroscopic studies of carbon-13 synthetic diamond. J. Phys. C 1988, 21, 1363–1376. [Google Scholar] [CrossRef]
- Collins, A.T.; Davies, G. Cathodoluminescence studies of carbon-13 diamond. J. Luminesc. 1988, 40–41, 865–866. [Google Scholar] [CrossRef]
- Collins, A.T.; Woad, P.J.; Woods, G.S.; Kanda, H. Localised vibrational modes in diamonds grown from mixed carbon isotopes. Diam. Relat. Mater. 1993, 2, 136–141. [Google Scholar] [CrossRef]
- Khmelnitsky, R.A.; Dravin, V.A.; Tal, A.A.; Latushko, M.I.; Khomich, A.A.; Khomich, A.V.; Trushin, A.S.; Alekseev, A.A.; Terentiev, S.A. Mechanical stresses and amorphization of ion-implanted diamond. Nucl. Instrum. Methods Phys. Res. B 2013, 304, 5–10. [Google Scholar] [CrossRef]
- Kozlova, M.V.; Khomich, A.A.; Khmelnitsky, R.A.; Averin, A.A.; Kovalev, A.I.; Poklonskaya, O.N.; Vlasov, I.I.; Khomich, A.V.; Ralchenko, V.G. Study of color centers in radiation-modified diamonds. J. Phys.Conf. Ser. 2021, 2103, 012223. [Google Scholar] [CrossRef]
- Ekimov, E.A.; Kondrin, M.V. Vacancy–impurity centers in diamond: Prospects for synthesis and applications. Phys. Uspekhi 2017, 60, 539–558. [Google Scholar] [CrossRef]
- Zaitsev, A.M.; Melnikov, A.A.; Denisenko, A.V.; Varichenko, V.S.; Job, R.; Fahrner, W.R. Luminescence characterization and application of diamond. MRS Online Proc. Libr. 1995, 416, 113. [Google Scholar] [CrossRef]
- Wang, C.; Kurtsiefer, C.; Weinfurter, H.; Burchard, B. Single photon emission from SiV centres in diamond produced by ion implantation. J. Phys. B 2005, 39, 37–41. [Google Scholar] [CrossRef]
- Aharonovich, I.; Castelletto, S.; Simpson, D.A.; Stacey, A.; McCallum, J.; Greentree, A.D.; Prawer, S. Two-level ultrabright single photon emission from diamond nanocrystals. Nano Lett. 2009, 9, 3191. [Google Scholar] [CrossRef]
- Neu, E.; Steinmetz, D.; Riedrich-Möller, J.; Gsell, S.; Fischer, M.; Schreck, M.; Becher, C. Single photon emission from silicon-vacancy colour centres in chemical vapour deposition nano-diamonds on iridium. New J. Phys. 2011, 13, 025012. [Google Scholar] [CrossRef]
- Walker, J. Optical absorption and luminescence in diamond. Rep. Prog. Phys. 1979, 42, 1605–1659. [Google Scholar] [CrossRef]
- Davies, G. Chemistry and Physics of Carbon; Walker, P.L., Thrower, P.A., Eds.; Marcel Dekker: New York, NY, USA, 1977; Volume 13, pp. 1–143. [Google Scholar]
- Beck, R.A.; Huang, Y.; Petrone, A.; Abbott, J.W.; Pauzauskie, P.J.; Li, X. Electronic Structures and Spectroscopic Signatures of Noble-Gas-Doped Nanodiamonds. ACS Phys. Chem. 2023, 3, 299–310. [Google Scholar] [CrossRef]
- Chowdhury, S.; Hillman, D.A.; Catledge, S.A.; Konovalov, V.V.; Vohra, Y.K. Synthesis of ultrasmooth nanostructured diamond films by microwave plasma chemical vapor deposition using a He/H2/CH4/N2 gas mixture. J. Mater. Res. 2006, 21, 2675–2682. [Google Scholar] [CrossRef]
- Cao, W.; Ma, Z.B.; Tao, L.P.; Gao, P.; Li, Y.C.; Fu, Q.M. Effect of helium on diamond films deposited using microwave PCVD. Spectr. Spectr. Anal. 2015, 35, 711–714. [Google Scholar]
- Zaitsev, A.M.; Moe, K.S.; Wang, W. Optical centers and their depth distribution in electron irradiated CVD diamond. Diam. Relat. Mater. 2017, 71, 38–52. [Google Scholar] [CrossRef]
- Poklonskaya, O.N.; Khomich, A.A. Raman scattering in a diamond crystal implanted by high-energy nickel ions. J. Appl. Spectrosc. 2013, 80, 715–720. [Google Scholar] [CrossRef]
- Boudou, J.P.; Curmi, P.A.; Jelezko, F.; Wrachtrup, J.; Aubert, P.; Sennour, M.; Balasubramanian, G.; Reuter, R.; Thorel, A.; Gaffet, E. High yield fabrication of fluorescent nanodiamonds. Nanotechnology 2009, 20, 235602. [Google Scholar] [CrossRef]
- Davydov, V.A.; Rakhmanina, A.V.; Lyapin, S.G.; Ilichev, I.D.; Boldyrev, K.N.; Shiryaev, A.A.; Agafonov, V.N. Production of nano-and microdiamonds with Si-V and NV luminescent centers at high pressures in systems based on mixtures of hydrocarbon and fluorocarbon compounds. JETP Lett. 2014, 99, 585–589. [Google Scholar] [CrossRef]
- Kaplyanskii, A.A. Noncubic centers in cubic crystals and their piezospectroscopic investigation. Opt. Spectr. 1964, 16, 329. [Google Scholar]
- Clark, C.D.; Norris, C.A. Photoluminescence associated with the 1.673, 1.944 and 2.498 eV centres in diamond. J. Phys. C 1971, 4, 2223–2229. [Google Scholar] [CrossRef]
- Bergman, A.A.; Zaitsev, A.M.; Gorokhovsky, A.A. Polarization of luminescence and site symmetry of the Xe center in diamond. J. Luminesc. 2007, 125, 92–96. [Google Scholar] [CrossRef]
- Neu, E.; Fischer, M.; Gsell, S.; Schreck, M.; Becher, C. Fluorescence and polarization spectroscopy of single silicon vacancy centers in heteroepitaxial nanodiamonds on iridium. Phys. Rev. B 2011, 84, 205211. [Google Scholar] [CrossRef]




| ZPL Maxima, nm | FWHM, nm | Data from Other Publications, nm |
|---|---|---|
| 535.9 (HR1) | 1.8 | 536.5 [13], 536.3 [14], 536.5 [15], 535.2 [16], 535.2 [25] |
| 537.1 | 2.0 | 537.5 [13], 536.5 [25] |
| 544.9 | 1.9 | 546 [25] |
| 546.5 | 1.4 | 547 [13] |
| 551.3 | 1.6 | 551.2 [25] |
| 560.6 (HR2) | 1.9 | 560.5 [13], 560.5 [14], 560.5 [15], 559.7 [16], 560.5 [25] |
| 562.2 | 1.6 | 563.3 [16], 562 [25] |
| 566.3 | 2.3 | |
| 576.9 (HR3) | 1.9 | 576 [13] |
| 579.1 | 1.5 | |
| 585.3 | 2.4 | 584 [13], 584.5 [16], 585.6 [25] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khomich, A.A.; Popovich, A.; Khomich, A.V. Photoluminescence Spectra of Helium Ion-Implanted Diamond. Materials 2024, 17, 5168. https://doi.org/10.3390/ma17215168
Khomich AA, Popovich A, Khomich AV. Photoluminescence Spectra of Helium Ion-Implanted Diamond. Materials. 2024; 17(21):5168. https://doi.org/10.3390/ma17215168
Chicago/Turabian StyleKhomich, Andrey A., Alexey Popovich, and Alexander V. Khomich. 2024. "Photoluminescence Spectra of Helium Ion-Implanted Diamond" Materials 17, no. 21: 5168. https://doi.org/10.3390/ma17215168
APA StyleKhomich, A. A., Popovich, A., & Khomich, A. V. (2024). Photoluminescence Spectra of Helium Ion-Implanted Diamond. Materials, 17(21), 5168. https://doi.org/10.3390/ma17215168






