Definition, Fabrication, and Compression Testing of Sandwich Structures with Novel TPMS-Based Cores
Abstract
1. Introduction
2. Materials and Methods
2.1. Topology Definition
2.2. Fabrication Method
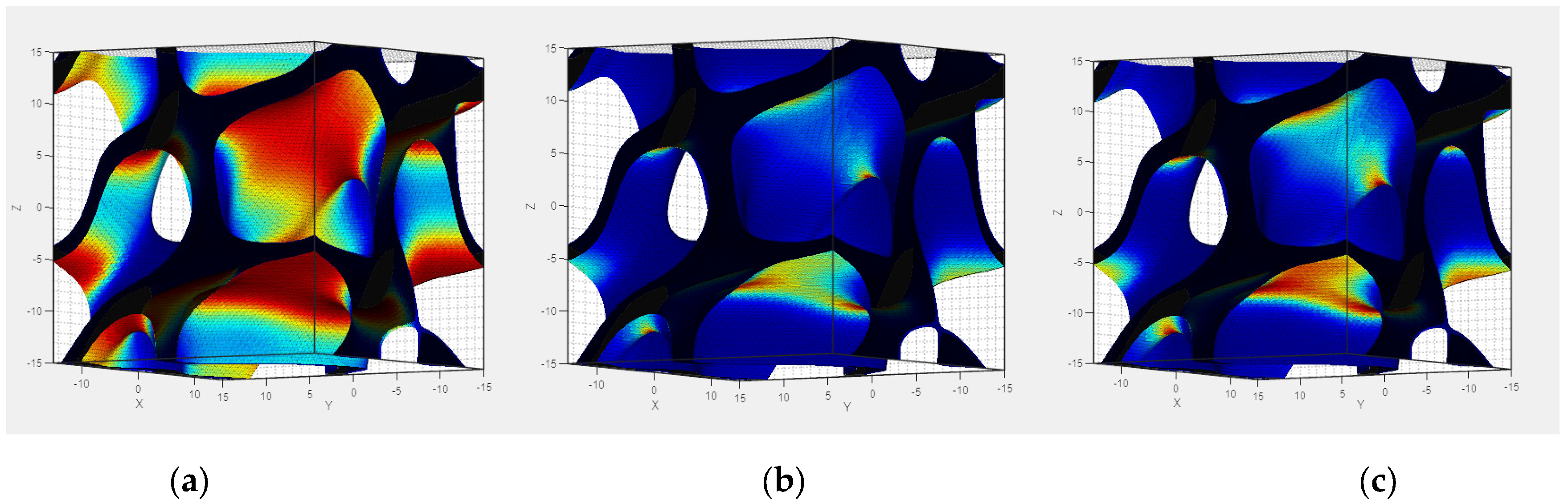
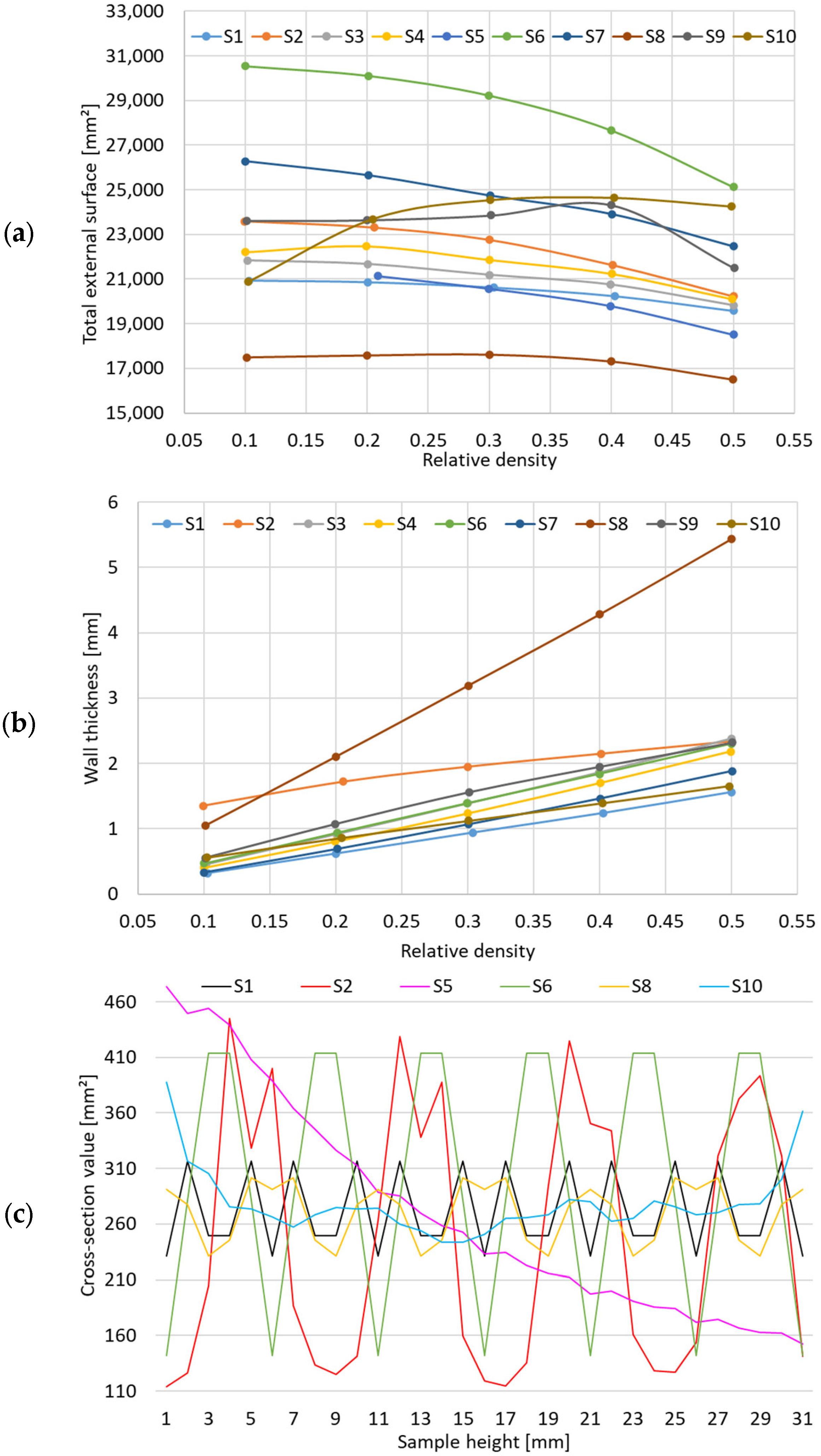
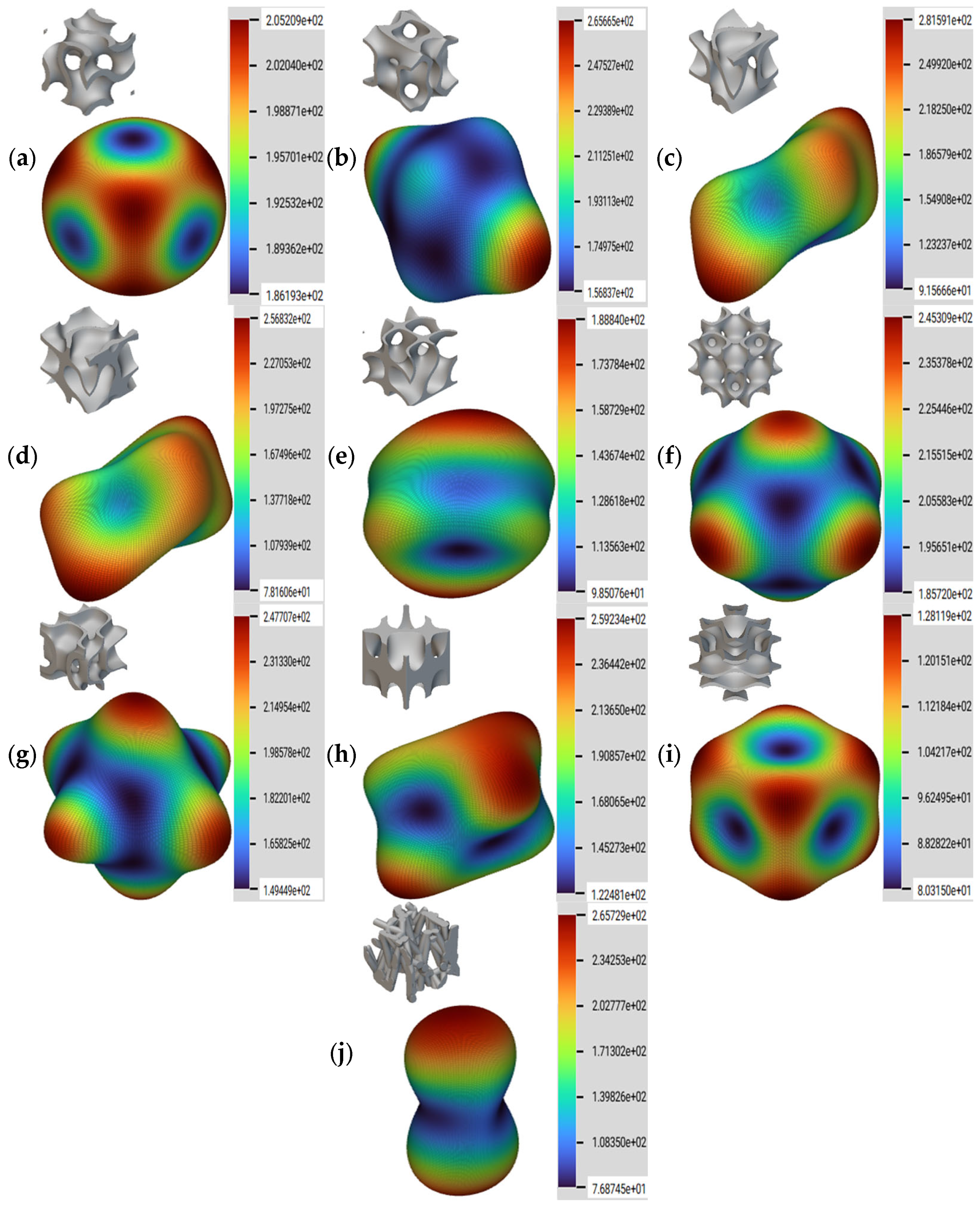
2.3. Geometry Analysis
3. Results
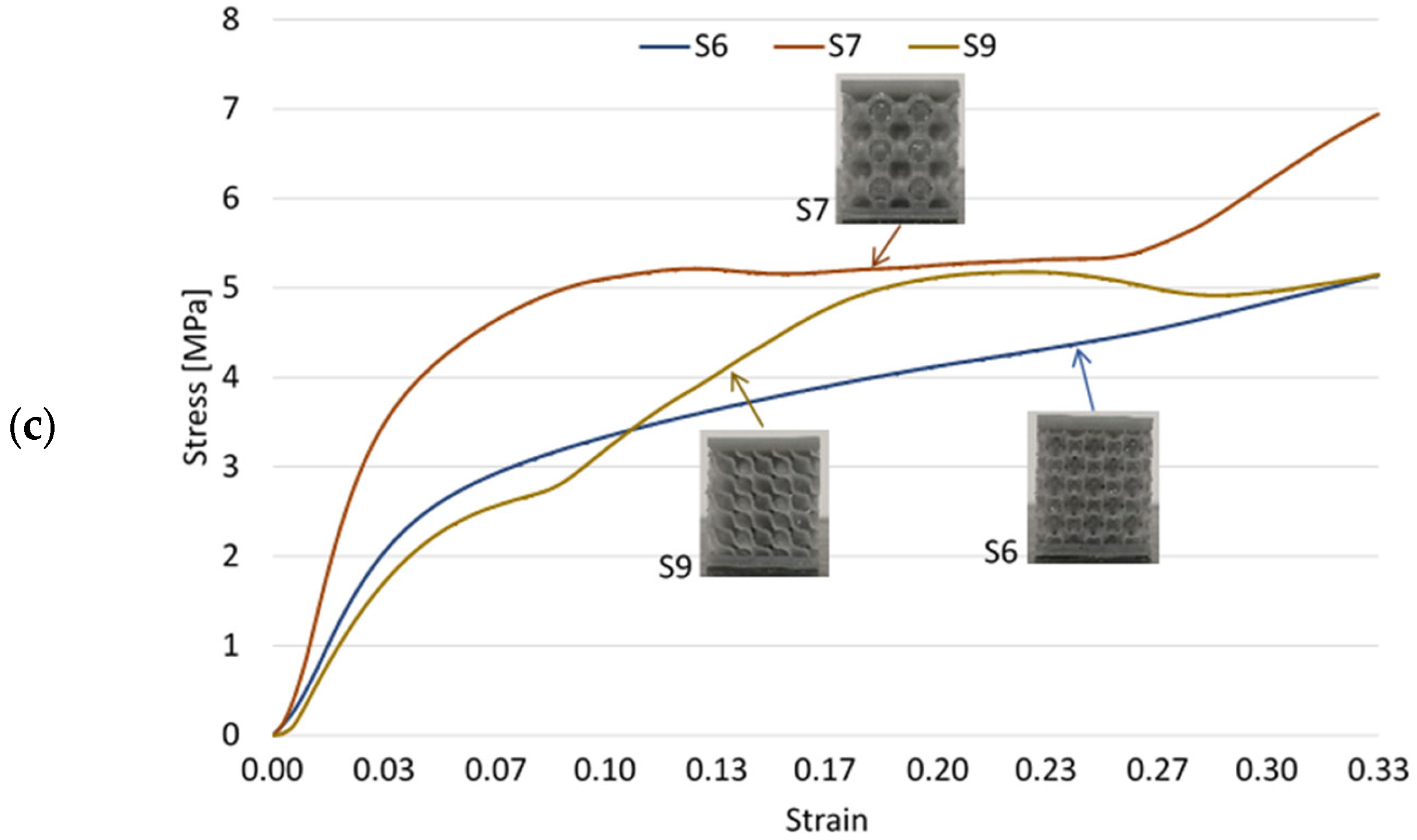
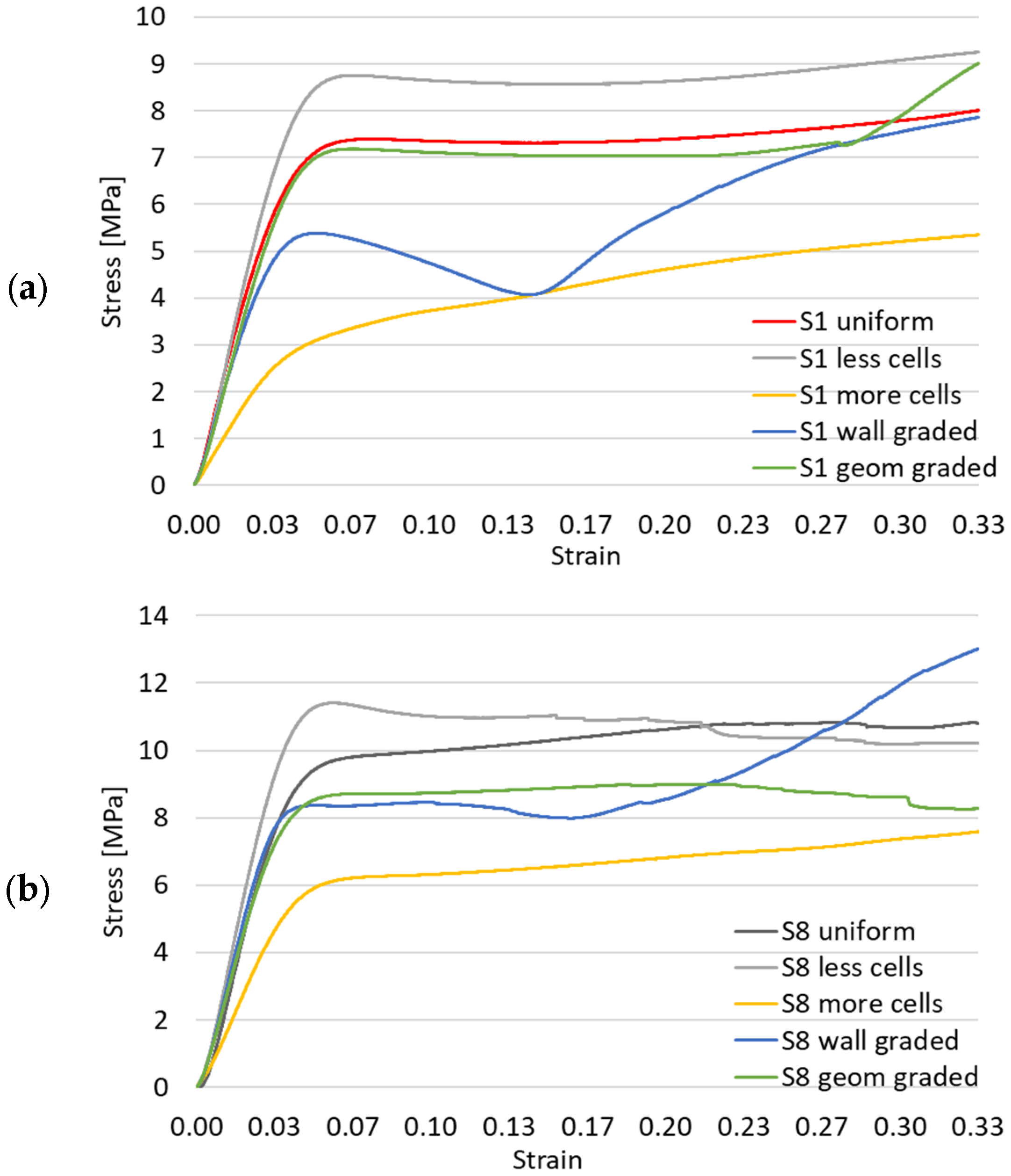
3.1. Compressive Testing
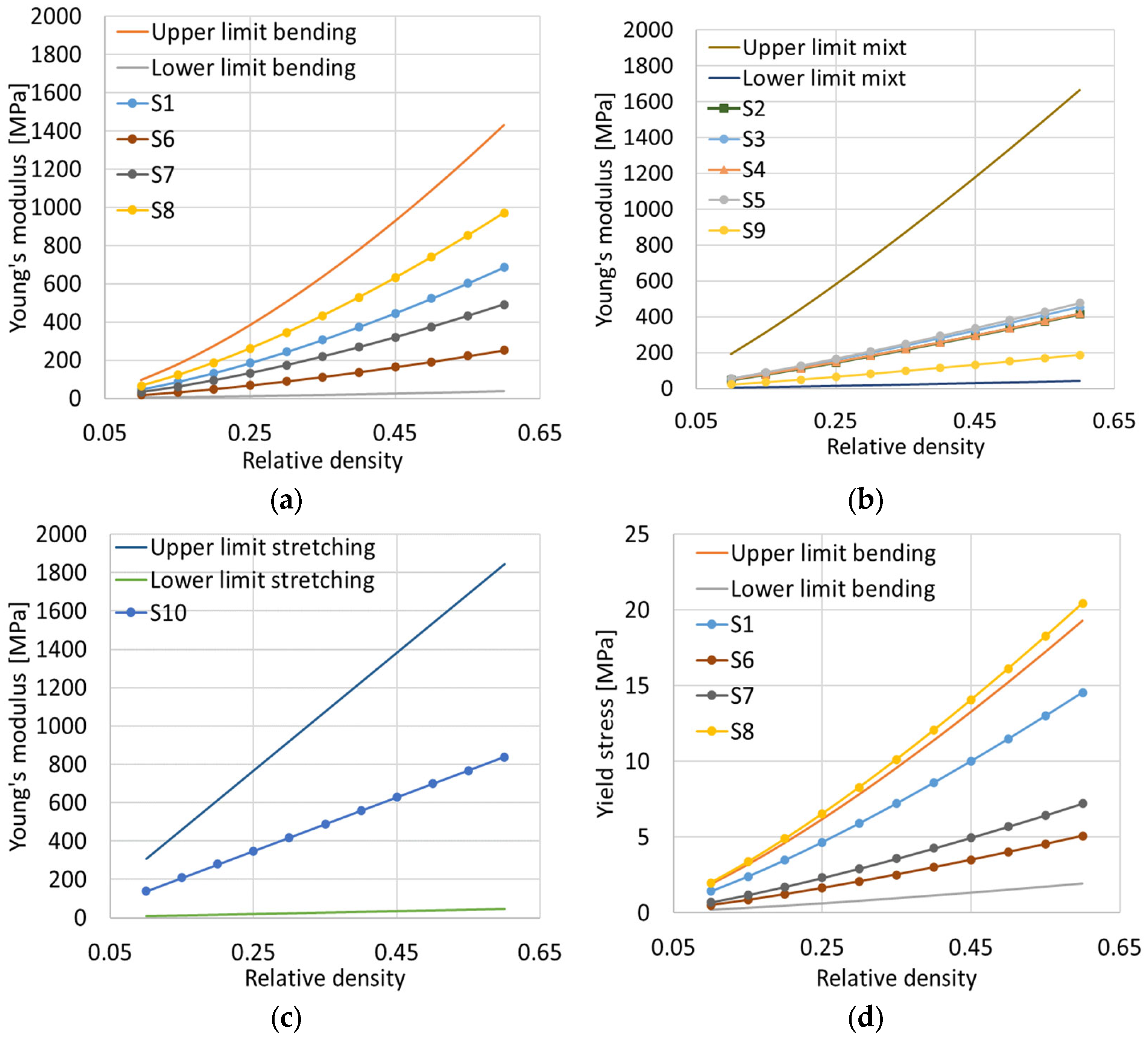
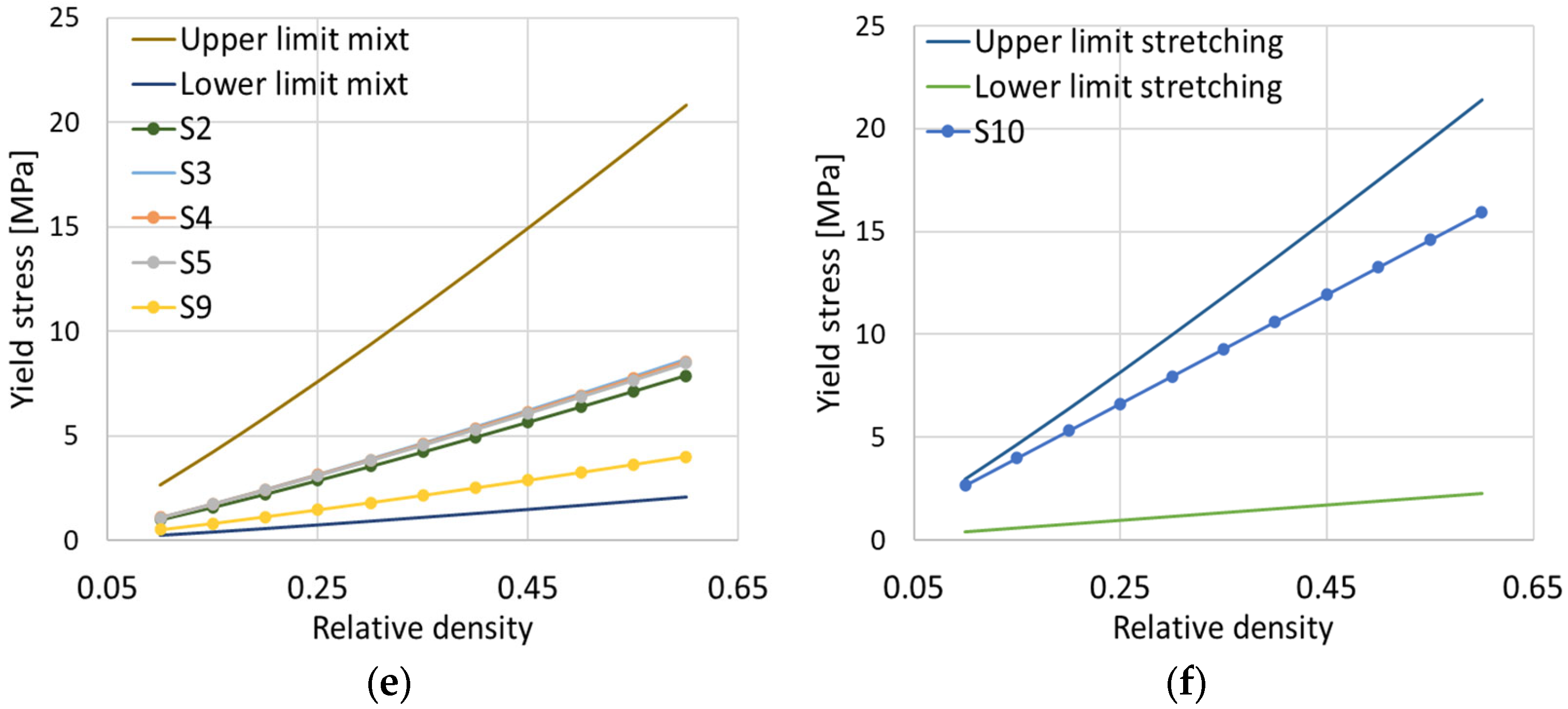
3.2. Influence of Relative Density
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Y.; Qiu, H.; Gao, Y.; Zheng, H.; Tan, J. Creative Design for Sandwich Structures: A Review. Int. J. Adv. Robot. Syst. 2020, 17. [Google Scholar] [CrossRef]
- Lu, C.; Hsieh, M.; Huang, Z.; Zhang, C.; Lin, Y.; Shen, Q.; Chen, F.; Zhang, L. Architectural Design and Additive Manufacturing of Mechanical Metamaterials: A Review. Engineering 2022, 17, 44–63. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical Metamaterials Associated with Stiffness, Rigidity and Compressibility: A Brief Review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Karalekas, D.; Tzetzis, D. Architected Materials for Additive Manufacturing: A Comprehensive Review. Materials 2022, 15, 5919. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rezgui, R.; Rowshan, R.; Du, H.; Fang, N.X.; Abu Al-Rub, R.K. Microarchitected Stretching-Dominated Mechanical Metamaterials with Minimal Surface Topologies. Adv. Eng. Mater. 2018, 20, 1800029. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy Absorption Characteristics of Metallic Triply Periodic Minimal Surface Sheet Structures under Compressive Loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-Mechanical Property Relationship of 3D Printed Strut, Skeletal, and Sheet Based Periodic Metallic Cellular Materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.W.; Rowshan, R.; Abu Al-Rub, R.K. Functionally Graded and Multi-Morphology Sheet TPMS Lattices: Design, Manufacturing, and Mechanical Properties. J. Mech. Behav. Biomed. Mater. 2020, 102, 103520. [Google Scholar] [CrossRef]
- Sang, L.; Wu, W.; Sun, Z.; Wang, F.; Xu, J.; Tian, J.; Zhao, Y.; Zhang, H. Reusability and Energy Absorption Behavior of 4D-Printed Heterogeneous Lattice Structures Based on Biomass Shape Memory Polyester. J. Mater. Res. Technol. 2023, 27, 1563–1578. [Google Scholar] [CrossRef]
- Novak, N.; Al-Ketan, O.; Krstulović-Opara, L.; Rowshan, R.; Abu Al-Rub, R.K.; Vesenjak, M.; Ren, Z. Quasi-Static and Dynamic Compressive Behaviour of Sheet TPMS Cellular Structures. Compos. Struct. 2021, 266, 113801. [Google Scholar] [CrossRef]
- Mishra, A.K.; Kumar, A. Compression Behavior of Triply Periodic Minimal Surface Polymer Lattice Structures. Exp. Mech. 2023, 63, 609–620. [Google Scholar] [CrossRef]
- Novak, N.; Borovinšek, M.; Al-Ketan, O.; Ren, Z.; Vesenjak, M. Impact and Blast Resistance of Uniform and Graded Sandwich Panels with TPMS Cellular Structures. Compos. Struct. 2022, 300, 116174. [Google Scholar] [CrossRef]
- Song, J.; Wang, M.; Li, D.; Zhang, J. Deformation and Energy Absorption Performance of Functionally Graded TPMS Structures Fabricated by Selective Laser Melting. Appl. Sci. 2024, 14, 2064. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. TPMS-Based Interpenetrating Lattice Structures: Design, Mechanical Properties and Multiscale Optimization. Int. J. Mech. Sci. 2023, 244, 108092. [Google Scholar] [CrossRef]
- Miralbes, R.; Ranz, D.; Pascual, F.J.; Zouzias, D.; Maza, M. Characterization of Additively Manufactured Triply Periodic Minimal Surface Structures under Compressive Loading. Mech. Adv. Mater. Struct. 2022, 29, 1841–1855. [Google Scholar] [CrossRef]
- Nazir, A.; Hussain, S.; Ali, H.M.; Waqar, S. Design and Mechanical Performance of Nature-Inspired Novel Hybrid Triply Periodic Minimal Surface Lattice Structures Fabricated Using Material Extrusion. Mater. Today Commun. 2024, 38, 108349. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Ibrahim, E.; Ahmad, Z. Compressive Behaviour of Neovius Triply Periodic Minimal Surface Cellular Structure Manufactured by Fused Deposition Modelling. Virtual Phys. Prototyp. 2019, 14, 360–370. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Compression and Buckling of Microarchitectured Neovius-Lattice. Extrem. Mech. Lett. 2020, 37, 100688. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Feng Lu, W. Pseudo-Ductile Fracture of 3D Printed Alumina Triply Periodic Minimal Surface Structures. J. Eur. Ceram. Soc. 2019, 40, 408–416. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.; Pang, S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Mechanical Properties of 3D Printed Polymeric Gyroid Cellular Structures: Experimental and Finite Element Study. Mater. Des. 2019, 165, 107597. [Google Scholar] [CrossRef]
- Saleh, M.; Anwar, S.; Al-Ahmari, A.M.; Alfaify, A. Compression Performance and Failure Analysis of 3D-Printed Carbon Fiber/PLA Composite TPMS Lattice Structures. Polymers 2022, 14, 4595. [Google Scholar] [CrossRef] [PubMed]
- Ronca, A.; Rollo, G.; Cerruti, P.; Fei, G.; Gan, X.; Buonocore, G.G.; Lavorgna, M.; Xia, H.; Silvestre, C.; Ambrosio, L. Selective Laser Sintering Fabricated Thermoplastic Polyurethane/Graphene Cellular Structures with Tailorable Properties and High Strain Sensitivity. Appl. Sci. 2019, 9, 864. [Google Scholar] [CrossRef]
- Gao, T.; Liu, K.; Wang, X.; Wei, K.; Wang, Z. Multi-Level Mechanism of Biomimetic TPMS Hybridizations with Tailorable Global Homogeneity and Heterogeneity. Extrem. Mech. Lett. 2024, 68, 102136. [Google Scholar] [CrossRef]
- Wei, Y.P.; Li, H.Q.; Han, J.J.; Ma, Y.C.; Zhou, H.R.; Cheng, J.C.; Shi, J.; Miao, Z.Q.; Yu, B.; Lin, F. Mechanical and Damping Performances of TPMS Lattice Metamaterials Fabricated by Laser Powder Bed Fusion. China Foundry 2024, 21, 327–333. [Google Scholar] [CrossRef]
- Yang, C.; Wu, W.; Fu, Z.; Zheng, H. Preparation and Thermal Insulation Properties of TPMS 3Y-TZP Ceramics Using DLP 3D Printing Technology. J. Mater. Sci. 2023, 58, 11992–12007. [Google Scholar] [CrossRef]
- Ramírez, E.A.; Béraud, N.; Pourroy, F.; Villeneuve, F.; Amaya, J.L.; Museau, M. Design Methodology of Functionally Graded Cellular Materials: Manipulating Design Parameters of Triply Periodic Minimal Surfaces through Three-Dimensional Density Distributions. Comput.-Aided Des. 2024, 177, 103778. [Google Scholar] [CrossRef]
- Viet, N.V.; Waheed, W.; Alazzam, A.; Zaki, W. Effective Compressive Behavior of Functionally Graded TPMS Titanium Implants with Ingrown Cortical or Trabecular Bone. Compos. Struct. 2023, 303, 116288. [Google Scholar] [CrossRef]
- Szatkiewicz, T.; Laskowska, D.; Bałasz, B.; Mitura, K. The Influence of the Structure Parameters on the Mechanical Properties of Cylindrically Mapped Gyroid TPMS Fabricated by Selective Laser Melting with 316L Stainless Steel Powder. Materials 2022, 15, 4352. [Google Scholar] [CrossRef]
- Wang, N.; Meenashisundaram, G.K.; Chang, S.; Fuh, J.Y.H.; Dheen, S.T.; Senthil Kumar, A. A Comparative Investigation on the Mechanical Properties and Cytotoxicity of Cubic, Octet, and TPMS Gyroid Structures Fabricated by Selective Laser Melting of Stainless Steel 316L. J. Mech. Behav. Biomed. Mater. 2022, 129, 105151. [Google Scholar] [CrossRef]
- Suryawanshi, C.M.; Sagar, S.; Bhallamudi, R.; Mishra, S. Effective Design and Mechanical Response of Gyroid Lattice Scaffold for Orthopedic Implants. Manuf. Lett. 2023, 35, 493–501. [Google Scholar] [CrossRef]
- Ozdemir, M.; Simsek, U.; Kiziltas, G.; Gayir, C.E.; Celik, A.; Sendur, P. A Novel Design Framework for Generating Functionally Graded Multi-Morphology Lattices via Hybrid Optimization and Blending Methods. Addit. Manuf. 2023, 70, 103560. [Google Scholar] [CrossRef]
- Yu, S.; Sun, J.; Bai, J. Investigation of Functionally Graded TPMS Structures Fabricated by Additive Manufacturing. Mater. Des. 2019, 182, 108021. [Google Scholar] [CrossRef]
- Li, M.; Jiang, J.; Liu, W.; Huang, X.; Wu, X.; Wei, W.; Zhu, H.; Zhang, J.; Xiao, J.; Dai, H. Bioadaptable Bioactive Glass-β-Tricalcium Phosphate Scaffolds with TPMS-Gyroid Structure by Stereolithography for Bone Regeneration. J. Mater. Sci. Technol. 2023, 155, 54–65. [Google Scholar] [CrossRef]
- Almesmari, A.; Baghous, N.; Ejeh, C.J.; Barsoum, I.; Abu Al-Rub, R.K. Review of Additively Manufactured Polymeric Metamaterials: Design, Fabrication, Testing and Modeling. Polymers 2023, 15, 3858. [Google Scholar] [CrossRef]
- Yuan, L.; Ding, S.; Wen, C. Additive Manufacturing Technology for Porous Metal Implant Applications and Triple Minimal Surface Structures: A Review. Bioact. Mater. 2019, 4, 56–70. [Google Scholar] [CrossRef]
- Schoen, A.H. Infinite Periodic Minimal Surfaces Without Self-Intersections; National Aeronautics and Space Administration: Washington, DC, USA, 1970.
- Jones, A.; Leary, M.; Bateman, S.; Easton, M. TPMS Designer: A Tool for Generating and Analyzing Triply Periodic Minimal Surfaces. Softw. Impacts 2021, 10, 100167. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.M.; Wu, X.; Wang, Z.; Li, Q.; Zhou, S. On Hybrid Cellular Materials Based on Triply Periodic Minimal Surfaces with Extreme Mechanical Properties. Mater. Des. 2019, 183, 108109. [Google Scholar] [CrossRef]
- Araya, M.; Jaskari, M.; Rautio, T.; Guillén, T.; Järvenpää, A. Assessing the Compressive and Tensile Properties of TPMS-Gyroid and Stochastic Ti64 Lattice Structures: A Study on Laser Powder Bed Fusion Manufacturing for Biomedical Implants. J. Sci. Adv. Mater. Devices 2024, 9, 100663. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.W.; Abu Al-Rub, R.K. Mechanical Properties of Additively-Manufactured Sheet-Based Gyroidal Stochastic Cellular Materials. Addit. Manuf. 2021, 48, 102418. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 1–510. [Google Scholar] [CrossRef]
- Mora Sierra, D.C.; Heydari Astaraee, A.; Guagliano, M.; Bagherifard, S. Numerical Investigation of Ti6Al4V Gradient Lattice Structures with Tailored Mechanical Response. Adv. Eng. Mater. 2022, 24, 2101760. [Google Scholar] [CrossRef]
- Ravichander, B.B.; Jagdale, S.H.; Kumar, G. Surface Morphology, Compressive Behavior, and Energy Absorption of Graded Triply Periodic Minimal Surface 316L Steel Cellular Structures Fabricated by Laser Powder Bed Fusion. Materials 2022, 15, 8294. [Google Scholar] [CrossRef] [PubMed]
- Ashby, M.F. The Properties of Foams and Lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]





| Sample | Sheet Network Lattice Implicit Function | Equation |
|---|---|---|
| S1 | f(x,y,z) = cos (x) × sin (y) + cos (y) × sin (z) + cos (z) × sin (x) | (1) |
| S2 | f(x,y,z) = 2 × [cos (x) × cos (y) + cos (y) × cos (z) + cos (z) × cos (x)] − [cos (2x) + cos (2y) + cos (2z)] | (2) |
| S3 | f(x,y,z) = cos (x) × cos (y) + cos (x) × cos (z) + cos (y) × cos (z) + sin (x) × cos (y) + sin (x) × cos (z)+ sin (y) × cos (z) + sin (y) × cos (z) + sin (z) × cos (x) + sin (z) × cos (y) | (3) |
| S4 | f(x,y,z) = cos (2x) × cos (y) × cos (z) + cos (2y) × cos (x) × cos (z) + cos (2z) × cos (x) × cos (y) + sin (x) × cos (y) + sin (x) × cos (z) + sin (y) × cos (z) + sin (y) × cos (z) + sin (z) × cos (x) + sin (z) × cos (y) | (4) |
| S5 | f(x,y,z) = sin (x) × cos (y) × z/2 + sin (y) × cos (z) × x/2 + sin (z) × cos (x) × y/2 | (5) |
| S6 | f(x,y,z) = 4 × cos (x) × cos (y) × cos (z) − [cos (2x) × cos (2y) + cos (2y) × cos (2z) + cos (2z) × cos (2x)] | (6) |
| S7 | f(x,y,z) = 4 × sin (x) × cos (y) × cos (z) − [cos (x) × cos (y) + cos (y) × cos (z) + cos (z) × cos (x)] | (7) |
| S8 | f(x,y,z) = 8 × cos (x/2) × cos (z/2) × sin (x/2)+ 8 × cos (y/2) × cos (z/2) × sin (y/2) + 8 × cos (x/2) × cos (y/2) × sin (z/2) | (8) |
| S9 | f(x,y,z) = sin (x) × sin (y) + sin (x) × sin (y) + sin (x) × sin (y) − 4 × cos (x) × cos (y) × cos (z) | (9) |
| Reference Values [41] | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.1–4 | 1.92 | 1.43 | 1.56 | 1.44 | 1.64 | 0.71 | 1.37 | 2.72 | 0.65 | 1.82 |
| C2 | 0.1–1 | 0.75 | 0.38 | 0.42 | 0.41 | 0.41 | 0.26 | 0.37 | 1.06 | 0.19 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasile, A.; Constantinescu, D.M.; Coropețchi, I.C.; Sorohan, Ș.; Apostol, D.A. Definition, Fabrication, and Compression Testing of Sandwich Structures with Novel TPMS-Based Cores. Materials 2024, 17, 5150. https://doi.org/10.3390/ma17215150
Vasile A, Constantinescu DM, Coropețchi IC, Sorohan Ș, Apostol DA. Definition, Fabrication, and Compression Testing of Sandwich Structures with Novel TPMS-Based Cores. Materials. 2024; 17(21):5150. https://doi.org/10.3390/ma17215150
Chicago/Turabian StyleVasile, Alexandru, Dan Mihai Constantinescu, Iulian Constantin Coropețchi, Ștefan Sorohan, and Dragoș Alexandru Apostol. 2024. "Definition, Fabrication, and Compression Testing of Sandwich Structures with Novel TPMS-Based Cores" Materials 17, no. 21: 5150. https://doi.org/10.3390/ma17215150
APA StyleVasile, A., Constantinescu, D. M., Coropețchi, I. C., Sorohan, Ș., & Apostol, D. A. (2024). Definition, Fabrication, and Compression Testing of Sandwich Structures with Novel TPMS-Based Cores. Materials, 17(21), 5150. https://doi.org/10.3390/ma17215150







