Appendix A.1. Helmholtz Decomposition of
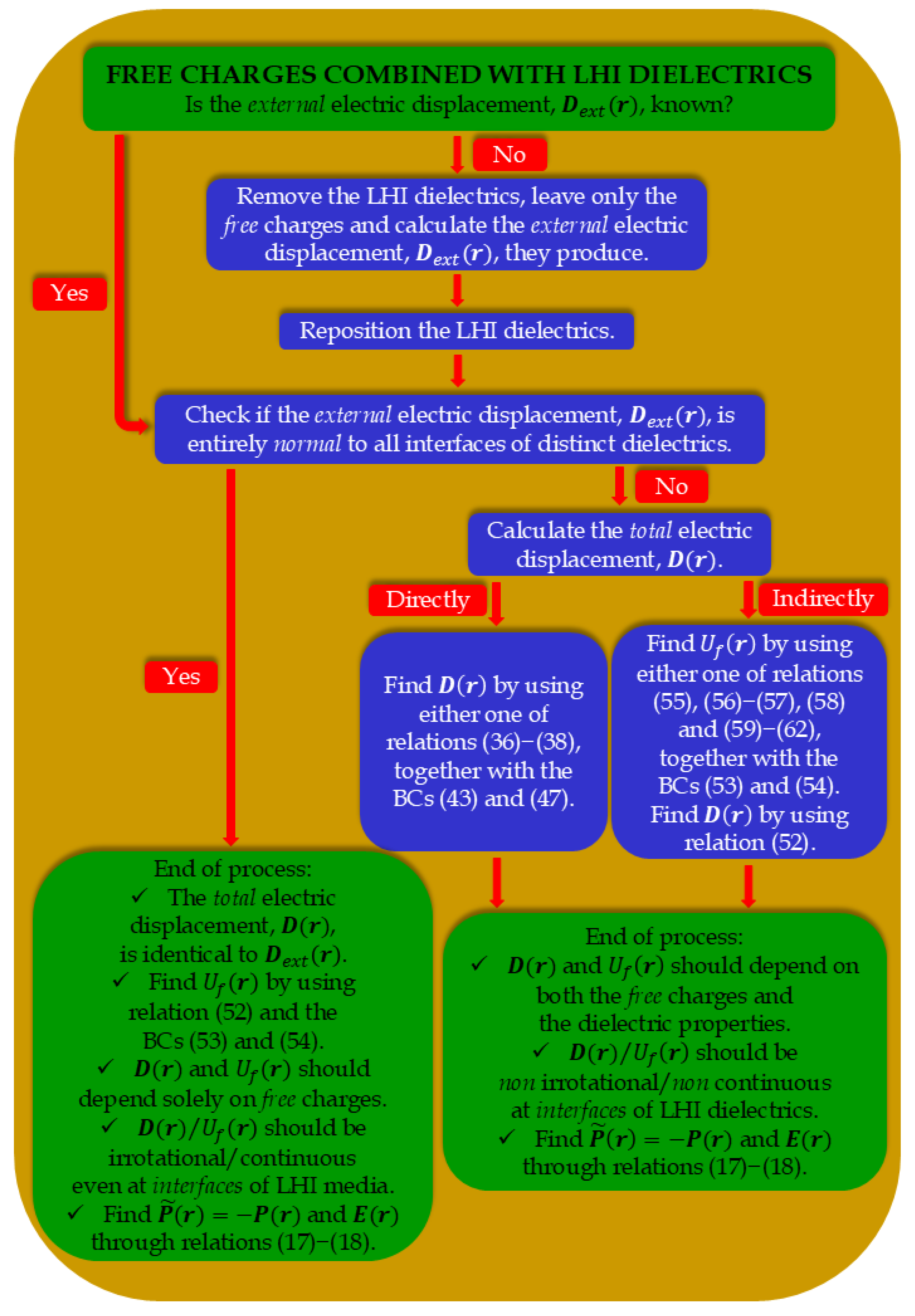
Here we investigate the Helmholtz decomposition of the electric displacement, , to clarify some important issues on both the foreground mathematics and the underlying physics of this vector field. We stress that the discussion below is exclusively focused on since in the P-D, , formulation, is the primary vector field that should be calculated beforehand, independently of the secondary vector fields, the reverse electric polarization, , and the electric field, . Then and can be easily calculated from .
The most important of the investigated issues is to determine the conditions under which depends solely on free charges or it depends on the dielectric properties, as well. Below, we document formally that, in the general case, does not depend solely on free charges. Under specific circumstances, the properties of the LHI dielectrics are imprinted onto through the relevant boundary conditions that should be satisfied at the interfaces of distinct media having different dielectric properties (thus, discontinuities of the electric polarization/susceptibility exist at such interfaces).
The most basic situation refers to a piecewise continuous
existing in the entire dielectric space (including vacuum as dielectric) which is divided in two distinct dielectric subspaces termed ‘in’ and ‘out’. By applying the Helmholtz theorem [
21,
22,
23,
24] on
we have the following expression:
Here, is the entire space, comprising of the interiors of subspaces ‘in’ and ‘out’, wherein and should be known, while the closed surface is the interface of subspaces ‘in’ and ‘out’ where and should be known, as well. Finally, refers to the unit vector that is normal to , directed from subspace ‘in’ to subspace ‘out’.
From these relations, we can define two functions, a scalar,
, (first parenthesis) and a vector,
, (second parenthesis) through:
and
Thus, in the general case,
can be determined through:
We call
the
free scalar potential and
the
bound vector potential for reasons that will become clear below. It is easily seen that for the case of electrostatics discussed here, the first relation is actually the law of Coulomb, where the two terms
and
act as volume and surface sources of
and consequently of
. Likewise, it is evident that the second relation is practically the law of Biot-Savart, where the two terms
and
act as volume and surface sources of
and consequently of
[
16,
17,
18].
Now, let us clarify the role of each one of the above candidate sources for the case of electrostatics in the systems comprising of
free charges and LHI dielectrics discussed here. Starting with the volume sources, obviously, at the
interior of subspaces ‘in’ and ‘out’, the relation
should hold wherever a non-zero
exists, else
0. In addition, at the
interior of subspaces ‘in’ and ‘out’,
is obviously irrotational,
. As we show below, this does not necessarily hold at the
interfaces between distinct dielectrics, even when they are LHI. Continuing with the surface sources, at the
interface , the following two fundamental conditions should hold for the electric field,
[
8,
9,
11,
13,
14,
15]. Below we review these boundary conditions on
which we ultimately ‘translate’ in respect to
since this is the
primary vector field according to the P-D,
, formulation.
The first fundamental boundary condition refers to the
normal to
component of
and reads:
Given that relations
and
hold, relation (A5) transforms into the two independent ones:
and
The second fundamental boundary condition on the
tangential to
components of
is:
Again, by using
, relation (A8) simply transforms to:
Thus, we have three independent boundary conditions on and given by relations (A6), (A7), and (A9). Below, we discuss each one of them to understand its physical content in respect to .
We start from the latter boundary condition, relation (A9). By recalling that in the P-D,
, formulation,
, relation (A9) evolves to:
that by simple rearrangement of terms further transforms to:
By recalling that in the P-D,
, formulation, the relative permittivity is given by
(relation (21) of the article), the above relation (A11) takes another equivalent version:
Relations (A11) and (A12) reveal that the
tangential components of
and
are linearly dependent at the
interface . Based on this fact, the former boundary condition obtains the following two, quite informative, equivalent forms:
In practical terms, relations (A11) and (A12) are the most useful of all versions since they are ready to be applied. More general, in any of its versions, (A10)–(A14), this is the most important boundary condition for the P-D, , formulation due to the following reasons: It is the only three boundary conditions that brings the dielectric properties (i.e., the P-D electric susceptibility, ) at the proscenium of the algebraic calculations and inevitably imprints onto all relevant physical entities of the problem (vector fields, scalar/vector potentials, etc.), obviously starting from the tangential components of the electric displacement, . Then, since and are directly calculated from , they should also depend on the properties of the LHI dielectrics, that is the electric susceptibility, . All other relevant physical entities, i.e., bound surface charge density, dipole moment, etc., will depend on the dielectric properties as well.
Next, we proceed with the second boundary condition, relation (A7). Once again, by recalling the basic relation
of the P-D,
, formulation, relation (A7) gets the form:
A superficial interpretation of this boundary condition will possibly lead to the following misleading message: this relation also imprints the P-D electric susceptibility, , onto the normal component of the electric displacement, , a situation completely analogous to the one discussed above, relations (A10)–(A14), for the tangential components of . However, this is not the case. Relation (A15) should only be used to accomplish the self-consistent solution of the problem through the determination of the bound surface charge density, , from the normal component of the electric displacement, , which should already be known. To recover this information, we turn our interest to the last boundary condition that refers to the normal component of as well.
Indeed, the third boundary condition, relation (A6), already refers to the
normal component of
, so we do not have much to do. We just reproduce it for convenience:
This relation clearly states that the discontinuity of the normal component of at the interface should depend solely on free charges. This information should be used in accordance with relation (A15) above, (that also relates to the normal component of ) for the determination of the bound surface charge density, .
The boundary conditions discussed until now, relations (A10)–(A16), refer to the
primary vector field of electrostatics,
, that relates to the
free scalar potential,
, and the
bound vector potential,
, respectively, through relation (A4). In turn,
and
are given by relation (A2) and relation (A3), respectively. By recalling that for the LHI dielectrics discussed here
and
and by using relations (A13) and (A16), the functions
and
become:
and
From the integral relation (A17), we clearly see that
relates solely on
free charges,
and
, thus we formally call it
free scalar electric potential. Similarly, the integral relation (A18) clearly reveals that
depends on any discontinuity/mismatch of the
tangential components of
, of the LHI dielectrics at the
interface of the two distinct subspaces ‘in’ and ‘out’, thus we assign the term
bound vector potential (else,
polarization vector potential). Most importantly, relations (A17) and (A18) evidence that in the general case,
depends on both the
free charges through
and the properties of the LHI dielectrics, i.e., the P-D electric susceptibility
, through
. Specifically, relation (A18) documents that the
bound vector potential,
, is non-zero when the following two conditions are fulfilled at the same time: first, the dielectric properties, i.e., the P-D electric susceptibility,
, of distinct dielectrics should be discontinuous at their
interface , and second,
and the induced
should have at least one component
tangential to the
interface . The first condition is determined by the intrinsic properties of the employed dielectrics, while the second is determined by external characteristics such as the geometry of the employed building units (i.e.,
free charges and LHI dielectrics) and their relative orientation (see
Section 5.3 and especially the rule of thumb illustrated in
Figure 1).
The discontinuity of
and the existence of at least one
tangential component at the
interface of distinct dielectric media have strong implications on both the physics and the mathematics of these systems; first, as already discussed above, it dictates that
should depend on both the
free charges and the properties of the employed LHI dielectrics, second, it determines the
non irrotational behavior of
, and, third, it defines the
non continuous character of
. These issues have been discussed in the article, as well (see
Section 5.2 and
Section 5.3 of the article). While the electric displacement,
, is irrotational and the
free scalar potential,
, is continuous at the
interior of any LHI dielectric medium, they do
not necessarily preserve this behavior at the
interface of distinct dielectric media. The boundary conditions (A10)–(A14) imply that a discontinuity in the
tangential components of
at the
interface of different dielectric media (that clearly always exists due to the discontinuous change of
) will result in a
non irrotational behavior of
at
. In turn, this will motivate a
non continuous character of
at the
interface , as well. We stress once again that in this case,
will depend on both the
free charges and the properties of the LHI dielectrics. In this case, the desired solution of
can be obtained straightforwardly by finding
through the integral relation (A17) and
through the integral relation (A18) so that
is ultimately calculated through relation (A4). However, alternative, more convenient practices can be employed to find
. First, we recall that the surface terms in relations (A17) and (A18) are actually the boundary conditions (A16) and equivalent forms (A10)–(A14), respectively. Second, we realize that
is determined only by the volume source of
,
. Indeed, since
has no volume source,
, it is actually involved only in the boundary condition of any of the equivalent relations (A10)–(A14). Third, from relation (A4) we realize that
can be used to exclusively satisfy all boundary conditions which
should obey, including the one in which
is involved. Once this is realized,
is no longer needed. However, the boundary conditions we have at hand, relations (A10)–(A14), (A15), and (A16), refer to
. Thus, we have to ‘translate’ them to be applicable to
. Accordingly, once we assume that the boundary conditions that
should obey at the
interface can be satisfied exclusively by
, relations (A10)–(A14), (A15), and (A16) obtain the form discussed below.
We start with relations (A10)–(A14) on the
tangential components of
. In respect to
, these relations take, one by one, the following forms:
else
else
else
Relations (A20) and (A21) are the most useful of all versions. First, they clearly address the linear dependence that the tangential components of the gradient of the free scalar potential, , should obey at the interface . Second, they are ready to be applied in any problem. In this way the P-D electric susceptibility, , will be introduced in , , etc.
Next, we proceed with relation (A7) that becomes:
As already discussed above, this relation should only be used to determine the bound surface charge density, , from the normal component of the gradient of the free scalar potential, , in a self-consistent way.
Finally, the third boundary condition, relation (A6), gets:
This relation should be used in close connection with the above relation (A24) to ultimately determine from all other known sources.
Now, we have at hand all information that we need on the boundary conditions for the calculation of both and by using the strategies presented in the article. Thus, we have completed the investigation for the case where and depend on both the free charges and the dielectric properties of the LHI dielectrics.
Finally, we discuss the case where
and
are exclusively
normal to the
interface . Now, the numerator of the integral in relation (A18) is zero so that
. Thus,
and
are formally coupled through:
In this case,
is irrotational and
is continuous in the entire space, that is, not only at the
interior of dielectric media, but also at the
interface (even when discontinuous change of the dielectric properties exists at
). In addition, the electric displacement,
, and the
free scalar potential,
, depend solely on
free charges. To calculate
and
we can employ any of the relevant strategies presented in the article. Referring to the boundary conditions, obviously, relations (A10)–(A14) on
and (A19)–(A23) on
, which refer to the
tangential components, are trivially satisfied and no longer can help to mathematically tackle the physical problem. On the contrary, relations (A15)–(A16) on
and (A24)–(A25) on
, which refer to the
normal components, still hold. Most importantly, in place of the non-active relations (A19)–(A23), we can employ the boundary condition on the continuity of
at the
interface . This property of
is now recovered due to the absence of the
tangential components of
. Thus, in this case, the following very useful relation holds:
The above discussion is clarified in great detail through some representative problems of electrostatics presented in
Section 7 of the article and in the following
Appendix A.2 of the
Appendix A. There, both cases are considered for
and
, when they depend solely on
free charges and when they also depend on the dielectric properties.
Finally, let us make two comments relevant to this section. First, above we applied our mathematical considerations to the newly introduced P-D, , formulation to clarify whether depends solely on the free charges or it also depends on the dielectric properties. With minor algebraic modifications, the same investigation can be applied to the standard P-E, , formulation, as well. Second, we underline that a relevant argumentation as the one mentioned above for , holds for the magnetic field in the case of magnetostatics: under specific circumstances, does not depend only on the free current density, it depends on the magnetic properties of the LHI materials as well. These issues will be addressed elsewhere.
Appendix A.2. Representative Problems in LHI Dielectrics
Following a basic example presented in
Section 7 of the article, in this section we survey some representative problems of electrostatics which we address with both formulations, the standard P-E,
, and the alternative P-D,
. With this, we aim to clarify the following issues which are important for the documentation of the P-D,
, description introduced here: (i) the somehow misleading causality/feedback between the electric polarization,
, and electric field,
, of the P-E,
, formulation, and the conceptual restoration by using the P-D,
, one; (ii) the nature of the depolarizing field/self field and its connection with the
reverse polarization in both formulations, P-E,
, and P-D,
; (iii) the dependence of the electric displacement,
, on both the
free charges and the dielectric properties of the LHI materials in both formulations, P-E,
, and P-D,
; and (iv) the overall quantitative equivalence of the two formulations, P-E,
, and P-D,
.
Problem (1): Dielectric LHI sphere of P-E/P-D electric susceptibility and radius a is placed with its center at the origin of the spherical coordinate system wherein a point electric charge, Q, is hosted.
Appendix A.2.1. Solution Based on the P-E Electric Susceptibility,
The standard formulation based on the P-E electric susceptibility, , focuses on the electric field, , and the respective scalar potential, , that relate through . We can use the integral form of Gauss’s law for , Laplace’s equation for etc. The following boundary conditions should hold on and , for the inside () and outside () spaces, as well as at the interface () of the two dielectrics (sphere and vacuum): (i) for , both and should diverge as and , respectively; (ii) for , both and should become zero; (iii) should be continuous at the interface of the two dielectric media, thus ; and (iv) the normal component of should satisfy the relation where since it translates to . Finally, the extra boundary condition on the continuity of the tangential components of (that is ), is trivially satisfied in this case.
The above information results in and for the scalar potential, and for the electric field, and for the electric polarization, and for the electric displacement.
Depolarizing field/self field: The surface density of bound charge that resides at the interface
is
, while the volume density of the charge is concentrated at
with
. The relevant
internal electric field (see [
25] of the article) produced by
and
at the inside space is simply
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field, or self field, that relates to
, else to the reverse
through
(see
Section 3 of the article and
Appendix A.2.2 below).
Dependence of on free charges and dielectric properties: Clearly, since the electric displacement that relates to the
external sources (point charge Q placed at
in this case),
, is
normal to the interface,
, of the two dielectric media (sphere with
and vacuum with
), we expect that the total
should depend solely on the
free charges. Thus,
should be identical to
. Indeed, this is the case, since
(see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
Appendix A.2.2. Solution Based on the P-D Electric Susceptibility,
The alternative formulation based on the P-D electric susceptibility,
, should focus on the electric displacement,
, and the respective
free scalar potential,
, that relate through
. Accordingly, we employ the solution of Laplace equation for the (obviously φ-independent)
free scalar potential,
, obtained through the method of separation of variables. For the outside space,
, the solution has the form
, while the inside space,
, reads
. The following boundary conditions should hold on
and
, for the inside (
) and outside (
) spaces, as well as at the interface (
) of the two dielectrics (sphere and vacuum): (i) for r = 0,
should diverge as
; (ii) for r
,
should become zero; (iii) the tangential components of
should satisfy the relation
that since
and
, gets
; and (iv) the normal component of
should satisfy the condition
where since
, translates to
. Finally, we recall that in contrast to the inherent continuity of
, the
free scalar potential,
, is
not necessarily continuous at the interface of two dielectric media, as indirectly reflected by the
tangential components of
in condition (iii) above (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
The above information results in and for the free scalar potential, while through we get for the electric displacement. In addition, through we get and for the electric polarization and finally through we obtain , for the electric field.
Depolarizing field/self field: The surface density of the bound charge that resides at the interface
is
, while the volume density of the charge concentrated at r = 0 is
. The relevant
internal electric field (see [
25] of the article) produced by
and
at the inside space is given by
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field or self field (see
Section 3 of the article).
Dependence of on free charges and dielectric properties: As already discussed above in
Appendix A.2.1 for the P-E,
, formulation, the electric displacement that relates to the
external sources,
, is entirely
normal to the surface of the dielectric sphere. Accordingly, we expect that the total
should depend solely on the
free charges, thus should be identical to
. This is expected even for the P-D,
, formulation discussed here. Indeed, this is observed (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
Non-continuity of the free scalar potential, , at the interface r = a: As discussed above and in the article, when
is entirely
normal at an interface,
and
should preserve the irrotational and continuous character, respectively, not only in the interior of dielectrics but also at the respective interfaces (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). In the present problem, we have
and
that is
normal to the interface
. Thus, we expect that
should be continuous at this site. Indeed, this is the case since
.
Comparison between the P-E, , and P-D, , formulations: The two descriptions, P-E,
, and P-D,
, should be equivalent on a quantitative basis. To this effect, it is expected that when we substitute
(relation (34) of the article) in the expressions obtained here in
Appendix A.2.2, we should get the exact same relations obtained above in
Appendix A.2.1. Indeed, this can be easily confirmed for all electric entities: displacement,
, polarization,
, field,
,
free scalar potential of the outside space (a
),
, and
bound surface charge density,
. In addition, we can easily verify that the relation
holds everywhere in space, where
is the
bound scalar potential that relates to the
reverse electric polarization,
, through
. For instance, at the outside space,
, the relation
holds, since
. For the inside space,
, we can easily find
and verify that indeed
(see
Section 6 of the article).
Appendix A.2.3. Solution Based on the P-E Electric Susceptibility, , by Means of Series
Here we employ a series approach with the standard formulation based on the P-E electric susceptibility, , and focus directly on the electric polarization, , and field, , to clarify their causality/feedback for the inside space, , of the LHI dielectric sphere.
Suppose that initially (before the dielectric sphere responds to the
external stimuli) the electric field is simply the one applied
externally,
. We call it the zeroth-order term of the electric field,
. The respective zeroth-order term of the electric polarization is
. As we showed in both
Appendix A.2.1 and
Appendix A.2.2 above, the sphere of polarization
produces an
internal electric field (depolarizing field/self field)
at the inside space. Thus, the zeroth-order term of the polarization
will produce a first-order term for the
internal electric field
(notice that the term
does not exist; the only zeroth-order electric field term is of
external origin,
). In turn, the first-order term,
, will induce a first-order term for the polarization
that subsequently will produce a second-order term for the
internal electric field
and so on. Thus, in general, the (i-1)-order term of the induced polarization is
, while the (i)-order term of the
internal electric field is
. Combining the last relations on
and
we get
. Accordingly, the total electric field will simply be
, else
. The geometric series results in
so that ultimately
. Since
this result is identical to the one obtained in
Appendix A.2.1 above, as expected.
The ‘infinite regress of the P-E polarization process’ applies, also, to the
bound surface charge density,
, that ultimately will be established at the interface,
, of the two dielectrics (sphere and vacuum) even for this case, as discussed analytically for a relevant problem in
Section 7.3 of the article.
This series-based approach of the ‘infinite regress of the P-E polarization process’ restores, somehow, the conceptually misleading causality/feedback between
and
that is inherent in the standard P-E,
, formulation (see [
8] pages 68 and 76; [
13] page 186). However, the serious obstacle discussed analytically for a relevant problem in
Section 7.3 of the article still exists: in strict mathematical terms, the above geometric series should converge only when
[
33], and since by definition
, the allowed interval should be
. Nevertheless, we do not raise any doubts or constraints on the obtained solution of
and use it in the entire range,
. This is one of the inherent ill-defined points of the standard P-E,
, formulation. The alternative P-D,
, formulation (
) is free of any misleading argumentation and controversial mathematics from which the standard P-E,
formulation suffers. This has been assessed analytically for a relevant problem in
Section 7.3 of the article.
Problem (2): Dielectric LHI cylinder of P-E/P-D electric susceptibility and radius a has infinite length, is placed along the z-axis of the cylindrical coordinate system, and is subjected to an external, uniform electric field along the x-axis, .
Appendix A.2.4. Solution Based on the P-E Electric Susceptibility,
The standard formulation based on the P-E electric susceptibility, , focuses on the electric field, , and the respective scalar potential, , that relate through . Our calculations will be exclusively focused on and as well. Accordingly, we employ the solution of Laplace equation for the scalar potential, , by means of separation of variables. The most general solution, for the outside space () is , while for the inside space () the respective candidate solution is . The following boundary conditions should hold on and , for the inside () and outside () spaces, as well as at the interface () of the two dielectrics (cylinder and vacuum): (i) for , should be finite; (ii) for , should be identical to the external scalar potential that produces , that is ; (iii) should be continuous at the interface of the two dielectric media, thus ; and (iv) the normal component of should satisfy the relation where since it translates to . Finally, notice that the extra boundary condition on the continuity of the tangential components of (that is ), reproduces the continuity of (condition (iii) above), thus, it does not add new information. Below, we briefly proceed with the solution.
Boundary condition (i) gives and for . Thus, for the inside space, the solution gets . Here, we have, also, adopted the obvious fact that for this problem, cannot exhibit linear dependence on or .
Boundary condition (ii) gives , for and for . Thus, for the outside space, the solution gets . Here, we have, also, adopted the obvious fact that for this problem, cannot exhibit linear dependence on or .
Boundary condition (iii) gives for , for , for and for .
Boundary condition (iv) gives that since it transforms to , else . The latter ultimately provides the desired relation that gives for , for , for and for .
The above set of relations results in (outside space) and (inside space) for the scalar potential.
Through we get the respective relations for the electric field and
Once we have found , we easily calculate the respective electric polarization, , and electric displacement, , since they relate to through expressions (1) and (2) of the article. Thus, we get and for the electric polarization, while and , where the external electric displacement.
Depolarizing field/self field: The surface density of bound charge that resides at the cylinder/vacuum interface
is given by
. The relevant
internal electric field (see [
25] of the article) produced by
at the inside space is simply
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field, or self field, that relates to
, else to the reverse
through
(see
Section 3 of the article, and below
Appendix A.2.5 of the
Appendix A).
Dependence of on free charges and dielectric properties: Here, the electric displacement that relates to the external sources,
, has component that is tangential to the surface of the dielectric cylinder. Thus, we expect that the total
, except for the free charges, should depend on the properties of the LHI dielectric cylinder (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). Indeed, this is what we observe here.
Appendix A.2.5. Solution Based on the P-D Electric Susceptibility,
The alternative formulation based on the P-D electric susceptibility,
, should focus on the electric displacement,
, and the respective
free scalar potential,
, that relate through
. Accordingly, we employ the solution of Laplace equation for the
free scalar potential,
, obtained by means of separation of variables. For the outside space (
) the most general solution has the form
, while for the inside space (
) it is
. The following boundary conditions should hold on
and
, for the inside (
) and outside (
) spaces, as well as at the interface (
) of the two dielectrics (cylinder and vacuum): (i) for
,
should be finite; (ii) for
,
should be identical to the
external scalar potential that produces
(
), that is
; (iii) the tangential components of
should satisfy the relation
that since
and
, gets
and (iv) the normal component of
should satisfy the condition
where since
, translates to
. Finally, notice that in contrast to the inherent continuity of
, the
free scalar potential,
, is
not necessarily continuous at the interface of two dielectric media (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). Thus, it is meaningless to ask for a boundary condition on the continuity of
at the interface
. As we will see below, indeed, the
is
non continuous at the interface
. Next, we briefly proceed with the solution.
Boundary condition (i) gives and for . Thus, for the inside space the solution gets . Here, we have also adopted the obvious fact that for this problem, cannot exhibit linear dependence on or .
Boundary condition (ii) gives , for and for . Thus, for the outside space, the solution gets . Here, we have also adopted the obvious fact that for this problem, cannot exhibit linear dependence on or .
To proceed with boundary conditions (iii) and (iv), we have to calculate the currently available version of through . We easily get and .
Boundary condition (iii) gives for , for and for .
Boundary condition (iv) gives for , for and for .
The above set of relations results in (outside space) and (inside space) for the free scalar potential.
Through we get the respective relations for the electric displacement and , where .
Once we have found , we easily calculate the respective reverse electric polarization, , (electric polarization, ) and electric field, , since they relate to through expressions (17) and (18) of the article. Thus, we get and for the reverse electric polarization, while and for the electric field.
Depolarizing field/self field: The surface density of
bound charges at ρ = a is
, where
. The relevant
internal electric field (see [
25] of the article) produced by
at the inside space is simply
. Also, we can easily obtain that
. We recall that
is the so-called depolarizing field or self field (see
Section 3 of the article).
Dependence of on free charges and dielectric properties: As already discussed above in
Appendix A.2.4 for the P-E,
, formulation, the electric displacement that relates to the
external sources,
, has component that is
tangential to the surface of the dielectric cylinder. Thus, we expect that the total
, except for the
free charges, should depend on the properties of the LHI dielectric cylinder (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). This is expected even for the P-D,
, formulation discussed here. Indeed, this is observed here.
Non-continuity of the free scalar potential, , at the interface ρ = a: The existence of a
tangential component of
and
at the interface of different dielectric media will result in a
non irrotational behavior of
, and a
non continuous character of
, locally at the interface (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). Indeed, here,
and
have a tangential component at the interface
. By using the expressions found above for
and
we see that
, while
. The respective discontinuity is
.
Comparison between the P-E, , and P-D, , formulations: The two descriptions, the standard P-E,
, employed today and the alternative P-D,
, introduced here, should be quantitatively equivalent. Thus, all physical entities of electrostatics (scalar potentials, vector fields, dipole moments, bound charge densities, etc.) should be the same irrespectively of which description we use. To this effect, it is expected that when we substitute
(relation (34) of the article) in the expressions obtained here in
Appendix A.2.5, we should get the exact same relations obtained above in
Appendix A.2.4. Indeed, this can be easily confirmed for all electric entities, displacement,
, polarization,
, field,
,
free scalar potential of the outside space (
),
, and
bound surface charge density,
. In addition, we can easily verify that the relation
holds everywhere in space, where
is the
bound scalar potential that relates to the
reverse electric polarization,
, through
. For instance, at the outside space,
, the relation
holds, since
. For the inside space,
, we can easily find
and verify that, indeed,
(see
Section 6 of the article).
Appendix A.2.6. Solution Based on the P-E Electric Susceptibility, , by Means of Series
Here we employ a series approach with the standard formulation based on the P-E electric susceptibility, , and focus directly on the electric polarization, , and field, , to clarify their causality/feedback for the inside space, , of the LHI dielectric cylinder.
Suppose that initially (before the dielectric cylinder responds to the
external stimuli), the electric field is simply the one applied
externally,
. We call it the zeroth-order term of the electric field,
. The respective zeroth-order term of the electric polarization,
, induced by
is
. As we showed in both
Appendix A.2.4 and
Appendix A.2.5 above, a uniformly polarized cylinder of polarization
produces an
internal electric field (depolarizing field/self field)
at the inside space. Thus, the zeroth-order term of the polarization
will produce a first-order term for the
internal electric field
(notice that the term
does not exist; the only zeroth-order electric field term is of
external origin,
). In turn, the first-order term,
, will induce a first-order term for the polarization
that subsequently will produce a second-order term for the
internal electric field
and so on. Thus, in general, the (i-1)-order term of the induced polarization is
, while the (i)-order term of the
internal electric field is
. Combining the last relations on
and
, we get
. Accordingly, the total electric field will simply be
, else
. The geometric series results in
so that ultimately
, else
. Since
this result is identical to the one obtained in
Appendix A.2.4 above as expected.
The ‘infinite regress of the P-E polarization process’ applies, also, to the
bound surface charge density,
, that ultimately will be established at the interface,
, of the two dielectrics (cylinder and vacuum) even for this case, as discussed analytically for a relevant problem in
Section 7.3 of the article.
This series-based approach of the ‘infinite regress of the P-E polarization process’ restores, somehow, the conceptually misleading causality/feedback between
and
that is inherent in the standard P-E,
, formulation (see [
8] pages 68 and 76; [
13] page 186, and
Section 4 of the article). However, the serious obstacle discussed above in
Appendix A.2.3 of the
Appendix A and in
Section 7.3 of the article still exists: in strict mathematical terms, the above geometric series should converge only when
[
33], and since by definition
, the allowed interval should be
. Nevertheless, we do not raise any doubts or constraints on the obtained solution of
and use it in the entire range,
. This is one of the inherent ill-defined points of the standard P-E,
, formulation. The alternative P-D,
, formulation (
) is free of any misleading argumentation and controversial mathematics from which the standard P-E,
formulation suffers. This has been assessed analytically for a relevant problem in
Section 7.3 of the article.
Problem (3): Dielectric LHI cylinder of P-E/P-D electric susceptibility and radius a, has infinite length, is placed along the z axis of the cylindrical coordinate system hosting a coaxial, homogeneous, linear charge density, .
Appendix A.2.7. Solution Based on the P-E Electric Susceptibility,
The standard formulation based on the P-E electric susceptibility, , focuses on the electric field, , and the respective scalar potential, , that relate through . We can use the integral form of Gauss’s law for , Laplace’s equation for etc. The following boundary conditions should hold on and , for the inside () and outside () spaces, as well as at the interface () of the two dielectrics (cylinder and vacuum): (i) for ρ = 0, both and should diverge as and , respectively; (ii) for , both and should become zero; (iii) should be continuous at the interface of the two dielectric media, thus ; and (iv) the normal component of should satisfy the relation where since it translates to . Finally, the extra boundary condition on the continuity of the tangential components of (that is ), is trivially satisfied in this case.
The above information results in and for the scalar potential, and for the electric field, and for the electric polarization, and for the electric displacement.
Depolarizing field/self field: The surface density of the bound charge that resides at the interface
is
, while the volume density of the bound charge concentrated at
is
. The relevant
internal electric field (see [
25] of the article) produced by
and
at the inside space is simply
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field, or self field, that relates to
, else to the reverse
through
(see
Section 3 of the article, and below
Appendix A.2.8 of the
Appendix A).
Dependence of on free charges and dielectric properties: Clearly, since the electric displacement that relates to the
external sources (linear charge density
placed at
in this case),
, is
normal to the interface,
, of the two dielectric media (cylinder with
and vacuum with
), we expect that the total
should depend solely on the
free charges. Thus,
should be identical to
. Indeed, this is the case, since
(see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
Appendix A.2.8. Solution Based on the P-D Electric Susceptibility,
The alternative formulation based on the P-D electric susceptibility,
, should focus on the electric displacement,
, and the respective
free scalar potential,
, that relate through
. We can use the integral form of Gauss’s law for
, Laplace’s equation for
, etc. The following boundary conditions should hold on
and
, for the inside (
) and outside (
) spaces, as well as at the interface (
) of the two dielectrics (cylinder and vacuum): (i) for
,
should diverge as
(ii) for
,
should become zero; (iii) the tangential components of
should satisfy the relation
that since
and
, gets
; and (iv) the normal component of
should satisfy the condition
where since
, translates to
. Finally, we recall that in contrast to the inherent continuity of
, the
free scalar potential,
, is
not necessarily continuous at the interface of two dielectric media, as indirectly reflected by the
tangential components of
in condition (iii) above (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). However, as we will see below, in this case the
external electric displacement,
, is absolutely normal to the interface
of the two dielectrics so that, ultimately,
.
The above information results in for the free scalar potential, while through we get for the electric displacement. In addition, through we get and for the electric polarization, and finally through we obtain , for the electric field.
Depolarizing field/self field: The surface density of the bound charge that resides at the interface ρ = a is given by
, while the volume density of the bound charge concentrated at ρ = 0 is
. The relevant
internal electric field (see [
25] of the article) produced by
and
at the inside space is given by
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field or self field (see
Section 3 of the article).
Dependence of on free charges and dielectric properties: As already discussed above in
Appendix A.2.7 for the P-E,
, formulation, the electric displacement that relates to the
external sources,
, is entirely
normal to the surface of the dielectric cylinder. Accordingly, we expect that the total
should depend solely on the
free charges, thus should be identical to
. This is expected even for the P-D,
, formulation discussed here. Indeed, this is observed (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
Non-continuity of the free scalar potential, , at the interface ρ = a: As discussed above and in the article, when
is entirely
normal at an interface,
and
should preserve the irrotational and continuous character, respectively, not only in the interior of dielectrics but also at the respective interfaces (see above
Appendix A.1 of the
Appendi A and
Section 5.2 and
Section 5.3 of the article). In the present problem, we have
and
that is
normal to the interface ρ = a. Thus, we expect that
should be continuous at this site. Indeed, this is the case since
.
Comparison between the P-E, , and P-D, , formulations: The two descriptions, P-E,
, and P-D,
, should be quantitatively equivalent. To this effect, it is expected that when we substitute
(relation (34) of the article) in the expressions obtained here in
Appendix A.2.8, we should get the exact same relations obtained above in
Appendix A.2.7. Indeed, this can be easily confirmed for all electric entities: displacement,
, polarization,
, field,
,
free scalar potential of the outside space (a
),
, and
bound surface charge densities, surface
and volume
. In addition, we can easily verify that the relation
holds everywhere in space, where
is the
bound scalar potential that relates to the
reverse electric polarization,
, through
. For instance, at the outside space,
, the relation
holds, since
. For the inside space,
, we can easily find
and verify that, indeed
(see
Section 6 of the article).
Appendix A.2.9. Solution Based on the P-E Electric Susceptibility, , by Means of Series
Here we employ a series approach with the standard formulation based on the P-E electric susceptibility, , and focus directly on the electric polarization, , and field, , to clarify their causality/feedback for the inside space, , of the LHI dielectric cylinder.
Suppose that initially (before the dielectric cylinder responds to the
external stimuli), the electric field is simply the one applied
externally,
. We call it the zeroth-order term of the electric field,
. The respective zeroth-order term of the electric polarization is
. As we showed in both
Appendix A.2.7 and
Appendix A.2.8 above, a uniformly polarized cylinder of polarization
produces an
internal electric field (depolarizing field/self field)
at the inside space. Thus, the zeroth-order term of the polarization
will produce a first-order term for the
internal electric field
(notice that the term
does not exist; the only zeroth-order electric field term is of
external origin,
). In turn, the first-order term,
, will induce a first-order term for the polarization
that subsequently will produce a second-order term for the
internal electric field
and so on. Thus, in general, the (i-1)-order term of the induced polarization is
, while the (i)-order term of the
internal electric field is
. Combining the last relations on
and
we get
. Accordingly, the total electric field will simply be
, else
. The geometric series results in
so that ultimately
. Since
this result is identical to the one obtained above in
Appendix A.2.7, as expected.
The ‘infinite regress of the P-E polarization process’ applies also to the
bound surface charge density,
, that ultimately will be established at the interface,
, of the two dielectrics (cylinder and vacuum) even for this case, as discussed analytically for a relevant problem in
Section 7.3 of the article.
This series-based approach of the ‘infinite regress of the P-E polarization process’ restores, somehow, the conceptually misleading causality/feedback between
and
that is inherent in the standard P-E,
, formulation (see [
8] pages 68 and 76; [
13] page 186). However, the serious obstacle discussed above in
Appendix A.2.3 and
Appendix A.2.6 of the
Appendix A and in
Section 7.3 of the article still exists: in strict mathematical terms, the above geometric series should converge only when
[
33], and since by definition
, the allowed interval should be
. Nevertheless, we do not raise any doubts or constraints on the obtained solution of
and use it in the entire range,
. This is one of the inherent ill-defined points of the standard P-E,
, formulation. The alternative P-D,
, formulation (
) is free of any misleading argumentation and controversial mathematics from which the standard P-E,
formulation suffers. This has been assessed analytically for a relevant problem in
Section 7.3 of the article.
Problem (4): Dielectric LHI slab (infinite on the xy-plane) of P-E/P-D electric susceptibility and thickness a, is placed normal to the z-axis with its midplane at z = 0 of the cartesian coordinate system and is subjected to an external, uniform electric field, .
Appendix A.2.10. Solution Based on the P-E Electric Susceptibility,
The standard formulation based on the P-E electric susceptibility, , focuses on the electric field, , and the respective scalar potential, . For the electric field, we easily get for and , for . For the scalar potential, with a bit of effort, we get for and and for , where when . Also, for and , for for the electric polarization and for for the electric displacement.
Depolarizing field/self field: The surface density of bound charges that reside at
is
. The relevant
internal electric field (see [
25] of the article) produced by
at the inside space is simply
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field, or self field, that relates to
, else to the
reverse through
(see
Section 3 of the article).
Dependence of on free charges and dielectric properties: Here, the electric displacement that relates to the
external sources,
, is entirely
normal to the interfaces,
, of the two dielectric media (slab with
and vacuum with
). Accordingly, the total
should depend solely on the
free charges, thus should be identical to the
external one,
. Indeed, this is what we observe here,
(see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
Appendix A.2.11. Solution Based on the P-D Electric Susceptibility,
The alternative formulation based on the P-D electric susceptibility, , focuses on the electric displacement, , and the respective free scalar potential, . We easily get for for the electric displacement and for for the free scalar potential. Then, we get for and , for for the electric polarization and for and , for for the electric field.
Depolarizing field/self field: The surface density of bound charges that reside at
is
. The relevant
internal electric field (see [
25] of the article) produced by
at the inside space is simply
. Also, we can easily obtain
. We recall that
is the so-called depolarizing field, or self field (see
Section 3 of the article).
Dependence of on free charges and dielectric properties: As already discussed above in
Appendix A.2.10 for the P-E,
, formulation, the electric displacement that relates to the
external sources,
, is entirely
normal to the interfaces,
, of the two dielectric media (slab with
and vacuum with
). Accordingly, the total
should depend solely on the
free charges, thus should be identical to the
external one,
. Indeed, this is observed in the P-D,
, description discussed here,
(see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article).
Non-continuity of the free scalar potential, , at the interfaces z = ±a/2: As discussed above and in the article, when
is entirely
normal at an interface,
and
should preserve the irrotational and continuous character, respectively, not only in the interior of dielectrics but also at the respective interfaces (see above
Appendix A.1 of the
Appendix A and
Section 5.2 and
Section 5.3 of the article). In the present problem, we have
and
that is
normal to both interfaces
. Thus, we expect that
should be continuous at these sites. Indeed, this is the case since
.
Comparison between the P-E, , and P-D, , formulations: The two descriptions, P-E,
, and P-D,
, should be equivalent. To this effect, it is expected that when we substitute
(relation (34) of the article) in the expressions obtained here in
Appendix A.2.11, we should get the exact same relations obtained above in
Appendix A.2.10. Indeed, this can be easily confirmed for all electric entities: displacement,
, polarization,
, field,
,
free scalar potential of the outside space (
and
),
, and
bound surface charge density,
. In addition, we can easily verify that everywhere in space
, where
is the
bound scalar potential that relates to the
reverse electric polarization,
, through
. For instance, at the outside space,
and
, the relation
holds, since
. For the inside space,
, we can easily find
and verify that, indeed,
(see
Section 6 of the article).
Appendix A.2.12. Solution Based on the P-E Electric Susceptibility, , by Means of Series
Here we employ a series approach with the standard formulation based on the P-E electric susceptibility, , and focus directly on the electric polarization, , and field, , to clarify their causality/feedback for the inside space, , of the LHI dielectric slab.
Suppose that initially (before the dielectric slab responds to the
external stimuli) the electric field is simply the one applied
externally,
. We call it the zeroth-order term of the electric field,
. The respective zeroth-order term of the electric polarization is
. As we showed in
Appendix A.2.10 above, a uniformly polarized slab of polarization
produces an
internal electric field (depolarizing field/self field)
at the inside space. Thus, the zeroth-order term of the polarization
will produce a first-order term for the
internal electric field
(notice that the term
does not exist; the only zeroth-order electric field term is of
external origin,
). In turn, the first-order term,
, will induce a first-order term for the polarization
that subsequently will produce a second-order term for the
internal electric field
and so on. Thus, in general, the (i-1)-order term of the induced polarization is
, while the (i)-order term of the
internal electric field is
. Combining the last relations on
and
we get
. Accordingly, the total electric field will simply be
, else
. The geometric series results in
so that ultimately
. Since
we finally get
. This result is identical to the one obtained above in
Appendix A.2.10.
The ‘infinite regress of the P-E polarization process’ applies, also, to the
bound surface charge density,
, that ultimately will be established at the interfaces,
, of the two dielectrics (slab and vacuum) even for this case, as discussed analytically for a relevant problem in
Section 7.3 of the article.
This series-based approach of the ‘infinite regress of the P-E polarization process’ restores, somehow, the conceptually misleading causality/feedback between
and
that is inherent in the standard P-E,
, formulation (see [
8] pages 68 and 76; [
13] page 186). However, the serious obstacle discussed above in
Appendix A.2.3,
Appendix A.2.6 and
Appendix A.2.9 of the
Appendix A and in
Section 7.3 of the article, exists in the present case as well: in strict mathematical terms, the above geometric series should converge only when
[
33], and since by definition
, the allowed interval should be
. Nevertheless, we do not raise any doubts or constraints on the obtained solution of
and use it in the entire range,
. This is one of the inherent ill-defined points of the standard P-E,
, formulation. The alternative P-D,
, formulation (
) is free of any misleading argumentation and controversial mathematics from which the standard P-E,
formulation suffers. This has been assessed analytically for a relevant problem in
Section 7.3 of the article.
Appendix A.3. Representative Example on a Physical Parameter in LHI Dielectrics: The Clausius-Mossotti Equation
The Clausius-Mossotti equation relates two basic properties of a LHI dielectric: a microscopic, polarizability α of a representative ‘test molecule’ of those the material comprises of, with a macroscopic, relative permittivity,
, of the material. Reference books present many different, and in some cases rather complicate, derivations of the Clausius-Mossotti equation [
8,
9,
11,
13,
14,
15,
38]. Most of these derivations treat the problem from an entirely macroscopic point of view; the one-by-one interaction of the neighboring electric dipoles/molecules with the ‘test molecule’ under investigation, one way or another is finally neglected, at least in most cases. Thus, in this relatively simple case, the standard Clausius-Mossotti equation is [
8,
9,
11,
13,
14,
15,
38]:
where
is the position-independent density of electric dipoles/molecules (number of entities per unit volume of the homogeneous dielectric).
Here, we present an alternative derivation of the Clausius-Mossotti equation. Instead of investigating what happens inside the ‘spherical cavity’ [
8,
9,
11,
13,
14,
15,
38], we are focusing on the processes that take place at the dielectric sphere that has been removed from the specimen.
Specifically, we consider a specimen of the LHI dielectric material of interest in the form of a sphere of radius R, subjected to a homogeneous, external electric field . Below, we treat the problem with both formulations, the P-E, , and the P-D, .
Standard P-E, , formulation: From the macroscopic point of view, we have to express the electric polarization,
, through the relative permittivity,
, of the material. In
Section 7.1 of the article, we have treated the exact same case and calculated all necessary physical entities. First, we recall the standard definition for the polarization at the inside space (
) of the LHI dielectric sphere:
where
is the
total electric field inside the specimen and
is the electric susceptibility. For reasons that will become clear below, we formally call
the
intrinsic electric susceptibility;
reflects the inherent properties of the material
per se and not of a specimen of particular shape and size characteristics used in a specific experiment. In addition, since
is the
total field, it takes into account two components: (i) the
external electric field
that is the stimulus applied to the dielectric sphere; and (ii) the
internal electric field
, else depolarizing field or self field, that is, the response of the dielectric sphere to
(for details, see
Section 3 and
Section 7.1, and [
25] of the article). For the inside space (
) of the dielectric sphere, we have:
By using relation (A29), relation (A28) transforms to
In these relations, is a component controlled/known during the experiment, while is a component not controlled/known, and in addition cannot be measured straightforwardly. This a serious obstacle; to practically obtain through relation (A30), we have to somehow get experimental access to . Else, from the experimental point of view, relations (A28) and (A30) are meaningless.
On the other hand, as mentioned above,
is a physical entity that is completely controlled/known during the experiment; it is the
external stimulus applied to the specimen by the user. Thus, if we express
through
we can ultimately obtain an equation that relates
and
exclusively. To this effect, an appropriate physical model should be adopted for
that will enable us to mathematically treat the electrostatic problem in a reliable way. Indeed, in
Section 7.1 of the article we obtained:
Thus, through relation (A31), relation (A30) becomes:
else
else
where
and
is the so-called
extrinsic susceptibility and
is the so-called depolarization (else, depolarizing) factor for the case under discussion where the specimen is a sphere. Here, let us make a comment trying to make the connection between the ideal theoretical expectation (relation (A28)) and the experimental realization (relation (A34)). First, we recall that since the
total electric field
inside the material is not experimentally accessible by any means, relation (A28) is useless in recording the
intrinsic susceptibility,
. On the contrary, relation (A34) is useful in obtaining information on the
extrinsic susceptibility,
, since we are able to experimentally record both
(it is controlled by the user) and
(probed through a closely relating voltage/current/capacitance signal). Thus, through the experimentally accessible
extrinsic susceptibility,
, we can eventually obtain the
intrinsic susceptibility,
, through relation (A35) as:
where
is the so-called depolarization factor for the case of a sphere as already defined above.
Here, let us clarify the above situation since (to non-experts) it can possibly appear as a misleading paradox: consider an experiment wherein we apply an
external electric field
to a specimen, trying to get information on its dielectric properties, susceptibility,
, relative permittivity,
, polarizability, α, etc. One could probably expect that the
external electric field
, applied by the user, would penetrate the specimen (thus, in the inside space
), and polarize it in an exclusive way in the sense that the following relation should hold
, i.e., the polarization of the specimen,
, should depend
solely on the
external electric field,
. However, this is
not the case. Here, we briefly clarify this issue. After subjection to the
external electric field,
, the specimen will be polarized. The discontinuity of its polarization,
, at the sphere-vacuum interface,
, will produce a
bound surface charge density,
. In turn,
acts as a
secondary source that produces the so-called
internal field (else, depolarizing field or self field),
, given by relation (A31) above (the
internal electric field relates to the polarization through
). Ultimately, the
internal electric field,
, (relation (A31)) adds to the
external one,
, (
) so that the
total field inside the specimen (relation (A29)) is given by:
A detailed description of these issues has been presented in
Section 7.1 of the article.
Still, we have to obtain
from the microscopic point of view, that is, to express
through the polarizability,
, of the electric dipoles/molecules. To this effect, we can define the electric polarization of the material in microscopic terms, through the relation:
where we recall that
is the position-independent density of electric dipoles/molecules, while
is the moment of each electric dipole/molecule. Here, we assume that the material comprises of one kind of electric dipoles/molecules so that
is position-independent, as well. Accordingly, based on relation (A38),
should be position-independent, thus homogeneous. Indeed, relations (A32)–(A34) give a consistent result; on the right-hand side all
,
and
are position-independent (the dielectric is homogeneous), while
is position-independent (
), as well.
Now, we have to define
through α. At first glance, we should employ the following relation:
where
is the
total local electric field inside the sphere. Notably, relation (A29) reveals that
comprises of two components, the
external,
and the
internal, else depolarizing field/self field,
. By definition, the polarizability, α, cannot depend on
internal electric fields, irrespectively of their origin [
8,
9,
11,
13,
14,
15,
38]. Thus, in our case, the
internal/depolarizing/self field
should be excluded so that relation (A39) gets:
where, now,
is the
externally applied electric field. Accordingly, relations (A38) and (A40) can be combined to provide an expression of
through the microscopic parameter of polarizability, α, of the material’s electric dipoles/molecules:
Combining relations (A33) and (A41) we finally get
This is the Clausius-Mossotti equation.
The Alternative P-D, , formulation: From the macroscopic point of view, we have to express the electric polarization,
, through the P-D relative permittivity,
, of the material. In
Section 7.2 of the article, we employed the alternative P-D,
, formulation and calculated all necessary physical entities. Briefly, first, we recall the standard definition for the
reverse electric polarization at the inside space (
) of the LHI dielectric sphere:
where the
total electric displacement inside the specimen is:
with
the
external electric displacement (originating from
free charges) applied by the user.
Combining relations (A43) and (A44), we get:
else
Relation (A41) still defines the electric polarization,
, in microscopic terms. By using the following version:
we define the D-related polarizability,
, (from the E-related one,
) through:
Thus, we get the expression of polarization that relate to
(instead of
):
By combining relations (A46) and (A49) we finally get:
Notice that since , the D-related polarizability, , is always positive, as it should. Also, starting from (A50), by using the above relation (A48) and (relation (34) of the article), we immediately obtain relation (A42), that is the Clausius-Mossotti, as expected. Thus, the P-D, , formulation is equivalent to the P-E, , one.