In Situ Investigation of Tensile Response for Inconel 718 Micro-Architected Materials Fabricated by Selective Laser Melting
Abstract
1. Introduction
2. Materials and Methods
2.1. The 3D Design of the Lattice Structure Specimens
2.2. The 3D Printing of the Lattice Structure Specimens
2.3. Microtensile Testing
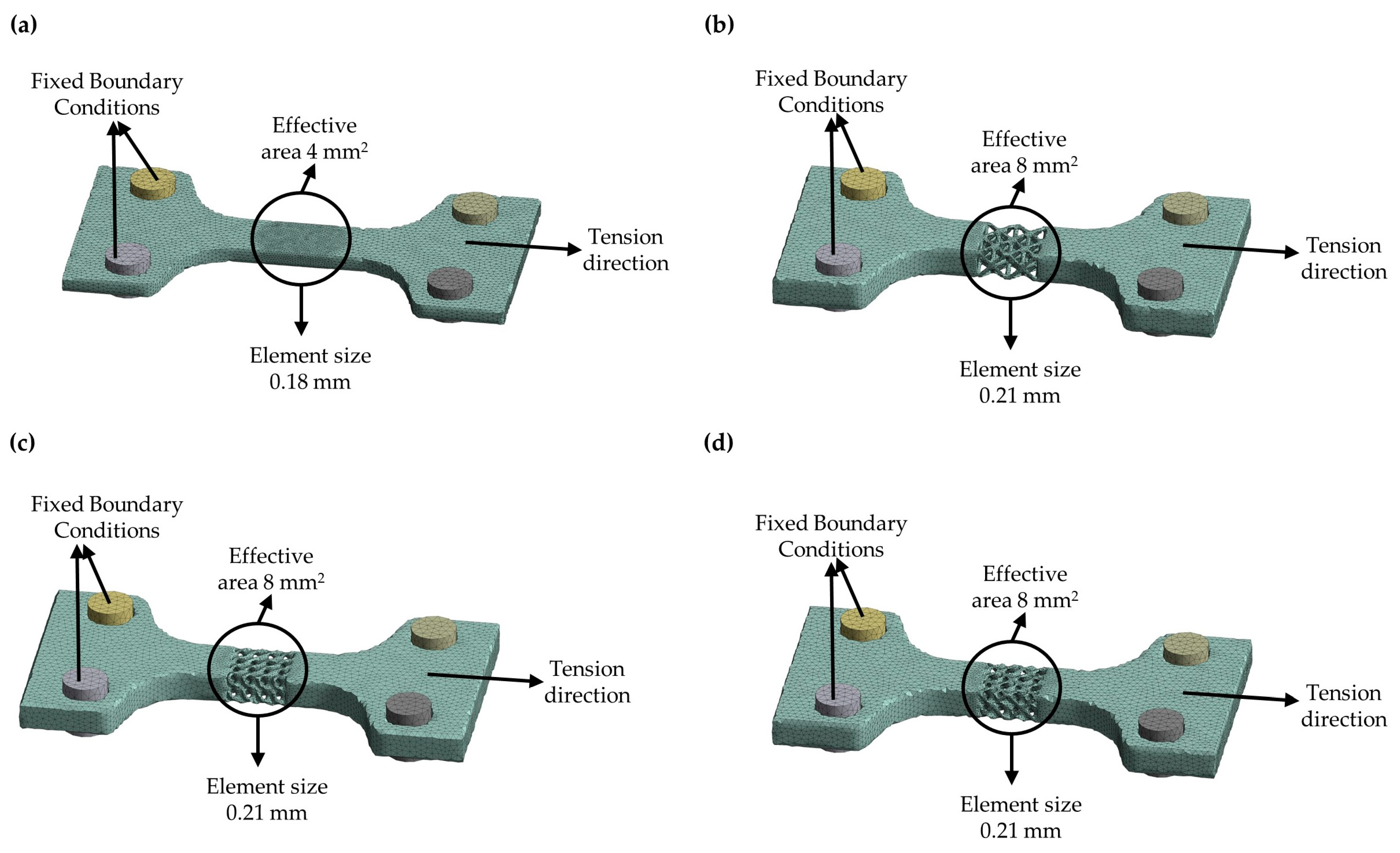
2.4. Finite Element Analysis
3. Results and Discussion
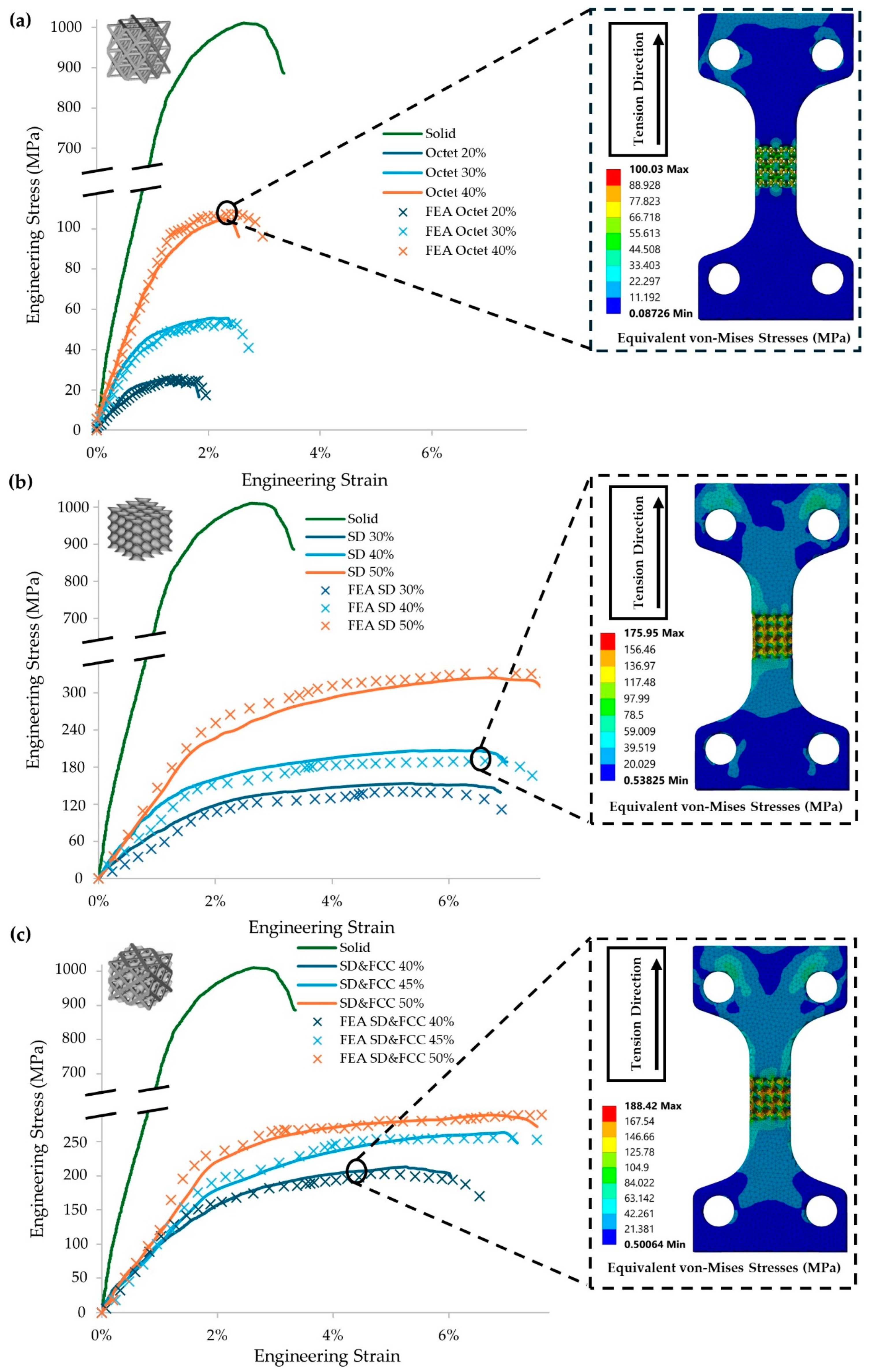
3.1. Mechanical Charaterization Assisted with FE Analysis
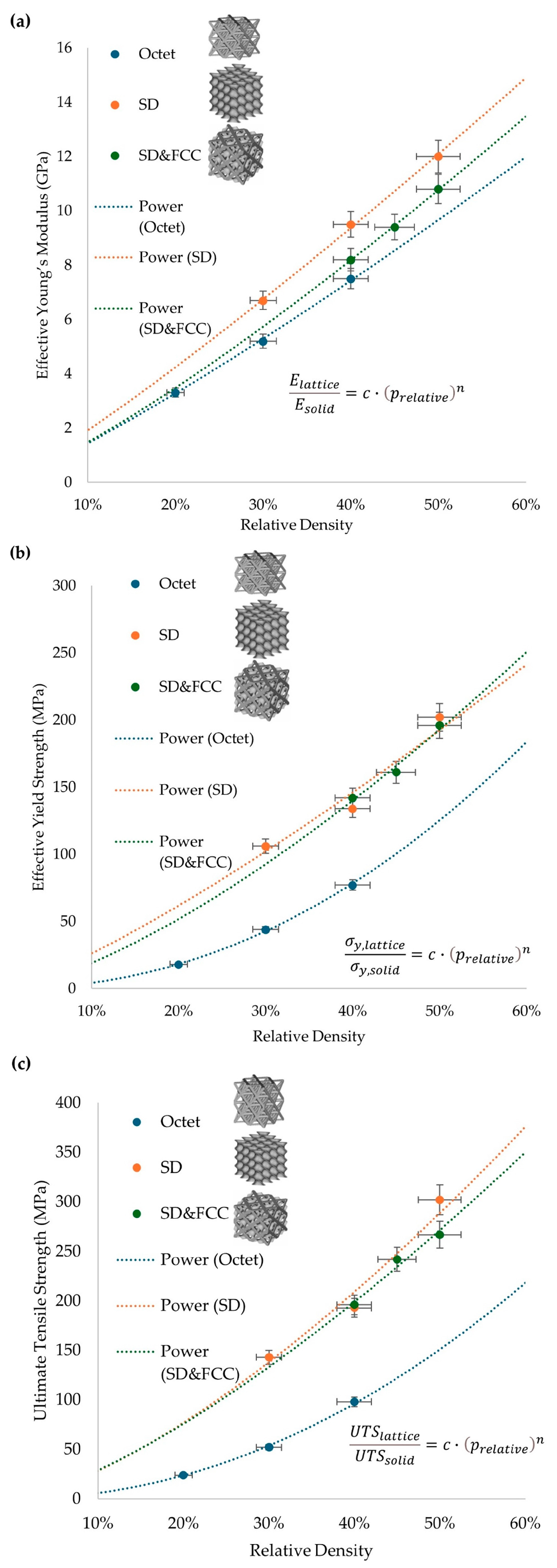
3.2. Identification of the Scaling Laws of Different Lattice Structures
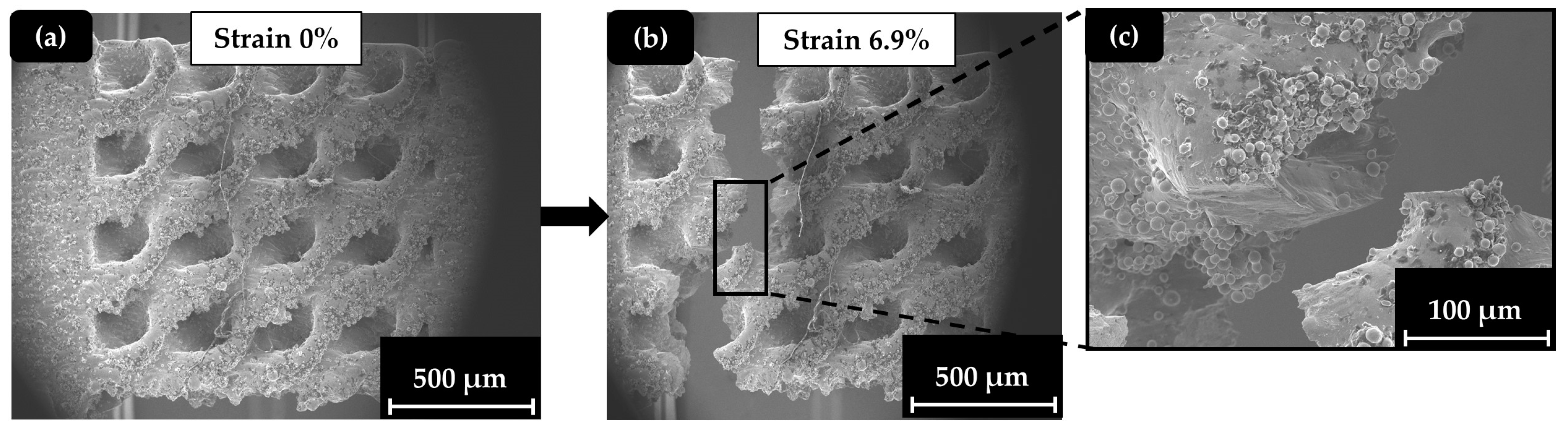
3.3. Identification of the Deformation Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kladovasilakis, N.; Tsongas, K.; Karalekas, D.; Tzetzis, D. Architected Materials for Additive Manufacturing: A Comprehensive Review. Materials 2022, 15, 5919. [Google Scholar] [CrossRef] [PubMed]
- Kladovasilakis, N.; Pechlivani, E.M.; Sfampa, I.K.; Tsongas, K.; Korlos, A.; David, C.; Tzovaras, D. Metal 3D-Printed Bioinspired Lattice Elevator Braking Pads for Enhanced Dynamic Friction Performance. Materials 2024, 17, 2765. [Google Scholar] [CrossRef] [PubMed]
- Kohale, V.; Jawade, S.; Kakandikar, G.M. Investigation on Mechanical Behaviour of Inconel 718 Manufactured through Additive Manufacturing. Int. J. Interact. Des. Manuf. 2023, 17, 1645–1651. [Google Scholar] [CrossRef]
- Kyriakidis, I.F.; Kladovasilakis, N.; Pechlivani, E.M.; Tsongas, K. Mechanical Performance of Recycled 3D Printed Sustainable Polymer-Based Composites: A Literature Review. J. Compos. Sci. 2024, 8, 215. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Grammatikos, S.; Papadakis, V.; Korlos, A.; Mountakis, N. High Performance Polycarbonate Nanocomposites Mechanically Boosted with Titanium Carbide in Material Extrusion Additive Manufacturing. Nanomaterials 2022, 12, 1068. [Google Scholar] [CrossRef]
- Giarmas, E.; Tsongas, K.; Tzimtzimis, E.K.; Korlos, A.; Tzetzis, D. Mechanical and FEA-Assisted Characterization of 3D Printed Continuous Glass Fiber Reinforced Nylon Cellular Structures. J. Compos. Sci. 2021, 5, 313. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, B.; Wen, Y.; Qu, X. Research Progress on Selective Laser Melting Processing for Nickel-Based Superalloy. Int. J. Miner. Metall. Mater. 2022, 29, 369–388. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Lu, F.; Wan, H.Y.; Ren, X.; Huang, L.; Liu, H.; Yi, X. Mechanical and Microstructural Characterization of Additive Manufactured Inconel 718 Alloy by Selective Laser Melting and Laser Metal Deposition. J. Iron Steel Res. Int. 2022, 29, 1322–1333. [Google Scholar] [CrossRef]
- Meng, G.; Gong, Y.; Zhang, J.; Jiang, Z.; Ren, Q.; Zhao, J. Microstructure and Mechanical Properties of Inconel 718 Thin Walls Prepared by Laser Direct Energy Deposition and Selective Laser Melting. Thin-Walled Struct. 2023, 193, 111284. [Google Scholar] [CrossRef]
- Borovitskaya, I.V.; Demin, A.C.; Komolova, O.A.; Latyshev, S.V.; Maslyaev, S.A.; Mikhailova, A.B.; Monakhov, I.S.; Morozov, E.V.; Pimenov, V.N.; Bondarenko, G.G.; et al. Effect of Pulsed Plasma Beams on the Structure and Mechanical Properties of the Surface Layer in an Inconel 718 Alloy. Russ. Metall. Met. 2023, 2023, 891–898. [Google Scholar] [CrossRef]
- Gruber, K.; Smolina, I.; Stopyra, W. Assessing Metal Powder Quality for Additive Manufacturing Using Diffuse Light Spectroscopy. Powder Technol. 2024, 434, 119366. [Google Scholar] [CrossRef]
- Kong, Y.S.; Peng, K.; Huang, H. Highly Controllable Additive Manufacturing of Heterostructured Nickel-Based Composites. Int. J. Mach. Tools Manuf. 2024, 195, 104112. [Google Scholar] [CrossRef]
- Macoretta, G.; Monelli, B.D. SLM Process Parameters Effects on the Fatigue Strength of AMed Inconel 718. Procedia Struct. Integr. 2022, 37, 632–643. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Charalampous, P.; Tsongas, K.; Kostavelis, I.; Tzovaras, D.; Tzetzis, D. Influence of Selective Laser Melting Additive Manufacturing Parameters in Inconel 718 Superalloy. Materials 2022, 15, 1362. [Google Scholar] [CrossRef] [PubMed]
- Kladovasilakis, N.; Bountourelis, T.; Tsongas, K.; Tzetzis, D. Computational Investigation of a Tibial Implant Using Topology Optimization and Finite Element Analysis. Technologies 2023, 11, 58. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Babamiri, B.B.; Zhou, Y.; Dargusch, M.; Hazeli, K.; Zhang, M. Enhancing Specific Energy Absorption of Additively Manufactured Titanium Lattice Structures through Simultaneous Manipulation of Architecture and Constituent Material. Addit. Manuf. 2022, 55, 102887. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Zhou, X.; Wang, D.; Zhang, M.; Gao, Y.; Wang, L.; Zhang, P. Evaluating Lattice Mechanical Properties for Lightweight Heat-Resistant Load-Bearing Structure Design. Materials 2020, 13, 4786. [Google Scholar] [CrossRef]
- Banait, S.; Liu, C.; Campos, M.; Pham, M.; Pérez-Prado, M.T. Coupled Effect of Microstructure and Topology on the Mechanical Behavior of Inconel718 Additively Manufactured Lattices. Mater. Des. 2022, 224, 111294. [Google Scholar] [CrossRef]
- Banait, S.; Jin, X.; Campos, M.; Pérez-Prado, M.T. Precipitation-Induced Transition in the Mechanical Behavior of 3D Printed Inconel 718 Bcc Lattices. Scr. Mater. 2021, 203, 114075. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R. Topology-Mechanical Property Relationship of 3D Printed Strut, Skeletal, and Sheet Based Periodic Metallic Cellular Materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Pemas, S.; Pechlivani, E.M. Computer-Aided Design of 3D-Printed Clay-Based Composite Mortars Reinforced with Bioinspired Lattice Structures. Biomimetics 2024, 9, 424. [Google Scholar] [CrossRef] [PubMed]
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Development of Novel Additive Manufactured Hybrid Architected Materials and Investigation of Their Mechanical Behavior. Mech. Mater. 2023, 176, 104525. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Barnes, B.; Soltani-Tehrani, A.; Shamsaei, N.; Hazeli, K. Designing Additively Manufactured Lattice Structures Based on Deformation Mechanisms. Addit. Manuf. 2021, 46, 102143. [Google Scholar] [CrossRef]
- Li, R.; Wang, H.; Li, X.; Ding, G.; Yang, C. A Micro-Tensile Method for Measuring Mechanical Properties of MEMS Materials. J. Micromechanics Microengineering 2008, 18, 065002. [Google Scholar] [CrossRef]
- AzoNano. The Benefits of Micro-Tensile Testing vs. Bulk Tensile Testing. Available online: https://www.azonano.com/article.aspx?ArticleID=5228 (accessed on 25 January 2024).
- Statnik, E.S.; Nyaza, K.V.; Salimon, A.I.; Ryabov, D.K.; Korsunsky, A.M. In Situ SEM Study of the Micro-Mechanical Behaviour of 3D-Printed Aluminium Alloy. Technologies 2021, 9, 21. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Askari, H.; Hazeli, K. Deformation Mechanisms and Post-Yielding Behavior of Additively Manufactured Lattice Structures. Mater. Des. 2020, 188, 108443. [Google Scholar] [CrossRef]
- Ravi, P.; Naragani, D.; Kenesei, P.; Park, J.-S.; Sangid, M.D. Direct Observations and Characterization of Crack Closure during Microstructurally Small Fatigue Crack Growth via In-Situ High-Energy X-ray Characterization. Acta Mater. 2021, 205, 116564. [Google Scholar] [CrossRef]
- Beyhaghi, M.; Rouhani, M.D.; Hobley, J.; Jeng, Y.-R. In-Situ and Ex-Situ Comparison of Oxidation of Inconel 718 Manufactured by Selective Laser Melting and Conventional Methods up to 650 °C. Appl. Surf. Sci. 2021, 569, 151037. [Google Scholar] [CrossRef]
- Sang, L.; Lü, J.; Jin, W.; Ullah, R.; Sun, X.; Zhang, Y.; Zhang, Z. In-Situ SEM Study of Temperature-Dependent Tensile Behavior of Inconel 718 Superalloy. J. Mater. Sci. 2021, 56, 16097–16112. [Google Scholar] [CrossRef]
- Teng, Q.; Li, S.; Wei, Q.; Shi, Y. Investigation on the Influence of Heat Treatment on Inconel 718 Fabricated by Selective Laser Melting: Microstructure and High Temperature Tensile Property. J. Manuf. Process. 2021, 61, 35–45. [Google Scholar] [CrossRef]
- ISO 6892-1; Metallic Materials—Tensile Testing—Part 1. ISO: Honk Kong, China, 2009.
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Mechanical and FEA-Assisted Characterization of Fused Filament Fabricated Triply Periodic Minimal Surface Structures. J. Compos. Sci. 2021, 5, 58. [Google Scholar] [CrossRef]
- Vock, S.; Klöden, B.; Kirchner, A.; Weißgärber, T.; Kieback, B. Powders for Powder Bed Fusion: A Review. Prog. Addit. Manuf. 2019, 4, 383–397. [Google Scholar] [CrossRef]
- ASTM ISO/ASTM52921-13; Standard Terminology for Additive Manufacturing-Coordinate Systems and Test Methodologies. ASTM International: West Conshohocken, PA, USA, 2013.
- Pechlivani, E.M.; Melidis, L.; Pemas, S.; Katakalos, K.; Tzovaras, D.; Konstantinidis, A.A. On the Effect of Volumetric Energy Density on the Characteristics of 3D-Printed Metals and Alloys. Metals 2023, 13, 1776. [Google Scholar] [CrossRef]
- Pechlivani, E.M.; Kampouris, A.K.; Melidis, L.; Katakalos, K.; Kontodina, T.; Tzovaras, D.; Konstantinidis, A.A. 3D Printed Inconel Mechanical Response Related to Volumetric Energy Density. Mater. Today Proc. 2023, 93, 39–47. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Michailidis, N.; David, C.; Mountakis, N.; Papadakis, V.; Sfakiotakis, E.; Sagris, D.; Spiridaki, M.; Argyros, A. Optimized PCL/CNF Bio-Nanocomposites for Medical Bio-Plotted Applications: Rheological, Structural, and Thermomechanical Aspects. Bioprinting 2023, 36, e00311. [Google Scholar] [CrossRef]


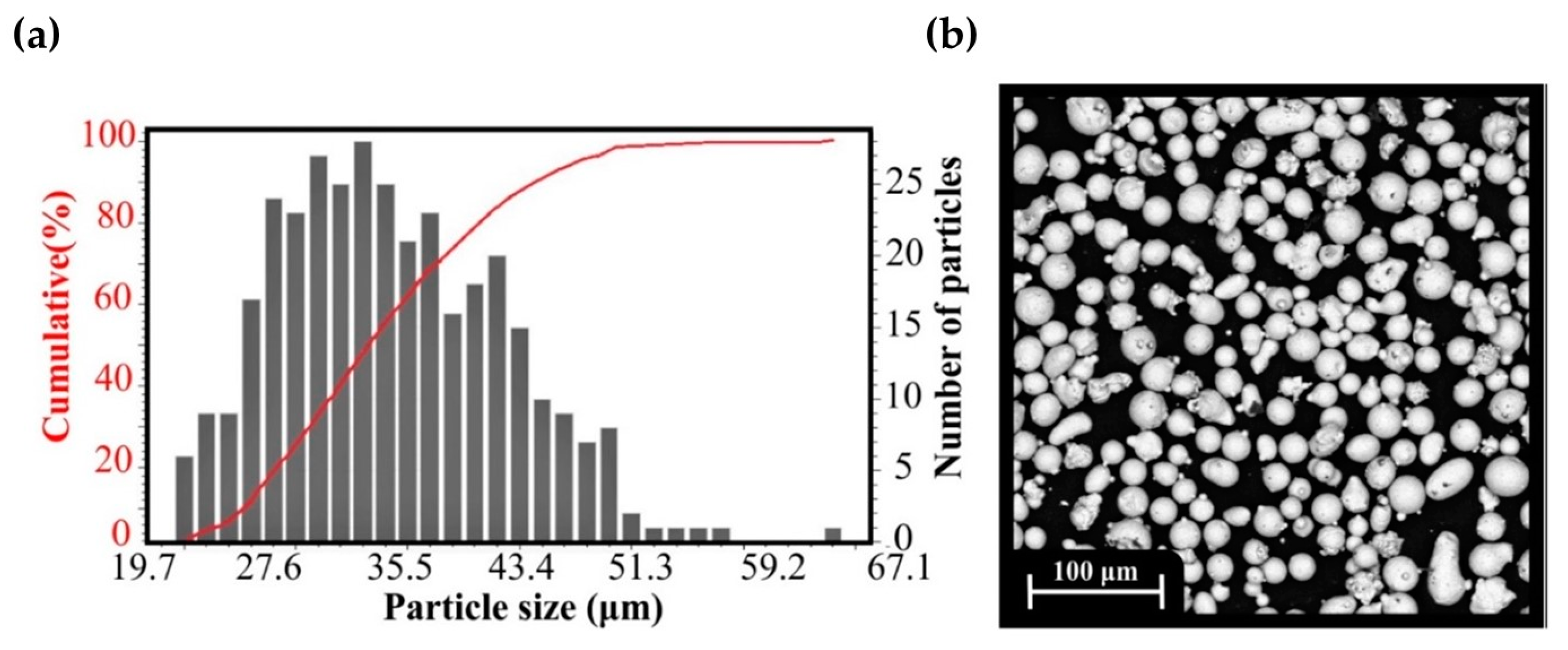







| Feedstock Material | Specimens’ Geometry | Relative Density | Unit Cell Length (mm) | Strut/Wall Thickness (mm) |
|---|---|---|---|---|
| Inconel 718 | Octet | 20% | 2 | 0.274 |
| 30% | 0.347 | |||
| 40% | 0.414 | |||
| Schwarz Diamond (SD) | 30% | 2 | 0.258 | |
| 40% | 0.344 | |||
| 50% | 0.428 | |||
| Schwarz Diamond and Face Centered Cubic (SD&FCC) | 40% | 2 | SD: 0.291 FCC: 0.291 | |
| 45% | SD: 0.325 FCC: 0.325 | |||
| 50% | SD: 0.360 FCC: 0.360 |
| Chemical Element | Chemical Composition (wt.%) |
|---|---|
| Nickel (Ni) | 54.11 |
| Chromium (Cr) | 18.14 |
| Iron (Fe) | 17.93 |
| Niobium (Nb) | 4.16 |
| Molybdenum (Mo) | 2.95 |
| Titanium (Ti) | 1.12 |
| Other | 1.59 |
| Specimens’ Geometry | Number of Elements | Element Size Range (mm) |
|---|---|---|
| Solid | 125,871 | 0.18–0.80 |
| Octet | 126,724 | 0.21–0.60 |
| SD | 127,020 | 0.21–0.60 |
| SD&FCC | 126,929 | 0.21–0.60 |
| Specimen’s Type | E (GPa) | Yield Strength (MPa) | UTS (MPa) | Elongation at Break (%) |
|---|---|---|---|---|
| Solid | 80.7 ± 7.3 | 811 ± 34 | 1010 ± 70 | 3.0 ± 0.4 |
| Octet 20% | 3.3 ± 0.5 | 19 ± 3 | 24 ± 5 | 1.5 ± 0.2 |
| Octet 30% | 5.2 ± 0.4 | 44 ± 4 | 52 ± 9 | 2.4 ± 0.3 |
| Octet 40% | 7.5 ± 0.4 | 77 ± 3 | 98 ± 5 | 2.5 ± 0.2 |
| SD 30% | 6.7 ± 0.6 | 106 ± 5 | 143 ± 6 | 6.8 ± 0.3 |
| SD 40% | 9.5 ± 0.7 | 134 ± 8 | 193 ± 8 | 6.9 ± 0.6 |
| SD 50% | 12.0 ± 1.1 | 202 ± 11 | 303 ± 16 | 7.5 ± 0.8 |
| SD&FCC 40% | 8.2 ± 0.6 | 142 ± 9 | 196 ± 13 | 6.0 ± 0.7 |
| SD&FCC 45% | 9.4 ± 0.5 | 161 ± 9 | 242 ± 15 | 6.8 ± 0.8 |
| SD&FCC 50% | 10.8 ± 1.4 | 199 ± 12 | 267 ± 19 | 7.5 ± 0.9 |
| Lattice Structures | Young’s Modulus (E) | Yield Strength (σy) | Ultimate Tensile Strength (UTS) | |||
|---|---|---|---|---|---|---|
| c | n | c | n | c | n | |
| Octet | 0.27 | 1.18 | 0.67 | 2.10 | 0.61 | 2.02 |
| SD | 0.33 | 1.14 | 0.56 | 1.24 | 0.78 | 1.44 |
| SD&FCC | 0.31 | 1.23 | 0.65 | 1.44 | 0.71 | 1.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyriakidis, I.F.; Kladovasilakis, N.; Pechlivani, E.M.; Korlos, A.; David, C.; Tsongas, K. In Situ Investigation of Tensile Response for Inconel 718 Micro-Architected Materials Fabricated by Selective Laser Melting. Materials 2024, 17, 4433. https://doi.org/10.3390/ma17174433
Kyriakidis IF, Kladovasilakis N, Pechlivani EM, Korlos A, David C, Tsongas K. In Situ Investigation of Tensile Response for Inconel 718 Micro-Architected Materials Fabricated by Selective Laser Melting. Materials. 2024; 17(17):4433. https://doi.org/10.3390/ma17174433
Chicago/Turabian StyleKyriakidis, Ioannis Filippos, Nikolaos Kladovasilakis, Eleftheria Maria Pechlivani, Apostolos Korlos, Constantine David, and Konstantinos Tsongas. 2024. "In Situ Investigation of Tensile Response for Inconel 718 Micro-Architected Materials Fabricated by Selective Laser Melting" Materials 17, no. 17: 4433. https://doi.org/10.3390/ma17174433
APA StyleKyriakidis, I. F., Kladovasilakis, N., Pechlivani, E. M., Korlos, A., David, C., & Tsongas, K. (2024). In Situ Investigation of Tensile Response for Inconel 718 Micro-Architected Materials Fabricated by Selective Laser Melting. Materials, 17(17), 4433. https://doi.org/10.3390/ma17174433











