Numerical Analysis of Cavitation Erosion in 316L Steel with CrN PVD Coating
Abstract
1. Introduction
2. Materials and Methods
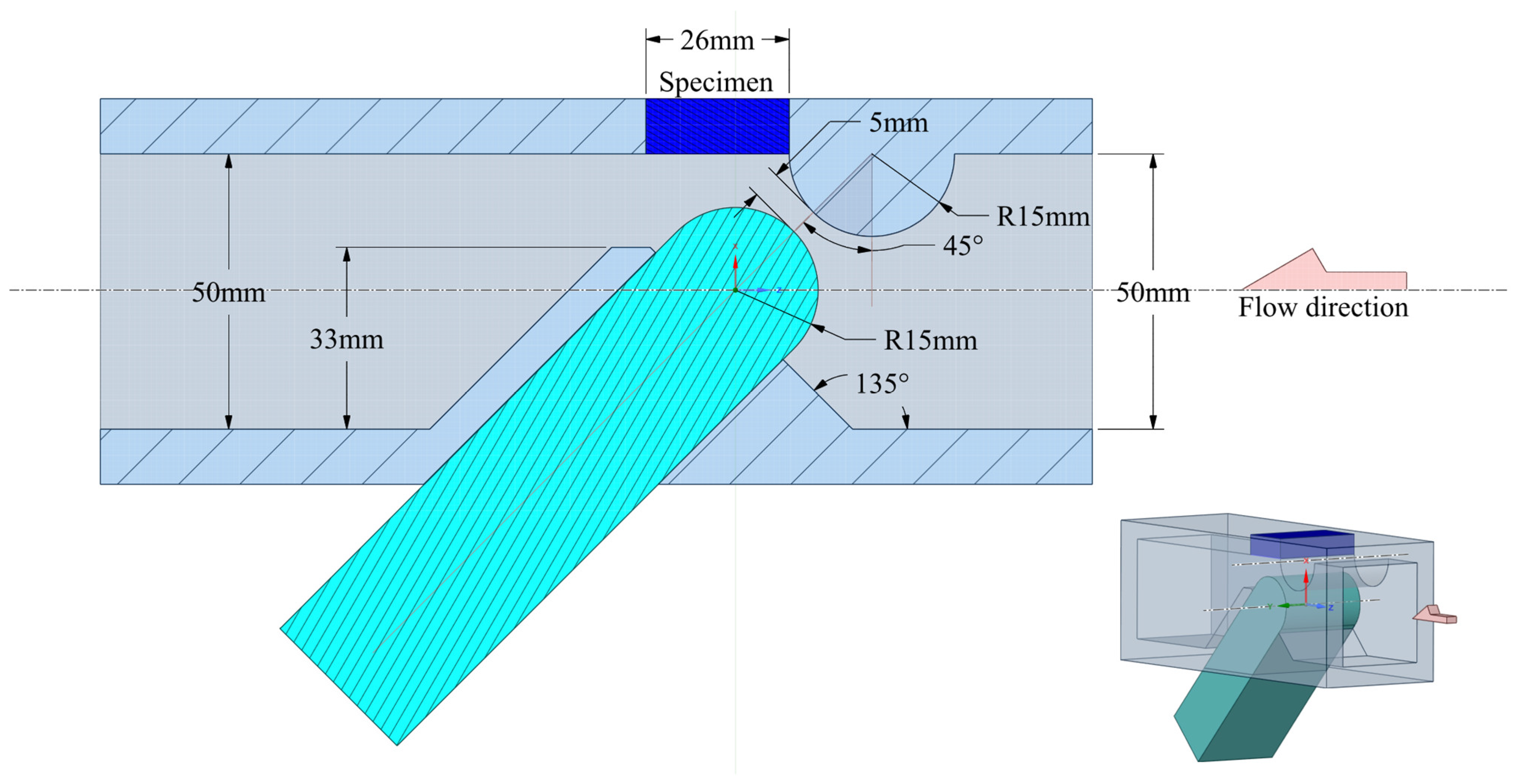
2.1. Cavitation Erosion Tests
2.2. Numerical Model
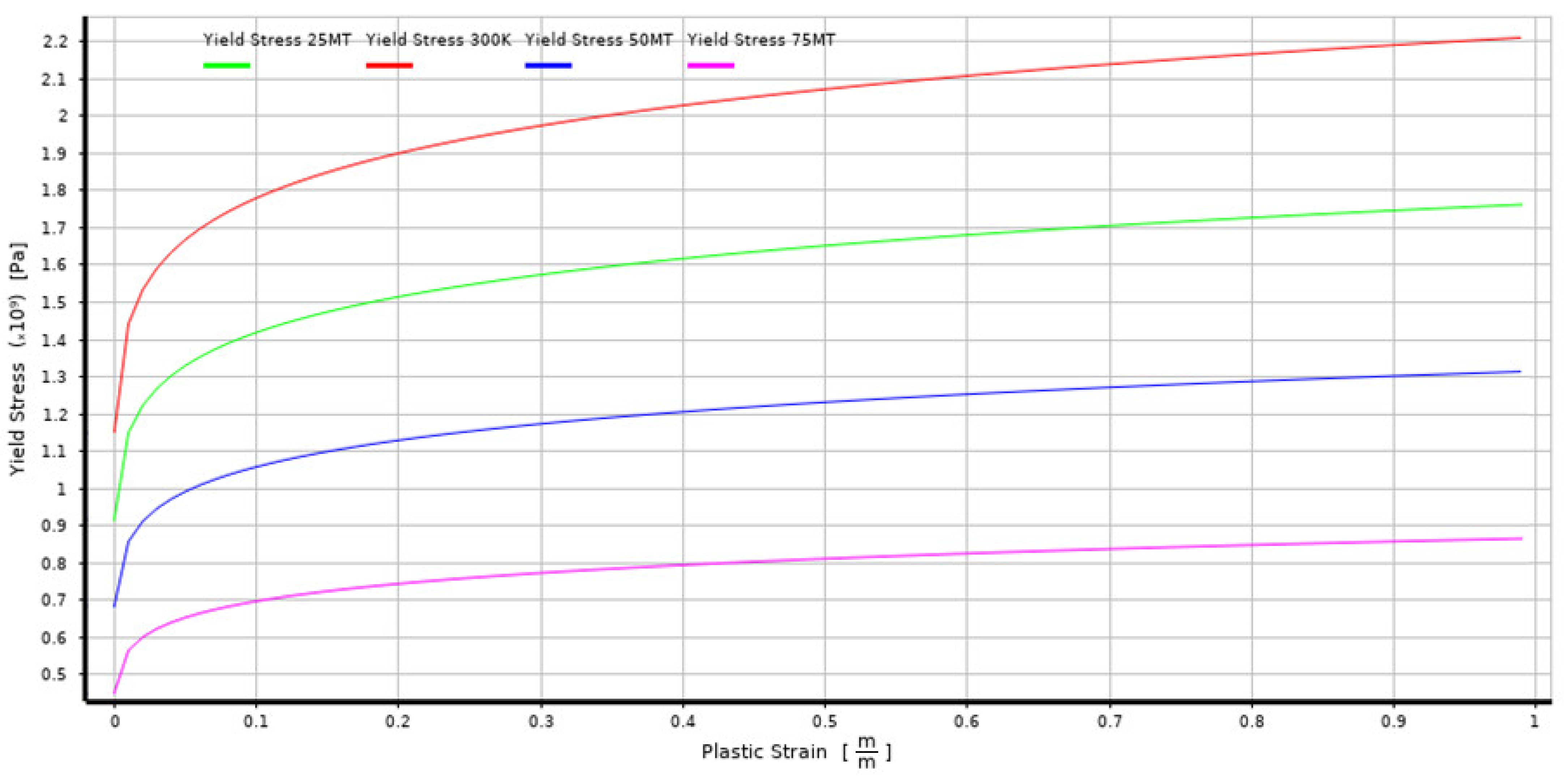
2.3. Johnson–Cook Strength Model
- -
- is the yield stress at reference strain rate and room temperature;
- -
- is the hardening modulus;
- -
- is the hardening exponent;
- -
- is the equivalent plastic strain;
- -
- is the equivalent plastic strain rate;
- -
- is the reference strain rate;
- -
- is the current temperature;
- -
- is the reference temperature;
- -
- is the melting temperature of the material;
- -
- is the thermal softening coefficient.
2.4. Steinberg–Guinan Strength Model
- -
- is the initial yield strength;
- -
- is the shear modulus as a function of plastic strain;
- -
- is a thermal softening coefficient;
- -
- is the current temperature;
- -
- is the reference temperature.
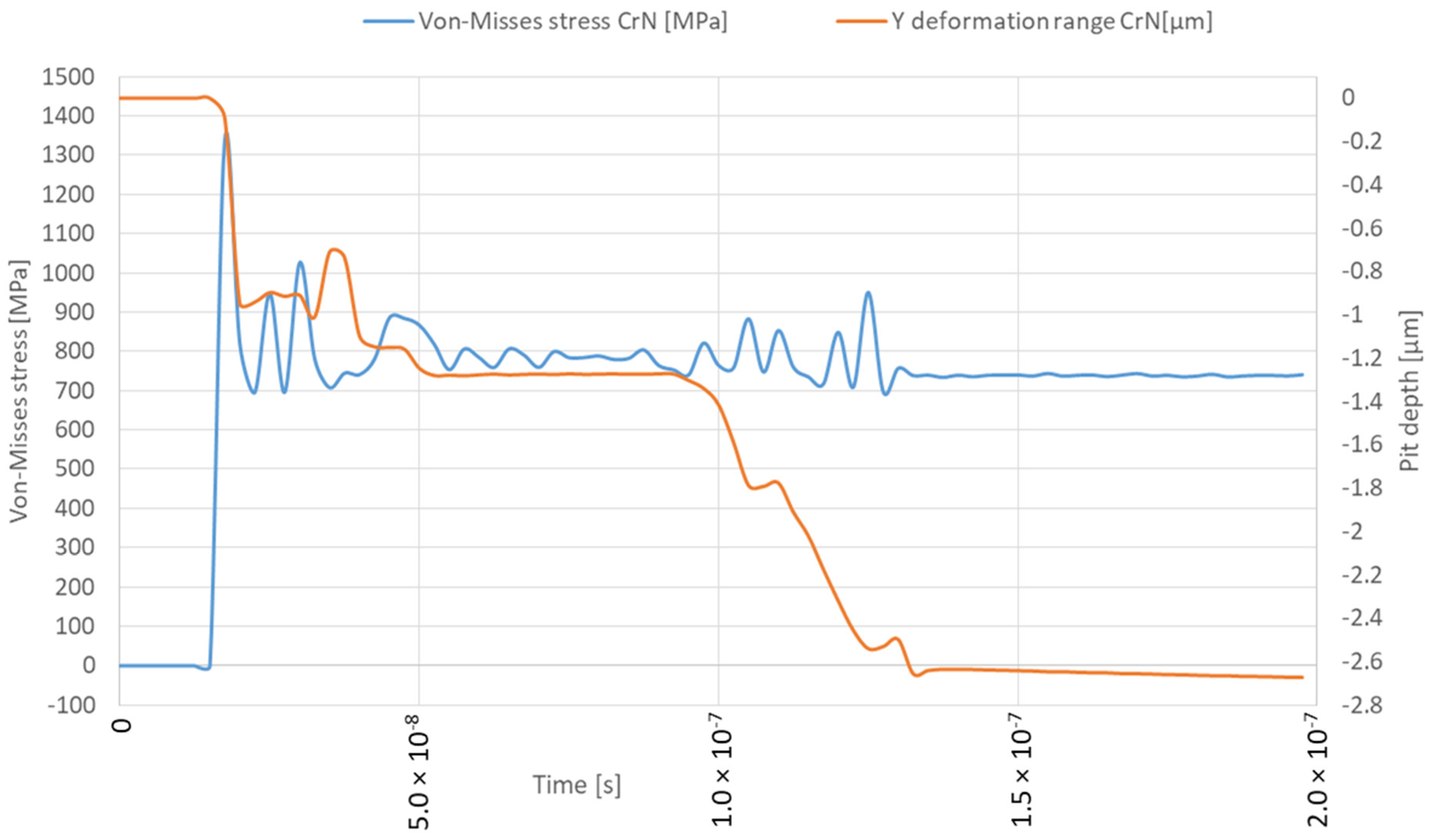
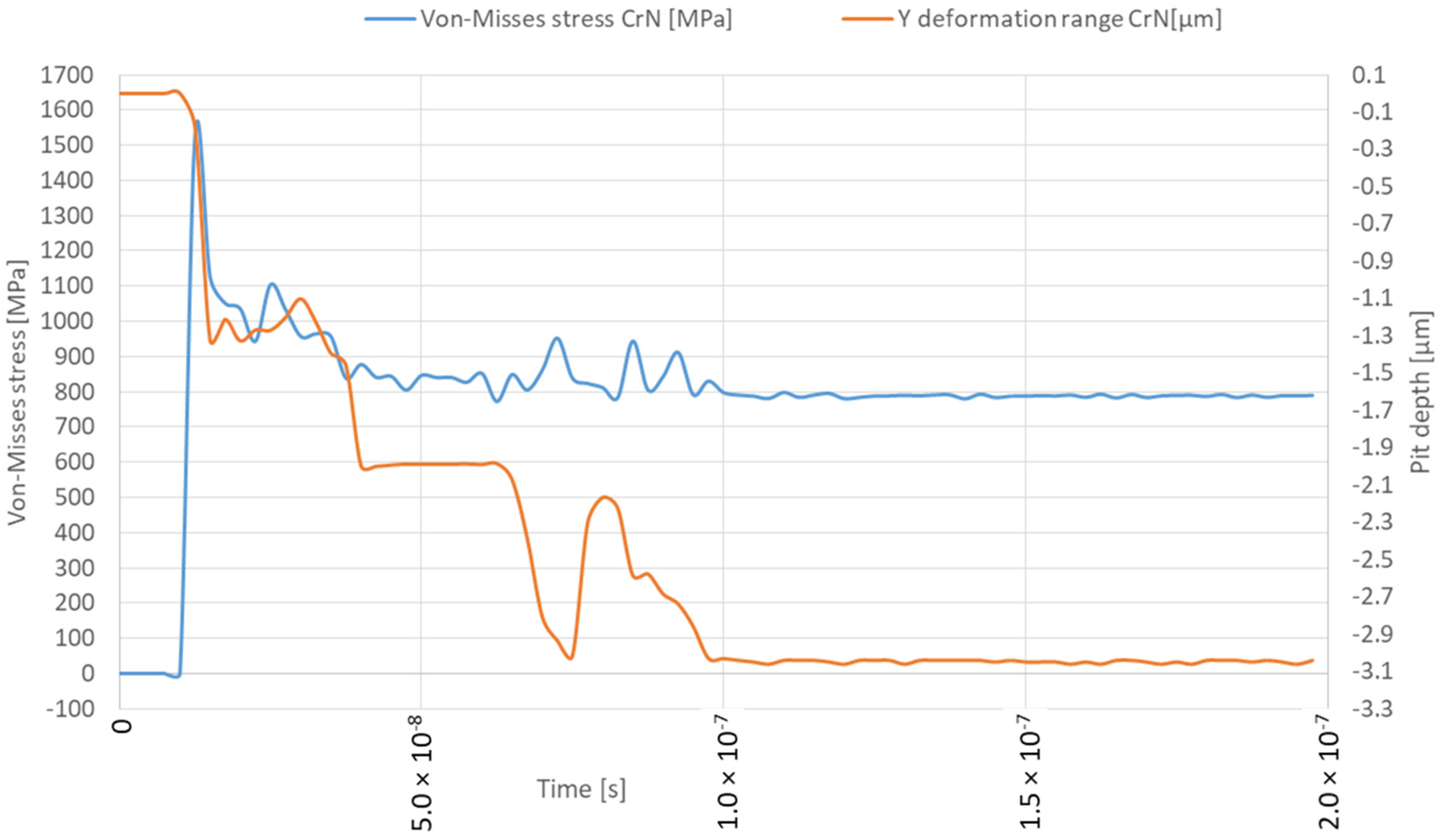
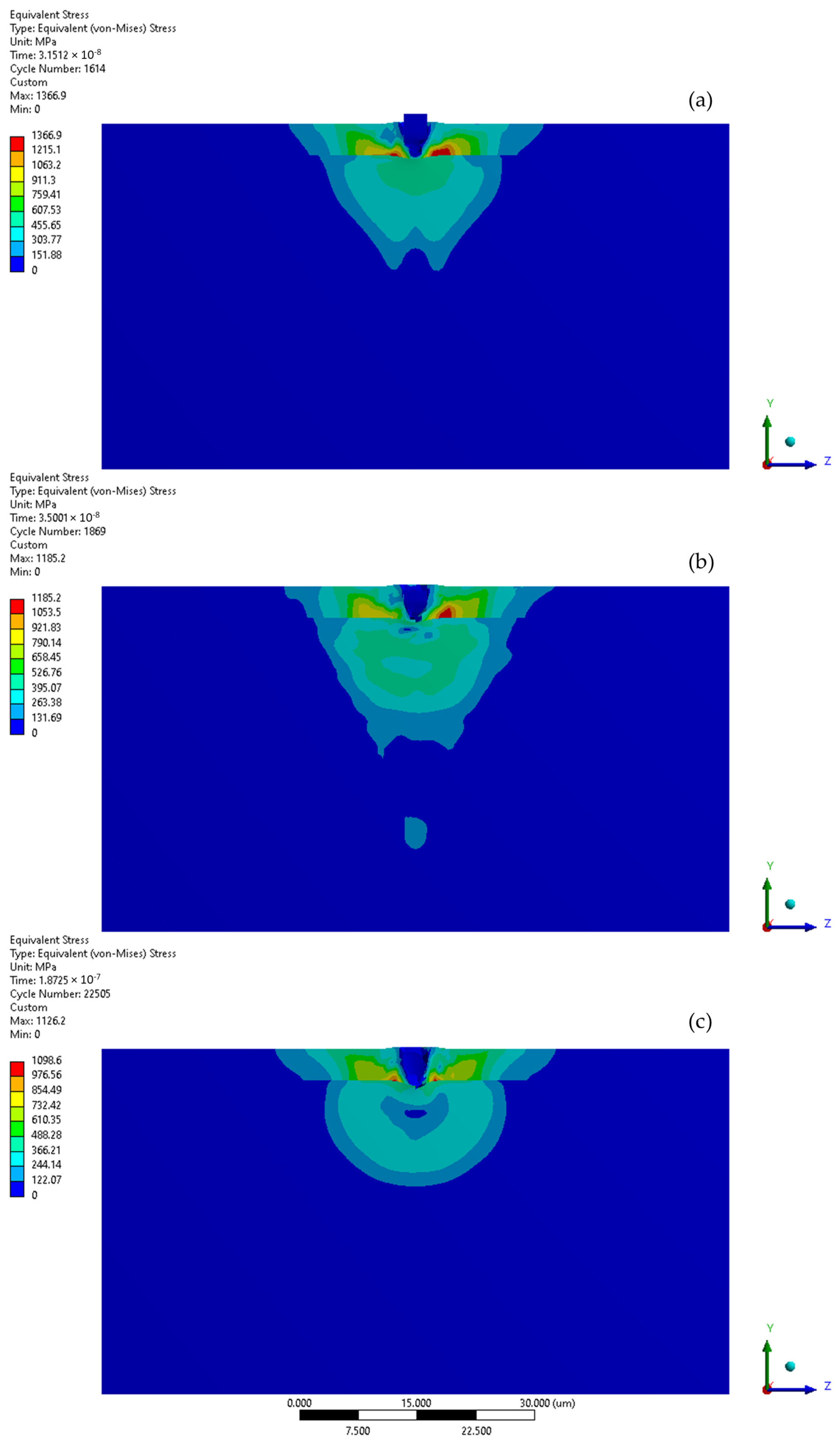
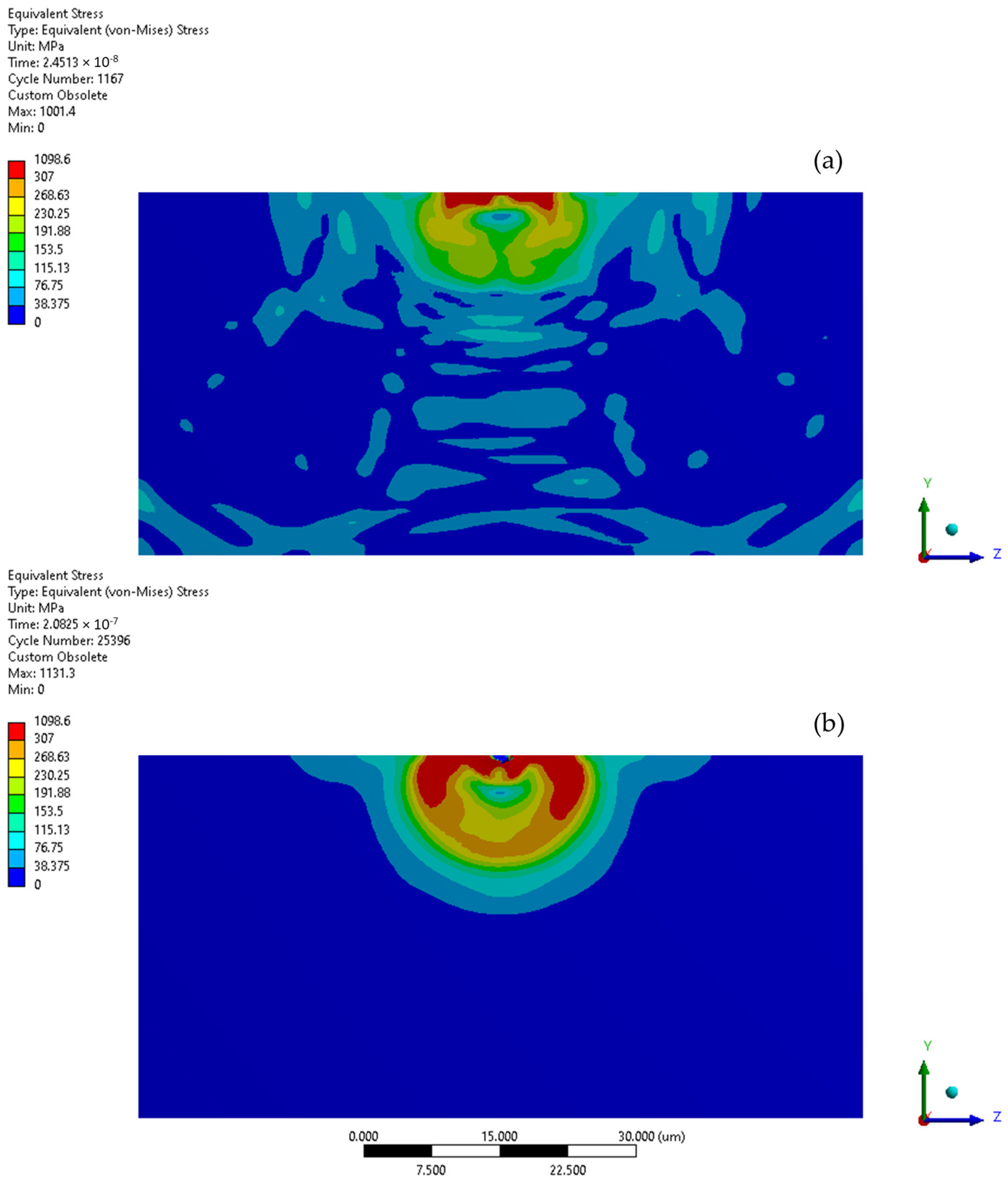
3. Analysis Results
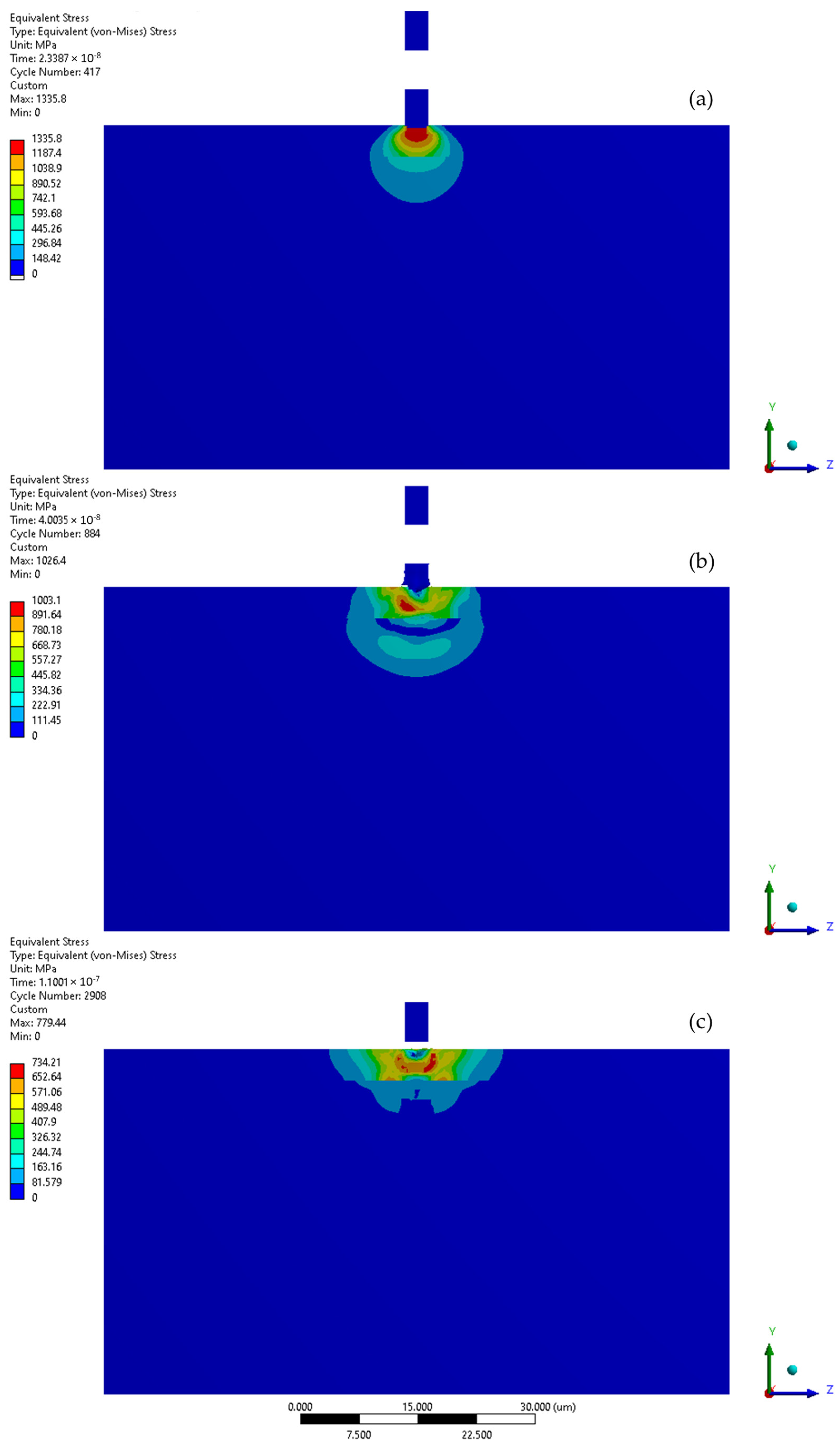
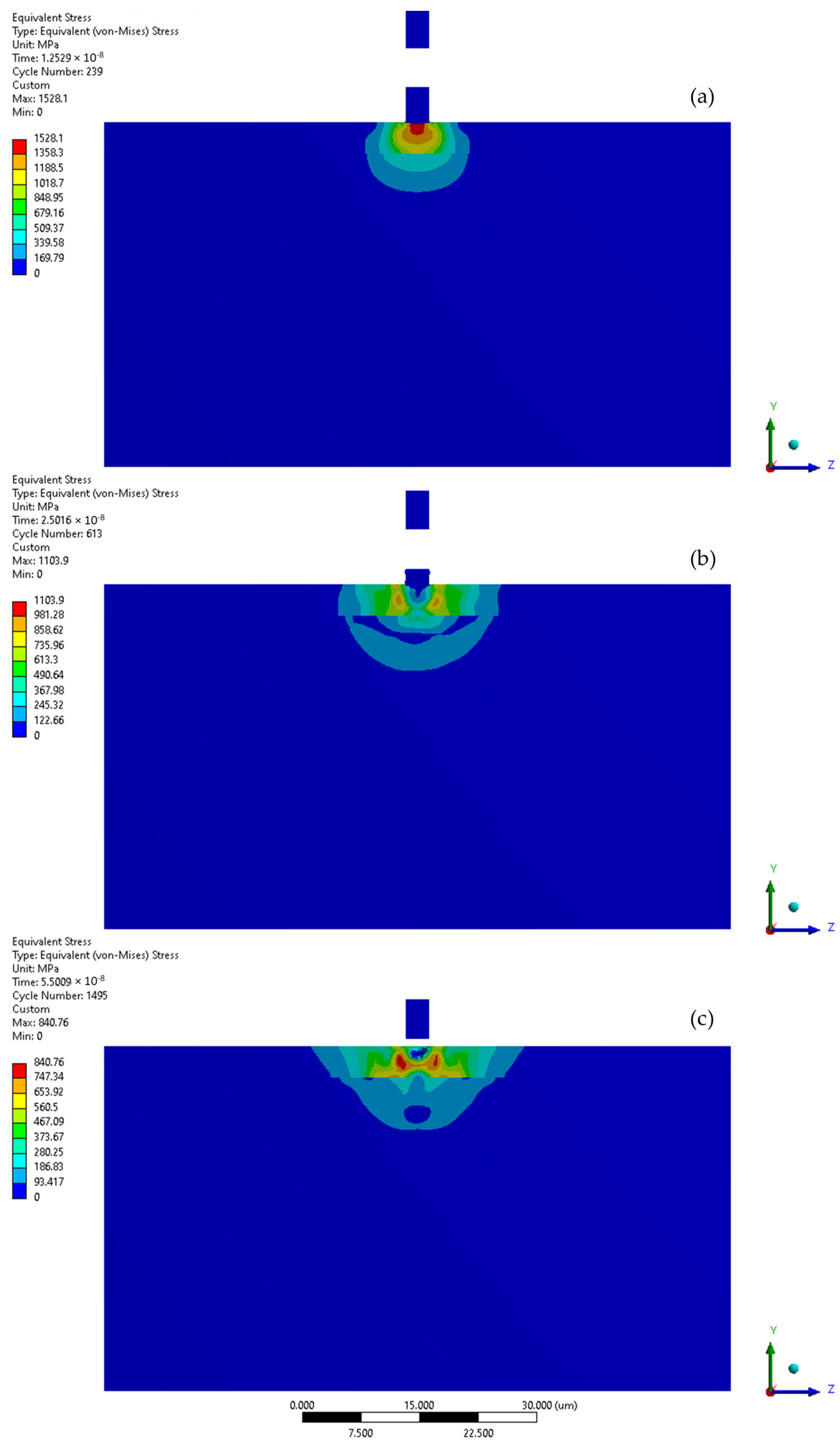
3.1. Microjet Collision at 100 m/s
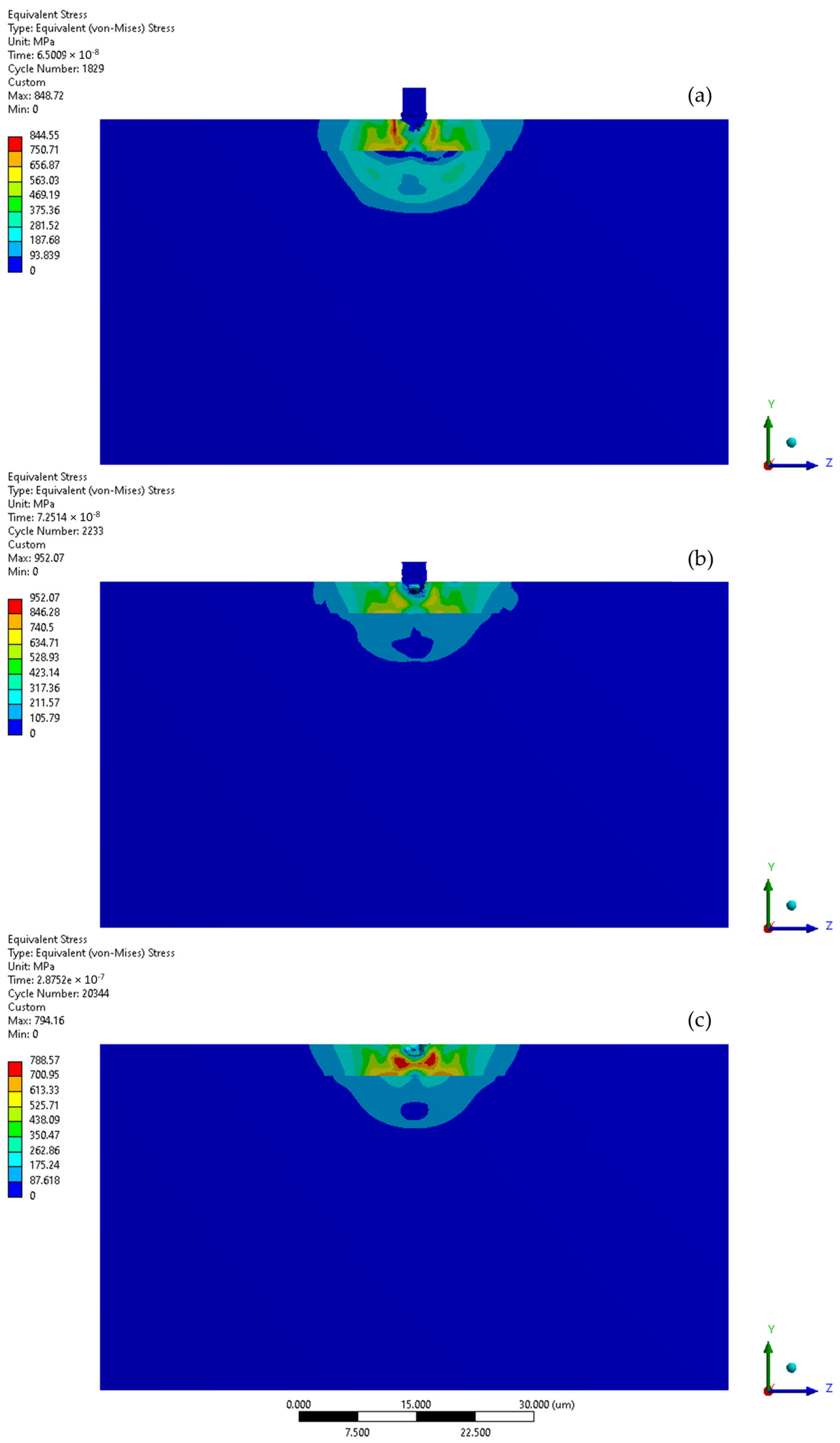
3.2. Microjet Collision at 200 m/s
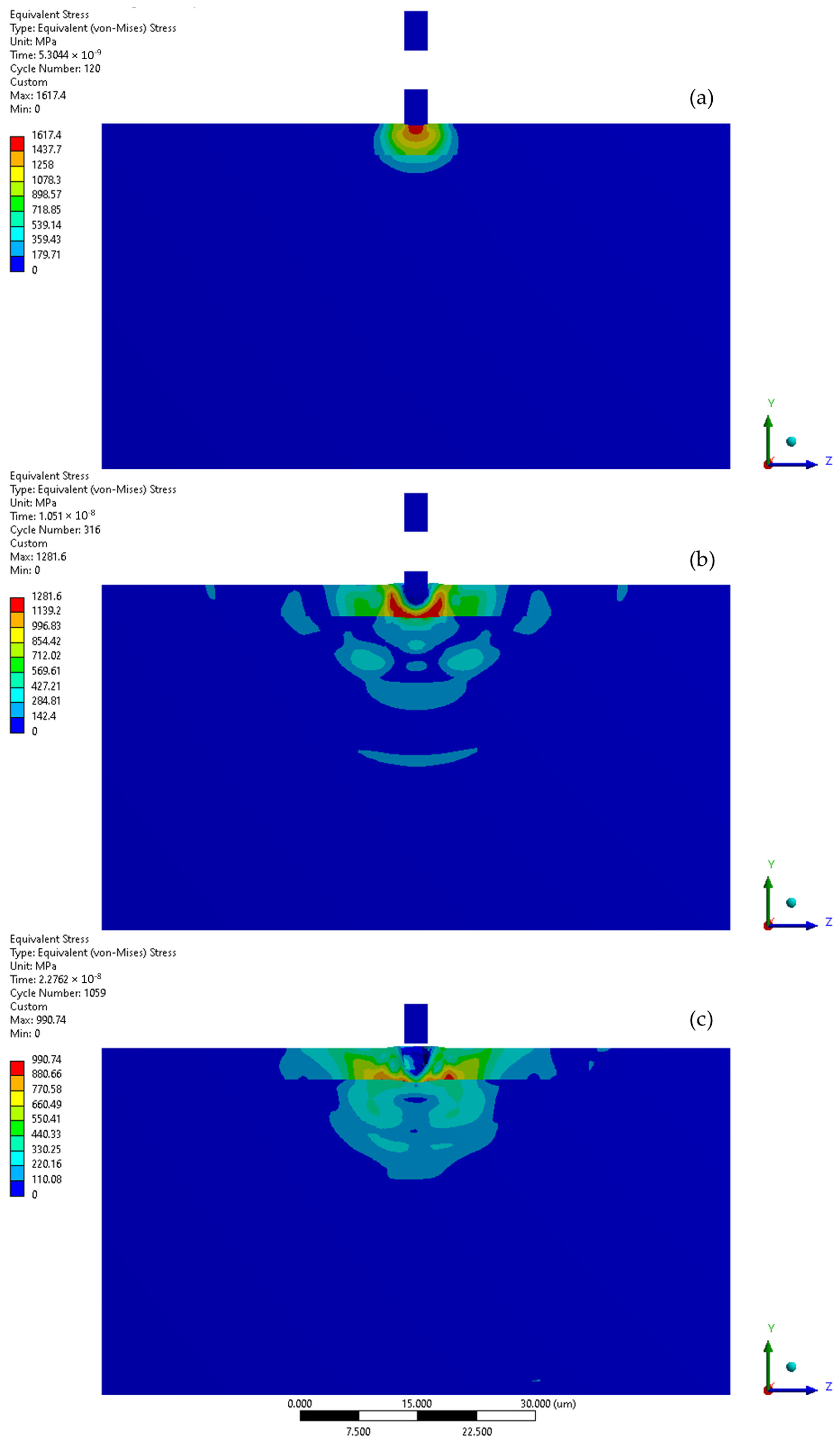
3.3. Microjet Collision at 500 m/s
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, N.; Wang, L.; Wu, S.; Likhachev, D.S. Research on cavitation erosion and wear resistance performance of coatings. Eng. Fail. Anal. 2015, 55, 208–223. [Google Scholar] [CrossRef]
- Aryal, S.; Chitrakar, S.; Shrestha, R.; Jha, A.K. Coating technology in hydro-Turbines for sediment affected power plants: A review. IOP Conf. Ser. Earth Environ. Sci. 2022, 1037, 012021. [Google Scholar] [CrossRef]
- Krella, A.K. Degradation and Protection of Materials from Cavitation Erosion: A Review. Materials 2023, 16, 2058. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press Inc.: Oxford, UK, 1995; Volume 9, ISBN 0-19-509409-3. [Google Scholar]
- Krella, A.K. Cavitation erosion of monolayer PVD coatings—An influence of deposition technique on the degradation process. Wear 2021, 478–479, 203762. [Google Scholar] [CrossRef]
- Jose, S.A.; John, M.; Menezes, P.L. Cermet Systems: Synthesis, Properties, and Applications. Ceramics 2022, 5, 210–236. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Ramachandran, C.S.; Guo, P.; Wang, A. Microstructure and Performance of High-Velocity Oxygen-Fuel Coupled Physical Vapor Deposition (HVOF-PVD) Duplex Protective Coatings: A Review. Coatings 2022, 12, 1395. [Google Scholar] [CrossRef]
- Jonda, E.; Szala, M.; Sroka, M.; Łatka, L.; Walczak, M. Investigations of cavitation erosion and wear resistance of cermet coatings manufactured by HVOF spraying. Appl. Surf. Sci. 2023, 608, 155071. [Google Scholar] [CrossRef]
- Hsiao, C.T.; Jayaprakash, A.; Kapahi, A.; Choi, J.K.; Chahine, G.L. Modelling of material pitting from cavitation bubble collapse. J. Fluid Mech. 2014, 755, 142–175. [Google Scholar] [CrossRef]
- Lindau, O.; Lauterborn, W. Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 2003, 479, 327–348. [Google Scholar] [CrossRef]
- Dular, M.; Požar, T.; Zevnik, J.; Petkovšek, R. High speed observation of damage created by a collapse of a single cavitation bubble. Wear 2019, 418–419, 13–23. [Google Scholar] [CrossRef]
- Xie, Z.; Shi, W.; Zheng, Y.; Tan, L.; Tian, Q. Simulation investigation on impact damage characteristics of metal plate by cavitating bubble micro-jet water hammer. Eng. Fail. Anal. 2020, 115, 104626. [Google Scholar] [CrossRef]
- Okada, T.; Iwai, Y.; Hattori, S.; Tanimura, N. Relation between impact load and the damage produced by cavitation bubble collapse. Wear 1995, 184, 231–239. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Formation; Cambrage University Press: New York, NY, USA, 1995; Volume 44, ISBN 9781107644762. [Google Scholar]
- Lauterborn, W.; Bolle, H. Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary. J. Fluid Mech. 1975, 72, 391. [Google Scholar] [CrossRef]
- Wright, M.M.; Epps, B.; Dropkin, A.; Truscott, T.T. Cavitation of a submerged jet. Exp. Fluids 2013, 54, 1541. [Google Scholar] [CrossRef]
- Bourne, N.K. On stress wave interactions in liquid impact. Wear 2005, 258, 588–595. [Google Scholar] [CrossRef]
- Field, J.E.; Camus, J.; Tinguely, M.; Obreschkow, D.; Farhat, M. Cavitation in impacted drops and jets and the effect on erosion damage thresholds. Wear 2012, 290–291, 154–160. [Google Scholar] [CrossRef]
- Smith, D.G.; Kinslow, R. Pressure Due to High-velocity Impact of a Water Jet. Exp. Mech. 1975, 16, 21–25. [Google Scholar] [CrossRef]
- Blake, J.R.; Tomita, Y.; Tong, R.P. The art, craft and science of modelling jet impact in a collapsing cavitation bubble. Appl. Sci. Res. 1998, 58, 77–90. [Google Scholar] [CrossRef]
- Lauterborn, W.; Kurz, T.; Geisler, R.; Schanz, D.; Lindau, O. Acoustic cavitation, bubble dynamics and sonoluminescence. Ultrason. Sonochem. 2007, 14, 484–491. [Google Scholar] [CrossRef]
- Zhang, S.; Duncan, J.H.; Chahine, G.L. The final stage of the collapse of a cavitation bubble near a rigid wall. J. Fluid Mech. 1993, 257, 147. [Google Scholar] [CrossRef]
- Wang, M.; Lv, M.; Zhang, R.; Tong, W.; Xu, X. Effect of ultrasonic cavitation micro-jet impact on corrosion of material in ultrasonic assisted electrochemical micromachining. J. Appl. Electrochem. 2023, 53, 1579–1593. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, X.; Li, J. SPH–FEM Analysis of Effect of Flow Impingement of Ultrasonic Honing Cavitation Microjet on Titanium–Tantalum Alloy Surface. Micromachines 2024, 15, 38. [Google Scholar] [CrossRef] [PubMed]
- Maurin, A. Numerical investigation of degradation of 316l steel caused by cavitation. Materials 2021, 14, 3131. [Google Scholar] [CrossRef] [PubMed]
- EN 10204; Metallic Products-Types of Inspection Documents Produits. CEN-European Committee for Standardization: Brussels, Belgium, 2004; 10p.
- Góral, M.; Sasiela, D.; Płoszaj, F.; Kościelniak, B.; Kubaszek, T.; Przybyło, A. The erosion resistance of Cr/CrN multilayer coating deposited using industrial Arc-PVD process for compressor blades application. Ochr. Przed Koroz. 2023, 66, 66–70. [Google Scholar] [CrossRef]
- Krella, A.; Czyzniewski, A. Investigation concerning the cavitation resistance of TiN coatings deposited on austenitic stainless steel at various temperatures. Wear 2008, 265, 72–80. [Google Scholar] [CrossRef]
- Zhang, Z.; Clifton, R.J. Shear band propagation from a crack tip subjected to Mode II shear wave loading. Int. J. Solids Struct. 2007, 44, 1900–1926. [Google Scholar] [CrossRef][Green Version]
- Krella, A.K.; Krupa, A. E ff ect of cavitation intensity on degradation of X6CrNiTi18-10 stainless steel. Wear 2018, 408–409, 180–189. [Google Scholar] [CrossRef]
- Muller, M.; Zima, P.; Unger, J. Energy dissipated during the cavitation bubble collapse close to a solid wall. Eighth Int. Symp. Cavitation 2012, 25, 146–151. [Google Scholar]
- Soyama, H.; Kumano, H.; Saka, M. A new parameter to predict cavitation erosion. In Proceedings of the CAV 2001: Fourth International Symposium on Cavitation, Pasadena, CA, USA, 20–23 June 2001; pp. 1–8. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A Computational Constitutive Model and Data for Metals Subjected to Large Strain, High Strain Rates and High Pressures. Seventh Int. Symp. Ballist. 1983, 21, 541–547. [Google Scholar]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; ISBN -0-521-25576-7. [Google Scholar]
- Krella, A.; Czyzniewski, A. Influence of the substrate hardness on the cavitation erosion resistance of TiN coating. Wear 2007, 263, 395–401. [Google Scholar] [CrossRef]







| C | Mn | Si | Ni | Ti | Cr | P | S |
|---|---|---|---|---|---|---|---|
| 0.01 | 1.79 | 0.53 | 9.56 | 0.15 | 17.05 | 0.025 | 0.027 |
| Element Size (μm) | Number of Elements | Max. Stress (MPa) | Max. Y Deformation (μm) | Run Time (h) |
|---|---|---|---|---|
| 0.8 | 455,312 | 1258 | −2.51 | 3 |
| 0.7 | 674,256 | 1289 | −2.57 | 4.5 |
| 0.6 | 1,090,955 | 1336 | −2.64 | 7 |
| 0.5 | 1,876,495 | 1343 | −2.65 | 13 |
| 0.4 | 3,546,584 | 1347 | −2.66 | 25 |
| Property | 316L | CrN | Unit |
|---|---|---|---|
| Density | 7990 | 5900 | kg/m3 |
| Young’s Modulus | 193 | 200 | GPa |
| Poisson’s Ratio | 0.3 | 0.2 | - |
| Bulk Modulus | 160.8 | 111.1 | GPa |
| Shear Modulus | 74.2 | 83.3 | GPa |
| Specific Heat | 452 | 477 | J/kgK |
| Strain Rate Correction | First-Order | First-Order | - |
| Initial Yield Stress | 307 | 950 | MPa |
| Hardening Exponent | 0.36 | 0.095 | MPa |
| Hardening Constant | 275 | 1000 | - |
| Strain Rate Constant | 0.022 | 0.012 | - |
| Thermal Softening Exponent | 1 | 1 | - |
| Melting Temperature | 1537.9 | 1436.9 | °C |
| Refresh Strain Rate | 1 | 1 | 1/s |
| Maximum Yield Stress | 600 | 2200 | MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maurin, A. Numerical Analysis of Cavitation Erosion in 316L Steel with CrN PVD Coating. Materials 2024, 17, 4397. https://doi.org/10.3390/ma17174397
Maurin A. Numerical Analysis of Cavitation Erosion in 316L Steel with CrN PVD Coating. Materials. 2024; 17(17):4397. https://doi.org/10.3390/ma17174397
Chicago/Turabian StyleMaurin, Artur. 2024. "Numerical Analysis of Cavitation Erosion in 316L Steel with CrN PVD Coating" Materials 17, no. 17: 4397. https://doi.org/10.3390/ma17174397
APA StyleMaurin, A. (2024). Numerical Analysis of Cavitation Erosion in 316L Steel with CrN PVD Coating. Materials, 17(17), 4397. https://doi.org/10.3390/ma17174397





