Electron Magnetic Resonance Study of Ni50.2Mn28.3Ga21.5 Powders
Abstract
1. Introduction
2. Materials and Methods
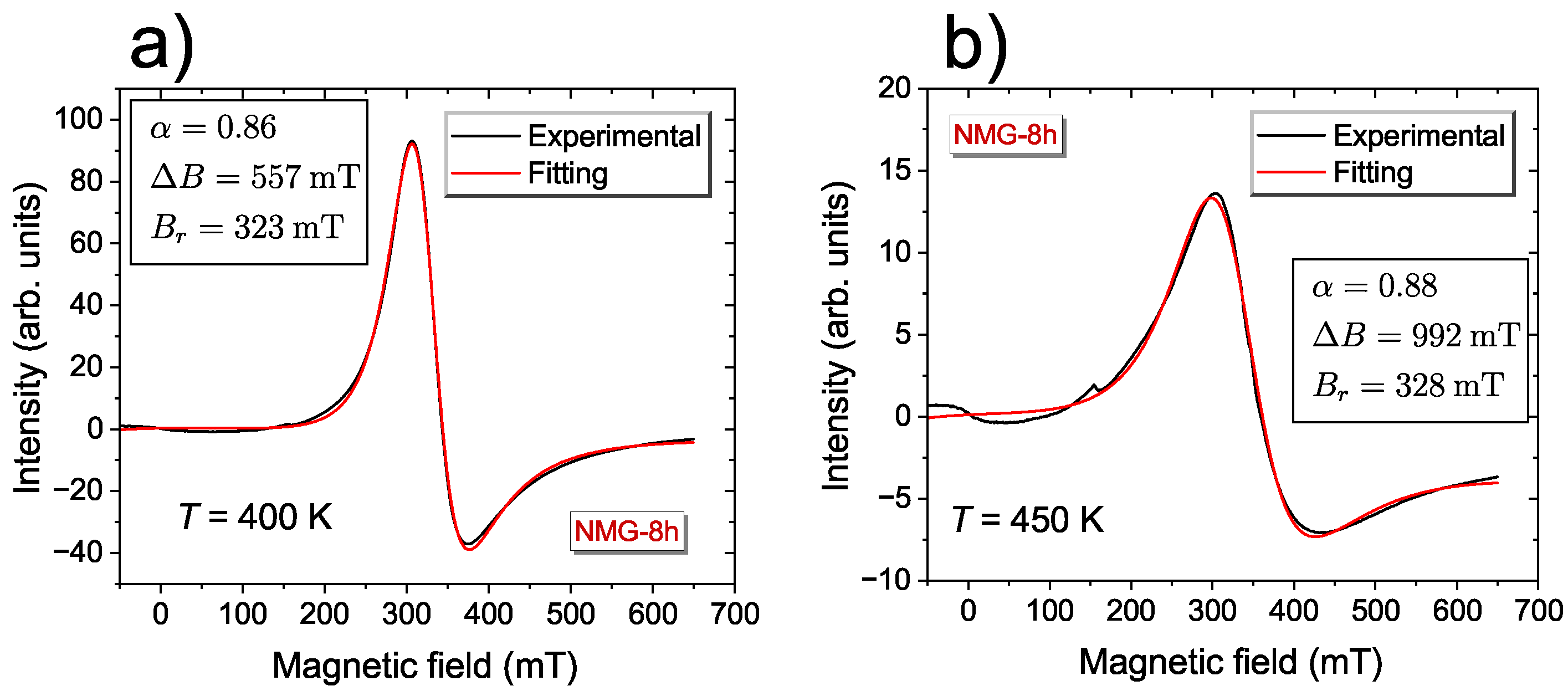
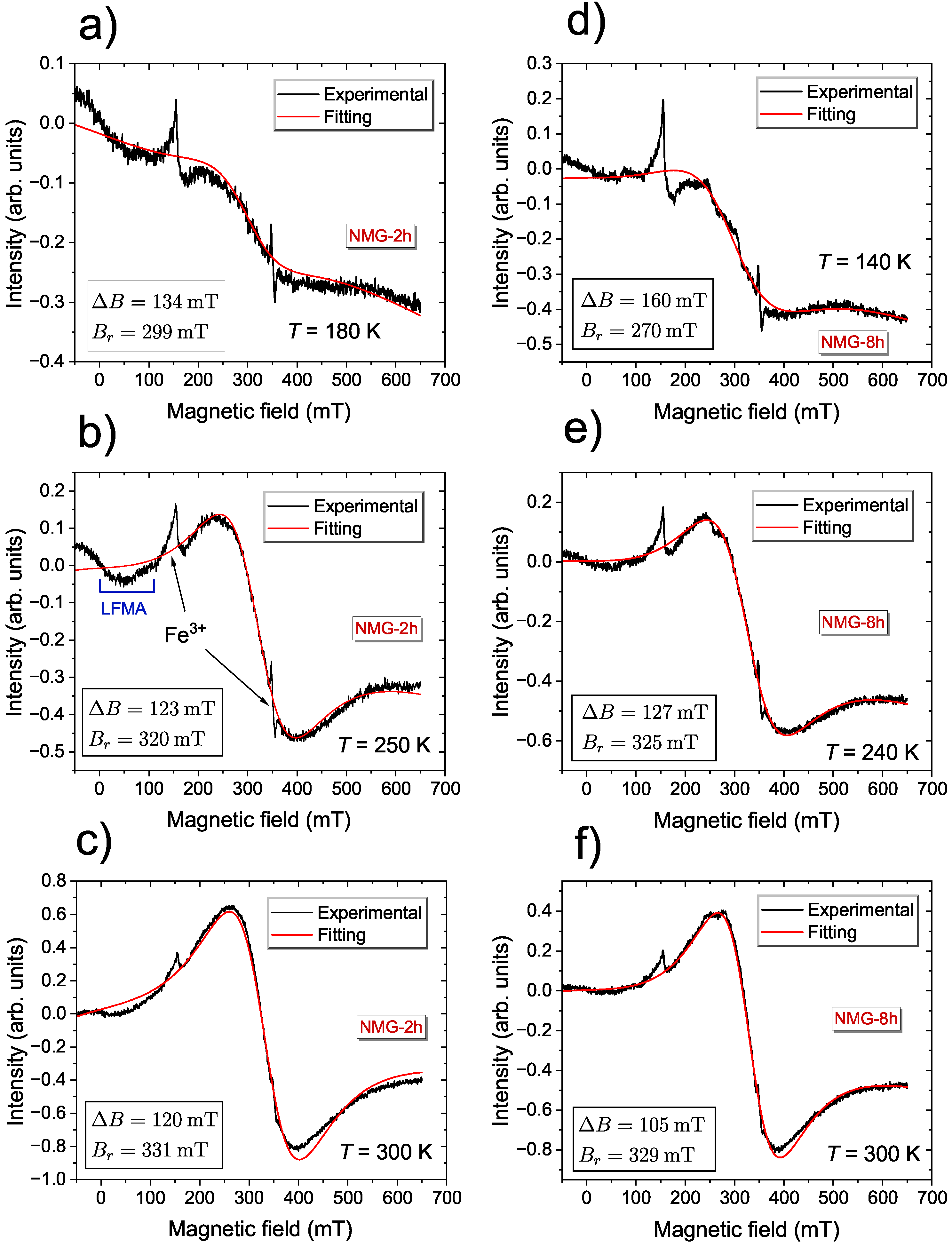
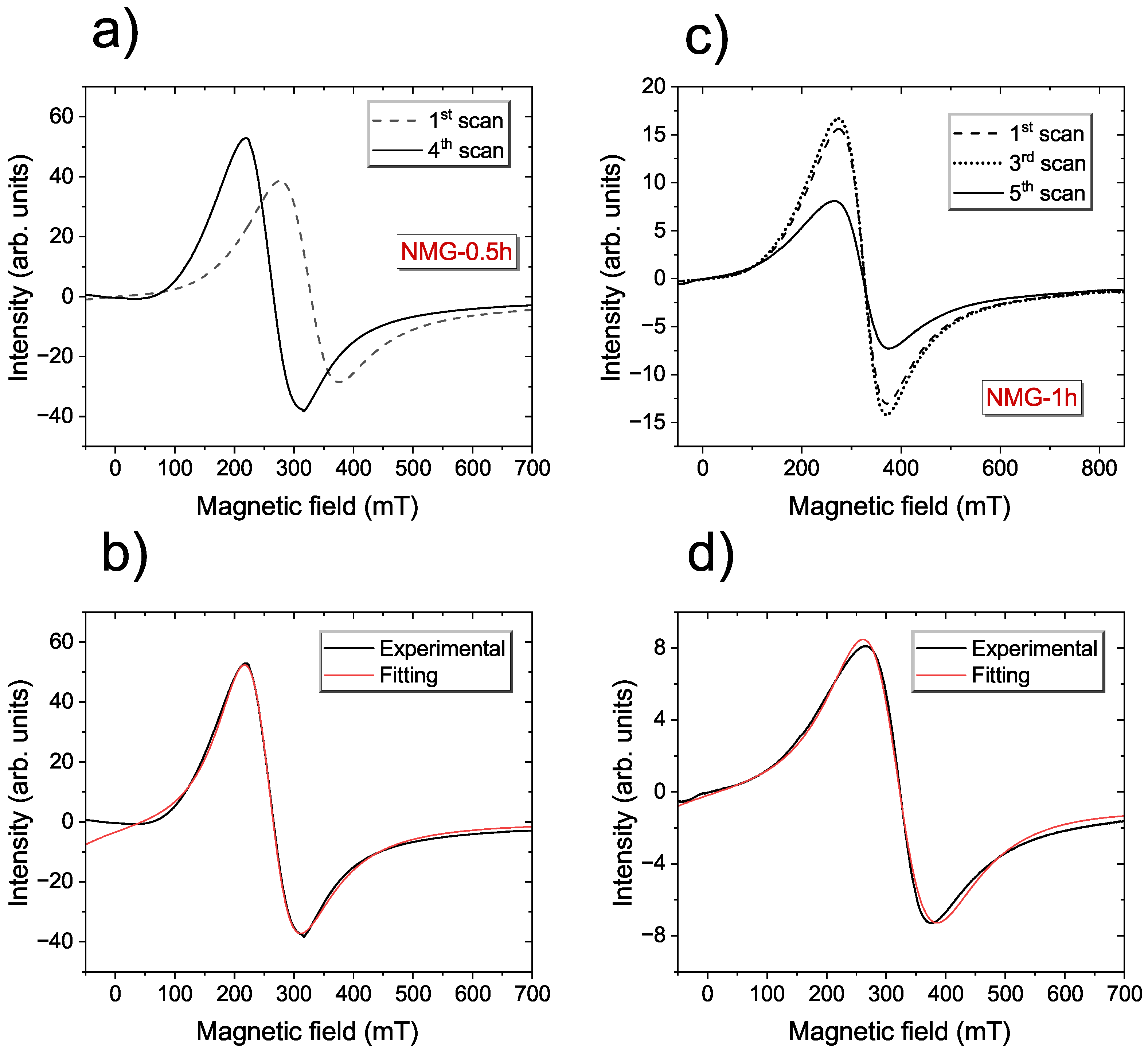
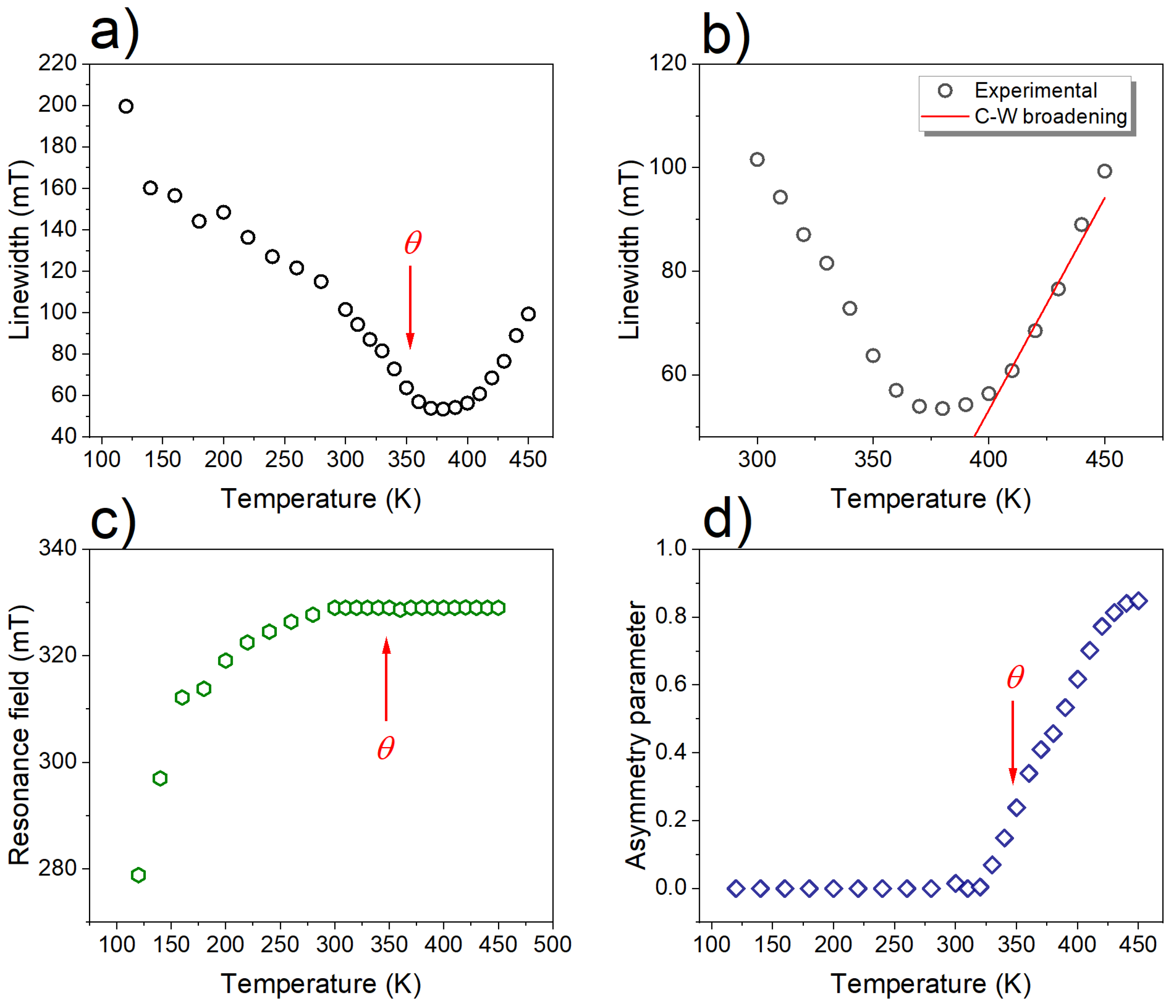
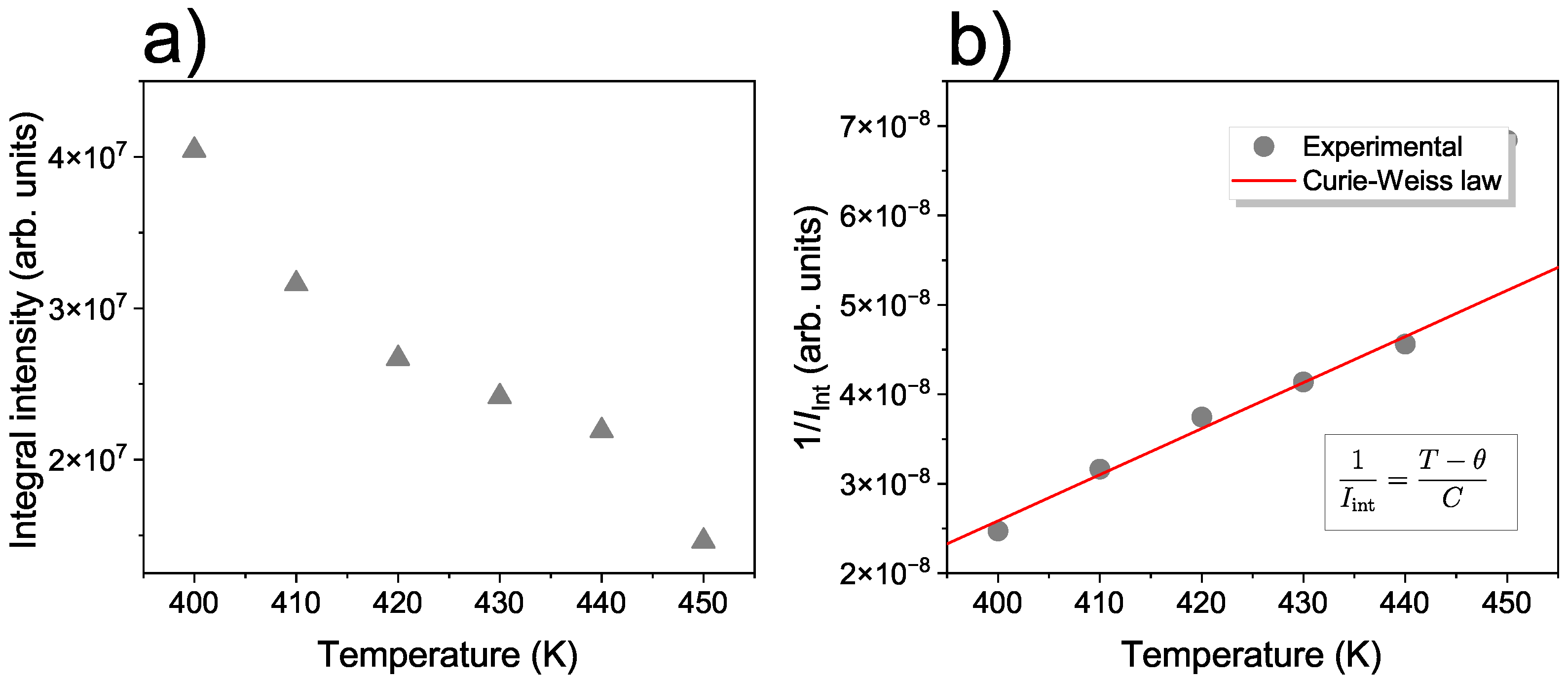
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Webster, P.; Ziebeck, K.; Town, S.; Peak, M. Magnetic order and phase transformation in Ni2MnGa. Philos. Mag. B 1984, 49, 295–310. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Sandratskii, L.; Bruno, P. Role of conduction electrons in mediating exchange interactions in Mn-based Heusler alloys. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 77, 064417. [Google Scholar] [CrossRef]
- Li, C.M.; Luo, H.B.; Hu, Q.M.; Yang, R.; Johansson, B.; Vitos, L. Role of magnetic and atomic ordering in the martensitic transformation of Ni-Mn-In from a first-principles study. Phys. Rev. B—Condens. Matter Mater. Phys. 2012, 86, 214205. [Google Scholar] [CrossRef]
- Chernenko, V.; Cesari, E.; Kokorin, V.; Vitenko, I. The development of new ferromagnetic shape memory alloys in Ni-Mn-Ga system. Scr. Metall. Mater. 1995, 33, 1239–1244. [Google Scholar] [CrossRef]
- Soto, D.; Hernández, F.A.; Flores-Zúñiga, H.; Moya, X.; Mañosa, L.; Planes, A.; Aksoy, S.; Acet, M.; Krenke, T. Phase diagram of Fe-doped Ni-Mn-Ga ferromagnetic shape-memory alloys. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 77, 184103. [Google Scholar] [CrossRef]
- Kanomata, T.; Yasuda, T.; Sasaki, S.; Nishihara, H.; Kainuma, R.; Ito, W.; Oikawa, K.; Ishida, K.; Neumann, K.U.; Ziebeck, K. Magnetic properties on shape memory alloys Ni2Mn1+xIn1−x. J. Magn. Magn. Mater. 2009, 321, 773–776. [Google Scholar] [CrossRef]
- Li, C.M.; Luo, H.B.; Hu, Q.M.; Yang, R.; Johansson, B.; Vitos, L. Site preference and elastic properties of Fe-, Co-, and Cu-doped Ni2MnGa shape memory alloys from first principles. Phys. Rev. B—Condens. Matter Mater. Phys. 2011, 84, 024206. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Sandratskii, L.; Bruno, P. First-principles calculation of the intersublattice exchange interactions and curie temperatures of the full Heusler alloys Ni2Mn X (X = Ga, in, Sn, Sb). Phys. Rev. B—Condens. Matter Mater. Phys. 2004, 70, 024427. [Google Scholar] [CrossRef]
- Zhou, L.; Kammerer, C.; Giri, A.; Cho, K.; Sohn, Y. Microstructural development and ternary interdiffusion in Ni-Mn-Ga alloys. Metall. Mater. Trans. A 2015, 46, 5572–5587. [Google Scholar] [CrossRef]
- Zheng, D.; Li, Z.; Zhang, Y.; Huang, P.; Xu, K.; Jing, C. Magnetostructural transformation and its multiple functional properties for Co-doped Ni56Mn18Ga26 Heusler alloy. J. Alloys Compd. 2017, 694, 532–538. [Google Scholar] [CrossRef]
- Entel, P.; Gruner, M.E.; Acet, M.; Çakır, A.; Arróyave, R.; Duong, T.; Sahoo, S.; Fähler, S.; Sokolovskiy, V.V. Properties and Decomposition of Heusler Alloys. Energy Technol. 2018, 6, 1478–1490. [Google Scholar] [CrossRef]
- Planes, A.; Mañosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter 2009, 21, 233201. [Google Scholar] [CrossRef] [PubMed]
- Kihara, T.; Roy, T.; Xu, X.; Miyake, A.; Tsujikawa, M.; Mitamura, H.; Tokunaga, M.; Adachi, Y.; Eto, T.; Kanomata, T. Observation of inverse magnetocaloric effect in magnetic-field-induced austenite phase of Heusler alloys Ni50−xCoxMn31.5Ga18.5 (x = 9 and 9.7). Phys. Rev. Mater. 2021, 5, 034416. [Google Scholar] [CrossRef]
- Koshkid’ko, Y.S.; Dilmieva, E.; Kamantsev, A.; Cwik, J.; Rogacki, K.; Mashirov, A.; Khovaylo, V.; Mejia, C.S.; Zagrebin, M.; Sokolovskiy, V.; et al. Magnetocaloric effect and magnetic phase diagram of Ni-Mn-Ga Heusler alloy in steady and pulsed magnetic fields. J. Alloys Compd. 2022, 904, 164051. [Google Scholar] [CrossRef]
- Zeng, M.; Or, S.W.; Zhu, Z.; Ho, S.L. Twin-variant reorientation-induced large magnetoresistance effect in Ni50Mn29Ga21 single crystal. J. Appl. Phys. 2010, 108, 053716. [Google Scholar] [CrossRef]
- Ullakko, K.; Huang, J.; Kantner, C.; O’handley, R.; Kokorin, V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett. 1996, 69, 1966–1968. [Google Scholar] [CrossRef]
- Heczko, O. Magnetoelastic coupling in Ni-Mn-Ga magnetic shape memory alloy. In Materials Science Forum; Trans Tech Publications Ltd.: Bäch, Switzerland, 2010; Volume 635, pp. 125–130. [Google Scholar]
- Bhattacharya, K.; James, R.D. The Material Is the Machine. Science 2005, 307, 53–54. [Google Scholar] [CrossRef] [PubMed]
- Wilson, S.A.; Jourdain, R.P.; Zhang, Q.; Dorey, R.A.; Bowen, C.R.; Willander, M.; Wahab, Q.U.; Willander, M.; Al-hilli, S.M.; Nur, O.; et al. New materials for micro-scale sensors and actuators: An engineering review. Mater. Sci. Eng. R Rep. 2007, 56, 1–129. [Google Scholar] [CrossRef]
- Krevet, B.; Pinneker, V.; Kohl, M. A magnetic shape memory foil actuator loaded by a spring. Smart Mater. Struct. 2012, 21, 094013. [Google Scholar] [CrossRef]
- Ullakko, K.; Wendell, L.; Smith, A.; Müllner, P.; Hampikian, G. A magnetic shape memory micropump: Contact-free, and compatible with PCR and human DNA profiling. Smart Mater. Struct. 2012, 21, 115020. [Google Scholar] [CrossRef]
- Barker, S.; Rhoads, E.; Lindquist, P.; Vreugdenhil, M.; Müllner, P. Magnetic shape memory micropump for submicroliter intracranial drug delivery in rats. J. Med. Devices 2016, 10, 041009. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Barandiarán, J.; Lázpita, P.; Segui, C.; Cesari, E. Magnetic properties of a rapidly quenched Ni–Mn–Ga shape memory alloy. Sens. Actuators A Phys. 2006, 129, 163–166. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, C.; Techapiesancharoenkij, R.; Bono, D.; Allen, S.M.; O’Handley, R.C. Microstructure and magnetic properties of melt spinning Ni–Mn–Ga. Intermetallics 2013, 32, 151–155. [Google Scholar] [CrossRef]
- Ullakko, K.; Ezer, Y.; Sozinov, A.; Kimmel, G.; Yakovenko, P.; Lindroos, V. Magnetic-field-induced strains in polycrystalline Ni-Mn-Ga at room temperature. Scr. Mater. 2001, 44, 475–480. [Google Scholar] [CrossRef]
- Gaitzsch, U.; Pötschke, M.; Roth, S.; Rellinghaus, B.; Schultz, L. A 1% magnetostrain in polycrystalline 5M Ni–Mn–Ga. Acta Mater. 2009, 57, 365–370. [Google Scholar] [CrossRef]
- Hürrich, C.; Roth, S.; Wendrock, H.; Pötschke, M.; Cong, D.; Rellinghaus, B.; Schultz, L. Influence of grain size and training temperature on strain of polycrystalline Ni50Mn29Ga21 samples. J. Phys. Conf. Ser. 2011, 303, 012080. [Google Scholar] [CrossRef]
- Laitinen, V.; Sozinov, A.; Saren, A.; Chmielus, M.; Ullakko, K. Characterization of as-built and heat-treated Ni-Mn-Ga magnetic shape memory alloy manufactured via laser powder bed fusion. Addit. Manuf. 2021, 39, 101854. [Google Scholar] [CrossRef]
- Mostafaei, A.; de Vecchis, P.R.; Stevens, E.L.; Chmielus, M. Sintering regimes and resulting microstructure and properties of binder jet 3D printed Ni-Mn-Ga magnetic shape memory alloys. Acta Mater. 2018, 154, 355–364. [Google Scholar] [CrossRef]
- Taylor, S.L.; Shah, R.N.; Dunand, D.C. Ni-Mn-Ga micro-trusses via sintering of 3D-printed inks containing elemental powders. Acta Mater. 2018, 143, 20–29. [Google Scholar] [CrossRef]
- Laitinen, V.; Sozinov, A.; Saren, A.; Salminen, A.; Ullakko, K. Laser powder bed fusion of Ni-Mn-Ga magnetic shape memory alloy. Addit. Manuf. 2019, 30, 100891. [Google Scholar] [CrossRef]
- Huang, M.; Lee, N.; Lee, Y.; Rhee, J.; Dubowik, J. Ferromagnetic resonance of Hensler Ni2 MnGa thin films. J. Korean Vac. Soc. 2003, 12, 116–119. [Google Scholar]
- Kharlan, J.; L’vov, V.; Golub, V. Ferromagnetic resonance in nanotwinned Ni–Mn–Ga film undergoing martensitic transformation. Low Temp. Phys. 2020, 46, 615–621. [Google Scholar] [CrossRef]
- Hoffmann, S.; Ulanov, V. Off-centre dynamic Jahn-Teller effect studied by electron spin relaxation of Cu2+ ions in SrF2 crystal. J. Phys. Condens. Matter 2000, 12, 1855. [Google Scholar] [CrossRef]
- Rudowicz, C.; Misra, S.K. Spin-Hamiltonian formalisms in electron magnetic resonance (EMR) and related spectroscopies. Appl. Spectrosc. Rev. 2001, 36, 11–63. [Google Scholar] [CrossRef]
- Gavriljuk, V.; Dobrinsky, A.; Shanina, B.; Kolesnik, S. A study of the magnetic resonance in a single-crystal Ni50.47Mn28.17Ga21.36 alloy. J. Phys. Condens. Matter 2006, 18, 7613. [Google Scholar] [CrossRef]
- Pandey, S.; Vyzulin, S.; Quetz, A.; Aryal, A.; Dubenko, I.; Granovsky, A.; Stadler, S.; Ali, N. Microwave absorption through the martensitic and Curie transitions in Ni45Cr5Mn37In13. AIP Adv. 2018, 8, 056707. [Google Scholar] [CrossRef]
- Dubiel, Ł.; Żywczak, A.; Maziarz, W.; Stefaniuk, I.; Wal, A. Magnetic Phase Transition and Exchange Bias in Ni45Co5Mn35.5In14.5 Heusler Alloy. Appl. Magn. Reson. 2019, 50, 809–818. [Google Scholar] [CrossRef]
- Abragam, A.; Bleaney, B. Electron Paramagnetic Resonance of Transition Ions; Clarendon P.: Oxford, UK, 1970. [Google Scholar]
- Wilamowski, Z.; Solnica, M.; Michaluk, E.; Havlicek, M.; Jantsch, W. EPR line shape and magnetometry—Chances and pitfalls. Semicond. Sci. Technol. 2011, 26, 064009. [Google Scholar] [CrossRef]
- Rieger, P. Electron Spin Resonance: Analysis and Interpretation; Royal Society of Chemistry: London, UK, 2007. [Google Scholar]
- Eaton, G.R.; Eaton, S.S.; Barr, D.P.; Weber, R.T. Quantitative EPR; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Dubiel, Ł.; Wal, A.; Stefaniuk, I.; Żywczak, A.; Maziarz, W. Electron magnetic resonance study of the Ni47Co3Mn35.5In14.5 ribbons. J. Magn. Magn. Mater. 2021, 530, 167930. [Google Scholar] [CrossRef]
- Maziarz, W.; Czaja, P.; Chulist, R.; Wójcik, A.; Żrodowski, Ł.; Morończyk, B.; Wróblewski, R.; Kowalczyk, M. Microstructure and Magnetic Properties of Selected Laser Melted Ni-Mn-Ga and Ni-Mn-Ga-Fe Powders Derived from as Melt-Spun Ribbons Precursors. Metals 2021, 11, 903. [Google Scholar] [CrossRef]
- Czaja, P.; Chulist, R.; Wójcik, A.; Kowalczyk, M.; Zackiewicz, P.; Szewczyk, A.; Schell, N.; Maziarz, W. Suppression and Recovery of Martensitic Transformation and Magnetism in Mechanically and Thermally Treated Magnetic Shape-Memory Ni-Mn-Ga Melt-Spun Ribbons. Adv. Eng. Mater. 2021, 23, 2100075. [Google Scholar] [CrossRef]
- Barnes, S. Theory of electron spin resonance of magnetic ions in metals. Adv. Phys. 1981, 30, 801–938. [Google Scholar] [CrossRef]
- Ivanshin, V.A.; Deisenhofer, J.; Krug von Nidda, H.A.; Loidl, A.; Mukhin, A.A.; Balbashov, A.M.; Eremin, M.V. ESR study in lightly doped La1−xSrxMnO3. Phys. Rev. B 2000, 61, 6213–6219. [Google Scholar] [CrossRef]
- Shanina, B.; Konchits, A.; Kolesnik, S.; Gavriljuk, V.; Glavatskij, I.; Glavatska, N.; Söderberg, O.; Lindroos, V.; Foct, J. Ferromagnetic resonance in non-stoichiometric Ni1−x−yMnxGay. J. Magn. Magn. Mater. 2001, 237, 309–326. [Google Scholar] [CrossRef]
- Vasyukov, V.; D’yakonov, V.; Shapovalov, V.; Aksimentyeva, E.; Szymczak, H.; Piechota, S. Temperature-induced change in the ESR spectrum of the Fe3+ ion in polyaniline. Low Temp. Phys. 2000, 26, 265–269. [Google Scholar] [CrossRef]
- Muralidhara, R.; Kesavulu, C.; Rao, J.; Anavekar, R.; Chakradhar, R. EPR and optical absorption studies of Fe3+ ions in sodium borophosphate glasses. J. Phys. Chem. Solids 2010, 71, 1651–1655. [Google Scholar] [CrossRef]
- Vasyukov, V. Manifestation of non-centrality effect in the EPR spectrum of Fe3+ ion in the polycrystalline materials. J. Phys. Conf. Ser. 2011, 324, 012024. [Google Scholar] [CrossRef]
- Parekh, K.; Upadhyay, R. Magnetization dynamics in rare earth Gd3+ doped Mn0.5Zn0.5Fe2O4 magnetic fluid: Electron spin resonance study. J. Magn. Reson. 2012, 225, 46–51. [Google Scholar] [CrossRef]
- Mozurkewich, G.; Elliott, J.; Hardiman, M.; Orbach, R. Exchange-narrowed anisotropy contribution to the EPR width and shift in the Ag-Mn spin-glass. Phys. Rev. B 1984, 29, 278. [Google Scholar] [CrossRef]
- Long, S.; Zhou, P.; Miller, J.S.; Epstein, A. Electron Spin Resonance Study of the Disorder in the V(TCNE)x·y(MeCN) High-Tc Molecule-Based Magnet. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1995, 272, 207–215. [Google Scholar] [CrossRef]
- Stewart, A. Simple Theory of the? Negative Residual Linewidth? in Reflection Spectroscopy of Magnetically Concentrated Local Moment Systems. Aust. J. Phys. 1980, 33, 1049–1054. [Google Scholar] [CrossRef][Green Version]
- Wolos, A.; Drabinska, A.; Borysiuk, J.; Sobczak, K.; Kaminska, M.; Hruban, A.; Strzelecka, S.G.; Materna, A.; Piersa, M.; Romaniec, M.; et al. High-spin configuration of Mn in Bi2Se3 three-dimensional topological insulator. J. Magn. Magn. Mater. 2016, 419, 301–308. [Google Scholar] [CrossRef]
- Graf, T.; Gjukic, M.; Hermann, M.; Brandt, M.S.; Stutzmann, M.; Ambacher, O. Spin resonance investigations of Mn2+ in wurtzite GaN and AlN films. Phys. Rev. B 2003, 67, 165215. [Google Scholar] [CrossRef]
- Deisenhofer, J.; von Nidda, H.A.K.; Loidl, A.; Sampathkumaran, E. ESR investigation of the spin dynamics in (Gd1−xYx)2PdSi3. Solid State Commun. 2003, 125, 327–331. [Google Scholar] [CrossRef][Green Version]

| Label | Composition | Milling Time in Hour |
|---|---|---|
| NMG-05 | 0.5 | |
| NMG-1 | 1 | |
| NMG-2 | 2 | |
| NMG-8 | 8 |
| Label | (mT) | (mT) | (K) | n |
|---|---|---|---|---|
| NMG-2 | 128 | 449 | 348 | 2 |
| NMG-8 | 104 | 183 | 364 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubiel, Ł.; Cieniek, B.; Maziarz, W.; Stefaniuk, I. Electron Magnetic Resonance Study of Ni50.2Mn28.3Ga21.5 Powders. Materials 2024, 17, 4391. https://doi.org/10.3390/ma17174391
Dubiel Ł, Cieniek B, Maziarz W, Stefaniuk I. Electron Magnetic Resonance Study of Ni50.2Mn28.3Ga21.5 Powders. Materials. 2024; 17(17):4391. https://doi.org/10.3390/ma17174391
Chicago/Turabian StyleDubiel, Łukasz, Bogumił Cieniek, Wojciech Maziarz, and Ireneusz Stefaniuk. 2024. "Electron Magnetic Resonance Study of Ni50.2Mn28.3Ga21.5 Powders" Materials 17, no. 17: 4391. https://doi.org/10.3390/ma17174391
APA StyleDubiel, Ł., Cieniek, B., Maziarz, W., & Stefaniuk, I. (2024). Electron Magnetic Resonance Study of Ni50.2Mn28.3Ga21.5 Powders. Materials, 17(17), 4391. https://doi.org/10.3390/ma17174391









