Theoretical Analysis of Stacking Fault Energy, Elastic Properties, Electronic Properties, and Work Function of MnxCoCrFeNi High-Entropy Alloy
Abstract
1. Introduction
2. Methods and Details
2.1. First-Principles Calculations
2.2. VCA Models
2.3. Stacking Fault Model and GSFE
2.4. Surface Energies
3. Results and Discussion
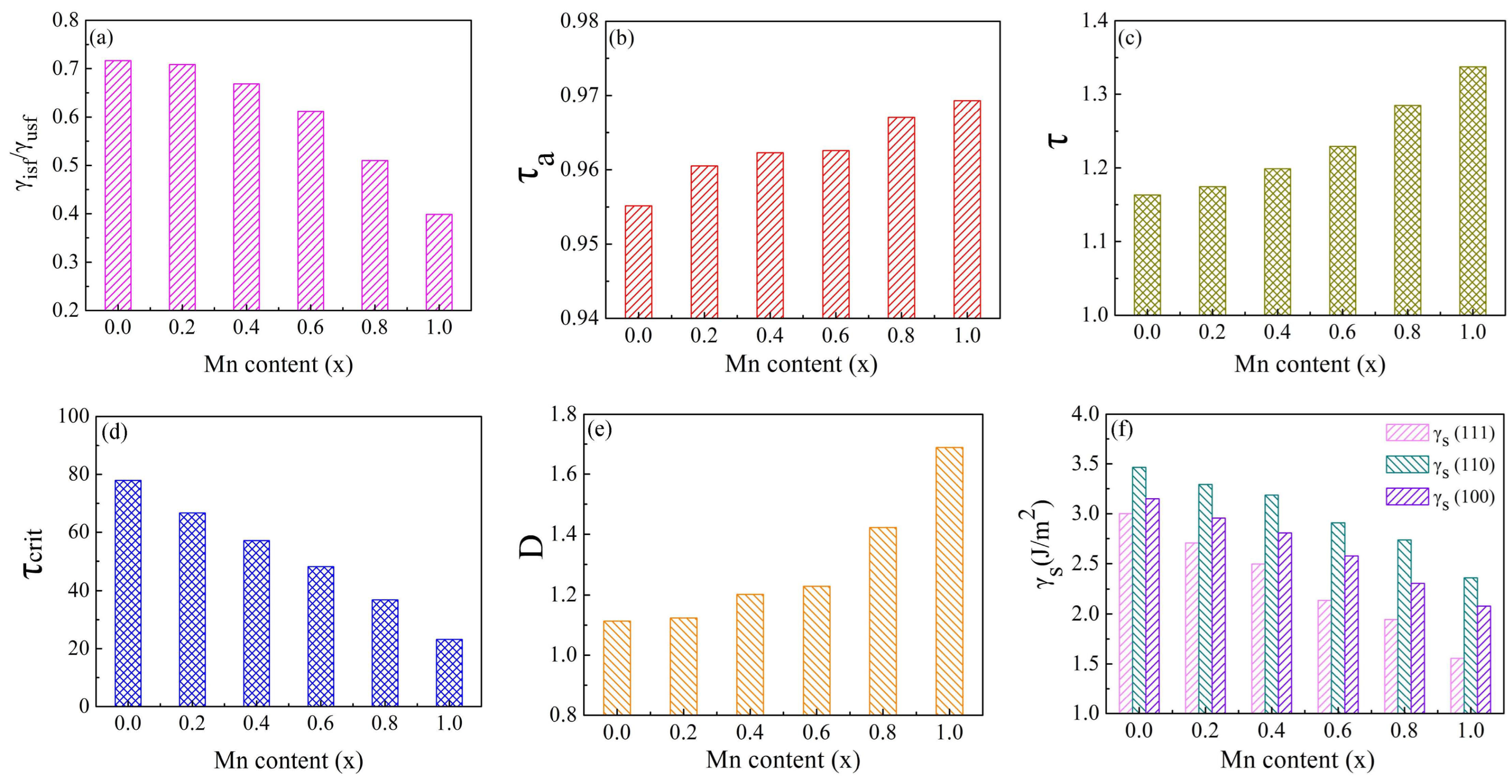
3.1. GSFE and Surface Energies
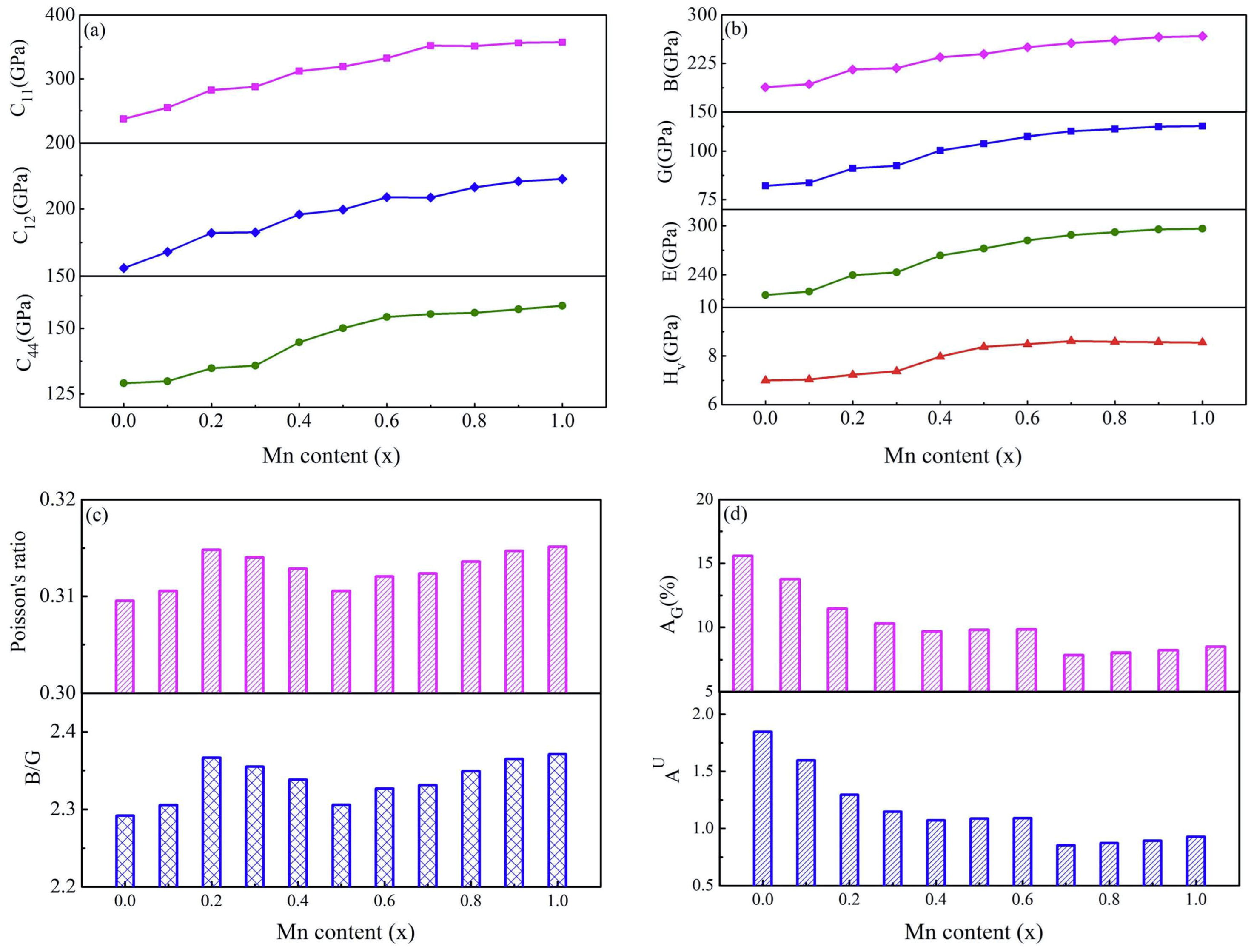
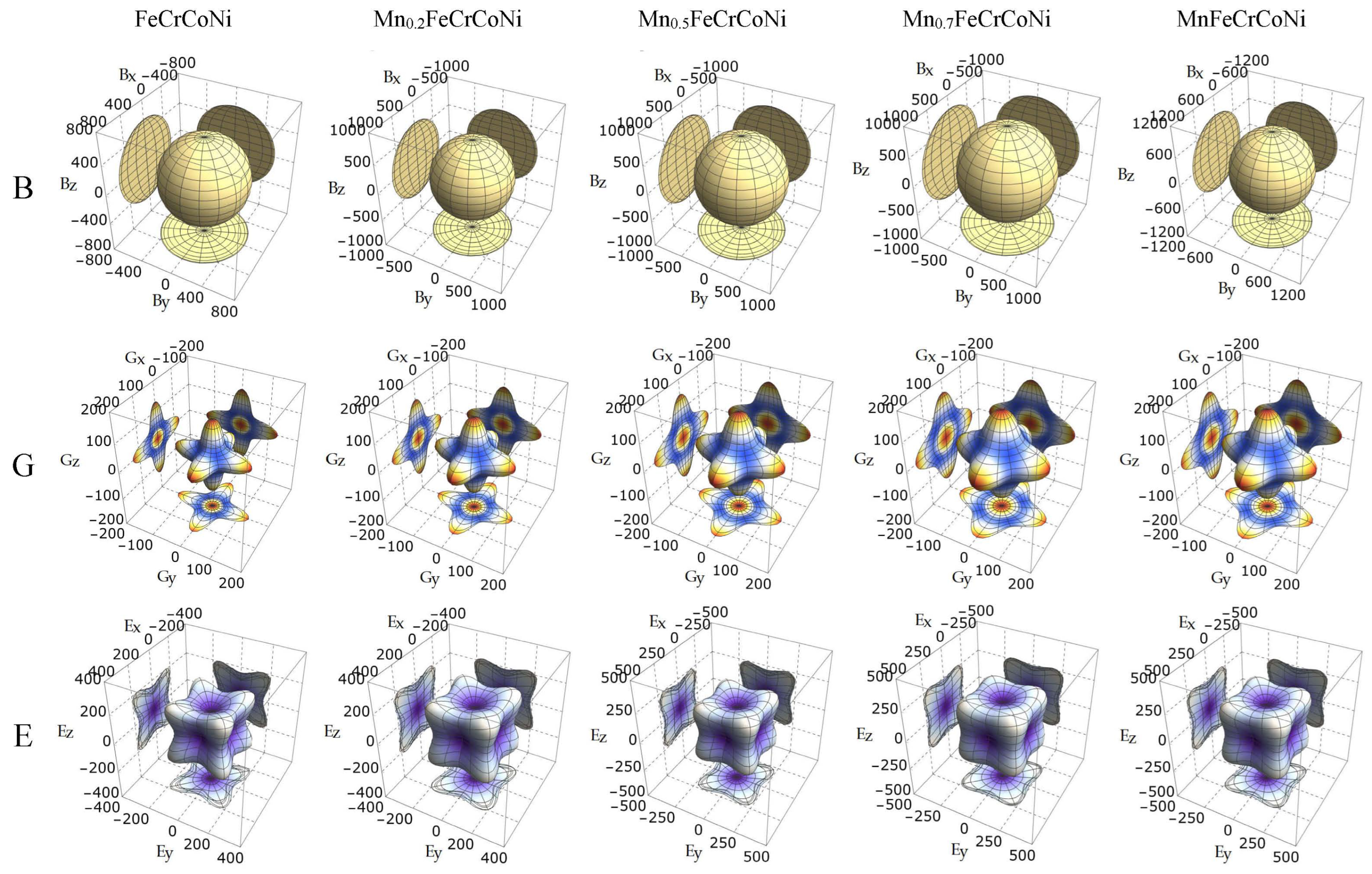
3.2. Elastic Properties
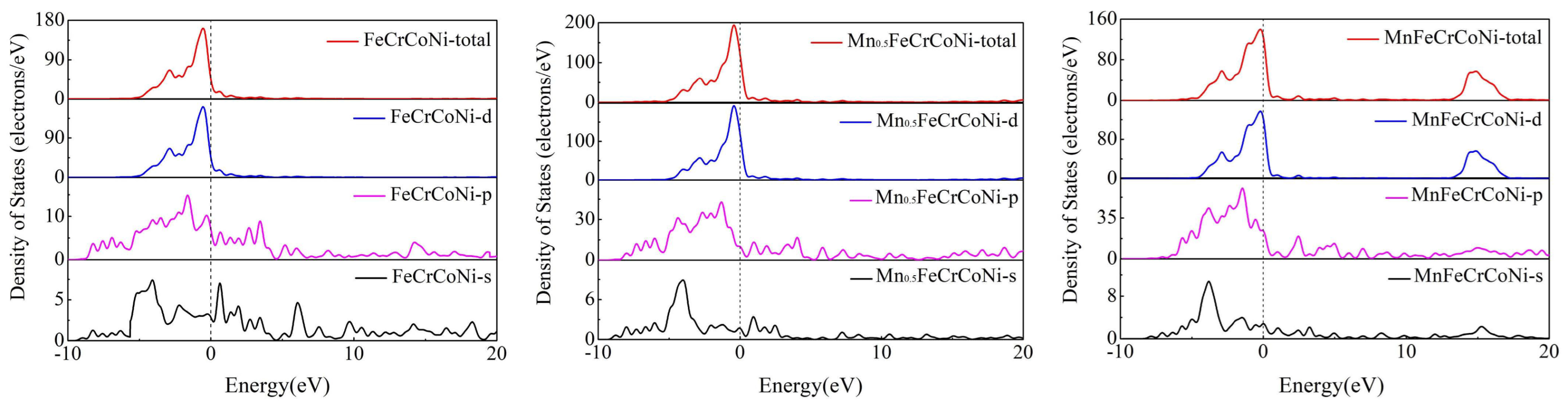
3.3. Electronic Properties
3.4. Work Function
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chan, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Liu, W.H.; Lu, Z.P.; He, J.Y.; Luan, J.H.; Wang, Z.J.; Liu, B.; Liu, Y.; Chen, M.W.; Liu, C.T. Ductile CoCrFeNiMox high entropy alloys strengthened by hard intermetallic phases. Acta Mater. 2016, 116, 332–342. [Google Scholar] [CrossRef]
- Tao, L.; Sun, M.; Zhou, Y.; Luo, M.; Lv, F.; Li, M.; Zhang, Q.; Gu, L.; Huang, B.; Guo, S. A general synthetic method for high-entropy alloy subnanometer ribbons. J. Am. Chem. Soc. 2022, 144, 10582–10590. [Google Scholar] [CrossRef]
- Tsai, K.Y.; Tsai, M.H.; Yeh, J.W. Sluggish diffusion in Co-Cr-Fe-Mn-Ni high-entropy alloys. Acta Mater. 2013, 61, 4887–4897. [Google Scholar] [CrossRef]
- Cao, B.; Wang, C.; Yang, T.; Liu, C. Cocktail effects in understanding the stability and properties of face-centered-cubic high-entropy alloys at ambient and cryogenic temperatures. Scr. Mater. 2020, 187, 250–255. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.; Fang, Q.; Jiang, C.; Liu, Y.; Liaw, P.K. Unraveling the dislocation–precipitate interactions in high-entropy alloys. Int. J. Plast. 2020, 133, 102819. [Google Scholar] [CrossRef]
- Ding, Q.; Zhang, Y.; Chen, X.; Fu, X.; Chen, D.; Chen, S.; Gu, L.; Wei, F.; Bei, H.; Gao, Y.; et al. Tuning element distribution, structure and properties by composition in high-entropy alloys. Nature 2019, 574, 223–227. [Google Scholar] [CrossRef]
- Ma, E. Unusual dislocation behavior in high-entropy alloys. Scr. Mater. 2020, 181, 127–133. [Google Scholar] [CrossRef]
- Qin, G.; Chen, R.; Liaw, P.K.; Gao, Y.; Li, X.; Zheng, H.; Wang, L.; Su, Y.; Guo, J.; Fu, H. A novel face-centered-cubic high-entropy alloy strengthened by nanoscale precipitates. Scr. Mater. 2019, 172, 51–55. [Google Scholar] [CrossRef]
- Yan, X.H.; Zhang, Y. Functional properties and promising applications of high entropy alloys. Scr. Mater. 2020, 187, 188–193. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Zhang, H.; Lu, S.; Ding, X.D.; Wang, Y.Z.; Vitos, L. Phase selection rule for Al-doped CrMnFeCoNi high-entropy alloys from first-principles. Acta Mater. 2017, 140, 366–374. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, X.; Lu, S.; Dong, Z.; Ding, X.; Wang, Y.; Vitos, L. Elastic properties of AlxCrMnFeCoNi (0 ≤ x ≤ 5) high-entropy alloys from ab initio theory. Acta Mater. 2018, 155, 12–22. [Google Scholar] [CrossRef]
- Shi, Y.Z.; Collins, L.; Feng, R.; Zhang, C.; Balke, N.; Liaw, P.K.; Yang, B. Homogenization of AlxCoCrFeNi high-entropy alloys with improved corrosion resistance. Corros. Sci. 2018, 133, 120–131. [Google Scholar] [CrossRef]
- Zhang, J.; Xiong, K.; Huang, L.; Xie, B.; Ren, D.; Tang, C.; Feng, W. Effect of Doping with Different Nb Contents on the Properties of CoCrFeNi High-Entropy Alloys. Materials 2023, 16, 6407. [Google Scholar] [CrossRef]
- Kivy, M.B.; Zaeem, M.A. Generalized stacking fault energies, ductilities, and twinnabilities of CoCrFeNi-based face-centered cubic high entropy alloys. Scr. Mater. 2017, 139, 83–86. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.G. First-principles calculations of generalized-stacking-fault-energy of Co-based alloys. Comput. Mater. Sci. 2016, 121, 86–96. [Google Scholar] [CrossRef]
- Liu, S.F.; Wu, Y.; Wang, H.T.; He, J.Y.; Liu, J.B.; Chen, C.X.; Liu, X.J.; Wang, H.; Lu, Z.P. Stacking fault energy of face-centered-cubic high entropy alloys. Intermetallics 2018, 93, 269–273. [Google Scholar] [CrossRef]
- Lu, J.; Hultman, L.; Holmström, E.; Antonsson, K.H.; Grehk, M.; Li, W.; Vitos, L.; Golpayegani, A. Stacking fault energies in austenitic stainless steels. Acta Mater. 2016, 111, 39–46. [Google Scholar] [CrossRef]
- Xu, X.; Liu, P.; Tang, Z.; Hirata, A.; Song, S.; Nieh, T.; Liaw, P.; Liu, C.; Chen, M. Transmission electron microscopy characterization of dislocation structure in a face-centered cubic high-entropy alloy Al0.1CoCrFeNi. Acta Mater. 2018, 144, 107–115. [Google Scholar] [CrossRef]
- Ullrich, C.; Eckner, R.; Krüger, L.; Martin, S.; Klemm, V.; Rafaja, D. Interplay of microstructure defects in austenitic steel with medium stacking fault energy. Mater. Sci. Eng. A 2016, 649, 390–399. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Chen, J.; Wu, C.; Kormout, K.S.; Ghosh, P.; Zhang, Z. On the stacking fault energy related deformation mechanism of nanocrystalline Cu and Cu alloys: A first-principles and TEM study. J. Alloys Compd. 2019, 776, 807–818. [Google Scholar] [CrossRef]
- Mayahi, R. An investigation concerning generalized stacking fault behavior of AlCoxCrFeNi (0.25 ≤ x ≤ 2) high entropy alloys: Insights from first-principles study. J. Alloys Compd. 2020, 818, 152928. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, J.; Fang, Q.; Feng, H. Effect of Al solute concentration on mechanical properties of AlxFeCuCrNi high entropy alloys: A first-principles study. Phys. B 2019, 566, 30–37. [Google Scholar] [CrossRef]
- Nong, Z.S.; Lei, Y.N.; Zhu, J.C. Wear and oxidation resistances of AlCrFeNiTi-based high entropy alloys. Intermetallics 2018, 101, 144–151. [Google Scholar] [CrossRef]
- Pan, Y.; Pu, D. First-principles investigation of oxidation behavior of Mo5SiB2. Ceram. Int. 2020, 46, 6698–6702. [Google Scholar] [CrossRef]
- Mitro, S.K.; Hossain, K.M.; Majumder, R.; Hasan, M.Z. Effect of the negative chemical pressure on physical properties of doped perovskite molybdates in the framework of DFT method. J. Alloys Compd. 2021, 854, 157088. [Google Scholar] [CrossRef]
- Vu, V.T.; Lavrentyev, A.A.; Gabrelian, B.V.; Parasyuk, O.V.; Ocheretova, V.A.; Khyzhun, O.Y. Electronic structure and optical properties of Ag2HgSnSe4: First-principles DFT calculations and X-ray spectroscopy studies. J. Alloys Compd. 2018, 732, 372–384. [Google Scholar] [CrossRef]
- Peivaste, I.; Alahyarizadeh, G.; Minuchehr, A.; Aghaie, M. Comparative study on mechanical properties of three different SiCpolytypes (3C, 4H and 6H) under high pressure: First-principle calculations. Vacuum 2018, 154, 37–43. [Google Scholar] [CrossRef]
- Chen, J.Y.; Zhang, X.D.; Ying, C.H.; Ma, H.; Li, J.; Wang, F.; Guo, H. The influence of vacancy defects on elastic and electronic properties of TaSi (5/3) desilicides from a first-principles calculations. Ceram. Int. 2020, 46, 10992–10999. [Google Scholar] [CrossRef]
- Pang, X.Z.; Yang, W.C.; Yang, J.B.; Pang, M.J.; Zhan, Y.Z. Atomic structure, stability and electronic properties of S(Al2CuMg)/Al interface: A first-principles study. Intermetallics 2018, 93, 329–337. [Google Scholar] [CrossRef]
- Chen, S.; Pan, Y.; Wang, D.; Deng, H. Structural stability and electronic and optical properties of bulk WS2 from first-principles investigations. Mat. Sci. Eng. B-Solid. 2020, 259, 114580. [Google Scholar] [CrossRef]
- Zaddach, A.J.; Niu, C.; Koch, C.C.; Irving, D.L. Mechanical properties and stacking fault energies of NiFeCrCoMn high-entropy alloy. Jom 2013, 65, 1780–1789. [Google Scholar] [CrossRef]
- Li, X.; Irving, D.L.; Vitos, L. First-principles investigation of the micromechanical properties of fcc-hcp polymorphic high-entropy alloys. Sci. Rep. 2018, 8, 11196. [Google Scholar] [CrossRef]
- Cantor, B. Multicomponent and high entropy alloys. Entropy 2014, 16, 4749–4768. [Google Scholar] [CrossRef]
- Udagawa, Y.; Yamaguchi, M.; Abe, H.; Sekimura, N.; Fuketa, T. Ab initio study on plane defects in zirconium-hydrogen solid solution and zirconium hydride. Acta Mater. 2010, 58, 3927–3938. [Google Scholar] [CrossRef]
- Swygenhoven, H.V.; Derlet, P.M.; Frøseth, A.G. Stacking fault energies and slip in nanocrystalline metals. Nat. Mater. 2004, 3, 399–403. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Hai, S. A Peierls criterion for the onset of deformation twinning at a crack tip. J. Mech. Phys. Solids 2003, 51, 765–779. [Google Scholar] [CrossRef]
- Asaro, R.J.; Suresh, S. Mechanistic models for the activation volume and rate sensitivity in metals with nanocrystalline grains and nano-scale twins. Acta Mater. 2005, 53, 3369–3382. [Google Scholar] [CrossRef]
- Kibey, S.; Liu, J.B.; Johnson, D.D.; Sehitoglu, H. Predicting twinning stress in fcc metals: Linking twin-energy pathways to twin nucleation. Acta Mater. 2007, 55, 6843–6851. [Google Scholar] [CrossRef]
- Rice, J.R. Dislocation nucleation from a crack tip an analysis based on the Peierls concept. J. Mech. Phys. Solids 1992, 40, 239–271. [Google Scholar] [CrossRef]
- Wen, Z.Q.; Zhao, Y.H.; Hou, H.; Wang, B.; Han, P.D. The mechanical and thermodynamic properties of Heusler compounds Ni2XAl (X = Sc, Ti, V) under pressure and temperature: A first-principles study. Mater. Des. 2017, 114, 398–403. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, G.; Liu, H.; Xu, H.; Fu, Y.; Li, D. Effect of transition-elements substitution on mechanical properties and electronic structures of B2-AlCu compounds. Results Phys. 2021, 21, 103765. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, G.; Ren, X.; Wang, M.; Xu, H.; Fu, Y.; Tang, Y.; Li, D. First-principles studies on phase stability, anisotropic elastic and electronic properties of Al-La binary system intermetallic compounds. Mater. Today Commun. 2020, 24, 101101. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Lu, H.; Liu, Z.; Yan, X.; Li, D.; Parent, L.; Tian, H. Electron work function-a promising guiding parameter for material design. Sci. Rep. 2016, 6, 24366. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |
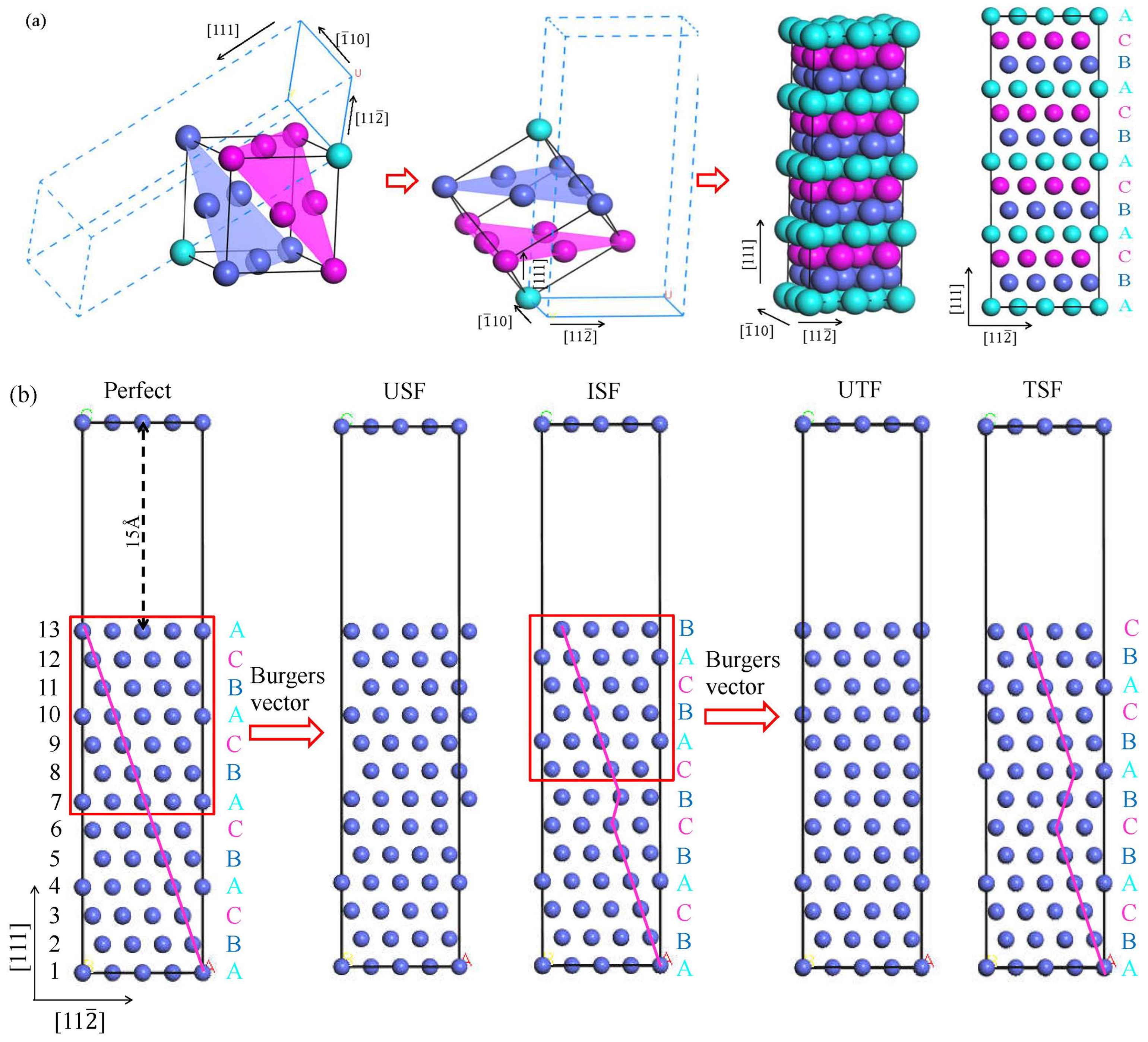
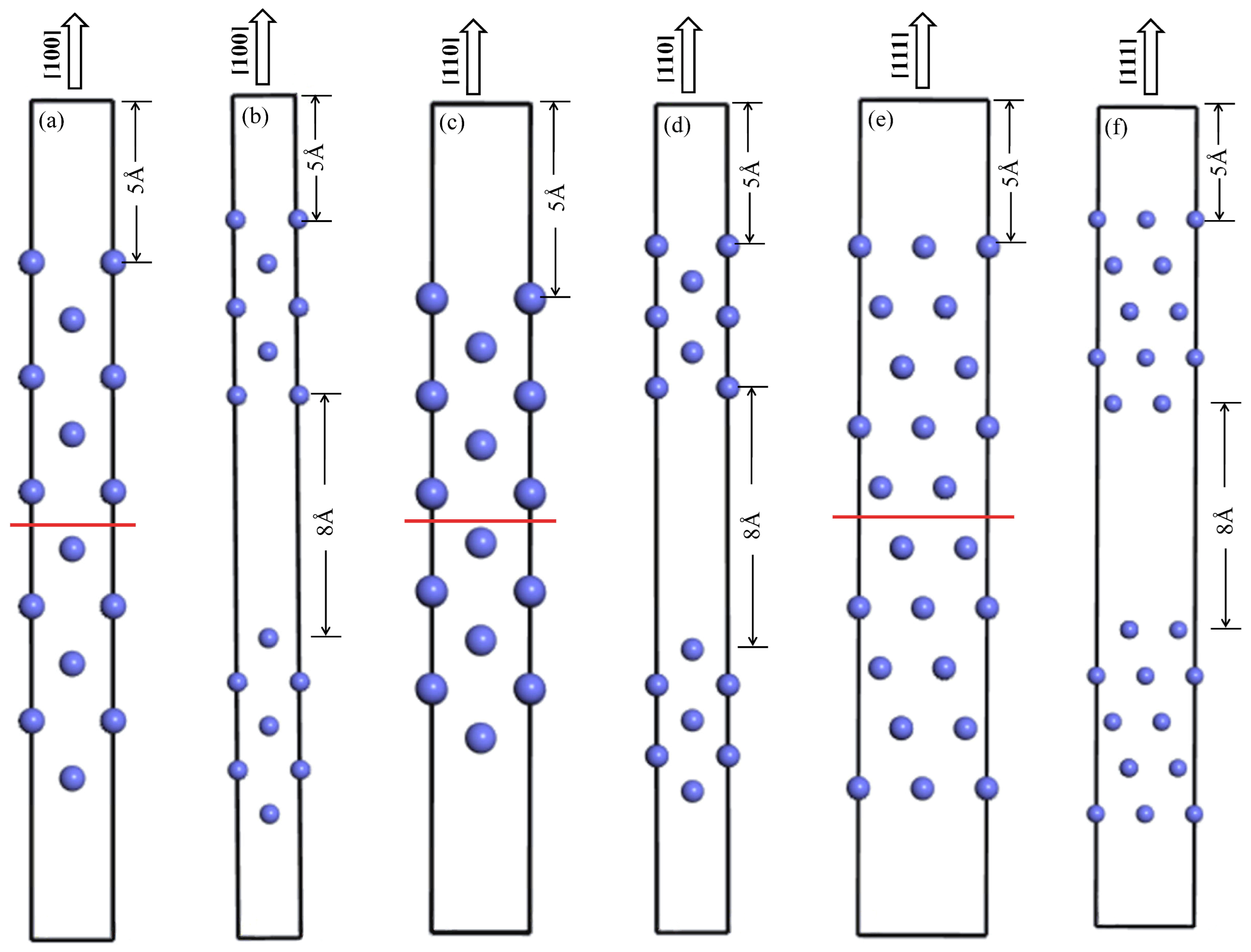



| HEAs | Mn (at.%) | Co (at.%) | Cr (at.%) | Fe (at.%) | Ni (at.%) |
|---|---|---|---|---|---|
| CoCrFeNi | 0 | 25.0 | 25.0 | 25.0 | 25.0 |
| Mn0.2CoCrFeNi | 2.4 | 24.4 | 24.4 | 24.4 | 24.4 |
| Mn0.4CoCrFeNi | 9.2 | 22.7 | 22.7 | 22.7 | 22.7 |
| Mn0.6CoCrFeNi | 13.2 | 21.7 | 21.7 | 21.7 | 21.7 |
| Mn0.8CoCrFeNi | 16.8 | 20.8 | 20.8 | 20.8 | 20.8 |
| MnCoCrFeNi | 20.0 | 20.0 | 20.0 | 20.0 | 20.0 |
| HEAs | a | |||
|---|---|---|---|---|
| CoCrFeNi | 3.415 | 3.540 [34] | 3.529 [35] | 3.575 [34] |
| MnCoCrFeNi | 3.517 | 3.540 [34] | 3.529 [35] | 3.597 [34] |
| 3.59 [36] |
| HEAs(x) | γusf | γisf | γutf | 2γtsf | γisf/γusf | γutf/γusf | D | γs(111) | γs(110) | γs(100) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 808.84 | 578.93 | 935.74 | 574.71 | 126.90 | 0.716 | 1.157 | 1.113 | 3.002 | 3.465 | 3.150 |
| 0.2 | 722.68 | 511.42 | 829.74 | 490.12 | 107.06 | 0.708 | 1.148 | 1.123 | 2.706 | 3.292 | 2.955 |
| 0.4 | 622.57 | 416.32 | 720.54 | 389.04 | 97.96 | 0.669 | 1.157 | 1.202 | 2.495 | 3.187 | 2.807 |
| 0.6 | 521.78 | 319.25 | 613.32 | 288.60 | 91.55 | 0.612 | 1.175 | 1.229 | 2.137 | 2.909 | 2.576 |
| 0.8 | 410.07 | 209.17 | 491.73 | 169.97 | 81.66 | 0.510 | 1.199 | 1.423 | 1.945 | 2.737 | 2.307 |
| 1.0 | 276.17 | 110.04 | 340.21 | 60.36 | 64.05 | 0.398 | 1.232 | 1.689 | 1.555 | 2.363 | 2.080 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, F.; Zhang, G.; Xu, H.; Li, D.; Fu, Y. Theoretical Analysis of Stacking Fault Energy, Elastic Properties, Electronic Properties, and Work Function of MnxCoCrFeNi High-Entropy Alloy. Materials 2024, 17, 4378. https://doi.org/10.3390/ma17174378
Sun F, Zhang G, Xu H, Li D, Fu Y. Theoretical Analysis of Stacking Fault Energy, Elastic Properties, Electronic Properties, and Work Function of MnxCoCrFeNi High-Entropy Alloy. Materials. 2024; 17(17):4378. https://doi.org/10.3390/ma17174378
Chicago/Turabian StyleSun, Fenger, Guowei Zhang, Hong Xu, Dongyang Li, and Yizheng Fu. 2024. "Theoretical Analysis of Stacking Fault Energy, Elastic Properties, Electronic Properties, and Work Function of MnxCoCrFeNi High-Entropy Alloy" Materials 17, no. 17: 4378. https://doi.org/10.3390/ma17174378
APA StyleSun, F., Zhang, G., Xu, H., Li, D., & Fu, Y. (2024). Theoretical Analysis of Stacking Fault Energy, Elastic Properties, Electronic Properties, and Work Function of MnxCoCrFeNi High-Entropy Alloy. Materials, 17(17), 4378. https://doi.org/10.3390/ma17174378






