The Effect of In Concentration and Temperature on Dissolution and Precipitation in Sn–Bi Alloys
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
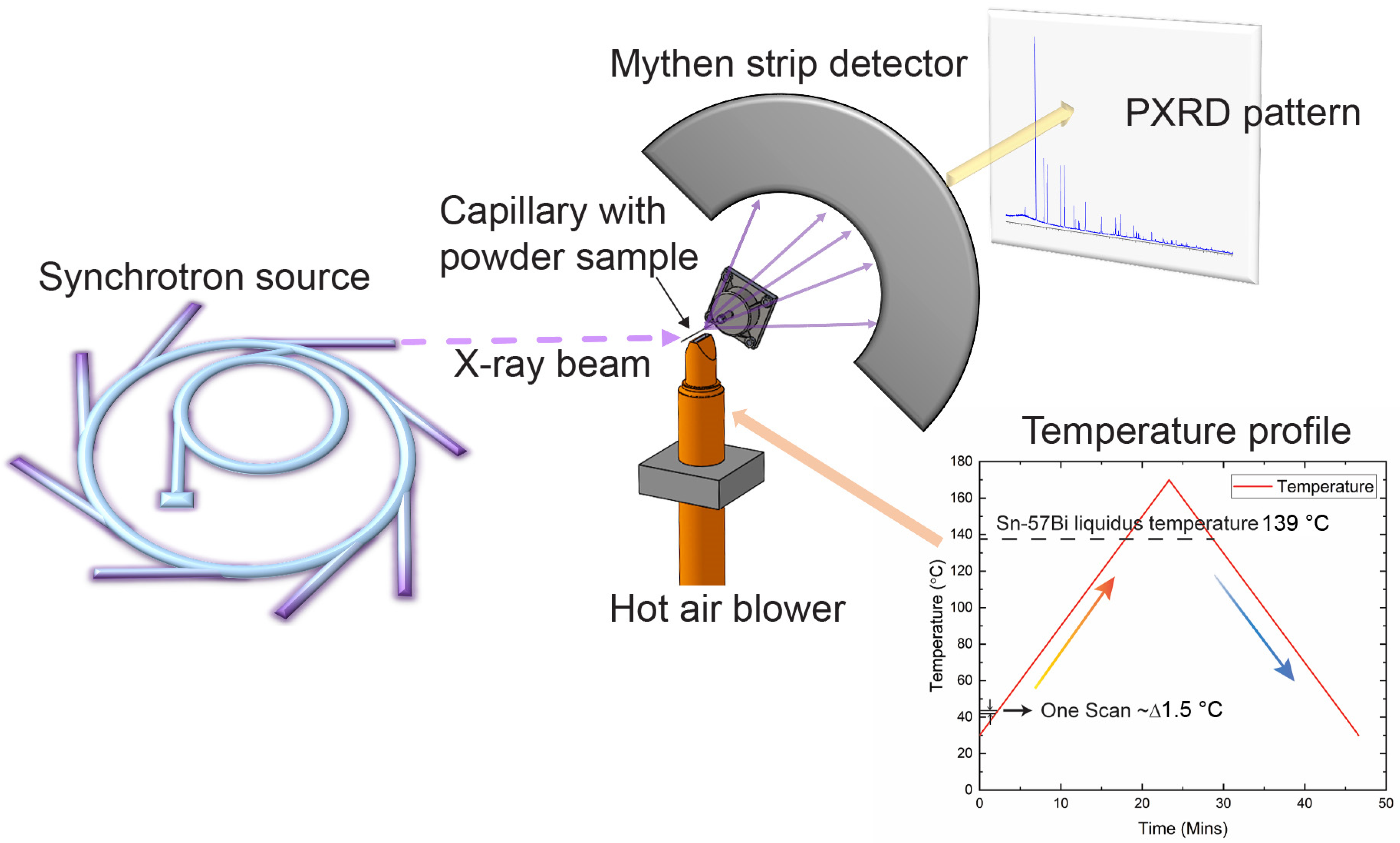
2.2. Material Characterisation
2.3. DFT Calculation
3. Results and Discussion
3.1. Microstructure
3.2. Cooling Curve Analysis
3.3. In Situ Synchrotron PXRD
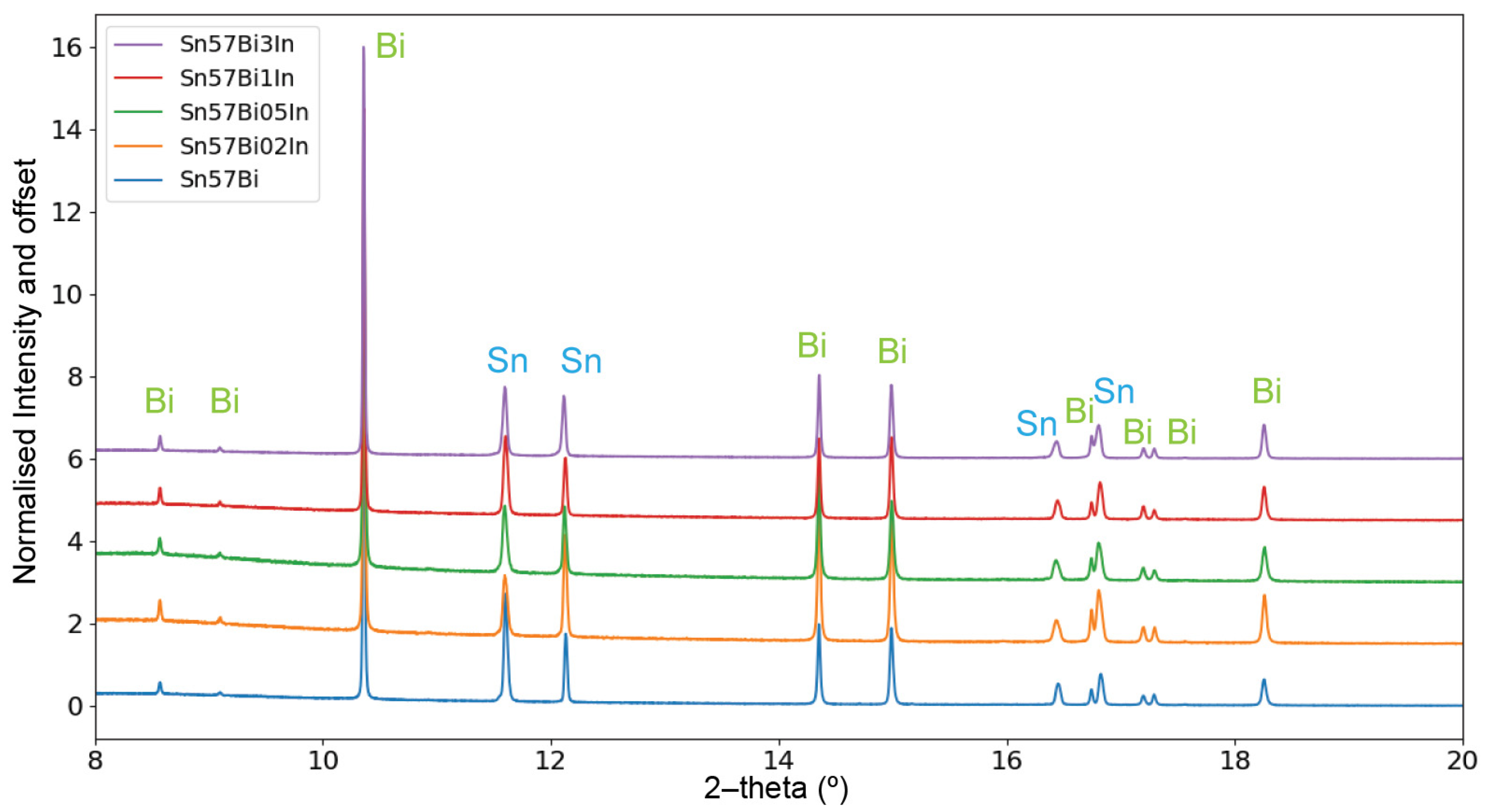
3.3.1. PXRD Patterns at Room Temperature
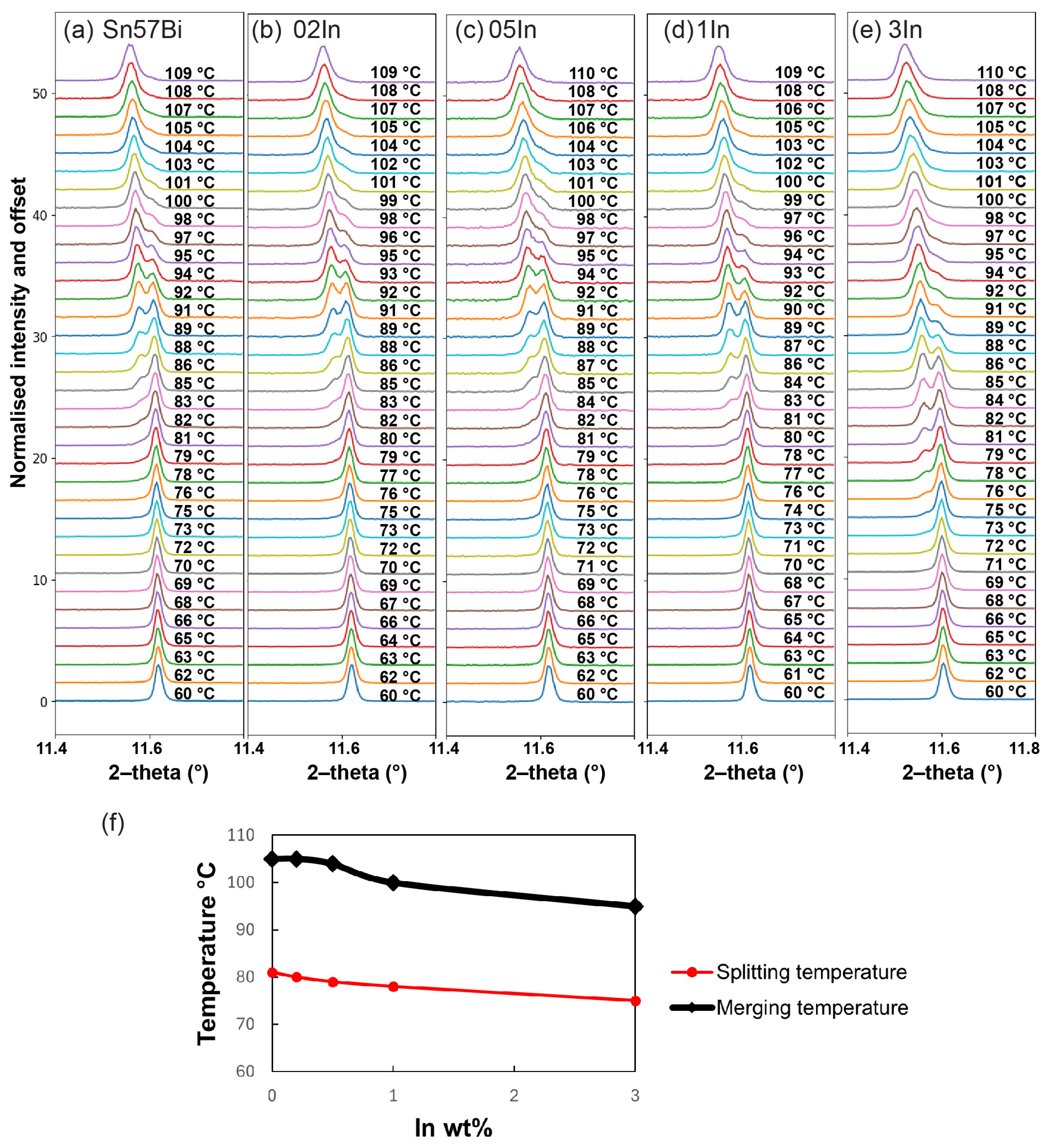
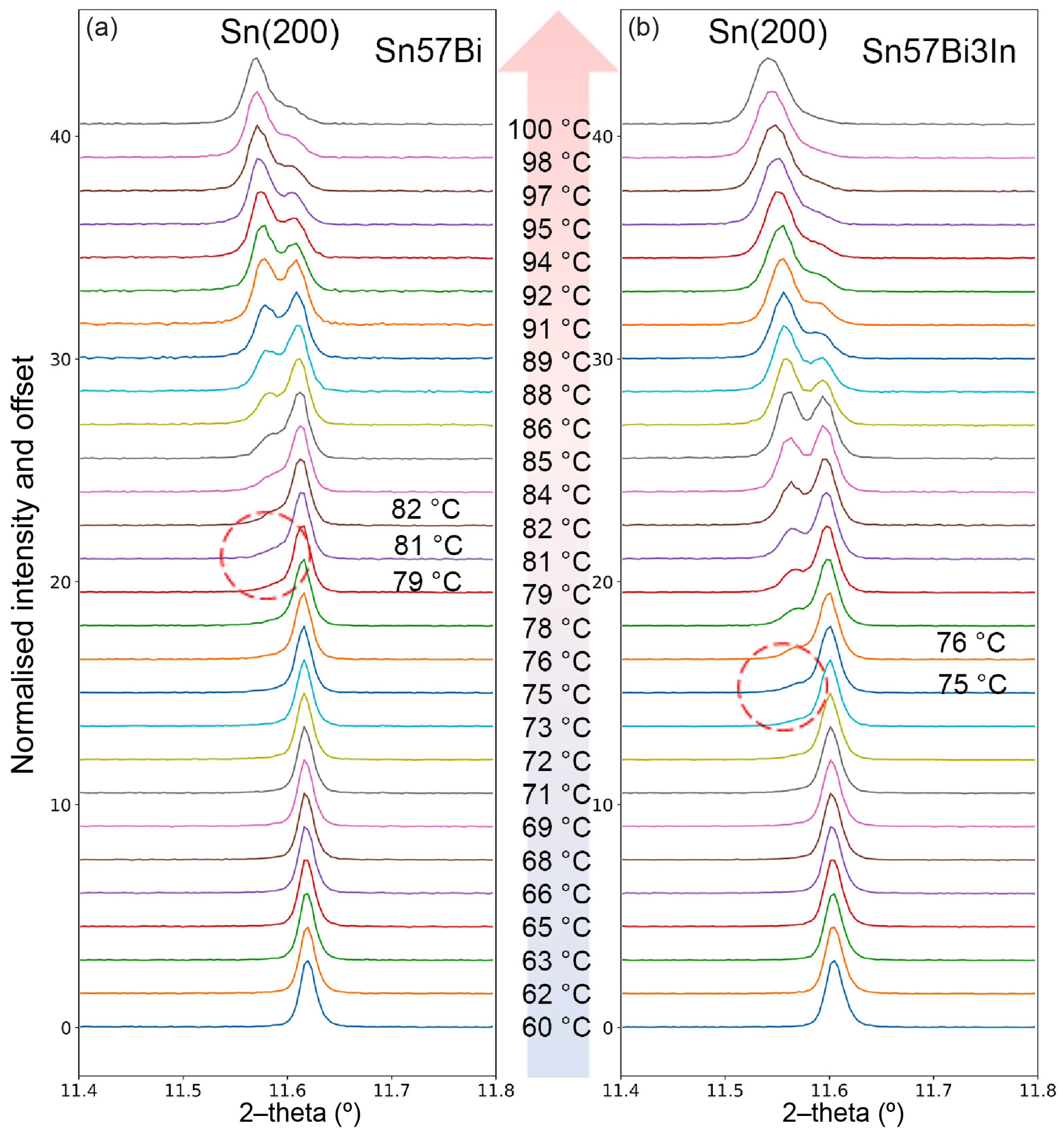
3.3.2. PXRD Patterns during Heating
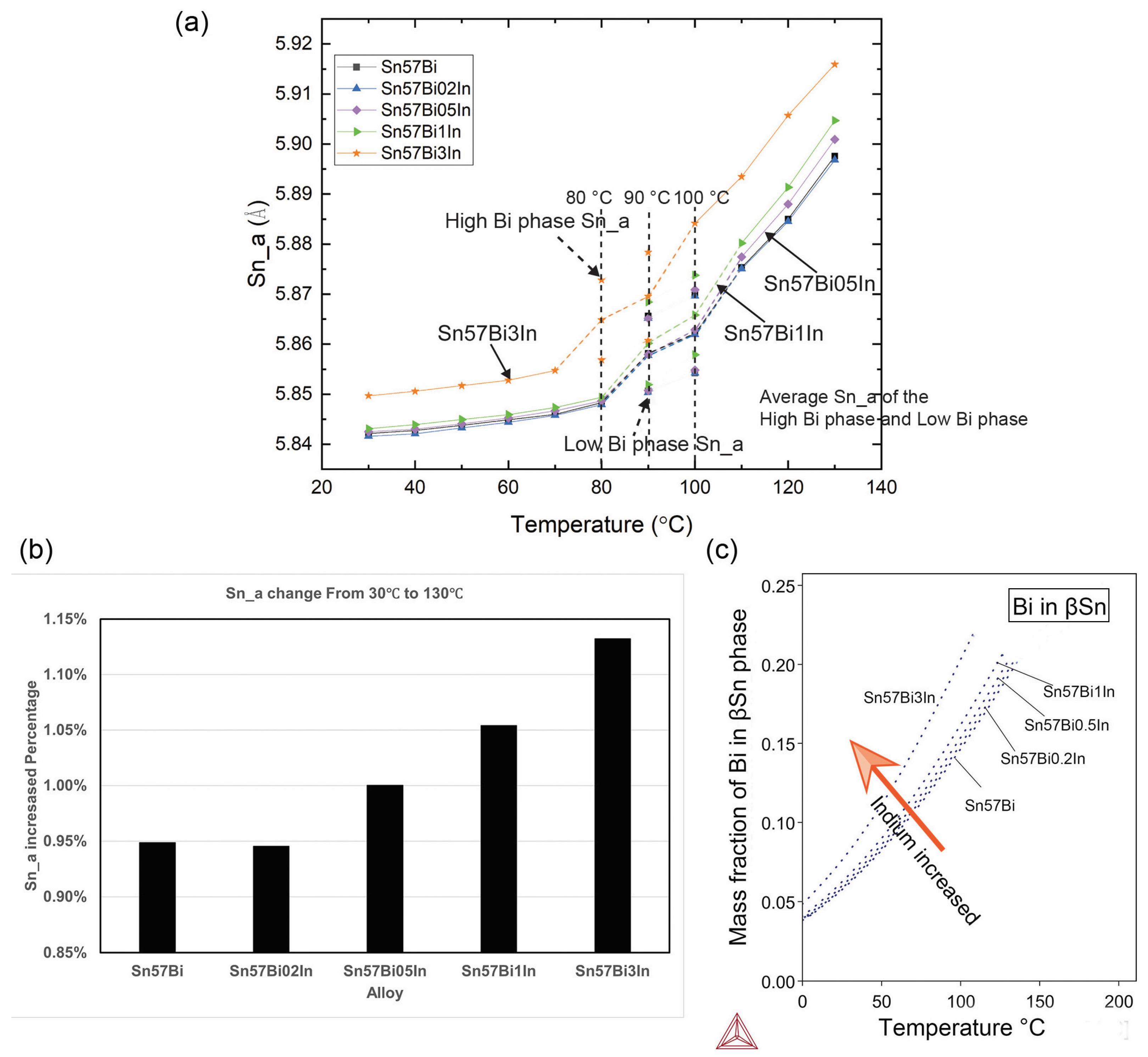
3.3.3. Lattice Parameters of Sn during Heating
3.3.4. PXRD Patterns during Cooling
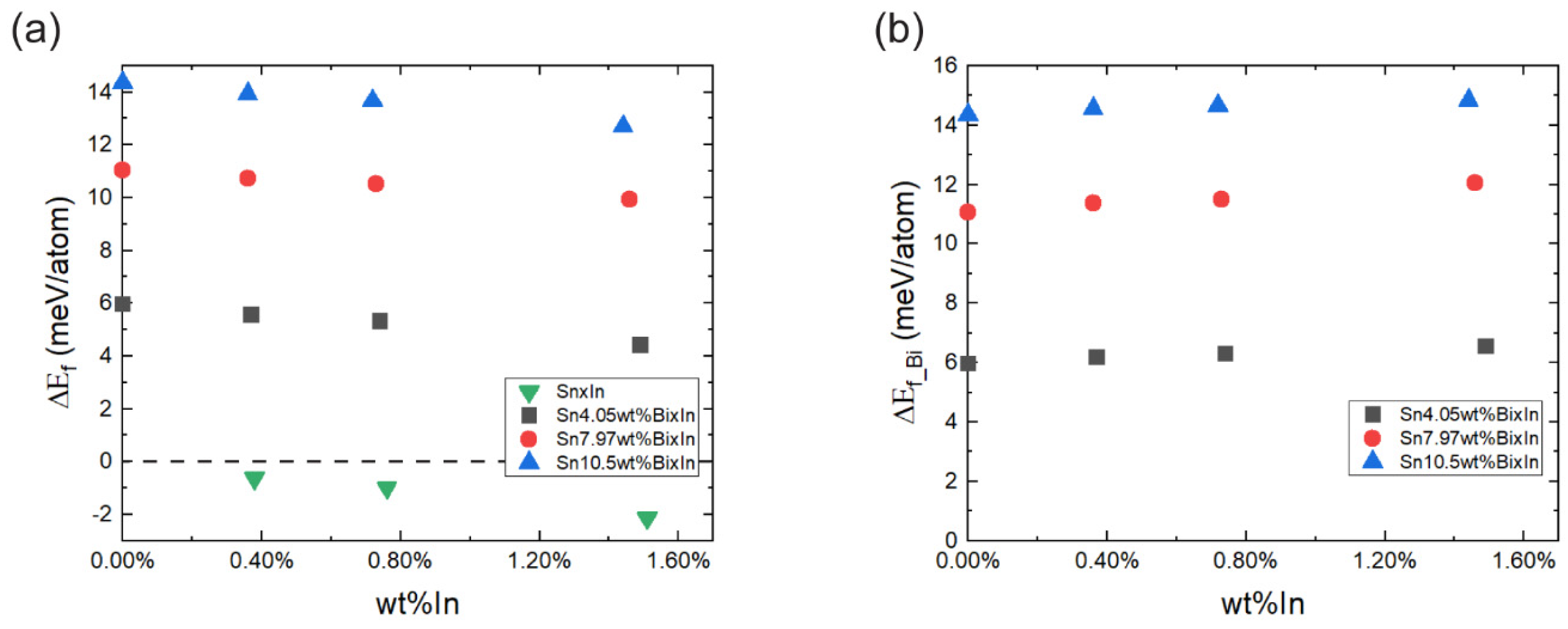
3.4. Atomistic Simulations
4. Conclusions
- (1)
- The addition of In into the Sn–Bi alloy system influences the morphology of the eutectic structure. Specifically, In enhances the refinement of the eutectic phase when present in concentrations of 1 wt% and below, whereas at a higher content of 3 wt%, it induces a coarsening effect;
- (2)
- The observed trends in terms of the recalescence with varying In concentrations, coupled with microstructural observations, point to In’s bifunctional influence: it first refines and then coarsens the eutectic structure as its content increases. These findings highlight In’s potential as a microstructure modifier in solder alloys;
- (3)
- In situ synchrotron PXRD analysis has yielded crucial insights into how In influences the dynamics of Bi dissolution and precipitation within the Sn matrix of Sn–Bi alloys. The findings demonstrate that In changes the homogeneous status during the Sn phase. During the heating process, the splitting temperature and merging temperature, which present an inhomogeneous status and a homogeneous status, respectively, decrease with the In concentration. Furthermore, the addition of In is confirmed to facilitate the dissolution of Bi into the Sn phase. In addition, there is an alloy-dependent temperature above which the dissolution speed of Bi into Sn increases significantly, and additions of In lower this temperature;
- (4)
- During the cooling phase, In appears to contribute to a more uniform distribution of Bi within Sn–Bi alloys. However, the precipitation behaviour is also dependent on the microstructure: an excessively coarse structure, characterised by widened Sn dendrites, can lead to non-uniformity, as observed in the Sn–57Bi–3In alloy. This indicates that while In acts as a homogenising agent, its effectiveness is contingent upon the microstructural context, underlining the complex interplay between alloy composition, structure, and thermal behaviour. Therefore, selecting an appropriate In concentration to optimise the decrease in the initial inhomogeneous temperature and achieve the benefit of homogeneous cooling after adding In is essential for improving the solder alloy’s stability. Based on the results presented in this article, it is recommended that the addition of 0.2 wt% to 1 wt% In is used to optimise both the heating and cooling processes during thermal cycling;
- (5)
- The DFT calculations further revealed the mechanism behind In’s effect, demonstrating that In stabilises the βSn phase and promotes more Bi dissolution in a given thermal condition. Despite a slight increase in the energy required for Bi dissolution and precipitation due to In, the abundance of thermal energy in micro-scale solder applications renders this increase negligible in practical experiments, resulting in an acceleration of the dissolution phenomena.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, N.C. Future Lead-Free Solder Alloys and Fluxes—Meeting Challenges of Miniaturization. In Proceedings of the 2008 10th Electronics Packaging Technology Conference, Singapore, 9–12 December 2008; pp. 864–872. [Google Scholar]
- Wang, F.; Chen, H.; Huang, Y.; Liu, L.; Zhang, Z. Recent progress on the development of Sn–Bi based low-temperature Pb-free solders. J. Mater. Sci. Mater. Electron. 2019, 30, 3222–3243. [Google Scholar] [CrossRef]
- Directive 2012/19/EU of the European Parliament and of the Council of 4 July 2012 on Waste Electrical and Electronic Equipment (WEEE) (Recast) (Text with EEA Relevance). Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:02012L0019-20180704 (accessed on 18 November 2023).
- Warwick, M. Implementing lead free soldering-European consortium research. J. Surf. Mt. Technol. 1999, 12, 1–12. [Google Scholar]
- Cheng, J.-C.; Li, J.-F.; Huang, C.-Y. Enablers for Adopting Restriction of Hazardous Substances Directives by Electronic Manufacturing Service Providers. Sustainability 2023, 15, 12341. [Google Scholar] [CrossRef]
- Li, M.-l.; Zhang, L.; Jiang, N.; Zhang, L.; Zhong, S.-j. Materials modification of the lead-free solders incorporated with micro/nano-sized particles: A review. Mater. Des. 2021, 197, 109224. [Google Scholar] [CrossRef]
- Feng, J.; Xu, D.E.; Tian, Y.; Mayer, M. SAC305 Solder Reflow: Identification of Melting and Solidification Using In-Process Resistance Monitoring. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 1623–1631. [Google Scholar] [CrossRef]
- Sungkhaphaitoon, P.; Chantaramanee, S. Effects of Indium Content on Microstructural, Mechanical Properties and Melting Temperature of SAC305 Solder Alloys. Russ. J. Non-Ferr. Met. 2018, 59, 385–392. [Google Scholar] [CrossRef]
- Sopoušek, J.í.; Palcut, M.; Hodúlová, E.; Janovec, J. Thermal Analysis of the Sn-Ag-Cu-In Solder Alloy. J. Electron. Mater. 2010, 39, 312–317. [Google Scholar] [CrossRef]
- Bath, J. Lead-Free Soldering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kang, H.; Rajendran, S.H.; Jung, J.P. Low Melting Temperature Sn-Bi Solder: Effect of Alloying and Nanoparticle Addition on the Microstructural, Thermal, Interfacial Bonding, and Mechanical Characteristics. Metals 2021, 11, 364. [Google Scholar] [CrossRef]
- Prakash, A.; Byrd, K.; Sidhu, R.; Elhalawaty, S.; Wu, N.; Okumura, H.; Erukula, S.; Lim, J. Challenges and key learnings in enabling Low Temperature Solder (LTS) technology at packaging components supply base. In Proceedings of the 2021 IEEE 71st Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 1 June–4 July 2021; pp. 635–642. [Google Scholar]
- Mei, Z.; Holder, H.A.; Vander Plas, H.A. Low-temperature solders. Hewlett Packard J. 1996, 47, 91–98. [Google Scholar]
- Hua, F.; Zequn, M.; Glazer, J. Eutectic Sn-Bi as an alternative to Pb-free solders. In Proceedings of the 1998 Proceedings. 48th Electronic Components and Technology Conference (Cat. No.98CH36206), Seattle, WA, USA, 25–28 May 1998; pp. 277–283. [Google Scholar]
- Yang, T.; Zhao, X.; Xiong, Z.; Tan, W.; Wei, Y.; Tan, C.; Yu, X.; Wang, Y. Improvement of microstructure and tensile properties of Sn–Bi–Ag alloy by heterogeneous nucleation of β-Sn on Ag3Sn. Mater. Sci. Eng. A 2020, 785, 139372. [Google Scholar] [CrossRef]
- Shen, J.; Pu, Y.; Yin, H.; Luo, D.; Chen, J. Effects of minor Cu and Zn additions on the thermal, microstructure and tensile properties of Sn–Bi-based solder alloys. J. Alloys Compd. 2014, 614, 63–70. [Google Scholar] [CrossRef]
- Tan, X.F.; Hao, Q.; Gu, Q.; McDonald, S.D.; Sweatman, K.; Bermingham, M.; Nogita, K. The effects of Sb on the lattice and microstructure characteristics of hypo-eutectic Sn-Bi alloys. Mater. Charact. 2023, 201, 112934. [Google Scholar] [CrossRef]
- Chen, X.; Xue, F.; Zhou, J.; Yao, Y. Effect of In on microstructure, thermodynamic characteristic and mechanical properties of Sn–Bi based lead-free solder. J. Alloys Compd. 2015, 633, 377–383. [Google Scholar] [CrossRef]
- Li, J.-G.; Ma, X.; Zhou, M.-B.; Ning, X.; Zhang, X.-P. Effects of Sb addition on the microstructure and mechanical performance of Sn58Bi based alloys and the solder joints. In Proceedings of the 2018 19th International Conference on Electronic Packaging Technology (ICEPT), Shanghai, China, 8–11 August 2018; pp. 457–461. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, S.-d.; Qian, G.-t.; Zhou, J.; Xue, F. Effect of Sb content on properties of Sn—Bi solders. Trans. Nonferrous Met. Soc. China 2014, 24, 184–191. [Google Scholar] [CrossRef]
- Wu, X.; Wu, J.; Wang, X.; Yang, J.; Xia, M.; Liu, B. Effect of In addition on microstructure and mechanical properties of Sn–40Bi alloys. J. Mater. Sci. 2020, 55, 3092–3106. [Google Scholar] [CrossRef]
- Young, K.; Badwe, N.; Aspandiar, R.; Walwadkar, S.; Lee, Y.-W.; Kim, H.-J.; Moon, J.-T.; Lee, T.-K. Low Melting Temperature Solder Interconnect Thermal Cycling Performance Enhancement Using Elemental Tuning. In Proceedings of the SMTA International, Minneapolis, MN, USA, 31 October–3 November 2022. [Google Scholar]
- Tan, X.F.; Hao, Q.; Zhou, J.; McDonald, S.D.; Sweatman, K.; Nogita, K. The Effect of Temperature on the Electrical Resistivity of Sn-Bi Alloys. J. Electron. Mater. 2024, 53, 1183–1191. [Google Scholar] [CrossRef]
- Tan, X.F.; Hao, Q.; Zhou, J.; Gu, Q.; McDonald, S.D.; Sweatman, K.; Ikeda, M.; Yasuda, K.; Bermingham, M.J.; Nogita, K. In-situ investigation of the time-temperature dependent lattice and microstructure of Sn-Bi alloys. Materialia 2024, 33, 101974. [Google Scholar] [CrossRef]
- Hao, Q.; Tan, X.F.; Gu, Q.; Sweatman, K.; McDonald, S.D.; Nogita, K. The Effects of Temperature and Solute Diffusion on Volume Change in Sn-Bi Solder Alloys. JOM 2022, 74, 1739–1750. [Google Scholar] [CrossRef]
- Hao, Q.; Tan, X.F.; McDonald, S.D.; Sweatman, K.; Akaiwa, T.; Nogita, K. Investigating the Effects of Rapid Precipitation of Bi in Sn on the Shear Strength of BGA Sn-Bi Alloys. J. Electron. Mater. 2024, 53, 1223–1238. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Paixão, J.L.; Gomes, L.F.; Reyes, R.V.; Garcia, A.; Spinelli, J.E.; Silva, B.L. Microstructure characterization and tensile properties of directionally solidified Sn-52 wt% Bi-1wt% Sb and Sn-52wt% Bi-2wt% Sb alloys. Mater. Charact. 2020, 166, 110445. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, X.; Zhong, H.; Xu, Z.; Li, L.; Gong, Y.; Miao, X.; Song, C.; Zhai, Q. Comparative study on the grain refinement of Al-Si alloy solidified under the impact of pulsed electric current and travelling magnetic field. Metals 2016, 6, 170. [Google Scholar] [CrossRef]


| Models | Atoms: Number of Elements | Weight Percent of Elements | |||
|---|---|---|---|---|---|
| Sn–xIn | Sn | Bi | In | wt%Bi | wt%In |
| Figure S5a | 512 | 0 | 0 | 0.00% | 0.00% |
| Figure S5b | 510 | 0 | 2 | 0.00% | 0.38% |
| Figure S5c | 508 | 0 | 4 | 0.00% | 0.76% |
| Figure S5d | 504 | 0 | 8 | 0.00% | 1.51% |
| Sn–12Bi–xIn | Sn | Bi | In | wt%Bi | wt%In |
| Figure S6a | 500 | 12 | 0 | 4.05% | 0.00% |
| Figure S6b | 498 | 12 | 2 | 4.05% | 0.37% |
| Figure S6c | 496 | 12 | 4 | 4.05% | 0.74% |
| Figure S6d | 492 | 12 | 8 | 4.06% | 1.49% |
| Sn–24Bi–xIn | Sn | Bi | In | wt%Bi | wt%In |
| Figure S6e | 488 | 24 | 0 | 7.97% | 0.00% |
| Figure S6f | 486 | 24 | 2 | 7.97% | 0.36% |
| Figure S6g | 484 | 24 | 4 | 7.97% | 0.73% |
| Figure S6h | 480 | 24 | 8 | 7.97% | 1.46% |
| Sn–32Bi–xIn | Sn | Bi | In | wt%Bi | wt%In |
| Figure S6i | 480 | 32 | 0 | 10.50% | 0.00% |
| Figure S6j | 478 | 32 | 2 | 10.50% | 0.36% |
| Figure S6k | 476 | 32 | 4 | 10.51% | 0.72% |
| Figure S6l | 472 | 32 | 8 | 10.51% | 1.44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Q.; Tan, X.; Gu, Q.; McDonald, S.D.; Nogita, K. The Effect of In Concentration and Temperature on Dissolution and Precipitation in Sn–Bi Alloys. Materials 2024, 17, 4372. https://doi.org/10.3390/ma17174372
Hao Q, Tan X, Gu Q, McDonald SD, Nogita K. The Effect of In Concentration and Temperature on Dissolution and Precipitation in Sn–Bi Alloys. Materials. 2024; 17(17):4372. https://doi.org/10.3390/ma17174372
Chicago/Turabian StyleHao, Qichao, Xinfu Tan, Qinfen Gu, Stuart D. McDonald, and Kazuhiro Nogita. 2024. "The Effect of In Concentration and Temperature on Dissolution and Precipitation in Sn–Bi Alloys" Materials 17, no. 17: 4372. https://doi.org/10.3390/ma17174372
APA StyleHao, Q., Tan, X., Gu, Q., McDonald, S. D., & Nogita, K. (2024). The Effect of In Concentration and Temperature on Dissolution and Precipitation in Sn–Bi Alloys. Materials, 17(17), 4372. https://doi.org/10.3390/ma17174372








