Dynamic Mechanical Properties and Modified Material Constitutive Model for Hot Forged Ti2AlNb over Wide Ranges of Temperature and Strain Rate
Abstract
1. Introduction
2. Material and Methods
2.1. Materials
2.2. Quasi-Static Compression Test
2.3. Split Hopkinson Pressure Bar Tests
3. Results and Discussion
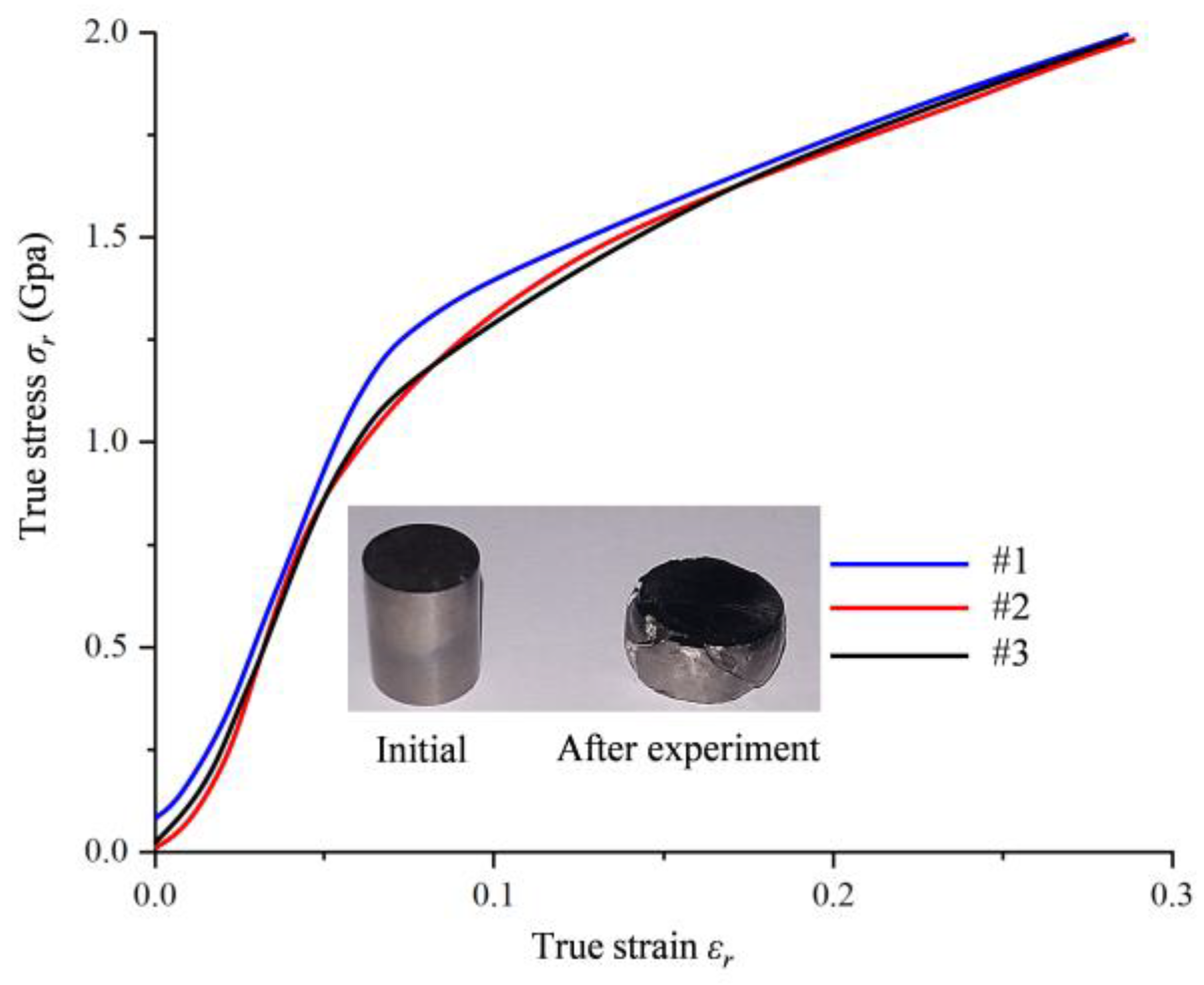
3.1. True Stress–Strain Curves of Hot Forged Ti2AlNb Alloy in Quasi-Static Compression Tests
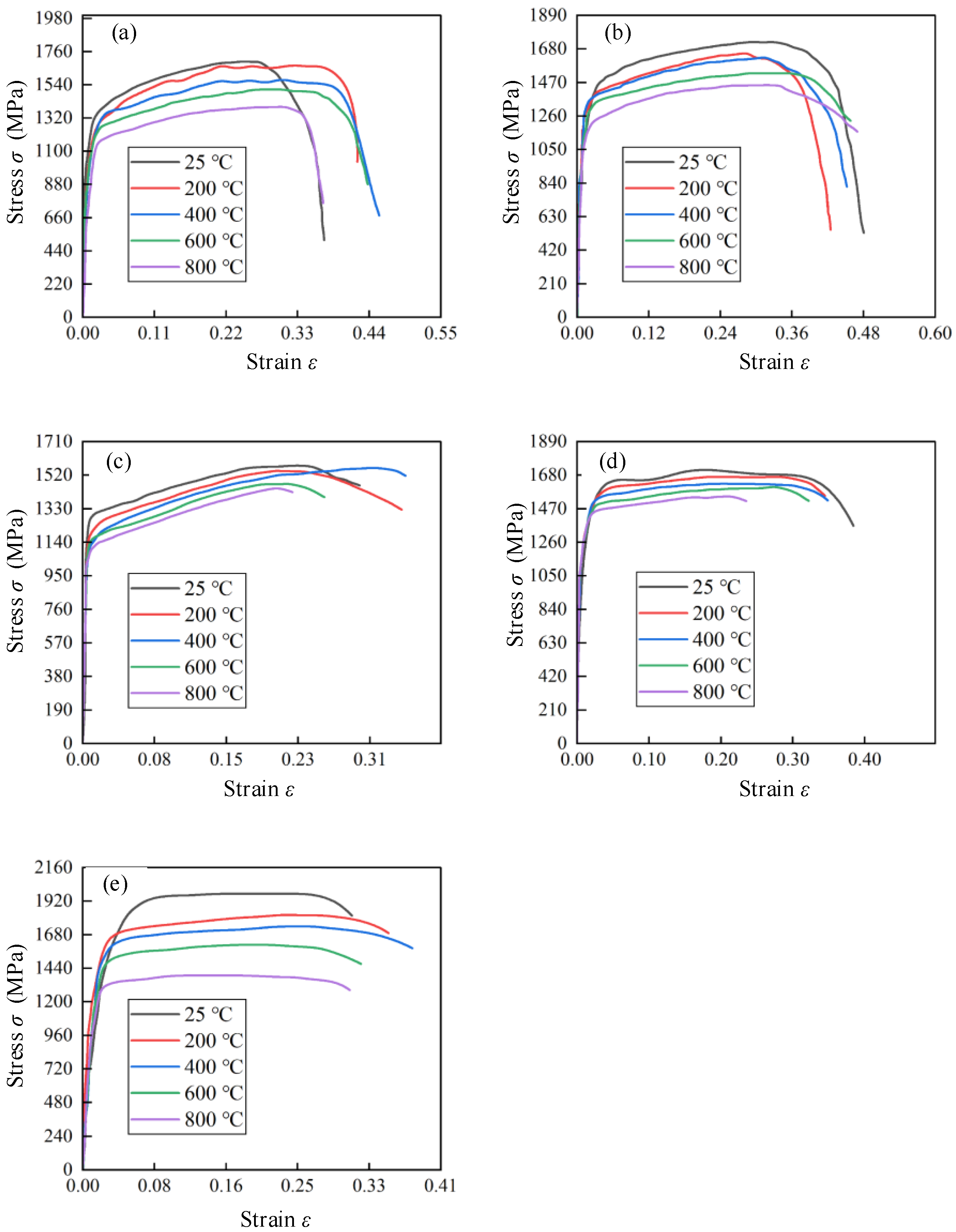
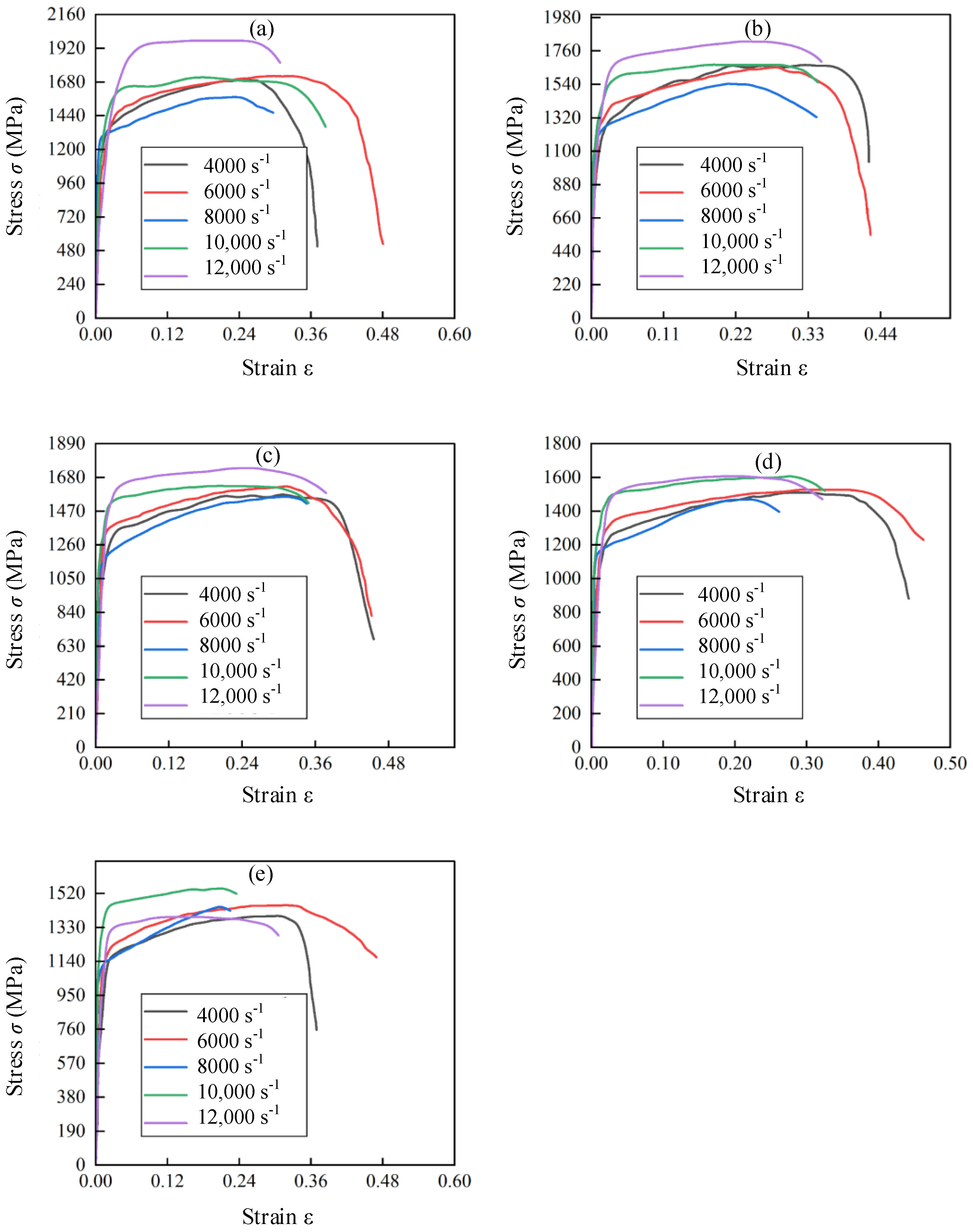
3.2. Deformation and Microstructure of Hot Forged Ti2AlNb in SHPB Tests
3.3. Stress–Strain Curves of hot Forged Ti2AlNb Alloy in SHPB Tests
4. Establishment and Verification of Modified J-C Constitutive Model
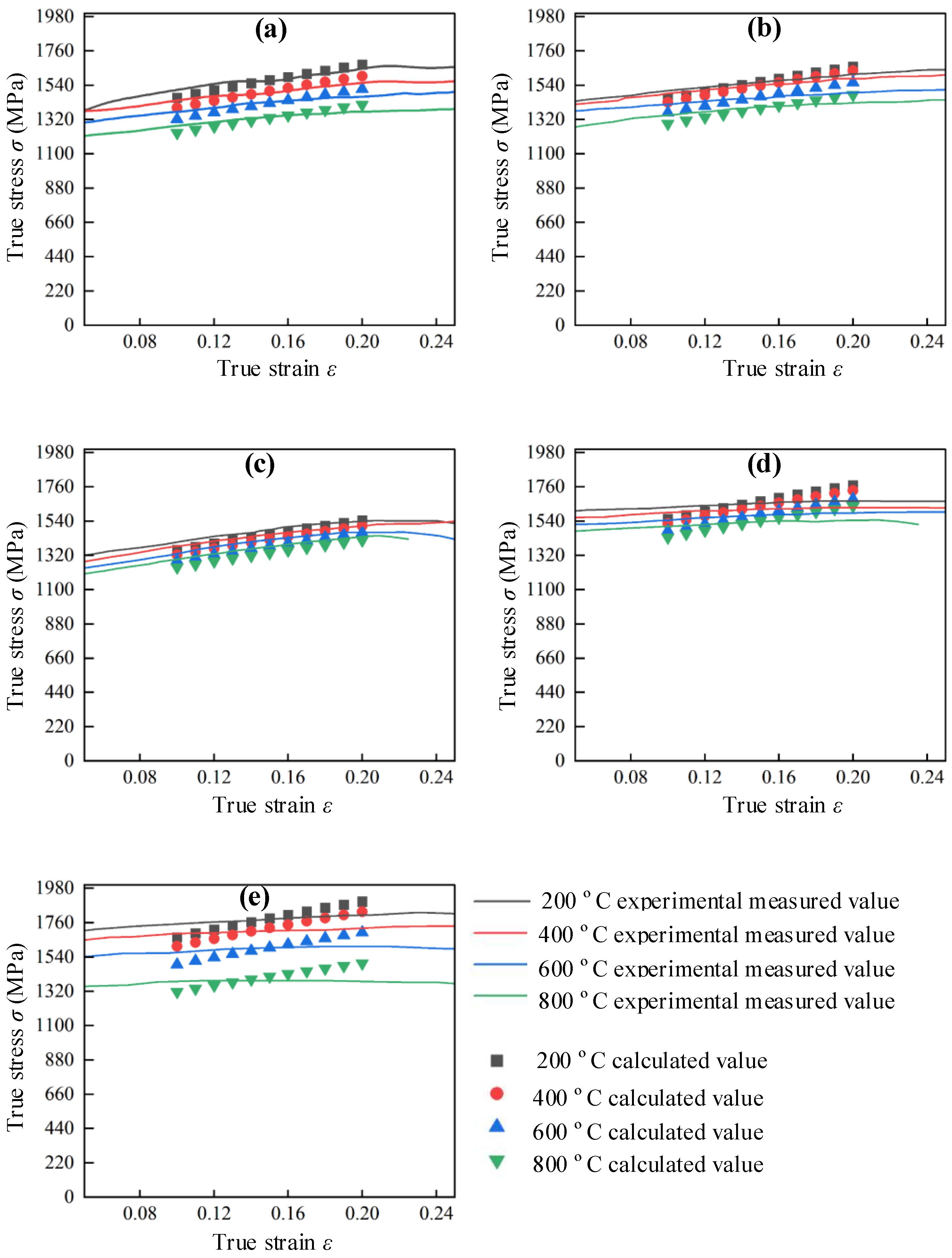
4.1. Establishment of Basic J-C Constitutive Model
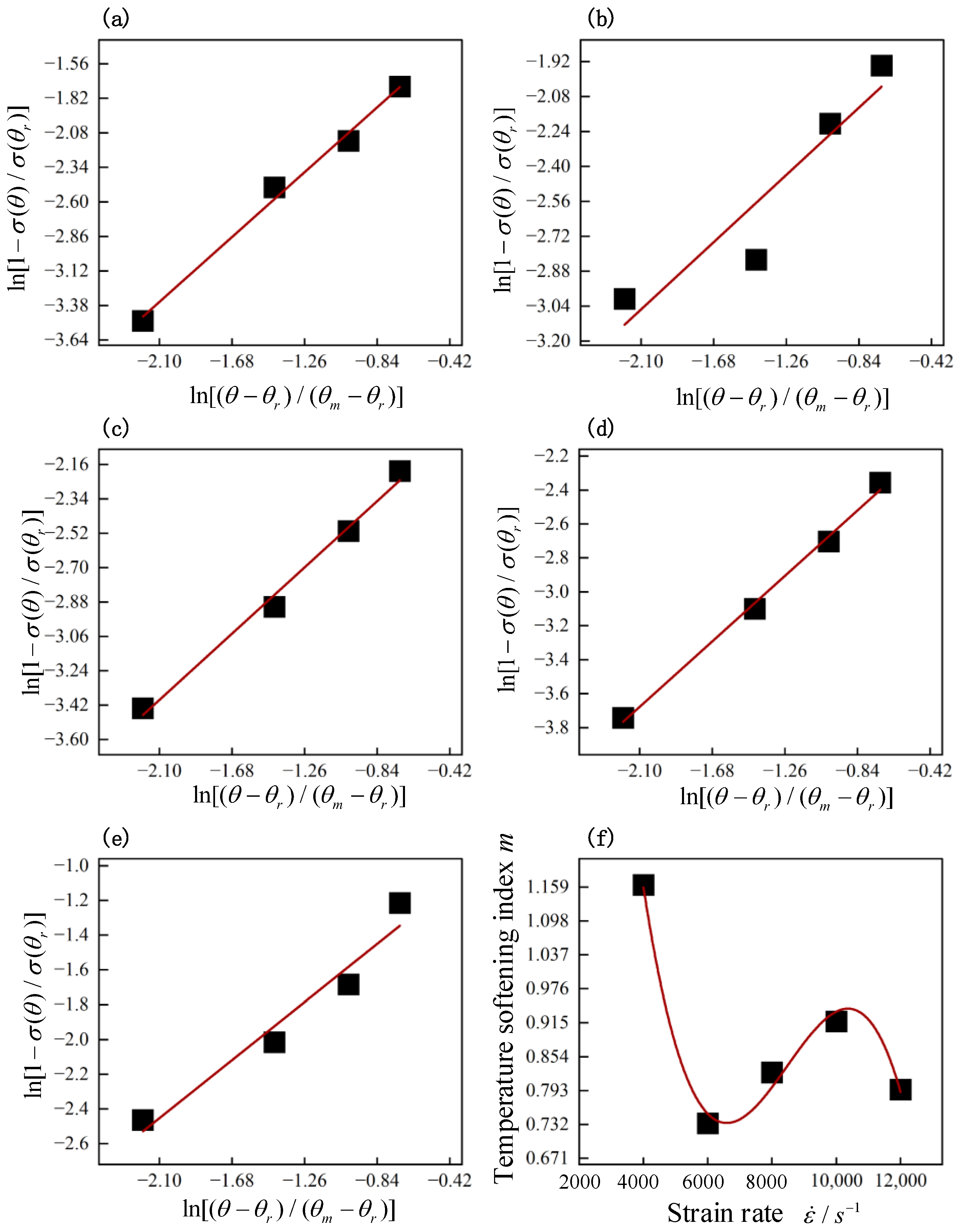
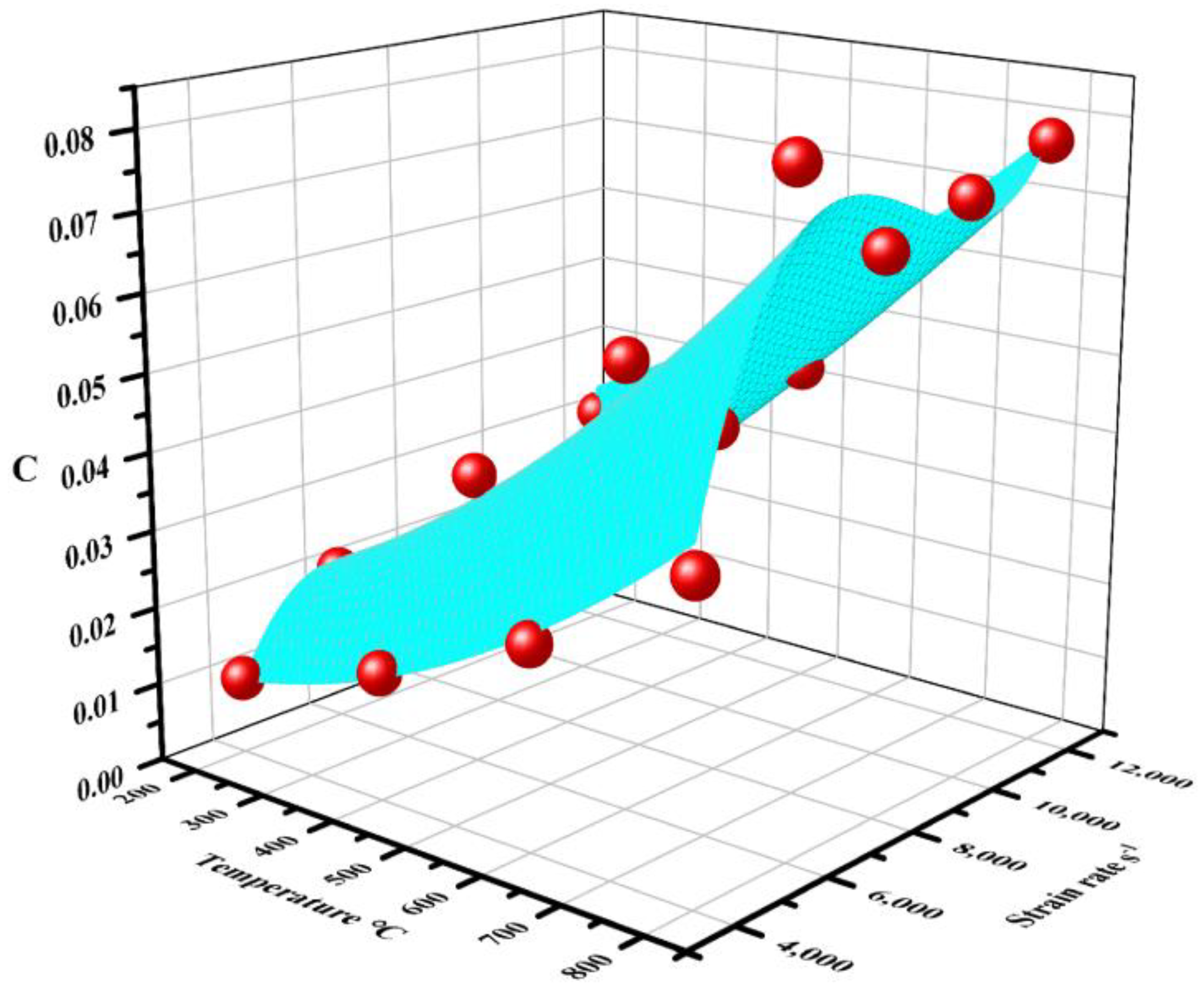
4.2. Modification of Basic J-C Constitutive Model
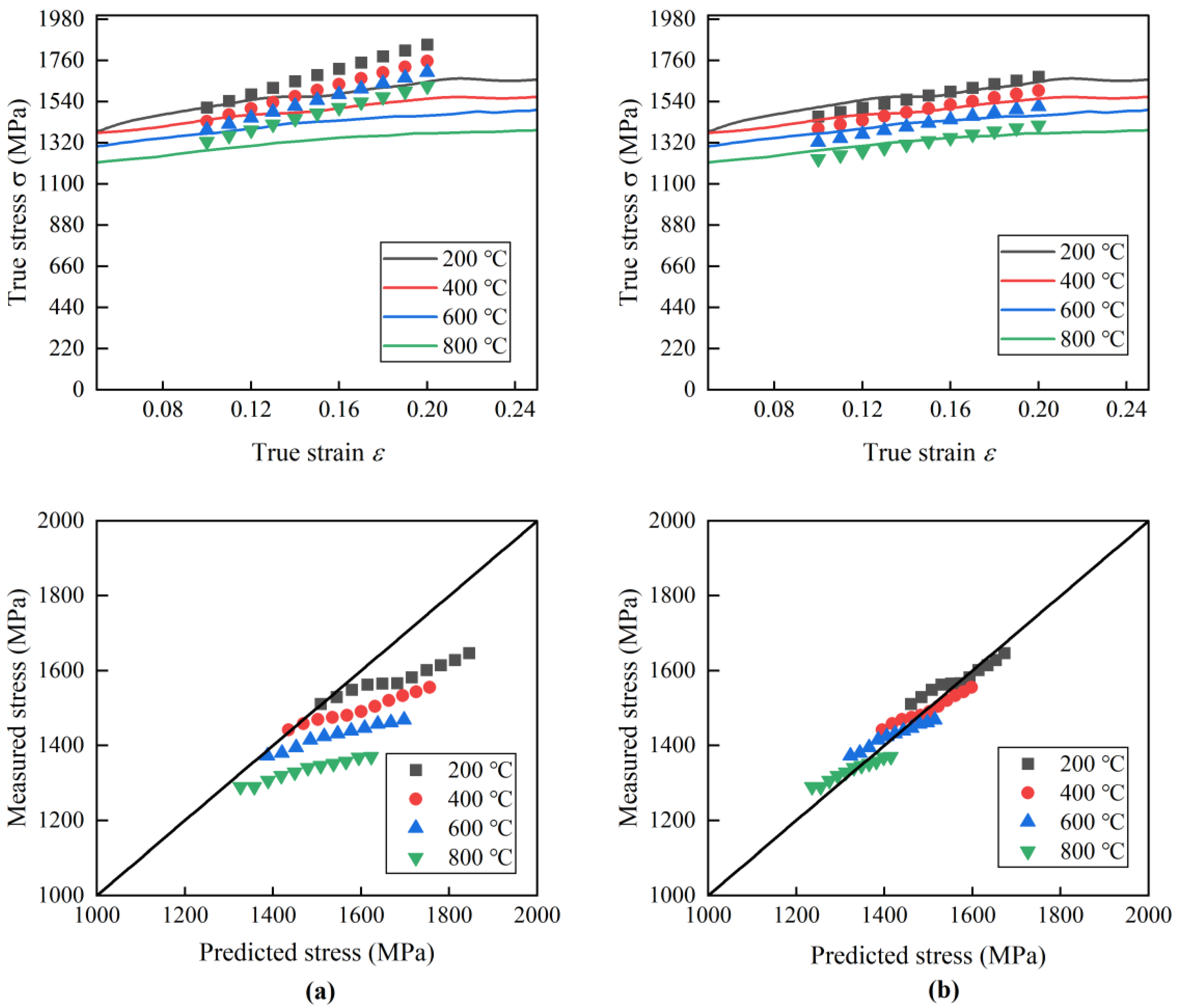
4.3. Verification of Modified J-C Constitutive Model
5. Conclusions
- Ti2AlNb showed work hardening under quasi-static compression without a significant yield phase; under high strain rate compression, the material’s deformation increased with strain rate, but no fracture occurred. Ti2AlNb exhibited the work hardening effect but does not show an obvious yield stage during quasi-static compression test. In the SHPB test, the deformation of specimens increased with the increase in strain rate, and no evident fracture was found.
- In the SHPB test, Ti2AlNb exhibited an evident temperature softening effect and low strain rate sensitivity. The strain rate strengthening effect was detected when the strain rate was 4000–6000 s−1. When the strain rate was more than 8000 s−1, the strain rate softening effect was detected, and the temperature softening effect also increased with the increase in strain rate.
- The basic J-C constitutive model could be modified well with the function describing the effect of strain rate on the strain rate strengthening parameters under various temperatures. The relative errors between the experimental measured values and predicted values in various experimental conditions with the modified J-C model were less than 5.0%. The results verified that the modified J-C model could accurately describe the dynamic mechanical properties of Ti2AlNb at high temperatures and strain rates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Yan, N.; Liang, H.; Liu, Y. Phase transformation and microstructure control of Ti2AlNb-based alloys: A review. J. Mater. Sci. Technol. 2021, 80, 203–216. [Google Scholar] [CrossRef]
- Goyal, K.; Sardana, N. Phase stability and microstructural evolution of Ti2AlNb alloys-a review. Mater. Today Proc. 2021, 41, 951–968. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, P.; Zhang, L.; Li, S.; Zhang, Z.; Yu, Q. Temperature effect on stacking fault energy and deformation mechanisms in titanium and titanium-aluminium alloy. Sci. Rep. 2020, 10, 3086. [Google Scholar] [CrossRef] [PubMed]
- Germann, L.; Banerjee, D.; Guédou, J.Y.; Strudel, J.L. Effect of composition on the mechanical properties of newly developed Ti2AlNb-based titanium aluminide. Intermetallics 2005, 13, 920–924. [Google Scholar] [CrossRef]
- Dressler, U.; Biallas, G.; Mercado, U.A. Friction stir welding of titanium alloy TiAl6V4 to aluminium alloy AA2024-T3. Mater. Sci. Eng. A 2009, 526, 113–117. [Google Scholar] [CrossRef]
- Fu, Z.; Gao, G.; Wang, Y.; Qiao, H.; Xiang, D.; Zhao, B. Research on dynamic mechanical properties and plastic constitutive relation of Ti3Al intermetallic compounds under mechanical-thermal coupling. J. Mater. Res. Technol. 2022, 19, 4154–4170. [Google Scholar] [CrossRef]
- Cao, X.; An, D.; Liu, Q.; Chen, G.; Li, X. Precipitation hardening characterization and stress prediction model in electrically-assisted Ti2AlNb uniaxial tension. Intermetallics 2024, 167, 108214. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; Liu, X.; Wang, S.; Wang, C.; Zhou, G.; Zhang, S.; Chen, L. Thermal deformation behavior investigation of Ti–10V–5Al-2.5 fe-0.1 B titanium alloy based on phenomenological constitutive models and a machine learning method. J. Mater. Res. Technol. 2024, 29, 589–608. [Google Scholar] [CrossRef]
- Cao, Y.; Lin, X.; Kang, N.; Ma, L.; Wei, L.; Zheng, M.; Yu, J.; Peng, D.; Huang, W. A novel high-efficient finite element analysis method of powder bed fusion additive manufacturing. Addit. Manuf. 2021, 46, 102187. [Google Scholar] [CrossRef]
- Ford, E.; Maneparambil, K.; Rajan, S.; Neithalath, N. Machine learning-based accelerated property prediction of two-phase materials using microstructural descriptors and finite element analysis. Comput. Mater. Sci. 2021, 191, 110328. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Ji, H.C.; Zhao, J.M.; Liu, B.X.; Pei, W.C. Johnson-Cook model for TC4 titanium alloy based on compression experiment. Metalurgija 2022, 61, 721–724. [Google Scholar]
- Lin, H.; Jin, G.; Zhan, Q.; Wang, G.; Han, J. Mechanical Properties and Constitutive Model of TC4 Titanium Alloy at Cryogenic. J. Mater. Eng. Perform. 2023, 1–13. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, D.; Ye, X.; Chen, X.; He, Y. A simplified Johnson-Cook model of TC4T for aeroengine foreign object damage prediction. Eng. Fract. Mech. 2022, 269, 108523. [Google Scholar] [CrossRef]
- Ling, C.; Ren, X.; Wang, X.; Li, Y.; Liu, Z.; Wang, B.; Zhao, J. Dynamic Mechanical Properties and Modified Johnson-Cook Model Considering Recrystallization Softening for Nickel-Based Powder Metallurgy Superalloys. Materials 2024, 17, 670. [Google Scholar] [CrossRef]
- Hou, X.; Liu, Z.; Wang, B.; Lv, W.; Liang, X.; Hua, Y. Stress-strain curves and modified material constitutive model for Ti-6Al-4V over the wide ranges of strain rate and temperature. Materials 2018, 11, 938. [Google Scholar] [CrossRef]
- Tian, X.; Yan, K.; Zhao, J.; Wang, Q.; Wang, Y.; Chen, X. Properties at Elevated Temperature and High Strain Rate and Establishment of Johnson-Cook Constitutive Model for GH2132. China Mech. Eng. 2022, 33, 872. [Google Scholar]
- Lin, M.; Pang, B.; Zhang, W.; Chi, R. Experimental investigation on a dynamic constitutive relationship of 5A06 Al alloy. Explos. Shock. Waves 2009, 29, 306–311. [Google Scholar]
- Zhou, X.; Zhao, C.M.; Li, L.; Huang, H.J. Numerical simulation of dynamic behavior of extruded AZ91D magnesium alloy based on SHPB experiment. Chin. J. Nonferrous Met. 2014, 24, 1968–1975. [Google Scholar]
- Hu, W.J.; Xie, R.Z.; Huang, X.C.; Yan, Y.X. Constitutive equation for V-5Cr-5Ti at high temperatures measured using the SHPB technique. Adv. Manuf. Technol. 2011, 314, 1154–1158. [Google Scholar] [CrossRef]
- He, Z.; Wang, Z.; Lin, P. A comparative study on Arrhenius and Johnson–Cook constitutive models for high-temperature deformation of Ti2AlNb-based alloys. Metals 2019, 9, 123. [Google Scholar] [CrossRef]
- Xue, K.; Guo, S.; Ji, X.; Meng, M.; Li, P. Investigation on Ultrasonic Vibration Effects on the Plastic Flow Behavior of Ti2AlNb Alloy: Johnson–Cook Model. J. Mater. Eng. Perform. 2023, 32, 7683–7694. [Google Scholar] [CrossRef]
- Sim, K.H.; Li, Y.C.; Li, C.H.; Kim, M.O.; Kim, H.C. Constitutive Modeling of a Fine-Grained Ti2AlNb-Based Alloy Fabricated by Mechanical Alloying and Subsequent Spark Plasma Sintering. Adv. Eng. Mater. 2021, 23, 2000987. [Google Scholar] [CrossRef]
- He, L.; Su, H.; Xu, J.; Liang, Z. Inverse identification of constitutive parameters of Ti2AlNb intermetallic alloys based on cooperative particle swarm optimization. Chin. J. Aeronaut. 2018, 31, 1774–1785. [Google Scholar] [CrossRef]
- He, L.; Su, H.; Xu, J.; Zhang, L. Study on dynamic chip formation mechanisms of Ti2AlNb intermetallic alloy. Int. J. Adv. Manuf. Technol. 2017, 92, 4415–4428. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, D.; Zhou, Y.; Sha, A.; Cheng, H.; Yan, Y. A Constitutive Relation Based on the Johnson–Cook Model for Ti-22Al-23Nb-2 (Mo, Zr) Alloy at Elevated Temperature. Crystals 2021, 11, 754. [Google Scholar] [CrossRef]
- GB/T 7314-2017; Metallic materials—Compression Test Method at Room Temperature. Standardization Administration of China: Beijing, China, 2017.
- GB/T 34108-2017; Metallic materials—High Strain Rate Compression Test Method at Ambient Temperature. Standardization Administration of China: Beijing, China, 2017.
- Badrish, C.A.; Morchhale, A.; Kotkunde, N.; Singh, S.K. Prediction of flow stress using integrated J-C-ZA constitutive model for Inconel 625 alloy. Mater. Today Proc. 2021, 46, 9287–9290. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, C.; Wang, K.; Jiang, Z. Simulation of ultrasonic vibration cutting performance of GH2132 superalloy. IOP Conf. Ser. Mater. Sci. Eng. 2019, 493, 012162. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Z.; Wang, Y.; Mao, P.; Kuang, X.; Zhang, Z.; Ju, Y.; Xu, X. The modified temperature term on Johnson-Cook constitutive model of AZ31 magnesium alloy with {0002} texture. J. Magnes. Alloys 2020, 8, 172–183. [Google Scholar] [CrossRef]






| Element | Al | Nb | Mo | Ti | Ni | Fe | Si | C | O | N | H |
|---|---|---|---|---|---|---|---|---|---|---|---|
| fraction% | 9.9~11.9 | 41.6~44.6 | ≤1.5 | Matrix | ≤0.10 | ≤0.30 | ≤0.10 | ≤0.10 | ≤0.10 | ≤0.02 | ≤0.01 |
| Strain Rate s−1 | Plastic Strain Range | Medium Strain |
|---|---|---|
| 4000 | 0.0579–0.2544 | 0.1562 |
| 6000 | 0.0537–0.2842 | 0.1689 |
| 8000 | 0.0250–0.1891 | 0.1071 |
| 10,000 | 0.0601–0.2006 | 0.1304 |
| 12,000 | 0.0819–0.2563 | 0.1691 |
| Strain rate (s−1) | 4000 | 6000 | 8000 | 10,000 | 12,000 |
| m | 1.16 | 0.73 | 0.83 | 0.92 | 0.80 |
| Strain Rate (s−1) | Temperature (°C) | |||
|---|---|---|---|---|
| 200 | 400 | 600 | 800 | |
| 4000 | 0.00983 | 0.01638 | 0.02583 | 0.03941 |
| 6000 | 0.01998 | 0.03728 | 0.056 | 0.08231 |
| 8000 | 0.01261 | 0.02647 | 0.04423 | 0.06953 |
| 10,000 | 0.01934 | 0.03215 | 0.04829 | 0.07314 |
| 12,000 | 0.03015 | 0.04592 | 0.06148 | 0.07753 |
| Strain rate s−1 | 0.001 | 4000 | 6000 | 8000 | 10,000 | 12,000 |
| Strain hardening rate | 2777.75 | 1581 | 1502 | 1483 | 1409 | 1354 |
| Strain Rate (s−1) | Temperature (°C) | |||
|---|---|---|---|---|
| 200 | 400 | 600 | 800 | |
| 4000 | 2.2% | 3.1% | 2.6% | 2.5% |
| 6000 | 2.5% | 2.7% | 3.3% | 3.4% |
| 8000 | 3.0% | 3.5% | 3.2% | 3.3% |
| 10,000 | 3.7% | 3.6% | 3.6% | 3.5% |
| 12,000 | 4.3% | 4.6% | 5.0% | 4.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Pan, X.; Zhang, Y.; Mu, J.; Zhao, J.; Dong, X.; Liu, Z. Dynamic Mechanical Properties and Modified Material Constitutive Model for Hot Forged Ti2AlNb over Wide Ranges of Temperature and Strain Rate. Materials 2024, 17, 2572. https://doi.org/10.3390/ma17112572
Li L, Pan X, Zhang Y, Mu J, Zhao J, Dong X, Liu Z. Dynamic Mechanical Properties and Modified Material Constitutive Model for Hot Forged Ti2AlNb over Wide Ranges of Temperature and Strain Rate. Materials. 2024; 17(11):2572. https://doi.org/10.3390/ma17112572
Chicago/Turabian StyleLi, Liangliang, Xin Pan, Yongliang Zhang, Jianwei Mu, Jinfu Zhao, Xiangmin Dong, and Zhifeng Liu. 2024. "Dynamic Mechanical Properties and Modified Material Constitutive Model for Hot Forged Ti2AlNb over Wide Ranges of Temperature and Strain Rate" Materials 17, no. 11: 2572. https://doi.org/10.3390/ma17112572
APA StyleLi, L., Pan, X., Zhang, Y., Mu, J., Zhao, J., Dong, X., & Liu, Z. (2024). Dynamic Mechanical Properties and Modified Material Constitutive Model for Hot Forged Ti2AlNb over Wide Ranges of Temperature and Strain Rate. Materials, 17(11), 2572. https://doi.org/10.3390/ma17112572







