A Macroscopic Interpretation of the Correlation between Electrical Percolation and Mechanical Properties of Poly-(Ethylene Vinyl Acetate)/Zn Composites
Abstract
1. Introduction
2. Materials and Methods
3. Results
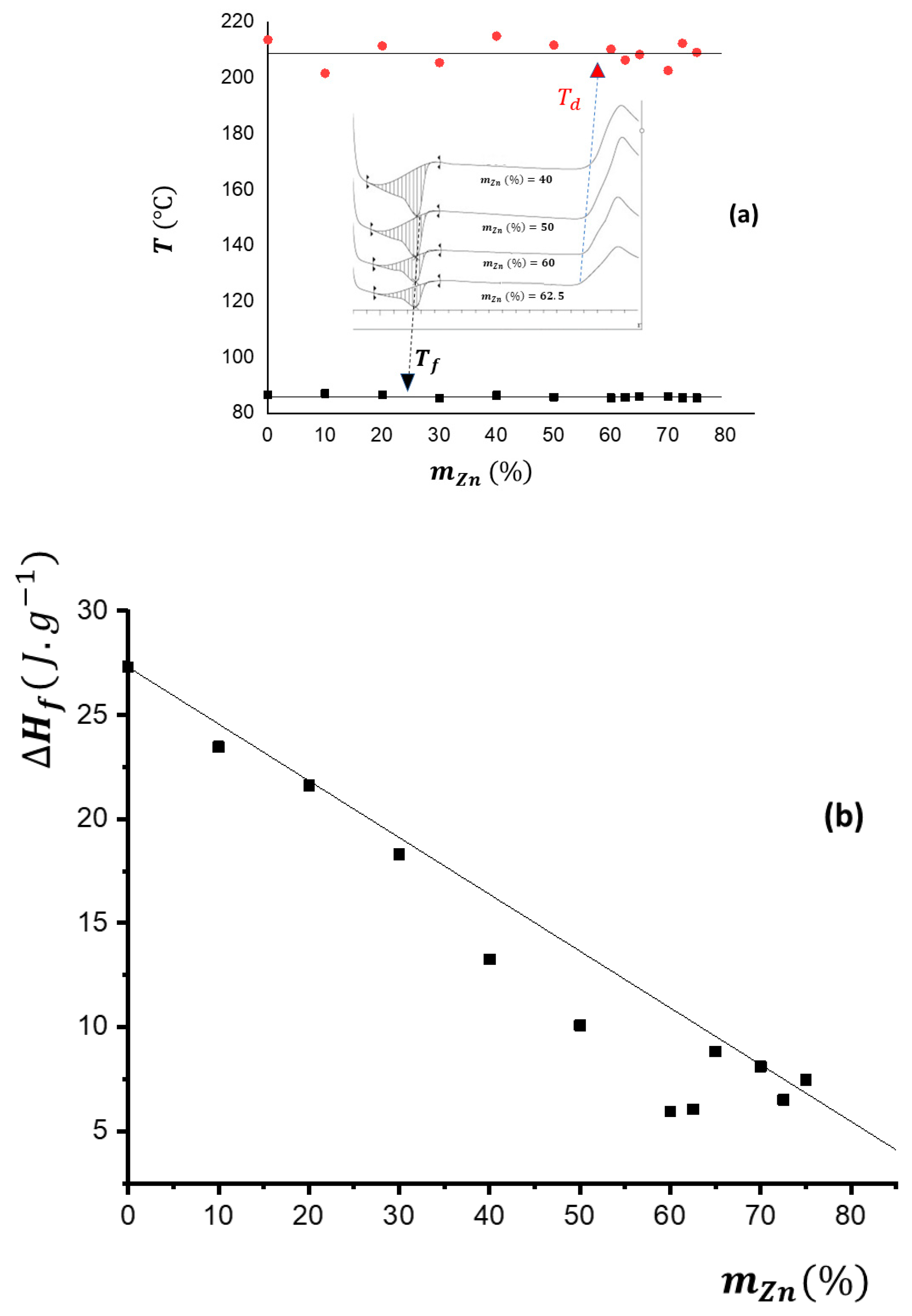
3.1. DSC Characterization
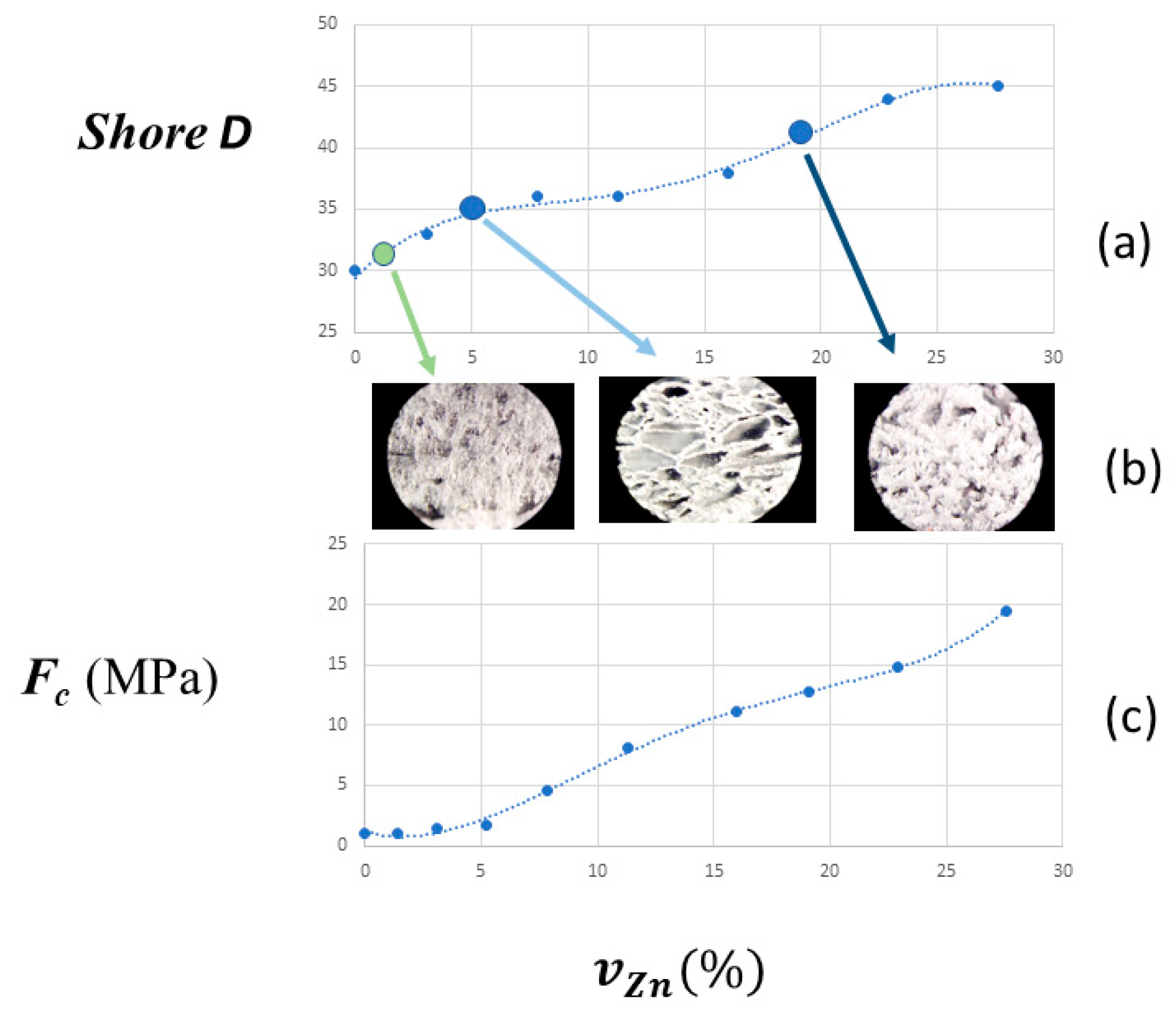
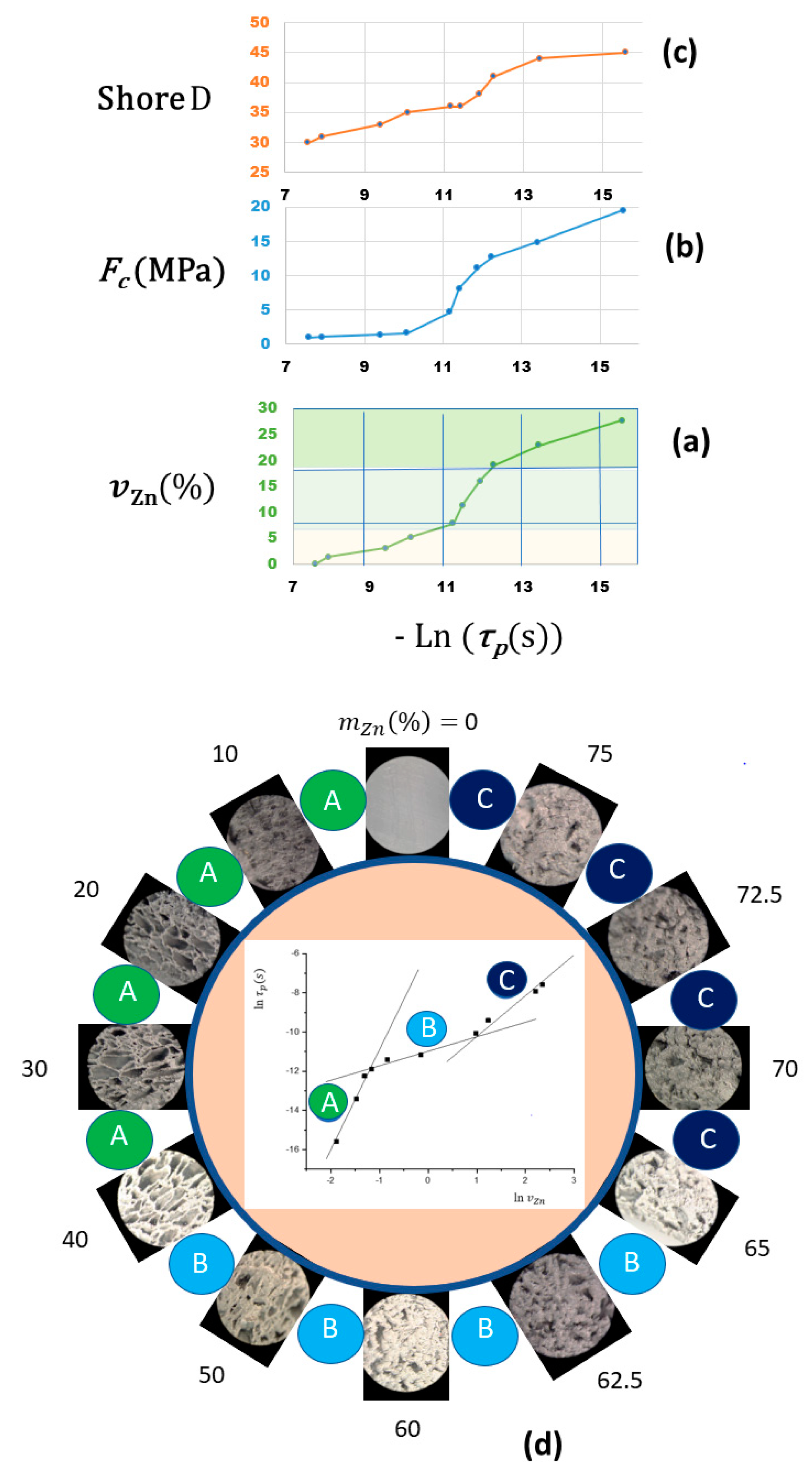
3.2. Mechanical Properties
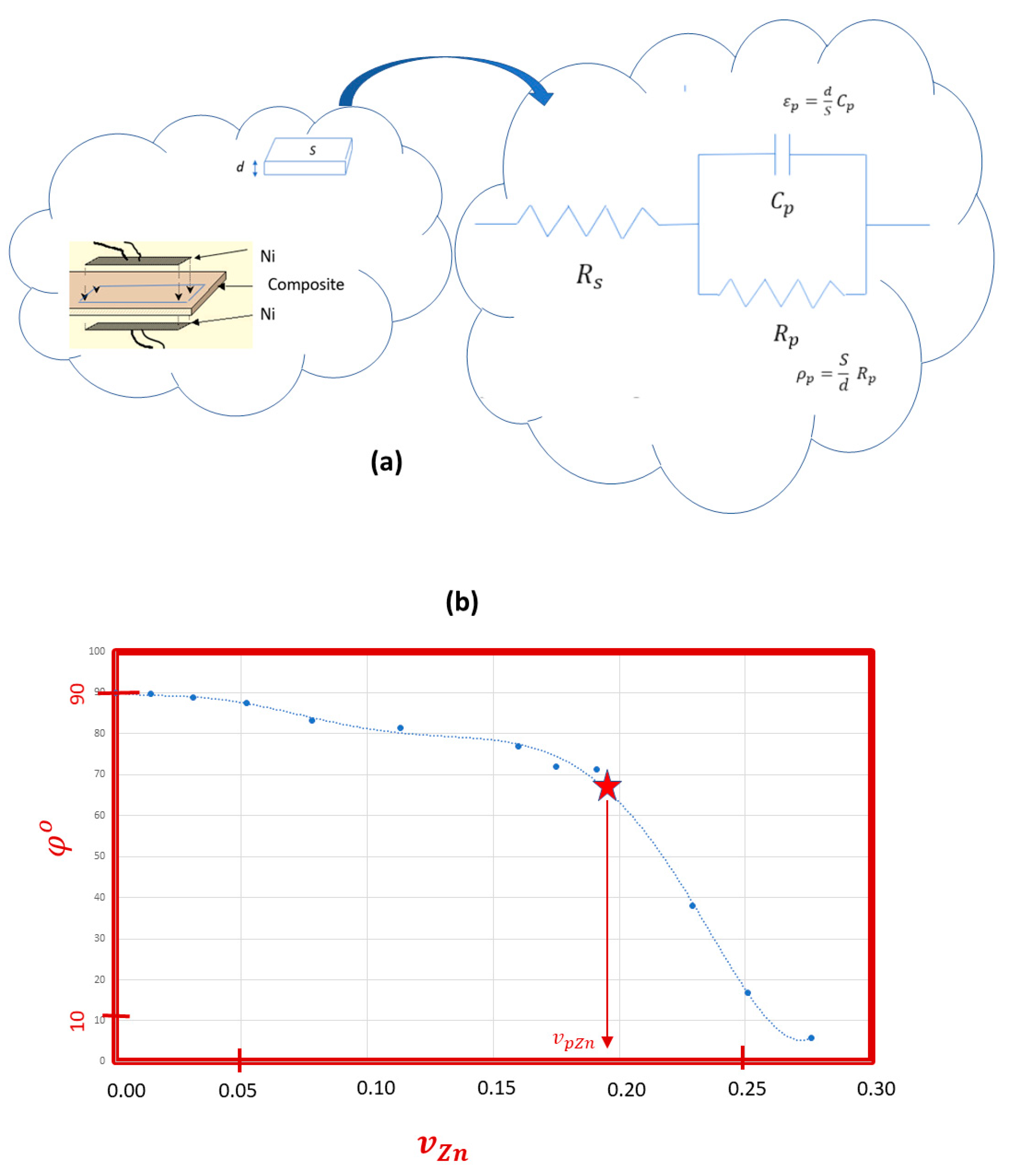
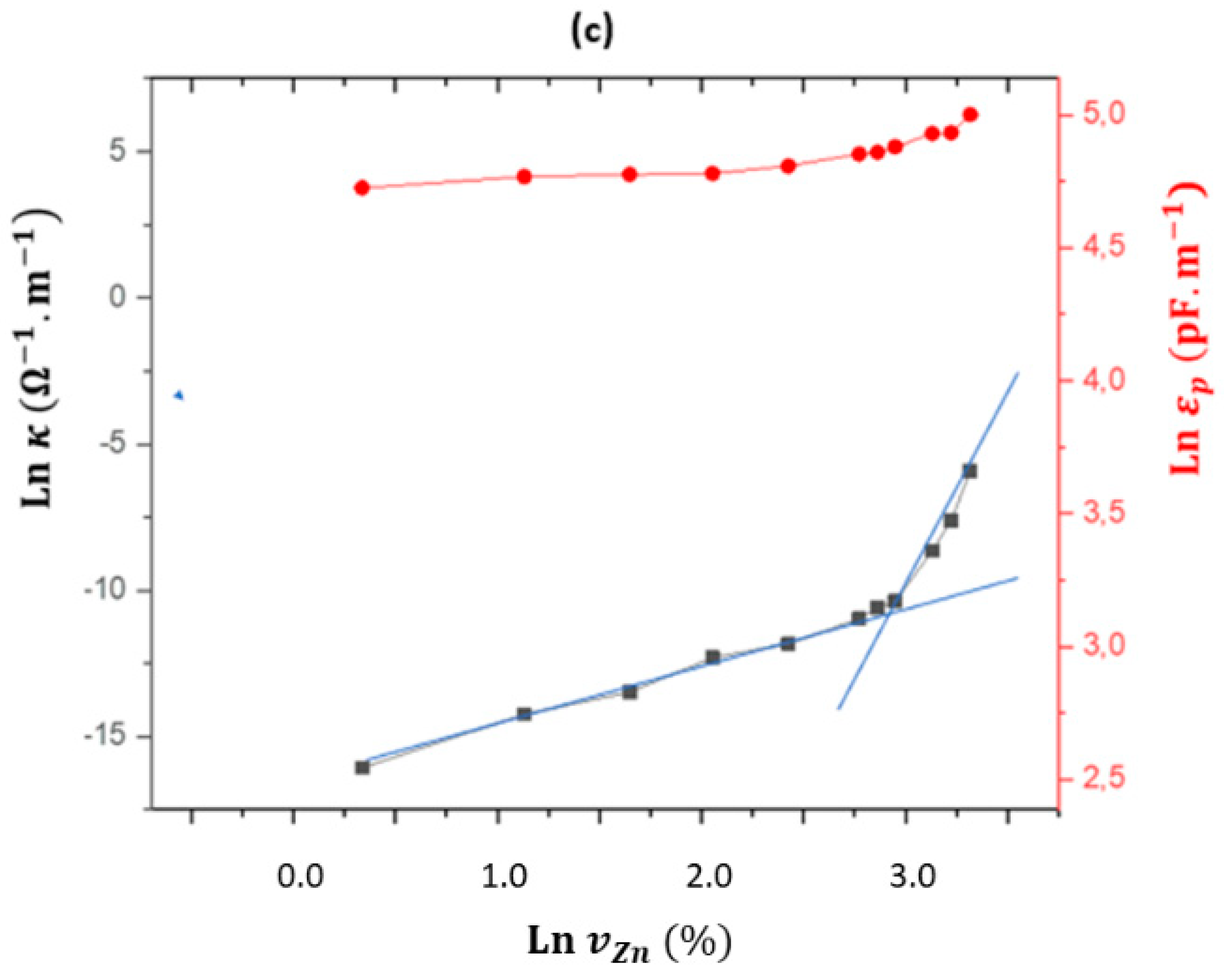
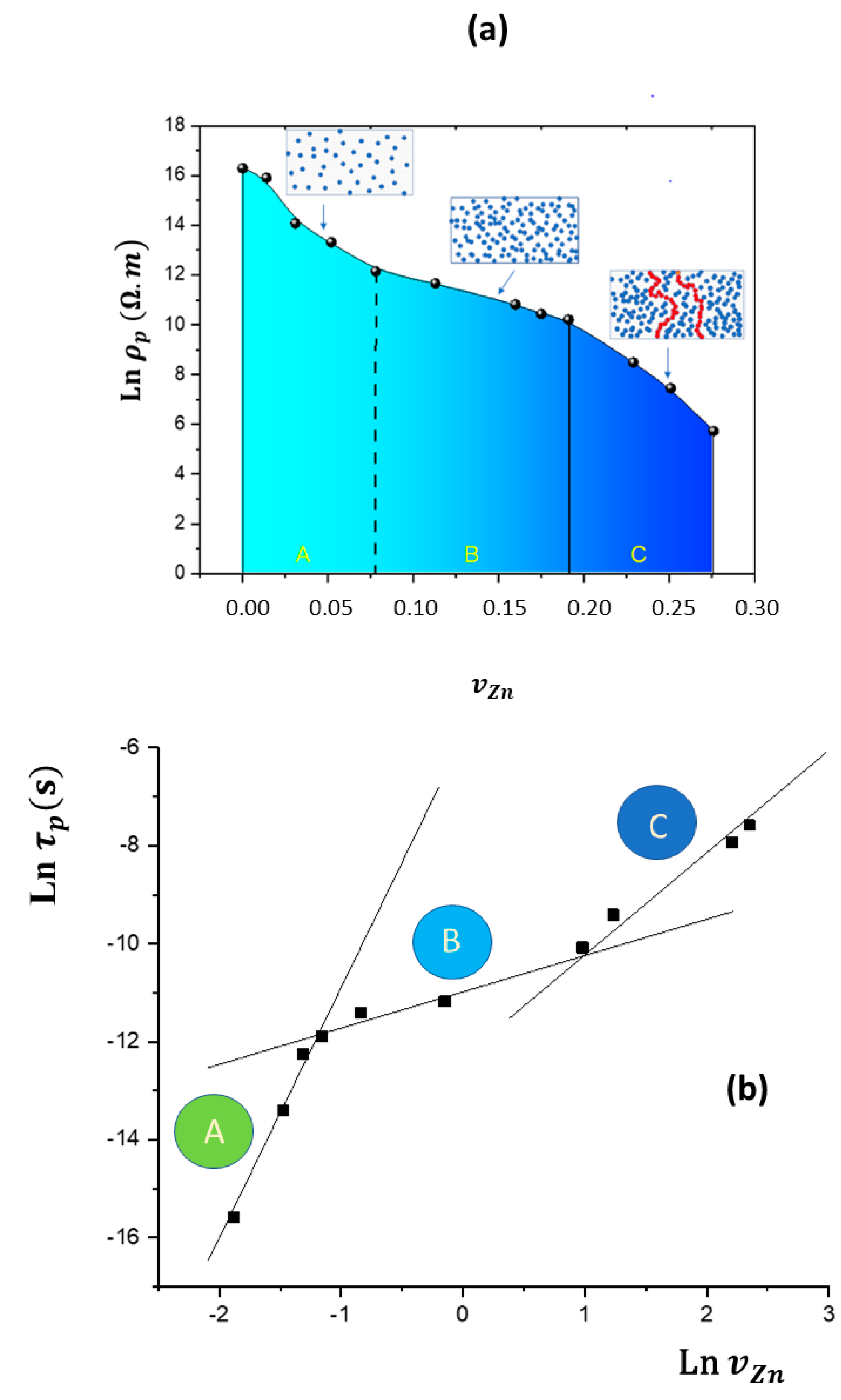
3.3. Electrical AC Characterization
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Xia, Y.; Tian, Y.; Wu, Y.; Liu, J.; He, Q.; Chen, D. Review—Recent Developments on Graphene-Based Electrochemical Sensors toward Nitrite. J. Electrochem. Soc. 2019, 166, B881. [Google Scholar] [CrossRef]
- Huang, W.Y.; Shen, J.W.; Chen, X.M. Effect of Composition on Phase Morphology and Mechanical Properties of PP/PA66 in Situ Composites via Extrusion-Drawing-Injection Method. J. Mater. Sci. 2003, 38, 541–547. [Google Scholar] [CrossRef]
- Rupnowski, P.; Gentz, M.; Sutter, J.K.; Kumosa, M. Mechanical Response of a Woven Graphite/Polyimide Composite to in-Plane Shear Dominated Loads at Room and Elevated Temperatures. Acta Mater. 2004, 52, 5603–5613. [Google Scholar] [CrossRef]
- Appetecchi, G.B.; Scaccia, S.; Passerini, S. Investigation on the Stability of the Lithium-Polymer Electrolyte Interface. J. Electrochem. Soc. 2000, 147, 4448. [Google Scholar] [CrossRef]
- Lee, B.; Dai, G. Influence of Interfacial Modification on the Thermal Conductivity of Polymer Composites. J. Mater. Sci. 2009, 44, 4848–4855. [Google Scholar] [CrossRef]
- Tchmutin, I.A.; Ponomarenko, A.T.; Krinichnaya, E.P.; Kozub, G.I.; Efimov, O.N. Electrical Properties of Composites Based on Conjugated Polymers and Conductive Fillers. Carbon 2003, 41, 1391–1395. [Google Scholar] [CrossRef]
- Navarro, J.; Roig, A.; Noguera, P.; Vicente, F.; Vilaplana, J.; López, J. Electrochemical Behaviour and Electrical Percolation in Graphite-Epoxy Electrodes. J. Mater. Sci. 1994, 29, 4604–4610. [Google Scholar] [CrossRef]
- Agrisuelas, J.; García-Jareño, J.J.; Guillén, E.; Vicente, F. RGB Video Electrochemistry of Copper Electrodeposition/Electrodissolution in Acid Media on a Ternary Graphite:Copper:Polypropylene Composite Electrode. Electrochim. Acta 2019, 305, 72–80. [Google Scholar] [CrossRef]
- Peinado, F.; Roig, A.; Vicente, F.; Vilaplana, J.; López, J. Electrochemical Characterization of Cement/Graphite and Cement/Aluminium Materials. J. Mater. Sci. Lett. 1994, 13, 609–612. [Google Scholar] [CrossRef]
- Aharoni, S.M. Electrical Resistivity of a Composite of Conducting Particles in an Insulating Matrix. J. Appl. Phys. 1972, 43, 2463–2465. [Google Scholar] [CrossRef]
- NavarroLaboulais, J.; Trijueque, J.; GarciaJareno, J.J.; Vicente, F. Ohmic Drop Effect on the Voltammetric Behaviour of Graphite plus Polyethylene Composite Electrodes. J. Electroanal. Chem. 1997, 422, 91–97. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L. A Route for Polymer Nanocomposites with Engineered Electrical Conductivity and Percolation Threshold. Materials 2010, 3, 1089–1103. [Google Scholar] [CrossRef]
- Knozowski, D.; Graczyk-Zajac, M.; Trykowski, G.; Wilamowska-Zawłocka, M. Silicon Oxycarbide-Graphite Electrodes for High-Power Energy Storage Devices. Materials 2020, 13, 4302. [Google Scholar] [CrossRef]
- Ionov, A.N.; Volkov, M.P.; Nikolaeva, M.N.; Smyslov, R.Y.; Bugrov, A.N. Magnetization of Ultraviolet-Reduced Graphene Oxide Flakes in Composites Based on Polystyrene. Materials 2021, 14, 2519. [Google Scholar] [CrossRef]
- Setnescu, R.; Lungulescu, E.-M.; Marinescu, V.E. Polymer Composites with Self-Regulating Temperature Behavior: Properties and Characterization. Materials 2022, 16, 157. [Google Scholar] [CrossRef]
- Lux, F. Models Proposed to Explain the Electrical Conductivity of Mixtures Made of Conductive and Insulating Materials. J. Mater. Sci. 1993, 28, 285–301. [Google Scholar] [CrossRef]
- Chen, X.B.; Issi, J.-P.; Devaux, J.; Billaud, D. The Conducting Behavior and Stability of Conducting Polymer Composites. Polym. Eng. Sci. 1995, 35, 637–641. [Google Scholar] [CrossRef]
- Dupasquier, A.; Fauvarque, J. Study of the Conductivity of Poly(ethylene Oxyde)/Polypyrrole Composites. J. Chim. Phys.-Chim. Biol. 1995, 92, 991–994. [Google Scholar] [CrossRef]
- Ruschau, G.; Yoshikawa, S.; Newnham, R. Resistivities of Conductive Composites. J. Appl. Phys. 1992, 72, 953–959. [Google Scholar] [CrossRef]
- Song, Y.; Noh, T.; Lee, S.; Gaines, J. Experimental-Study of the 3-Dimensional Ac Conductivity and Dielectric-Constant of a Conductor-Insulator Composite Near the Percolation-Threshold. Phys. Rev. B 1986, 33, 904–908. [Google Scholar] [CrossRef]
- Choi, M.; Kim, W.; Lee, S. Conductivity Distribution of Resistor-Capacitor Composites. Phys. Rev. B 1994, 49, 15348–15351. [Google Scholar] [CrossRef]
- Ishigure, Y.; Iijima, S.; Ito, H.; Ota, T.; Unuma, H.; Takahashi, M.; Hikichi, Y.; Suzuki, H. Electrical and Elastic Properties of Conductor-Polymer Composites. J. Mater. Sci. 1999, 34, 2979–2985. [Google Scholar] [CrossRef]
- Balberg, I. A Comprehensive Picture of the Electrical Phenomena in Carbon Black-Polymer Composites. Carbon 2002, 40, 139–143. [Google Scholar] [CrossRef]
- Verbeek, C.J.R. The Influence of Interfacial Adhesion, Particle Size and Size Distribution on the Predicted Mechanical Properties of Particulate Thermoplastic Composites. Mater. Lett. 2003, 57, 1919–1924. [Google Scholar] [CrossRef]
- Xue, Q. The Influence of Particle Shape and Size on Electric Conductivity of Metal–Polymer Composites. Eur. Polym. J. 2004, 40, 323–327. [Google Scholar] [CrossRef]
- Ahmad, Z.; Aleem, B.J.A. Degradation of Aluminum Metal Matrix Composites in Salt Water and Its Control. Mater. Des. 2002, 23, 173–180. [Google Scholar] [CrossRef]
- Malla, P.; Khedmatgozar Dolati, S.S.; Ortiz, J.D.; Mehrabi, A.B.; Nanni, A.; Ding, J. Damage Detection in FRP-Reinforced Concrete Elements. Materials 2024, 17, 1171. [Google Scholar] [CrossRef]
- Dang, Z.M.; Fan, L.Z.; Zhao, S.J.; Nan, C.W. Dielectric Properties and Morphologies of Composites Filled with Whisker and Nanosized Zinc Oxide. Mater. Res. Bull. 2003, 38, 499–507. [Google Scholar] [CrossRef]
- Rusu, M.; Sofian, N.; Rusu, D. Mechanical and Thermal Properties of Zinc Powder Filled High Density Polyethylene Composites. Polym. Test. 2001, 20, 409–417. [Google Scholar] [CrossRef]
- Telli, L.; Hammouche, A.; Brahimi, B.; De Doncker, R.W. Elaboration of a New Anode Material for All-Solid State Zn/MnO2 Protonic Cells. J. Power Sources 2002, 103, 201–206. [Google Scholar] [CrossRef]
- Brito, Z.; Sanchez, G. Influence of Metallic Fillers on the Thermal and Mechanical Behaviour in Composites of Epoxy Matrix. Compos. Struct. 2000, 48, 79–81. [Google Scholar] [CrossRef]
- Das, N.C.; Maiti, S. Electromagnetic Interference Shielding of Carbon Nanotube/Ethylene Vinyl Acetate Composites. J. Mater. Sci. 2008, 43, 1920–1925. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Sun, J.; Gu, X.; Li, H.; Zhang, S. Improving Flame Retardant and Mechanical Properties of Ethylene–Vinyl Acetate by Cured Compound Silicone Decorated Magnesium Hydroxide. J. Mater. Sci. 2022, 57, 2243–2256. [Google Scholar] [CrossRef]
- Singla, R.K.; Maiti, S.N.; Ghosh, A.K. Mechanical, Morphological, and Solid-State Viscoelastic Responses of Poly(Lactic Acid)/Ethylene-Co-Vinyl-Acetate Super-Tough Blend Reinforced with Halloysite Nanotubes. J. Mater. Sci. 2016, 51, 10278–10292. [Google Scholar] [CrossRef]
- Wang, Z.; Tao, J.; Shen, Y.; Liu, S. Molecular Design and Preparation of an Integrated CNT@EVA/PVDF Composite Film Heater for Effective Deicing Applications. J. Mater. Sci. 2022, 57, 1019–1035. [Google Scholar] [CrossRef]
- Baiamonte, M.; Morici, E.; Colletti, C.; Dintcheva, N.T. Polar Wax as Adhesion Promoter in Polymeric Blend Films for Durable Photovoltaic Encapsulants. Materials 2022, 15, 6751. [Google Scholar] [CrossRef]
- Liu, G.-Y.; Sun, W.-F.; Lei, Q.-Q. Charge Injection and Dielectric Characteristics of Polyethylene Terephthalate Based on Semiconductor Electrodes. Materials 2021, 14, 1344. [Google Scholar] [CrossRef]
- Zuo, S.; Xiao, J.; Yuan, Q. Comparative Study on the New-Old Mortar Interface Deterioration after Wet-Dry Cycles and Heat-Cool Cycles. Constr. Build. Mater. 2020, 244, 118374. [Google Scholar] [CrossRef]
- Zeng, L.; Liang, M.; Cai, W.; Tang, J.; Liu, G.; Zhang, J.; Wang, S.; Yang, K. Investigation on Effect of EVA on Properties of Desert Sand-Based Permeable Materials. Case Stud. Constr. Mater. 2023, 18, e02038. [Google Scholar] [CrossRef]
- Udi, U.J.; Yussof, M.M.; Isa, F.N.; Abdullah, L.C. Analysis of Environmental Stresses on the Mechanical Properties of Laminated Glass Composites: A Review of Experimental Results and Outlook. JST 2023, 31, 2339–2359. [Google Scholar] [CrossRef]
- Yan, X.; Wu, D.; Hu, K.; Zhang, W.; Xing, J.; Cui, L.; Shi, S.; Yang, J.; Yang, C. The Modification Mechanism, Evaluation Method, and Construction Technology of Direct-to-Plant SBS Modifiers in Asphalt Mixture: A Review. Polymers 2023, 15, 2768. [Google Scholar] [CrossRef]
- Moroni, S.; Bischi, F.; Aluigi, A.; Campana, R.; Tiboni, M.; Casettari, L. 3D Printing Fabrication of Ethylene-Vinyl Acetate (EVA) Based Intravaginal Rings for Antifungal Therapy. J. Drug Deliv. Sci. Technol. 2023, 84, 104469. [Google Scholar] [CrossRef]
- Slonov, A.; Musov, I.; Zhansitov, A.; Khashirov, A.; Tlupov, A.; Musov, K.; Rzhevskaya, E.; Fomicheva, I.; Potapov, A.; Khashirova, S. Investigation of the Properties of Polyethylene and Ethylene-Vinyl Acetate Copolymer Blends for 3D Printing Applications. Polymers 2023, 15, 4129. [Google Scholar] [CrossRef]
- Padhi, S.; Priyadarsini Jena, D.; Nayak, N.C. Dielectric Behaviour of Ethylene Vinyl Acetate/Cenosphere Composites. Mater. Today Proc. 2020, 30, 355–359. [Google Scholar] [CrossRef]
- Shelenkov, P.G.; Pantyukhov, P.V.; Poletto, M.; Popov, A.A. Influence of Vinyl Acetate Content and Melt Flow Index of Ethylene-Vinyl Acetate Copolymer on Physico-Mechanical and Physico-Chemical Properties of Highly Filled Biocomposites. Polymers 2023, 15, 2639. [Google Scholar] [CrossRef]
- Lim, S.; Ahn, H.-S.; Gasonoo, A.; Lee, J.-H.; Choi, Y. Fabrication of Color Glass by Pearlescent Pigments and Dissolved EVA Film. Materials 2022, 15, 5570. [Google Scholar] [CrossRef]
- Wu, D.; Wessel, P.; Zhu, J.; Montiel-Chicharro, D.; Betts, T.R.; Mordvinkin, A.; Gottschalg, R. Influence of Lamination Conditions of EVA Encapsulation on Photovoltaic Module Durability. Materials 2023, 16, 6945. [Google Scholar] [CrossRef]
- Buczyński, P.; Iwański, M.; Mazurek, G.; Krasowski, J.; Krasowski, M. Effects of Portland Cement and Polymer Powder on the Properties of Cement-Bound Road Base Mixtures. Materials 2020, 13, 4253. [Google Scholar] [CrossRef]
- Brachaczek, W.; Chleboś, A.; Giergiczny, Z. Influence of Polymer Modifiers on Selected Properties and Microstructure of Cement Waterproofing Mortars. Materials 2021, 14, 7558. [Google Scholar] [CrossRef]
- Cao, R.; Yang, J.; Li, G.; Niu, M. Effect of Sulfuric Acid on Cementitious Composites Containing Ethylene-Vinyl Acetate and Styrene-Butadiene Rubber. J. Build. Eng. 2023, 80, 108024. [Google Scholar] [CrossRef]
- Kou, Y.; Cheng, X.; Macosko, C.W. Degradation and Breakdown of Polymer/Graphene Composites under Strong Electric Field. J. Compos. Sci. 2022, 6, 139. [Google Scholar] [CrossRef]
- Ferri, J.M.; Garcia-Garcia, D.; Rayón, E.; Samper, M.D.; Balart, R. Compatibilization and Characterization of Polylactide and Biopolyethylene Binary Blends by Non-Reactive and Reactive Compatibilization Approaches. Polymers 2020, 12, 1344. [Google Scholar] [CrossRef]
- Wang, P.; Song, T.; Abo-Dief, H.M.; Song, J.; Alanazi, A.K.; Fan, B.; Huang, M.; Lin, Z.; Altalhi, A.A.; Gao, S.; et al. Effect of Carbon Nanotubes on the Interface Evolution and Dielectric Properties of Polylactic Acid/Ethylene–Vinyl Acetate Copolymer Nanocomposites. Adv. Compos. Hybrid. Mater. 2022, 5, 1100–1110. [Google Scholar] [CrossRef]
- Stalmann, G.; Matic, A.; Jacobsson, P.; Tranchida, D.; Gitsas, A.; Gkourmpis, T. Crystallisation Kinetics and Associated Electrical Conductivity Dynamics of Poly(Ethylene Vinyl Acetate) Nanocomposites in the Melt State. Nanomaterials 2022, 12, 3602. [Google Scholar] [CrossRef]
- Shang, H.; Hou, G.; Sun, C.; Lu, D.; Zhao, X.; Fan, L. EVA Enhanced Cementitious Materials Based Coatings for the Improvement of Steel Reinforcement Corrosion Protection Performance. J. Build. Eng. 2023, 75, 107080. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data; CRC Press: Boca Raton, FL, USA, 1995; ISBN 978-0-8493-0595-5. [Google Scholar]
- EN ISO 527-2:2012; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. International Organization for Standardization: Geneva, Switzerland, 2012.
- Krupa, I.; Chodak, I. Physical Properties of Thermoplastic/Graphite Composites. Eur. Polym. J. 2001, 37, 2159–2168. [Google Scholar] [CrossRef]
- Krupa, I.; Novak, I.; Chodak, I. Electrically and Thermally Conductive Polyethylene/Graphite Composites and Their Mechanical Properties. Synth. Met. 2004, 145, 245–252. [Google Scholar] [CrossRef]
- Novak, I.; Krupa, I. Electro-Conductive Resins Filled with Graphite for Casting Applications. Eur. Polym. J. 2004, 40, 1417–1422. [Google Scholar] [CrossRef]
- Segurado, J.; Gonzalez, C.; Llorca, J. A Numerical Investigation of the Effect of Particle Clustering on the Mechanical Properties of Composites. Acta Mater. 2003, 51, 2355–2369. [Google Scholar] [CrossRef]
- Buchdahl, R. Mechanical Properties of Polymers and Composites—Vols. I and II, Lawrence E. Nielsen, Marcel Dekker, Inc., New York, 1974, Vol. I 255 Pp. Vol. II 301 Pp. Vol. I $24.50, Vol. II $28.75. J. Polym. Sci. Polym. Lett. Ed. 1975, 13, 120–121. [Google Scholar] [CrossRef]
- Chalivendra, V.B.; Shukla, A.; Bose, A.; Parameswaran, V. Processing and Mechanical Characterization of Lightweight Polyurethane Composites. J. Mater. Sci. 2003, 38, 1631–1643. [Google Scholar] [CrossRef]
- Guth, E. Theory of Filler Reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]
- Zhang, Q.-H.; Chen, D.-J. Percolation Threshold and Morphology of Composites of Conducting Carbon Black/Polypropylene/EVA. J. Mater. Sci. 2004, 39, 1751–1757. [Google Scholar] [CrossRef]
- Novak, I.; Krupa, I.; Chodak, I. Analysis of Correlation between Percolation Concentration and Elongation at Break in Filled Electroconductive Epoxy-Based Adhesives. Eur. Polym. J. 2003, 39, 585–592. [Google Scholar] [CrossRef]
- Navarro-Laboulais, J.; García-Jareño, J.J.; Vicente, F. Kramers–Kronig Transformation, Dc Behaviour and Steady State Response of the Warburg Impedance for a Disk Electrode Inlaid in an Insulating Surface. J. Electroanal. Chem. 2002, 536, 11–18. [Google Scholar] [CrossRef]
- Beaunier, L.; Keddam, M.; Garcia-Jareno, J.J.; Vicente, F.; Navarro-Laboulais, J. Surface Structure Determination by SEM Image Processing and Electrochemical Impedance of Graphite plus Polyethylene Composite Electrodes. J. Electroanal. Chem. 2004, 566, 159–167. [Google Scholar] [CrossRef]
- Trijueque, J.; García-Jareño, J.J.; Navarro-Laboulais, J.; Sanmatías, A.; Vicente, F. Ohmic Drop of Prussian-Blue/Graphite+epoxy Electrodes. Electrochim. Acta 1999, 45, 789–795. [Google Scholar] [CrossRef]
- Gimenezromero, D. Correlation between the Fractal Dimension of the Electrode Surface and the EIS of the Zinc Anodic Dissolution for Different Kinds of Galvanized Steel. Electrochem. Commun. 2004, 6, 148–152. [Google Scholar] [CrossRef]
- García-Jareño, J.J.; Giménez-Romero, D.; Keddam, M.; Vicente, F. Graphical Analysis of Electrochemical Impedance Spectroscopy of Two Consecutive Irreversible Electron Transfers. 2. Zinc Anodic Dissolution in Acid Media. J. Phys. Chem. B 2005, 109, 4593–4598. [Google Scholar] [CrossRef]
- Himadri Reddy, P.C.; Amalraj, J.; Ranganatha, S.; Patil, S.S.; Chandrasekaran, S. A Review on Effect of Conducting Polymers on Carbon-Based Electrode Materials for Electrochemical Supercapacitors. Synth. Met. 2023, 298, 117447. [Google Scholar] [CrossRef]
- Fang, H.; Yang, D.; Su, Z.; Sun, X.; Ren, J.; Li, L.; Wang, K. Preparation and Application of Graphene and Derived Carbon Materials in Supercapacitors: A Review. Coatings 2022, 12, 1312. [Google Scholar] [CrossRef]
- Meng, Q.; Cai, K.; Chen, Y.; Chen, L. Research Progress on Conducting Polymer Based Supercapacitor Electrode Materials. Nano Energy 2017, 36, 268–285. [Google Scholar] [CrossRef]
- Faga, M.; Duraccio, D.; Di Maro, M.; Pedraza, R.; Bartoli, M.; d’Ayala, G.; Torsello, D.; Ghigo, G.; Malucelli, G. Ethylene-Vinyl Acetate (EVA) Containing Waste Hemp-Derived Biochar Fibers: Mechanical, Electrical, Thermal and Tribological Behavior. Polymers 2022, 14, 4171. [Google Scholar] [CrossRef]
- Parida, S.; Malik, R.; Parida, R.K.; Parida, B.N.; Nayak, N.C. Dielectric Behavior of EVA/EOC/xGnP Ternary Microcellular Nanocomposites. J. Mater. Sci. Mater. Electron. 2022, 33, 23693–23702. [Google Scholar] [CrossRef]
- Li, S.; Gao, W.; Zhang, Q.; Jiang, Z.; Chen, L. The Strain Sensoring Behavior of the Melt-Extruded Ethylene-Vinyl Acetate (EVA)/Carbon Black Composites Filament. Mater. Plast. 2001, 59, 165–176. [Google Scholar] [CrossRef]
- Sandu, I.-L.; Stan, F.; Fetecau, C. Mechanical Recycling of Ethylene-Vinyl Acetate/Carbon Nanotube Nanocomposites: Processing, Thermal, Rheological, Mechanical and Electrical Behavior. Polymers 2023, 15, 583. [Google Scholar] [CrossRef]
- Rahaman, M.; Gupta, P.; Hossain, M.; Periyasami, G.; Das, P. Effect of Carbons’ Structure and Type on AC Electrical Properties of Polymer Composites: Predicting the Percolation Threshold of Permittivity through Different Models. Colloid. Polym. Sci. 2023, 301, 1001–1019. [Google Scholar] [CrossRef]
- Agrisuelas, J.; García-Jareño, J.J.; Piedras, M.; Vicente, F. Quality and Efficiency Control of Electrodeposition and Electrodissolution of Ni on a Ternary Composite Electrode Followed by Digital Video Electrochemistry. J. Electrochem. Soc. 2023, 170, 072505. [Google Scholar] [CrossRef]
- Subiela, J.R.; López, J.; Balart, R.; García-Jareño, J.J.; Vicente, F. Electrical Properties of EVA Filled by Zinc Powder. J. Mater. Sci. 2006, 41, 6396–6402. [Google Scholar] [CrossRef]
- García-Jareño, J.J.; Agrisuelas, J.; Vicente, F. Overview and Recent Advances in Hyphenated Electrochemical Techniques for the Characterization of Electroactive Materials. Materials 2023, 16, 4226. [Google Scholar] [CrossRef]


| Shore D | FC | ||||
|---|---|---|---|---|---|
| (%) | (%) | (%) | MPa | MPa | |
| 0 | 0 | 30 | 10.47 | 10.18 | 0.97 |
| 10 | 1.4 | 31 | 9.11 | 9.34 | 1.03 |
| 20 | 3.1 | 33 | 3.43 | 4.73 | 1.38 |
| 30 | 5.2 | 35 | 2.66 | 4.36 | 1.64 |
| 40 | 7.8 | 36 | 0.86 | 3.97 | 4.62 |
| 50 | 11.3 | 36 | 0.43 | 3.49 | 8.08 |
| 60 | 16.0 | 38 | 0.31 | 3.48 | 11.09 |
| 65 | 19.1 | 41 | 0.27 | 3.44 | 12.71 |
| 70 | 22.9 | 44 | 0.23 | 3.40 | 14.86 |
| 75 | 27.6 | 45 | 0.15 | 2.98 | 19.51 |
Degree | Ω·m | pF·m-1 | µs | ||
|---|---|---|---|---|---|
| 0 | 0 | 89.9 | 1.19 × 107 | 43 | 510 |
| 10 | 0 | 89.8 | 8.13 × 106 | 44 | 360 |
| 20 | 0 | 88.9 | 1.30 × 106 | 63 | 82 |
| 30 | 0 | 87.4 | 6.09 × 105 | 69 | 42 |
| 40 | 0 | 83.2 | 1.89 × 105 | 70 | 14 |
| 50 | 0 | 81.5 | 1.17 × 105 | 92 | 11 |
| 60 | 0 | 77.0 | 4.99 × 104 | 137 | 6.9 |
| 62.5 | 0 | 72.0 | 3.39 × 104 | 145 | 4.9 |
| 65 | 0 | 71.2 | 2.73 × 104 | 175 | 4.8 |
| 70 | 0 | 38.1 | 4.87 × 103 | 300 | 0.15 |
| 75 | 0 | 5.8 | 3.09 × 102 | 544 | 0.17 |
| 0 | 50 | 72.0 | 1.83 × 104 | 267 | 4.9 |
| 10 | 50 | 20.6 | 5.74 × 102 | 1000 | 0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrisuelas, J.; Balart, R.; García-Jareño, J.J.; López-Martínez, J.; Vicente, F. A Macroscopic Interpretation of the Correlation between Electrical Percolation and Mechanical Properties of Poly-(Ethylene Vinyl Acetate)/Zn Composites. Materials 2024, 17, 2527. https://doi.org/10.3390/ma17112527
Agrisuelas J, Balart R, García-Jareño JJ, López-Martínez J, Vicente F. A Macroscopic Interpretation of the Correlation between Electrical Percolation and Mechanical Properties of Poly-(Ethylene Vinyl Acetate)/Zn Composites. Materials. 2024; 17(11):2527. https://doi.org/10.3390/ma17112527
Chicago/Turabian StyleAgrisuelas, Jerónimo, Rafael Balart, José J. García-Jareño, Juan López-Martínez, and Francisco Vicente. 2024. "A Macroscopic Interpretation of the Correlation between Electrical Percolation and Mechanical Properties of Poly-(Ethylene Vinyl Acetate)/Zn Composites" Materials 17, no. 11: 2527. https://doi.org/10.3390/ma17112527
APA StyleAgrisuelas, J., Balart, R., García-Jareño, J. J., López-Martínez, J., & Vicente, F. (2024). A Macroscopic Interpretation of the Correlation between Electrical Percolation and Mechanical Properties of Poly-(Ethylene Vinyl Acetate)/Zn Composites. Materials, 17(11), 2527. https://doi.org/10.3390/ma17112527









