Effect of Strain Rate on Mechanical Deformation Behavior in CuZr Metallic Glass
Abstract
1. Introduction
2. Model and Method
3. Results and Discussions
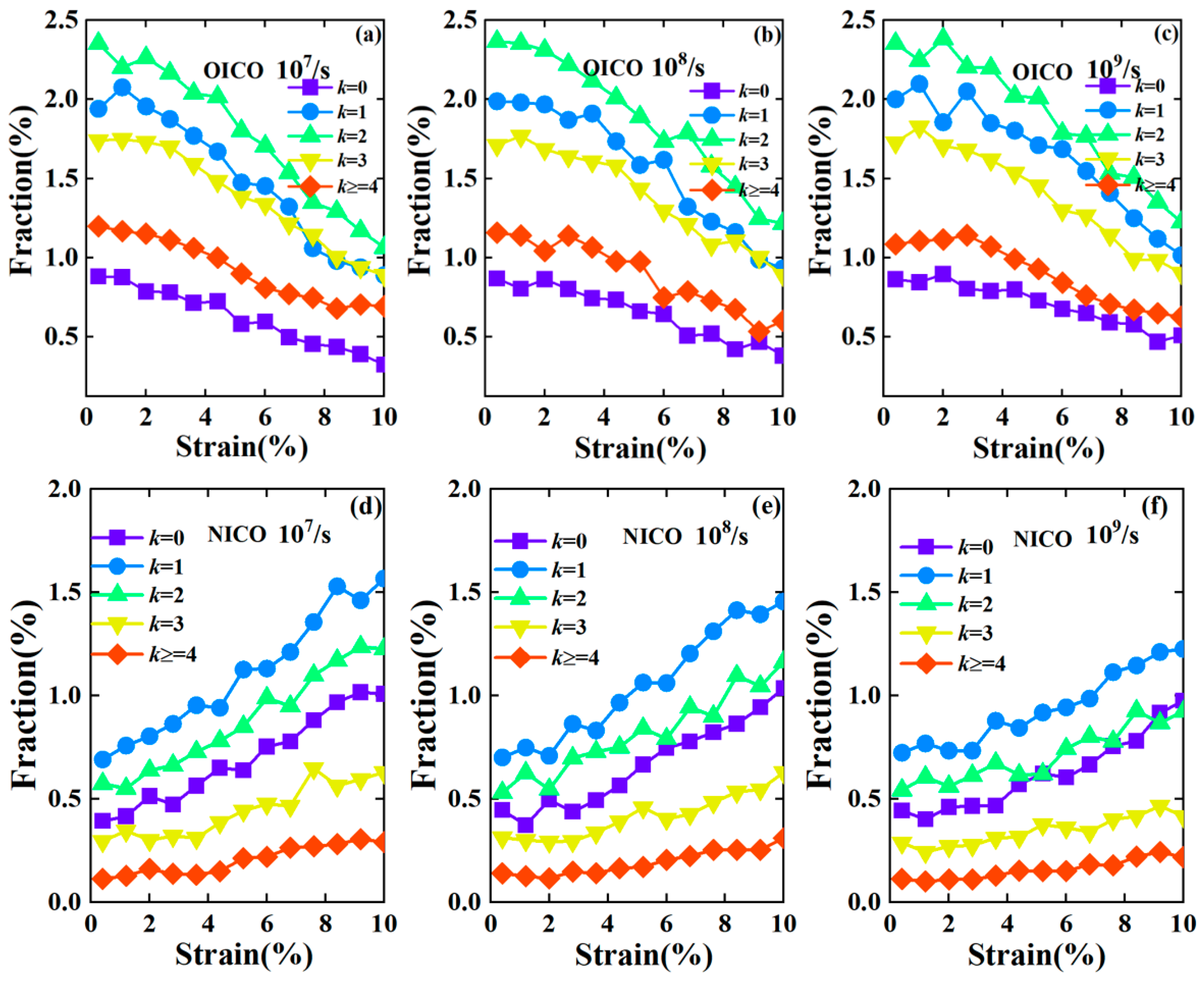
3.1. Atomic Structural Evolution with Different Strain Rates
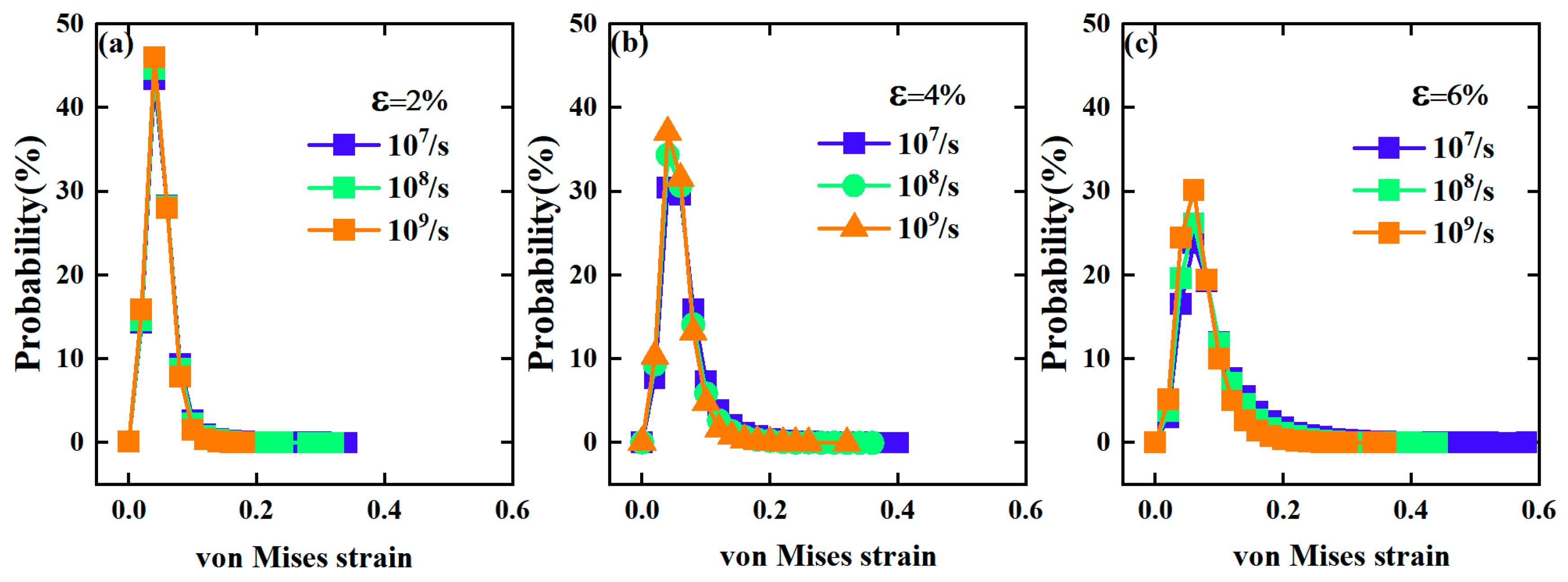
3.2. Mechanical Response to Different Strain Rates
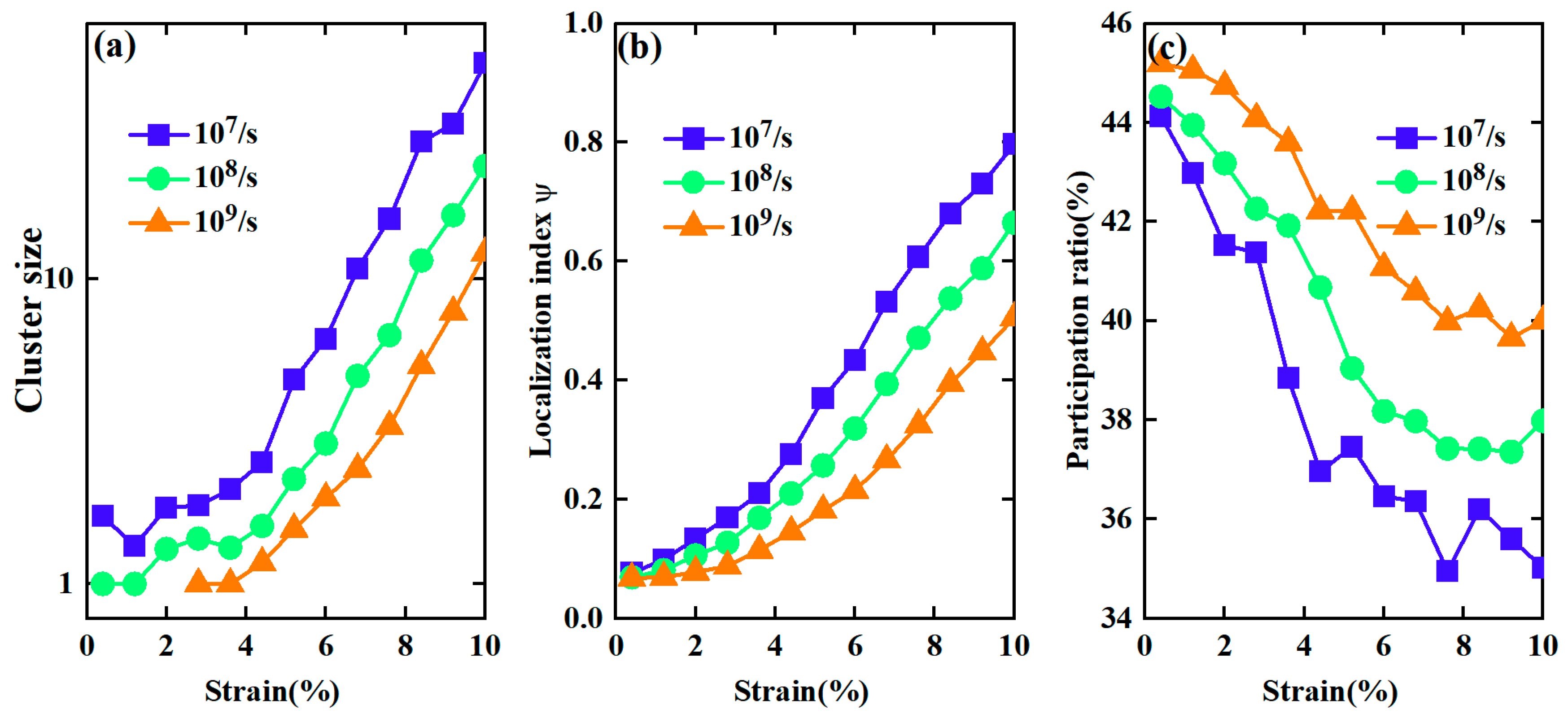
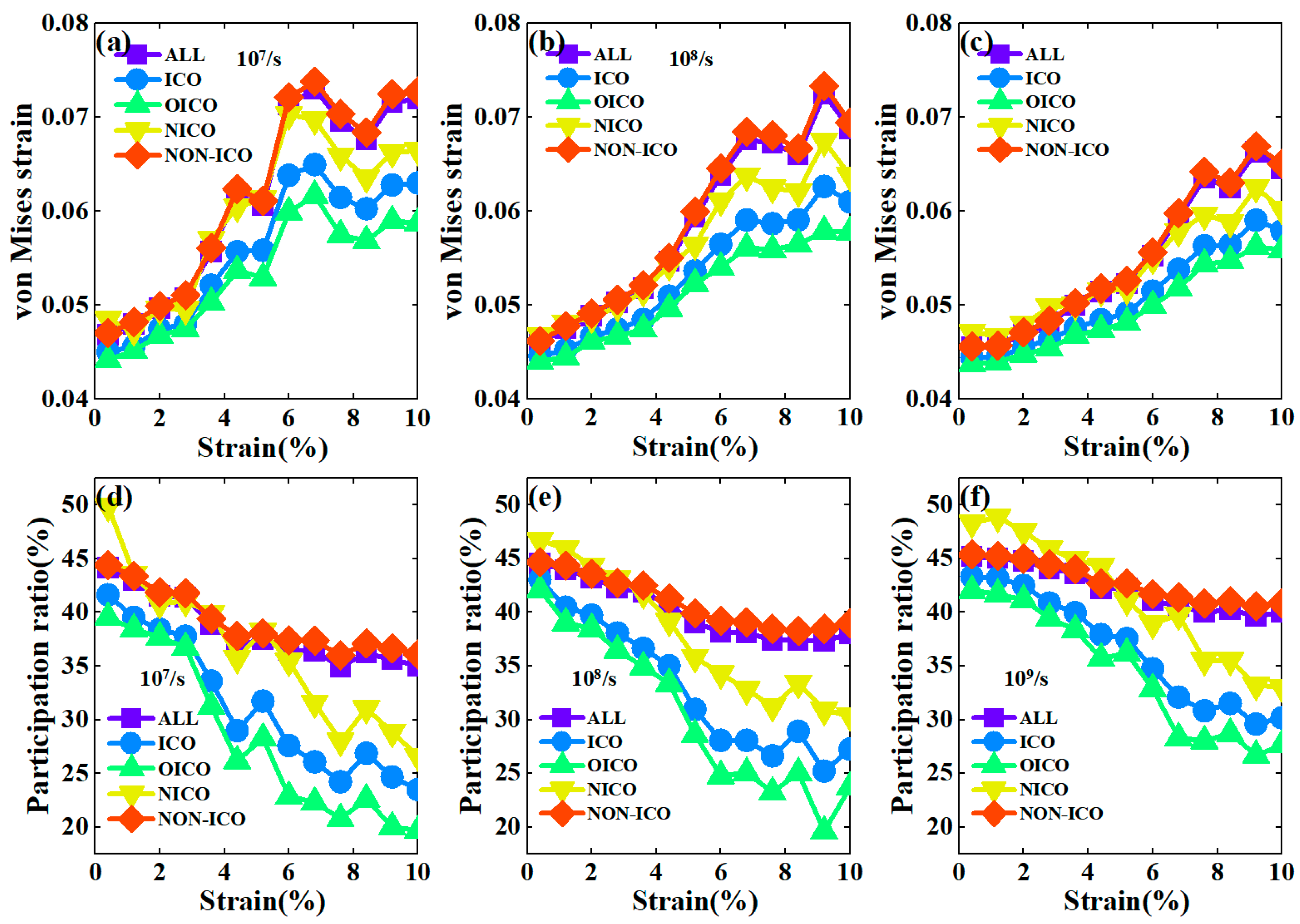
3.3. Correlation between Atomic Structure and Mechanical Response
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.H. The elastic properties, elastic models and elastic perspectives of metallic glasses. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar] [CrossRef]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta. Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Shi, H.Q.; Zhao, W.B.; Wei, X.W.; Ding, Y.; Shen, X.D.; Liu, W.J. Effect of Ti addition on mechanical properties and corrosion resistance of Ni-free Zr-based bulk metallic glasses for potential biomedical applications. J. Alloys Compd. 2020, 815, 152636. [Google Scholar] [CrossRef]
- Yang, L.Q.; Fan, J.T.; Vu-Bac, N.; Rabczuk, T. A nanoscale study of the negative strain rate dependency of the strength of metallic glasses by molecular dynamics simulations. Phys. Chem. Chem. Phys. 2018, 20, 26552–26557. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, J.J.; Greer, A.L. Temperature rise at shear bands in metallic glassed. Nat. Mater. 2006, 5, 15–18. [Google Scholar] [CrossRef]
- Guo, H.; Yan, P.F.; Wang, Y.B.; Tan, J.; Zhang, Z.F.; Sui, M.L.; Ma, E. Tensile ductility and necking of metallic glass. Nat. Mater. 2007, 10, 735–739. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.C.; Jian, W.R.; Huang, J.Y.; Zhao, F.; Li, C.; Xiao, X.H.; Yao, X.H.; Luo, S.N. Spall damage of a Ta particle-reinforced metallic glass matrix composite under high strain rate loading. Mater. Sci. Eng. A 2018, 711, 284–292. [Google Scholar] [CrossRef]
- Huang, C.M.; Li, S.; Bai, S.X. Quasi-static and impact-initiated response of Zr55Ni5Al10Cu30 alloy. J. Non-Cryst. Solids 2018, 481, 59–64. [Google Scholar] [CrossRef]
- Wang, C.T.; He, Y.; Ji, C.; He, Y.; Han, W.; Pan, X.C. Investigation on shock-induced reaction characteristics of a Zr-based metallic glass. Intermetallics 2018, 93, 383–388. [Google Scholar] [CrossRef]
- Lyu, G.J.; Qiao, J.C.; Pelletier, J.M.; Yao, Y. The dynamic mechanical characteristics of Zr-based bulk metallic glasses and composites. Mater. Sci. Eng. A 2018, 711, 356–363. [Google Scholar] [CrossRef]
- Ma, W.F.; Kou, H.C.; Li, J.S.; Chang, H.; Zhou, L. Effect of strain rate on compressive behavior of Ti-based bulk metallic glass at room temperature. J. Alloys Compd. 2009, 472, 214–218. [Google Scholar] [CrossRef]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Natl. Acad. Sci. USA 2008, 105, 14769–14772. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.X.; Cheng, M.; Meng, L.Y.; Yao, X.H. Microstructural evolution of shear bands formation of metallic glasses under different loading conditions and strain rates. J. Non-Cryst. Solids 2022, 584, 121525. [Google Scholar] [CrossRef]
- Yuan, X.; Şopu, D.; Moitzi, F.; Song, K.K.; Eckert, J. Intrinsic and extrinsic effects on the brittle-to-ductile transition in metallic glasses. J. Appl. Phys. 2020, 128, 125102. [Google Scholar] [CrossRef]
- Albe, K.; Ritter, Y.; Şopu, D. Enhancing the plasticity of metallic glasses: Shear band formation, nanocomposites and nanoglasses investigated by molecular dynamics simulations. Mech. Mater. 2013, 67, 94–103. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, Y.J.; Wang, G.Y.; Liaw, P.K.; Shen, J. Influence of Strain Rate on Compressive Deformation Behavior of a Zr-Cu-Ni-Al Bulk Metallic Glass at Room Temperature. Metall. Mater. Trans. A 2011, 42, 1491–1498. [Google Scholar] [CrossRef]
- Li, H.; Subhash, G.; Gao, X.L.; Kecskes, L.J.; Dowding, R.J. Negative strain rate sensitivity and compositional dependence of fracture strength in Zr/Hf based bulk metallic glasses. Scr. Mater. 2003, 49, 1087–1092. [Google Scholar] [CrossRef]
- Mukai, T.; Nieh, T.G.; Kawamura, Y.; Inoue, A.; Higashi, K. Dynamic response of a Pd40Ni40P20 bulk metallic glass in tension. Scr. Mater. 2002, 46, 43–47. [Google Scholar] [CrossRef]
- Tokunaga, H.; Fujita, K.; Yokoyama, Y. Tensile Plastic Deformation Behavior of Zr70Ni16Cu6Al8 Bulk Metallic Glass at Cryogenic Temperature. Mater. Trans. 2012, 53, 1395–1399. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Eckert, J.; Schultz, L. Difference in compressive and tensile fracture mechanisms of Zr59Cu20Al10Ni8Ti3 bulk metallic glass. Acta Mater. 2003, 51, 1167–1179. [Google Scholar] [CrossRef]
- Zhang, W.J.; Tao, P.J.; Chen, Y.; Si, J.F.; Long, Z.Y.; Huang, S.K.; He, H.J.; Huang, Z.H.; Yang, Y.Z. Structural evolutionary behavior of Zr-based bulk metallic glasses under thermoplastic deformation. Intermetallics 2023, 155, 107831. [Google Scholar] [CrossRef]
- Samiri, A.; Khmich, A.; Haouas, H.; Hassani, A.; Hasnaoui, A. Structural and mechanical behaviors of Mg-Al metallic glasses investigated by molecular dynamics simulations. Comput. Mater. Sci. 2020, 184, 109895. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Kramer, M.J.; Ott, R.T.; Sordelet, D.J.; Yagodin, P.; Popel, P. Development of suitable interatomic potentials for simulation of liquid and amorphous Cu–Zr alloys. Philos. Mag. 2009, 89, 967. [Google Scholar] [CrossRef]
- Li, F.X.; Li, M.Z. Local environments of atomic clusters and the effect on dynamics in CuZr metallic glass-forming liquids. J. Appl. Phys. 2017, 122, 225103. [Google Scholar] [CrossRef]
- Wu, Z.W.; Li, M.Z.; Wang, W.H.; Liu, K.X. Correlation between structural relaxation and connectivity of icosahedral clusters in CuZr metallic glass-forming liquids. Phys. Rev. B 2013, 88, 054202. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Cao, A.J.; Sheng, H.W.; Ma, E. Local order influences initiation of plastic flow in metallic glass: Effects of alloy composition and sample cooling history. Acta Mater. 2008, 56, 5263–5275. [Google Scholar] [CrossRef]
- Cao, A.J.; Cheng, Y.Q.; Ma, E. Structural processes that initiate shear localization in metallic glass. Acta Mater. 2009, 57, 5146–5155. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Ma, E. Intrinsic shear strength of metallic glass. Acta Mater. 2011, 59, 1800–1807. [Google Scholar] [CrossRef]
- Yue, X.X.; Brechtl, J.; Wang, F.; Chang, Z.; Liaw, P.K.; Fan, C. Deformation behavior of annealed Cu64Zr36 metallic glass via molecular dynamics simulations. Mater. Des. 2020, 191, 108660. [Google Scholar] [CrossRef]
- Voronoi, G. New parametric applications concerning the theory of quadratic forms-second announcement, J. R. Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Li, M.Z.; Wang, C.Z.; Hao, S.G.; Kramer, M.J.; Ho, K.M. Structural heterogeneity and medium-range order in ZrxCu100 − x metallic glasses. Phys. Rev. B 2009, 80, 184201. [Google Scholar] [CrossRef]
- Shimizu, F.; Ogata, S.; Li, J. Theory of shear banding in metallic glasses and molecular dynamics calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Cao, A.J.; Ma, E. Correlation between the elastic modulus and the intrinsic plastic behavior of metallic glasses: The roles of atomic configuration and alloy composition. Acta Mater. 2009, 57, 3253–3267. [Google Scholar] [CrossRef]
- Şopu, D.; Yuan, X.; Moitzi, F.; Spieckermann, F.; Bian, X.; Eckert, J. From elastic excitations to macroscopic plasticity in metallic glasses. Appl. Mater. Today 2021, 22, 100958. [Google Scholar] [CrossRef]
- Shi, Y.F.; Falk, M.L. Atomic-scale simulations of strain localization in three-dimensional model amorphous solids. Phys. Rev. B 2006, 73, 214201. [Google Scholar] [CrossRef]
- Wang, C.C.; Wong, C.H. Different icosahedra in metallic glasses: Stability and response to shear transformation. Scr. Mater. 2012, 66, 610–613. [Google Scholar] [CrossRef]
- Wang, P.F.; Peng, C.X.; Cheng, Y.; Jia, L.J.; Wang, Y.Y.; Wang, L. Atomic structure evolution of (CuZr)100-xAgx glass under compression deformation. J. Alloys Compd. 2019, 777, 44–51. [Google Scholar] [CrossRef]
- Fan, B.B.; Li, M.Z. Topology of icosahedral network responsible for yielding in CuZr metallic glasses. Comput. Mater. Sci. 2024, 233, 112682. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, B.; Li, M. Effect of Strain Rate on Mechanical Deformation Behavior in CuZr Metallic Glass. Materials 2024, 17, 2507. https://doi.org/10.3390/ma17112507
Fan B, Li M. Effect of Strain Rate on Mechanical Deformation Behavior in CuZr Metallic Glass. Materials. 2024; 17(11):2507. https://doi.org/10.3390/ma17112507
Chicago/Turabian StyleFan, Beibei, and Maozhi Li. 2024. "Effect of Strain Rate on Mechanical Deformation Behavior in CuZr Metallic Glass" Materials 17, no. 11: 2507. https://doi.org/10.3390/ma17112507
APA StyleFan, B., & Li, M. (2024). Effect of Strain Rate on Mechanical Deformation Behavior in CuZr Metallic Glass. Materials, 17(11), 2507. https://doi.org/10.3390/ma17112507





