Microhardness Variation with Indentation Depth for Body-Centered Cubic Steels Pertinent to Grain Size and Ferrite Content
Abstract
1. Introduction
2. Experiments and Data
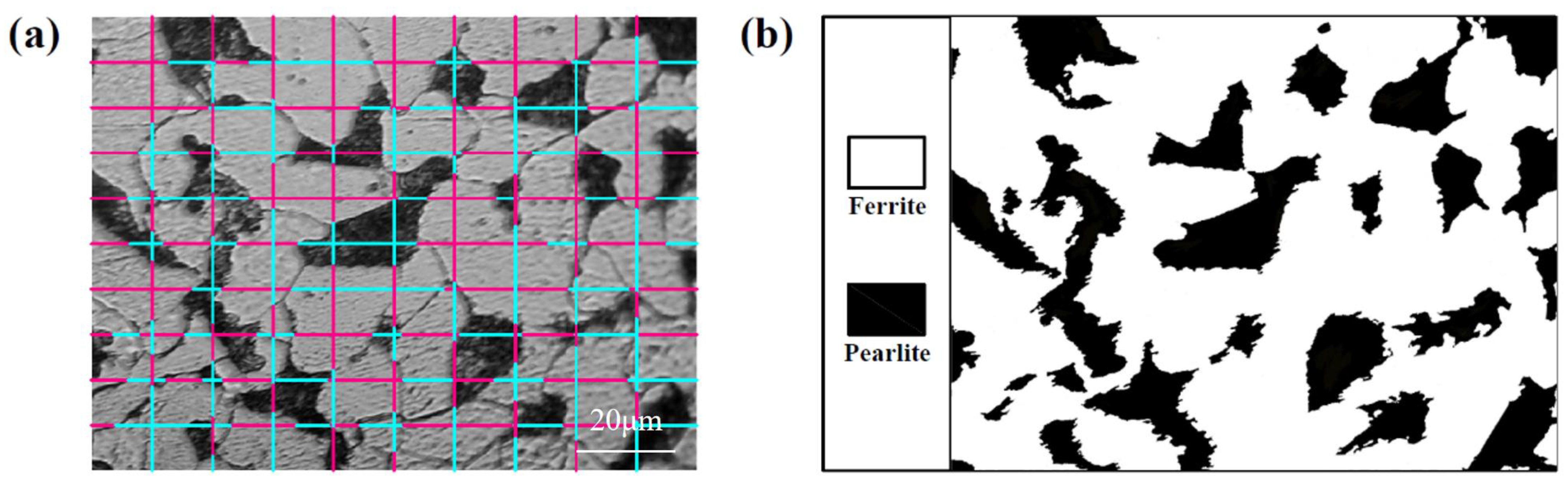
2.1. Measurements on Hardness, Grain Size and Ferrite Volume Fraction
2.2. Experimental Data
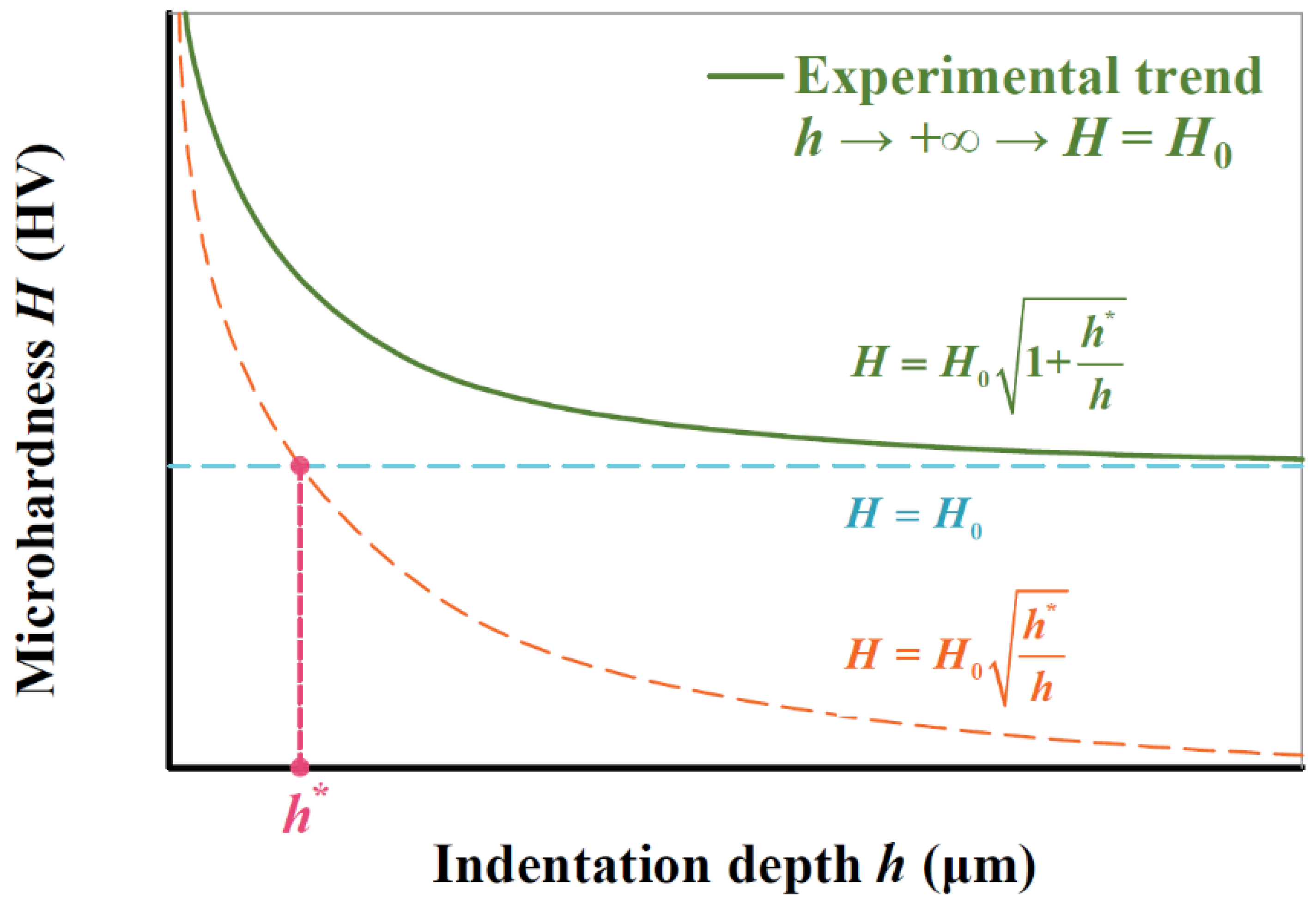
3. Analytical H–H0 Relation by Linking h* to G and VF
3.1. Theoretical Derivation
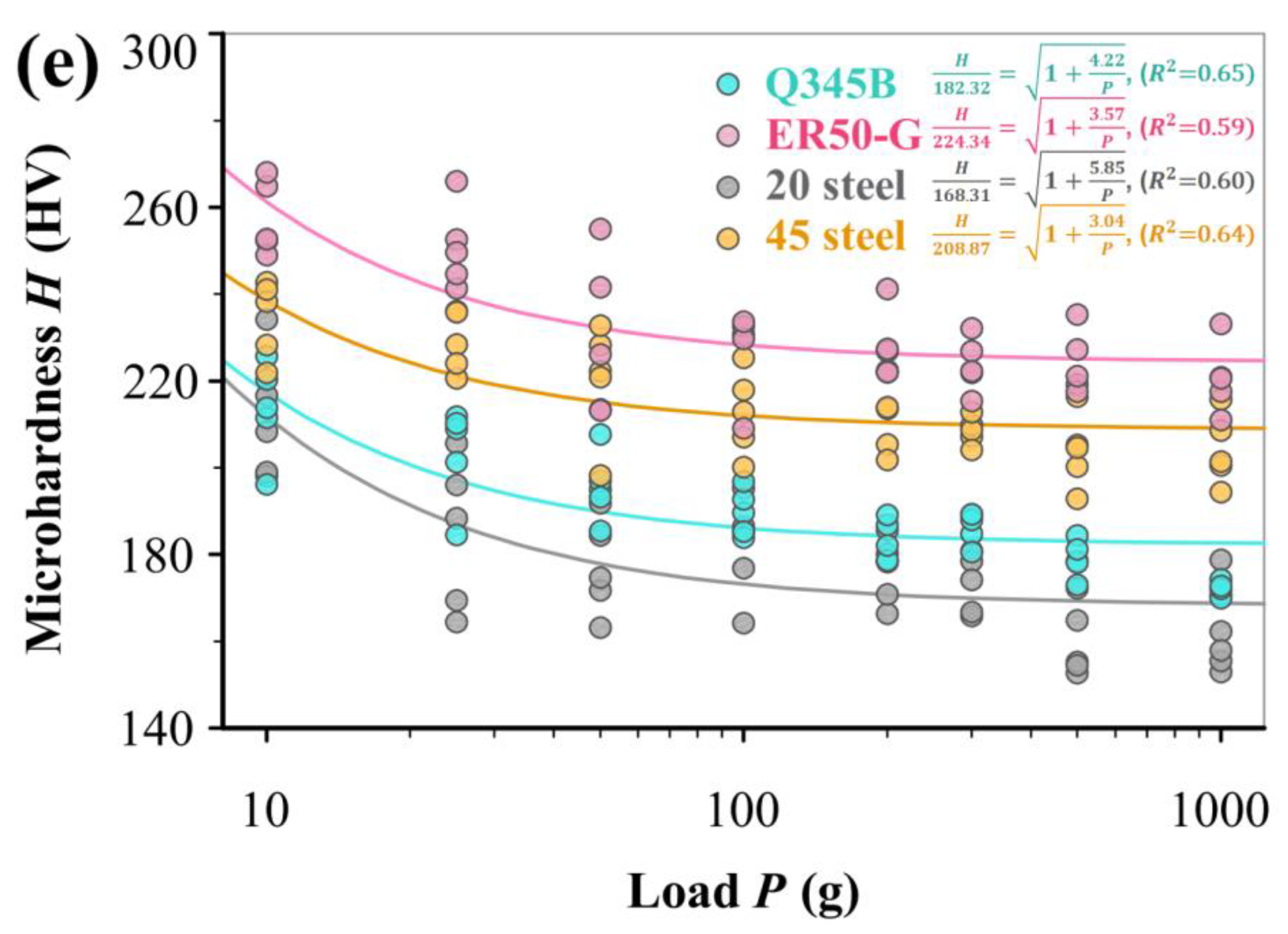
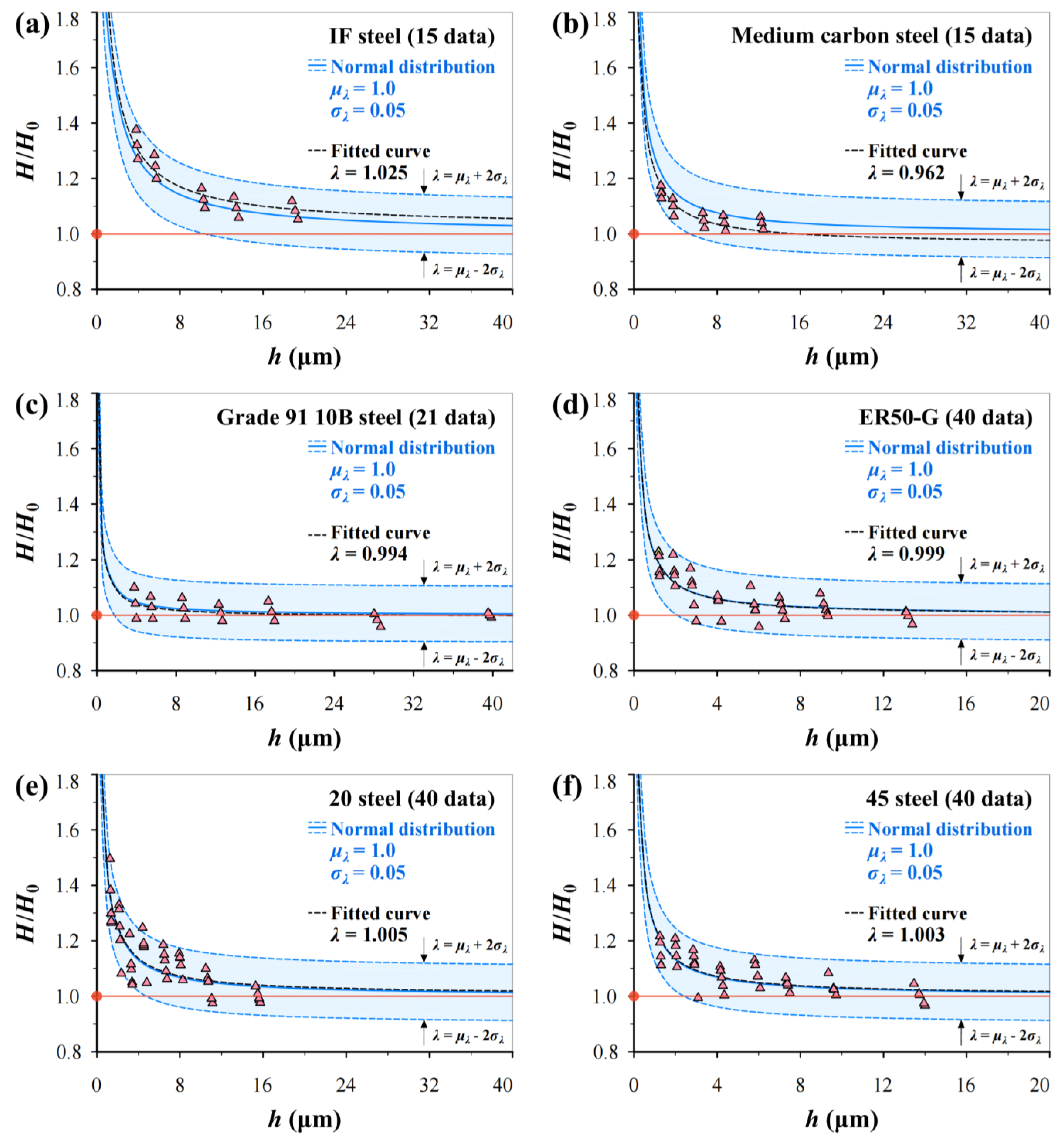
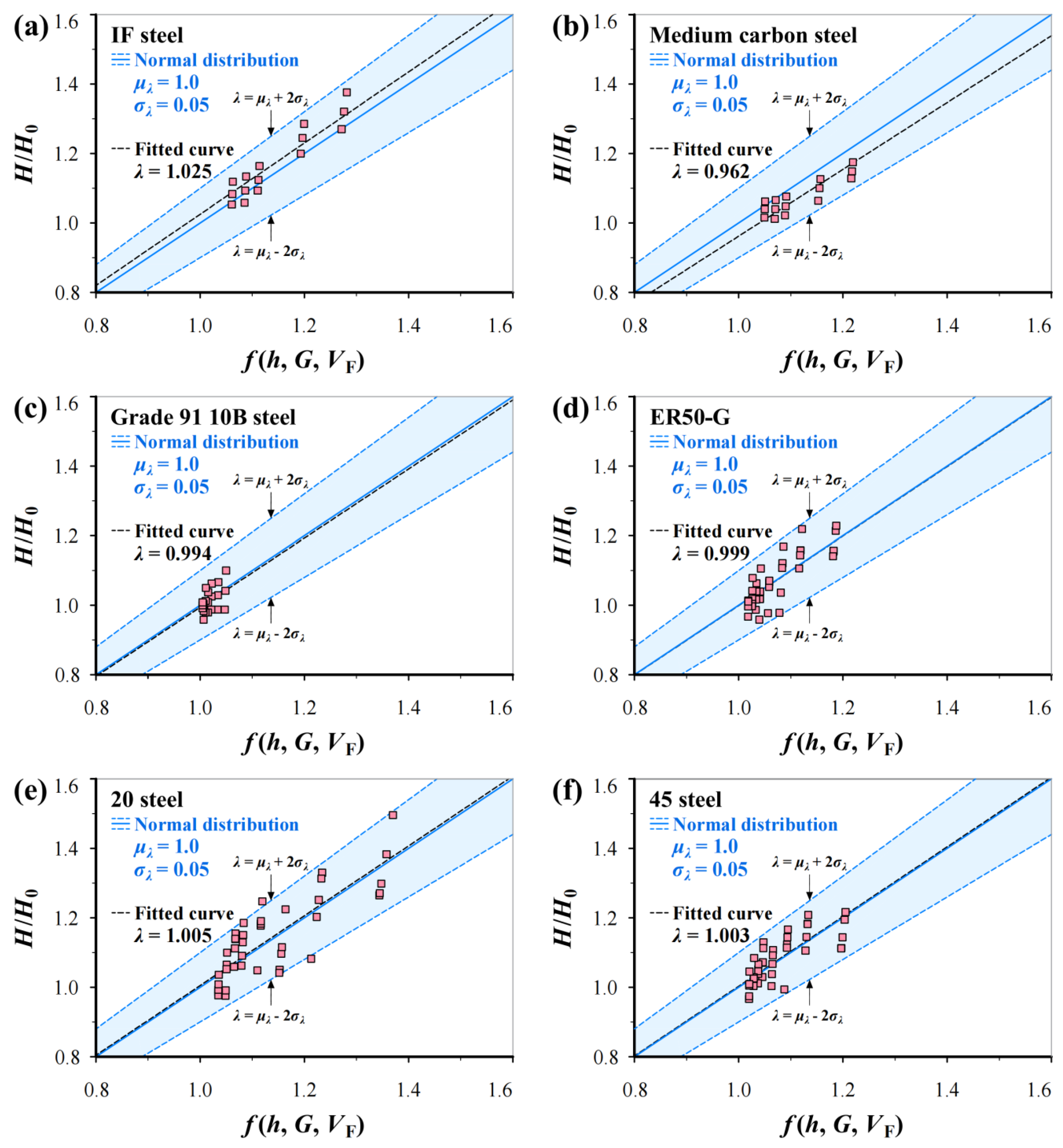
3.2. Analysis of Experimental Data
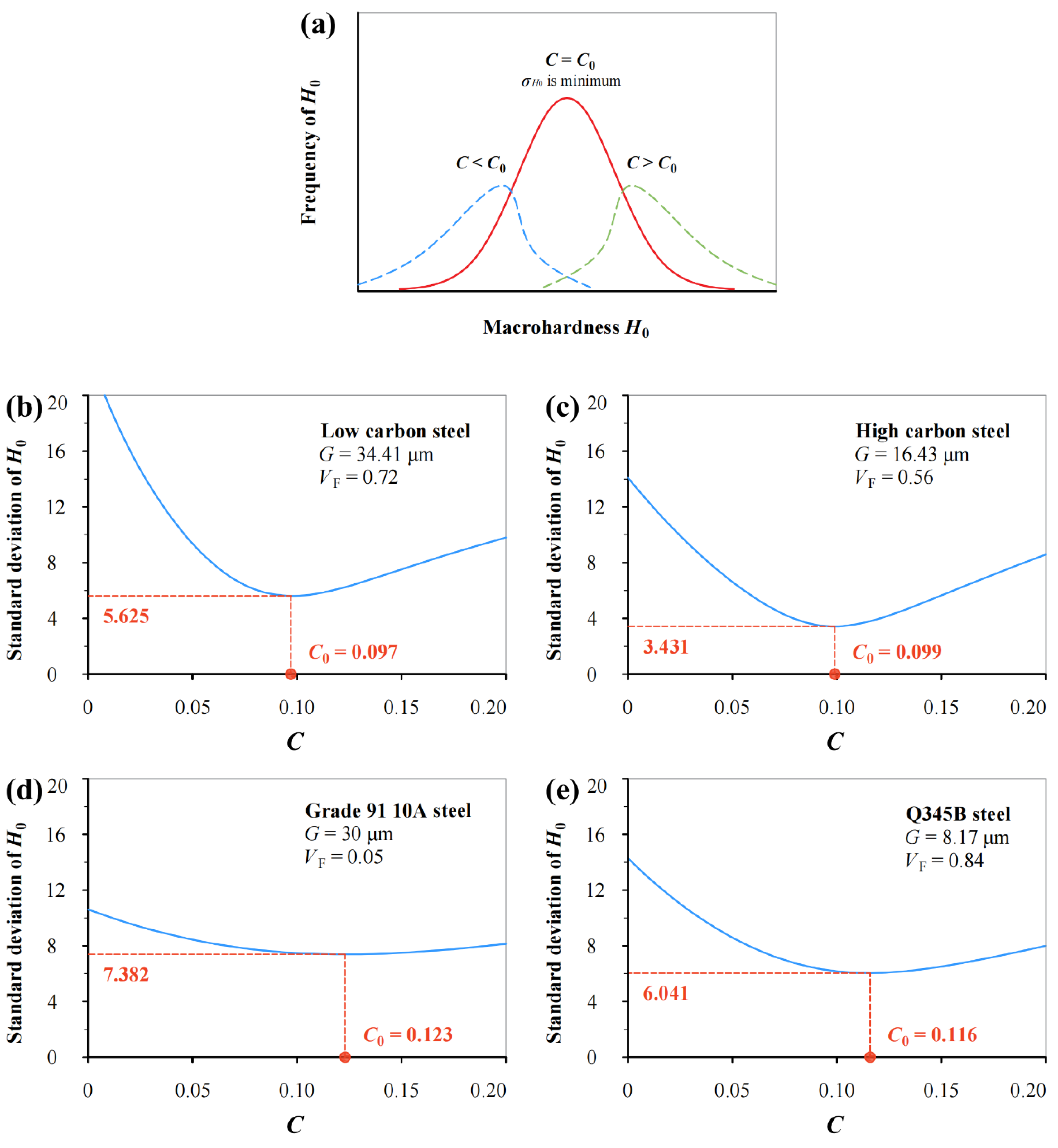
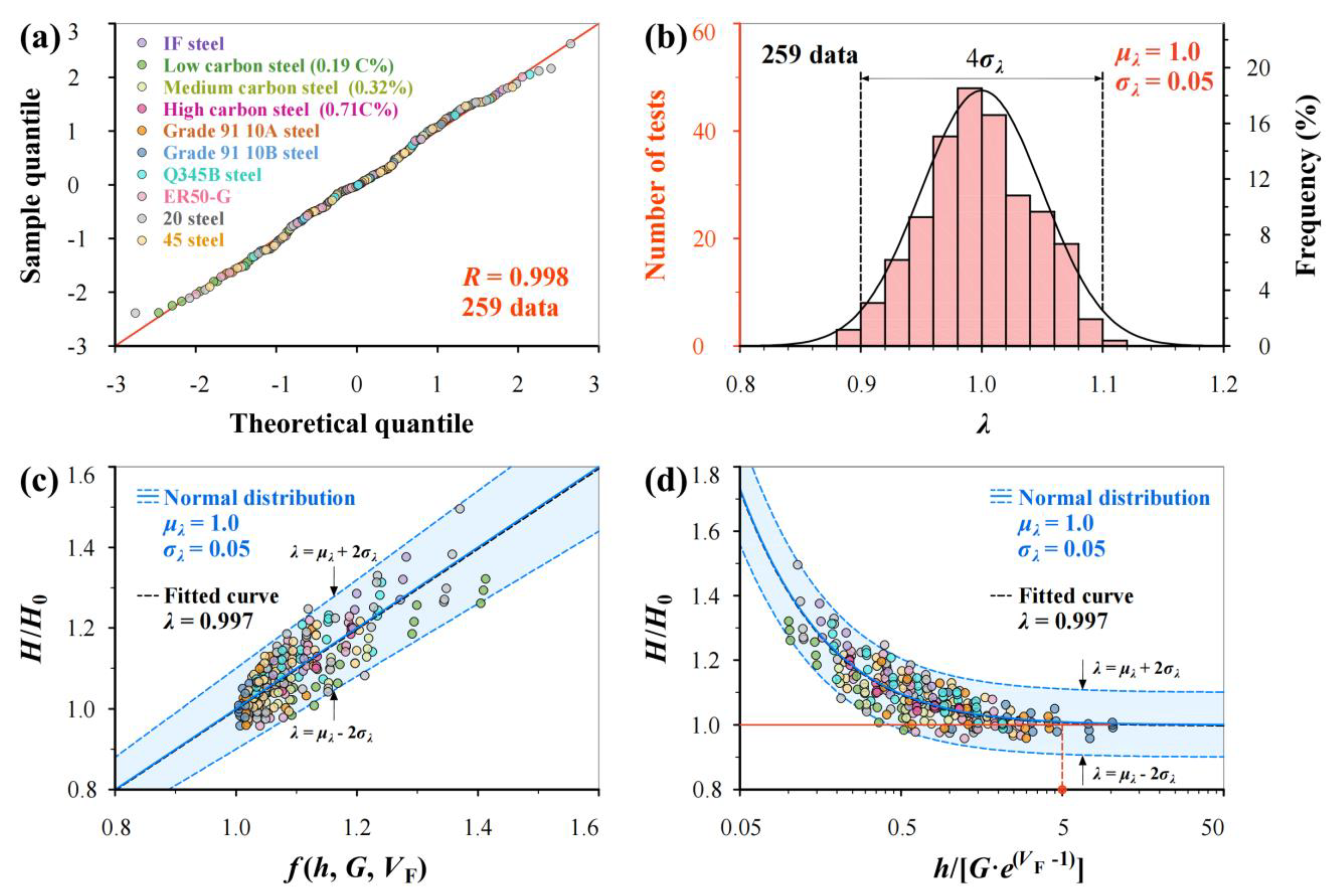
3.3. Normal Distribution Analysis for Inevitable Scatter of H/H0
4. Verification
5. Discussion
6. Conclusions
- Based on the Nix–Gao model, an analytical relation between H/H0 and h is proposed, which can replace the fitting method commonly used. Through the proposed model, the hardness of a material H0 can be calculated based on tested data (h, H) under any loads.
- The characteristic indentation depth h* indicates the translation from infinite hardness to macrohardness H0 in H-h curve. By two methods, h* is explicitly linked to average grain size G and ferrite volume fraction VF of BCC steels, i.e., h* = 0.1G∙e(VF−1).
- In micro-indentation hardness tests, when the indentation depth h is more than 5G∙e(VF−1), the tested value H ≤ 1.025H0 which can be regarded as material hardness H0.
- Normal distribution theory is incorporated successfully to quantify the inevitable scatter of hardness measurements resulting from the microstructure heterogeneity of a material and machining/testing errors. After considering scatter, this model includes both mean, and upper and lower bounds with 96% reliability, which ensue effective application for material testing and quality control.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| H | Tested hardness or microhardness |
| H0 | Material hardness or macrohardness |
| h | Indentation depth |
| h* | Characteristic indentation depth as the translation from infinite hardness to H0 |
| G | Average grain size |
| VF | Ferrite volume fraction |
| b | Burgers vector |
| μ | Shear modulus |
| θ | Indenter geometry parameter |
| f | Scaling factor |
| σy | Yield strength |
| σGB | The contribution of grain boundaries to strength |
| σ0 | The contribution of strengthening other than grain boundaries strengthening. |
| Gr | Relative grain size |
| ρG | The density of geometrically necessary dislocation |
| ρS | The density of statistically stored dislocation |
| L | Dislocation mean free path |
| λ | Non-dimensional parameter |
| μλ | Mean of a group of λ |
| σλ | Standard deviation of a group of λ |
References
- Luo, Q.; Kitchen, M. Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel. Materials 2023, 16, 1117. [Google Scholar] [CrossRef] [PubMed]
- Broitman, E. Indentation Hardness Measurements at Macro-, Micro-, and Nanoscale: A Critical Overview. Tribol. Lett. 2016, 65, 2–18. [Google Scholar] [CrossRef]
- Yang, B.; Vehoff, H. Dependence of nanohardness upon indentation size and grain size—A local examination of the interaction between dislocations and grain boundaries. Acta Mater. 2007, 55, 849–856. [Google Scholar] [CrossRef]
- Hu, J.; Sun, W.; Jiang, Z.; Zhang, W.; Lu, J.; Huo, W.; Zhang, Y.; Zhang, P. Indentation size effect on hardness in the body-centered cubic coarse-grained and nanocrystalline tantalum. Mater. Sci. Eng. A 2017, 686, 19–25. [Google Scholar] [CrossRef]
- Bond, T.; Badmos, A.; Ahmed, R.A.; Obayemi, J.D.; Salifu, A.; Rahbar, N.; Soboyejo, W.O. Indentation size effects in aluminum and titanium alloys. Mater. Sci. Eng. A 2022, 839, 142542. [Google Scholar] [CrossRef]
- Mattucci, M.A.; Cherubin, I.; Changizian, P.; Skippon, T.; Daymond, M.R. Indentation size effect, geometrically necessary dislocations and pile-up effects in hardness testing of irradiated nickel. Acta Mater. 2021, 207, 116702. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Manika, I.; Maniks, J. Size effects in micro- and nanoscale indentation. Acta Mater. 2006, 54, 2049–2056. [Google Scholar] [CrossRef]
- Jung, B.; Lee, H.; Park, H. Effect of grain size on the indentation hardness for polycrystalline materials by the modified strain gradient theory. Int. J. Solids Struct. 2013, 50, 2719–2724. [Google Scholar] [CrossRef]
- Durst, K.; Backes, B.; Göken, M. Indentation size effect in metallic materials: Correcting for the size of the plastic zone. Scr. Mater. 2005, 52, 1093–1097. [Google Scholar] [CrossRef]
- Qu, S.; Huang, Y.; Pharr, G.M.; Hwang, K.C. The indentation size effect in the spherical indentation of iridium: A study via the conventional theory of mechanism-based strain gradient plasticity. Int. J. Plast. 2006, 22, 1265–1286. [Google Scholar] [CrossRef]
- Sarangi, S.S.; Lavakumar, A.; Singh, P.K.; Katiyar, P.K.; Ray, R.K. Indentation size effect in steels with different carbon contents and microstructures. Mater. Sci. Technol. 2022, 39, 338–346. [Google Scholar] [CrossRef]
- Chicot, D. Hardness length-scale factor to model nano- and micro-indentation size effects. Mater. Sci. Eng. A 2009, 499, 454–461. [Google Scholar] [CrossRef]
- Seekala, H.; Bathini, L.; Wasekar, N.P.; Krishnaswamy, H.; Sudharshan Phani, P. A unified approach to quantify the material and geometrical effects in indentation size effect. J. Mater. Res. 2023, 38, 1740–1755. [Google Scholar] [CrossRef]
- Qin, J.; Huang, Y.; Hwang, K.C.; Song, J.; Pharr, G.M. The effect of indenter angle on the microindentation hardness. Acta Mater. 2007, 55, 6127–6132. [Google Scholar] [CrossRef]
- Shen, F.; Münstermann, S.; Lian, J.A. unified fracture criterion considering stress state dependent transition of failure mechanisms in bcc steels at –196 °C. Int. J. Plast. 2022, 156, 103365. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, L.; Zhang, G.; Zhao, L.; Shao, Q.; Huang, D.; Zhu, Y.; Wang, X.; Shen, Z.; Yang, H. Correlation of microstructure and hardness distribution of high-speed train wheels under original and service statuses. Eng. Fail. Anal. 2024, 158, 107994. [Google Scholar] [CrossRef]
- Mendas, M.; Benayoun, S.; Miloud, M.H.; Zidane, I. Microhardness model based on geometrically necessary dislocations for heterogeneous material. J. Mater. Res. Technol. 2021, 15, 2792–2801. [Google Scholar] [CrossRef]
- Ramazani, A.; Mukherjee, K.; Prahl, U.; Bleck, W. Modelling the effect of microstructural banding on the flow curve behaviour of dual-phase (DP) steels. Comput. Mater. Sci. 2012, 52, 46–54. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X.; Sercombe, T.; Li, Q.; Wu, Z.; Lu, P. Prediction of ceramic fracture with normal distribution pertinent to grain size. Acta Mater. 2018, 145, 41–48. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, S. Probabilistic prediction of strength and fracture toughness scatters for ceramics using normal distribution. Materials 2019, 12, 727. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Gu, H.; Zhu, S.; Li, K.; Wang, J.; Wang, X.; Hideo, M.; Zhang, X.; Tu, S. A data-driven roadmap for creep-fatigue reliability assessment and its implementation in low-pressure turbine disk at elevated temperatures. Reliab. Eng. Syst. Saf. 2022, 225, 108523. [Google Scholar] [CrossRef]
- Gu, H.; Wang, R.; Zhu, S.; Wang, X.; Wang, D.; Zhang, G.; Fan, Z.; Zhang, X.; Tu, S. Machine learning assisted probabilistic creep-fatigue damage assessment. Int. J. Fatigue 2022, 156, 106677. [Google Scholar] [CrossRef]
- ASTM E92; Standard Test Methods for Vickers Hardness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM E112; Standard Test Methods for Determining Average Grain Size. ASTM International: West Conshohocken, PA, USA, 2012.
- Kobayashi, S.; Sawada, K.; Hara, T.; Kushima, H.; Kimura, K. The formation and dissolution of residual δ ferrite in ASME Grade 91 steel plates. Mater. Sci. Eng. A 2014, 592, 241–248. [Google Scholar] [CrossRef]
- Ragab, M.; Liu, H.; Ahmed, M.M.Z.; Yang, G.; Lou, Z.; Mehboob, G. Microstructure evolution during friction stir welding of 1Cr11Ni2W2MoV martensitic stainless steel at different tool rotation rates. Mater. Charact. 2021, 182, 11561. [Google Scholar] [CrossRef]
- Lavakumar, A.; Sarangi, S.S.; Chilla, V.; Narsimhachary, D.; Ray, R.K. A “new” empirical equation to describe the strain hardening behavior of steels and other metallic materials. Mater. Sci. Eng. A 2021, 802, 140641. [Google Scholar] [CrossRef]
- Siefert, J.A.; Shingledecker, J.P.; Parker, J.D. Optimization of Vickers hardness parameters for micro- and macro-indentation of Grade 91 steel. J. Test. Eval. 2013, 41, 778–787. [Google Scholar] [CrossRef]
- Yaguchi, M.; Tomobe, M.; Komazaki, S.-I.; Kumada, A. Thickness of small sample for creep property evaluation of 9Cr steel base metal of piping on site. Trans. JSME 2022, 88, 00302. (In Japanese) [Google Scholar] [CrossRef]
- Sawada, K.; Kushima, H.; Tabuchi, M.; Kimura, K. Microstructural degradation of Gr.91 steel during creep under low stress. Mater. Sci. Eng. A 2011, 528, 5511–5518. [Google Scholar] [CrossRef]
- Cui, L.; Yu, C.; Jiang, S.; Sun, X.; Peng, R.; Lundgren, J.; Moverare, J. A new approach for determining GND and SSD densities based on indentation size effect: An application to additive-manufactured Hastelloy X. J. Mater. Sci. Technol. 2022, 96, 295–307. [Google Scholar] [CrossRef]
- Iza-Mendia, A.; Gutiérrez, I. Generalization of the existing relations between microstructure and yield stress from ferrite-pearlite to high strength steels. Mater. Sci. Eng. A 2013, 561, 40–51. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and ageing of mild steel: III Discussion of results. Proc. Phys. Soc. 1951, 64, 747. [Google Scholar] [CrossRef]
- Jiang, L.; Fu, H.; Zhang, H.; Xie, J. Physical mechanism interpretation of polycrystalline metals’ yield strength via a data-driven method: A novel Hall-Petch relationship. Acta Mater. 2022, 231, 117868. [Google Scholar] [CrossRef]
- Seok, M.; Choi, I.; Moon, J.; Kim, S.; Ramamurty, U.; Jang, J. Estimation of the Hall-Petch strengthening coefficient of steels through nanoindentation. Scr. Mater. 2014, 87, 49–52. [Google Scholar] [CrossRef]
- Tabor, D. The hardness and strength of metals. J. Inst. Met. 1951, 79, 1–18. [Google Scholar]
- Hernot, X.; Moussa, C.; Bartier, O. Study of the concept of representative strain and constraint factor introduced by Vickers indentation. Mech. Mater. 2014, 68, 1–14. [Google Scholar] [CrossRef]
- Gutierrez, I. AME modelling the mechanical behaviour of steels with mixed microstructures. J. Metall. Mater. Eng. 2005, 11, 201–214. [Google Scholar]

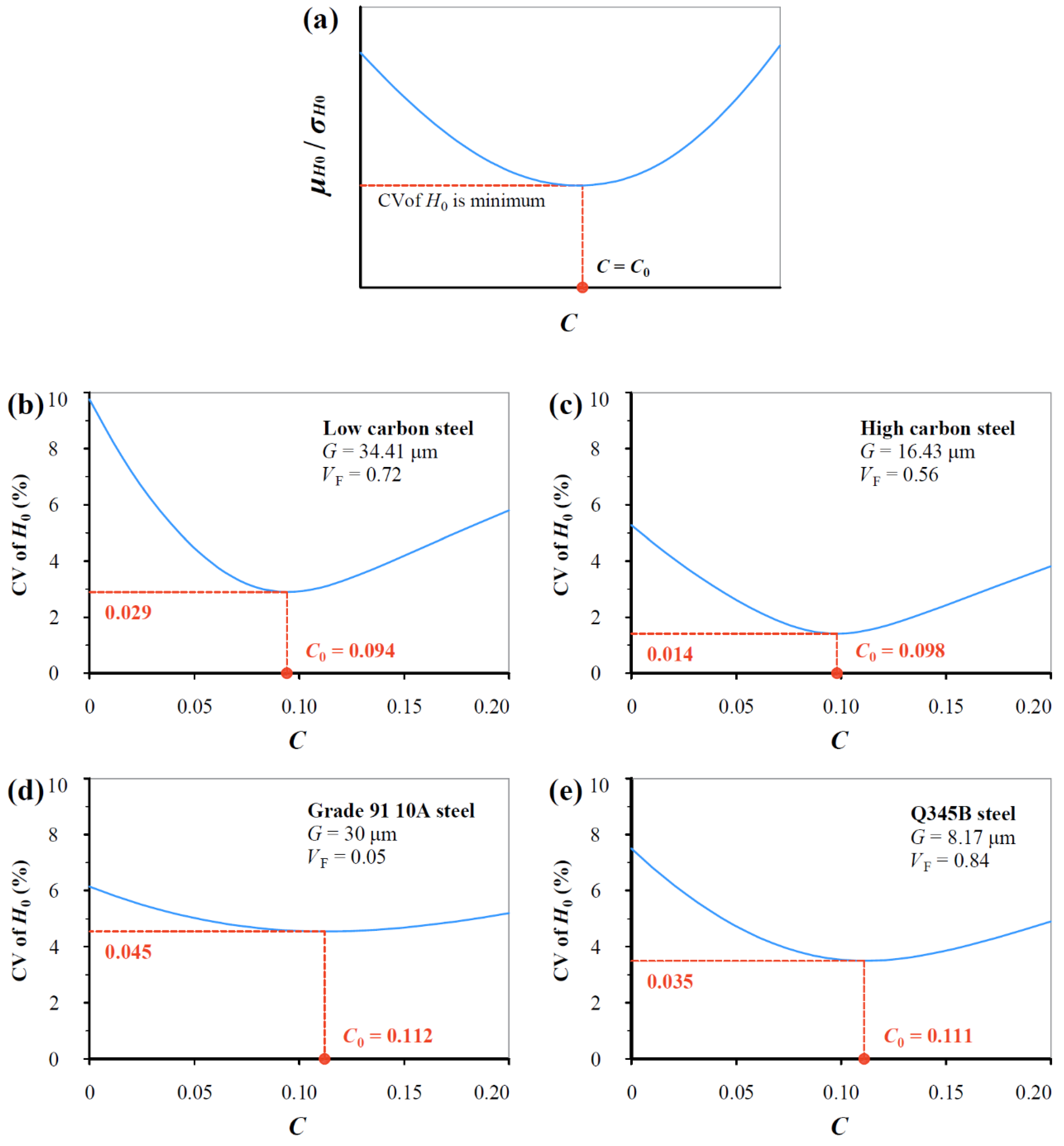
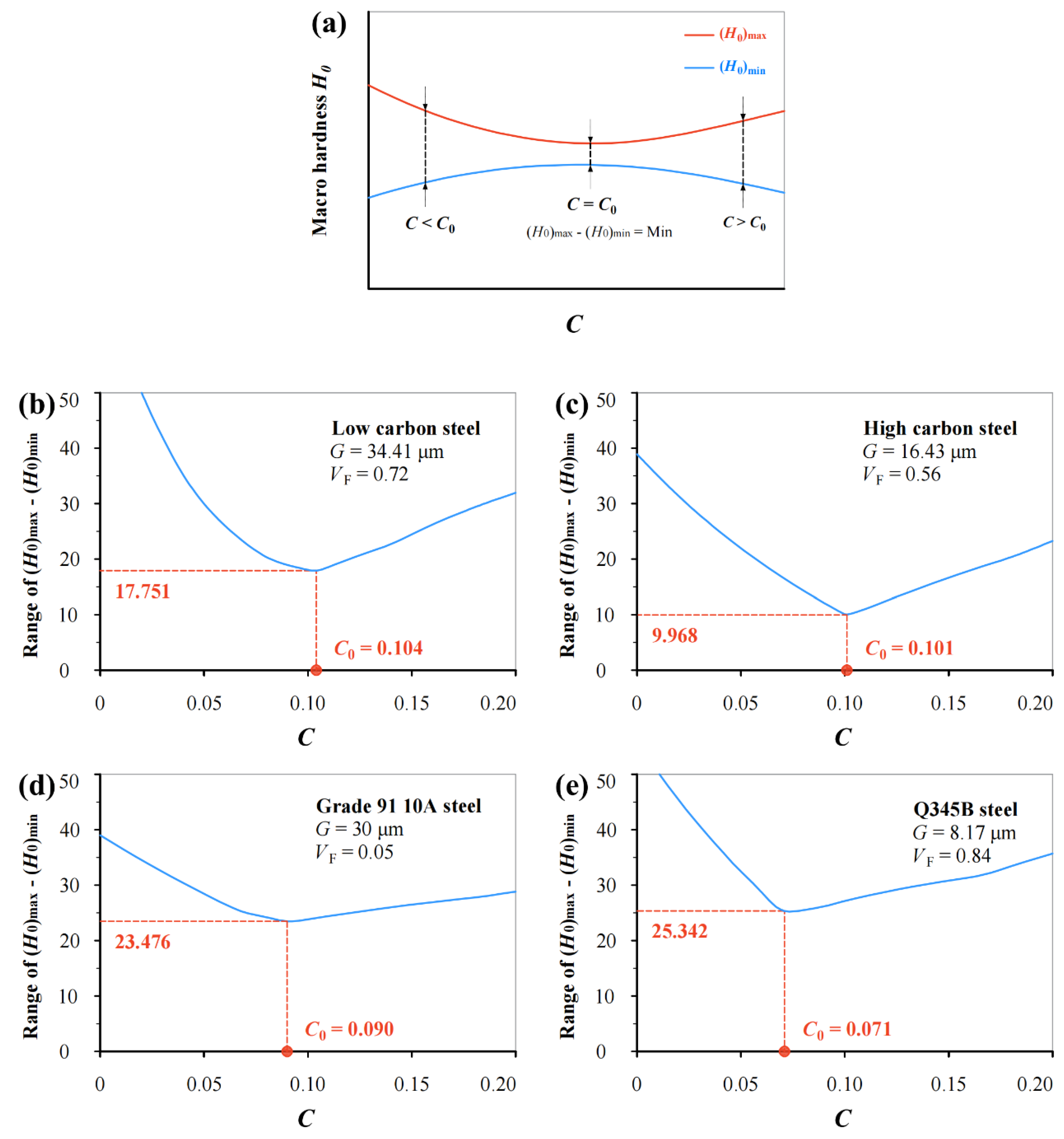
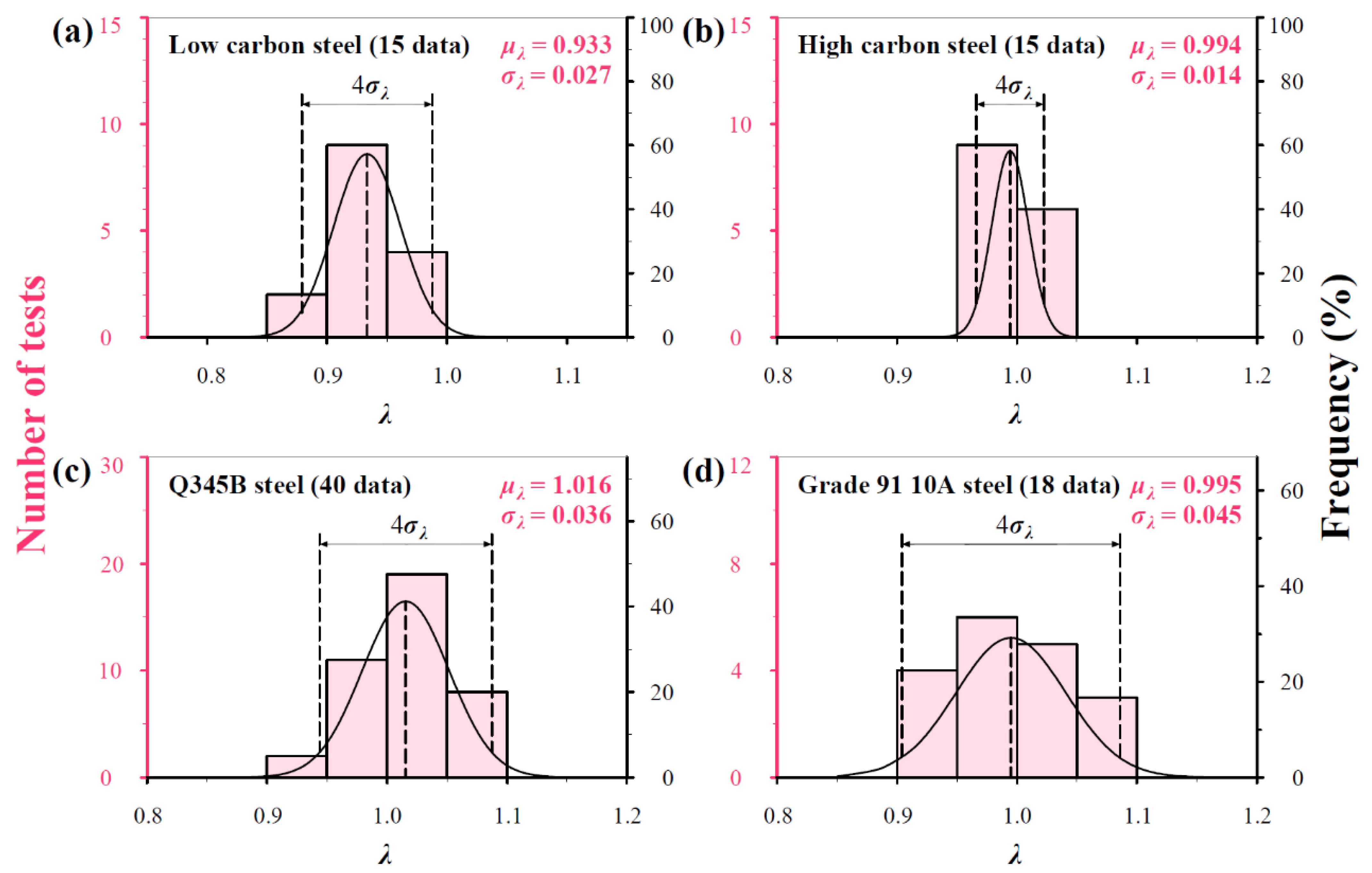
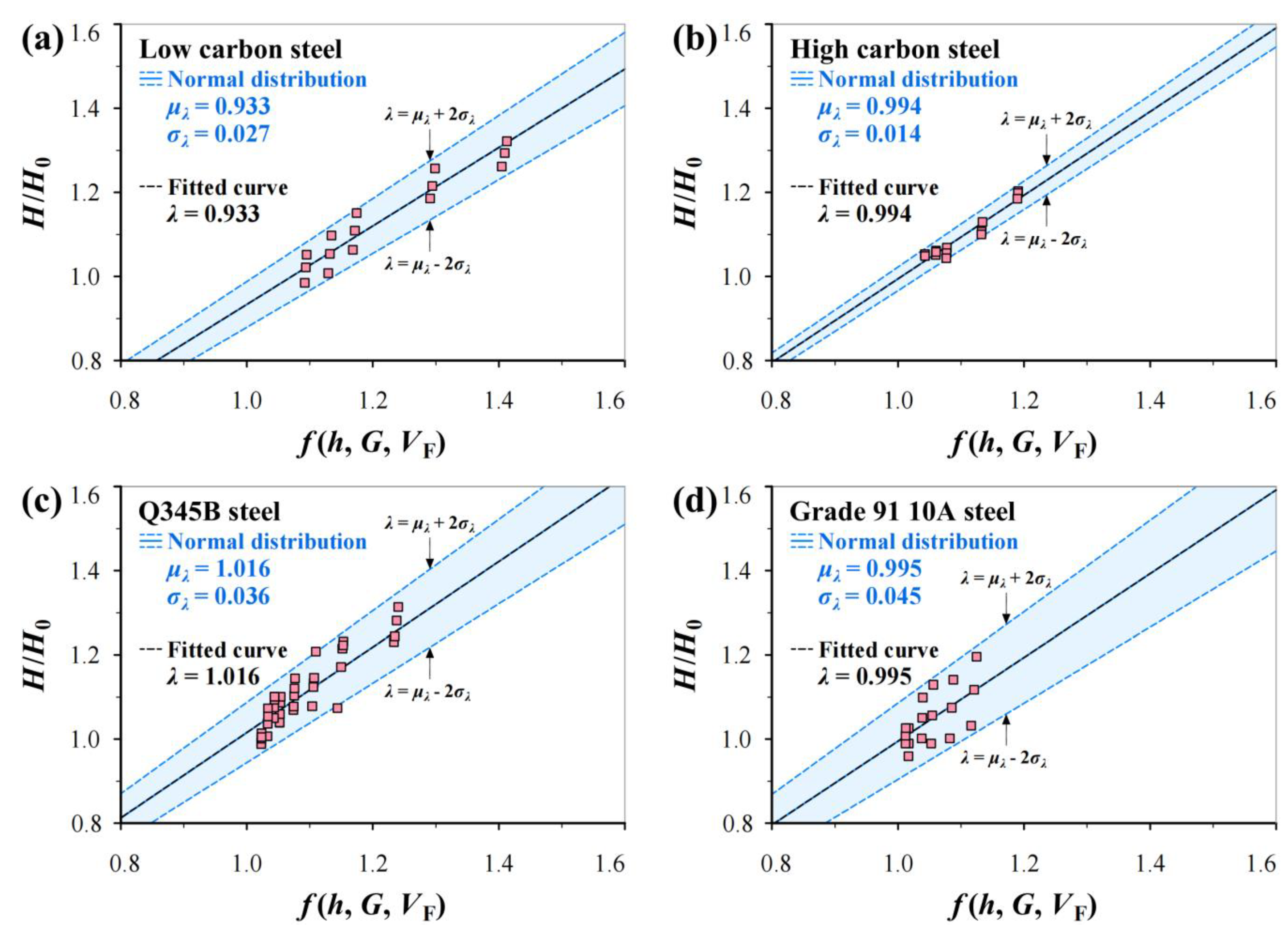
| Materials | C | Si | Mn | P | S | Cu | Cr | Ni | Fe |
|---|---|---|---|---|---|---|---|---|---|
| Q345B | 0.14 | 0.5 | 1.7 | 0.035 | 0.035 | 0.30 | 0.3 | 0.05 | Balance * |
| ER50-G | 0.07 | 0.9 | 1.5 | 0.012 | 0.011 | 0.5 | 0.02 | 0.02 | Balance |
| 20 steel | 0.2 | 0.22 | 0.53 | 0.035 | 0.035 | 0.07 | 0.04 | 0.01 | Balance |
| 45 steel | 0.45 | 0.17 | 0.5 | 0.035 | 0.035 | 0.25 | 0.25 | 0.25 | Balance |
| Materials | Phase | VF | G (μm) | H0 (HV) |
|---|---|---|---|---|
| Q345B | F * + P * | 84% | 8.17 | 171.9 |
| ER50-G | F + P | 94% | 5.19 | 218.2 |
| 20 steel | F + P | 76% | 14.14 | 156.6 |
| 45 steel | F + P | 43% | 10.01 | 199.5 |
| IF steel [12] | F | 100% [28] | 24.29 [12] | 94.5 [12] |
| Low carbon steel (0.19% C) [12] | F + P | 72% [28] | 34.41 [12] | 206.7 [12] |
| Medium carbon steel (0.32% C) [12] | F + P | 58% [28] | 19.23 [12] | 237.0 [12] |
| High carbon steel (0.71% C) [12] | F + SC * | 56% | 16.43 [12] | 244.1 [12] |
| Grade 91 10A steel [29] | F + M * | 5% [26] | 30.00 [30] | 164.7 [29] |
| Grade 91 10B steel [29] | F + M | 5% [26] | 10.00 [31] | 240.0 [29] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, A.; Song, X.; Ye, M.; Wan, Y.; Zhang, C. Microhardness Variation with Indentation Depth for Body-Centered Cubic Steels Pertinent to Grain Size and Ferrite Content. Materials 2024, 17, 2371. https://doi.org/10.3390/ma17102371
Xu A, Song X, Ye M, Wan Y, Zhang C. Microhardness Variation with Indentation Depth for Body-Centered Cubic Steels Pertinent to Grain Size and Ferrite Content. Materials. 2024; 17(10):2371. https://doi.org/10.3390/ma17102371
Chicago/Turabian StyleXu, Anye, Xuding Song, Min Ye, Yipin Wan, and Chunguo Zhang. 2024. "Microhardness Variation with Indentation Depth for Body-Centered Cubic Steels Pertinent to Grain Size and Ferrite Content" Materials 17, no. 10: 2371. https://doi.org/10.3390/ma17102371
APA StyleXu, A., Song, X., Ye, M., Wan, Y., & Zhang, C. (2024). Microhardness Variation with Indentation Depth for Body-Centered Cubic Steels Pertinent to Grain Size and Ferrite Content. Materials, 17(10), 2371. https://doi.org/10.3390/ma17102371







