Computationally Efficient Algorithm for Modeling Grain Growth Using Hillert’s Mean-Field Approach
Abstract
1. Introduction
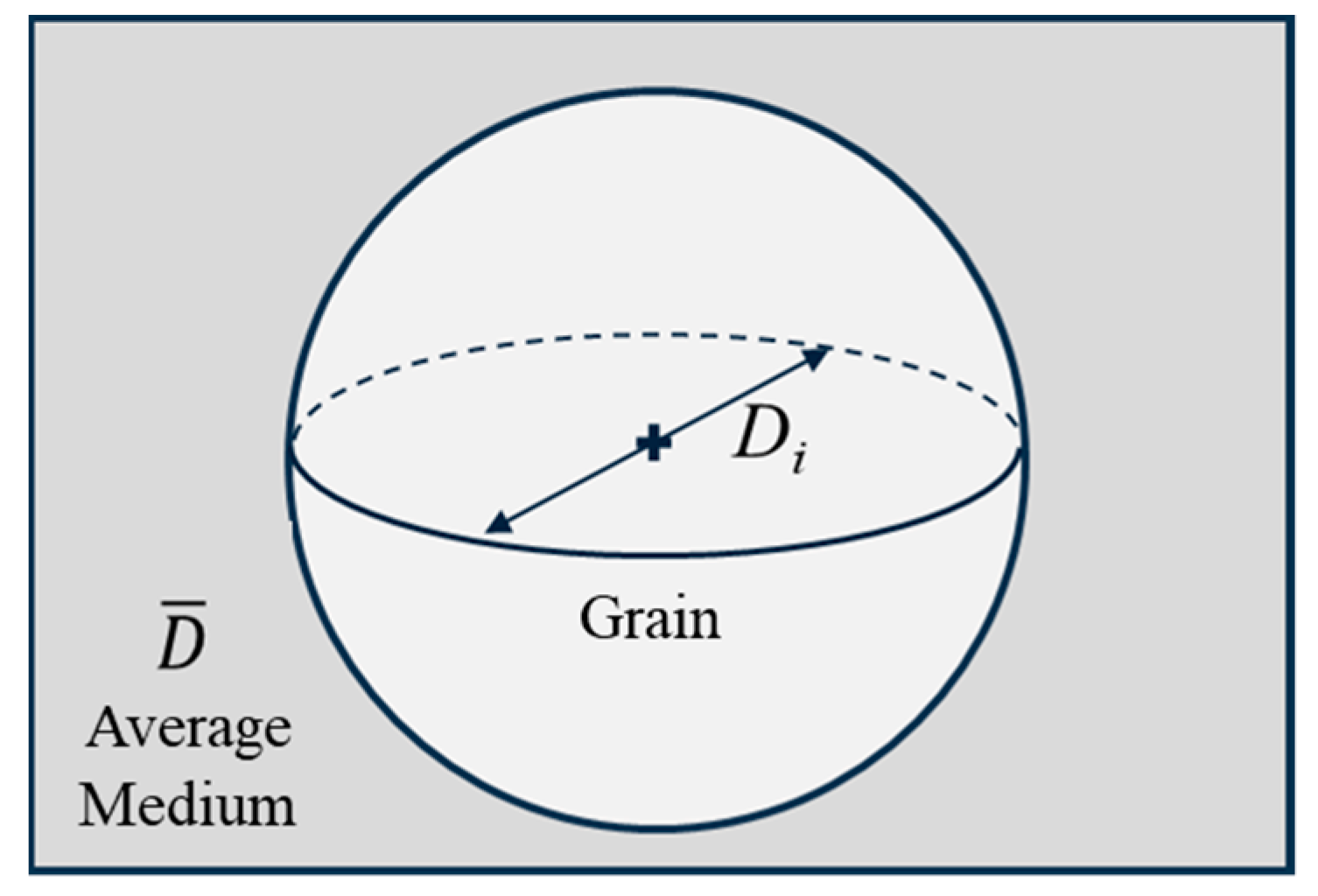
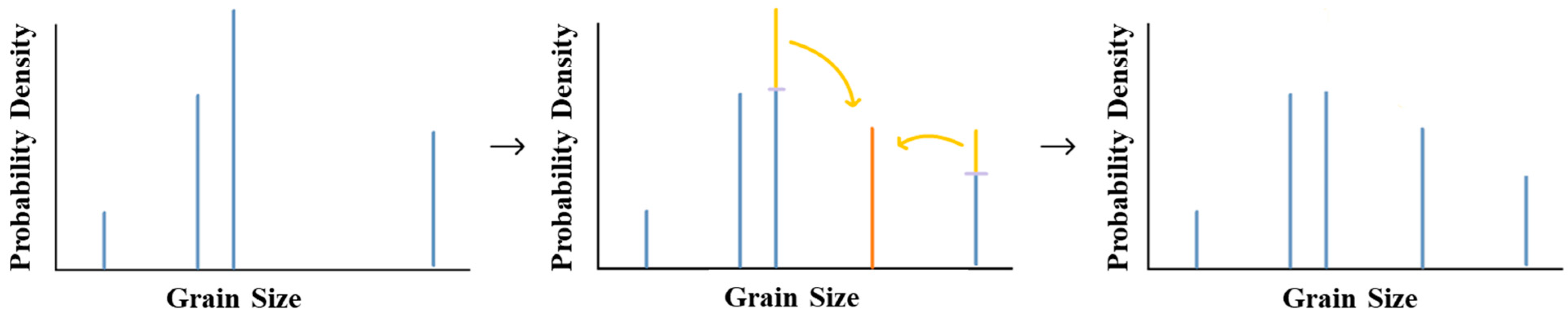
2. Modeling Framework
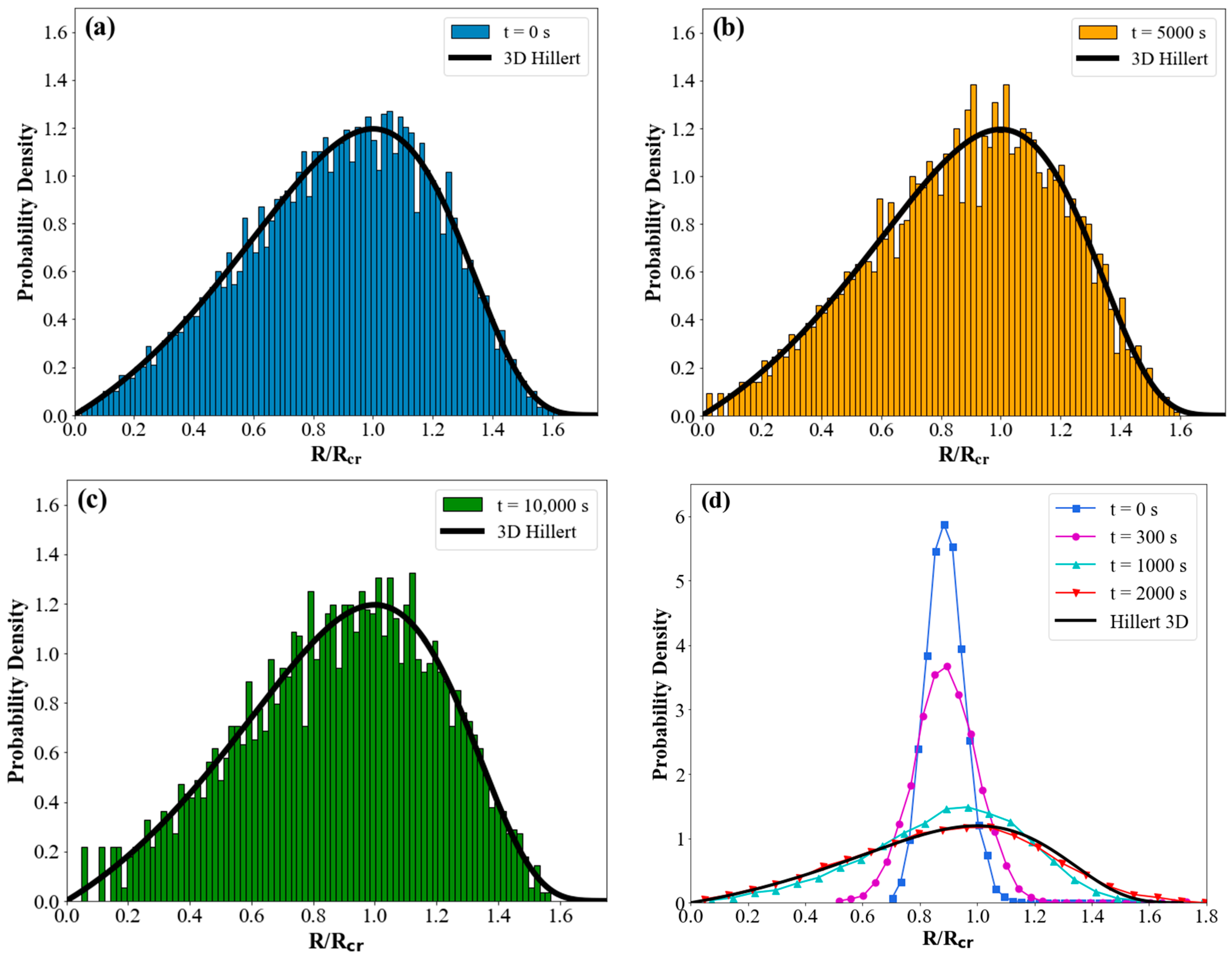
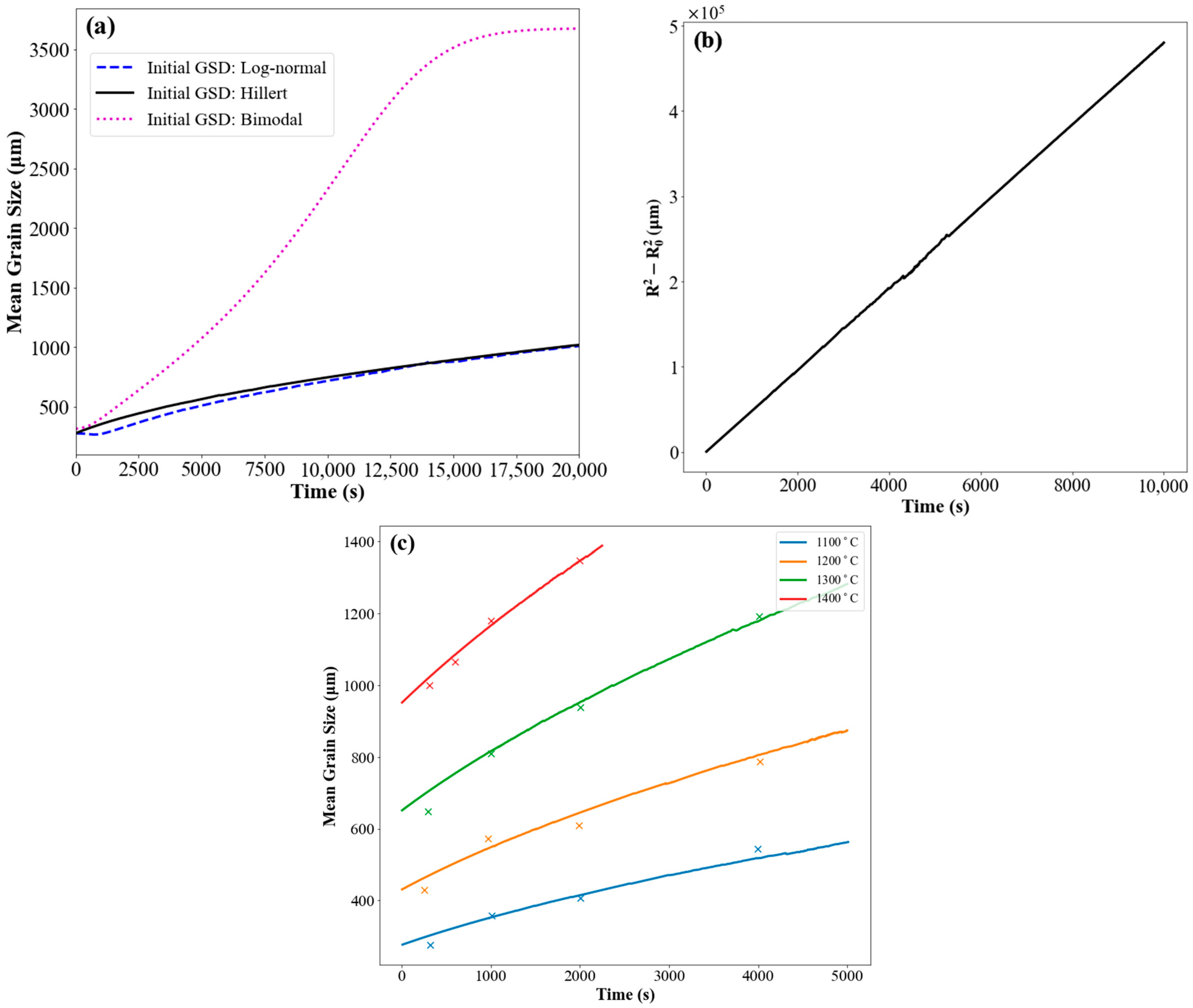
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sellars, C.M. Modelling microstructural development during hot rolling. Mater. Sci. Technol. 1990, 6, 1072–1081. [Google Scholar] [CrossRef]
- Hodgson, P.D. A mathematical model to predict the mechanical properties of hot rolled C-Mn and microalloyed steels. ISIJ Int. 1992, 32, 1329–1338. [Google Scholar] [CrossRef]
- Hodgson, P.D. Models of the recrystallization behaviour of C-Mn and Nb microalloyed steels during hot working processes. Met. Forum 1993, 17, 403–408. [Google Scholar]
- Dunlop, J.W.C.; Bréchet, Y.J.M.; Legras, L.; Zurob, H.S. Modelling isothermal and non-isothermal recrystallisation kinetics: Application to Zircaloy-4. J. Nucl. Mater. 2007, 366, 178–186. [Google Scholar] [CrossRef]
- Rehman, K.; Zurob, H.S. Novel approach to model static recrystallization of austenite during hot-rolling of Nb-Microalloyed steel: Effect of precipitates. Mater. Sci. Forum 2013, 753, 417–422. [Google Scholar] [CrossRef]
- Pietrzyk, M. Through-process modelling of microstructure evolution in hot forming of steels. J. Mater. Process. Technol. 2002, 125–126, 53–62. [Google Scholar] [CrossRef]
- Elder, K.R.; Katakowski, M.; Haataja, M.; Grant, M. Modeling Elasticity in Crystal Growth. Phys. Rev. Lett. 2002, 88, 245701. [Google Scholar] [CrossRef] [PubMed]
- Militzer, M.; Hawbolt, E.; Meadowcroft, T. Microstructural model for hot strip rolling of high-strength low-alloy steels. Metall. Mater. Trans. A 2000, 31, 1247–1259. [Google Scholar] [CrossRef]
- Zurob, H.S.; Hutchinson, C.R.; Brechet, Y.; Purdy, G. Modeling recrystallization of microalloyed austenite: Effect of coupling recovery, precipitation and recrystallization. Acta Mater. 2002, 50, 3077–3094. [Google Scholar] [CrossRef]
- Zurob, H.S.; Brechet, Y.; Purdy, G. A model for the competition of precipitation and recrystallization in deformed austenite. Acta Mater. 2001, 49, 4183–4190. [Google Scholar] [CrossRef]
- Hoffman, A.K.; Umretiya, R.V.; Crawford, C.; Spinelli, I.; Huang, S.; Buresh, S.; Perlee, C.; Mandal, T.; Abouelella, H.; Rebak, R.B. The relationship between grain size distribution and ductile to brittle transition temperature in FeCrAl alloys. Mater. Lett. 2023, 331, 133427. [Google Scholar] [CrossRef]
- Atkinson, H.V. Overview no. 65: Theories of normal grain growth in pure single phase systems. Acta Metall. 1988, 36, 469–491. [Google Scholar] [CrossRef]
- Shirdel, M.; Mirzadeh, H.; Habibi Parsa, M. Microstructural evolution during normal/abnormal grain growth in austenitic stainless steel. Metall. Mater. Trans. A 2014, 45, 5185–5193. [Google Scholar] [CrossRef]
- Benson, W.; Wert, J. The effect of initial grain size distribution on abnormal grain growth in single-phase materials. Acta Mater. 1998, 46, 5323–5333. [Google Scholar] [CrossRef]
- Krill III, C.E.; Holm, E.A.; Dake, J.M.; Cohn, R.; Holíková, K.; Andorfer, F. Extreme Abnormal Grain Growth: Connecting Mechanisms to Microstructural Outcomes. Annu. Rev. Mater. Res. 2023, 53, 319–345. [Google Scholar] [CrossRef]
- Burke, J.E.; Turnbull, D. Recrystallization and grain growth. Prog. Met. Phys. 1952, 3, 220–292. [Google Scholar] [CrossRef]
- Smith, C. Grain Shapes and Other Metallurgical Applications of Topology Metal Interfaces; American Society for Metals: Cleveland, OH, USA, 1952. [Google Scholar]
- Feltham, P. Grain growth in metals. Acta Metall. 1957, 5, 97–105. [Google Scholar] [CrossRef]
- Louat, N.P. On the theory of normal grain growth. Acta Metall. 1974, 22, 721–724. [Google Scholar] [CrossRef]
- Enomoto, M.; Hayashi, K. Estimation of austenite grain boundary mobility in low-carbon steel by grain growth. J. Mater. Sci. 2023, 58, 4603–4620. [Google Scholar] [CrossRef]
- Abbruzzese, G.; Lücke, K. A theory of texture controlled grain growth—I. Derivation and general discussion of the model. Acta Metall. 1986, 34, 905–914. [Google Scholar] [CrossRef]
- Eichelkraut, H.; Abbruzzese, G.; Lücke, K. A theory of texture controlled grain growth—II. Numerical and analytical treatment of grain growth in the presence of two texture components. Acta Metall. 1988, 36, 55–68. [Google Scholar] [CrossRef]
- Wu, K.; Jeppsson, J.; Mason, P. Mean Field Modeling of Grain Growth and Zener Pinning. J. Phase Equilibria Diffus. 2022, 43, 866–875. [Google Scholar] [CrossRef]
- Maire, L.; Scholtes, B.; Moussa, C.; Bozzolo, N.; Pino Muñoz, D.; Bernacki, M. Improvement of 3D mean field models for capillarity-driven grain growth based on full field simulations. J. Mater. Sci. 2016, 51, 10970–10981. [Google Scholar] [CrossRef]
- Roth, M.; Flipon, B.; Bozzolo, N.; Bernacki, M. Comparison of Grain-Growth Mean-Field Models Regarding Predicted Grain Size Distributions. Materials 2023, 16, 6761. [Google Scholar] [CrossRef]
- Hillert, M. On the theory of normal and abnormal grain growth. Acta Metall. 1965, 13, 227–238. [Google Scholar] [CrossRef]
- Abbruzzese, G.; Heckelmann, I.; Lücke, K. Statistical theory of two-dimensional grain growth—I. The topological foundation. Acta Metall. Mater. 1992, 40, 519–532. [Google Scholar] [CrossRef]
- Maire, L.; Fausty, J.; Bernacki, M.; Bozzolo, N.; De Micheli, P.; Moussa, C. A new topological approach for the mean field modeling of dynamic recrystallization. Mater. Des. 2018, 146, 194–207. [Google Scholar] [CrossRef]
- Andersson, J.-O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar]
- Upmanyu, M.; Hassold, G.N.; Kazaryan, A.; Holm, E.A.; Wang, Y.; Patton, B.; Srolovitz, D.J. Boundary mobility and energy anisotropy effects on microstructural evolution during grain growth. Interface Sci. 2002, 10, 201–216. [Google Scholar] [CrossRef]
- Bulatov, V.V.; Reed, B.W.; Kumar, M. Grain boundary energy function for fcc metals. Acta Mater. 2014, 65, 161–175. [Google Scholar] [CrossRef]
- Darvishi Kamachali, R.; Steinbach, I. 3-D phase-field simulation of grain growth: Topological analysis versus mean-field approximations. Acta Mater. 2012, 60, 2719–2728. [Google Scholar] [CrossRef]
- Rios, P.R. Comparison between a grain size distribution obtained by a Monte Carlo Potts model and by an analytical mean field model. Scr. Mater. 1999, 41, 1283–1287. [Google Scholar] [CrossRef]
- Blikstein, P.; Tschiptschin, A.P. Monte Carlo simulation of grain growth. Mater. Res. 1999, 2, 133–137. [Google Scholar] [CrossRef]
- Xiaoyan, S.; Guoquan, L.; Nanju, G. Re-analysis on grain size distribution during normal grain growth based on Monte Carlo simulation. Scr. Mater. 2000, 43, 355–359. [Google Scholar] [CrossRef]
- Zöllner, D.; Streitenberger, P. Three-dimensional normal grain growth: Monte Carlo Potts model simulation and analytical mean field theory. Scr. Mater. 2006, 54, 1697–1702. [Google Scholar] [CrossRef]
- Ivasishin, O.M.; Shevchenko, S.V.; Vasiliev, N.L.; Semiatin, S.L. 3D Monte-Carlo simulation of texture-controlled grain growth. Acta Mater. 2003, 51, 1019–1034. [Google Scholar] [CrossRef]
- Brakke, K.A. The surface evolver. Exp. Math. 1992, 1, 141–165. [Google Scholar] [CrossRef]
- Marthinsen, K.; Hunderi, O.; Ryum, N. The influence of spatial grain size correlation and topology on normal grain growth in two dimensions. Acta Mater. 1996, 44, 1681–1689. [Google Scholar] [CrossRef]
- Wakai, F.; Enomoto, N.; Ogawa, H. Three-dimensional microstructural evolution in ideal grain growth—General statistics. Acta Mater. 2000, 48, 1297–1311. [Google Scholar] [CrossRef]
- Weygand, D.; Bréchet, Y.; Lépinoux, J.; Gust, W. Three-dimensional grain growth: A vertex dynamics simulation. Philos. Mag. B 1999, 79, 703–716. [Google Scholar] [CrossRef]
- Fuchizaki, K.; Kusaba, T.; Kawasaki, K. Computer modelling of three-dimensional cellular pattern growth. Philos. Mag. B 1995, 71, 333–357. [Google Scholar] [CrossRef]
- Marsh, S.; Masumura, R.; Pande, C. A curvature-driven vertex model for two-dimensional grain growth. Philos. Mag. Lett. 1995, 72, 429–434. [Google Scholar] [CrossRef]
- Fullman, R. Boundary migration during grain growth. In Met. Interfaces; National Metal Congress: Detroit, MI, USA, 1952; pp. 179–207. [Google Scholar]
- Bronsard, L.; Wetton, B.T. A numerical method for tracking curve networks moving with curvature motion. J. Comput. Phys. 1995, 120, 66–87. [Google Scholar] [CrossRef]
- Frost, H.J.; Thompson, C.V. Computer simulation of grain growth. Curr. Opin. Solid. State Mater. Sci. 1996, 1, 361–368. [Google Scholar] [CrossRef]
- Fayad, W.; Thompson, C.; Frost, H. Steady-state grain-size distributions resulting from grain growth in two dimensions. Scr. Mater. 1999, 40, 1199–1204. [Google Scholar] [CrossRef]
- Krill Iii, C.E.; Chen, L.Q. Computer simulation of 3-D grain growth using a phase-field model. Acta Mater. 2002, 50, 3059–3075. [Google Scholar] [CrossRef]
- Yadav, V.; Vanherpe, L.; Moelans, N. Effect of volume fractions on microstructure evolution in isotropic volume-conserved two-phase alloys: A phase-field study. Comput. Mater. Sci. 2016, 125, 297–308. [Google Scholar] [CrossRef]
- Yadav, V.; Moelans, N. Investigation on the existence of a ‘Hillert regime’in normal grain growth. Scr. Mater. 2018, 142, 148–152. [Google Scholar] [CrossRef]
- Gao, J.; Wei, M.; Zhang, L.; Du, Y.; Liu, Z.; Huang, B. Effect of Different Initial Structures on the Simulation of Microstructure Evolution During Normal Grain Growth via Phase-Field Modeling. Metall. Mater. Trans. A 2018, 49, 6442–6456. [Google Scholar] [CrossRef]
- Szeliga, D.; Bzowski, K.; Rauch, Ł.; Kuziak, R.; Pietrzyk, M. Mean field and full field modelling of microstructure evolution and phase transformations during hot forming and cooling of low carbon steels. Comp. Methods Mater. Sci. 2020, 20, 121–132. [Google Scholar] [CrossRef]
- Després, A.; Greenwood, M.; Sinclair, C. A mean-field model of static recrystallization considering orientation spreads and their time-evolution. Acta Mater. 2020, 199, 116–128. [Google Scholar] [CrossRef]
- Cram, D.; Zurob, H.S.; Brechet, Y.; Hutchinson, C. Modelling discontinuous dynamic recrystallization using a physically based model for nucleation. Acta Mater. 2009, 57, 5218–5228. [Google Scholar] [CrossRef]
- Piot, D.; Smagghe, G.; Jonas, J.J.; Desrayaud, C.; Montheillet, F.; Perrin, G.; Montouchet, A.; Kermouche, G. A semitopological mean-field model of discontinuous dynamic recrystallization: Toward a correct and rapid prediction of grain-size distribution. J. Mater. Sci. 2018, 53, 8554–8566. [Google Scholar] [CrossRef]
- Anderson, M.; Srolovitz, D.; Grest, G.; Sahni, P. Computer simulation of grain growth—I. Kinetics. Acta Metall. 1984, 32, 783–791. [Google Scholar] [CrossRef]
- Ponge, D.; Gottstein, G. Necklace formation during dynamic recrystallization: Mechanisms and impact on flow behavior. Acta Mater. 1998, 46, 69–80. [Google Scholar] [CrossRef]
- Montheillet, F.; Lurdos, O.; Damamme, G. A grain scale approach for modeling steady-state discontinuous dynamic recrystallization. Acta Mater. 2009, 57, 1602–1612. [Google Scholar] [CrossRef]
- Darvishi Kamachali, R.; Abbondandolo, A.; Siburg, K.F.; Steinbach, I. Geometrical grounds of mean field solutions for normal grain growth. Acta Mater. 2015, 90, 252–258. [Google Scholar] [CrossRef]
- Rios, P.R.; Dalpian, T.G.; Brandão, V.S.; Castro, J.A.; Oliveira, A.C.L. Comparison of analytical grain size distributions with three-dimensional computer simulations and experimental data. Scr. Mater. 2006, 54, 1633–1637. [Google Scholar] [CrossRef]
- Dumitrescu, D.; Boiangiu, C.-A. A Study of Image Upsampling and Downsampling Filters. Computers 2019, 8, 30. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M. B-spline signal processing. II. Efficiency design and applications. IEEE Trans. Signal Process. 1993, 41, 834–848. [Google Scholar] [CrossRef]
- Fattal, R. Image upsampling via imposed edge statistics. In ACM SIGGRAPH 2007 Papers; ACM: New York, NY, USA, 2007; p. 95-es. [Google Scholar]
- Monno, Y.; Tanaka, M.; Okutomi, M. Multispectral demosaicking using adaptive kernel upsampling. In Proceedings of the 2011 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 3157–3160. [Google Scholar]
- Li, Y.; Liu, D.; Li, H.; Li, L.; Wu, F.; Zhang, H.; Yang, H. Convolutional neural network-based block up-sampling for intra frame coding. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2316–2330. [Google Scholar] [CrossRef]
- Furumai, K.; Wang, X.; Zurob, H.; Phillion, A. Evaluating the Effect of the Competition between NbC Precipitation and Grain Size Evolution on the Hot Ductility of Nb Containing Steels. ISIJ Int. 2019, 59, 1064–1071. [Google Scholar] [CrossRef]
- Zhou, T.; O’malley, R.J.; Zurob, H.S. Study of grain-growth kinetics in delta-ferrite and austenite with application to thin-slab cast direct-rolling microalloyed steels. Metall. Mater. Trans. A 2010, 41, 2112–2120. [Google Scholar] [CrossRef]
- Cahn, J.W. The impurity-drag effect in grain boundary motion. Acta Metall. 1962, 10, 789–798. [Google Scholar] [CrossRef]
- Cruz-Fabiano, A.L.; Logé, R.; Bernacki, M. Assessment of simplified 2D grain growth models from numerical experiments based on a level set framework. Comput. Mater. Sci. 2014, 92, 305–312. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, D.I.; Kim, W.T.; Park, Y.B. Computer simulations of two-dimensional and three-dimensional ideal grain growth. Phys. Rev. E 2006, 74, 061605. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zhou, T.H.; Zurob, H.S. Abnormal and post-abnormal austenite grain growth kinetics in Nb–Ti microalloyed steels. Can. Metall. Q. 2011, 50, 389–395. [Google Scholar] [CrossRef]

| Final Ensemble Size | tmax (s) | r2 | RMSE |
|---|---|---|---|
| Auto | NA | 0.98 | 14.84 |
| 1000 | 6000 | 0.96 | 15.24 |
| 500 | 4000 | 0.96 | 16.38 |
| 100 | 1700 | 0.90 | 23.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatroudi, S.F.; Cicoria, R.; Zurob, H.S. Computationally Efficient Algorithm for Modeling Grain Growth Using Hillert’s Mean-Field Approach. Materials 2024, 17, 2341. https://doi.org/10.3390/ma17102341
Chatroudi SF, Cicoria R, Zurob HS. Computationally Efficient Algorithm for Modeling Grain Growth Using Hillert’s Mean-Field Approach. Materials. 2024; 17(10):2341. https://doi.org/10.3390/ma17102341
Chicago/Turabian StyleChatroudi, Shabnam Fadaei, Robert Cicoria, and Hatem S. Zurob. 2024. "Computationally Efficient Algorithm for Modeling Grain Growth Using Hillert’s Mean-Field Approach" Materials 17, no. 10: 2341. https://doi.org/10.3390/ma17102341
APA StyleChatroudi, S. F., Cicoria, R., & Zurob, H. S. (2024). Computationally Efficient Algorithm for Modeling Grain Growth Using Hillert’s Mean-Field Approach. Materials, 17(10), 2341. https://doi.org/10.3390/ma17102341






