Development and Calibration of a Phenomenological Material Model for Steel-Fiber-Reinforced High-Performance Concrete Based on Unit Cell Calculations
Abstract
1. Introduction
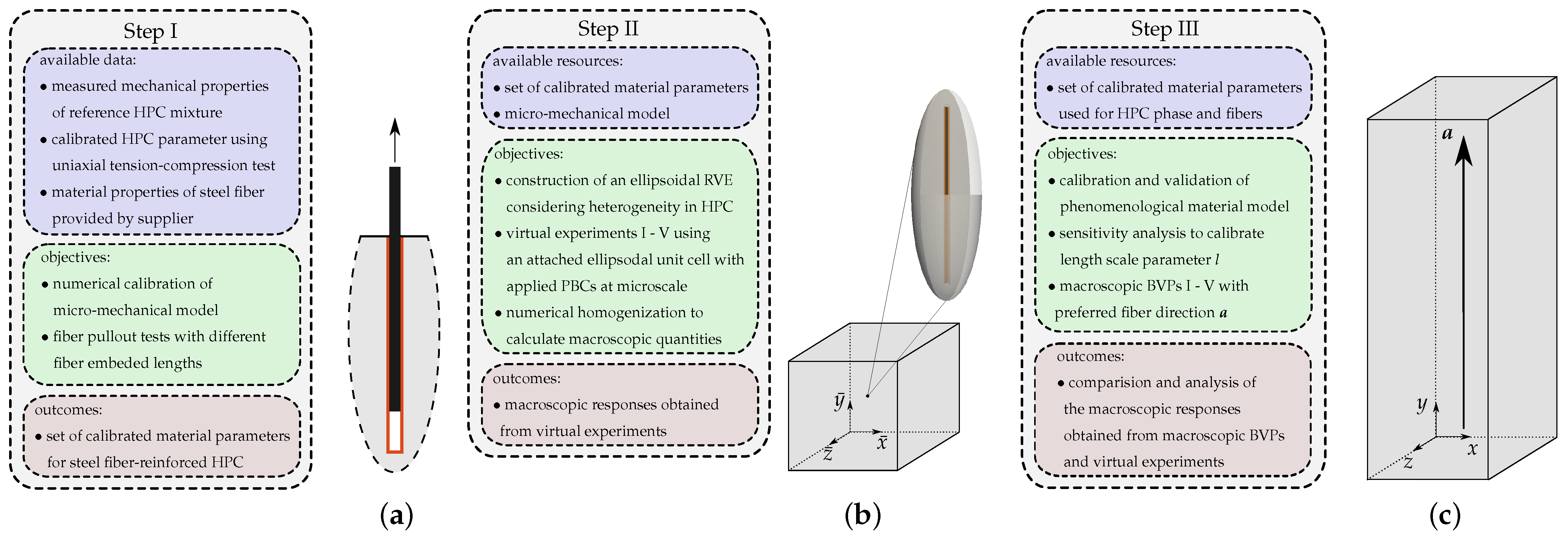
- Numerical calibration of a micro-mechanical model using single-fiber pullout tests;
- Analysis of the effective macroscopic behavior of fiber-reinforced HPC through virtual experiments based on unit cell calculations using a micro-mechanical model;
- Calibration and validation of the phenomenological material model by comparing the macroscopic responses obtained from macroscopic BVPs and virtual experiments.
2. Numerical Calibration of the Micro-Mechanical Model Using Fiber Pullout Tests
2.1. Constitutive Framework of a Small-Strain Elasto-Plastic Phase-Field Model for Fractures
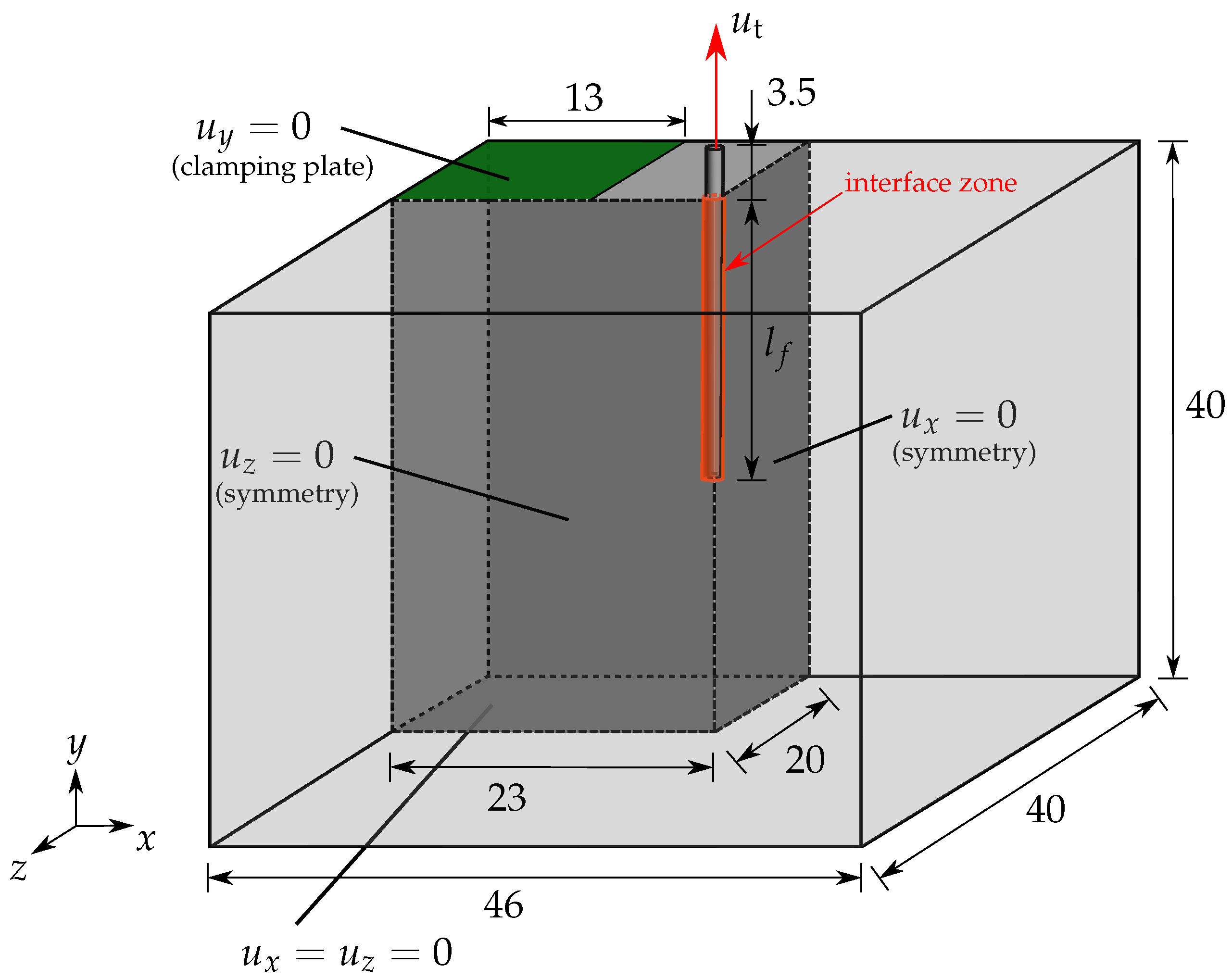
2.2. Numerical Simulations of Pullout Tests of a Steel Fiber Embedded in HPC
3. Virtual Experiments Based on Ellipsoidal RVEs
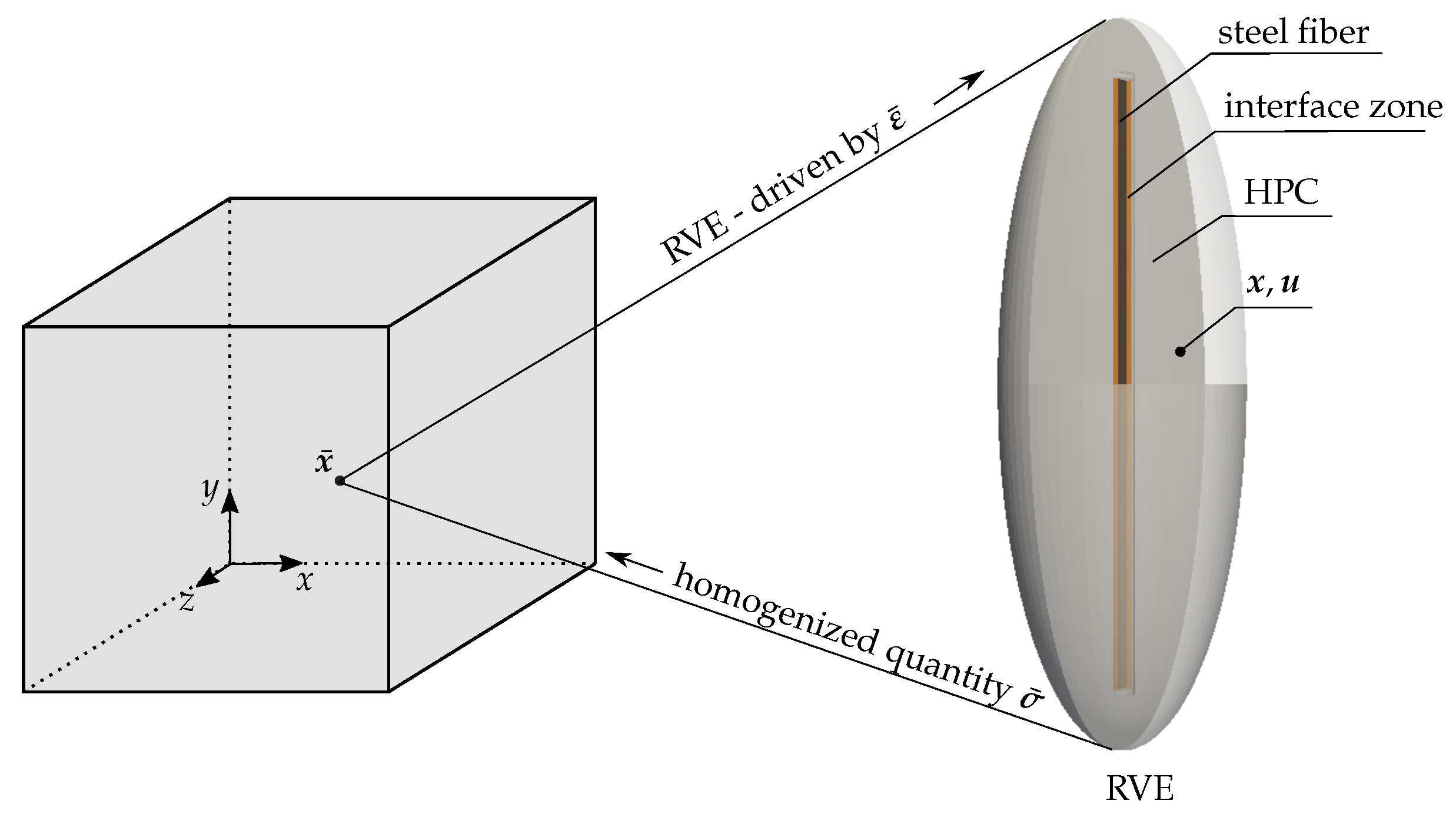
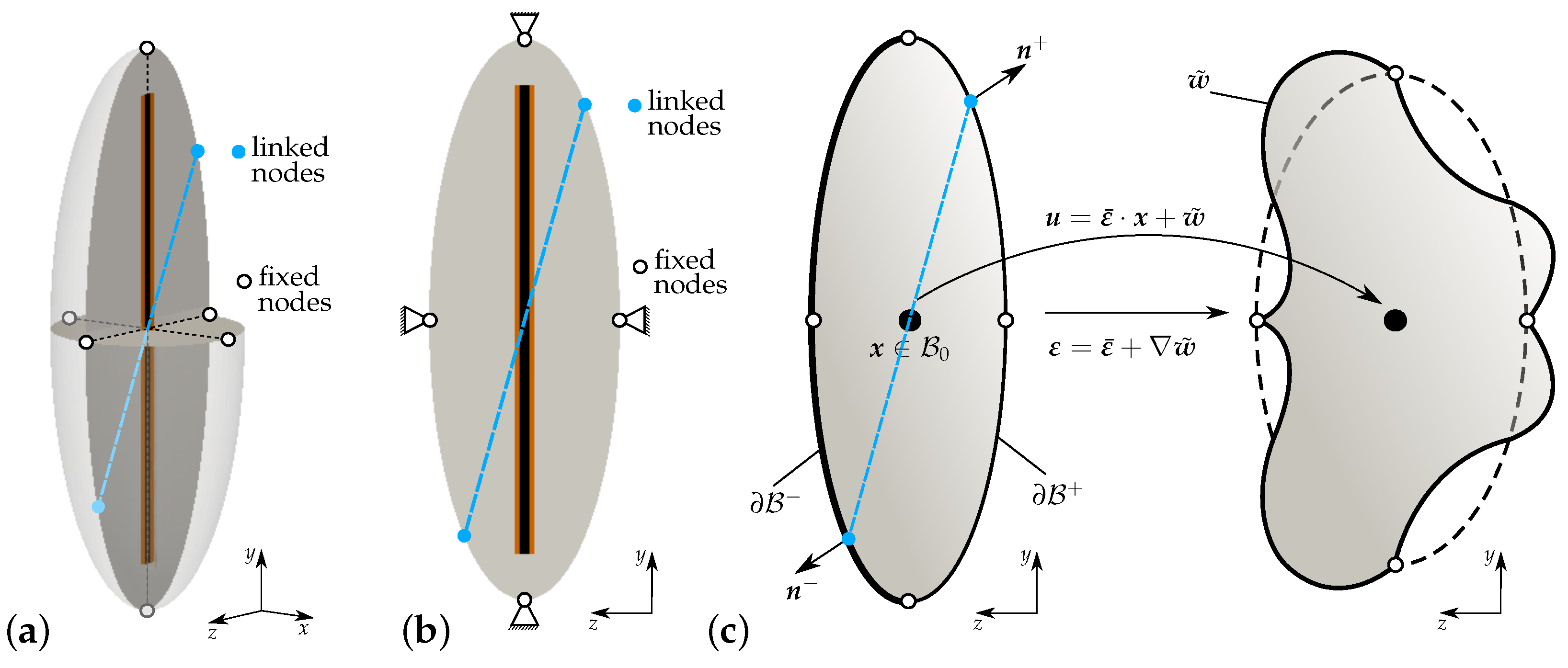
3.1. Kinematics and Concept of Numerical Homogenization
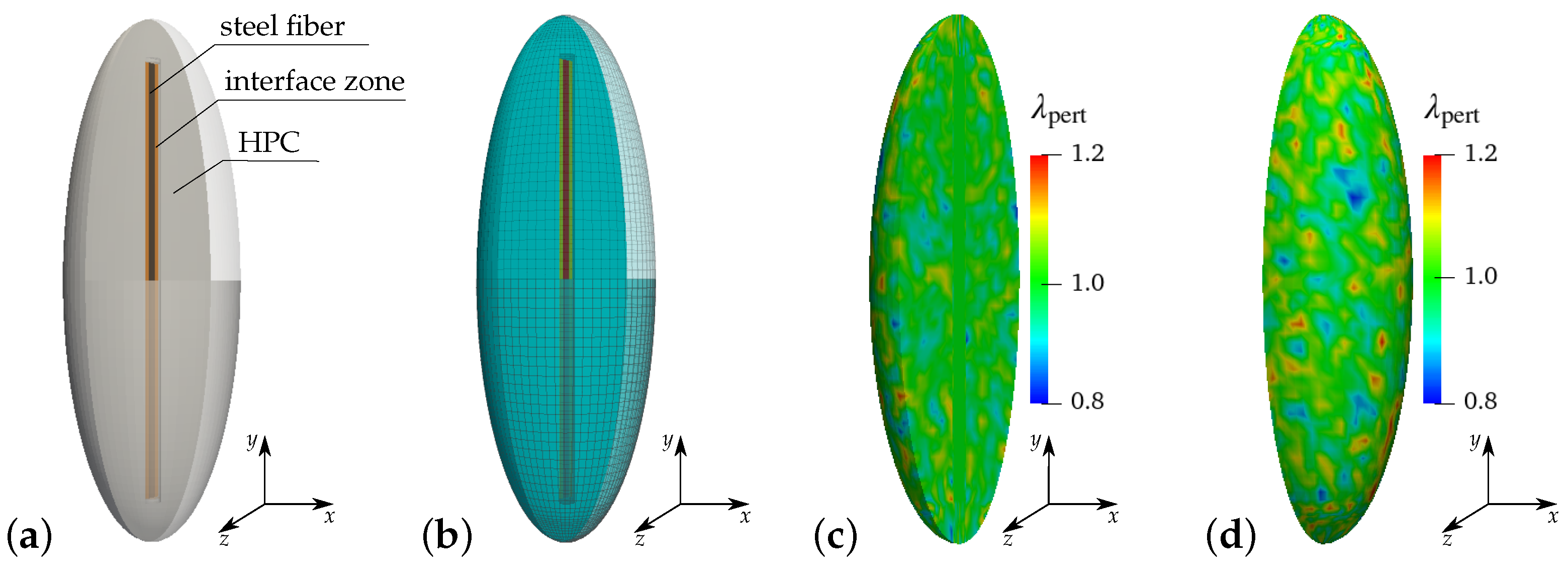
3.2. Ellipsoidal RVE for Fiber-Reinforced HPC
3.3. Failure Analysis of Pure and Reinforced HPC in Virtual Experiments
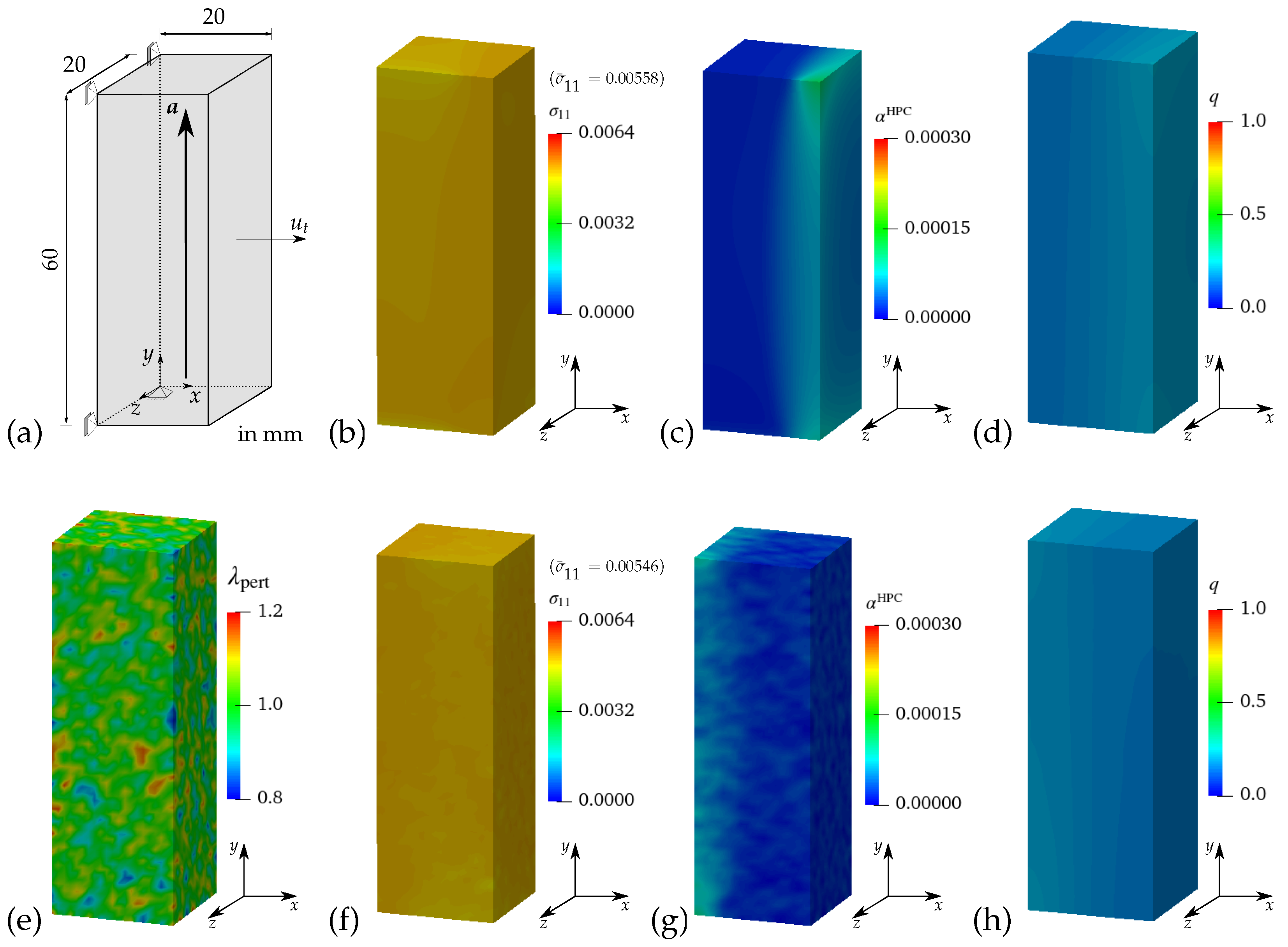
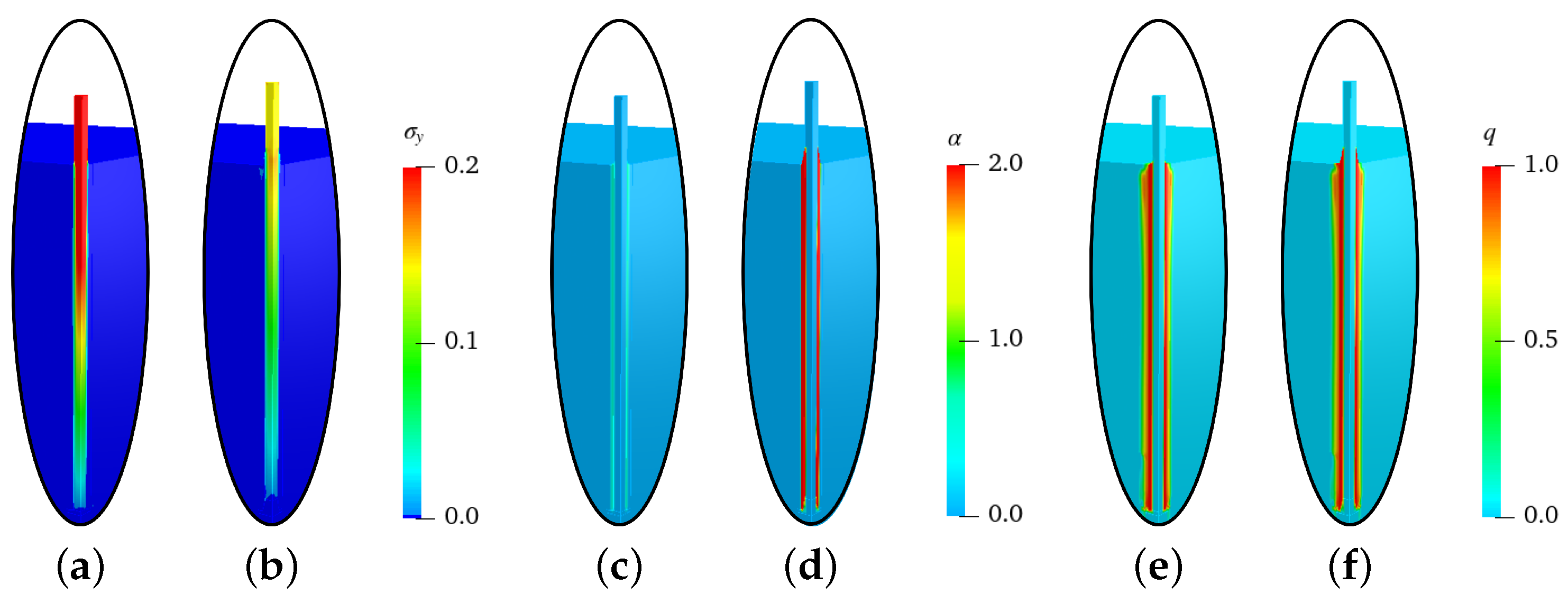
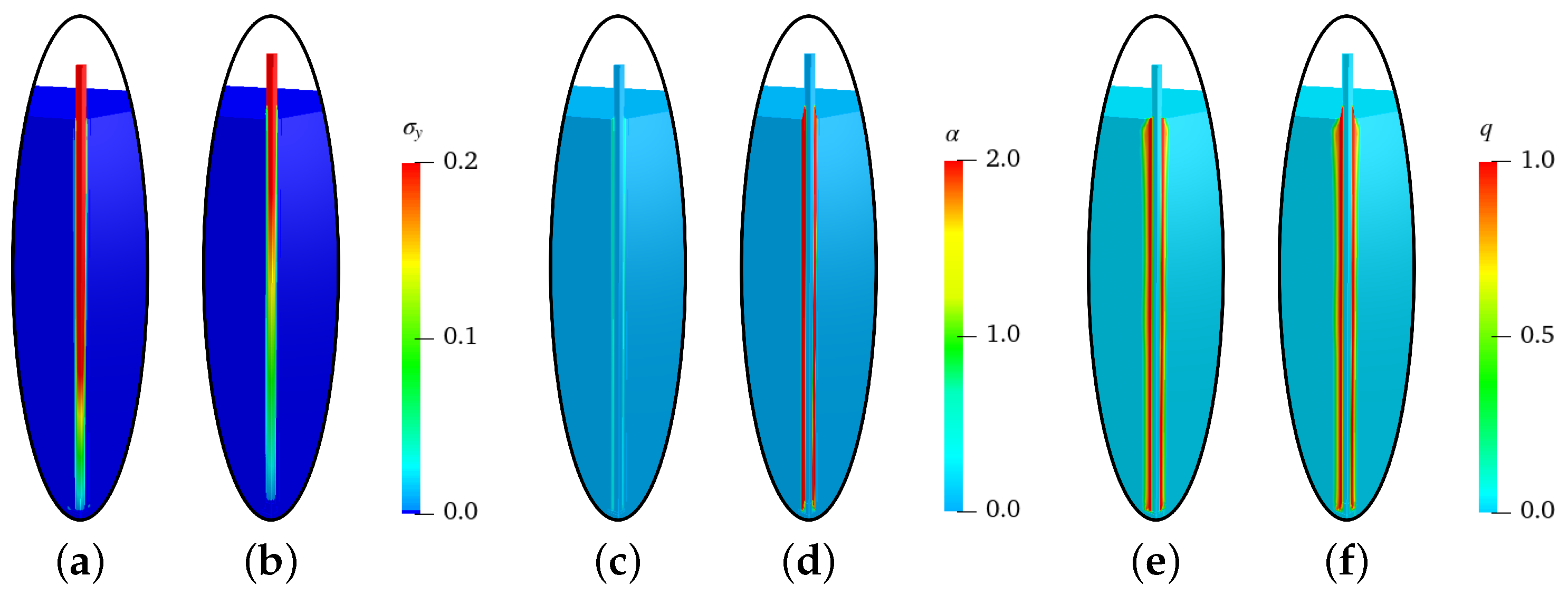
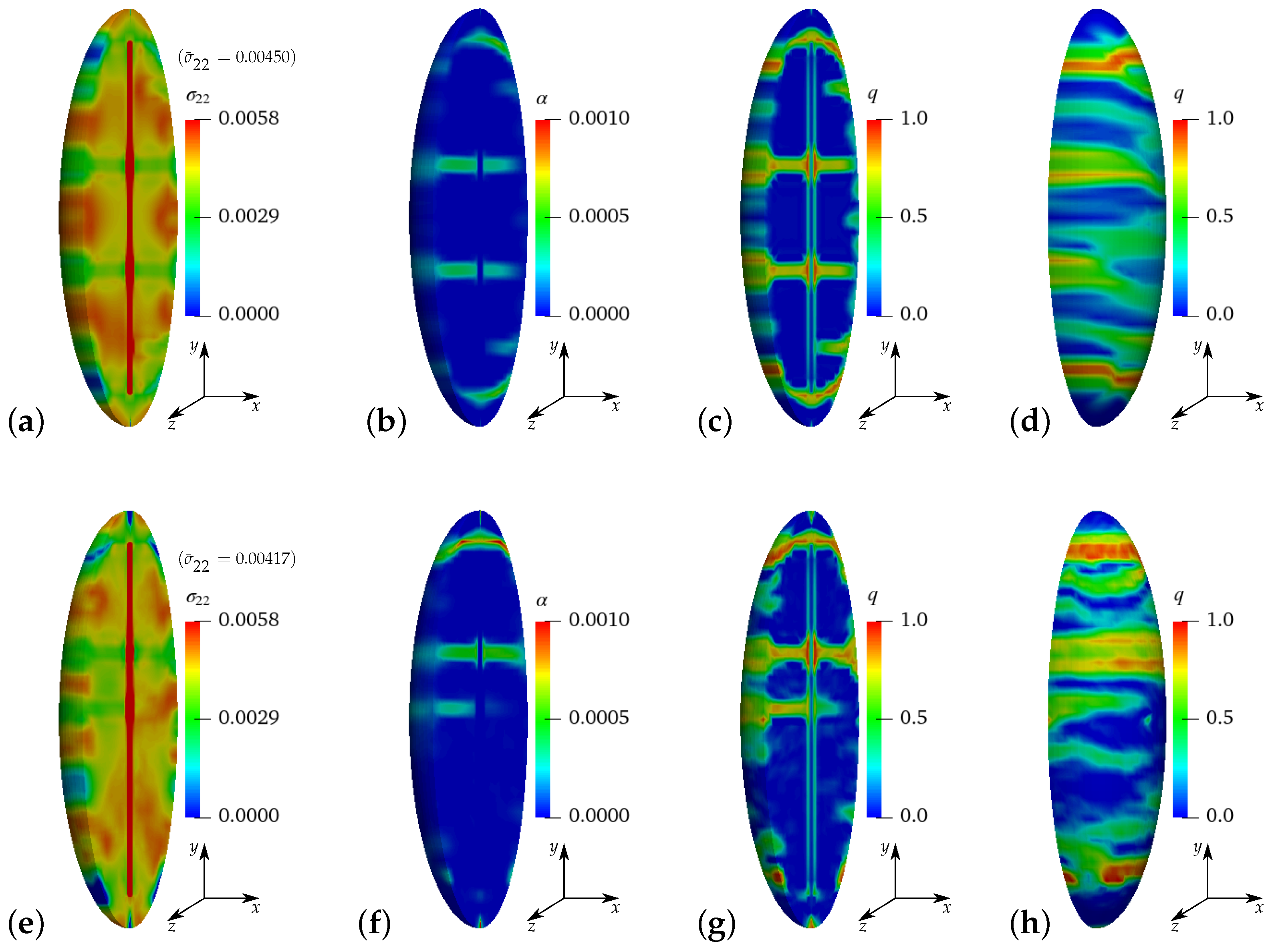
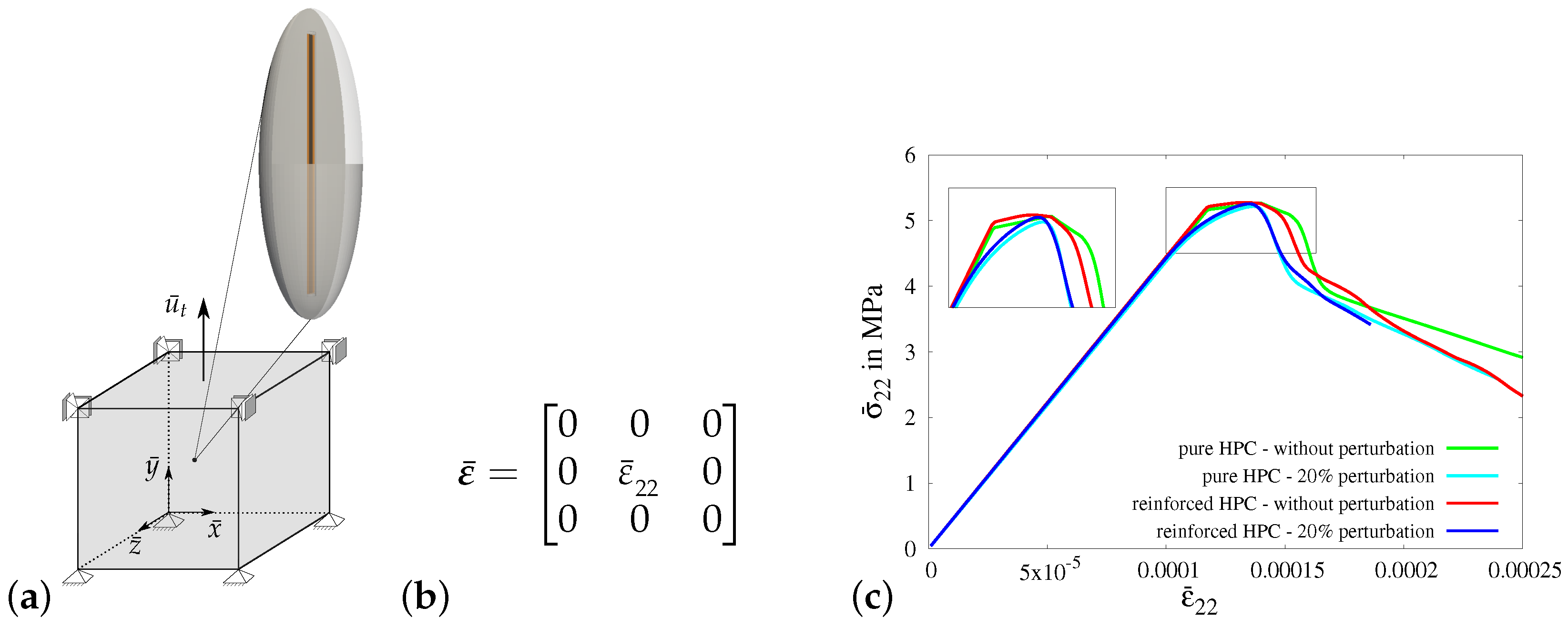
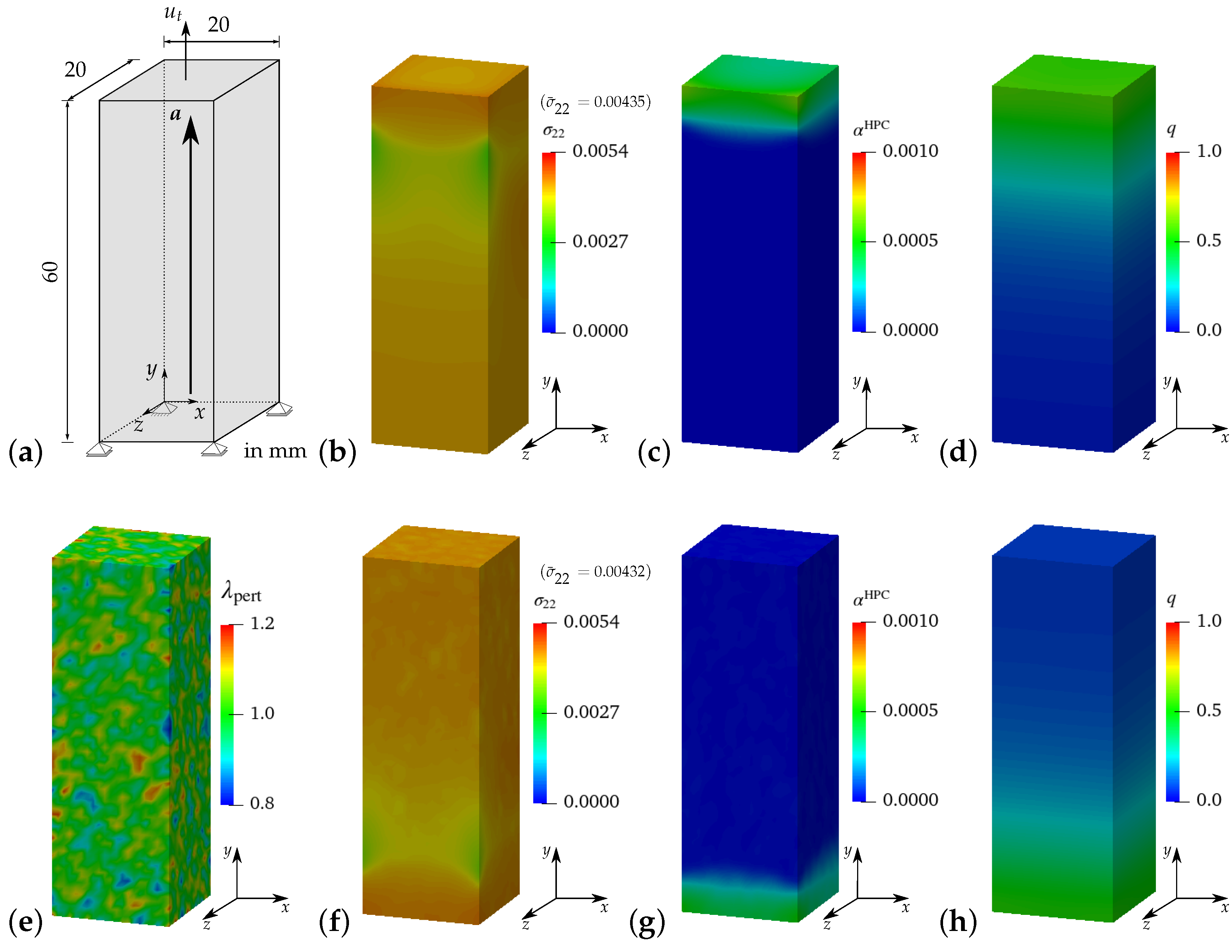
3.3.1. Virtual Experiment I—Uniaxial Tensile Test with Vanishing Transverse Stresses
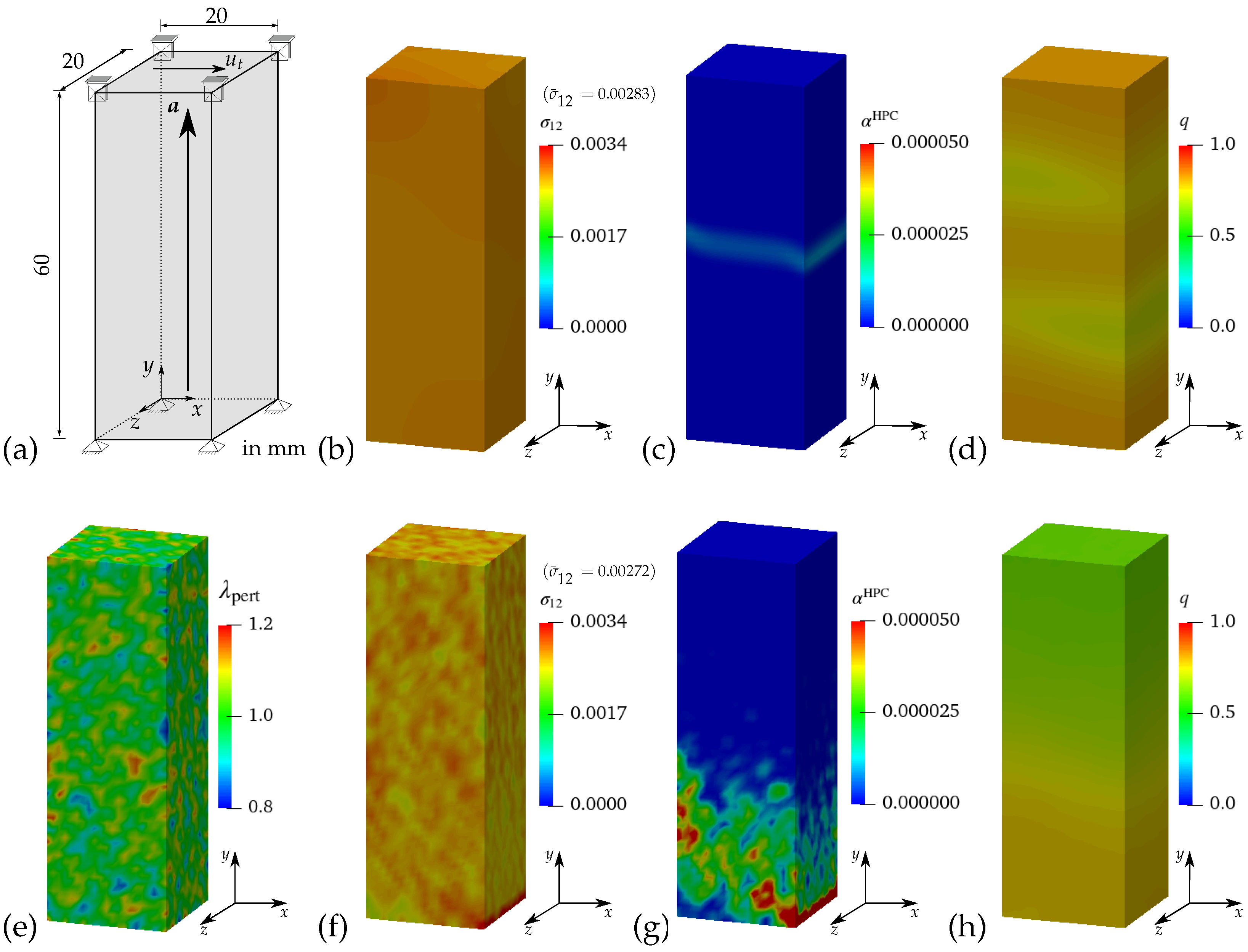
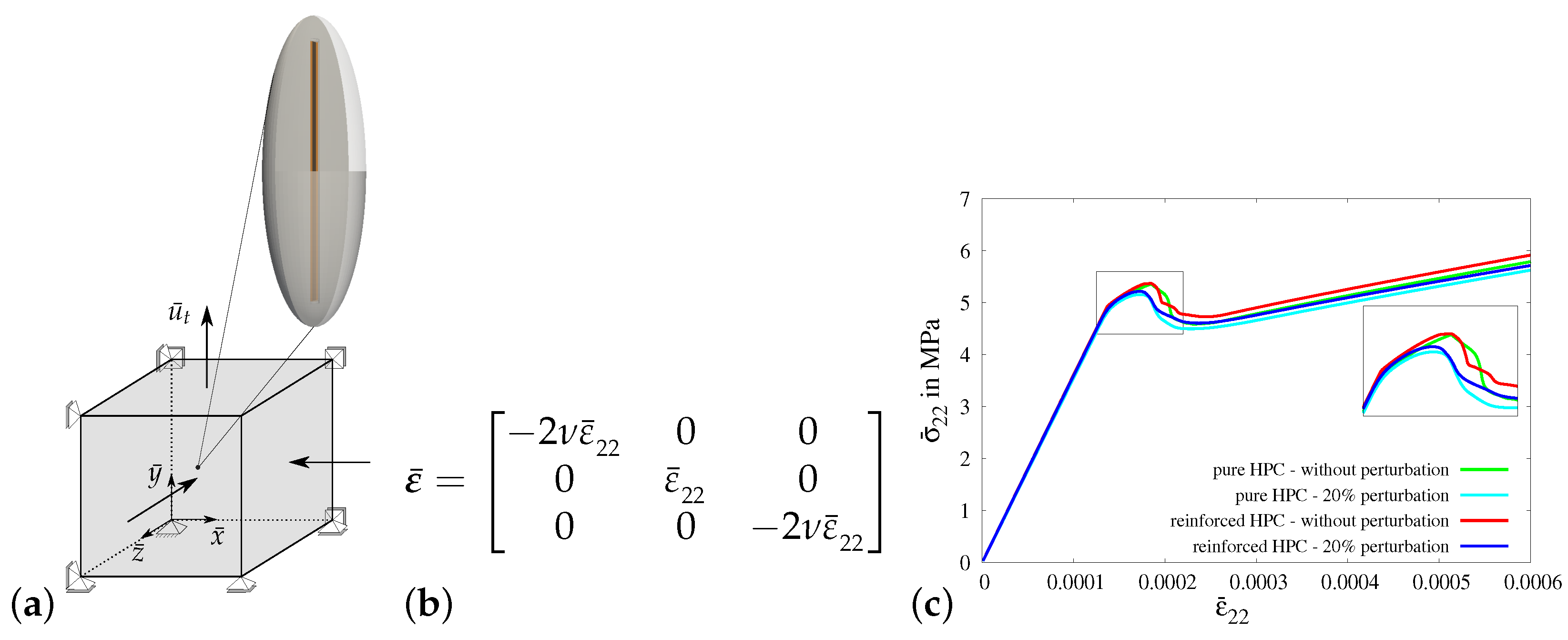
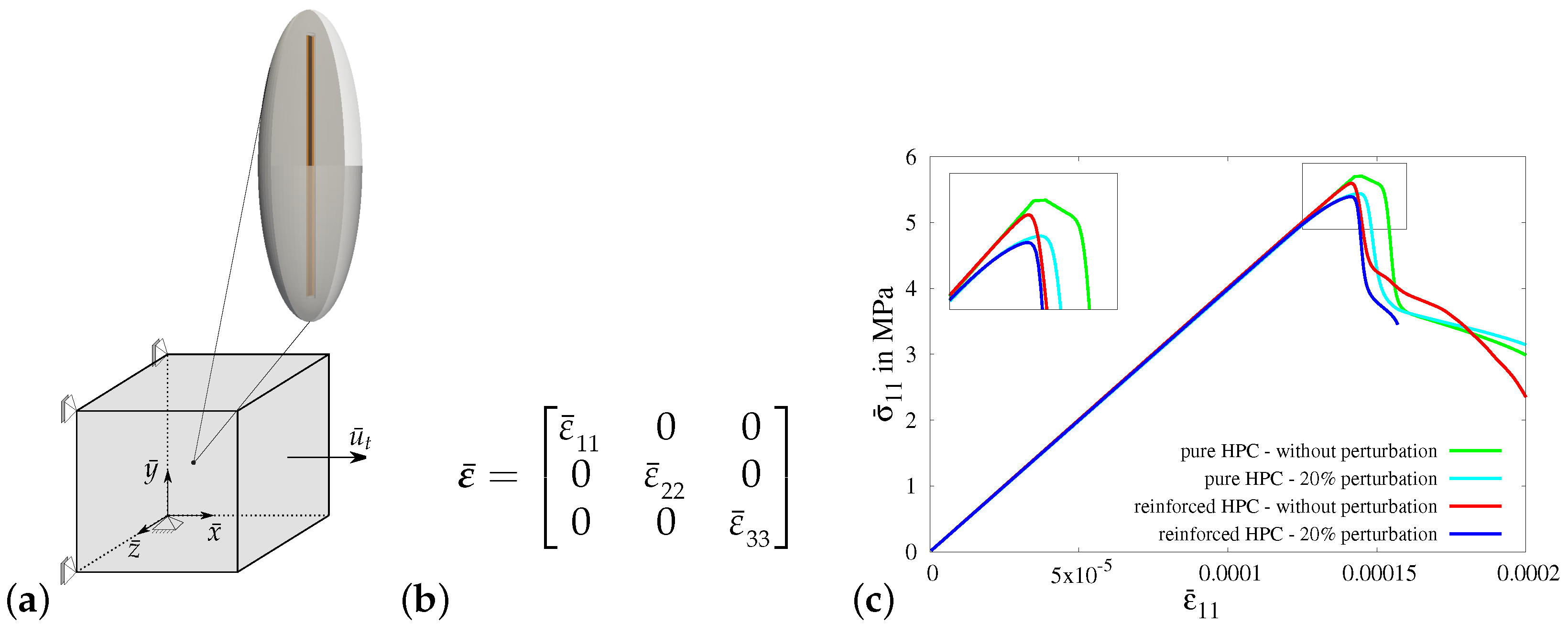
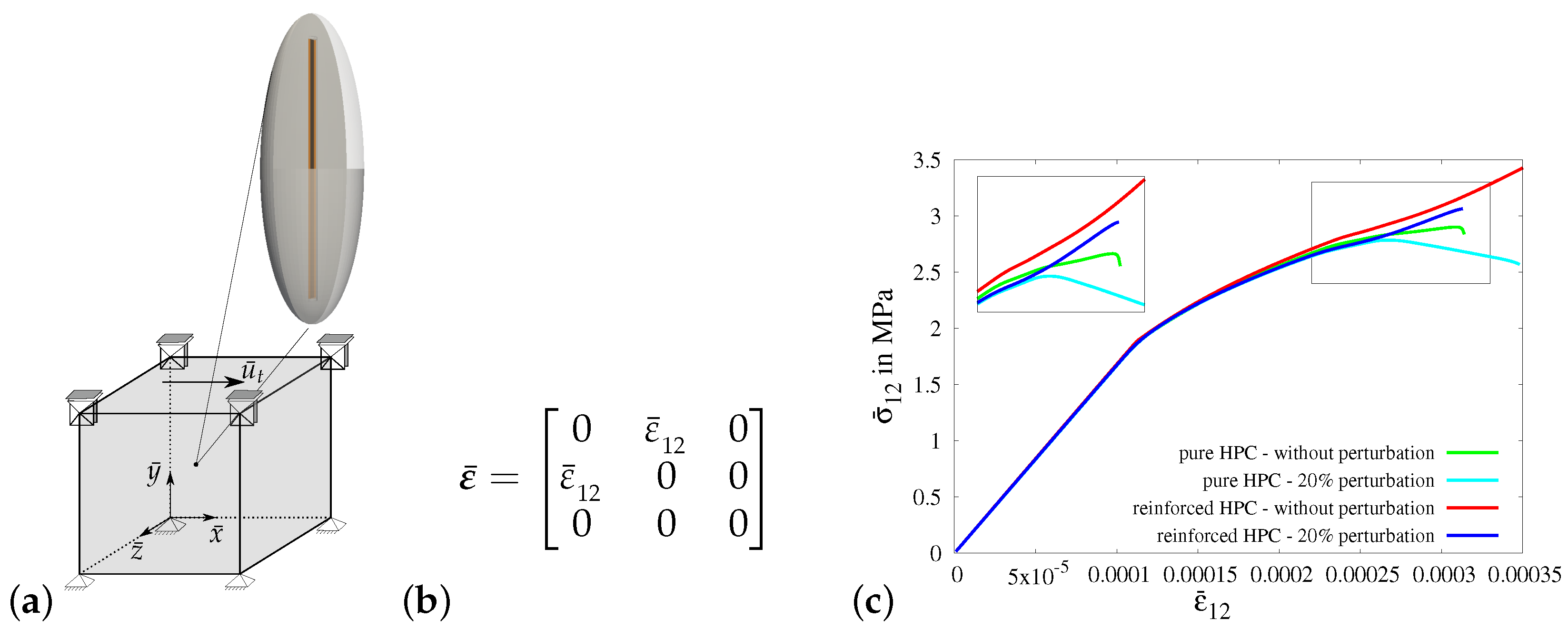
3.3.2. Numerical Results of Virtual Experiments II–V
4. Phenomenological Material Model for Fiber-Reinforced HPC
4.1. Constitutive Framework
4.1.1. Yield Criteria and Flow Rules
4.1.2. Consistent Elasto-Plastic Tangent Moduli

4.2. Numerical Calibration and Validation Using Unit Cell Calculations
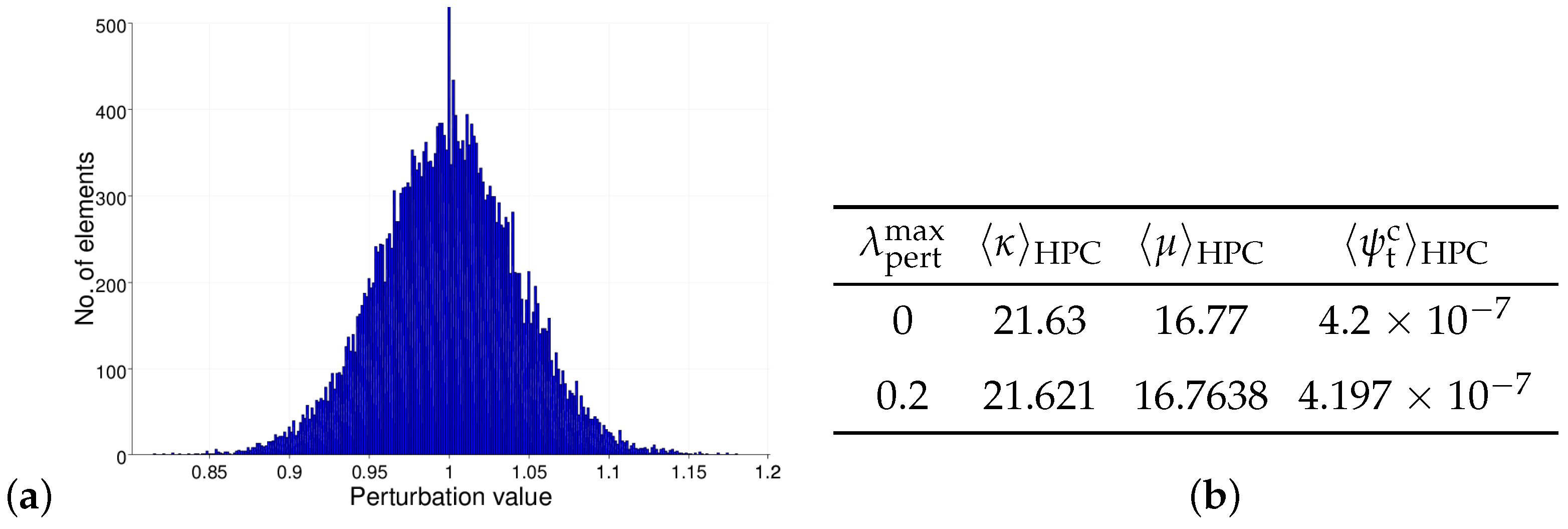
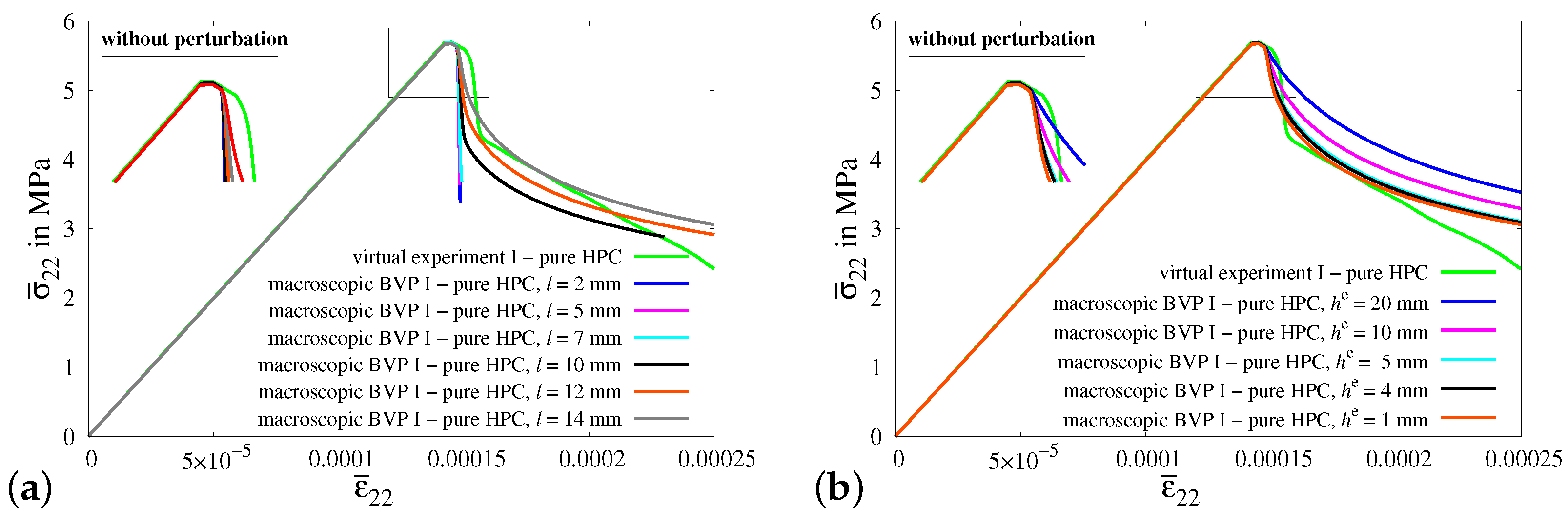
4.2.1. Sensitivity Analysis for the Calibration of the Length-Scale Parameter l
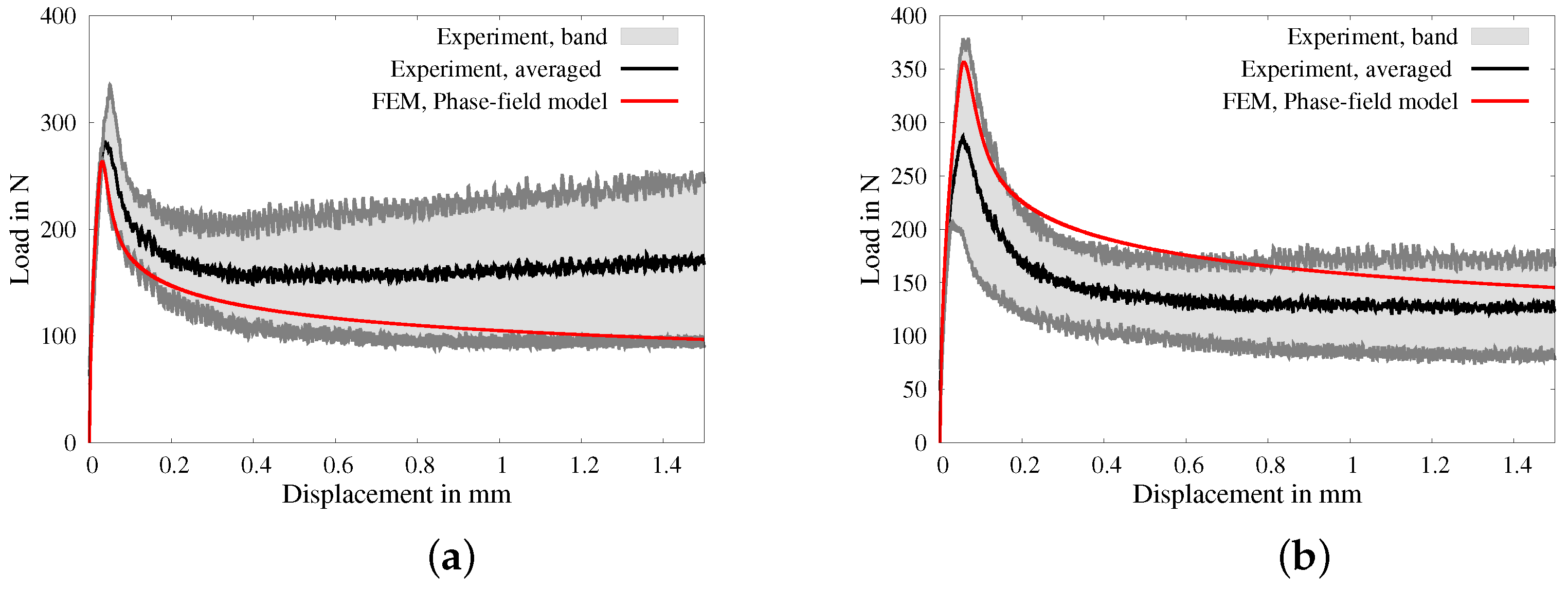
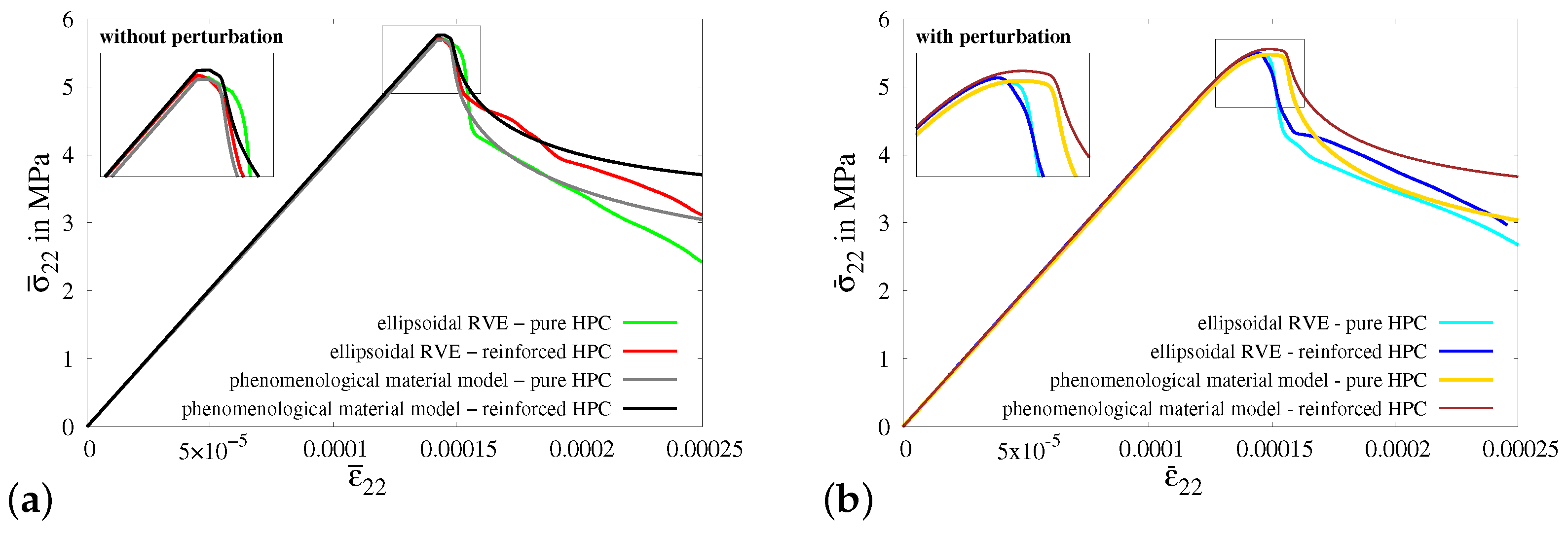
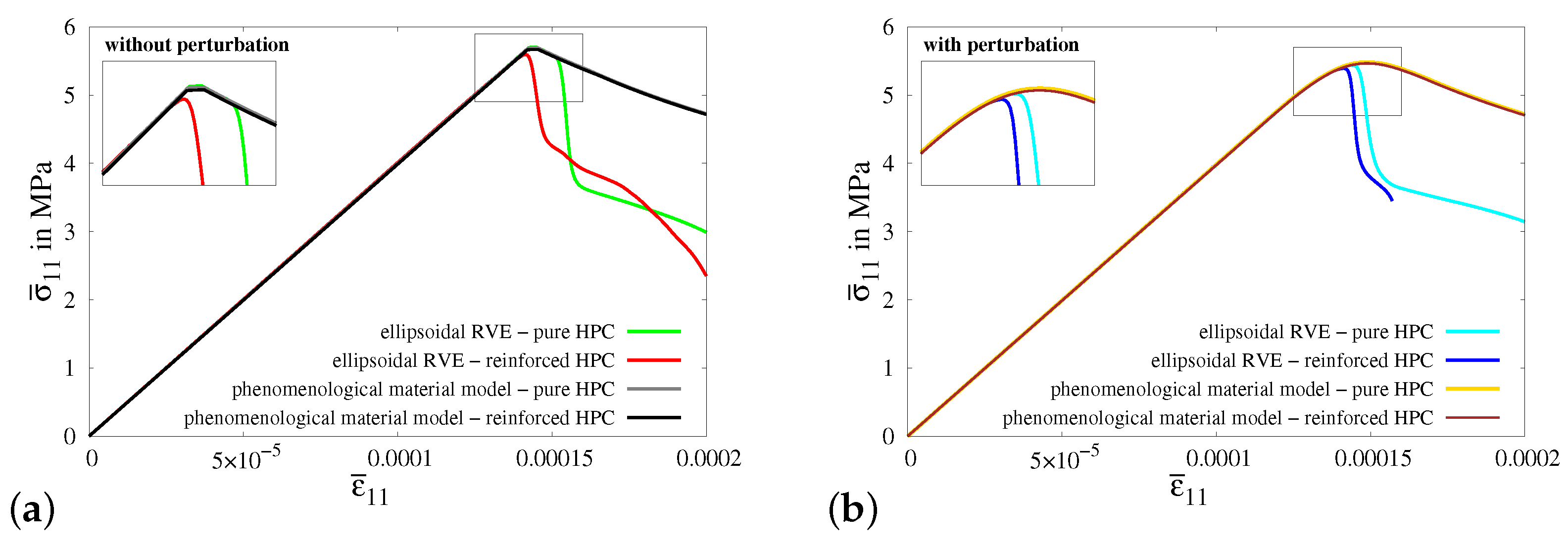
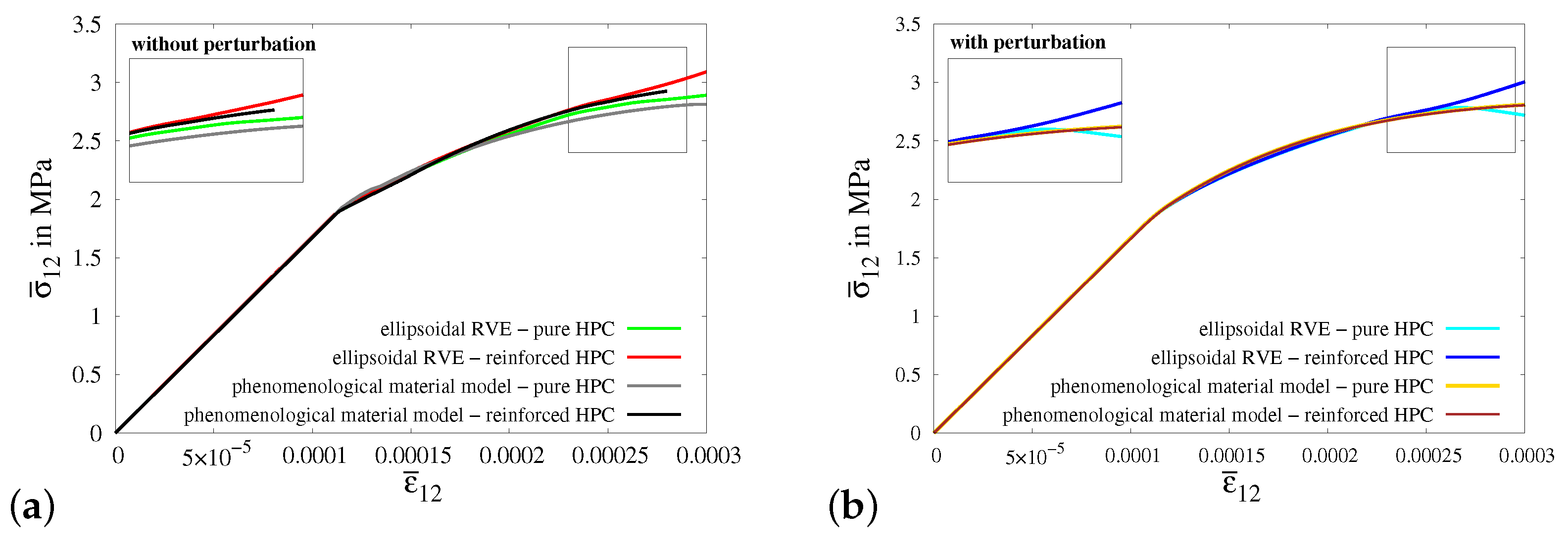
4.2.2. Macroscopic BVP I—Uniaxial Tensile Test with Vanishing Transverse Stresses
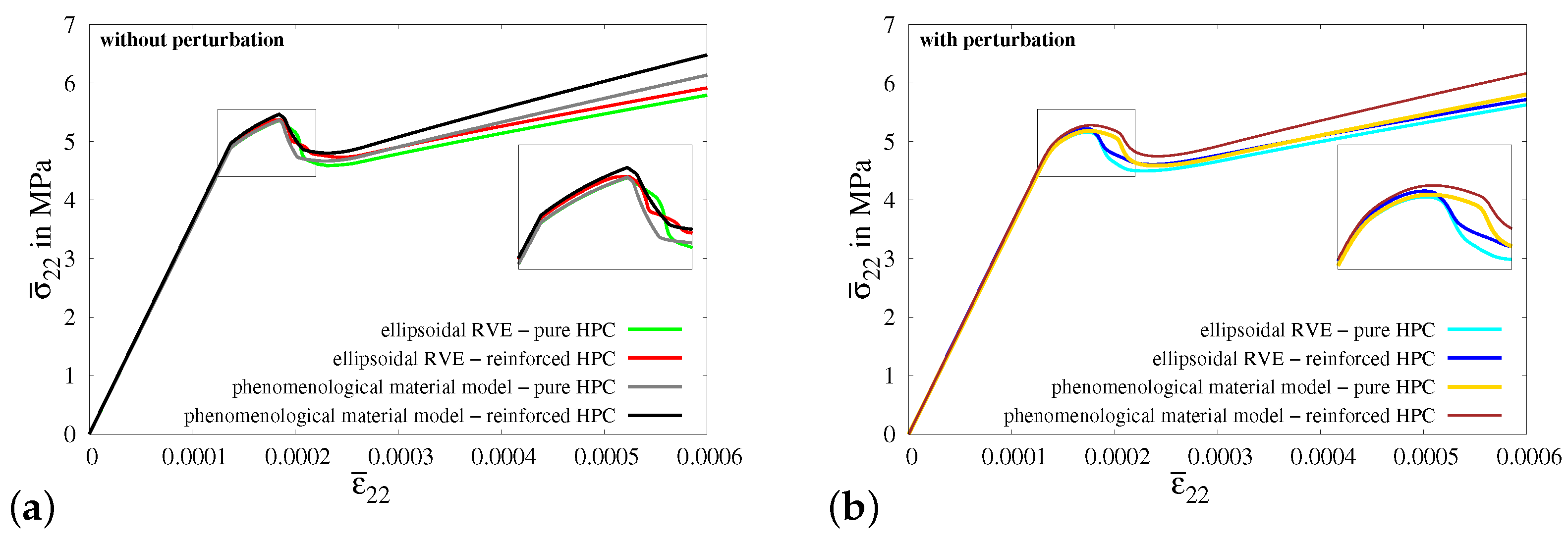
4.2.3. Numerical Simulations of Macroscopic BVPs II–V
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Simulation Results of Virtual Experiments II–V
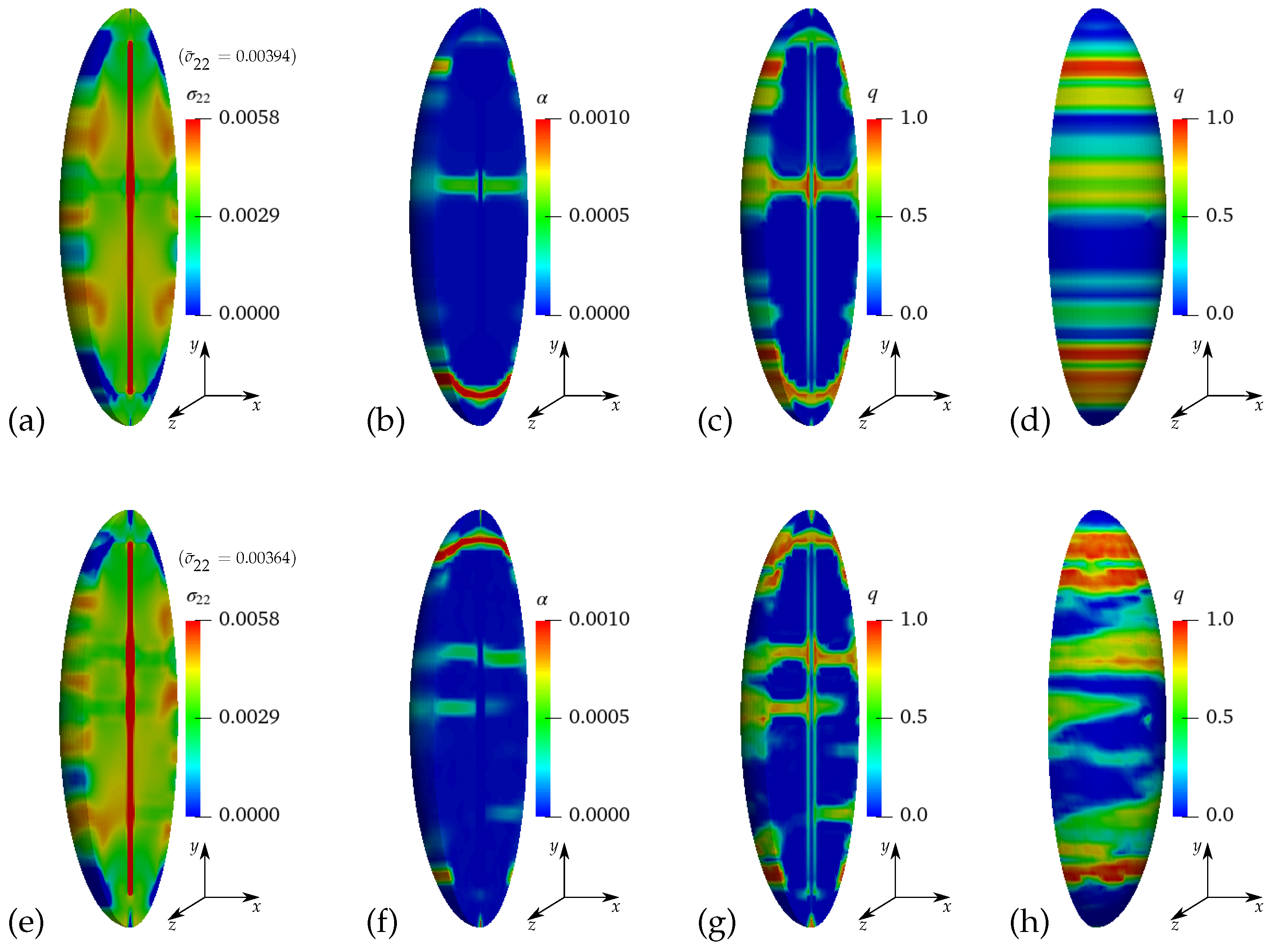
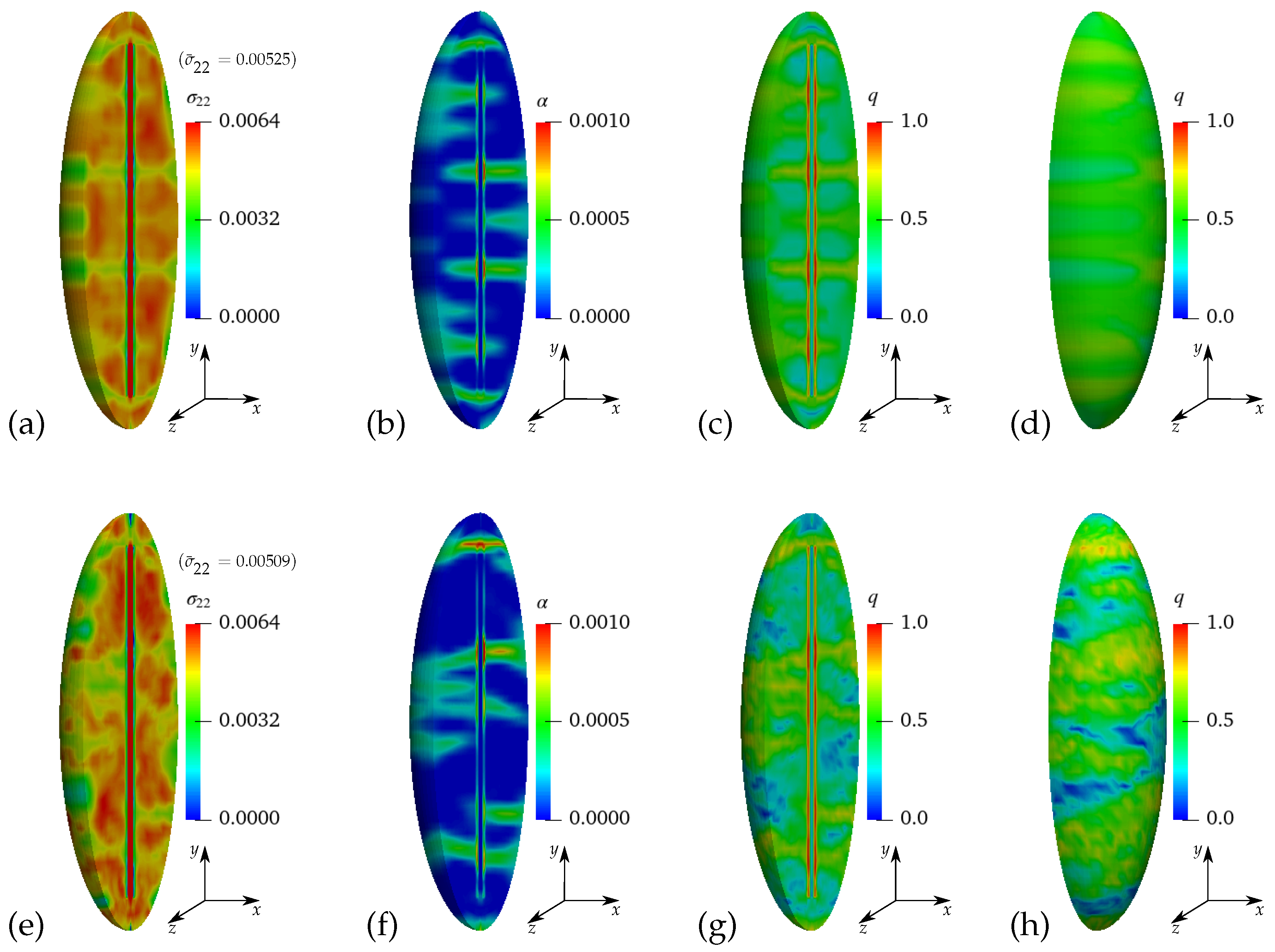


Appendix A.2. Simulations Results of Macroscopic BVPs II–V
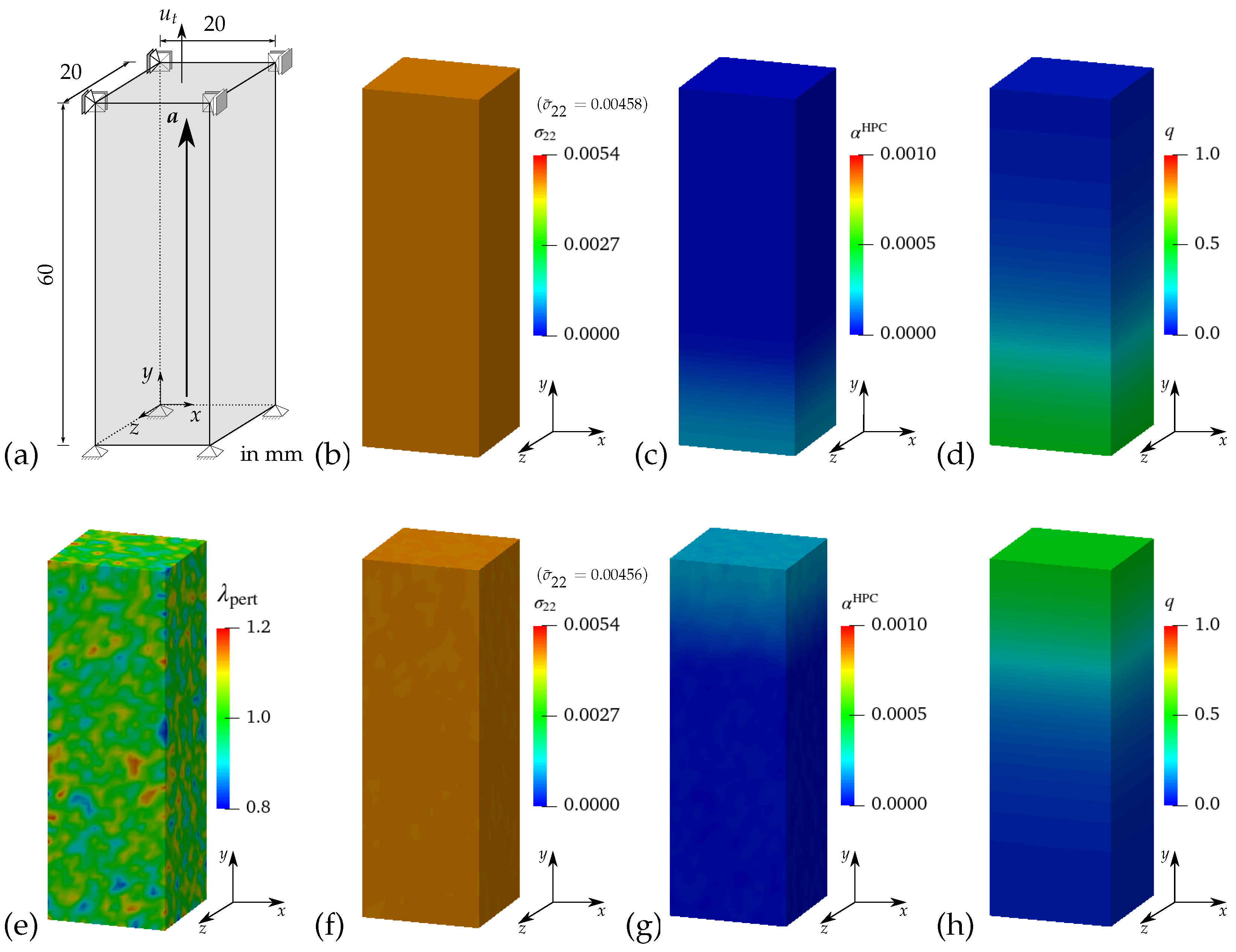
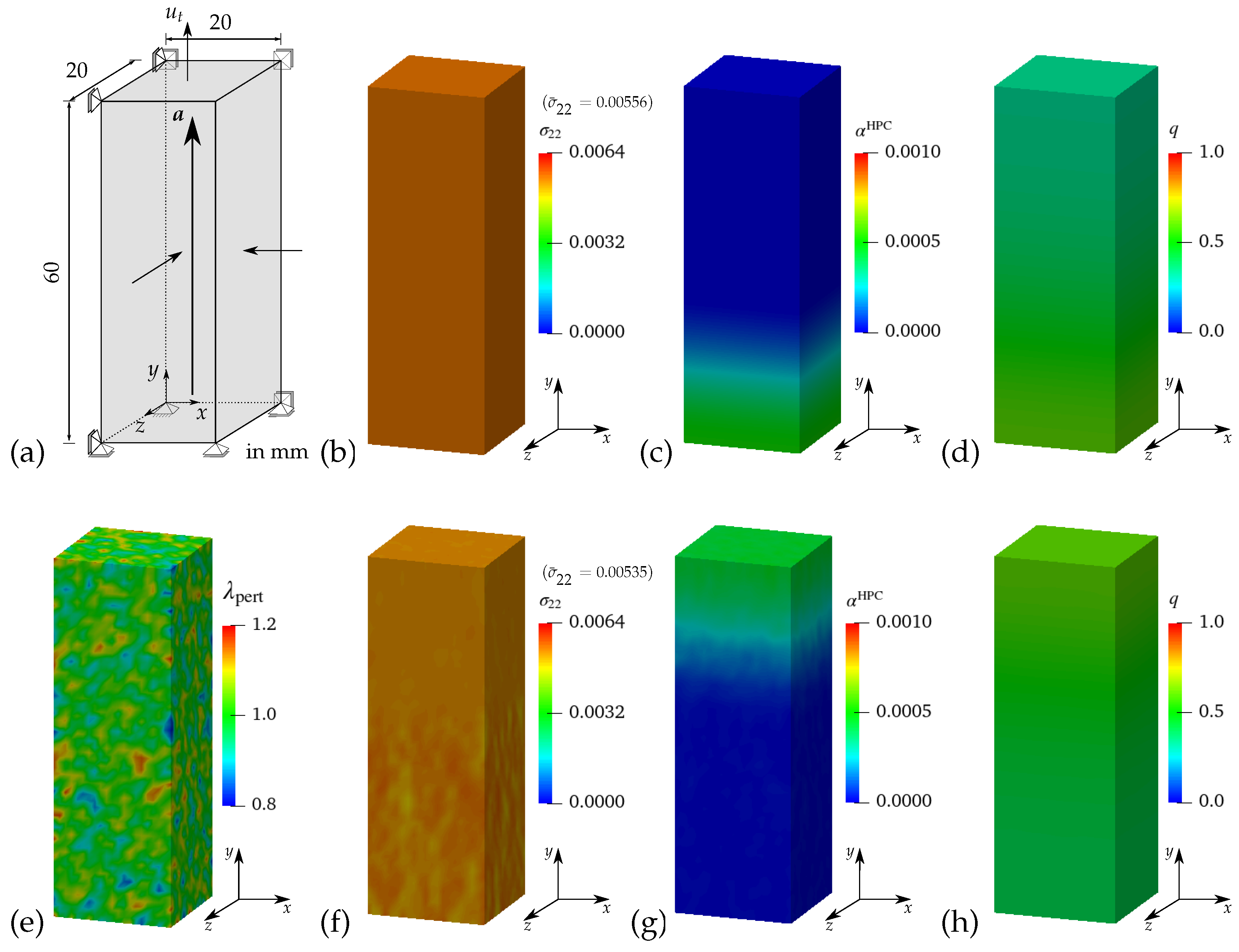
References
- Aïtcin, P.C. High-Performance Concrete; E & FN Spon: London, UK, 1998. [Google Scholar]
- Reinhardt, H.W.; Naaman, A.E. (Eds.) High Performance Fiber Reinforced Cement Composites: Proceedings of the International RILEM/ACI Workshop; E & FN Spon: London, UK, 1992. [Google Scholar]
- Malier, Y. (Ed.) High-Performance Concrete: From Material to Structure; E & FN Spon: London, UK, 1998. [Google Scholar]
- Zhang, J. Fatigue Fracture of Fibre Reinforced Concrete. Ph.D. Thesis, Technische Universität von Dänemark, Kongens Lyngby, Denmark, 1998. [Google Scholar]
- Krasnikovs, A.; Kononova, O.; Khabbaz, A.; Machanovsky, E.; Machanovsky, A. Post-cracking behaviour of high strength fiber concrete prediction and validation. World Acad. Sci. Eng. Technol. Int. J. Mech. Mechatronics Eng. 2011, 5, 2183–2187. [Google Scholar]
- Germano, F.; Tiberti, G.; Plizzari, G. Post-peak fatigue performance of steel fiber reinforced concrete under flexure. Mater. Struct. 2016, 49, 4229–4245. [Google Scholar] [CrossRef]
- Elsmeier, K.; Hümme, J.; Oneschkow, N.; Lohaus, L. Prüftechnische Einflüsse auf das Ermüdungsverhalten hochfester feinkörninger Vergussbetone. Beton- Und Stahlbetonbau 2016, 111, 233–240. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Zhou, X. Pull-out behaivour of hooked end steel fibres embedded in ultra-high peformance mortar with various W/B ratios. Int. J. Concr. Struct. Mater. 2017, 11, 301–313. [Google Scholar] [CrossRef]
- Sivakumar, A.; Santhanam, M. Mechanical properties of high strength concrete reinforced with metallic and non-metallic fibres. Cem. Concr. Compos. 2007, 29, 603–608. [Google Scholar] [CrossRef]
- Žirgulis, G.; Švec, O.; Sarmiento, E.V.; Geiker, M.R.; Cwirzen, A.; Kanstad, T. Importance of quantification of steel fibre orientation for residual flexural tensile strength in FRC. Mater. Struct. 2016, 49, 3861–3877. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Nematollahi, B.; Qiu, J.; Yang, E.H.; Sanjayan, J. Microscale investigation of fiber-matrix interface properties of strain-hardening geopolymer composite. Ceram. Int. 2017, 43, 15616–15625. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. ASCE 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Wu, J.Y.; Li, J.; Faria, R. An energy release rate-based plastic-damage model for concrete. Int. J. Solids Struct. 2006, 43, 583–612. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Kappos, A.J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef]
- Cicekli, U.; Voyiadjis, G.Z.; Abu Al-Rub, R.K. A plasticity and anisotropic damage model for plain concrete. Int. J. Plast. 2007, 23, 1874–1900. [Google Scholar] [CrossRef]
- Zhou, F.; Cheng, G. A Coupled Plastic Damage Model for Concrete considering the Effect of Damage on Plastic Flow. Math. Probl. Eng. 2015, 2015, 867979. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Ju, J.W. 3D elastoplastic damage model for concrete based on novel decomposition of stress. Int. J. Solids Struct. 2016, 94–95, 125–137. [Google Scholar] [CrossRef]
- Ambrosio, L.; Tortorelli, V. Approximation of functionals depending on jumps by elliptic functionals via Γ-convergence. Commun. Pure Appl. Math. 1990, 43, 999–1036. [Google Scholar] [CrossRef]
- Mumford, D.; Shah, J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.; Marigo, J. The variational approach to fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Francfort, G.; Marigo, J. Revisiting brittle fracture as an energy minimisation problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Kuhn, K.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.R.; Landis, C.M.; Verhoosel, C.V. A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework. Comput. Methods Appl. Mech. Eng. 2014, 273, 100–118. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Kästner, M.; Hennig, P.; Linse, T.; Ulbricht, V. Phase-field modelling of damage and fracture–convergence and local mesh refinement. In Advanced Methods of Continuum Mechanics for Materials and Structures; Naumenko, K., Aßmus, M., Eds.; Springer: Singapore, 2016; pp. 307–324. [Google Scholar]
- Nguyen, T.T.; Yvonnet, J.; Bornert, M.; Chateau, C.; Sab, K.; Romani, R.; Le Roy, R. On the choice of parameters in the phase field method for simulating crack initiation with experimental validation. Int. J. Fract. 2016, 197, 213–226. [Google Scholar] [CrossRef]
- Linse, T.; Hennig, P.; Kästner, M.; de Borst, R. A convergence study of phase-field models for brittle fracture. Eng. Fract. Mech. 2017, 184, 307–318. [Google Scholar] [CrossRef]
- Zhang, X.; Vignes, C.; Sloan, S.W.; Sheng, D. Numerical evaluation of the phase-field model for brittle fracture with emphasis on the length scale. Comput. Mech. 2017, 59, 737–752. [Google Scholar] [CrossRef]
- Steinke, C.; Kaliske, M. A phase-field crack model based on directional stress decomposition. Comput. Mech. 2019, 63, 1019–1046. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Hofacker, M.; Miehe, C. A phase field model of dynamic fracture: Robust field updates for the analysis of complex crack patterns. Int. J. Numer. Methods Eng. 2013, 93, 276–301. [Google Scholar] [CrossRef]
- Schlüter, A.; Willenbücher, A.; Kuhn, C.; Müller, R. Phase field approximation of dynamic brittle fracture. Comput. Mech. 2014, 54, 1141–1161. [Google Scholar] [CrossRef]
- Liu, G.; Li, Q.; Msekh, M.A.; Zuo, Z. Abaqus implementation of monolithic and staggered schemes for quasi-static and dynamic fracture phase-field model. Comput. Mater. Sci. 2016, 121, 35–47. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Duda, F.P.; Ciarbonetti, A.; Sánchez, P.J.; Huespe, A.E. A phase-field/gradient damage model for brittle fracture in elastic-plastic solids. Int. J. Plast. 2015, 65, 269–296. [Google Scholar] [CrossRef]
- Kuhn, C.; Noll, T.; Müller, R. On phase field modeling of ductile fracture. GAMM-Mitteilungen 2016, 39, 35–54. [Google Scholar] [CrossRef]
- Miehe, C.; Aldakheel, F.; Raina, A. Phase field modeling of ductile fracture at finite strains: A variational gradient-extended plasticity-damage theory. Int. J. Plast. 2016, 84, 1–32. [Google Scholar] [CrossRef]
- Borden, M.; Hughes, T.; Landis, C.; Anvari, A.; Lee, I. A phase-field formulation for fracture in ductile materials: Finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Int. J. Numer. Methods Eng. 2016, 312, 130–166. [Google Scholar] [CrossRef]
- Miehe, C.; Teichtmeister, S.; Aldakheel, F. Phase-field modelling of ductile fracture: A variational gradient-extended plasticity-damage theory and its micromorphic regularization. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150170. [Google Scholar] [CrossRef]
- Aldakheel, F.; Wriggers, P.; Miehe, C. A modified Gurson-type plasticity model at finite strains: Formulation, numerical analysis and phase-field coupling. Comput. Mech. 2018, 62, 815–833. [Google Scholar] [CrossRef]
- Alessi, R.; Ambati, M.; Gerasimov, T.; Vidoli, S.; De Lorenzis, L. Comparison of Phase-Field Models of Fracture Coupled with Plasticity. In Advances in Computational Plasticity: A Book in Honour of D. Roger J. Owen; Oñate, E., Peric, D., de Souza Neto, E., Chiumenti, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–21. [Google Scholar]
- Yin, B.; Kaliske, M. A ductile phase-field model based on degrading the fracture toughness: Theory and implementation at small strain. Comput. Methods Appl. Mech. Eng. 2020, 366, 113068. [Google Scholar] [CrossRef]
- Krüger, M.; Dittmann, M.; Aldakheel, F.; Härtel, A.; Wriggers, P.; Hesch, C. Porous-ductile fracture in thermo-elasto-plastic solids with contact applications. Comput. Mech. 2020, 65, 941–966. [Google Scholar] [CrossRef]
- Noll, T.; Kuhn, C.; Olesch, D.; Müller, R. 3D phase field simulations of ductile fracture. GAMM-Mitteilungen 2020, 43, e202000008. [Google Scholar] [CrossRef]
- Choo, J.; Sun, W. Coupled phase-field and plasticity modeling of geological materials: From brittle fracture to ductile flow. Comput. Methods Appl. Mech. Eng. 2018, 330, 1–32. [Google Scholar] [CrossRef]
- Kienle, D.; Aldakheel, F.; Keip, M.A. A finite-strain phase-field approach to ductile failure of frictional materials. Int. J. Solids Struct. 2019, 172–173, 147–162. [Google Scholar] [CrossRef]
- Pise, M.; Bluhm, J.; Schröder, J. Elasto-plastic phase-field model of hydraulic fracture in saturated binary porous media. Int. J. Multiscale Comput. Eng. 2019, 17, 201–221. [Google Scholar] [CrossRef]
- Aldakheel, F. A microscale model for concrete failure in poro-elasto-plastic media. Theor. Appl. Fract. Mech. 2020, 107, 102517. [Google Scholar] [CrossRef]
- You, T.; Zhu, Q.Z.; Li, P.F.; Shao, J.F. Incorporation of tension-compression asymmetry into plastic damage phase-field modeling of quasi brittle geomaterials. Int. J. Plast. 2020, 124, 71–95. [Google Scholar] [CrossRef]
- Späth, M.; Herrmann, C.; Prajapati, N.; Schneider, D.; Schwab, F.; Selzer, M.; Nestler, B. Multiphase-field modelling of crack propagation in geological materials and porous media with Drucker-Prager plasticity. Comput. Geosci. 2021, 25, 325–343. [Google Scholar] [CrossRef]
- Schröder, J. A numerical two-scale homogenization scheme: The FE2-method. In Plasticity and Beyond—Microstructures, Crystal-Plasticity and PhaseTransitions; Schröder, J., Hackl, K., Eds.; CISM Lectures Notes; Springer: Vienna, Austria, 2014; Volume 550, pp. 1–64. [Google Scholar]
- Raous, M.; Cangémi, L.; Cocu, M. A consistent model coupling adhesion, friction, and unilateral contact. Comput. Methods Appl. Mech. Eng. 1999, 177, 383–399. [Google Scholar] [CrossRef]
- Raous, M.; Karray, M.A. Model coupling friction and adhesionfor steel-concrete interfaces. Int. J. Comput. Appl. Technol. 2009, 177, 383–399. [Google Scholar]
- Breitenbücher, R.; Meschke, G.; Song, F.; Zhan, Y. Experimental, analytical and numerical analysis of the pullout behaviour of steel fibres considering different fibre types, inclinations and concrete strengths. Struct. Concr. 2013, 15, 126–135. [Google Scholar] [CrossRef]
- Zhan, Y.; Meschke, G. Analytical Model for the Pullout Behavior of Straight and Hooked-End Steel Fibers. J. Eng. Mech. 2014, 140, 04014091. [Google Scholar] [CrossRef]
- Tai, Y.S.; El-Tawil, S. High loading-rate pullout behavior of inclined deformed steel fibers embedded in ultra-high performance concrete. Constr. Build. Mater. 2017, 148, 204–218. [Google Scholar] [CrossRef]
- Deng, F.; Ding, X.; Chi, Y.; Xu, L.; Wang, L. The pull-out behavior of straight and hooked-end steel fiber from hybrid fiber reinforced cementitious composite: Experimental study and analytical modelling. Compos. Struct. 2018, 206, 693–712. [Google Scholar] [CrossRef]
- Ranjbarian, M.; Mechtcherine, V.; Zhang, Z.; Curosu, I.; Storm, J.; Kaliske, M. Locking Front Model for pull-out behaviour of PVA microfibre embedded in cementitious matrix. Cem. Concr. Compos. 2019, 103, 318–330. [Google Scholar] [CrossRef]
- Gudžulić, V.; Neu, G.E.; Gebuhr, G.; Meschke, G.; Anders, S. Numerisches Mehrebenen-Modell für Stahlfaserbeton Von der Faser-zur Strukturebebe—Mehrstufige Validierung anhand einer experimentellen Studie an hochfestem Faserbeton. Beton- und Stahlbetonbau 2019, 115, 146–157. [Google Scholar] [CrossRef]
- Gebuhr, G.; Pise, M.; Sarhil, M.; Anders, S.; Brands, D.; Schröder, J. Analysis and evaluation of the pull-out behavior of hooked steel fibers embedded in high and ultra-high performance concrete for calibration of numerical models. Struct. Concr. 2019, 20, 1254–1264. [Google Scholar] [CrossRef]
- Pise, M.; Brands, D.; Sarhil, M.; Schröder, J.; Gebuhr, G.; Anders, S. Numerical calibration of elasto-plastic phase-field modeling of fracture for experimental pullout tests of single steel fibres embedded in high-performance concrete. In Advances in Engineering Materials, Structures and Systems: Innovations, Mechanics and Applications: Proceedings of the 7th International Conference on Structural Engineering, Mechanics and Computation (SEMC 2019), Cape Town, South Africa; Zingoni, A., Ed.; Taylor & Francis Group: London, UK, 2019; pp. 1391–1396. [Google Scholar]
- Storm, J.; Pise, M.; Brands, D.; Schröder, J.; Kaliske, M. A comparative study of micro-mechanical models for fiber pullout behavior of reinforced high performance concrete. Eng. Fract. Mech. 2021, 243, 107506. [Google Scholar] [CrossRef]
- Taylor, R.L. FEAP—Finite Element Analysis Program, Version 8.2. 2008. Available online: http://projects.ce.berkeley.edu/feap/ (accessed on 1 March 2008).
- Schröder, J.; Pise, M.; Brands, D.; Gebuhr, G.; Anders, S. Phase-field modeling of fracture in high performance concrete during low-cycle fatigue: Numerical calibration and experimental validation. Comput. Methods Appl. Mech. Eng. 2022, 398, 1179. [Google Scholar] [CrossRef]
- Kuhn, C.; Schlüter, A.; Müller, R. On degradation functions in phase field fracture models. Comput. Mater. Sci. 2015, 108, 374–384. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. part ii. coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic-plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- von Mises, R. Mechanik der festen Körper im plastisch-deformablen Zustand. Nachrichten Von Der Ges. Der Wiss. GÖttingen-Math.-Phys. Kl. 1913, 1913, 582–592. [Google Scholar]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Seleš, K.; Aldakheel, F.; Tonković, Z.; Sorić, J.; Wriggers, P. A general phase-field model for fatigue failure in brittle and ductile solids. Comput. Mech. 2021, 67, 1431–1452. [Google Scholar] [CrossRef]
- Seleš, K.; Lesičar, T.; Tonković, Z.; Sorić, J. A residual control staggered solution scheme for the phase-field modeling of brittle fracture. Eng. Fract. Mech. 2019, 205, 370–386. [Google Scholar] [CrossRef]
- Pise, M.; Brands, D.; Schröder, J. Data Publication: Numerical Simulations of Pullout Test of Steel Fiber Embedded in High Performance Concrete (HPC). Zenodo 2024. [Google Scholar] [CrossRef]
- Pise, M.; Brands, D.; Schröder, J. Data Publication: Virtual Experiments for Steel Fiber Reinforced High Performance Concrete (HPC). Zenodo 2024. [Google Scholar] [CrossRef]
- Pise, M.; Brands, D.; Schröder, J.; Gebuhr, G.; Anders, S. On the application of representative volume elements for steel fiber reinforced high performance concrete - a numerical study. Proc. Appl. Math. Mech. 2021, 20, e202000323. [Google Scholar] [CrossRef]
- Hill, R. Theory and mechanical properties of fibre-strengthened materials. 3. selfconsistent model. J. Mech. Phys. Solids 1965, 13, 189–198. [Google Scholar] [CrossRef]
- Mandel, J. Plasticité Classique et Viscoplasticité; CISM Course Nr. 97; Springer: Wien, Austria, 1972. [Google Scholar]
- Larsson, F.; Runesson, K.; Saroukhani, S.; Vafadari, R. Computational homogenization based on a weak format of micro-periodicity for RVE-problems. Comput. Methods Appl. Mech. Eng. 2011, 200, 11–26. [Google Scholar] [CrossRef]
- Glüge, R. Generalized boundary conditions on representative volume elements and their use in determining the effective material properties. Comput. Mater. Sci. 2013, 79, 408–416. [Google Scholar] [CrossRef]
- Zeman, J. Analysis of Composite Materials with Random Microstructure. Ph.D. Thesis, University of Prague, Prague, Czechia, 2003. [Google Scholar]
- Saavedra Flores, E.I.; de Souza Neto, E.A. Remarks on symmetry conditions in computational homogenisation problems. Int. J. Comput.-Aided Eng. Softw. 2010, 27, 551–575. [Google Scholar] [CrossRef]
- von Hoegen, Y.; Hellebrand, S.; Scheunemann, L.; Schröder, J. On the realization of periodic boundary conditions for hexagonal unit cells. Finite Elem. Anal. Des. 2024, 229, 104067. [Google Scholar] [CrossRef]
- Pise, M.; Brands, D.; Schröder, J.; Gebuhr, G.; Anders, S. Macroscopic model for steel fiber reinforced high performance concrete based on unit cell calculations. Proc. Appl. Math. Mech. 2021, 21, e202100180. [Google Scholar] [CrossRef]
- Pise, M.; Brands, D.; Schröder, J.; Gebuhr, G.; Anders, S. Macroscopic model based on application of representative volume element for steel fiber reinforced high performance concrete. In Current Perspectives and New Directions in Mechanics, Modelling and Design of Structural Systems: Proceedings of the Eigth International Conference on Structural Engineering, Mechanics and Computation (SEMC 2022), Cape Town, South Africa; Zingoni, A., Ed.; CRC Press: Oxon, UK, 2022; pp. 1300–1306. [Google Scholar]
- Simo, J.; Hughes, T. Computational Inelasticity; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2000. [Google Scholar]
- de Souza Neto, E.A.; Peric, D.; Owen, D.R.J. Computational Methods for Plasticity: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ambati, M.; De Lorenzis, L. Phase-field modeling of brittle and ductile fracture in shells with isogeometric NURBS-based solid-shell elements. Comput. Methods Appl. Mech. Eng. 2016, 312, 351–373. [Google Scholar] [CrossRef]
- Čermák, M.; Sysala, S.; Valdman, J. Efficient and flexible MATLAB implementation of 2D and 3D elastoplastic problems. Appl. Math. Comput. 2019, 355, 595–614. [Google Scholar]
- Pise, M.; Brands, D.; Schröder, J. Data Publication: Simulation of Macroscopic Boundary Value Problems Using Phenomenological Material Model for Steel Fiber Reinforced High Performance Concrete (HPC). Zenodo 2024. [Google Scholar] [CrossRef]


| E | h | l | m | |||||||||
| GPa | − | MPa | MPa | MPa | MPa | − | − | mm | − | − | ||
| Steel | 210 | 0.3 | 1150 | – | 0.4 | 0.4 | 660 | 0 | 130 | 0.4 | 0.6 | 0.5 |
| Interface | 39.976 | 0.192 | – | – | 2 × 10−4 | 2 × 10−4 | 6.263 | 0 | 0 | 0.4 | 0.3 | 0.5 |
| HPC | 39.976 | 0.192 | 5.7 | 112 | 4.2 × 10−4 | 0.12 | 6.263 | 0.5218 | 2000 | 0.4 | 0.6 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pise, M.; Brands, D.; Schröder, J. Development and Calibration of a Phenomenological Material Model for Steel-Fiber-Reinforced High-Performance Concrete Based on Unit Cell Calculations. Materials 2024, 17, 2247. https://doi.org/10.3390/ma17102247
Pise M, Brands D, Schröder J. Development and Calibration of a Phenomenological Material Model for Steel-Fiber-Reinforced High-Performance Concrete Based on Unit Cell Calculations. Materials. 2024; 17(10):2247. https://doi.org/10.3390/ma17102247
Chicago/Turabian StylePise, Mangesh, Dominik Brands, and Jörg Schröder. 2024. "Development and Calibration of a Phenomenological Material Model for Steel-Fiber-Reinforced High-Performance Concrete Based on Unit Cell Calculations" Materials 17, no. 10: 2247. https://doi.org/10.3390/ma17102247
APA StylePise, M., Brands, D., & Schröder, J. (2024). Development and Calibration of a Phenomenological Material Model for Steel-Fiber-Reinforced High-Performance Concrete Based on Unit Cell Calculations. Materials, 17(10), 2247. https://doi.org/10.3390/ma17102247







