Study of Complexity of Numerical Models of a Strengthened Timber Beam
Abstract
1. Introduction
- Constitutive law for wood, CFRP tapes, and adhesive,
- Cohesive behavior and traction separation of an adhesive layer,
- Material orientation,
- Proper recreation of damage and delamination,
- Convergence of solution of non-linear FEM problem.
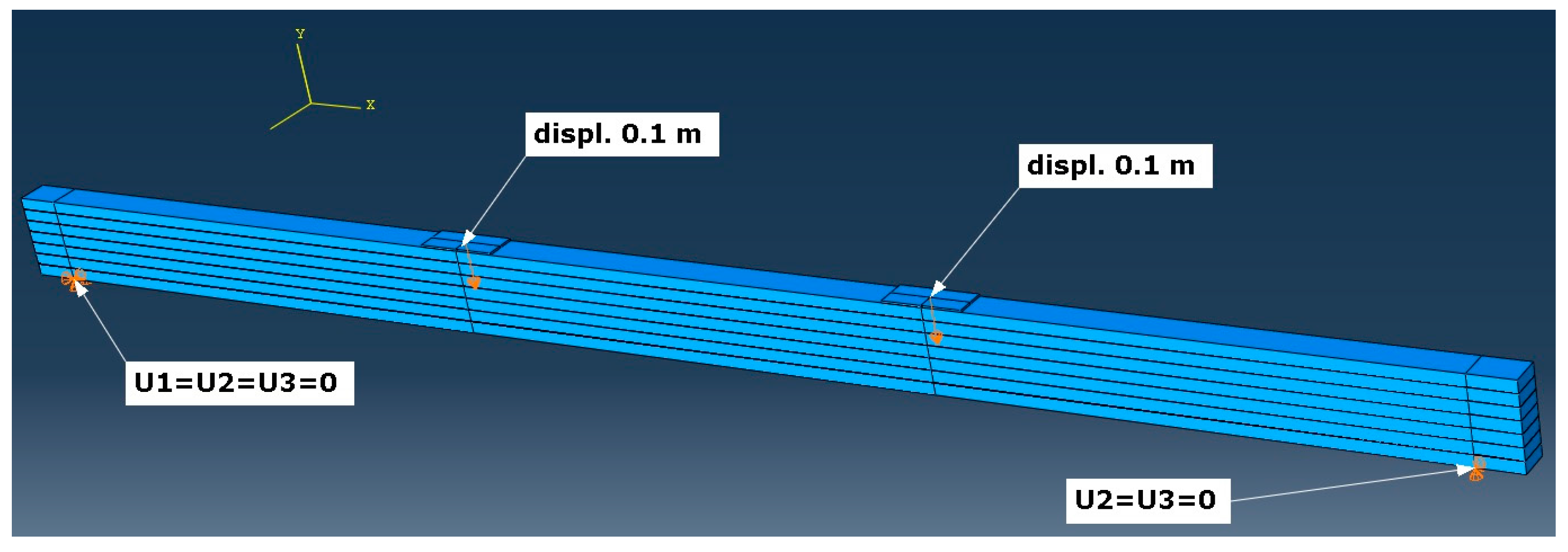
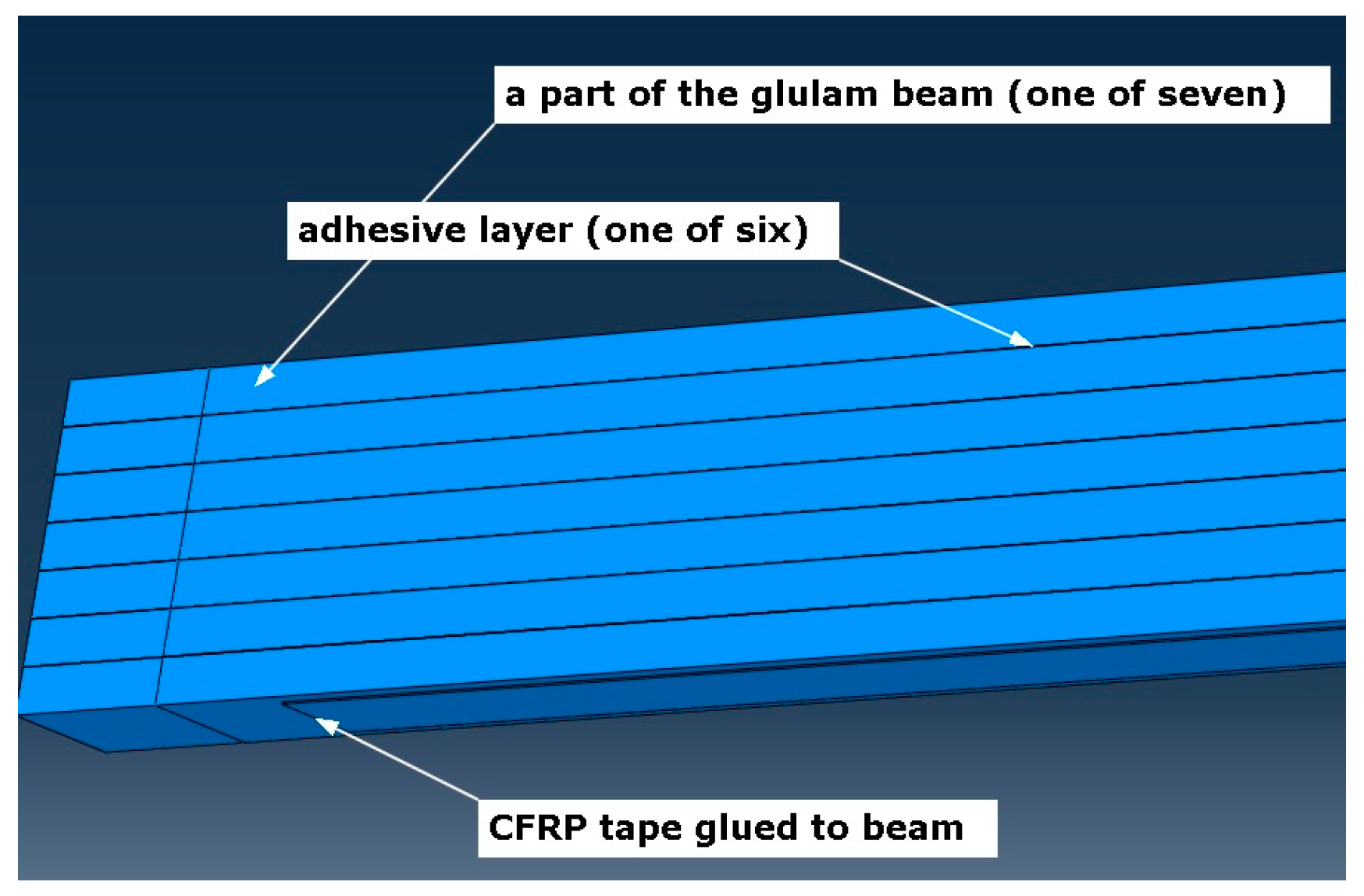
2. Materials and Methods
2.1. Materials
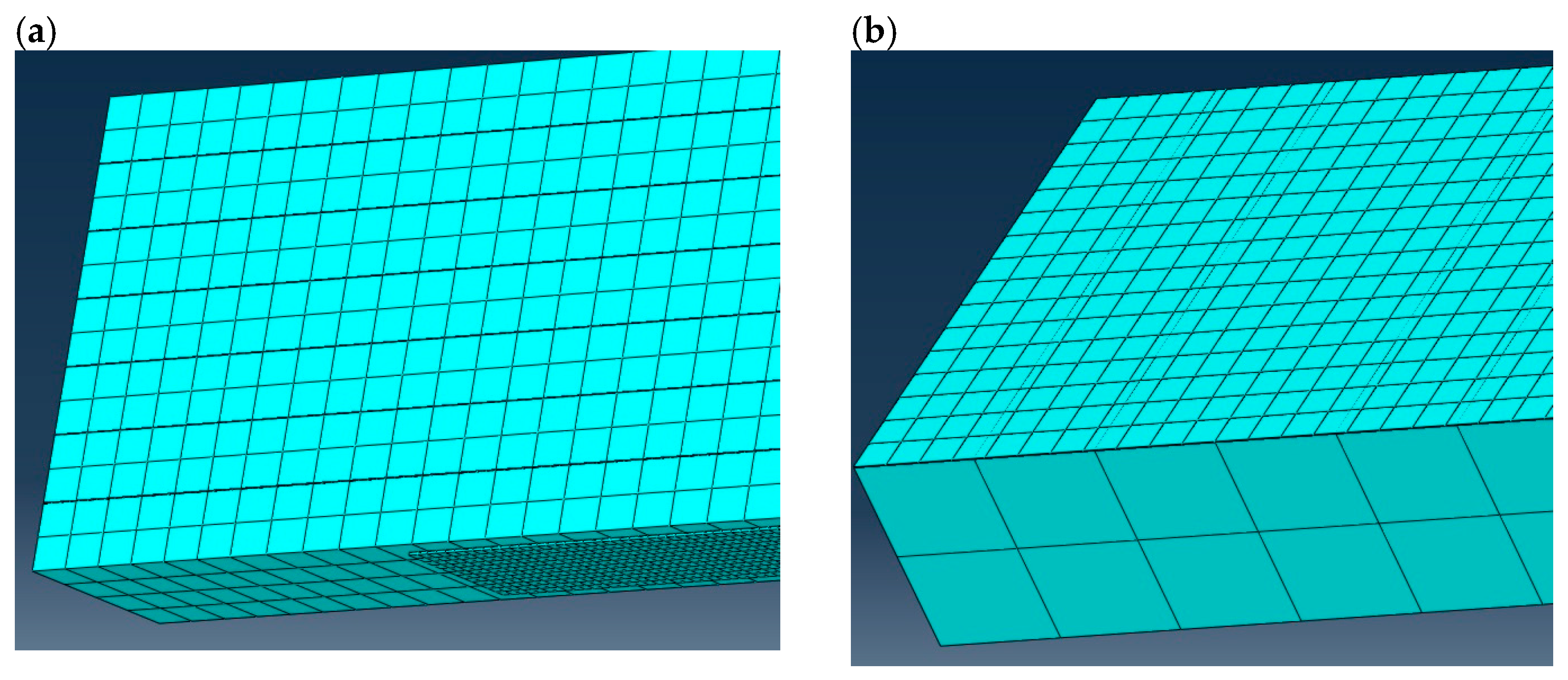
2.2. Methods
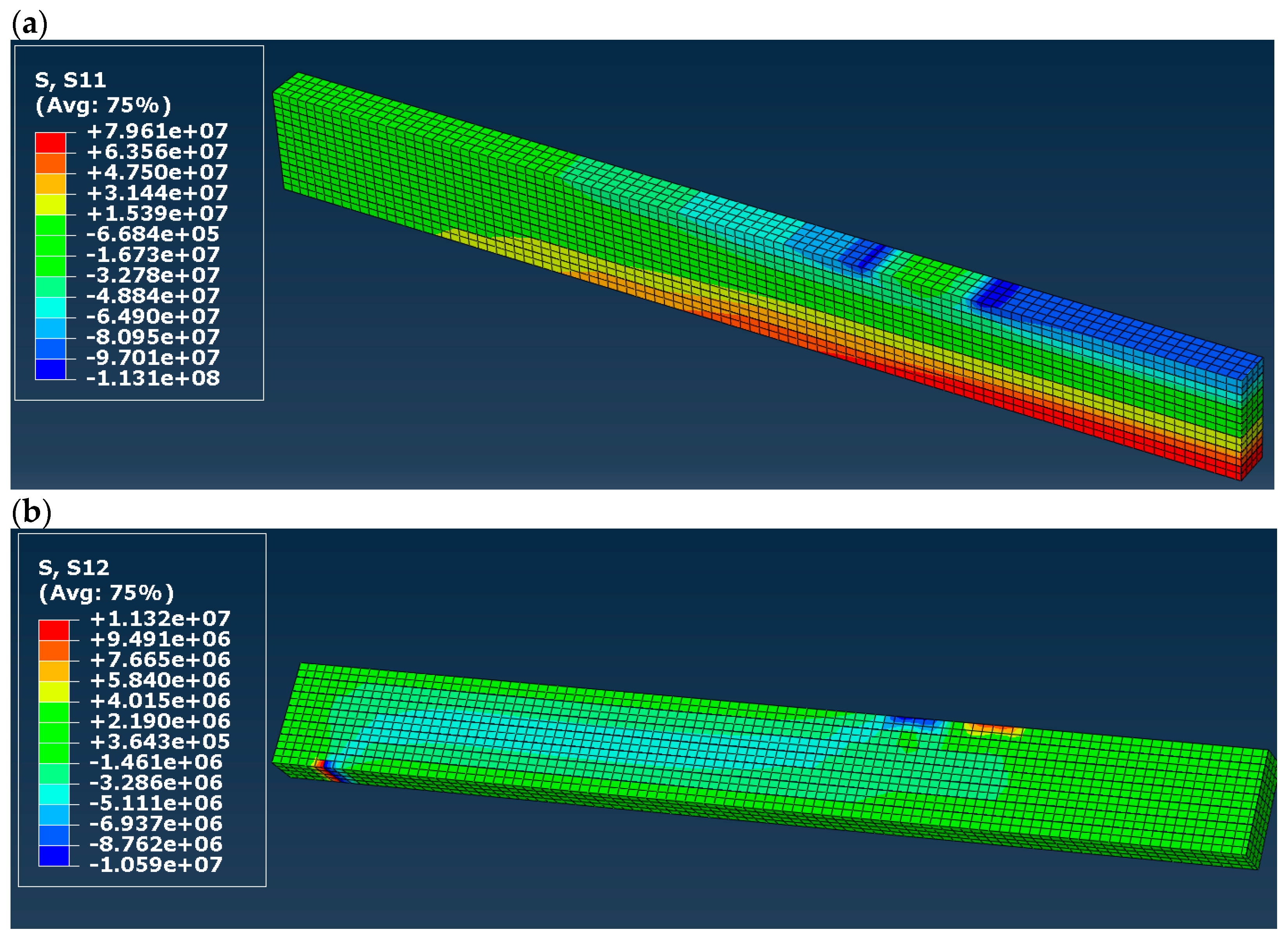
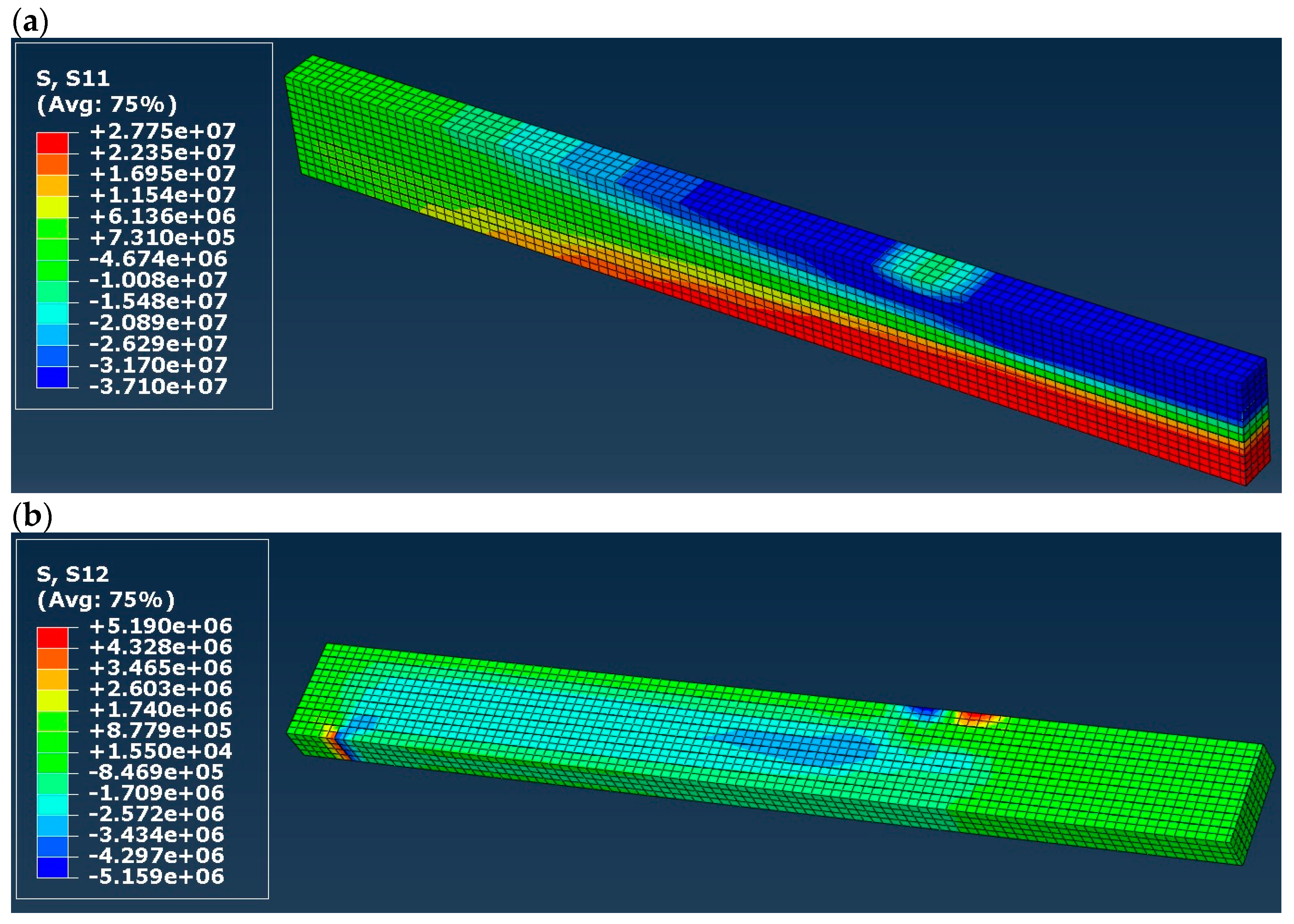
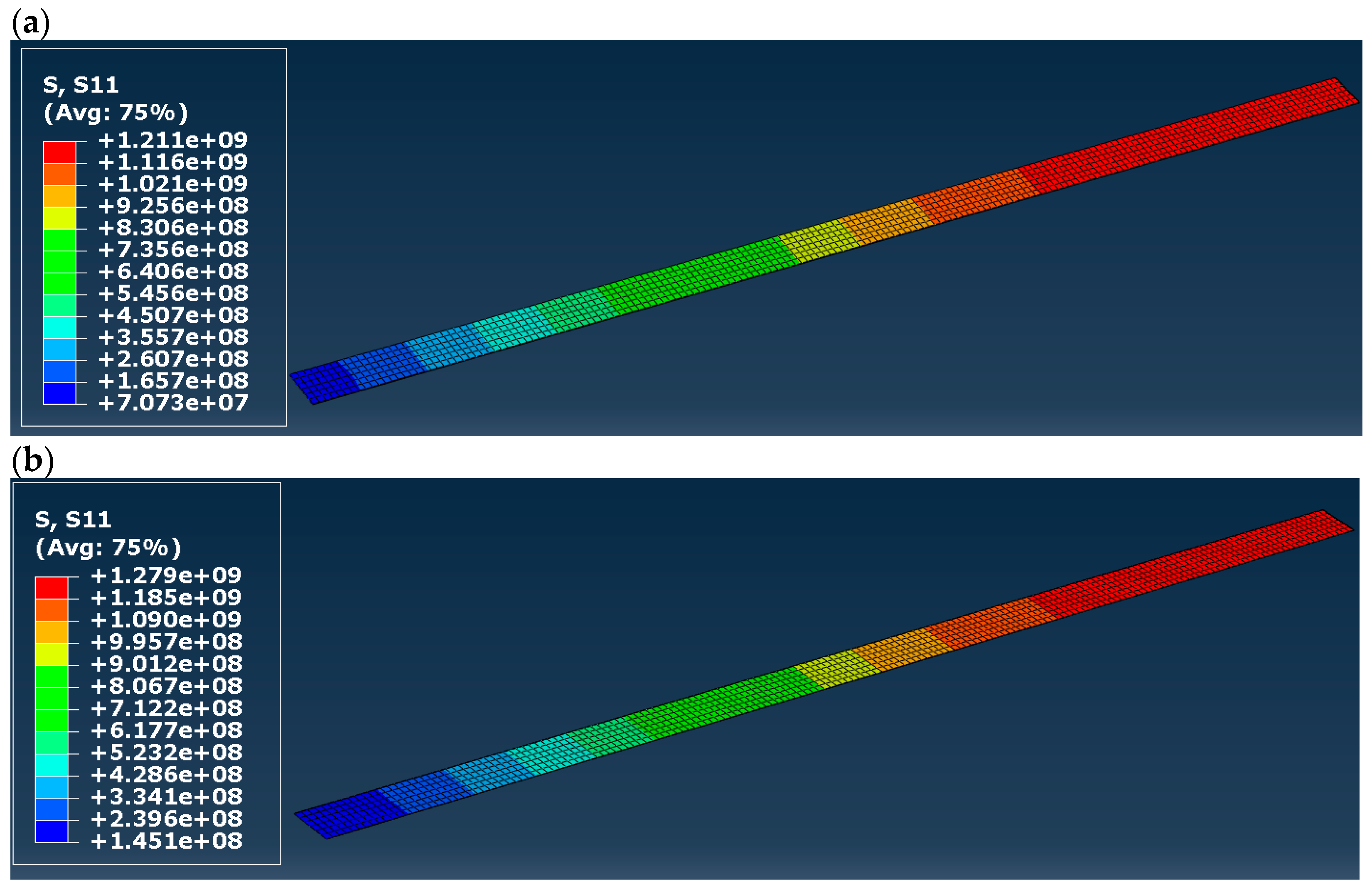
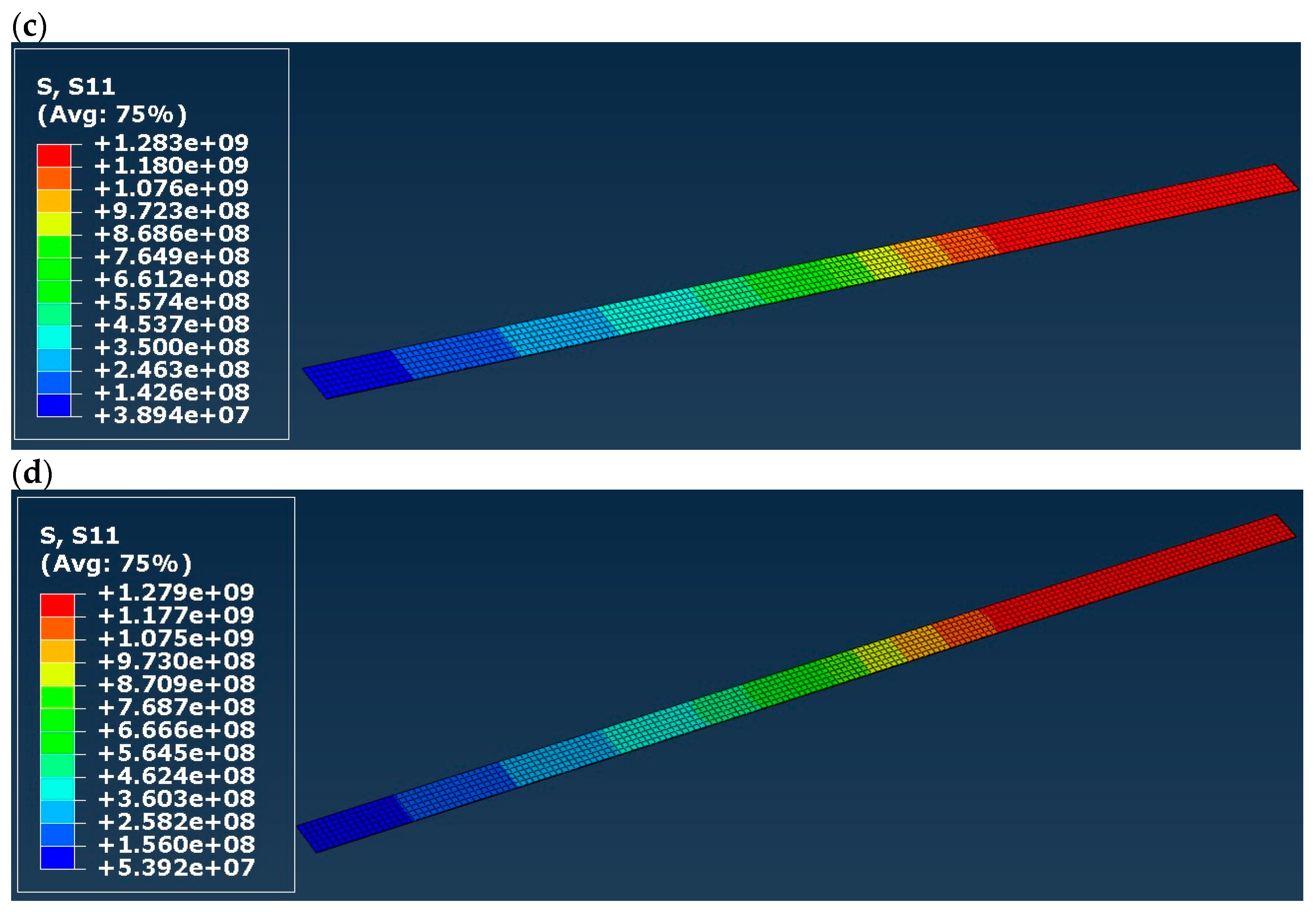
3. Results
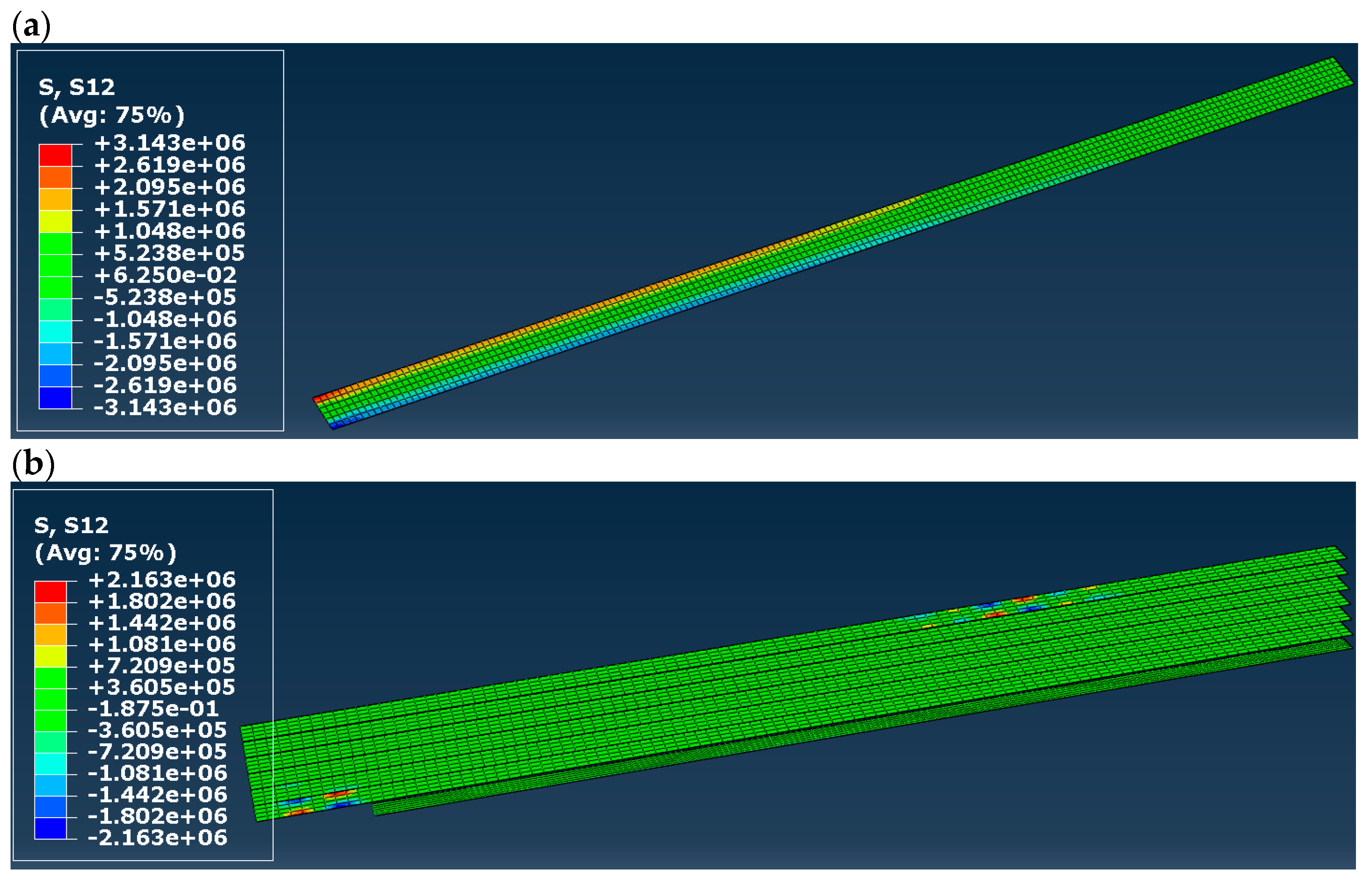
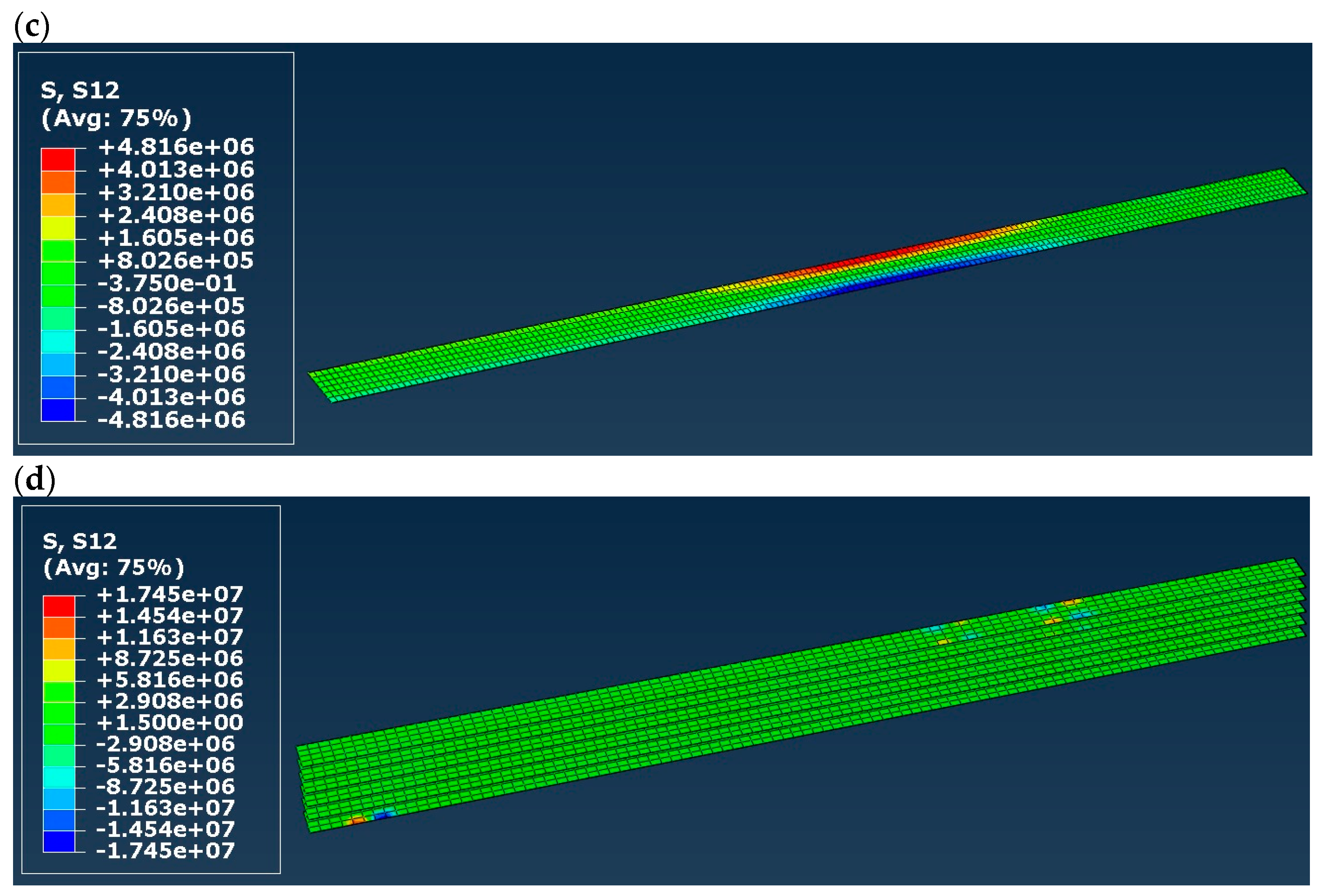
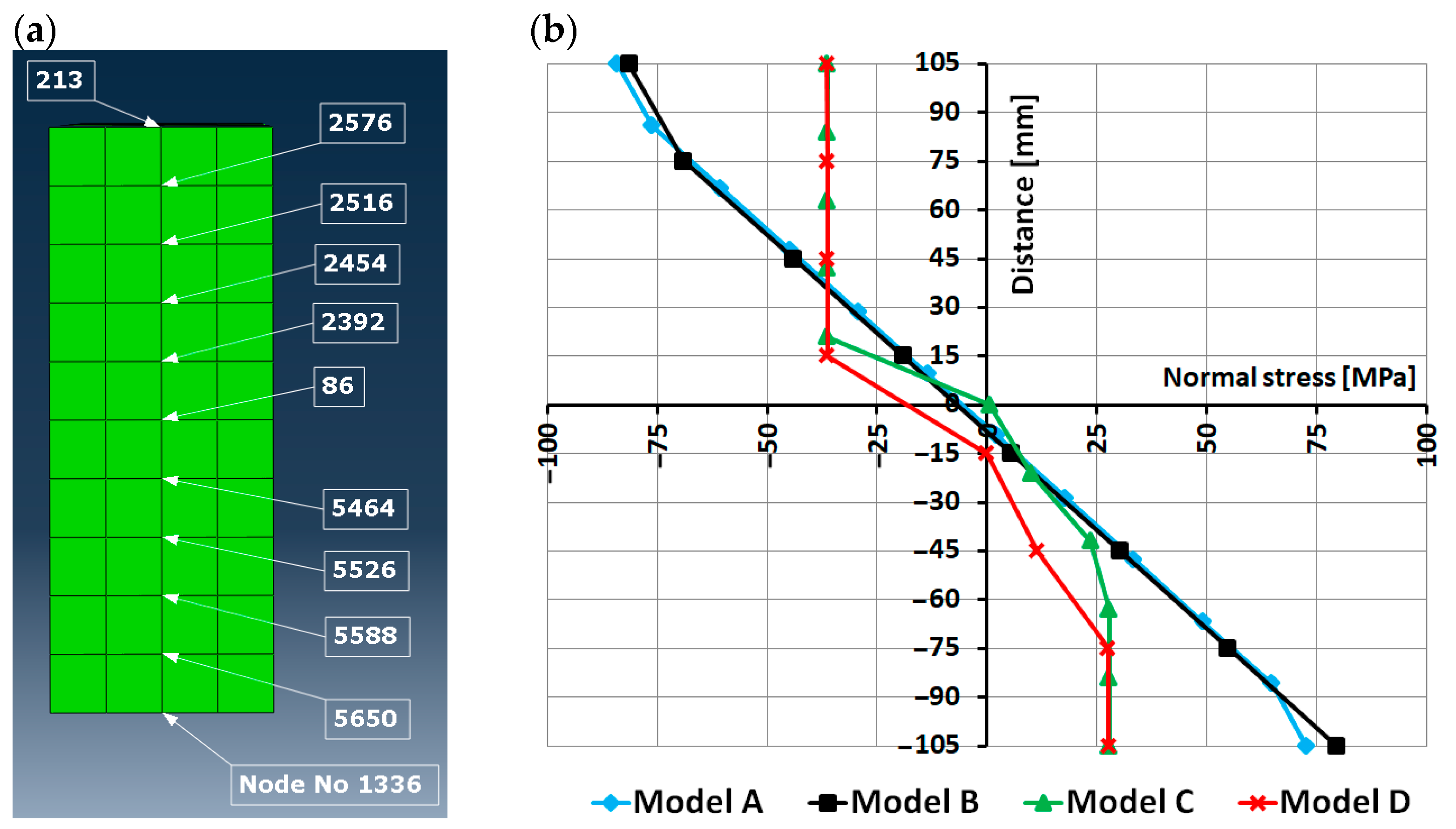
- Stress distribution in timber and CFRP tape;
- Force–deflection relationship for a point in the mid-span of the beam;
- Shear stress in adhesive layers.
4. Discussion
5. Conclusions
- An orthotropic linear elastic model seems not to be a proper model to reproduce the mechanical response of a glulam structural element; structural engineers should be aware of this fact when designing a structural element made of timber strengthened with CFRP tapes (the model can be valid only for relatively small values of mid-span deflection);
- Exceptionally, an orthotropic linear elastic model in the case of a cross-section divided into laminates (model B in the paper) can reproduce reality quite well, but it is limited to small values of deflection of a glulam beam;
- An orthotropic elastic–plastic model behaves well in comparison to a laboratory test; generally speaking, a structural engineer, when designing a timber glulam beam strengthened with CFRP tapes, should seriously consider the use of the plastic model;
- A division of a cross-section into laminates does not significantly affect the results of the FEM calculations.
Funding

Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bakalarz, M.M.; Kossakowski, P.G. Strengthening of full-scale laminated veneer lumber beams with CFRP sheets. Materials 2022, 15, 6526. [Google Scholar] [CrossRef] [PubMed]
- Andor, K.; Lengyel, A.; Polgar, R.; Fodor, T.; Karacsonyi, Z. Experimental and statistical analysis of spruce timber beams reinforced with CFRP fabric. Constr. Build. Mater. 2015, 99, 200–207. [Google Scholar] [CrossRef]
- Nowak, T.P.; Jasieńko, J.; Czepiżak, D. Experimental tests and numerical analysis of historic bent timber elements reinforced with CFRP strips. Constr. Build. Mater. 2013, 40, 197–206. [Google Scholar] [CrossRef]
- Wdowiak-Postulak, A. Strengthening of structural flexural glued laminated beams of ashlar with cords and carbon laminates. Materials 2022, 15, 8303. [Google Scholar] [CrossRef]
- Glisović, I.; Pavlović, M.; Stevanović, B.; Todorović, M. Numerical analysis of glulam beams reinforced with CFRP plates. J. Civ. Eng. Manag. 2017, 23, 868–879. [Google Scholar] [CrossRef]
- Vahedian, A.; Shrestha, R.; Crews, K. Experimental and analytical investigation on CFRP strengthened glulam laminated timber beams: Full-scale experiments. Compos. Part B 2019, 164, 377–389. [Google Scholar] [CrossRef]
- Baño, V.; Arriaga, F.; Soilan, A.; Guaita, M. Prediction of bending load capacity of timber beams using a finite element method simulation of knots and grain deviation. Biosyst. Eng. 2011, 109, 241–249. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Grazini, A. A method for flexural reinforcement of old wood beams with CFRP materials. Compos. Part B 2005, 36, 143–153. [Google Scholar] [CrossRef]
- Jardim, P.I.L.G.; Mascarenhas, F.J.R.; de Almeida, D.H.; Lahr, F.A.R.; Christoforo, A.L. Numerical analysis of hardwood timber beams reinforced with steel plate screwed. Rev. Arvore 2022, 46, e4619. [Google Scholar] [CrossRef]
- Kozłowski, M. Experimental and Numerical Analysis of Hybrid Timber-Glass Beams. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2014. [Google Scholar]
- Navaratnam, S.; Small, D.W.; Corradi, M.; Gatheeshgar, P.; Poologanathan, K.; Higgins, C. Numerical modelling of timber beams with GFRP pultruded reinforcement. Buildings 2022, 12, 1992. [Google Scholar] [CrossRef]
- Thorhallsson, E.R.; Hinriksson, G.I.; Snæbjörnsson, J.T. Strength and stiffness of glulam beams reinforced with glass and basalt fibres. Compos. Part B 2017, 115, 300–307. [Google Scholar] [CrossRef]
- Wdowiak-Postulak, A. Basalt fibre reinforcement of bent heterogeneous glued laminated beams. Materials 2021, 14, 51. [Google Scholar] [CrossRef]
- Wdowiak-Postulak, A. Ductility, load capacity and bending stiffness of scandinavian pine beams from waste timber strengthened with jute fibres. Drew. Pr. Nauk. Doniesienia Komun. 2022, 65, 1–20. [Google Scholar] [CrossRef]
- Kawecki, B. Guidelines for FEM modelling of wood-CFRP beams using ABAQUS. Arch. Civ. Eng. 2021, 67, 175–191. [Google Scholar] [CrossRef]
- Mirianon, F.; Fortino, S.; Toratti, T. A Method to Model Wood by Using ABAQUS Finite Element Software Part 1. Constitutive Model and Computational Details; VTT Technical Research Centre of Finland: Espoo, Finland, 2008. [Google Scholar]
- Kim, Y.J.; Harries, K.A. Modeling of timber beams strengthened with various CFRP composites. Eng. Struct. 2010, 32, 3225–3234. [Google Scholar] [CrossRef]
- Raftery, G.M.; Annette, M.H. Nonlinear numerical modelling of FRP reinforced glued laminated timber. Compos. Part B 2013, 52, 40–50. [Google Scholar] [CrossRef]
- O’Ceallaigh, C.; Sikora, K.; McPolin, D.; Harte, A.M. Modelling the hygro-mechanical creep behaviour of FRP reinforced timber elements. Constr. Build. Mater. 2020, 259, 119899. [Google Scholar] [CrossRef]
- Kawecki, B.; Podgórski, J. 3D abaqus simulation of bent softwood elements. Arch. Civ. Eng. 2020, 66, 323–337. [Google Scholar] [CrossRef]
- Kawecki, B.; Podgórski, J. The effect of glue cohesive stiffness on the elastic performance of bent wood–CFRP beams. Materials 2020, 13, 5075. [Google Scholar] [CrossRef]
- Eslami, H.; Jayasinghe, L.B.; Waldmann, D. Nonlinear three-dimensional anisotropic material model for failure analysis of timber. Eng. Fail. Anal. 2021, 130, 105764. [Google Scholar] [CrossRef]
- CEN. Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Braun, M.; Pełczyński, J.; Al Sabouni-Zawadzka, A.; Kromoser, B. Calibration and validation of a linear-elastic numerical model for timber step joints based on the results of experimental investigations. Materials 2022, 15, 1639. [Google Scholar] [CrossRef] [PubMed]
- Brol, J.; Nowak, T.; Wdowiak, A. Numerical analysis and modelling of timber elements strengthened with FRP materials. Ann. WULS-SGGW Wood Technol. 2018, 104, 274–282. [Google Scholar]
- Palatas, F.; Karolak, A.; Nowak, T.P. Numerical analyses of timber beams with stop-splayed scarf carpentry joints. Eng. Struct. 2022, 266, 114626. [Google Scholar] [CrossRef]
- Kawecki, B. Numerical modelling and experimental testing on polyurethane adhesively bonded joints behaviour in wood-wood and wood-carbon fibre reinforced polymer layouts. Adv. Sci. Technol. Res. J. 2023, 17, 36–52. [Google Scholar] [CrossRef]
- Abaqus/CAE. User’s Guide, Version 2017; Dassault Systemes Simulia Corp: Johnston, RI, USA, 2016. [Google Scholar]




| Modulus of Elasticity [MPa] | Shear Modulus [MPa] | Poisson’s Ratio [-] | ||||||
|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | G12 | G13 | G23 | ν12 | ν13 | ν23 |
| 11,080 | 886 | 554 | 791 | 744 | 79 | 0.37 | 0.42 | 0.47 |
| Modulus of Elasticity [MPa] | Shear Modulus [MPa] | Poisson’s Ratio [-] | ||||||
|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | G12 | G13 | G23 | ν12 | ν13 | ν23 |
| 165,543 | 10,000 | 10,000 | 5000 | 5000 | 1000 | 0.30 | 0.30 | 0.03 |
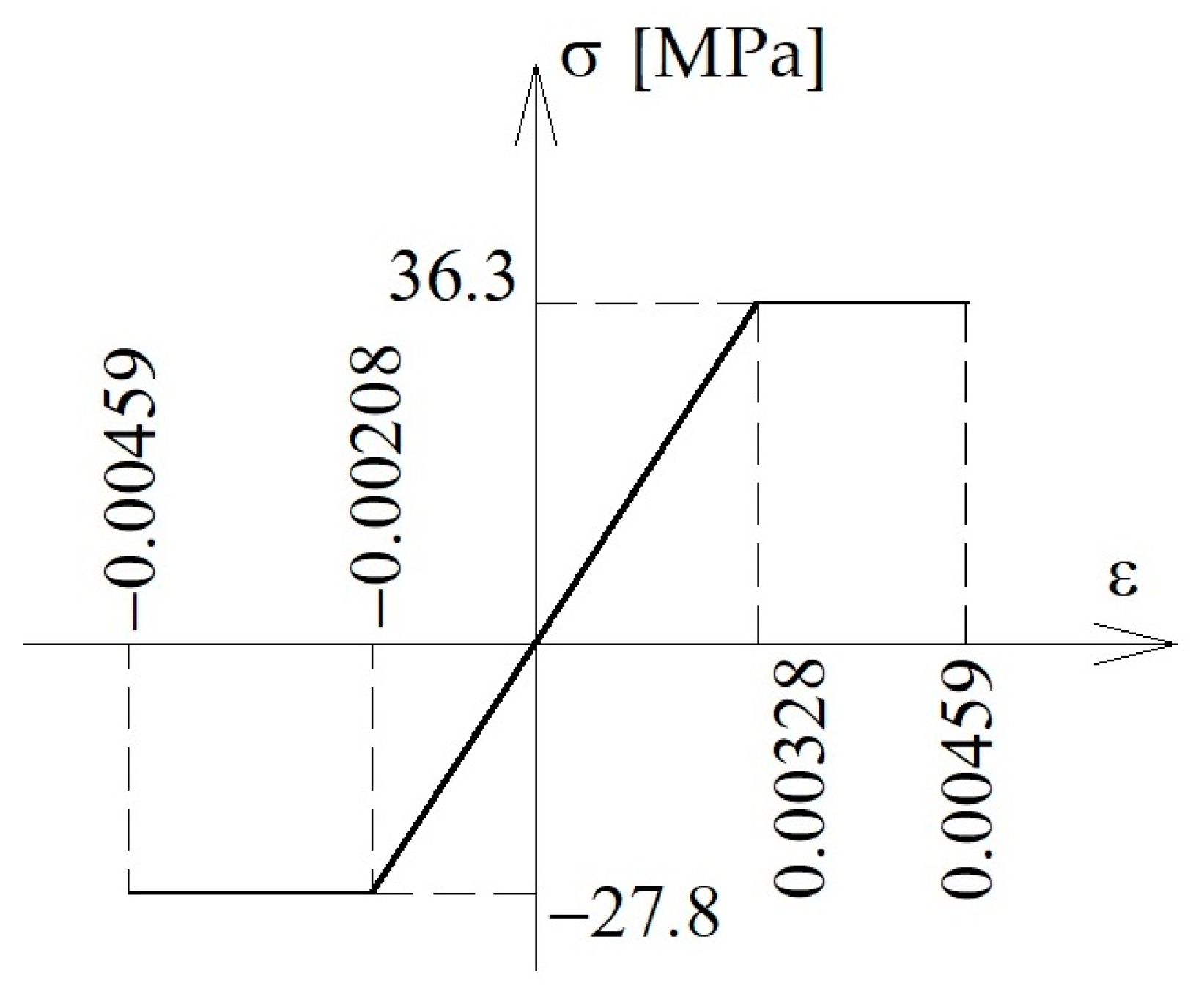
| Property | Timber | CFRP | Adhesive Layer |
|---|---|---|---|
| Compressive strength [MPa] | 36.3 | - | 70.0 |
| Tensile strength [MPa] | 27.8 | 2846.0 | 24.0 |
| Bending strength [MPa] | 42.5 | - | - |
| Shear strength [MPa] | - | - | 18.0 |
| Model Name | Cross-Section | Timber Definition |
|---|---|---|
| A | whole section, no division | orthotropic, linear elastic |
| B | divided into 7 parts, glued with adhesive | orthotropic, linear elastic |
| C | whole section, no division | orthotropic, plastic |
| D | divided into 7 parts, glued with adhesive | orthotropic, plastic |
| R11 | R22 | R33 | R12 | R13 | R23 |
|---|---|---|---|---|---|
| 1.000 | 0.138 | 0.138 | 0.291 | 0.291 | 0.143 |
| Criterion | Model A | Model B | Model C | Model D |
|---|---|---|---|---|
| Force vs deflection curve | Overestimated, no plateau | Similar to laboratory tests, with plateau | ||
| Normal stress in timber | Very overestimated | Restricted to the yield stress value, maps similar to [5] | ||
| Shear stress in timber | Overestimated, but maps similar to [5] in a qualitative sense | Maps and values similar to [5] | ||
| Normal stress in CFRP tapes | Practically identical in all models, below the tensile strength and clearly higher than in the laboratory tests | |||
| Shear stress in adhesive layer(s) | Clearly below the shear strength, no delamination | Similar to the laboratory tests, clearly below the shear strength, no delamination | Clearly higher than in the tests, but still below the shear strength, no delamination | |
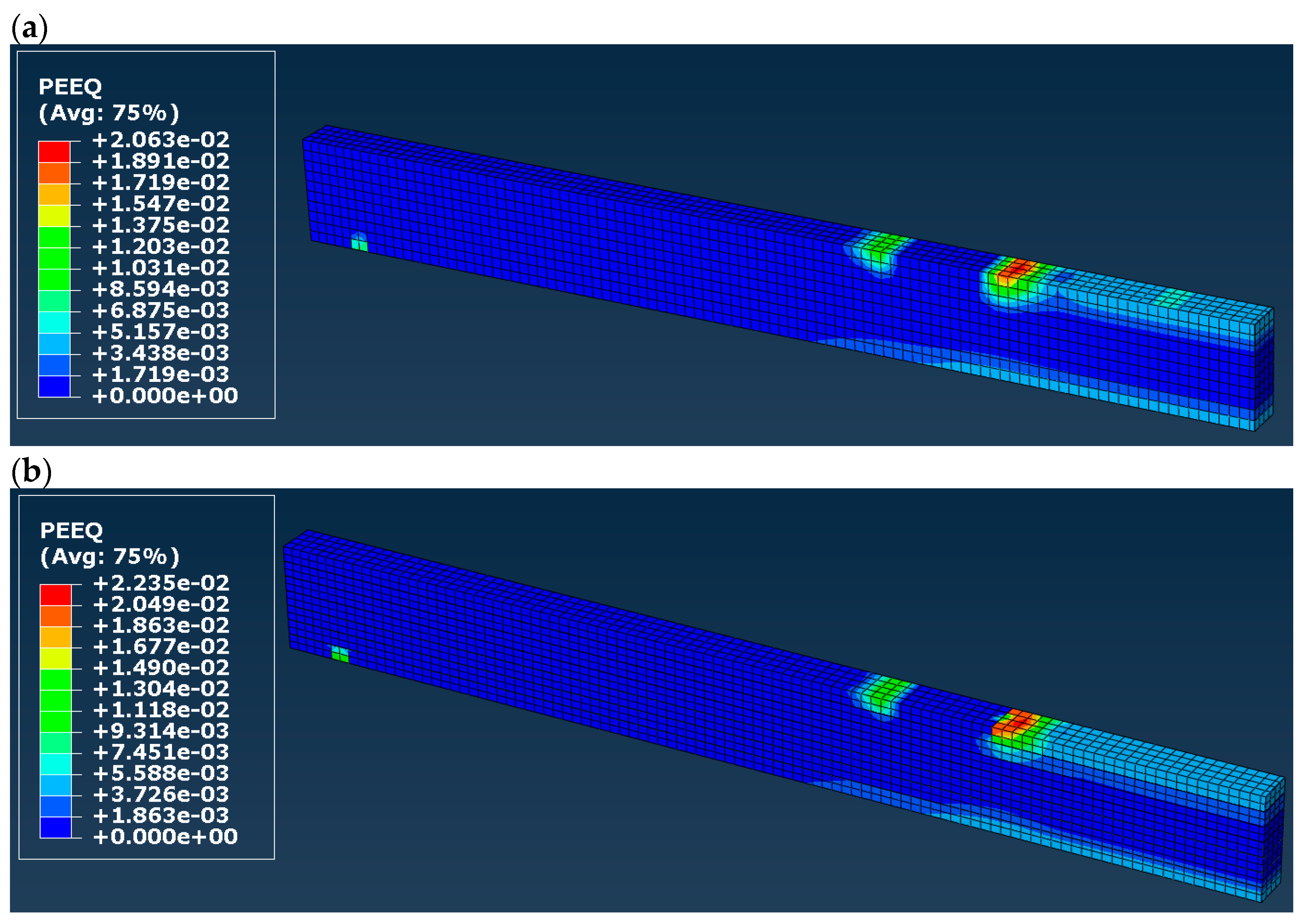
| Plastic strains | (not applicable) | Very similar in both models, concentration in the support and loading zones | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szczecina, M. Study of Complexity of Numerical Models of a Strengthened Timber Beam. Materials 2023, 16, 3466. https://doi.org/10.3390/ma16093466
Szczecina M. Study of Complexity of Numerical Models of a Strengthened Timber Beam. Materials. 2023; 16(9):3466. https://doi.org/10.3390/ma16093466
Chicago/Turabian StyleSzczecina, Michał. 2023. "Study of Complexity of Numerical Models of a Strengthened Timber Beam" Materials 16, no. 9: 3466. https://doi.org/10.3390/ma16093466
APA StyleSzczecina, M. (2023). Study of Complexity of Numerical Models of a Strengthened Timber Beam. Materials, 16(9), 3466. https://doi.org/10.3390/ma16093466







