Investigation into the Dynamic Stability of Nanobeams by Using the Levinson Beam Model
Abstract
1. Introduction
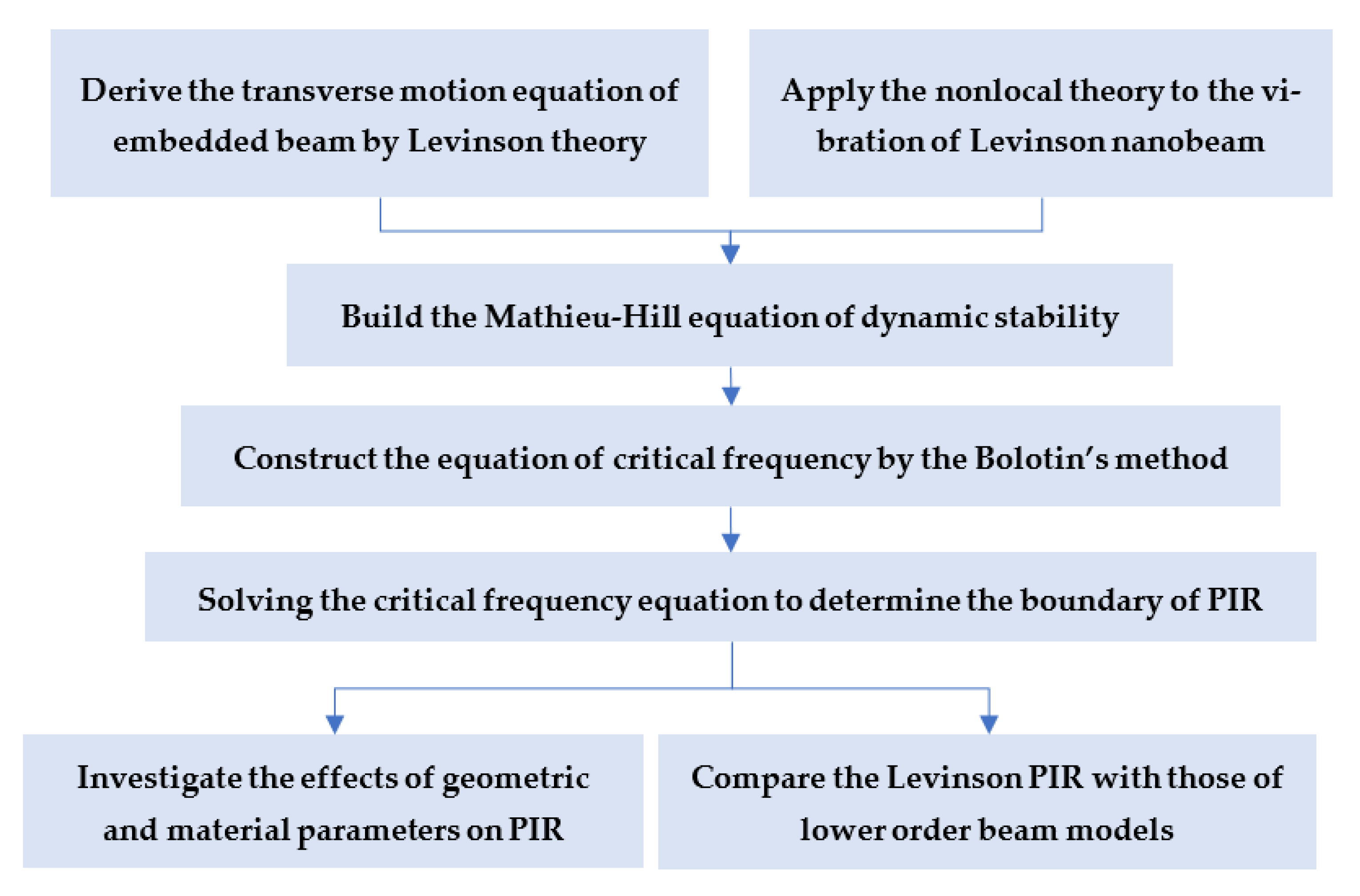
2. Formulation of Dynamic Stability of Levison Nanobeam
2.1. Transverse Vibration of Embedded Levinson Beam
2.2. Vibration Equation of Nonlocal Levinson Beam
2.3. Governing Equation of Dynamic Stability of Nonlocal Levinson Beam
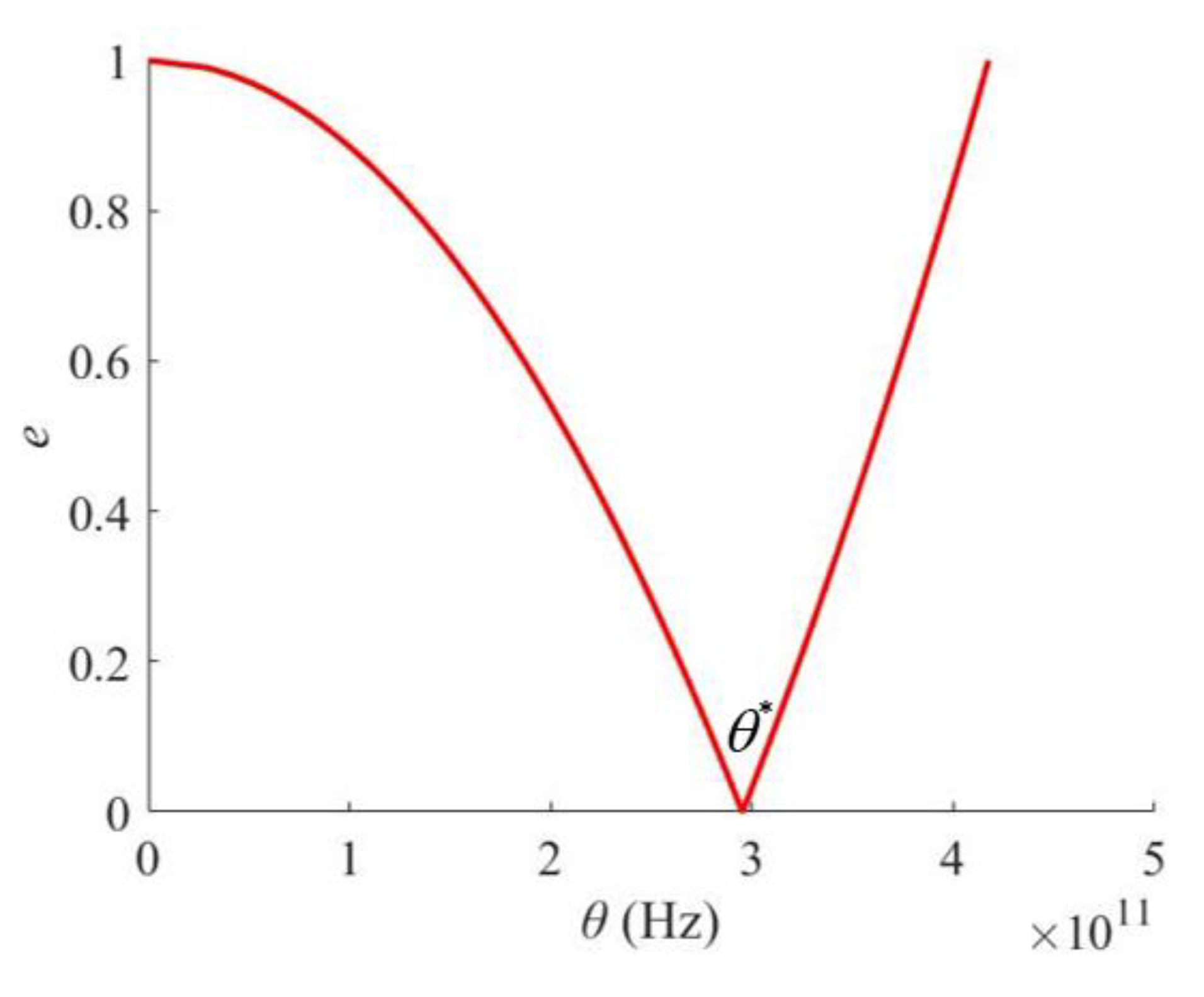
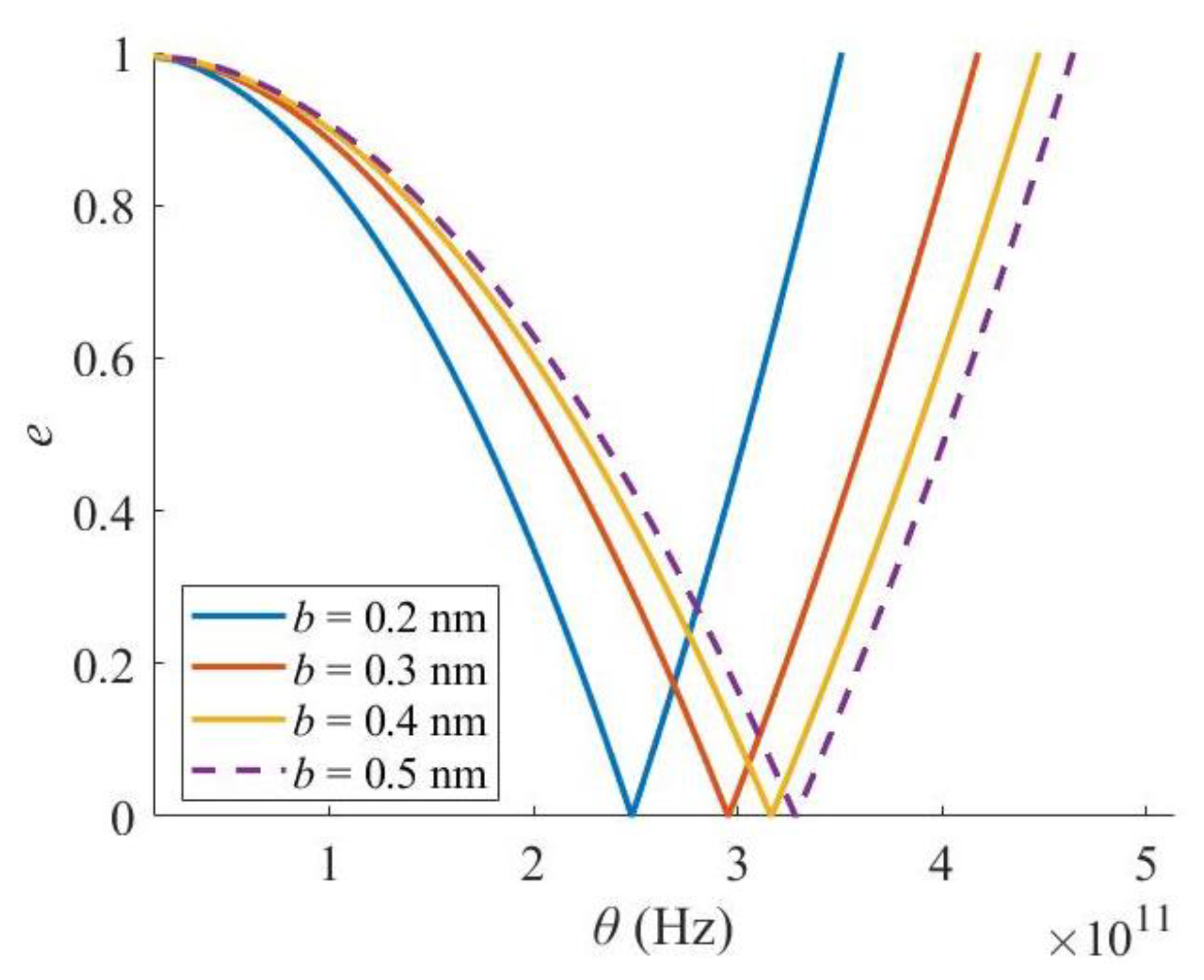
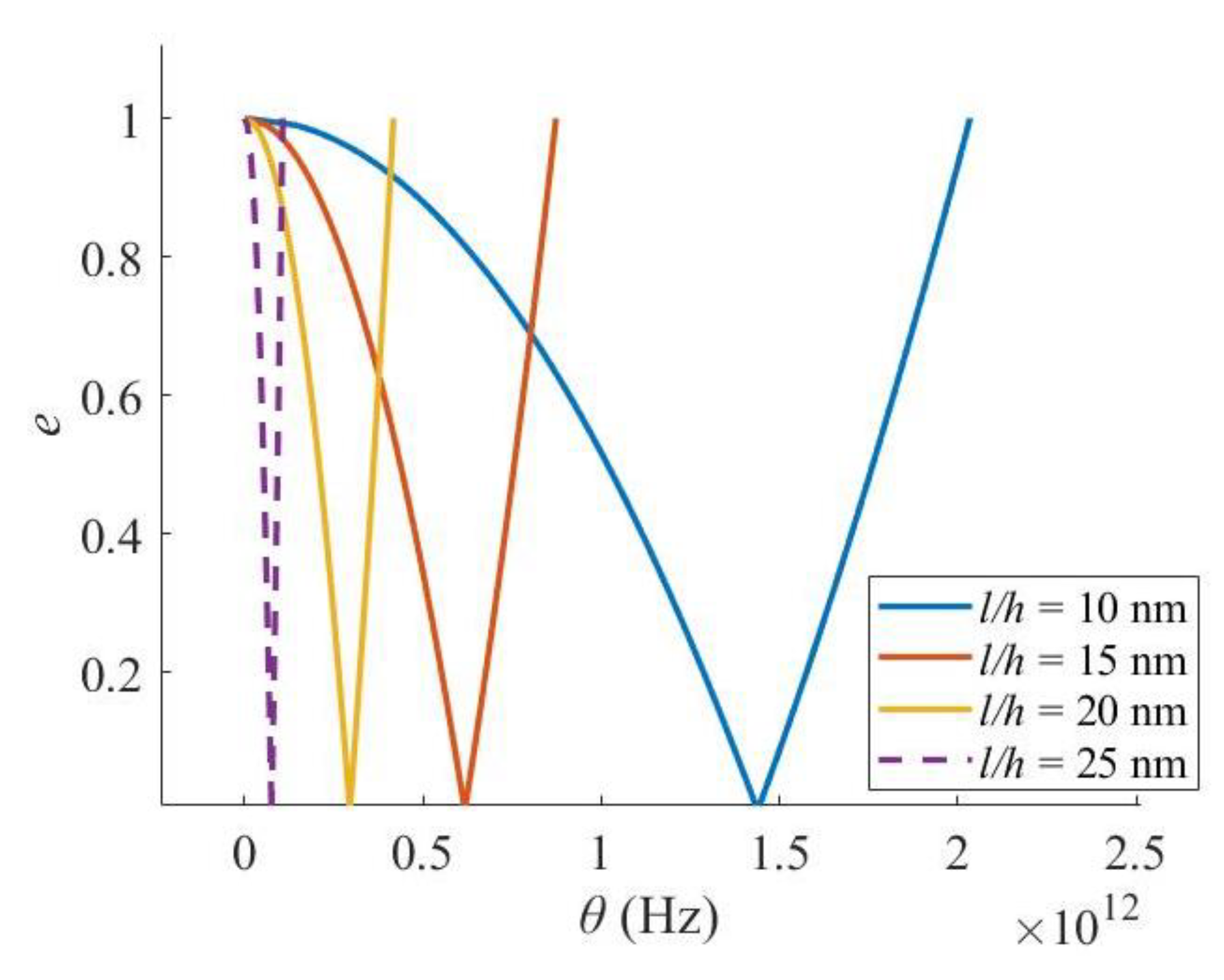
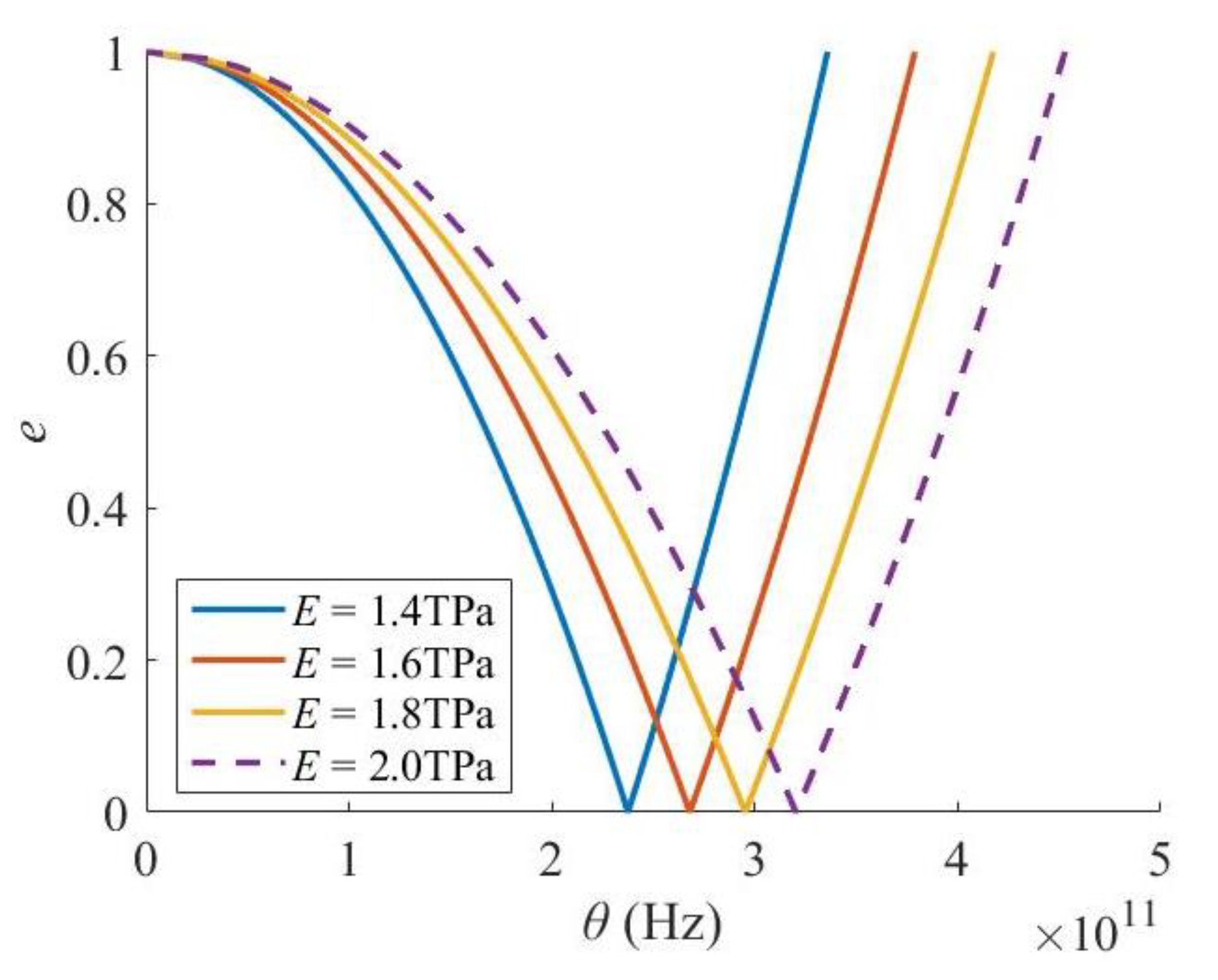
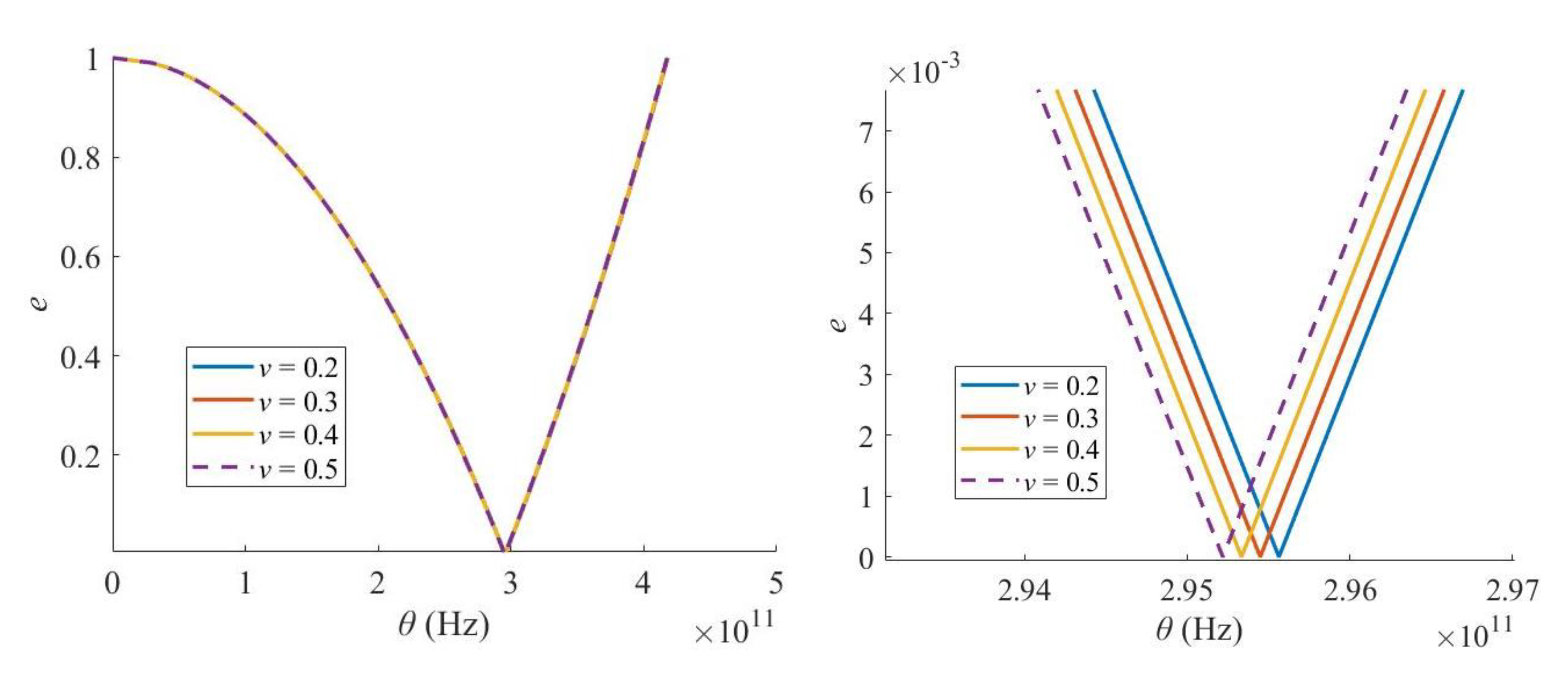
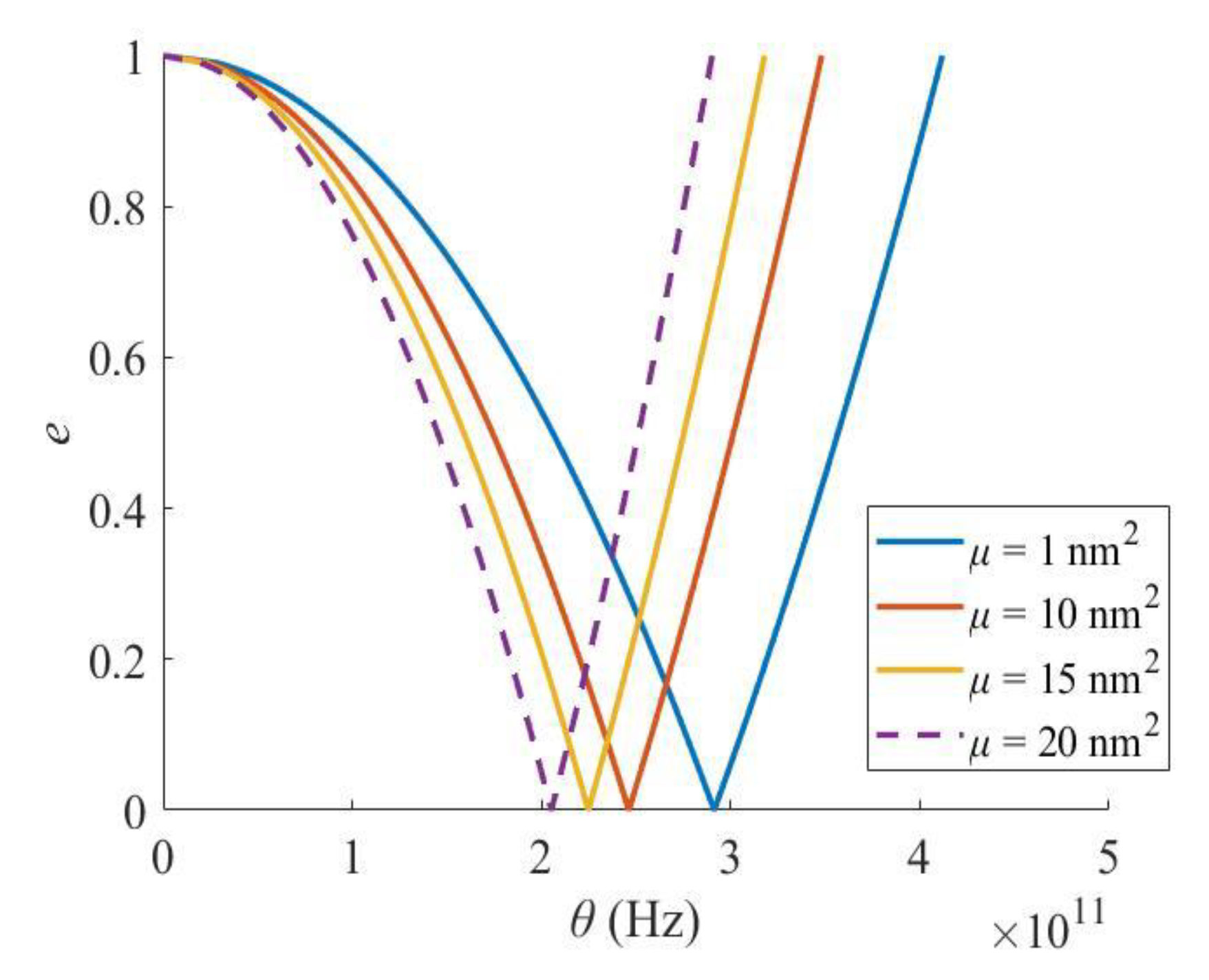
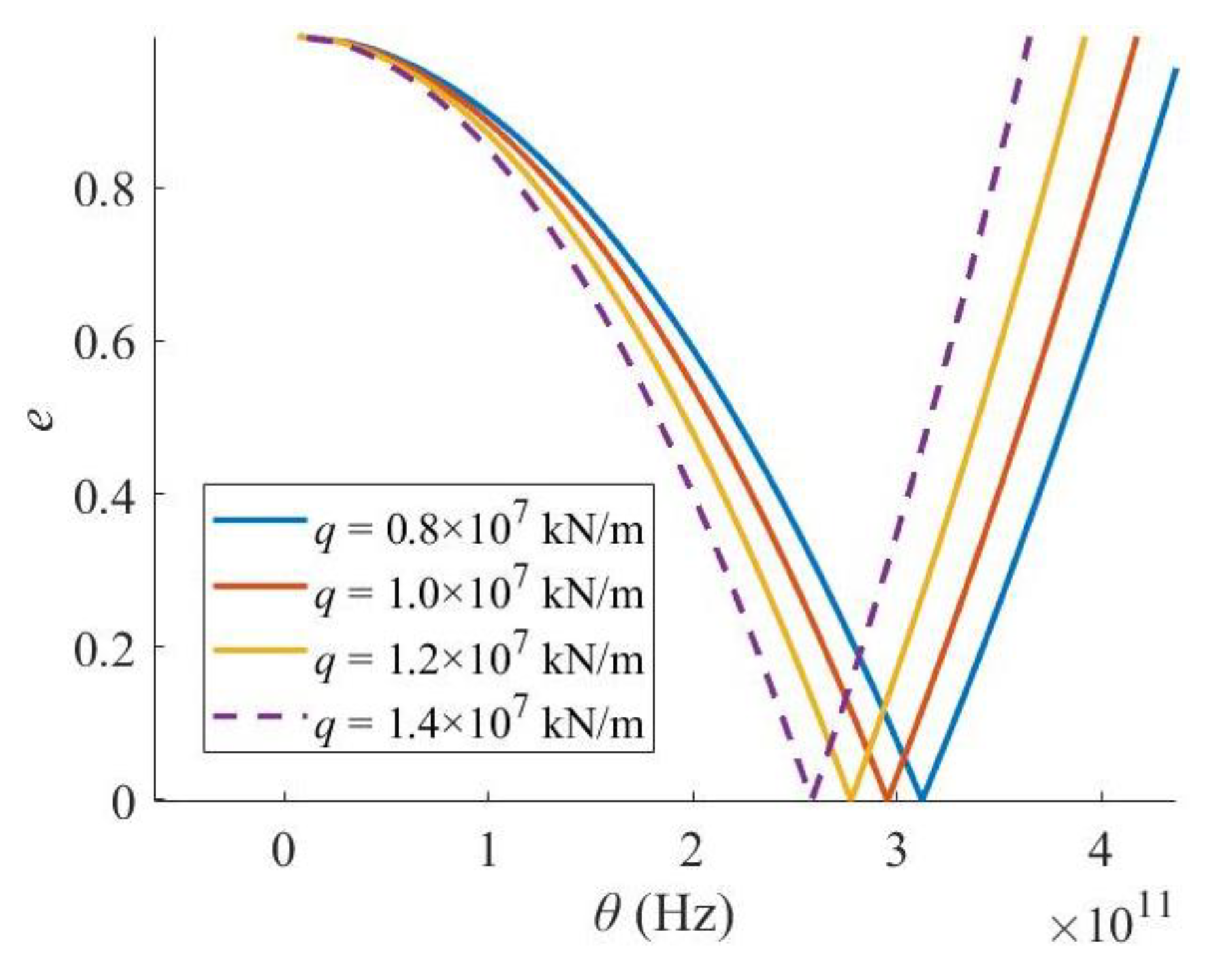
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, M.; Zhuang, Q.R.; Yu, H.; Chen, W. MnCo2S4 nanosheet arrays modified with vermicular polypyrrole for advanced free-standing flexible electrodes. Electrochim. Acta 2023, 447, 142167. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Gu, D.H.; Ding, H.; Lacarbonara, W. Nonlinear vibration isolation via a circular ring. Mech. Syst. Signal Process. 2020, 136, 106490. [Google Scholar] [CrossRef]
- Xiao, X.H.; Zhang, Q.; Zheng, J.X.; Li, Z.C. Analytical model for the nonlinear buckling responses of the confined polyhedral FGP-GPLs lining subjected to crown point loading. Eng. Struct. 2023, 282, 115780. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, H.Q.; Xu, X.H.; Bao, L.L.; Wang, Y.N.; Lin, H.W.; Zheng, C.Y. Construction of a novel lanthanum carbonate-grafted ZSM-5 zeolite for effective highly selective phosphate removal from wastewater. Microporous Microporous Mater. 2021, 324, 111289. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Sahmani, S.; Norouzzadeh, A.; Bazdid-Vahdati, M. Dynamic stability analysis of embedded multi-walled carbon nanotubes in thermal environment. Acta Mech. Solida Sin. 2015, 28, 659–667. [Google Scholar] [CrossRef]
- Pham, Q.H.; Nhan, H.T.; Tran, V.K.; Zenkour, A.M. Hygro-thermo-mechanical vibration analysis of functionally graded porous curved nanobeams resting on elastic foundations. Waves Random Complex 2023, 33, 1–32. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 1, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories. Springer-Verlag, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Ghadiri, M.; Hosseini, S.H.S. Parametric excitation of Euler–Bernoulli nanobeams under thermo-magneto-mechanical loads: Nonlinear vibration and dynamic instability. Compos. Part B Eng. 2019, 173, 106928. [Google Scholar] [CrossRef]
- Sourani, P.; Hashemian, M.; Pirmoradian, M.; Toghraie, D. A comparison of the Bolotin and incremental harmonic balance methods in the dynamic stability analysis of an Euler–Bernoulli nanobeam based on the nonlocal strain gradient theory and surface effects. Mech. Mater. 2020, 145, 103403. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Dynamic stability analysis of multi-walled carbon nanotubes with arbitrary boundary conditions based on the nonlocal elasticity theory. Mech. Adv. Mater. Struct. 2017, 24, 1180–1188. [Google Scholar] [CrossRef]
- Saffari, S.; Hashemian, M.; Toghraie, D. Dynamic stability of functionally graded nanobeam based on nonlocal Timoshenko theory considering surface effects. Physica B 2017, 520, 97–105. [Google Scholar] [CrossRef]
- Hashemian, M.; Falsafifioon, M.; Pirmoradian, M.; Toghrai, D. Nonlocal dynamic stability analysis of a Timoshenko nanobeam subjected to a sequence of moving nanoparticles considering surface effects. Mech. Mater. 2020, 148, 103452. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Selim, B.A.; Zhang, L.W.; Liew, K.M. Vibration analysis of CNT reinforced functionally graded composite plates in a thermal environment based on Reddy’s higher-order shear deformation theory. Compos. Struct. 2016, 156, 276–290. [Google Scholar] [CrossRef]
- Balireddy, S.N.; Pitchaimani, J. Stability and dynamic behaviour of bi-directional functionally graded beam subjected to variable axial load. Mater. Today Commun. 2022, 32, 104043. [Google Scholar] [CrossRef]
- Iwase, B.T.; Hirashima, K. High-accuracy analysis of beams of bimodulus materials. J. Eng. Mech. 2000, 126, 149–156. [Google Scholar] [CrossRef]
- Li, S.R.; Wang, X.; Wan, Z. Classical and homogenized expressions for buckling solutions of functionally graded material Levinson beams. Acta Mech. Solida Sin. 2015, 28, 0894–9166. [Google Scholar] [CrossRef]
- Li, S.R.; Wan, Z.Q. Homogenized and classical expressions for static bending solutions for functionally graded material Levinson beams. Appl. Math. Mech. Engl. 2015, 36, 895–910. [Google Scholar] [CrossRef]
- Karttunen, A.T.; Hertzen, R. Variational formulation of the static Levinson beam theory. Mech. Res. Commun. 2015, 66, 15–19. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.R. Free vibration analysis of functionally graded material beams based on Levinson beam theory. Appl. Math. Mech. Engl. 2016, 37, 861–878. [Google Scholar] [CrossRef]
- Kryskoa, A.V.; Awrejcewiczc, J.; Zhigalove, M.V.; Pavlove, S.P.; Krysko, V.A. Nonlinear behaviour of different flexible size-dependent beams models based on the modified couple stress theory. Part 1: Governing equations and static analysis of flexible beams. Int. J. Non-Linear Mech. 2017, 93, 96–105. [Google Scholar] [CrossRef]
- Kryskoa, A.V.; Awrejcewiczc, J.; Zhigalove, M.V.; Pavlove, S.P.; Krysko, V.A. Nonlinear behaviour of different flexible size-dependent beams models based on the modified couple stress theory. Part 2. Chaotic dynamics of flexible beams. Int. J. Non-Linear Mech. 2017, 93, 106–121. [Google Scholar] [CrossRef]
- Kryskoa, A.V.; Awrejcewiczc, J.; Zhigalove, M.V.; Pavlove, S.P.; Krysko, V.A. Chaotic dynamics of the size-dependent non-linear micro-beam model. Commun. Non-Linear Sci. 2017, 50, 16–28. [Google Scholar] [CrossRef]
- Golbakhshi, H.; Dashtbayazi, M.R.; Site, A.R. A new theoretical framework for couple stress analysis of Reddy-Levinson micro-beams. Int. J. Appl. Mech. 2022, 14, 2250069. [Google Scholar] [CrossRef]
- Huang, Y.Q.; Huang, R.H.; Zhang, J.C. Dynamic stability of nanobeams based on the Reddy’s beam theory. Materials 2023, 16, 1626. [Google Scholar] [CrossRef]
- Xiao, Q.; Huang, Z.K.; Zeng, Z.G.; Huang, T.W.; Lewis, F.L. Stability of homogeneous positive systems with time-varying delays. Automatica 2023, 152, 110965. [Google Scholar] [CrossRef]
- Dao, P.N.; Liu, Y.C. Adaptive reinforcement learning in control design for cooperating manipulator systems. Asian J. Control 2022, 24, 1088–1103. [Google Scholar] [CrossRef]
- Dao, P.N.; Nguyen, V.T.; Liu, Y.C. Finite-time convergence for bilateral teleoperation systems with disturbance and time-varying delays. IET Control Theory Appl. 2021, 15, 1736–1748. [Google Scholar] [CrossRef]
- Levinson, M. A new rectangular beam theory. J. Sound Vib. 1981, 74, 81–87. [Google Scholar] [CrossRef]
- Karličić, D.; Kozić, P.; Pavlović, R.; Nešić, N. Dynamic stability of single-walled carbon nanotube embedded in a viscoelastic medium under the influence of the axially harmonic load. Compos. Struct. 2017, 162, 227–243. [Google Scholar] [CrossRef]
- Huang, Y.Q.; Fu, J.Y.; Liu, A.R. Dynamic instability of Euler–Bernoulli nanobeams subject to parametric excitation. Compos. Part B Eng. 2019, 164, 226–234. [Google Scholar] [CrossRef]
- Bolotin, V.V. The Dynamic Stability of Elastic Systems; Holden-Day Inc.: San Francisco, CA, USA, 1964. [Google Scholar]
- Ansari, R.; Gholami, R.; Sahmani, S. On the dynamic stability of embedded single-walled carbon nanotubes including thermal environment effects. Sci. Iran. 2012, 19, 919–925. [Google Scholar] [CrossRef]



| Material Parameters | Geometric Parameter | ||
|---|---|---|---|
| E (TPa) | 1.8 | l (nm) | 20 |
| ρ (kg/m3) | 1300 | h (nm) | 1 |
| υ | 0.5 | b (nm) | 0.3 |
| q (GPa) | 0.1 | μ (nm2) | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Huang, R.; Huang, Y. Investigation into the Dynamic Stability of Nanobeams by Using the Levinson Beam Model. Materials 2023, 16, 3404. https://doi.org/10.3390/ma16093404
Huang Y, Huang R, Huang Y. Investigation into the Dynamic Stability of Nanobeams by Using the Levinson Beam Model. Materials. 2023; 16(9):3404. https://doi.org/10.3390/ma16093404
Chicago/Turabian StyleHuang, Youqin, Richeng Huang, and Yonghui Huang. 2023. "Investigation into the Dynamic Stability of Nanobeams by Using the Levinson Beam Model" Materials 16, no. 9: 3404. https://doi.org/10.3390/ma16093404
APA StyleHuang, Y., Huang, R., & Huang, Y. (2023). Investigation into the Dynamic Stability of Nanobeams by Using the Levinson Beam Model. Materials, 16(9), 3404. https://doi.org/10.3390/ma16093404







